Hostname: page-component-77c89778f8-m8s7h Total loading time: 0 Render date: 2024-07-19T19:21:54.517Z Has data issue: false hasContentIssue false
  • English
  • Français

The dimension of graphs with respect to the direct powers of a two-element graph

Published online by Cambridge University Press:  17 April 2009

Klaus Kriegel ,
Reinhard Pöschel  and
Walter Wessel
Klaus Kriegel
Affiliation:
Karl-Weierstrass-Institut für Mathematik, Akademie der Wissenschaften der DDR, Mohrenstr. 39 (Postfach 1304), Berlin, DDR-1086
Reinhard Pöschel
Affiliation:
Karl-Weierstrass-Institut für Mathematik, Akademie der Wissenschaften der DDR, Mohrenstr. 39 (Postfach 1304), Berlin, DDR-1086
Walter Wessel
Affiliation:
Karl-Weierstrass-Institut für Mathematik, Akademie der Wissenschaften der DDR, Mohrenstr. 39 (Postfach 1304), Berlin, DDR-1086
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Every finite loopless undirected graph G is isomorphic to an induced subgraph of a suitable finite direct power 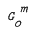of the undirected graph G0 with two adjacent vertices 0,1 and one loop at vertex 1. The least natural number m such that G can be represented in this way is called its G0-dimension. We give some upper and lower bounds of this dimension depending on certain other graph invariants and determine its exact values for some special classes of graphs. Some methods to determine a concrete G0-representation, that is an embedding of G into 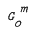, are presented. Moreover we show that the problem of determining the G0-dimension of a graph is NP-complete.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 36 , Issue 2 , October 1987 , pp. 251 - 265
Copyright
Copyright © Australian Mathematical Society 1987

References

[1]Buer, H. and Möhring, R.H., “A fast algorithm for the decomposition of graphs and posets”, Math. Oper. Res. 8 (1983), 170–184.CrossRefGoogle Scholar
[2]Garey, M.R. and Johnson, D.S., Computers and intractability, a guide to the theory of NP-completeness. (Freeman and Company, 1979).Google Scholar
[3]Golumbic, H.Ch., Algorithmic graph theory and perfect graphs. (Academic Press, New York 1980).Google Scholar
[4]Kiss, E., “A note on varieties of graph algebras”, Lecture Notes in Math. 1149 (1985), 163–166.Google Scholar
[5]McNulty, G.F. and Shallon, C., “Inherently nonfinitely based finite algebras”, Lecture Notes in Math. 1004 (1983), 206–231.CrossRefGoogle Scholar
[6]Möhring, R.H. and Rademacher, F.J., “Substitution decomposition for discrete structures and connections with combinatorial optimization”, Ann. Discrete Math. 19 (1984), 257–356.Google Scholar
[7]Oates-Williams, S., “Murskii's algebra does not satisfy MIN”, Bull. Austral. Math. Soc. 22 (1980), 199–203.CrossRefGoogle Scholar
[8]Oates-Williams, S., “Graphs and universal algebras”, Lecture Notes in Math. 884 (1981), 351–354.CrossRefGoogle Scholar
[9]Pöschel, R., “Graph algebras and graph varieties”, (Manuscript 1985, submitted to Algebra Universalis).Google Scholar
[10]Pöschel, R. and Wessel, W., “Classes of graphs definable by graph algebra identities or quasi-identities”, Comment Math. Univ. Carolin. (to appear).Google Scholar
[11]Pouzet, M. and Rosenberg, I.G., “Embeddings and absolute retracts of relational systems”, Preprint CRM-1265, Montreal, Febr. 1985.Google Scholar
[12]Pultr, A., “On productive classes of graphs determined by prohibiting given subgraphs”, Colloq. Math. Soc. Janos. Bolyai 18 (1976), 805–820.Google Scholar
[13]Pultr, A., “On product dimensions in general and that of graphs in particular”, Weiterbildungszentrum Math. Kybernet Rechentech., 27 (1977), 66–79.Google Scholar
[14]Pultr, A. and Vinárek, J., “Productive classes and subdirect irreducibility, in particular for graphs, Discrete Math. 20 (1977), 159–176.Google Scholar
[15]Shallon, C.R., Nonfinitely based finite algebras derived from lattices. (Ph.D. Dissertation, University of California, Los Angeles, 1979.)Google Scholar