Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T09:43:34.694Z Has data issue: false hasContentIssue false
  • English
  • Français

CLASSIFICATION OF THE SUBLATTICES OF A LATTICE

Part of: Discrete geometry Structure and classification of infinite or finite groups Geometry of numbers

Published online by Cambridge University Press:  13 April 2020

CHUANMING ZONG
CHUANMING ZONG*
Affiliation:
Center for Applied Mathematics,Tianjin University, Tianjin300072, China email cmzong@math.pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1945–1946, C. L. Siegel proved that an $n$-dimensional lattice 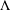$\unicode[STIX]{x1D6EC}$ of determinant 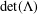$\text{det}(\unicode[STIX]{x1D6EC})$ has at most 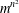$m^{n^{2}}$ different sublattices of determinant 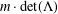$m\cdot \text{det}(\unicode[STIX]{x1D6EC})$. In 1997, the exact number of the different sublattices of index $m$ was determined by Baake. We present a systematic treatment for counting the sublattices and derive a formula for the number of the sublattice classes under unimodular equivalence.

Keywords

latticesublattice

MSC classification

Primary: 11H06: Lattices and convex bodies
Secondary: 20E07: Subgroup theorems; subgroup growth 52C05: Lattices and convex bodies in $2$ dimensions 52C07: Lattices and convex bodies in $n$ dimensions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 50 - 61
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the National Natural Science Foundation of China (NSFC11921001) and the National Key Research and Development Program of China (2018YFA0704701).

References

Andrews, G. E. and Eriksson, K., Integer Partitions (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Baake, M., ‘Solution of the coincidence problem in dimensions d ≤ 4’, in: The Mathematics of Long-Range Aperiodic Order (ed. Moody, R. V.) (Kluwer, Dordrecht, 1997), 9–44.CrossRefGoogle Scholar
Baake, M., Scharlau, R. and Zeiner, P., ‘Similar sublattices of planar lattices’, Canad. J. Math. 63 (2011), 1220–1237.CrossRefGoogle Scholar
Baake, M., Scharlau, R. and Zeiner, P., ‘Well-rounded sublattices of planar lattices’, Acta Arith. 166 (2014), 301–334.CrossRefGoogle Scholar
Bernstein, M., Sloane, N. J. A. and Wright, P. E., ‘On sublattices of the hexagonal lattice’, Discrete Math. 170 (1997), 29–39.CrossRefGoogle Scholar
Cassels, J. W. S., An Introduction to the Geometry of Numbers (Springer, Berlin, 1959).CrossRefGoogle Scholar
Fukshansky, L., ‘On distribution of well-rounded sublattices of ℤ2’, J. Number Theory 128 (2008), 2359–2393.CrossRefGoogle Scholar
Fukshansky, L., ‘On similarity classes of well-rounded sublattices of ℤ2’, J. Number Theory 129 (2009), 2530–2556.CrossRefGoogle Scholar
Goldfeld, D., Lubotzky, A. and Pyber, L., ‘Counting congruence subgroups’, Acta Math. 193 (2004), 73–104.CrossRefGoogle Scholar
Gruber, B., ‘Alternative formulae for the number of sublattices’, Acta Crystallogr. Sect. A 53 (1997), 807–808.CrossRefGoogle Scholar
Gruber, P. M., Convex and Discrete Geometry (Springer, New York, 2007).Google Scholar
Gruber, P. M. and Lekkerkerker, C. G., Geometry of Numbers (North-Holland, Amsterdam, 1987).Google Scholar
Grunewald, F. J., Segal, D. and Smith, G. C., ‘Subgroups of finite index in nilpotent groups’, Invent. Math. 93 (1988), 185–223.CrossRefGoogle Scholar
Hua, L. K., Introduction to Number Theory (Springer, Berlin–Heidelberg, 1987).Google Scholar
Lubotzky, A. and Segal, D., Subgroup Growth, Progress in Mathematics, 212 (Birkhäuser, Basel, 2003).CrossRefGoogle Scholar
Martinet, J., Perfect Lattices in Euclidean Spaces (Springer, Berlin, 2003).CrossRefGoogle Scholar
Minkowski, H., Diophantische Approximationen (Chelsea, New York, 1957; Teubner, Leipzig, 1907).CrossRefGoogle Scholar
Scheja, G. and Storch, U., Lehrbuch der Algebra, Teil 2 (Teubner, Stuttgart, 1988).CrossRefGoogle Scholar
Schmidt, W. M., ‘The distribution of the sublattices of ℤn’, Monatsh. Math. 125 (1998), 37–81.CrossRefGoogle Scholar
Schmidt, W. M., ‘Integer matrices, sublattices of ℤn, and Frobenius numbers’, Monatsh. Math. 178 (2015), 405–451.CrossRefGoogle Scholar
Serre, J.-P., A Course in Arithmetic (Springer, New York, 1973).CrossRefGoogle Scholar
Siegel, C. L., Lectures on the Geometry of Numbers (Springer, Berlin, 1989).CrossRefGoogle Scholar