No CrossRef data available.
Article contents
A characterization of the existence of a Souslin line
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The main purpose of this paper is to show that there exists a Souslin line if and only if there exists a countable chain condition space which is not weak-separable but has a generic π-base. If I is the closure of the isolated points in a space X, then X is said to be weak-separable if a first category set is dense in X – I. A π-base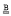 
is said to be generic if, whenever a member of 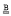is included in the disjoint union of members of 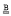it is included in one of them.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1982
References
[1]Engelking, Ryszard, General topology (Monografie Mathematyczne, 60. PWN – Polish Scientific Publishers, Warsaw, 1977).Google Scholar
[2]Kunen, Kenneth, Set theory. An introduction to independence proofs (Studies in Logic and the Foundations of Mathematics, 102. North-Holland, Amsterdam, New York, Oxford, 1980).Google Scholar
[3]Marczewski, Edward, “Séparabilité et multiplication cartesienne des espaces topologiques”, Fund. Math. 34 (1947), 127–143.Google Scholar
[4]Miller, Edwin W., “A note on Souslin's problem”, Amer. J. Math. 65 (1943), 673–678.Google Scholar
[5]Pondiczery, E.S., “Power problems in abstract spaces”, Duke Math. J. 11 (1944), 835–837.Google Scholar
[6]Solovay, R.M. and Tennenbaum, S., “Iterated Cohen extensions and Souslin's problem”, Ann. of Math. (2) 94 (1971), 201–245.Google Scholar
[7]Tall, Franklin D., “Stalking the Souslin tree – a topological guide”, Canad. Math. Bull. 19 (1976), 337–341.Google Scholar
You have
Access