No CrossRef data available.
Article contents
UNIFORM LOWER BOUND AND LIOUVILLE TYPE THEOREM FOR FRACTIONAL LICHNEROWICZ EQUATIONS
Published online by Cambridge University Press: 21 April 2021
Abstract
We study the fractional parabolic Lichnerowicz equation
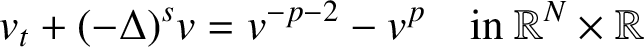
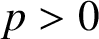 $p>0$
and
$p>0$
and
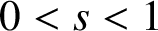 $ 0<s<1 $
. We establish a Liouville-type theorem for positive solutions in the case
$ 0<s<1 $
. We establish a Liouville-type theorem for positive solutions in the case
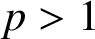 $p>1$
and give a uniform lower bound of positive solutions when
$p>1$
and give a uniform lower bound of positive solutions when
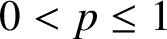 $0<p\leq 1$
. In particular, when v is independent of the time variable, we obtain a similar result for the fractional elliptic Lichnerowicz equation
$0<p\leq 1$
. In particular, when v is independent of the time variable, we obtain a similar result for the fractional elliptic Lichnerowicz equation 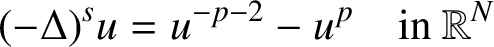
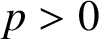 $p>0$
and
$p>0$
and
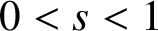 $0<s<1$
. This extends the result of Brézis [‘Comments on two notes by L. Ma and X. Xu’, C. R. Math. Acad. Sci. Paris349(5–6) (2011), 269–271] to the fractional Laplacian.
$0<s<1$
. This extends the result of Brézis [‘Comments on two notes by L. Ma and X. Xu’, C. R. Math. Acad. Sci. Paris349(5–6) (2011), 269–271] to the fractional Laplacian.
Keywords
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 484 - 492
- Copyright
- ©2021 Australian Mathematical Publishing Association Inc.
Footnotes
The research of A. T. Duong is funded by the Vietnam Ministry of Education and Training under grant number B2021-SPH-15.





