Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Hongxia
2022.
Sharp conditions on fractional ID-(g, f)-factor-critical covered graphs.
RAIRO - Operations Research,
Vol. 56,
Issue. 5,
p.
3257.
Gao, Wei
Wang, Weifan
and
Chen, Yaojun
2022.
Tight isolated toughness bound for fractional (k,n)-critical graphs.
Discrete Applied Mathematics,
Vol. 322,
Issue. ,
p.
194.
Liu, Hongxia
2022.
Sun toughness and path-factor uniform graphs.
RAIRO - Operations Research,
Vol. 56,
Issue. 6,
p.
4057.
He, Zhengyue
Liang, Li
and
Gao, Wei
2022.
Isolated toughness variant and fractional κ-factor.
RAIRO - Operations Research,
Vol. 56,
Issue. 5,
p.
3675.
Zhou, Sizhong
Wu, Jiancheng
and
Liu, Hongxia
2022.
Independence number and connectivity for fractional (a, b, k)-critical covered graphs.
RAIRO - Operations Research,
Vol. 56,
Issue. 4,
p.
2535.
Wang, Sufang
and
Zhang, Wei
2022.
Isolated toughness for path factors in networks.
RAIRO - Operations Research,
Vol. 56,
Issue. 4,
p.
2613.
Zhou, Si-zhong
and
Liu, Hong-xia
2022.
Discussions on Orthogonal Factorizations in Digraphs.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 38,
Issue. 2,
p.
417.
Chen, Yuan
and
Dai, Guowei
2022.
Binding number and path-factor critical deleted graphs.
AKCE International Journal of Graphs and Combinatorics,
Vol. 19,
Issue. 3,
p.
197.
Zhang, Wei
and
Wang, Su-fang
2022.
Discussion on Fractional (a, b, k)-critical Covered Graphs.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 38,
Issue. 2,
p.
304.
Wu, Jie
2022.
Path-factor critical covered graphs and path-factor uniform graphs.
RAIRO - Operations Research,
Vol. 56,
Issue. 6,
p.
4317.
Zhou, Sizhong
and
Bian, Qiuxiang
2022.
The existence of path-factor uniform graphs with large connectivity.
RAIRO - Operations Research,
Vol. 56,
Issue. 4,
p.
2919.
Dai, Guowei
2023.
Degree sum conditions for path-factor uniform graphs.
Indian Journal of Pure and Applied Mathematics,
Gao, Wei
Wang, Weifan
and
Chen, Yaojun
2023.
Isolated toughness and fractional (
a,b,n
)-critical graphs
.
Connection Science,
Vol. 35,
Issue. 1,
Zhou, Sizhong
and
Zhang, Yuli
2023.
Sufficient conditions for graphs to have strong parity factors.
RAIRO - Operations Research,
Vol. 57,
Issue. 5,
p.
2465.
Zhou, Sizhong
Sun, Zhiren
and
Liu, Hongxia
2023.
Some sufficient conditions for path-factor uniform graphs.
Aequationes mathematicae,
Vol. 97,
Issue. 3,
p.
489.
Dai, Guowei
Zhang, Zan-Bo
and
Zhang, Xiaoyan
2023.
Remarks on component factors in K1,r-free graphs.
RAIRO - Operations Research,
Vol. 57,
Issue. 2,
p.
837.
Zhou, Sizhong
Sun, Zhiren
and
Bian, Qiuxiang
2023.
Isolated toughness and path-factor uniform graphs (II).
Indian Journal of Pure and Applied Mathematics,
Vol. 54,
Issue. 3,
p.
689.
Wang, Sufang
and
Zhang, Wei
2023.
Degree conditions for the existence of a {P2, P5}-factor in a graph.
RAIRO - Operations Research,
Vol. 57,
Issue. 4,
p.
2231.
He, Zhengyue
Liang, Li
Baskonus, Haci Mehmet
and
Gao, Wei
2023.
Remarks on path-factor critical avoidable graphs.
International Journal of Cognitive Computing in Engineering,
Vol. 4,
Issue. ,
p.
65.
Feng, Xinge
and
Deng, Xingchao
2023.
Toughness and binding number bounds of star-like and path factor.
RAIRO - Operations Research,
Vol. 57,
Issue. 3,
p.
1167.
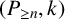 $(P_{\geq n},k)$
-factor-critical covered graph if for any
$(P_{\geq n},k)$
-factor-critical covered graph if for any
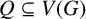 $Q\subseteq V(G)$
with
$Q\subseteq V(G)$
with
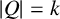 $|Q|=k$
and any
$|Q|=k$
and any
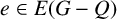 $e\in E(G-Q)$
,
$e\in E(G-Q)$
,
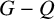 $G-Q$
has a
$G-Q$
has a
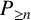 $P_{\geq n}$
-factor covering e. We demonstrate that (i) a
$P_{\geq n}$
-factor covering e. We demonstrate that (i) a
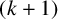 $(k+1)$
-connected graph G with at least
$(k+1)$
-connected graph G with at least
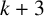 $k+3$
vertices is a
$k+3$
vertices is a
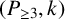 $(P_{\geq 3},k)$
-factor-critical covered graph if its toughness
$(P_{\geq 3},k)$
-factor-critical covered graph if its toughness
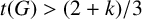 $t(G)>{(2+k)}/{3}$
; (ii) a
$t(G)>{(2+k)}/{3}$
; (ii) a
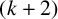 $(k+2)$
-connected graph G is a
$(k+2)$
-connected graph G is a
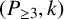 $(P_{\geq 3},k)$
-factor-critical covered graph if its isolated toughness
$(P_{\geq 3},k)$
-factor-critical covered graph if its isolated toughness
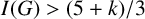 $I(G)>{(5+k)}/{3}$
. Furthermore, we show that the conditions on
$I(G)>{(5+k)}/{3}$
. Furthermore, we show that the conditions on
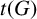 $t(G)$
and
$t(G)$
and
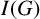 $I(G)$
are sharp.
$I(G)$
are sharp.




