Article contents
ON THE INCREASING PARTIAL QUOTIENTS OF CONTINUED FRACTIONS OF POINTS IN THE PLANE
Published online by Cambridge University Press: 17 December 2021
Abstract
For any x in
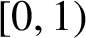 $[0,1)$
, let
$[0,1)$
, let
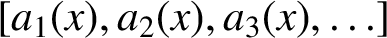 $[a_1(x),a_2(x),a_3(x),\ldots ]$
be its continued fraction. Let
$[a_1(x),a_2(x),a_3(x),\ldots ]$
be its continued fraction. Let
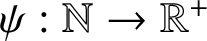 $\psi :\mathbb {N}\to \mathbb {R}^+$
be such that
$\psi :\mathbb {N}\to \mathbb {R}^+$
be such that
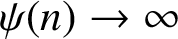 $\psi (n) \to \infty $
as
$\psi (n) \to \infty $
as
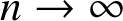 $n\to \infty $
. For any positive integers s and t, we study the set
$n\to \infty $
. For any positive integers s and t, we study the set
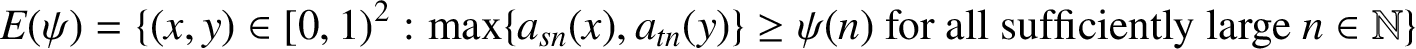 $$ \begin{align*}E(\psi)=\{(x,y)\in [0,1)^2: \max\{a_{sn}(x), a_{tn}(y)\}\ge \psi(n) \ {\text{for all sufficiently large}}\ n\in \mathbb{N}\} \end{align*} $$
$$ \begin{align*}E(\psi)=\{(x,y)\in [0,1)^2: \max\{a_{sn}(x), a_{tn}(y)\}\ge \psi(n) \ {\text{for all sufficiently large}}\ n\in \mathbb{N}\} \end{align*} $$
and determine its Hausdorff dimension.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the Program of Chongqing Municipal Education Commission (Nos. KJQN202100528 and KJQN202000531), Projects from Chongqing Municipal Science and Technology Commission (No. cstc2018jcyjAX0277) and the Foundation of Chongqing Normal University (No. 20XLB030).
References
- 2
- Cited by



