Article contents
A NOTE ON LARGE VALUES OF 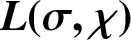 $\boldsymbol{L(\sigma ,\chi )}$
$\boldsymbol{L(\sigma ,\chi )}$
Published online by Cambridge University Press: 04 October 2021
Abstract
In this note, by introducing a new variant of the resonator function, we give an explicit version of the lower bound for
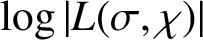 $\log |L(\sigma ,\chi )|$
in the strip
$\log |L(\sigma ,\chi )|$
in the strip
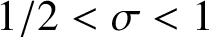 $1/2<\sigma <1$
, which improves the result of Aistleitner et al. [‘On large values of
$1/2<\sigma <1$
, which improves the result of Aistleitner et al. [‘On large values of
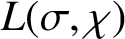 $L(\sigma ,\chi )$
’, Q. J. Math. 70 (2019), 831–848].
$L(\sigma ,\chi )$
’, Q. J. Math. 70 (2019), 831–848].
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work is supported by the Science and Technology Development Fund, Macau SAR (File no. 0095/2018/A3).
References
- 1
- Cited by



