Article contents
A NEW 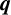 $\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
$\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
Published online by Cambridge University Press: 20 May 2022
Abstract
We give a new q-analogue of the (A.2) supercongruence of Van Hamme. Our proof employs Andrews’ multiseries generalisation of Watson’s
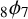 $_{8}\phi _{7}$
transformation, Andrews’ terminating q-analogue of Watson’s
$_{8}\phi _{7}$
transformation, Andrews’ terminating q-analogue of Watson’s
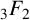 $_{3}F_{2}$
summation, a q-Watson-type summation due to Wei–Gong–Li and the creative microscoping method, developed by the author and Zudilin [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358]. As a conclusion, we confirm a weaker form of Conjecture 4.5 by the author [‘Some generalizations of a supercongruence of van Hamme’, Integral Transforms Spec. Funct. 28 (2017), 888–899].
$_{3}F_{2}$
summation, a q-Watson-type summation due to Wei–Gong–Li and the creative microscoping method, developed by the author and Zudilin [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358]. As a conclusion, we confirm a weaker form of Conjecture 4.5 by the author [‘Some generalizations of a supercongruence of van Hamme’, Integral Transforms Spec. Funct. 28 (2017), 888–899].
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 22 - 30
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by



