No CrossRef data available.
Article contents
EULER PRODUCT ASYMPTOTICS FOR DIRICHLET 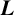 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
Published online by Cambridge University Press: 07 January 2022
Abstract
The aim of this article is to establish the behaviour of partial Euler products for Dirichlet L-functions under the generalised Riemann hypothesis (GRH) via Ramanujan’s work. To understand the behaviour of Euler products on the critical line, we invoke the deep Riemann hypothesis (DRH). This work clarifies the relation between GRH and DRH.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.





