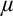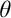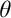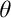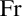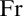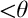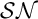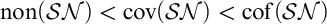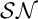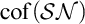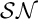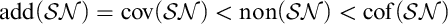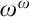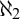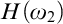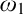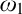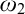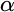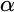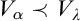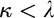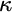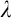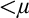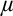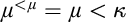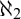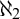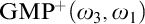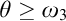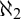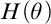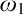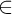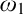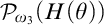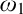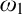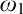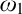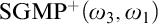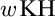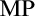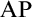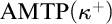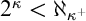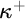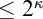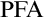The Theme. Strong forcing axioms like Martin’s Maximum give a reasonably satisfactory structural analysis of 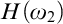 $H(\omega _2)$. A broad program in modern Set Theory is searching for strong forcing axioms beyond
$H(\omega _2)$. A broad program in modern Set Theory is searching for strong forcing axioms beyond 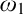 $\omega _1$. In other words, one would like to figure out the structural properties of taller initial segments of the universe. However, the classical techniques of forcing iterations seem unable to bypass the obstacles, as the resulting forcings axioms beyond
$\omega _1$. In other words, one would like to figure out the structural properties of taller initial segments of the universe. However, the classical techniques of forcing iterations seem unable to bypass the obstacles, as the resulting forcings axioms beyond 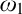 $\omega _1$ have not thus far been strong enough! However, with his celebrated work on generalised side conditions, I. Neeman introduced us to a novel paradigm to iterate forcings. In particular, he could, among other things, reprove the consistency of the Proper Forcing Axiom using an iterated forcing with finite supports. In 2015, using his technology of virtual models, Veličković built up an iteration of semi-proper forcings with finite supports, hence reproving the consistency of Martin’s Maximum, an achievement leading to the notion of a virtual model.
$\omega _1$ have not thus far been strong enough! However, with his celebrated work on generalised side conditions, I. Neeman introduced us to a novel paradigm to iterate forcings. In particular, he could, among other things, reprove the consistency of the Proper Forcing Axiom using an iterated forcing with finite supports. In 2015, using his technology of virtual models, Veličković built up an iteration of semi-proper forcings with finite supports, hence reproving the consistency of Martin’s Maximum, an achievement leading to the notion of a virtual model.
In this thesis, we are interested in constructing forcing notions with finitely many virtual models as side conditions to preserve three uncountable cardinals. The thesis constitutes six chapters and three appendices that amount to 118 pages, where Section 1 is devoted to preliminaries, and Section 2 is a warm-up about the scaffolding poset of a proper forcing. In Section 3, we present the general theory of virtual models in the context of forcing with sets of models of two types, where we, e.g., define the “meet” between two virtual models and prove its properties.
The main results are joint with Boban Veličković, and partly appeared in Guessing models and the approachability ideal, J. Math. Log. 21 (2021).
Pure Side Conditions. In Section 4, we use two types of virtual models (countable and large non-transitive ones induced by a supercompact cardinal, which we call Magidor models) to construct our forcing with pure side conditions. The forcing covertly uses a third type of models that are transitive. We also add decorations to the conditions to add many clubs in the generic 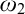 $\omega _2$. In contrast to Neeman’s method, we do not have a single chain, but
$\omega _2$. In contrast to Neeman’s method, we do not have a single chain, but 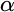 $\alpha $-chains, for an ordinal
$\alpha $-chains, for an ordinal 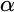 $\alpha $ with
$\alpha $ with 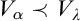 $V_\alpha \prec V_\lambda $. Thus, starting from suitable large cardinals
$V_\alpha \prec V_\lambda $. Thus, starting from suitable large cardinals 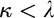 $\kappa <\lambda $, we construct a forcing notion whose conditions are finite sets of virtual models described earlier. The forcing is strongly proper, preserves
$\kappa <\lambda $, we construct a forcing notion whose conditions are finite sets of virtual models described earlier. The forcing is strongly proper, preserves 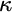 $\kappa $, and has the
$\kappa $, and has the 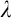 $\lambda $-Knaster property. The relevant quotients of the forcing are strongly proper, which helps us prove strong guessing model principles. The construction is generalisable to a
$\lambda $-Knaster property. The relevant quotients of the forcing are strongly proper, which helps us prove strong guessing model principles. The construction is generalisable to a 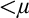 ${<}\mu $-closed forcing, for any given cardinal
${<}\mu $-closed forcing, for any given cardinal 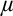 $\mu $ with
$\mu $ with 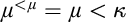 $\mu ^{<\mu }=\mu <\kappa $.
$\mu ^{<\mu }=\mu <\kappa $.
The Iteration Theorem. In Section 5, we use the forcing with pure side conditions to iterate a subclass of proper and 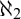 $\aleph _2$-c.c. forcings and obtain a forcing axiom at the level of
$\aleph _2$-c.c. forcings and obtain a forcing axiom at the level of 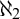 $\aleph _2$. The iterable class is closely related to Asperó–Mota’s forcing axiom for finitely proper forcings.
$\aleph _2$. The iterable class is closely related to Asperó–Mota’s forcing axiom for finitely proper forcings.
Guessing Model Principles. Section 6 encompasses the main parts of the thesis. We prove the consistency of the guessing principle 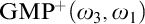 $\mathrm {GMP}^+(\omega _3,\omega _1)$ that states for any cardinal
$\mathrm {GMP}^+(\omega _3,\omega _1)$ that states for any cardinal 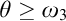 ${\theta \geq \omega _3}$, the set of
${\theta \geq \omega _3}$, the set of 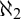 $\aleph _2$-sized elementary submodels M of
$\aleph _2$-sized elementary submodels M of 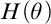 $H(\theta )$, which are the union of an
$H(\theta )$, which are the union of an 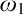 $\omega _1$-continuous
$\omega _1$-continuous 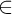 $\in $-chain of
$\in $-chain of 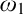 $\omega _1$-guessing, I.C. models is stationary in
$\omega _1$-guessing, I.C. models is stationary in 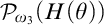 $\mathcal P_{\omega _3}(H(\theta ))$. The consistency and consequences of this principle are demonstrated in the following diagram. We also prove that one can obtain the above guessing models in a way that the
$\mathcal P_{\omega _3}(H(\theta ))$. The consistency and consequences of this principle are demonstrated in the following diagram. We also prove that one can obtain the above guessing models in a way that the 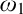 $\omega _1$-sized
$\omega _1$-sized 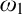 $\omega _1$-guessing models remain
$\omega _1$-guessing models remain 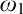 $\omega _1$-guessing model in any outer transitive model with the same
$\omega _1$-guessing model in any outer transitive model with the same 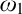 $\omega _1$, and we denote this principle by
$\omega _1$, and we denote this principle by 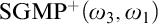 $\rm{SGMP}^+(\omega_3,\omega_1)$.
$\rm{SGMP}^+(\omega_3,\omega_1)$.
In the following diagram,  $\mathrm{TP}$ stands for the tree property;
$\mathrm{TP}$ stands for the tree property; 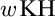 $w\mathrm{KH}$ stands for the weak Kurepa Hypothesis;
$w\mathrm{KH}$ stands for the weak Kurepa Hypothesis; 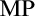 $\mathrm{MP}$ stands for Mitchell property, i.e., the approachability ideal is trivial modulo the nonstationary ideal;
$\mathrm{MP}$ stands for Mitchell property, i.e., the approachability ideal is trivial modulo the nonstationary ideal; 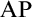 $\mathrm{AP}$ stands for the approachability property;
$\mathrm{AP}$ stands for the approachability property; 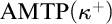 $\mathrm {AMTP}(\kappa ^+)$ states that if
$\mathrm {AMTP}(\kappa ^+)$ states that if 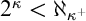 $2^\kappa <\aleph _{\kappa ^+}$, then every forcing which adds a new subset of
$2^\kappa <\aleph _{\kappa ^+}$, then every forcing which adds a new subset of 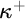 $\kappa ^+$ whose initial segments are in the ground model, collapses some cardinal
$\kappa ^+$ whose initial segments are in the ground model, collapses some cardinal 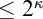 $\leq 2^{\kappa }$. The dotted arrow denotes the relative consistency, while others are logical implications.
$\leq 2^{\kappa }$. The dotted arrow denotes the relative consistency, while others are logical implications.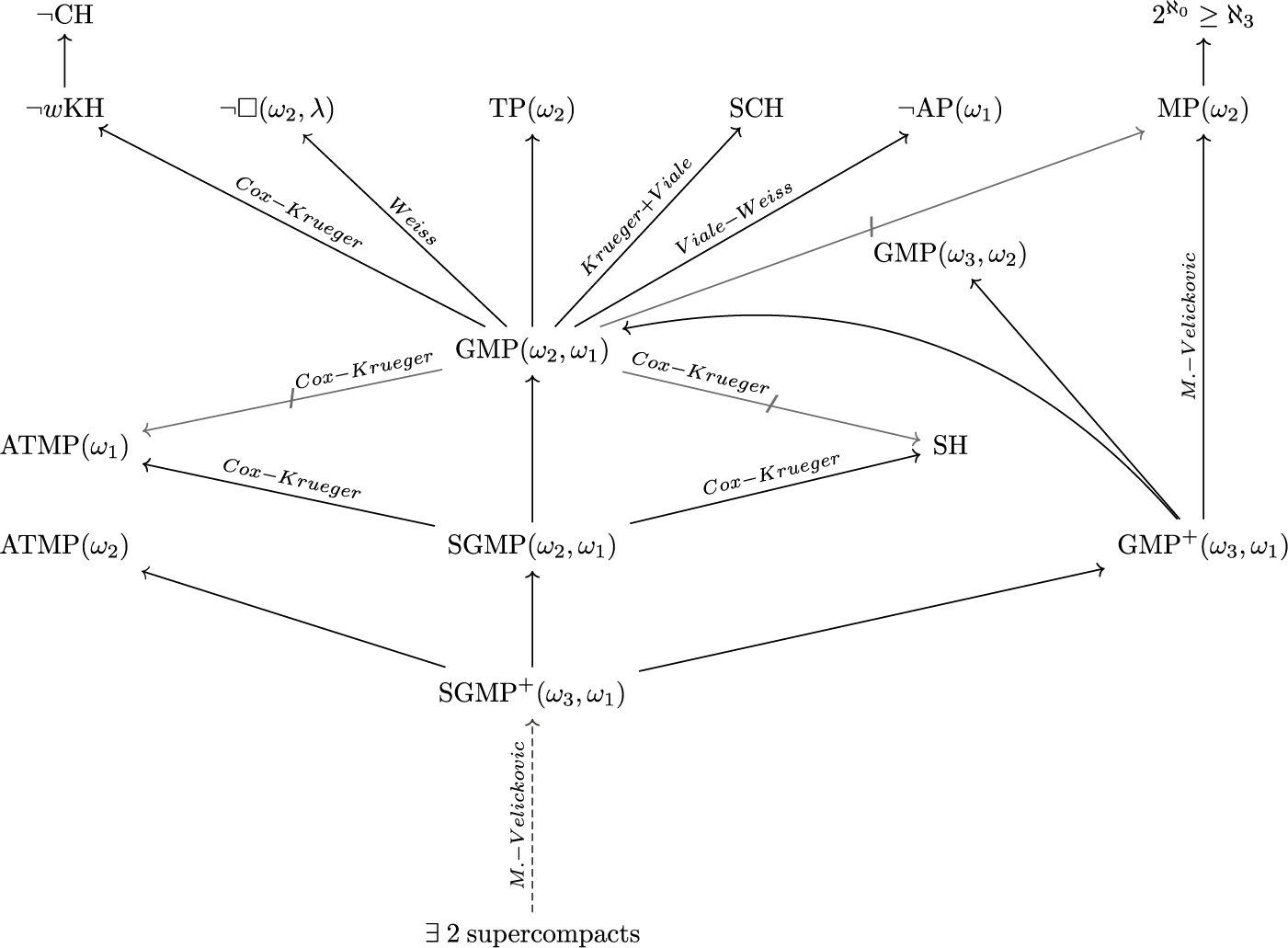
Appendices. Appendix A includes merely the above diagram. Appendix B presents a proof of the Mapping Reflection Principle with finite conditions under 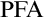 $\mathrm {PFA}$. Appendix C contains open problems. Finally, the thesis’s bibliography consists of 42 items.
$\mathrm {PFA}$. Appendix C contains open problems. Finally, the thesis’s bibliography consists of 42 items.
Abstract prepared by Rahman Mohammadpour
E-mail: rahmanmohammadpour@gmail.com
URL: https://theses.hal.science/tel-03209264