Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-28T08:18:24.434Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERLEAVING LOGIC AND COUNTING

Part of: Philosophical aspects of logic and foundations General logic

Published online by Cambridge University Press:  26 July 2023

JOHAN VAN BENTHEM  and
THOMAS ICARD
JOHAN VAN BENTHEM
Affiliation:
INSTITUTE FOR LOGIC, LANGUAGE, AND COMPUTATION UNIVERSITEIT VAN AMSTERDAM SCIENCE PARK 107, 1098 XG AMSTERDAM NETHERLANDS E-mail: johan@stanford.edu
THOMAS ICARD
Affiliation:
DEPARTMENT OF PHILOSOPHY, STANFORD UNIVERSITY 450 JANE STANFORD WAY, MAIN QUAD, BUILDING 90 STANFORD, CA 94305, USA E-mail: icard@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Reasoning with quantifier expressions in natural language combines logical and arithmetical features, transcending strict divides between qualitative and quantitative. Our topic is this cooperation of styles as it occurs in common linguistic usage and its extension into the broader practice of natural language plus ‘grassroots mathematics’.

We begin with a brief review of 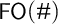$\mathsf {FO}(\#)$, first-order logic with counting operators and cardinality comparisons. This system is known to be of very high complexity, and drowns out finer aspects of the combination of logic and counting. We therefore move to a small fragment that can represent numerical syllogisms and basic reasoning about comparative size: monadic first-order logic with counting, 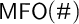$\mathsf {MFO}(\#)$. We provide normal forms that allow for axiomatization, determine which arithmetical notions can be defined on finite and on infinite models, and conversely, we discuss which logical notions can be defined out of purely arithmetical ones, and what sort of (non-)classical logics can be induced.

Next, we investigate a series of strengthenings of 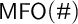$\mathsf {MFO}(\#)$, again using normal form methods. The monadic second-order version is close, in a precise sense, to additive Presburger Arithmetic, while versions with the natural device of tuple counting take us to Diophantine equations, making the logic undecidable. We also define a system 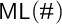$\mathsf {ML}(\#)$ that combines basic modal logic over binary accessibility relations with counting, needed to formulate ubiquitous reasoning patterns such as the Pigeonhole Principle. We prove decidability of $\mathsf {ML}(\#)$, and provide a new kind of bisimulation matching the expressive power of the language.

As a complement to the fragment approach pursued here, we also discuss two other ways of lowering the complexity of 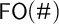$\mathsf {FO}(\#)$ by changing the semantics of counting in natural ways. A first approach replaces cardinalities by abstract but well-motivated values of ‘mass’ or other mereological aggregating notions. A second approach keeps the cardinalities but generalizes the meaning of counting to work in models that allow dependencies between variables.

Finally, we return to our starting point in natural language, confronting the architecture of our formal systems with linguistic quantifier vocabulary and syntax, as well as with natural reasoning modules such as the monotonicity calculus. In addition to these encounters with formal semantics, we discuss the role of counting in semantic evaluation procedures for quantifier expressions and determine, for instance, which binary quantifiers are computable by finite ‘semantic automata’. We conclude with some general thoughts on yet further entanglements of logic and counting in formal systems, on rethinking the qualitative/quantitative divide, and on connecting our analysis to empirical findings in cognitive science.

Keywords

logicarithmeticcountingqualitativequantitativecardinality

MSC classification

Primary: 03A05: Philosophical and critical
Secondary: 03B45: Modal logic (including the logic of norms) 03B65: Logic of natural languages 03B70: Logic in computer science
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 29 , Issue 4 , December 2023 , pp. 503 - 587
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ackermann, W., Solvable Cases of the Decision Problem , Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1954.Google Scholar
Antonelli, G. A., Numerical abstraction via the Frege quantifier . Notre Dame Journal of Formal Logic , vol. 51 (2010), no. 2, pp. 161–179.CrossRefGoogle Scholar
Baader, F. and De Bortoli, F., On the expressive power of description logics with cardinality constraints on finite and infinite sets. , Frontiers of Combining Systems (Herzig, A. and Popescu, A., editors), Springer, Cham, 2019, pp. 203–219.CrossRefGoogle Scholar
Bacchus, F., Representing and Reasoning with Probabilistic Knowledge , MIT Press, Cambridge, 1990.Google Scholar
Baltag, A. and van Benthem, J., A simple logic of functional dependence . Journal of Philosophical Logic , vol. 50 (2021), pp. 939–1005.CrossRefGoogle Scholar
Barceló, P., Kostylev, E. V., Monet, M., Pérez, J., Reutter, J., and Silva, J. P., The logical expressiveness of graph neural networks , Proceedings of the International Conference on Learning Representations (ICLR) , 2020.Google Scholar
Barner, D., Chow, K., and Yang, S.-J., Finding one’s meaning: A test of the relation between quantifiers and integers in language development . Cognitive Psychology , vol. 58 (2009), no. 2, pp. 195–219.CrossRefGoogle ScholarPubMed
Barwise, J. and Cooper, R., Generalized quantifiers and natural language . Linguistics and Philosophy , vol. 4 (1981), no. 2, pp. 159–219.CrossRefGoogle Scholar
Barwise, J. and Feferman, S., Model-Theoretic Logics , Association for Symbolic Logic, 1985.Google Scholar
Bednarczyk, B., Demri, S., Fervari, R., and Mansutti, A., Modal logics with composition on finite forests: Expressivity and complexity , Proceedings of the 35th Annual ACM/IEEE Symposium on Logic in Computer Science , Association for Computing Machinery, New York, 2020, pp. 167–180.CrossRefGoogle Scholar
van Benthem, J., Essays in Logical Semantics , Reidel, Dordrecht, 1986.CrossRefGoogle Scholar
van Benthem, J., Language in Action: Categories, Lambdas, and Dynamic Logic , Studies in Logic, vol. 130, Elsevier, Amsterdam, 1991.Google Scholar
van Benthem, J., Program constructions that are safe for bisimulation . Studia Logica , vol. 60 (1998), pp. 311–330.CrossRefGoogle Scholar
van Benthem, J., Guards, bounds, and generalized semantics . Journal of Logic, Language, and Information , vol. 14 (2005), no. 3, pp. 263–279.CrossRefGoogle Scholar
van Benthem, J. and Liu, F., New logical perspectives on monotonicity , Monotonicity in Logic and Language (Deng, D., Liu, F., Liu, M., and Westerståhl, D., editors), Springer, 2020.Google Scholar
van Benthem, J., Mierzewski, K., and Zaffora Blando, F., The modal logic of stepwise removal . The Review of Symbolic Logic , vol. 15 (2022), no. 1, pp. 36–63.CrossRefGoogle Scholar
Blackburn, P., de Rijke, M., and Venema, Y., Modal Logic , Cambridge University Press, New York, 2001.CrossRefGoogle Scholar
Borosh, I. and Treybig, L. B., Bounds on positive integral solutions of linear Diophantine equations . Proceedings of the American Mathematical Society , vol. 55 (1976), no. 2, pp. 299–304.CrossRefGoogle Scholar
Brasoveanu, A., Sentence-internal different as quantifier-internal anaphora . Linguistics and Philosophy. 34(2011), 93–168.CrossRefGoogle Scholar
Bumford, D., Incremental quantification and the dynamics of pair-list phenomena . Semantics and Pragmatics , vol. 8 (2015), no. 9, pp. 1–70.CrossRefGoogle Scholar
Burgess, J. P., Axiomatizing the logic of comparative probability . Notre Dame Journal of Formal Logic , vol. 51 (2010), no. 1, pp. 119–126.CrossRefGoogle Scholar
Cai, J.-Y., Fürer, M., and Immerman, N., An optimal lower bound on the number of variables for graph identification . Combinatorica , vol. 12 (1992), pp. 389–410.CrossRefGoogle Scholar
Carey, S., The Origin of Concepts , Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
Carreiro, F., Facchini, A., Venema, Y., and Zanasi, F., Model theory of monadic predicate logic with the infinity quantifier . Archive for Mathematical Logic , vol. 61 (2022), pp. 465–502.CrossRefGoogle Scholar
Clarke, S. and Beck, J., The number sense represents (rational) numbers . Behavioral and Brain Sciences , vol. 44 (2021), p. e178.CrossRefGoogle ScholarPubMed
Cook, S. A. and Reckhow, R. A., The relative efficiency of propositional proof systems . Journal of Symbolic Logic , vol. 44 (1979), no. 1, pp. 36–50.CrossRefGoogle Scholar
Corcoran, J., Frank, W., and Maloney, M., String theory . The Journal of Symbolic Logic , vol. 39 (1974), no. 4, pp. 625–637.CrossRefGoogle Scholar
van Deemter, K., Generalized quantifiers: Finite versus infinite , Generalized Quantifiers in Natural Language (van Benthem, J. and ter Meulen, A., editors), Foris, Dordrecht, 1984, pp. 145–160.Google Scholar
Dehaene, S., The Number Sense , Oxford University Press, Oxford, 2011.Google Scholar
Demri, S. and Lugiez, D., Complexity of modal logics with Presburger constraints . Journal of Applied Logic , vol. 8 (2010), no. 3, pp. 233–252.CrossRefGoogle Scholar
Denison, S. and Xu, F., The origins of probabilistic inference in human infants . Cognition , vol. 130 (2014), no. 3, pp. 335–347.CrossRefGoogle ScholarPubMed
Ding, Y., Harrison-Trainor, M., and Holliday, W. H., The logic of comparative cardinality . The Journal of Symbolic Logic , vol. 83 (2020), no. 3, pp. 972–1005.CrossRefGoogle Scholar
Ding, Y., Holliday, W. H., and Icard, T. F., Regularity for relative likelihood, Peking University, University of California, Berkeley, and Stanford University, manuscript, 2021.Google Scholar
Ehrenfeucht, A., Haussler, D., and Rozenberg, G., On regularity of context-free languages . Theoretical Computer Science , vol. 27 (1983), no. 3, pp. 311–332.CrossRefGoogle Scholar
Eilenberg, S. and Schützenberger, M.-P., Rational sets in commutative monoids . Journal of Algebra , vol. 13 (1969), no. 2, pp. 173–191.CrossRefGoogle Scholar
Endrullis, J. and Moss, L. S., Syllogistic logic with “most” . Mathematical Structures in Computer Science , vol. 29 (2019), no. 6, pp. 763–782.CrossRefGoogle Scholar
Fagin, R., Halpern, J. Y., and Megiddo, N., A logic for reasoning about probabilities . Information and Computation , vol. 87 (1990), pp. 78–128.CrossRefGoogle Scholar
Feferman, S. and Vaught, R., The first-order properties of products of algebraic systems . Fundamenta Mathematicae , vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
Feigenson, L., Dehaene, S., and Spelke, E., Core systems of number . Trends in Cognitive Sciences , vol. 8 (2003), no. 7, pp. 307–314.CrossRefGoogle Scholar
Fine, K., Propositional quantifiers in modal logic . Theoria , vol. 36 (1970), pp. 336–346.CrossRefGoogle Scholar
Fine, K., In so many possible worlds . Notre Dame Journal of Formal Logic , vol. 13 (1972), no. 4, 516–520.CrossRefGoogle Scholar
Fu, X. and Zhao, Z., Modal logic with counting: Definability, semilinear sets and correspondence theory, unpublished manuscript, China University of Political Science and Law, Beijing and School of Mathematics and Statistics, Taishan University, 2023.Google Scholar
Gärdenfors, P., Qualitative probability as an intensional logic . Journal of Philosophical Logic , vol. 4 (1975), no. 2, pp. 171–185.CrossRefGoogle Scholar
Ginsburg, S. and Spanier, E. H., Semigroups, Presburger formulas, and languages . Pacific Journal of Mathematics , vol. 16 (1966), no. 2, pp. 285–296.CrossRefGoogle Scholar
Grädel, E., Otto, M., and Rosen, E., Two-variable logic with counting is decidable , Proceedings of Twelfth Annual IEEE Symposium on Logic in Computer Science (LICS ‘97) , IEEE Computer Society, Warsaw, 1997, pp. 306–317.CrossRefGoogle Scholar
Grädel, E., Otto, M., and Rosen, E., Undecidability results on two-variable logics . Archive for Mathematical Logic , vol. 38 (1999), pp. 313–353.Google Scholar
Graf, T., A subregular bound on the complexity of lexical quantifiers , Proceedings of the 22nd Amsterdam Colloquium (Schlöder, J. J., McHugh, D., and Roelofsen, F., editors), 2019, pp. 455–464.Google Scholar
Grumbach, S. and Tollu, C., On the expressive power of counting . Theoretical Computer Science , vol. 149 (1995), pp. 67–99.CrossRefGoogle Scholar
Grzegorczyk, A., Undecidability without arithmetization . Studia Logica , vol. 79 (2005), pp. 163–230.CrossRefGoogle Scholar
Hale, B. and Wright, C., The Reason’s Proper Study: Essays towards a Neo-Fregean Philosophy of Mathematics , Oxford University Press, Oxford, 2001.CrossRefGoogle Scholar
Hall, P., On representatives of subsets . Journal of the London Mathematical Society , vol. 10 (1935), no. 1, pp. 26–30.CrossRefGoogle Scholar
Halpern, J. Y., An analysis of first-order logics of probability . Artificial Intelligence , vol. 46 (1990), pp. 311–350.CrossRefGoogle Scholar
Harel, D., Recurring dominoes: Making the highly undecidable highly understandable . Annals of Discrete Mathematics , vol. 24 (1985), pp. 51–72.Google Scholar
Harrison-Trainor, M., Holliday, W. H., and Icard, T. F., Inferring probability comparisons . Mathematical Social Sciences , vol. 91 (2018), pp. 61–70.CrossRefGoogle Scholar
Hartogs, F., Über das Problem der Wohlordnung . Mathematische Annalen , 76 (1915), 438–443.CrossRefGoogle Scholar
Herre, H., Krynicki, M., Pinus, A., and Väänänen, J., The Härtig quantifier: A survey . The Journal of Symbolic Logic , vol. 56 (1991), no. 4, 1153–1183.CrossRefGoogle Scholar
Hilbert, D., On the foundations of logic and arithmetic . The Monist , vol. 15 (1905), no. 3, pp. 338–352.CrossRefGoogle Scholar
van der Hoek, W. and deRijke, M., Generalized quantifier and modal logic . Journal of Logic, Language, and Information , vol. 2 (1993), pp. 19–58.CrossRefGoogle Scholar
van der Hoek, W., Qualitative modalities . International Journal of Uncertainty, Fuzziness, and Knowledge-Based Systems , vol. 4 (1996), no. 1, pp. 45–59.CrossRefGoogle Scholar
Hoeksema, J., Plurality and conjunction , Studies in Model-Theoretic Semantics (ter Meulen, A., editor), Foris, Dordrecht, 1983, pp. 63–83.CrossRefGoogle Scholar
Hoffmann, S., Commutative regular languages—Properties and state complexity , Algebraic Informatics (Ćirić, M., Droste, M., and Pin, J.-É., editors), Springer, 2019, pp. 151–163.CrossRefGoogle Scholar
Holliday, W. H. and Icard, T. F., Axiomatization in the meaning sciences , The Science of Meaning (Ball, D., and Rabern, B., editors), Oxford University Press, Oxford, 2018.Google Scholar
Ibeling, D., Icard, T., Mierzewski, K., and Mossé, M., Probing the quantitative–qualitative divide in probabilistic reasoning . Annals of Pure and Applied Logic (2023), p. 103339, forthcoming.CrossRefGoogle Scholar
Icard, T. F. and Moss, L. S., Recent progress on monotonicity . Linguistic Issues in Language Technology , vol. 9 (2014), no. 7, 167–194.Google Scholar
Icard, T. F., Moss, L. S., and Tune, W., A monotonicity calculus and its completeness , Proceedings of the 15th Meeting on the Mathematics of Language (Kanazawa, M., de Groote, P., and Sadrzadeh, M., editors), Association for Computational Linguistics, London, 2017, pp. 75–87.CrossRefGoogle Scholar
Kanazawa, M., Monadic quantifiers recognized by deterministic pushdown automata , Proceedings of the 19th Amsterdam Colloquium (Aloni, M., Franke, M., and Roelofsen, F., editors), 2013, pp. 139–146.Google Scholar
Karp, R. M., Reducibility among combinatorial problems , Complexity of Computer Computations (Miller, R. E., Thatcher, J. W., and Bohlinger, J. D., editors), Springer, Boston, 1972, pp. 85–103.CrossRefGoogle Scholar
Keenan, E. and Paperno, D., Overview , Handbook of Quantifiers in Natural Language , Studies in Linguistics and Philosophy, vol. 90, Springer, 2012, pp. 941–950.CrossRefGoogle Scholar
Kieroński, E., Pratt-Hartmann, I., and Tendera, L., Two-variable logics with counting and semantic constraints . ACM SIGLOG News, vol. 5 (2018), no. 3, pp. 22–43.CrossRefGoogle Scholar
Kirschhock, M. E., Ditz, H. M., and Nieder, A., Behavioral and neuronal representation of numerosity zero in the crow . Journal of Neuroscience , vol. 41 (2021), no. 22, pp. 4889–4896.CrossRefGoogle ScholarPubMed
Kisby, C., Blanco, S. A., Kruckman, A., and Moss, L. S., Logics for sizes with union or intersection . Proceedings of the AAAI Conference on Artificial Intelligence , vol. 34, 2020, no. 3, pp. 2870–2876.CrossRefGoogle Scholar
Knowlton, T., Hunter, T., Odic, D., Wellwood, A., Halberda, J., Pietroski, P., and Lidz, J., Linguistic meanings as cognitive instructions . Annals of the New York Academy of Sciences , vol. 1500 (2021a), no. 1, pp. 134–144.CrossRefGoogle ScholarPubMed
Knowlton, T., Pietroski, P., Halberda, J., and Lidz, J., The mental representation of universal quantifiers . Linguistics and Philosophy , vol. 45 (2021b), pp. 911–941.CrossRefGoogle Scholar
Kraft, C. H., Pratt, J. W., and Seidenberg, A., Intuitive probability on finite sets . The Annals of Mathematical Statistics , vol. 30 (1959), no. 2, pp. 408–419.CrossRefGoogle Scholar
Krajíček, J., Proof Complexity , Cambridge University Press, Cambridge, 2019.CrossRefGoogle Scholar
Krantz, D. H., Luce, R. D., Suppes, P., and Tversky, A., Foundations of Measurement , vol. 1, Academic Press, New York, 1971.Google Scholar
Kuske, D. and Schweikardt, N., First-order logic with counting: At least, weak hanf normal forms always exist and can be computed! , Proceedings of the 32nd Annual ACM/IEEE Symposium on Logic in Computer Science , IEEE, 2017, pp. 1–12.Google Scholar
Lai, T., Endrullis, J., and Moss, L. S., Majority digraphs . Proceedings of the American Mathematical Society , vol. 144 (2016), no. 9, pp. 3701–3715.CrossRefGoogle Scholar
Leśniewski, S., O podstawach matematyki . Przegląd Filozoficzny , vol. 30 (1927), pp. 164–206.Google Scholar
Lewis, H. R., Complexity results for classes of quantificational formulas . Journal of Computer and System Sciences , vol. 23 (1980), no. 3, pp. 317–353.CrossRefGoogle Scholar
Lidz, J., Pietroski, P., Halberda, J., and Hunter, T., Interface transparency and the psychosemantics of most. Natural Language Semantics , vol. 19 (2011), pp. 227–256.CrossRefGoogle Scholar
Lindström, P., First order predicate logic with generalized quantifiers . Theoria , vol. 32 (1966), no. 3, pp. 186–195.CrossRefGoogle Scholar
Link, G., Algebraic Semantics in Language and Philosophy , Cambridge University Press, Cambridge, 1998.Google Scholar
Lipshitz, L., The Diophantine problem for addition and divisibility . Transactions of the American Mathematical Society , vol. 235 (1978), pp. 271–283.CrossRefGoogle Scholar
Marx, M. and Venema, Y., Multi-Dimensional Modal Logic , Springer, Dordrecht, 1997.CrossRefGoogle Scholar
Mayer, T., An investigation of the negationless fragment of the Rescher–Härtig quantifier. Bachelor’s thesis in Mathematics, Stanford University, 2023.Google Scholar
Mercier, H., Politzer, G., and Sperber, D., What causes failure to apply the pigeonhole principle in simple reasoning problems? Thinking & Reasoning , vol. 23 (2017), no. 2, pp. 184–189.CrossRefGoogle Scholar
Moreno, L. E. and Waldegg, G., The conceptual evolution of actual mathematical infinity . Educational Studies in Mathematics , vol. 22 (1991), no. 3, pp. 211–231.Google Scholar
Mortimer, M., On languages with two variables . Mathematical Logic Quarterly , vol. 21 (1975), no. 1, pp. 135–140.CrossRefGoogle Scholar
Moss, L. S., Natural logic , Handbook of Contemporary Semantic Theory , second ed., Wiley-Blackwell, Oxford, 2015, pp. 646–681.Google Scholar
Moss, L. S., Syllogistic logic with cardinality comparisons , J. Michael Dunn on Information Based Logics (Bimbó, K., editor), Springer, Cham, 2016, pp. 391–415.CrossRefGoogle Scholar
Moss, L. S. and Topal, S., Syllogistic logic with cardinality comparisons, on infinite sets . The Review of Symbolic Logic , vol. 13 (2020), no. 1, pp. 1–22.CrossRefGoogle Scholar
Mossé, M., Ibeling, D., and Icard, T., Is causal reasoning harder than probabilistic reasoning? The Review of Symbolic Logic (2022), pp. 1–26, forthcoming.CrossRefGoogle Scholar
Mostowski, A. and Tarski, A., Arithmetical classes and types of well-ordered systems . Bulletin of the American Mathematical Society , vol. 55 (1949), p. 65.Google Scholar
Mostowski, M., Computational semantics for monadic quantifiers . Journal of Applied Non-Classical Logics , vol. 8 (1998), pp. 107–121.CrossRefGoogle Scholar
Németi, I., Fine-structure analysis of first-order logic , Arrow Logic and Multidimensional Logic (Marx, M., Masuch, M., and Pólos, L., editors), CSLI Publications, Stanford, 1996, pp. 221–247.Google Scholar
Oppen, D. C., A ${2}^{2^{2^{pn}}}$ upper bound on the complexity of Presburger Arithmetic. Journal of Computer and System Sciences, vol. 16 (1978), no. 3, pp. 323–332.CrossRefGoogle Scholar
Otto, M., Bounded Variable Logics and Counting , Springer, New York, 1997.CrossRefGoogle Scholar
Parikh, R., On context-free languages . Journal of the ACM , vol. 13 (1966), no. 4, pp. 570–581.CrossRefGoogle Scholar
Peters, S. and Westerståhl, D., Quantifiers in Language and Logic , Oxford University Press, Oxford, 2006.Google Scholar
Piaget, J. and Garcia, R., Psychogenèse et Histoire des Sciences , Flammarion, Paris, 1983.Google Scholar
Pietroski, P., Lidz, J., Hunter, T., and Halberda, J., The meaning of “most”: Semantics, numerosity and psychology . Mind & Language , vol. 24 (2009), no. 5, pp. 554–585.CrossRefGoogle Scholar
Pratt-Hartmann, I., Complexity of the two-variable fragment with counting quantifiers . Journal of Logic, Language and Information , vol. 14 (2005), no. 3, pp. 369–395.CrossRefGoogle Scholar
Pratt-Hartmann, I., On the computational complexity of the numerically definite syllogistic and related logics, this Journal, vol. 14 (2008), no. 1, pp. 1–28.Google Scholar
Pratt-Hartmann, I., No syllogisms for the numerical syllogistic , Languages: From Formal to Natural , Lecture Notes in Computer Science, vol. 5533, Springer, Berlin–Heidelberg, 2009, pp. 129–203.Google Scholar
Putnam, H., Trial and error predicates and the solution to a problem of Mostowski . The Journal of Symbolic Logic , vol. 30 (1965), no. 1, pp. 49–57.CrossRefGoogle Scholar
Quine, W. V., Concatenation as a basis for arithmetic . The Journal of Symbolic Logic , vol. 11 (1946), no. 4, pp. 105–114.CrossRefGoogle Scholar
Reichenbach, H., The Direction of Time , University of California Press, Berkeley, 1956.CrossRefGoogle Scholar
Rescher, N., Plurality quantification . The Journal of Symbolic Logic , vol. 27 (1962), pp. 373–374.Google Scholar
Restall, G., An Introduction to Substructural Logics , Routledge, London and New York, 2000.CrossRefGoogle Scholar
Rett, J., The semantics of many, much, few, and little. Language and Linguistics Compass , vol. 12 (2018), no. 1, p. e12269.CrossRefGoogle Scholar
Robinson, J., Definability and decision problems in arithmetic . The Journal of Symbolic Logic , vol. 14 (1949), no. 2, pp. 98–114.CrossRefGoogle Scholar
Rothstein, S., Counting and the mass/count distinction . Journal of Semantics , vol. 27 (2010), no. 3, pp. 343–397.CrossRefGoogle Scholar
Sánchez-Valencia, V., Studies on natural logic and categorial grammar. PhD thesis, Universiteit van Amsterdam, 1991.Google Scholar
Schrijver, A., Theory of Linear and Integer Programming , Wiley, Chichester, 1998.Google Scholar
Schweikardt, N., Arithmetic, first-order logic, and counting quantifiers . ACM Transactions on Compututational Logic , vol. 6 (2005), no. 3, pp. 634–671.CrossRefGoogle Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers , The Theory of Models (Addition, J., Henkin, L., and Tarski, A., editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
Seidenberg, A., A simple proof of a theorem of Erdős and Szekeres . Journal of the London Mathematical Society , vol. s1–34 (1959), no. 3, p. 352.CrossRefGoogle Scholar
Skølem, T., Diophantische Gleichungen , Ergebnisse der Mathematik und ihrer Grenzgebiete, Springer, Berlin, 1938.Google Scholar
Slomson, A., The monadic fragment of predicate calculus with the Chang quantifier and equality , Proceedings of the Summer School in Logic Leeds, 1967 (Löb, M. H., editor), Springer, Berlin–Heidelberg, 1968, pp. 279–301.CrossRefGoogle Scholar
Steinert-Threlkeld, S. and Icard, T. F., Iterating semantic automata . Linguistics and Philosophy , vol. 36 (2013), no. 2, pp. 151–173.CrossRefGoogle Scholar
Steinhorn, C., Borel structures for first-order and extended logics , Harvey Friedman’s Research on the Foundations of Mathematics (Harrington, L., Morley, M., Svêdrov, A., and Simpson, S., editors), Studies in Logic and the Foundations of Mathematics, vol. 117, Elsevier, 1985, pp. 161–178.CrossRefGoogle Scholar
Sun, Z. and Liu, F., The inference pattern Mou in Mohist logic—A montonicity reasoning view . Roczniki Filozoficzne , vol. 68 (2020), pp. 257–270.CrossRefGoogle Scholar
Szymanik, J., Quantifiers and Cognition: Logical and Computational Perspectives , Springer, Berlin, 2016.CrossRefGoogle Scholar
Tarski, A., Mostowski, A., and Robinson, R. M., Undecidable Theories , North-Holland, Amsterdam, 1953.Google Scholar
Väänänen, J., Remarks on generalized quantifiers and second-order logics , Set Theory and Hierarchy Theory , vol. 14 , Prace Naukowe Instytutu Matematyki Politechniki Wroclawskiej, Wroclaw, 1977, pp. 117–123.Google Scholar
Visser, A., Growing commas: A study of sequentiality and concatenation . Notre Dame Journal of Formal Logic , vol. 50 (2009), no. 1, pp. 61–85.CrossRefGoogle Scholar
Westerståhl, D., Logical constants in quantifier languages . Linguistics and Philosophy , vol. 8 (1985), pp. 387–413.CrossRefGoogle Scholar