Estimates indicate that by the year 2013, 62 % of the obese population of the world lived in low- and middle-income countries(Reference Ng, Fleming and Robinson1). It is also known that young adult women are the group with the highest increase in excess weight prevalence in these countries(Reference Ford, Patel and Narayan2). In Brazil, national surveys indicate that there is an interaction between formal education levels, a proxy of income and excess weight prevalence in women. Those women with fewer years of formal education present the highest and still increasing prevalence of excess weight, whereas those with more years of formal education show the lowest and stagnated prevalence(3).
It is considered that weight gain arises from an energy imbalance, defined as when the energy intake of an individual exceeds his/her total energy expenditure (TEE). TEE is composed of the sum of the BMR, the physical activity (PA) energy expenditure and the thermic effect of food. Hence, it is a pivotal step of the nutritional care to adequately estimate the TEE of any individual seeking to lose weight, so that an energy deficit may be established(Reference Psota and Chen4,5) .
There is a myriad of methods available to assess TEE, being the doubly labelled water (DLW) usually considered the ‘gold standard’ one(Reference Westerterp6). Nonetheless, this method has a high operational cost, turning its use in large studies and clinical practice prohibitive(Reference Scagliusi and Lancha Júnior7). Hence, clinicians and researchers frequently use other methods that yield an estimate of the TEE in order to estimate the daily energy requirement of individuals. The use of predictive equations is rapid and smooth, with no associated costs, being the most feasible method to be used with outpatients, especially in low-income settings. However, its results are often discrepant, given that different equations were built using diverse populations and methods. In addition, few studies have validated the use of these equations in low-income populations.
Furthermore, these equations do not estimate the TEE itself, but rather, it usually estimates the BMR or the RMR(Reference Henry8,Reference Weijs9) . Briefly, the BMR is the rate of energy expenditure that occurs while the individual is at rest, in the post-absorptive state (12–14 h after food intake), thus, without the influence of recent food intake and PA(5). In turn, RMR tends to be somewhat higher (10–20 %) than the BMR since it is affected by recent food intake and recent PA(5). Predictive equations usually extrapolate the resulting BMR or RMR to a 24-h period, expressed in kJ/24-h, to be more meaningful, referred to as the basal energy expenditure or the resting energy expenditure, respectively(5). Noteworthy, these terms are often used interchangeably in the literature; hence, studies may state that the same predictive equation yields an estimate of the BMR(Reference Sabounchi, Rahmandad and Ammerman10) or the RMR(Reference Frankenfield, Roth-Yousey and Compher11) or of the resting energy expenditure(Reference Cancello, Soranna and Brunani12), making it challenging to maintain a constant nomenclature use.
Nevertheless, in clinical practice, it is more useful to estimate the TEE and not the BMR, since the energy deficit, as already pointed out, must be calculated considering the TEE(13). Hence, clinicians and researchers need to multiply the result of such an equation by a factor that represents the PA energy expenditure of the individuals. This factor is also known as the PA level (PAL), which is the ratio between TEE and BMR, expressed as multiples of BMR. Nevertheless, it is also a challenge to estimate PA energy expenditure, and consequently PAL, in clinical practice, since it is difficult to be objectively measured. Given that the use of accurate methods, such as triaxial accelerometers, is also expensive, the use of questionnaires, which are usually imprecise, is common(Reference Lee and Shiroma14).
Hence, the objective of the present study was to determine, in low-income women with excess weight, which calculated-TEE, obtained through the multiplication of the BMR resulting from different predictive equations by the metabolic equivalent of task (MET) obtained with triaxial accelerometers, shows higher agreement compared with the TEE obtained with the use of DLW (TEE-DLW).
Methods
Ethical aspects
The human experimental procedures conducted were all approved by the Ethical in Research Committee of the Centro de Estudos Superiores de Maceió, under protocol number 1588/12. All women provided written consent to participate in the study.
Population and sample
Low-income women with excess weight (BMI > 25 and < 40 kg/m2), aged 19–45 years, were included, using a non-probabilistic, convenience sampling approach. These women are mothers of undernourished children treated at the Centre for Nutrition Education and Recovery, a non-governmental institution, which aims to nutritionally recover undernourished children, located in a shantytown on the outskirts of Maceió-AL, a city with approximately 1 million inhabitants and a homicide rate of sixty-four per 100 000 per year in 2017. In the specific region of the shantytown, Human Development index is lower than 0·600, with a severe lack of infrastructure. Individuals living there usually come from the countryside, with an almost complete absence of a social network, since they do not bring any family or friend with them.
All mothers were invited to a screening at the centre. Pregnant and lactating women, those with physical impairment that interfered with anthropometric evaluation, those who self-reported to be dieting or presented with weight change in the previous month or during the 14 d of DLW assessment, and those who reported doing upper-body weight-resisted exercise, which cannot be detected by the triaxial accelerometers, were not included. All women underwent blood collection to determine concentrations of thyroid hormones, fasting blood glucose and insulin, and those with altered parameters were not included. Those who reported using antidiabetic or diuretic drugs or were doing thyroid hormones replacement were also not included.
Socio-economic and demographic data
A structured questionnaire was used to assess primary socio-economic and demographic data, such as age, years of formal schooling, number of children, the household crowding index (the number of individuals living in the household divided by the number of rooms in the household), labour situation and if the household receives financial aid from the government(Reference Florêncio, Bueno and Clemente15).
Anthropometric measurements
Body weight was measured using a digital scale (Filizola), and height was measured using a portable stadiometer(16). BMI was calculated and classified according to the WHO cut-off points(16).
Dietary intake data
Energy intake was estimated through the application of three 24-h dietary recalls in each participant, one of which at weekend day, with the aid of a photo book to assist in the quantification of food portions(Reference Monteiro17). In order to take into account the within-subject variance in the multiple 24-h dietary recalls, the de-attenuation method was used(5). The same nutritionist undertook all the 24-h dietary recalls via in-person interviews and performed the coding and analysis of dietary assessments. More details can be found in another publication of the present study(Reference Lins, Bueno and Grotti Clemente18).
Doubly labelled water analysis
The TEE of the participants was estimated using the multiple-point DLW (2H2 18O) technique, according to the recommendations of the International Dietary Energy Consultancy Group(Reference Coward, Roberts and Cole19). In order to receive the DLW dosage, the volunteers could not be febrile, present oedema, should neither have practised intense exercises the day before nor have received intravenous fluids the week before the study. Also, they could not travel outside the State of Alagoas within 14 d after the administration, as this would cause a change in the source of drinking water. Initially, a 10-h fasting urine sample of all participants was collected to serve as isotope-free basal urine. Then, all women received a single dose of DLW. The dose of DLW was formulated considering the estimated total body water of the included women and was composed of 0·12 g of 99·8 % 2H-labelled water and 2 g of 10 % 18O-labelled water/kg of estimated body water. Body water was assumed to be 50 % of the women’s body weight(20). Next, urine samples of each volunteer were collected on the 1st, 2nd, 3rd, 7th, 12th, 13th and 14th day after dose administration.
Isotopic analysis of the samples by isotope ratio MS for 18O (ANCA 20-20; Europe Scientific) and for 2H (ANCA 20-22; Sercon) was performed at the Mass Spectrometry Laboratory of the School of Medicine of Ribeirão Preto, which is accredited by the International Atomic Energy Agency. The 2H and 18O elimination rates were calculated according to Speakman(Reference Speakman21). Tap water was collected and analysed, and all calculations were adjusted for the content of isotopes in the drinking water. The rate of carbon dioxide production was calculated according to Coward et al.(Reference Coward, Roberts and Cole19). The isotope dilution spaces and TEE were calculated by the comparison of the enrichment of the baseline sample with that of the 1st, 2nd, 3rd, 7th, 12th, 13th and 14th day samples when a plateau of enrichment must have been reached. The enrichment of samples collected 14 d after dosing was used to draw the 2H and 18O elimination rate. A respiratory quotient of 0·85 was assumed to calculate TEE. The following criteria were established for the measurements: the ratio between the 2H dilution space and the 18O dilution space should be from 1·01 to 1·07 and the differences in the sample triplicates should be 5 deltas for 2H and 0·5 deltas for 18O(Reference Florêncio, Bueno and Clemente15,Reference Monteiro17) .
Physical activity level
In order to estimate the PAL of the participants, triaxial accelerometer motion sensors (ActivPAL®) were used. The participants used the equipment for seven consecutive days, in the anterior portion of their thigh, with the aid of an impermeable medical dressing (TegaDerm®, 3M), during the DLW period, and were advised not to withdraw it until the end of the specified period. ActivPAL® has been thoroughly validated in adults. It is a reliable measure during everyday physical activities of posture and motion(Reference Grant, Ryan and Tigbe22), and of walking, with an absolute percentage error of approximately 1 % for step number and cadence, regardless of walking speed(Reference Ryan, Grant and Tigbe23). It also accurately classifies activity intensity categories in healthy adults(Reference Lyden, Keadle and Staudenmayer24), and it has been used as the criterion validity measure in studies of occupational sitting and standing(Reference van Nassau, Chau and Lakerveld25), sedentary behaviour(Reference Kozey-Keadle, Libertine and Lyden26) and light-intensity PA(Reference Alberto, Nathanael and Mathew27). Considering that mostly sedentary women composed our sample, we believe that ActivPAL® would be a reliable way of measuring their PAL.
ActivPAL® computes the time that the individuals spend lying/sitting, standing, walking and running at every tenth of a second and then provides a MET estimate for the whole period of use based on default values for sitting/lying (1·25 MET), standing (1·40 MET) and stepping at a cadence of 120 steps per min (four MET). These MET values are taken from the WHO report(28) and James & Schofield(Reference James and Schofield29). The software analysis of the accelerometers’ data provides the MET value for the entire period that the individuals wore them by multiplying the MET value for each activity by the duration of the activity. For cadences that differ from 120 steps per min, the following equation is used to compute the MET estimate: MET.h = (1·4 × d) + (4 − 1·4) × (c/120) × d, where c is the cadence (steps per min) and d is the activity duration (in h). The ActivPAL® internal equation performed reasonably well in estimating energy expenditure during treadmill walking in females aged 15–25 years, especially in lower intensities’ activities, which is the case of the sample from the present study(Reference Harrington, Welk and Donnelly30).
The MET value yielded by the accelerometer analysis is closely related to the physical activity ratio concept, which is used to estimate the PAL of an individual when using questionnaires of PA(31). When one estimate PAL through questionnaires, it is necessary to record the time allocated (in h) to different activities performed by the individual in a day (from time spent working in a sedentary job to physical exercise such as jogging or swimming) and multiply it by the reference values for MET for each of these activities. The result of this multiplication is then divided by the total hours (usually 24 h) to yield the mean PAL of the individual, as a multiple of the 24-h BMR(31). Proceeding in a similar way, in the present study, the total MET value obtained in the 7-d period of the accelerometer analysis was divided by the total amount of hours that the individuals used the accelerometer (168 h), yielding a proxy of the individual’s PAL (estimated PAL), as a multiple of the 24-h BMR.
MET has a widely accepted definition of the amount of O2 consumed while sitting at rest and is equal to 3·5 ml O2 per kg body weight × min, or as 4·184 kJ/kg per h, and is roughly equal to the cost of sitting quietly(Reference Ainsworth, Haskell and Whitt32). It is a simple concept that may express the energy cost of PA as a multiple of the RMR, regardless of individual characteristics and type of activity(Reference Jetté, Sidney and Blümchen33). Nevertheless, there are several critiques regarding the adoption of this value for every individual, since it was obtained in a sitting 40-year-old male adult(Reference Byrne, Hills and Hunter34). More recently, the use of corrected MET values has been suggested, which would better represent the BMR of individuals, usually obtained as a multiple of supine RMR rather than seated RMR. Corrected MET values are systematically lower than the standard MET values(Reference Kozey, Lyden and Staudenmayer35). In a similar sample of obese women from the same population of the present study, we found a mean amount of O2 consumption of 2·82 ml/kg body weight × min, which is roughly equal to 3·52 kJ/kg per h, considering 1 ml of O2 consumed yields 20·92 kJ, similar to the values reported by Byrne et al.(Reference Byrne, Hills and Hunter34). These values were used in the present study in order to assess the accuracy and precision of the estimates of energy expenditure based on the MET values obtained from the accelerometry analysis; in other words, the estimated PAL obtained for each woman was multiplied by her body weight (in kg), by 3·52 (kJ) and by 24 (h).
Calculation of estimated total energy expenditure
In their seminal paper, Harris & Benedict(Reference Harris and Benedict36) stated that BMR should be measured with the individual ‘in a state of complete muscular repose 12–14 hours after the last meal’. Hence, in the present study, when the seminal paper of an equation reported that it was derived from indirect calorimetry measures conducted in individuals with at least 12-h fasting, the equation was considered to yield an estimation of the BMR. The only exception was the equation provided by the Dietary Reference Intake (DRI)(5).
The following eleven predictive equations of the BMR of the participants were used in the present study, after a review of the recent literature of studies using equations to assess energy expenditure in female Brazilian populations: Anjos et al.(Reference Anjos, Wahrlich and Vasconcellos37), DRI(5), FAO/WHO/UNU(31), Harris & Benedict(Reference Harris and Benedict36), Henry & Rees(Reference Henry and Rees38), Mifflin et al.(Reference Mifflin, St Jeor and Hill39), Owen(Reference Owen, Kavle and Owen40), Oxford(Reference Henry8), Rodrigues et al.(Reference Rodrigues, Mancini and Dalcanale41), Schofield(Reference Schofield42) and Siervo et al.(Reference Siervo, Boschi and Falconi43). The formulae for these equations are found in Table 1. As the present investigation is intended to aid low-income settings, equations that use parameters that are not easily collected, such as lean mass and fat mass, were not included. The equation by Rodrigues et al.(Reference Rodrigues, Mancini and Dalcanale41) does not clearly state if individuals were in 12-h fasting in the indirect calorimetry measurements. However, as it was conducted with a female Brazilian population, we included it in the present analysis.
Table 1. Predictive equations used to estimate energy expenditure in female populations found in the literature review (n 11)
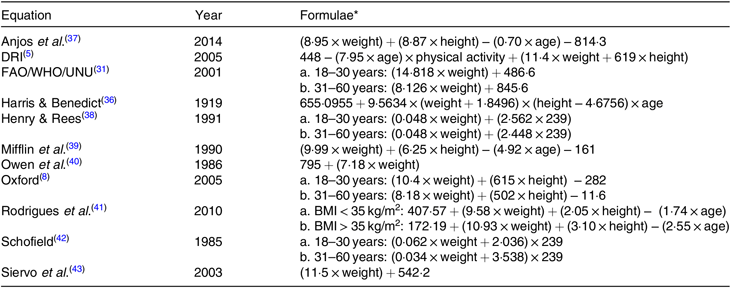
DRI, Dietary Reference Intakes.
* The unit of measurement for weight is kg, for height is cm, for age is years. For DRI and Oxford, the height was in metres.
The calculated-TEE of each participant was calculated using the factorial approach (i.e. TEE = BMR × PAL)(13). First, each predictive equation was calculated for each participant, yielding an estimated measure of the individuals’ BMR. The equations that yielded results in kcal were transformed into kJ, by multiplying it by 4·184. Then, this estimated BMR was multiplied by the estimated PAL yielded by the accelerometry analysis, for each participant, to yield the calculated-TEE. According to the FAO/WHO/UNU joint report(31), thermic effect of food is already accounted for in the PAL when TEE is estimated using the factorial approach. The factorial method was not applied to the DRI equation. This equation contains a PA coefficient, which is based on the PAL, and predicts the estimated energy requirements of the individuals, which is already a proxy of the TEE. According to the equation instructions, the PA coefficient was equal to 1·00 if PAL was estimated to be ≥ 1·0 < 1·4, equal to 1·12 if PAL was estimated ≥ 1·4 < 1·6, equal to 1·27 if PAL was estimated to be ≥ 1·6 < 1·9 and equal to 1·45 if PAL was estimated to be ≥ 1·9 < 2·5(5).
Statistical analyses
Three different methods assessed the agreement between the calculated-TEE obtained with the predictive equations and accelerometry analysis and the TEE-DLW. Firstly, the method of Bland and Altman, using the percentage differences, was used, since it diminishes the proportionality bias in the analysis(Reference Bland and Altman44). Limits of agreement and its 95 % CI were calculated. In order to assess which calculated-TEE yielded by the equations did not present significant bias compared with the TEE-DLW, a paired-sample ‘t’ test between the calculated-TEE and the TEE-DLW was conducted. Those equations that did not show significant differences between calculated-TEE and TEE-DLW were considered to present a non-significant bias. To determine the maximum allowed difference between methods in the Bland and Altman analysis, the within-subject variance coefficient of the energy dietary intake of the sample obtained with the use of three 24-h food records was used as a proxy, considering that, if the energy intake of an individual with stable body weight varies from day to day, the estimation of the TEE may also vary. This coefficient was 23·9 %(Reference Lins, Bueno and Grotti Clemente18), so a maximum allowed difference of 24 % was defined as acceptable.
Secondly, the root-mean-square error between each calculated-TEE and the TEE-DLW was calculated, in which the lowest values show better agreement between methods. Thirdly, the concordance correlation coefficient (CCC), which considers both the precision (the Pearson correlation coefficient) and the accuracy (using a bias correction factor that measures how far the best-fit line deviates from the 45° line) for each pair of measurements, was also analysed(Reference Lin45). The CCC equation is as follows:
where S XY = covariance(X, Y), S x = var(X), S y = var(Y). The Spearman rank correlation was used to explore the relationship between the PAL estimated with the accelerometers and the bias in the calculated-TEE using the predictive equations.
Sample size was determined according to the method of Lu et al.(Reference Lu, Zhong and Liu46). Based on the study by Raveli et al.(Reference Ravelli, Schoeller and Crisp47), where the two best equations showed a mean difference of 2·5 % compared with the TEE-DLW, and considering the mean TEE-DLW of our sample (8983 kJ), the expected mean of the differences for the present study would be 222 kJ. In order to obtain a sample that yielded an α value of 5 % and a β value of 20 %, considering an expected standard deviation of three times the mean difference (666 kJ) and a maximum allowed difference of 24 % (2154 kJ), the minimum required number of pairs for the Bland and Altman analysis would be thirty-one.
All analyses were conducted using the statistical package MedCalc Statistical Software version 18.11.3 (MedCalc Software bvba) and an α value of 5 % was adopted.
Results
From the sixty-seven women who were mothers or relatives to the undernourished children treated at the centre and received a DLW dose in the study, nineteen were excluded from the present analysis due to being in the normal BMI range. From forty-eight remaining women, three were excluded due to presenting less than 7 d of accelerometer data, resulting in forty-five women included in the present investigation. Descriptive characteristics of the women are shown in Table 2. Regarding their estimated PAL, the lowest value was 1·35 and the highest value was 1·65. PAL categories were distributed as follows: Three women (6·6 %) < 1·4; forty women (88·9 %) ≥ 1·4 and < 1·6 and two women (4·4 %) ≥ 1·6. The agreement between the calculated-TEE yielded by the equations’ results multiplied by the estimated-PAL yielded by the accelerometry analysis and the TEE-DLW is found in Table 3, which also shows the agreement between the estimates of energy expenditure based on the estimated PAL yielded by the accelerometer analysis and the TEE-DLW.
Table 2. Characteristics of the included women (n 45)
(Mean values and standard deviations; frequencies and percentages)
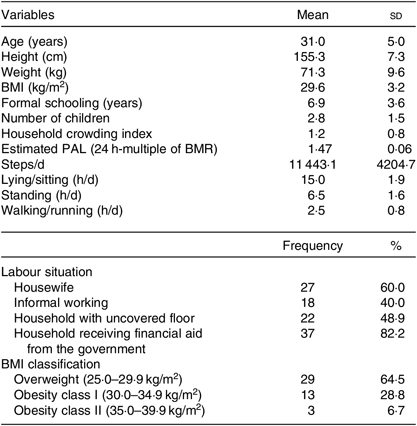
PAL, physical activity level.
Table 3. Assessment of the agreement between the calculated total energy requirements yielded by the predictive equations multiplied by the estimated physical activity level (PAL) and the total energy expenditure (TEE) measured with doubly labelled water (DLW) in low-income women with excess weight (n 45)
(Mean values and standard deviations and 95 % confidence intervals)
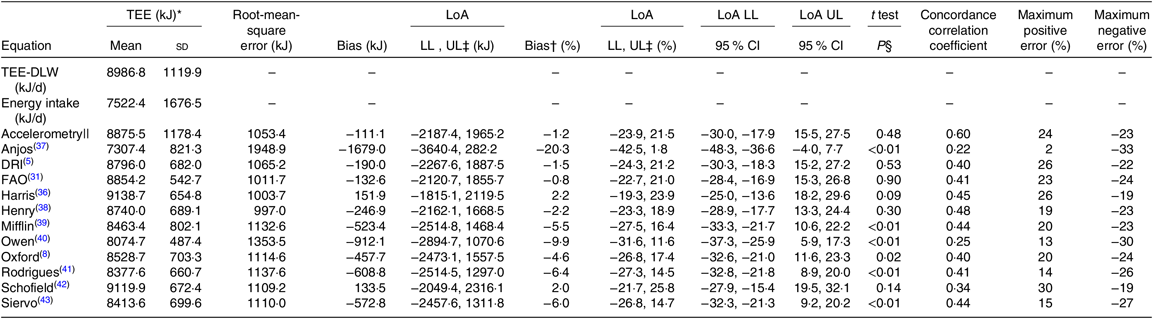
LoA, limits of agreement; UL, upper limit; LL, lower limit; DRI, Dietary Reference Intakes.
* Mean calculated-TEE. Obtained from the multiplication of the BMR resulting from each equation by the estimated PAL, for each woman.
† Bland–Altman percentage mean differences. Calculated by dividing the difference between the calculated-TEE and TEE-DLW by the mean between the calculated-TEE and TEE-DLW, multiplied by 100.
‡ Lower limit and upper limit of the Bland–Altman LoA, where 95 % of the differences is expected to lie between.
§ P value for a ‘t’ test for paired samples, comparing the mean calculated-TEE with the mean TEE-DLW.
|| Estimates of energy expenditure based on the estimated PAL given by the accelerometry.
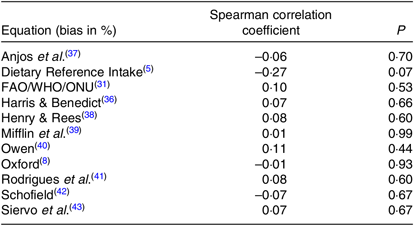
Accelerometry derived estimates of energy expenditure showed good agreement with the TEE-DLW, with a bias of –1·2 % and a CCC of 0·60. Considering all eleven equations, only five provided a calculated-TEE that did not present a significant bias compared with the TEE-DLW: DRI(5), FAO/WHO/UNU(31), Harris & Benedict(Reference Harris and Benedict36), Henry & Rees(Reference Henry and Rees38) and Schofield(Reference Schofield42). The mean percentage difference and limits of agreement between the calculated-TEE of each of these equations and the TEE-DLW were 1·57 (–21·1, 24·3) %; 0·81 (–21·0, 22·6); –2·28 (–23·8, 19·3) %; 2·21 (–18·8, 23·2) % and –2·05 (–25·7, 21·6) %, respectively. From these, DRI(5) and Schofield(Reference Schofield42) showed wider limits of agreement than the pre-defined maximum allowed difference of 24 % and lower CCC. Root-mean-square error was roughly equal between the three remaining equations. Nevertheless, no equation presented the CI of the limits of agreement within the pre-defined maximum allowed difference range. The Bland–Altman scatterplots for the five equations are found in Fig. 1. Table 4 shows the Spearman rank correlation coefficients for the bias, in percentage, from each calculated-TEE and the estimated PAL. All coefficients were equal to or lower than 0·10, except for DRI equation, which was equal to 0·27.
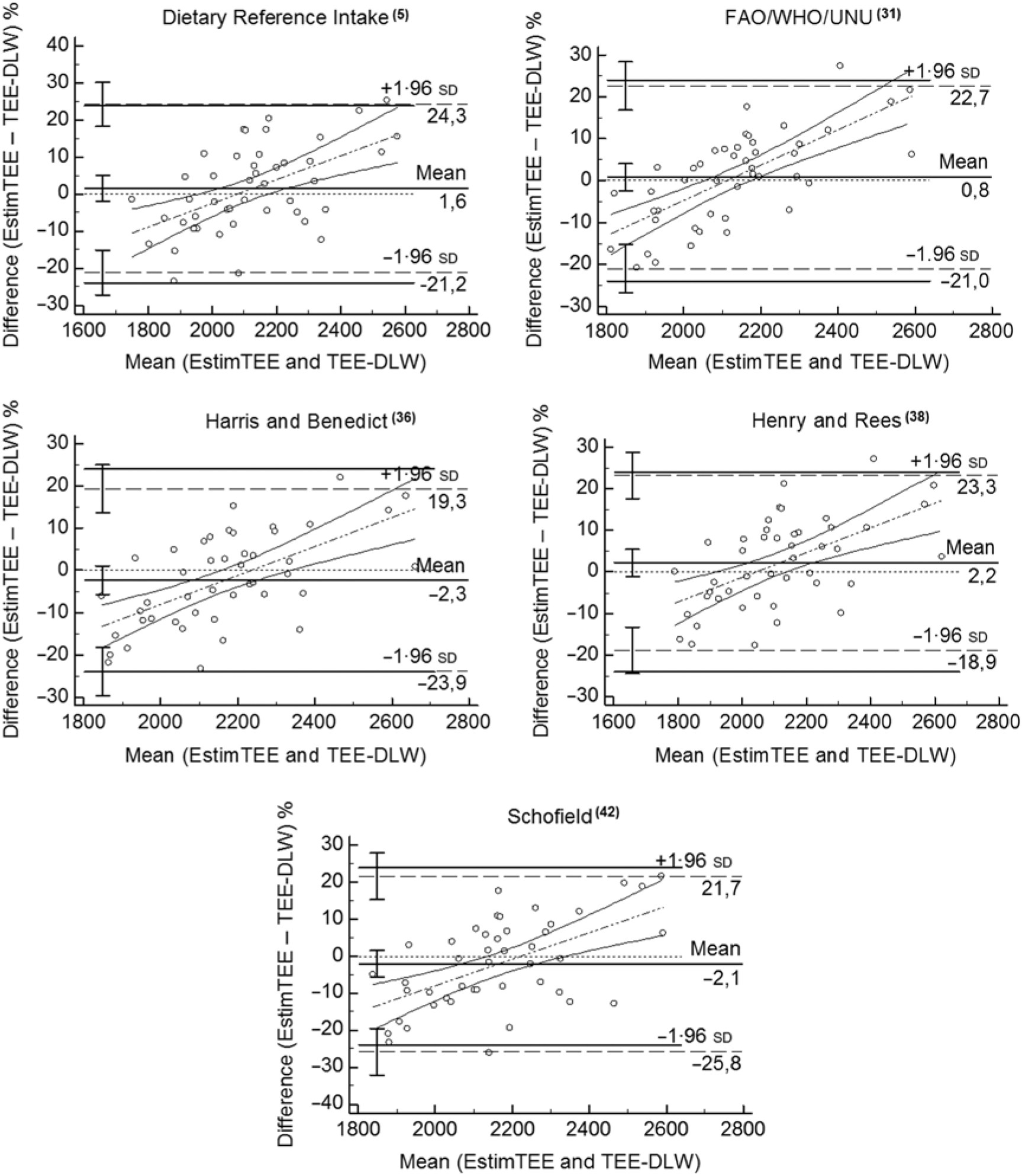
Fig. 1. Bland and Altman plots for the five equations that did not show significant bias when compared with the total energy expenditure measured with the doubly labelled water method (TEE-DLW).
Table 4. Correlation matrix between the estimated physical activity level and bias (in %) yielded by each calculated-total energy expenditure
Discussion
The present study demonstrated that, in low-income women with excess weight, the calculated-TEE derived from the combination between the estimated PAL and estimated BMR from five out of eleven studied predictive equations did not show significant bias when compared with the TEE-DLW. Three calculated-TEE presented its limits of agreement within the pre-defined maximum allowed difference range, with roughly equal root-mean-square error. Considering all parameters, the calculated-TEE obtained with the BMR yielded by the FAO/WHO/UNU(31) equation performed slightly better than the others. Nevertheless, it is noteworthy that all calculated-TEE showed the CI of the limits of agreement wider than the pre-defined maximum allowed difference range of 24 %, indicating that none of the calculated-TEE satisfactorily estimates the TEE-DLW in the present sample. Furthermore, estimates of energy expenditure yielded by the accelerometry analysis showed good agreement with the TEE-DLW, presenting a considerably low bias and the highest CCC when compared with the calculated-TEE.
The majority of studies validate predictive equations against data derived from indirect calorimetry, including in Brazilian populations, which is because equations are usually built to estimate BMR(Reference Santos, Suen and Marchini48–Reference Poli, Sanches and Moraes50). Nevertheless, as pointed by Madden et al.(Reference Madden, Mulrooney and Shah51), in clinical practice, it is arguably more critical to use equations to estimate TEE rather than to estimate BMR, since energy deficit must be calculated considering the former and not the latter. In their recent systematic review, Madden et al.(Reference Madden, Mulrooney and Shah51) report that only four studies comparing the agreement between calculated-TEE that uses the BMR derived from predictive equations and TEE-DLW in overweight/obese adults met their inclusion criteria regarding the quality of the assessment, as compared with twenty-one studies comparing results of the equations against measured BMR.
The four studies above(Reference Blanc, Schoeller and Bauer52–Reference Tooze, Schoeller and Subar55) were all conducted in US populations, with diverse backgrounds. Blanc et al.(Reference Blanc, Schoeller and Bauer52) studied seventy-three obese individuals aged 70–79 years, whereas Mahabir et al.(Reference Mahabir, Baer and Giffen53) evaluated forty-four post-menopausal women with excess weight. Das et al.(Reference Das, Saltzman and McCrory54), in turn, assessed the agreement in a group of twenty severely obese women, with a mean age approximately 37 years old. At last, Tooze et al.(Reference Tooze, Schoeller and Subar55) evaluated 314 adults with excess weight, aged 40–69 years. Hence, the comparability of our results with the studies available in the literature is somewhat complex.
More recently, Ravelli et al.(Reference Ravelli, Schoeller and Crisp47) investigated the agreement between the calculated-TEE obtained using the factorial method (i.e. multiplying equations-derived BMR by the estimated PAL) and the TEE-DLW in twenty severely obese Brazilian women before and after bariatric surgery. Although the population studied in their investigation differs from ours, since their study was conducted in the Brazilian southeast, the wealthiest region in the country, they also found that none of the investigated equations had a high accuracy when estimating the TEE-DLW of the women, especially after the weight loss induced by the bariatric surgery. Considering before-surgery values, Harris & Benedict(Reference Harris and Benedict36) and DRI(5) equations were indicated by the authors as the most suitable equations that could be used in the absence of specific equations to the target population.
It is noteworthy that two of the equations analysed in the present study, the one proposed by Anjos et al.(Reference Anjos, Wahrlich and Vasconcellos37) and the other proposed by Rodrigues et al.(Reference Rodrigues, Mancini and Dalcanale41), were both specifically developed in Brazilian studies and included women with excess weight in their samples. Nevertheless, the calculated-TEE derived using the BMR yielded by both of them presented significant bias in our investigation, being the calculated-TEE obtained using Anjos et al.(Reference Anjos, Wahrlich and Vasconcellos37), the one with the highest bias of all eleven calculated-TEE. Indeed, these two equations are not very used in clinical practice, maybe due to the almost inexistent number of validation studies, like the present one, investigating these equations for Brazilian populations. Although it is a usual concern that one should only use an equation for a specific population if that equation was developed for similar populations, in the present study, the most well-known equations, such as Harris & Benedict(Reference Harris and Benedict36), FAO/WHO/UNU(31) and Henry & Rees(Reference Henry and Rees38), which were not developed in similar populations to ours, presented a lower bias than the equations developed explicitly for Brazilian populations. This may indicate that the fact that an equation was developed using a specific population does not necessarily turn that equation the most suitable one for similar populations. At last, several studies have shown that one of the most accurate equations to predict BMR in obese individuals is proposed by Mifflin et al.(Reference Frankenfield, Roth-Yousey and Compher11,Reference Mifflin, St Jeor and Hill39,Reference Mahabir, Baer and Giffen53) , which did show significant bias (5·5 %) and poor overall agreement in our study. Similar findings were also reported by Ravelli et al.(Reference Ravelli, Schoeller and Crisp47), which may prevent the counselling of using this equation in Brazilian populations, at least if the objective is to estimate TEE, through the factorial method, in excess weight women.
As expected in a group of obese women, the self-reported energy intake was considerably lower than the TEE-DLW. Given that the women were weight stable, it may be concluded that there was a critical underreporting of energy intake, which is a long-discussed issue(Reference Schoeller56), and a common phenomenon, especially in obese individuals(Reference Heitmann and Lissner57). It has also been demonstrated in Brazilian women(Reference Scagliusi, Ferrioli and Pfrimer58). This issue is thoroughly discussed elsewhere, with regard to the present sample(Reference Lins, Bueno and Grotti Clemente18).
Some authors opt to include a factor to represent thermic effect of food in the calculations of the factorial method, usually 10 % of the individuals’ calculated-TEE(Reference Ravelli, Schoeller and Crisp47). In our data, this approach led to a worse overall agreement between calculated-TEE and TEE-DLW, overestimating the bias in the equations (data not shown). This overestimation may be explained by the fact that, by definition, the TEE is the result of the multiplication of the BMR by the PAL(31). Consequently, we opted only to discuss the analysis that did not include the 10 % addition of thermic effect of food in the calculated-TEE.
Regarding the estimated PAL of our sample, it indicates that the vast majority of women are sedentary and few of them are light-active. Although comparison of this data with other Brazilian women population is difficult, since few studies report it using the same data that were reported here, it is possible to conclude that our sample is much less active than other Brazilian samples. Raveli et al.(Reference Ravelli, Schoeller and Crisp47) found an estimated PAL of 1·65 in twenty severely obese women before bariatric surgery, which is substantially higher than that found in the present study. As already outlined, Raveli et al.(Reference Ravelli, Schoeller and Crisp47) studied a significantly different population when compared with ours. Fassini et al.(Reference Fassini, Pfrimer and Ferriolli59) studying Brazilian individuals with short bowel syndrome found an estimated PAL of 1·4 for those with the disease and of 1·75 for the sex-, age- and BMI-matched controls. Vasconcellos et al.(Reference Vasconcellos and Anjos60), using data from 267 000 Brazilian individuals, suggested a PAL of 1·53 for Brazilian women aged 20–44 years, which was substantially lower than the recommended PAL of 1·67 and close to the PAL found in the present study. It is noteworthy that the estimated PAL found in our sample is compatible with the definition given by the FAO/WHO/UNU report(31), which states, as an example of sedentary or light activity lifestyle ‘[…] rural women living in villages that have electricity, piped water and nearby paved roads, who spend most of the time selling produce at home or in the marketplace, or doing light household chores and caring for children in or around their houses’. This definition matches the setting of the present study, except for the fact that our study was conducted in a metropolitan region, rather than in a rural area. Nevertheless, the benefits that a regular metropolitan area may offer in terms of PA are possibly not seen by the women in our sample, given the extremely violent setting and severe lack of infrastructure they are inserted, which makes a walk around the streets, or doing some jogging, often not a feasible option. Hence, we believe that for this population of low-income women with excess weight, the mean PAL of 1·47 may be initially used to estimate the TEE using the factorial method.
Our study presents two crucial limitations. The first is the lack of data regarding the BMR of the sample, which could be an enriching information for the comparisons with the predictive equations. However, as the study aimed to compare the calculated-TEE obtained by the factorial method using results of the equations and accelerometers’ analysis, with the TEE-DLW, and not with the BMR, the DLW method was sufficient for the analyses.
The second limitation is that it is pivotal to consider that all of our calculations are severely dependent on the reliability of the estimated PAL; hence, if PAL was not reasonably estimated in the sample, all calculated-TEE are negatively affected. Estimates of energy expenditure based on the estimated PAL and a suitable MET value for the present sample (3·52 kJ/kg per h) were calculated in order to quantify the accuracy and precision of the accelerometry analysis compared with the TEE-DLW. Although it performed better than all calculated-TEE, based on the considerably higher CCC and roughly equal bias and root-mean-square error, it is only possible to say that the accelerometry estimates of energy expenditure agreement with the TEE-DLW are moderate at best, in the present sample. Besides, the estimation of PAL with the use of triaxial accelerometry data, which yield MET values, may have some concerns, given that the basal O2 volume consumption varies among individuals, which reduces the precision of MET usage(Reference Byrne, Hills and Hunter34). As already pointed out, corrected MET values could better represent the BMR of individuals; however, ActivPAL does not make it clear in its manual, which MET values it, uses, although it suggests the use of standard MET values (i.e. 1 kcal/kg per h or 4·184 kJ/kg per h) which may introduce important bias in our analysis.
Nevertheless, in clinical practice, the estimation of PAL is much less precise, since the practitioner relies on the reported physical activities done by the individuals, who also need to specify the amount of time they spent in each activity, and then, the practitioner matches these activities with pre-specified MET values available in the literature. Hence, although the use of accelerometers may show some imprecision, in this context, it surely may be considered a more reliable way to estimate the PAL of the individuals, supported by several studies, as outlined in the methods section(Reference Grant, Ryan and Tigbe22–Reference Kozey-Keadle, Libertine and Lyden26) especially in this sample of sedentary and light-physically active adults(Reference Alberto, Nathanael and Mathew27). Furthermore, the correlation analysis showed that there were no associations between the estimated PAL and the bias between each calculated-TEE and the TEE-DLW. Indeed, the equation that showed the higher correlation coefficient, but still a weak coefficient, was the DRI equation(5), precisely the one that asks to categorize the PAL into a PA coefficient.
Conclusion
In conclusion, none of the eleven calculated-TEE, estimated using the factorial method, showed the CI of the limits of agreement within the pre-defined maximum acceptable difference range of 24 %. This indicates that the use of these equations may not be sufficiently precise to estimate TEE using the factorial method in the context of the present study. Nevertheless, in the absence of specific equations for this population of low-income women with excess weight, the use of the equations of FAO/WHO/UNU(31) may be considered in conjunction with a mean PAL of 1·47 to estimate the TEE, using the factorial method.
Acknowledgements
The present study is funded by the Brazilian National Council for Scientific and Technologic Development (CNPq), process no. 552194/2011-5. CNPq had no role in the design, analysis or writing of this article.
M. L. M., I. S. V. M., A. G. C., K. P., E. F., I. R. O. M. P. and N. B. B. collected and analysed the data; M. L. M., I. S. V. M., I. R. O. M. P. and N. B. B. wrote the draft of the manuscript and H. S. F., T. M. T. F. and A. L. S. critically reviewed the manuscript. All authors read and approved the final version of the manuscript.
The authors declare no conflicts of interest.








