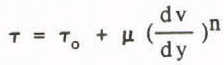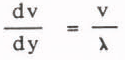INTRODUCTION
In modeling snow avalanche motion the application of hydrodynamic theory and equations was first introduced by Voellmy (1955). Although the theory strictly applies only to uniform, steady flow conditions, this method has continued to be used to predict avalanche runout speeds and distances. This is undoubtedly because of the simplicity of the equations involved, compared to what would be the alternative with transient viscous fluid dynamic equations. In continued use of the Voellmy formulation, principal criticism over the years has been in selection of the drag coefficients in the governing dynamic equation, which tend to vary over a wide range for different avalanche paths and different snow and terrain conditions. While part of this variation is caused by varying material and surface conditions, another part is related to the restrictions imposed in formulation of the governing equation of motion. Recent findings on the flow properties of granulamed snow, namely the property of snow to "lock up" as velocity gradients become small, provide a new basis in considering the formulation of equations of motion for avalanching snow. While the material locking property cannot be introduced explicitly into the hydrodynamic equations for uniform, steady flow, the physical concepts involved may be used to set up alternate forms of the drag terms. The intent in this is to determine if the range of the drag coefficients can be reduced in defining alternate forms of the drag terms. Evaluation of the range of these parameters is carried out by analyzing the runout of two avalanches, one constituted from dry mid-winter snow and the other of coastal wet snow.
GOVERNING EQUATION OF MOTION
The hydrodynamic equation of motion developed by Voellmy has the form

This is an equation for acceleration, a, of the fluid mass in terms of the gravitational driving force g sine, frictional drag ug cose, and v2 or dynamic drag with coefficient g/h. In this coefficient, g is the acceleration of gravity, h is the fluid flow depth, and is the turbulence coefficient. In typical applications of this equation, (Buser, Frutiger 1980; Martinelli and others 1980) the two drag coefficients μ and have a reported range of

depending upon avalanche path and field conditions.
Another version of the acceleration (per unit mass) equation, reported by Cheng and Perla (1979), and made applicable to computer based analysis of avalanche runout, is
where the only change is in the dynamic drag coefficient, namely D/M, which is treated as a single parameter. The ranges of the parameters reported by Cheng and Perla are:

in which the friction coefficient μ is unchanged from the Voellmy friction parameter, but the dynamic drag coefficient, M/D, increases over that of t. The difference is in the account taken of flow depth h, a parameter difficult to evaluate if considered a variable over the path of avalanche runout.
To pursue further the effect of flow depth h on avalanche flow, and its incorporation into equations of motion, the following physical conditions are considered:
-
At low shear stresses in flowing granular snow, the snow has a tendency to lock up (Dent and Lang 1983). The constitutive law for this Bingham type fluid is
where τo is the shear locking stress, u is the viscosity coefficient and dv/dy is the velocity gradient. A true Bingham fluid corresponds to n = 1; however, in order to retain v2 type dynamic drag, the exponent is set at n = 2, which in fluid mechanics is termed the Boussinesq formulation (Shames 1982).(3)
-
Flow of avalanches involves bulk flow of the major portion of the moving material riding upon a high velocity gradient boundary layer of granularized snow (Lang and Dent 1983). Designating the boundary layer thickness by λ, then the velocity gradient may be approximated by (Figure 1),
which assumes a linear velocity profile over the thickness of the boundary layer (Lang and Dent 1983).(4)
At present, not enough data exist to physically relate the boundary layer thickness λ to the flow depth h of the material. However, recognizing the degree of approximation involved in the model under consideration, two assumed relationships are investigated as a means of studying two additional versions of the equation of motion.
In one case the granular layer is taken to be proportional to h, and the constant of proportionality is combined with the viscosity coefficient v in the final equation. The equation of motion is then obtained by summing forces in the x direction (in Figure 1) and using the equation for the locking shear stress to obtain

In this equation the locking shear stress, τ0, is contained in the coefficient η, so that the mechanism of material locking reverts to the same type of term that surface friction contributes in previous derivations. In the v2 drag term the form is the same except that flow depth appears to second power in the denominator of the dynamic friction coefficient.

Fig. 1. Fİg.l. Bulk flow forces, kinematics, and boundary layer.
As another example, if λ is taken proportional to h, then h3 appears in the v2 drag term. In numerical studies this proved to be too severe a motion retardation unless a "fast-stop" mechanism is introduced, that has been proposed from observations of the appearance-wise accelerated slow-down of avalanches as they come to a stop. Lang and others (1979) define a slow speed viscosity function of the form
to represent a fast-stop mechanism. In this equation v0 is the nominal high-speed viscosity, and C and α are constants that are evaluated from avalanche outflow analyses. Using this equation for viscosity, the governing equation of motion becomes:

to represent a fast-stop mechanism. In this equation v0 is the nominal high-speed viscosity, and C and α are constants that are evaluated from avalanche outflow analyses. Using this equation for viscosity, the governing equation of motion becomes: Note that in these equations the viscosity referred to has different units based upon the different dependencies on h.
The next step, namely evaluation of the coefficients for specific avalanche cases, involves integration of the equations of motion. This was carried out by computer methodology using the Cheng-Perla (1979) code with some modifications. First, h was set equal to the average depth of the released snow slab and not updated as the flow progressed. This is not considered a serious error, since the avalanches studied are sheet-flow types without significant lateral confinement. Under this assumption the Voellmy, Cheng-Perla and Material Locking equations become identical in form, and any one of the three can be evaluated using the Cheng-Perla code. In what follows the Material Locking equation is evaluated, and the Voellmy and Cheng-Perla coefficients are computed for reference purposes only. However, if h were to be treated as a variable, then the procedure could be adapted as was necessary in the case of the Fast-Stop equation. In this equation velocity, v, appears in the argument of the exponential function, which negates easy integration of the equation, as is necessary to obtain an equation for velocity as a function of distance traveled for the Cheng-Perla code. Rather than try to find an integrated form of the Fast-Stop equation, an alternate option of equivalent linearization was introduced. At the slower flow speeds (v < 8 m s-1) where the viscosity changes, the length of segment was reduced to the point where coefficient values were essentially constant over the interval of integration. An added benefit of this finite differencing is that it is also easy to determine the segment in which flow speed becomes negligible and the avalanche stops. This negates the need to use an integrated form of the equation that, in the case of the other three versions of the equations of motion, contains an instability condition for this calculation.
AVALANCHE ANALYSES
Evaluations of the drag coefficients in the Material Locking and Fast-Stop equations are carried out for two avalanche paths. One is the nominal 35° Ironton Park path in southwestern Colorado where, after an elevation drop of 350 m, runout is onto a frozen lake bed. For this avalanche path a 2 m deep release slab of mid-winter dry snow is known to have traversed a path distance of 910 m, while a 1 m deep release traverses a path distance of 690 m (Lang, Dawson, Martinelli 1979). The second avalanche path is located on Mt Myoko, 23 km from the Sea of Japan in central Honshu Islands Japan. The slope extends from 800 to 1100 m (34° average slope), on which a 2.0 m average depth wet snow avalanche was artificially released on IS February 1966 (Nakamura and others 1984). Avalanche distance of travel was 570 m. For these avalanche cases the two versions of the hydrodynamic equations of motion were factored into a computer analysis to determine values of the drag coefficients in order to match the travel distances of the avalanches. Results of these evaluations are summarized in Table 1. In matching the avalanche runout distances, maximum velocities were also matched, which are also listed in Table I for the two cases. For reference purposes we show also the corresponding coefficients of the Voellmy and Cheng-Perla equations, computed directly from the Materials Locking coefficient values.
CONCLUSIONS
Results of the analysis allow two comparisons to be made. One comparison is between dry and wet snow avalanches of equal release depth (h => 2 m). In the case of the Material Locking model the variation in the friction coefficient between the dry and wet snow avalanches is from η = 0.053 to η = 0.075 respectively (Table 1), a factor of 1.4, which however fall below the published range of this parameter, namely 0.1η0.5. In the case of the Fast-Stop model, η = 0.12 to 0.08, respectively, a factor of 0.8; friction values somewhat greater than those of Material Locking. For the dynamic drag coefficients v and v0, the difference is a factor of 4 between the dry and wet snow avalanches, for both flow models, although the corresponding values differ by a factor of 2. Thus the dominant difference is reflected in the viscous pan of the flow models relative to the wetness of the snow in these avalanches.
The second comparison is in regard to difference in flow depth of the avalanches. For friction the variation is about a factor of 2 for a comparable change in depth in the case of Material Locking, but virtually no change with Fast-Stop. Change in the coefficient v for Material Locking, is by a factor of 0.6 from h=l m toh = 2m flow depth, and by 1.16 for Fast-Stop, for the same depth change. Thus there is a decrease in the range of the coefficients with Fast-Stop compared to Material Locking relative to flow depth change.
The characteristic of the Fast-Stop model that distinguishes it from the other models is that the total drag force decreases in magnitude in a low to mid velocity range. For example, in the case of the Mt Myoko avalanche, the total drag force drops in the velocity range 3 < v < 11 ms -1. Above v = 11 m s-1 the v2 drag becomes dominant and continues to increase up to the maximum velocity of the avalanche at v = 20.8 m s-1. This drop in drag force over an intermediate avalanche speed range is reported also by Schaerer (1975) from drag force studies of avalanches at Rodger's Pass, Canada. Schaerer introduces a kinetic friction term Equation1= which he applies over a speed range 10 < v < 50 m s -1 , based upon numerical fitting of the drag coefficients to more than 35 control released avalanches. Using this representation for drag, an intermediate range occurs, in which the total drag force decreases in magnitude, similar to that of Fast-Stop. That drag force decreases with increasing speed has also been directly measured on a granular snow layer, subjected to overburden pressure representing that in an avalanche at speeds up to v = 12 ms-1 by Lang and Dent (1984). While the Fast-Stop model stems from empirical origins, it appears that the essential ingredient in the mechanism of drag force reduction at mid-range speeds of avalanches warrants further consideration as a means of reducing the current wide range in the motion parameters associated with the hydro-dynamic flow representation of avalanches.
One objective in this study was to attempt to incorporate recently determined flow conditions into the fluid flow equations for snow avalanches. What was determined was that in starting with the hydrodynamic equation for uniform, steady flow, that conditions of material locking and bulk flow on an active boundary layer could not be incorporated in a distinctive way from the usual form of the equation. The basic property of Material Locking at low speed, known to be a property of granular flowing snow, cannot be accounted for in a "single block" model, wherein the shear locking stress coefficient reverts instead to the sliding friction term of the ordinary equation. Through this reversion the application of the locking stress τ having dependence upon the magnitude of the velocity gradient, the basic characteristic of a Bingham type fluid, is lost. Thus if account is to be taken of the somewhat unique flow properties of avalanching snow, a more refined flow model is needed than what is associated with uniform flow hydrodynamics.
In regard to the numerical aspects of this investigation, the segmentation of the avalanche path in the terminal part of the flow facilitated rapid determination of the location where the avalanche stops. This modification to the Cheng-Perla code resulted in an insignificant increment in computer running time, yet simplified the numerical algorithm.
Table 1. Friction And Dynamic Drag Coefficients And Maximum Velocities Of Three Avalanches.