List Of Symbols
-
Ā Complex conjugate value of A
-
α Coefficient of attenuation of the propagation of an acoustic wave through the snow
-
B Prandtl number
-
Cair Sound velocity in free air
-
Cv,Cp Specific heats
-
d Density
-
e Backing length
-
f Frequency
-
ϕ Phase of the characteristic impedance W of snow
-
γ Propagation constant
-
γm Propagation constant measured with impedance tube
-
h Acoustic porosity
-
hg Gravimetric porosity
-
Im (A) Imaginary part of A
-
j Imaginary unit
-
Ji Bessel’s function of order i
-
k Coefficient of structure
-
 Ratio of specific heats
Ratio of specific heats -
l Sample length
-
λ Wavelength in free air
-
λapp Apparent thermal conductivity
-
λh Thermal conductivity
-
λmin Minimal wavelength in air according to a planewave condition in a tube
-
p− Reflected component of p1
-
p+ Incident component of p1
-
Pi Fourier transform of acoustic pressure at microphone i
-
q Coefficient of tortuosity
-
R Pore radius
-
R2 Coefficient of determination
-
r Complex reflection coefficient at sample surface
-
ρ Volumetric mass
-
ρe Equivalent complex volumetric mass
Real(A) Real part of A
-
Rth Pore radius taking into account thermal effects
-
Rv Pore radius taking into account viscous effects
-
Sp Pore-shape ratio factor
-
υ Cinematic viscosity of air
-
W Characteristic impedance ratio with respect to the free-air wave impedance
-
ω Radian frequency
-
Wm Characteristic impedance ratio measured with the impedance tube
-
Z Sample normal acoustic impedance ratio

Introduction
In this paper, the notation of Reference Zwikker and Kosten.Zwikker and Kosten (1949) will be used. No derivations of the formulae will be given, because they can be found in Reference Zwikker and Kosten.Zwikker and Kosten (1949).
The experiments were performed to seek phenomenological relationships between acoustic parameters and snow density. For light snow (ρ < 300 kg m−3), Reference ŌuraŌura (1952) indicated that the air contained in the snow propagates the acoustic wave. His observations were confirmed by Reference IshidaIshida’s (1965) and Reference BuserBuser’s (1986) experiments. For the dense snow (400 kg m−3 ≤ ρ ≤ 900 kg m−3) of Greenland, Reference SmithSmith (1965) found a linear correlation between density and the longitudinal acoustic wave velocity in the ice frame. According to Reference Bogorodskiy, Gavrilo and Nitikin.Bogorodskiy and others (1974), Reference SommerfeldSommerfeld (1982) and Reference Lee and RogersLee and Rogers (1985), it seems clear that below 200 kg m−3, the pore air is more important in sound propagation, whereas above 300 kg m−3 propagation in the ice frame is more important. Reference JohnsonJohnson (1982) tried to explain this phenomenon by using the theory of Reference BiotBiot (1962) which predicts the existence of two longitudinal acoustic waves. They involve coupled motion between the interstitial air and the ice frame. Reference BuserBuser (1986) and Reference Attenborough and Buser.Attenborough and Buser (1988) suggested the rigid-frame model of porous media for snow when only the movement of pore air is of interest, which has been validated up to 400 kg m−3.
To measure the density of all sorts of snow, the method used by Reference SmithSmith (1965) would be the best if measurements of the longitudinal wave pressure in the frame did not require a perfect contact between the sensors and the ice grains of the skeleton. However, Reference Zephoris, Martin and Pontikis.Zephoris and others (1975) showed that this experimental constraint is very difficult to meet with light snow (ρ ≤ 300 kg m−3). For these densities, Reference Buser and Good.Buser and Good (1987) found that the acoustic porosity, h, a parameter of Zwikker’s and Kosten’s (1949, p. 18–21) rigid-frame model is identical to the gravimetric porosity up to a density of 400 kg m−3.
Our final goal is to find a method of measuring the density inside the body of a flowing dense avalanche where the density of the snow can reach 700 kg m−3.
In this paper, experiments were performed, first to seek a correlation between the density of dense snow (up to 680 kg m−3) and one of its acoustic parameters, and secondly to verify the validity of the rigid-frame model to describe acoustic waves in the pore air for this dense snow.
Experimental Procedure
The selection of snow samples and the method used to measure their acoustic parameters are the main aspects of the experimental procedure to be described.
Sampling
Naturally deposited snow density varies from 200 to 500 kg m−3. Snow is a porous medium in which the ice grains form a skeleton. The shape and the size of these grains vary according to the state of snow metamorphism and deposited snow density is not entirely independent of the ice-grain shape. Usually, light snow is a compound of fresh or branched snow and dense snow is composed of more rounded particles produced by metamorphosis. Sound propagation through snow pores may be influenced by the frame structure. In this study, snow samples of each kind were compacted mechanically to obtain 55 snow samples with ρ varying from 142 to 682 kg m−3 (Fig. 1). This sampling includes and extends that used by Reference BuserBuser (1986).

Fig. 1. Snow samples.
The snow samples have a diameter of 3 cm. Their thickness is between 6 and 4 cm when ρ < 400 kg m−3; and between 2 and 1 cm for dense snow.
To allow the snow-sample temperature to reach equili-brium with the cold-room temperature, the snow samples were prepared not less than 1 day before they were used for acoustic measurements. They were stored in a cold room at −10°C.
An hydraulic press was used to compact the snow in the cold room (1 mm min−1). This procedure (Fig. 2) provided homogeneous snow samples.

Fig. 2. The experimental procedure for preparing the compacting snow sample.
Acoustic measurements
The characteristic acoustic parameters of a material are W, the characteristic impedance ratio with respect to the free-air wave impedance, and γ, the propagation constant (see list of symbols). A two-microphone impedance-measurement tube was used. This method was developed by Reference Chung and Blaser.Chung and Blaser (1980a, Reference Chung and Blaser.b), and the associated error analysis was studied by Reference Seybert and Soenarko.Seybert and Soenarko (1980) and Reference Bodén and Åbom.Bodén and Åbom (1986).
The basic principle of the two-microphone method is to measure the acoustic pressure of a broad-band stationary random signal by microphones at two locations on the wall of the tube. After a Fourier transform, the acoustic pressure Spectra at microphone 1 and microphone 2 (Fig. 3) may be written as:

where f = w/2Π is a frequency for which there is a plane wave in the tube, pi is the Fourier transform of acoustic pressure at microphone i, p+ and p− are respectively the incident and reflected component of p1 and Cair is the speed of sound. Using the notation of Figure 3, the complex reflection coefficient at the surface of the sample is:

Using Equations (1) and (2), one obtains:

Then the normal acoustic impedance ratio Z is:
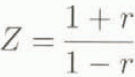
So, with only one measurement, the two-microphone method can give Z for each frequency of the plane-wave domain. To calculate W and γ, one needs two values of Z for different backing distances e. With the two-microphone method, it is impossible, for a random signal, to work with only one wavelength. To obtain W and γ one uses the basic equations:


with
Or,

So, Equation (8) implies

If one chooses 0 < e < λmin/2 (λmin is the smallest wavelength in air satisfying the condition for plane waves in the tube), one obtains from Equations (6) and (7):
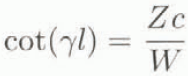

Fig. 3. The basic configuration of the two-microphone method.
The real part of W is positive and there is only one pair of complex solutions (W,γ).
For the experiments presented in this paper, we used Brüel and Kjær’s two-microphone impedance measurement tube type 4206 with the high-frequency tube (from 500 to 6.4 kHz). This tube is supplied with two specially designed ¼inch condenser microphones type 4187 with preamplifiers (type 2633) and application software BZ 5050. The measurement set-up is controlled by a Brüel and Kjær (1983) multi-channel analysis system. With this equipment, the time that the snow sample was in the sample holder was never longer than 10 minutes. This is important when investigating snow, even in a cold room at −10°C.
According to Reference BuserBuser’s (1986) work, the frequency range of interest is 500–4096 Hz. Zc and Z0 were calculated for 25 different frequencies with a step of 150 ± 2 Hz and e (Fig. 3) was taken equal to 0.01 m.
Relationship Between Density and the Acoustic Parameters of Snow
The acoustic properties of snow are defined by the two complex numbers, ![]() and
and ![]()
Four real numbers can be distinguished:
![]() and ϕ, respectively the modulus and the phase of the characteristic impedance W of the snow.
and ϕ, respectively the modulus and the phase of the characteristic impedance W of the snow.
α and C respectively the coefficient of attenuation and the velocity of propagation of an acoustic wave through snow.
Relationship between d and Respectively α and ϕ
Figures 4 and 5 show there is no straightforward relationship between density d and the coefficient of attenuation α of propagation of an acoustic wave through snow or the phase ϕ of the characteristic impedance ratio W of snow.

Fig. 4. Relation between density d and phase ϕ of the characteristic impedance ratio W; data from Reference BuserBuser (1986) (∎) and this study (Δ).

Fig. 5. Relation between density d and attenuation coefficient α; data from Reference BuserBuser (1986) (∎) and this study (Δ).
Relationship between d and c
The density is not the main explicative parameter of sound velocity. Measurements only show that the tendency of the velocity is to decrease when the density increases (Fig. 6). This can be explained by the fact that acoustic waves are propagated through the pores of the snow. The higher the density, the narrower and more tortuous the pores are. The scatter observed is caused by the shapes of the ice grains. The relation hetween d and C cannot be used to obtain an acceptable estimate of d from a measurement of C.

Fig. 6. Relation between density d and sound velocity C. o rounded particles; • compacted rounded particles: ○ small grains; ● compacted small grains: × branched snow; \ compacted branched snow; Δ depth hoar crystal; ○ wet snow.
Relationship between d and 
There is a very good relation between log ![]() and d (Fig. 7). One obtains:
and d (Fig. 7). One obtains:


Fig. 7. Relation between density d and the modulus of characteristic impedance ratio ![]() . ☐ this study; ∎ Reference BuserBuser (1986); ● ice grains in front of the surface of the sample; ▲ sample with a chipped surface.
. ☐ this study; ∎ Reference BuserBuser (1986); ● ice grains in front of the surface of the sample; ▲ sample with a chipped surface.
This relation indicates that the propagation of an acoustic wave through a snow sample cannot be compared to a phenomenon of percolation, because the propagation becomes impossible only when there are no pores in the snow (d = 1). This result does not depend on the quality of the surface of the sample.
The Rigid-Frame Model
Presentation
In this third part, the derivation of the theory developed by Reference Zwikker and Kosten.Zwikker and Kostcn (1949, p. 25–48), restated by Reference BuserBuser (1986) and Reference MarcoMarco (1994) and revised by Reference AttenboroughAttenborough (1982), will not be presented. According to this theory and the frequency range of interest, W and γ are given by the following mathematical expressions (Reference AttenboroughAttenborough, 1982):


Ji
is the Bessel’s function of order i; B is the Prandtl Number; K = Cv/Cp
is the ratio of specific heats; ![]() with V the kinematic viscosity of air included in the pores. The three parameters of this wave-propagation model are :
with V the kinematic viscosity of air included in the pores. The three parameters of this wave-propagation model are :
-
R. Average radius of pores compared to cylindrical uniform tubes which are not interconnected. One may also assume slits of uniform width. But according to Atten-borough and Reference BuserBuser (1988), significant variations in pore cross-sections along their length and between pores might require different values of R in the density and stiffness calculation. Attenborough suggested the use of 2sp R in place of R. Sp is frequency-dependent if the pores are non-cylindrical and has a constant value of 0.5 if the pores are cylindrical. Reference BuserBuser (1986) suggested that, if this model needs a fourth parameter, one has the possibility of considering two radii Rv and Rth, the first one for the viscous effects (taken into account by an equivalent complex density calculation) and the second one for the thermal effects (taken into account by an equivalent complex compressibility calculation).
-
h Acoustic porosity. In the equation of motion, this porosity is taken as air in the main pores per unit of volume (that means without closed or side holes where the air is at rest (Reference Zwikker and Kosten.Zwikker and Kosten, 1949, p. 19–21). For snow, up to 400 kg m−3, the value of the acoustic porosity parameter of this rigid-frame model is equal to the value of gravimetric porosity (= 1 – 1.09ρsnow/ρice ).
-
k Structure constant. According to Reference Zwikker and Kosten.Zwikker and Kosten (1949, p. 25–48), this parameter comes mainly from two effects. The structural properties of the material plays the most important part (orientation of the pores and ratio of the total air content to that of the main pores). The second effect can come from a possible light vibration of the small parts of the solid skeleton. This parameter is always greater than 1. Reference AttenboroughAttenborough (1982) replaced the structure constant by parameter q(= √k),, called tortuosity. In this paper the last parameter will be used.
Considering practical materials, Reference Zwikker and Kosten.Zwikker and Kosten (1949, p.25–48) also introduced a further constant, the apparent thermal conductivity λapp which is smaller than the real thermal conductivity λh(λapp/λh < 1). Similarly, we get an apparent Prandtl number Bapp with Bapp/B = λh/λapp. This assumption is equivalent to the use of two radii with Rv/Rth = λapp/λh. The meaning of this fourth parameter Rth or λapp is that the effects of viscosity, for a same pore, are more important than the thermal ones (Rth > Rv). For a medium consisting of spheres, situated on a cubic lattice, λapp/λh is constant and equal to 0.45 and independent of frequency radius of the spheres and porosity (Reference Zwikker and Kosten.Zwikker and Kosten, 1949, p.43).
In the first step, we obtain simultaneously the three parameters by fitting the frequency dependent W and γ.
Before each experiment, air pressure and temperature in the cold room are measured to calculate the speed of sound and characteristic impedance of the air. Then, functions W(q = 1,h = 1,R, f) and γ(q = 1, h = 1, R, f) are determined with Bequal to 0,86. Values issued from experiments, Wm(f) and γμ(f) are obtained for 25 frequencies. According to the least-squares fitting method, and assuming that the three parameters are independent of the frequency, the solution (h, q, R) must minimize the function S:

We obtain the functions q(R) and h(R) such that ∂S/∂h = 0 and ∂S/∂q = 0.


Real (A): real part of complex A.
Ā: complex conjugate value of A.
So, we need only one parameter R to minimize the function S(h(R),q(R), R). The mathematical software MAT-LAB of Scientific Software Group (Mathworks, 1994), has been used to fit R for each snow sample. Then, h and q are calculated easily.
Results
In another paper (Reference Marco, Buser and Villemain.Marco and others, 1996), we show that the rigid-frame model proposed by Reference Zwikker and Kosten.Zwikker and Kosten (1949) for porous media cannot explain the acoustic wave propagation through all snow types, especially not for dense snow. Certainly, one or more of its three parameters are not constant in the frequency range used.
The only interesting result for our problem is the very good correlation between the acoustic porosity h determined by minimising S and the gravimetric porosity hg
(Fig. 8). With the phenomenological relationship obtained between d and ![]() , the use of the three-parameter model seems not to be the most convenient way to determine the density of snow from measurements of its acoustic parameters.
, the use of the three-parameter model seems not to be the most convenient way to determine the density of snow from measurements of its acoustic parameters.

Fig. 8. Relation between acoustic porosity h and gravimetric porosity hg. □ this study; ■Reference BuserBuser (1986); Δ ice grains in front of the surface of the sample; O sample with a chipped surface.
Conclusion
From experiments in a cold laboratory, we found a good relationship between the density of snow and the modulus of its characteristic impedance. This estimate is much more convenient than the one obtained by using the existing three-parameter model describing the propagation of an acoustic wave through not very dense snow.
The main difficulties for conducting field measurements to determine density are the uncertainties associated with the experimental parameters. For example, the exact distance between the microphones and the surface of the snow sample has to be known. Unfortunately, this condition will be very difficult to fulfill for measurements inside the body of a flowing avalanche and even in a natural snow cover.












