Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-27T16:45:11.824Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral Analysis of Markov Kernels and Application to the Convergence Rate Of Discrete Random Walks

Part of: Markov processes Special classes of linear operators

Published online by Cambridge University Press:  22 February 2016

Loïc Hervé  and
James Ledoux
Loïc Hervé*
Affiliation:
INSA de Rennes
James Ledoux*
Affiliation:
INSA de Rennes
*
∗ Postal address: INSA de Rennes, IRMAR CNRS-UMR 6625, 20 avenue des Buttes de Coesmes, CS 70 839, 35708 Rennes cedex 7, France.
∗ Postal address: INSA de Rennes, IRMAR CNRS-UMR 6625, 20 avenue des Buttes de Coesmes, CS 70 839, 35708 Rennes cedex 7, France.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let {Xn}n∈ℕ be a Markov chain on a measurable space 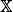with transition kernel P, and let 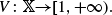The Markov kernel P is here considered as a linear bounded operator on the weighted-supremum space 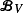associated with V. Then the combination of quasicompactness arguments with precise analysis of eigenelements of P allows us to estimate the geometric rate of convergence ρV(P) of {Xn}n∈ℕ to its invariant probability measure in operator norm on 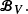A general procedure to compute ρV(P) for discrete Markov random walks with identically distributed bounded increments is specified.

Keywords

V-geometric ergodicityquasicompactnessdrift conditionbirth-and-death Markov chain

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 47B07: Operators defined by compactness properties
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 46 , Issue 4 , December 2014 , pp. 1036 - 1058
Copyright
© Applied Probability Trust 

References

Baxendale, P. H. (2005). Renewal theory and computable convergence rates for geometrically ergodic Markov chains. Ann. Appl. Prob. 15, 700–738.CrossRefGoogle Scholar
Guibourg, D., Hervé, L. and Ledoux, J. (2011). Quasi-compactness of Markov kernels on weighted-supremum spaces and geometrical ergodicity. Preprint. Available at http://uk.arxiv.org/abs/1110.3240.Google Scholar
Hennion, H. (1993). Sur un théorème spectral et son application aux noyaux lipchitziens. Proc. Amer. Math. Soc. 118, 627–634.Google Scholar
Hervé, L. and Ledoux, J. (2014). Approximating Markov chains and V-geometric ergodicity via weak perturbation theory. Stoch. Process. Appl. 124, 613–638.CrossRefGoogle Scholar
Hordijk, A. and Spieksma, F. (1992). On ergodicity and recurrence properties of a Markov chain with an application to an open Jackson network. Adv. Appl. Prob. 24, 343–376.CrossRefGoogle Scholar
Klimenok, V. and Dudin, A. (2006). Multi-dimensional asymptotically quasi-Toeplitz Markov chains and their application in queueing theory. Queueing Systems. 54, 245–259.CrossRefGoogle Scholar
Kontoyiannis, I. and Meyn, S. P. (2003). Spectral theory and limit theorems for geometrically ergodic Markov processes. Ann. Appl. Prob. 13, 304–362.CrossRefGoogle Scholar
Kontoyiannis, I. and Meyn, S. P. (2012). Geometric ergodicity and the spectral gap of non-reversible Markov chains. Prob. Theory Relat. Fields 154, 327–339.CrossRefGoogle Scholar
Kovchegov, Y. (2009). Orthogonality and probability: beyond nearest neighbor transitions. Electron. Commun. Prob. 14, 90–103.CrossRefGoogle Scholar
Lund, R. B. and Tweedie, R. L. (1996). Geometric convergence rates for stochastically ordered Markov chains. Math. Operat. Res. 21, 182–194.CrossRefGoogle Scholar
Malyshev, V. A. and Spieksma, F. M. (1995). Intrinsic convergence rate of countable Markov chains. Markov Process. Relat. Fields 1, 203–266.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1993). Markov Chains and Stochastic Stability. Springer, London.CrossRefGoogle Scholar
Meyn, S. P. and Tweedie, R. L. (1994). Computable bounds for geometric convergence rates of Markov chains. Ann. Appl. Prob. 4, 981–1011.CrossRefGoogle Scholar
Roberts, G. O. and Tweedie, R. L. (1999). Bounds on regeneration times and convergence rates for Markov chains. Stoch. Process. Appl. 80, 211–229. (Corrigendum: 91 (2001), 337–338.)CrossRefGoogle Scholar
Rosenthal, J. S. (1996). Markov chain convergence: from finite to infinite. Stoch. Process. Appl. 62, 55–72.CrossRefGoogle Scholar
Van Doorn, E. A. and Schrijner, P. (1995). Geometric ergodicity and quasi-stationarity in discrete-time birth–death processes. J. Austral. Math. Soc. B 37, 121–144.CrossRefGoogle Scholar
Wu, L. (2004). Essential spectral radius for Markov semigroups. I. Discrete time case. Prob. Theory Relat. Fields 128, 255–321.CrossRefGoogle Scholar