Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-07-05T23:14:30.267Z Has data issue: false hasContentIssue false
  • English
  • Français

Sentry Selection in Wireless Networks

Part of: Graph theory Equilibrium statistical mechanics Geometric probability and stochastic geometry

Published online by Cambridge University Press:  01 July 2016

Paul Balister ,
Béla Bollobás ,
Amites Sarkar  and
Mark Walters
Paul Balister*
Affiliation:
University of Memphis
Béla Bollobás*
Affiliation:
Trinity College Cambridge and University of Memphis
Amites Sarkar*
Affiliation:
Western Washington University
Mark Walters*
Affiliation:
Queen Mary, University of London
*
∗ Postal address: Department of Mathematical Sciences, University of Memphis, Dunn Hall, 3725 Norriswood, Memphis, TN 38152, USA. Email address: pbalistr@memphis.edu
∗∗ Postal address: Trinity College, Cambridge, CB2 1TQ, UK. Email address: b.bollobas@dpmms.cam.ac.uk
∗∗∗ Postal address: Department of Mathematics, Western Washington University, Bellingham, WA 98225, USA. Email address: amites.sarkar@wwu.edu
∗∗∗∗ Postal address: School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London, E1 4NS, UK. Email address: m.walters@qmul.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 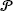be a Poisson process of intensity one in the infinite plane ℝ2. We surround each point x of 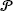by the open disc of radius r centred at x. Now let Sn be a fixed disc of area n, and let Cr(Sn) be the set of discs which intersect Sn. Write Erk for the event that Cr(Sn) is a k-cover of Sn, and Frk for the event that Cr(Sn) may be partitioned into k disjoint single covers of Sn. We prove that P(Erk ∖ Frk) ≤ ck / logn, and that this result is best possible. We also give improved estimates for P(Erk). Finally, we study the obstructions to k-partitionability in more detail. As part of this study, we prove a classification theorem for (deterministic) covers of ℝ2 with half-planes that cannot be partitioned into two single covers.

Keywords

Poisson processcoveragepartition

MSC classification

Primary: 05C80: Random graphs
Secondary: 60D05: Geometric probability and stochastic geometry 82B43: Percolation
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 42 , Issue 1 , March 2010 , pp. 1 - 25
Copyright
Copyright © Applied Probability Trust 2010 

Footnotes

Supported by NSF grant CCF-0728928.

Supported by ARO grant W911NF-06-1-0076, and NSF grants CNS-0721983, CCF-0728928, and DMS-0906634.

References

Arratia, R., Goldstein, L. and Gordon, L. (1989). Two moments suffice for poisson approximations: the Chen-Stein method. Ann. Prob. 17, 9–25.Google Scholar
Bollobás, B. (2001). Random Graphs, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Bollobás, B. (2006). The Art of Mathematics. Cambridge University Press.CrossRefGoogle Scholar
Gilbert, E. N. (1961). Random plane networks. J. Soc. Indust. Appl. Math. 9, 533–543.Google Scholar
Gilbert, E. N. (1965). The probability of covering a sphere with N circular caps. Biometrika 56, 323–330.Google Scholar
Hall, P. (1985). On the coverage of k-dimensional space by k-dimensional spheres. Ann. Prob. 13, 991–1002.Google Scholar
Janson, S. (1986). Random coverings in several dimensions. Acta Math. 156, 83–118.CrossRefGoogle Scholar
Kumar, S., Lai, T. H. and Balogh, J. (2004). On k-coverage in a mostly sleeping sensor network. In Proc. 10th Internat. Mobile Comput. Networking, ACM, New York, pp. 144–158.Google Scholar
Wan, P.-J. and Yi, C.-W. (2006). Coverage by randomly deployed wireless sensor networks. IEEE Trans. Inf. Theory 52, 2658–2669.Google Scholar
Zhang, H. and Hou, J. (2004). On deriving the upper bound of α-lifetime for large sensor networks. In Proc. 5th ACM Internat. Symp. Mobile Ad Hoc Network Comput., ACM, New York, pp. 121–132.Google Scholar