Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T04:38:14.057Z Has data issue: false hasContentIssue false
  • English
  • Français

Phenotypic diversity and population growth in a fluctuating environment

Part of: Markov processes Special processes

Published online by Cambridge University Press:  01 July 2016

Clément Dombry ,
Christian Mazza  and
Vincent Bansaye
Clément Dombry*
Affiliation:
Université de Poitiers
Christian Mazza*
Affiliation:
Université de Fribourg
Vincent Bansaye*
Affiliation:
École Polytechnique
*
∗ Postal address: Laboratoire de Mathématiques et Applications, Téléport 2-BP30179, Boulevard Pierre et Marie Curie, 86962 Futuroscope Chasseneuil Cedex, France. Email address: clement.dombry@math.univ-poitiers.fr
∗∗ Postal address: Département de Mathématique, Université de Fribourg, Chemin du Musée 23, CH-1700 Fribourg, Switzerland. Email address: christian.mazza@unifr.ch
∗∗∗ Postal address: CMAP, Ecole Polytechnique, Route de Saclay, 91128 Palaiseau Cedex, France. Email address: bansaye@polytechnique.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Organisms adapt to fluctuating environments by regulating their dynamics, and by adjusting their phenotypes to environmental changes. We model population growth using multitype branching processes in random environments, where the offspring distribution of some organism having trait t ∈ 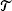in environment e ∈ ε is given by some (fixed) distribution ϒt,e on ℕ. Then, the phenotypes are attributed using a distribution (strategy) πt,e on the trait space 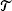. We look for the optimal strategy πt,e, t ∈ 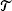, e ∈ ε, maximizing the net growth rate or Lyapounov exponent, and characterize the set of optimal strategies. This is considered for various models of interest in biology: hereditary versus nonhereditary strategies and strategies involving or not involving a sensing mechanism. Our main results are obtained in the setting of nonhereditary strategies: thanks to a reduction to simple branching processes in a random environment, we derive an exact expression for the net growth rate and a characterization of optimal strategies. We also focus on typical genealogies, that is, we consider the problem of finding the typical lineage of a randomly chosen organism.

Keywords

Branching process in a random environmentphenotypic diversityLyapounov exponentoptimal strategyextinctiontypical genealogy

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60K37: Processes in random environments
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 43 , Issue 2 , June 2011 , pp. 375 - 398
Copyright
Copyright © Applied Probability Trust 2011 

References

Afanasyev, V. I., Geiger, J., Kersting, G. and Vatutin, V. A. (2005). Criticality for branching processes in random environment. Ann. Prob. 33, 645–673.CrossRefGoogle Scholar
Athreya, K. B. and Karlin, S. (1971). On branching processes with random environments. I. Extinction probabilities. Ann. Math. Statist. 42, 1499–1520.CrossRefGoogle Scholar
Athreya, K. B. and Karlin, S. (1971). Branching processes with random environment. II. Limit theorems. Ann. Math. Statist. 42, 1843–1858.Google Scholar
Baake, E. and Georgii, H.-O. (2007). Mutation, selection, and ancestry in branching models: a variational approach. J. Math. Biol. 54, 257–303.Google Scholar
Bonnans, J. F., Gilbert, J. C., Lemaréchal, C. and Sagastizábal, C. A. (2006). Numerical Optimization, 2nd edn. Springer, Berlin.Google Scholar
Gander, M. J., Mazza, C. and Rummler, H. (2007). Stochastic gene expression in switching environments. J. Math. Biol. 55, 249–269.CrossRefGoogle ScholarPubMed
Geiger, J., Kersting, G. and Vatutin, V. A. (2003). Limit theorems for subcritical branching processes in random environment. Ann. Inst. H. Poincaré Prob. Statist. 39, 593–620.CrossRefGoogle Scholar
Georgii, H.-O. and Baake, E. (2003). Supercritical multitype branching processes: the ancestral types of typical individuals. Adv. Appl. Prob. 35, 1090–1110.Google Scholar
Haccou, P. and Iwasa, Y. (1995). Optimal mixed strategies in stochastic environments. Theoret. Pop. Biol. 47, 212–243.Google Scholar
Kussel, E. and Leibler, S. (2005). Phenotypic diversity, population growth and information in fluctuating environments. Science 309, 2075–2078.CrossRefGoogle Scholar
Smith, W. L. and Wilkinson, W. E. (1969). On branching processes in random environments. Ann. Math. Statist. 40, 814–827.Google Scholar
Tanny, D. (1977). Limit theorems for branching processes in a random environment. Ann. Prob. 5, 100–116.Google Scholar
Thattai, M. and van Oudenaarden, A. (2004). Stochastic gene expression in fluctuating environments. Genetics 167, 523–530.CrossRefGoogle ScholarPubMed
Visco, P., Allen, R. J., Majumda, S. N. and Evans, M.R. (2010). Switching and growth for microbial populations in catastrophic responsive environments. Preprint. Available at http://arxiv.org/abs/0908.1351v2.Google Scholar