Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Foster, Dean P.
and
Vohra, Rakesh V.
1989.
Probabilistic analysis of a heuristics for the dual bin packing problem.
Information Processing Letters,
Vol. 31,
Issue. 6,
p.
287.
Coffman, E.G.
Fayolle, G.
Jacquet, P.
and
Robert, P.
1990.
Largest-first sequential selection with a sum constraint.
Operations Research Letters,
Vol. 9,
Issue. 3,
p.
141.
Rhee, Wansoo
and
Talagrand, Michel
1991.
A note on the selection of random variables under a sum constraint.
Journal of Applied Probability,
Vol. 28,
Issue. 4,
p.
919.
Bruss, F. Thomas
and
Robertson, James B.
1991.
‘Wald's Lemma' for sums of order statistics of i.i.d. random variables.
Advances in Applied Probability,
Vol. 23,
Issue. 3,
p.
612.
Preater, J.
1994.
A Multiple Stopping Problem.
Probability in the Engineering and Informational Sciences,
Vol. 8,
Issue. 2,
p.
169.
Almeida, Rui
Gaver, Donald P.
and
Jacobs, Patricia A.
1995.
Simple probability models for assessing the value of information in defense against missile attack.
Naval Research Logistics,
Vol. 42,
Issue. 4,
p.
535.
Li, K.
1998.
Average-case performance analysis of an approximation algorithm for maximum subset sum using recurrence relations.
Computers & Mathematics with Applications,
Vol. 36,
Issue. 6,
p.
63.
Gnedin, Alexander V.
1999.
Sequential selection of an increasing subsequence from a sample of random size.
Journal of Applied Probability,
Vol. 36,
Issue. 4,
p.
1074.
Boshuizen, Frans A.
and
Kertz, Robert P.
1999.
Smallest-fit selection of random sizes under a sum constraint: weak convergence and moment comparisons.
Advances in Applied Probability,
Vol. 31,
Issue. 1,
p.
178.
Gnedin, Alexander V.
1999.
Sequential selection of an increasing subsequence from a sample of random size.
Journal of Applied Probability,
Vol. 36,
Issue. 4,
p.
1074.
Baryshnikov, Yuliy M.
and
Gnedin, Alexander V.
2000.
Sequential selection of an increasing sequence from a multidimensional random sample.
The Annals of Applied Probability,
Vol. 10,
Issue. 1,
Bruss, F.Thomas
and
Delbaen, Freddy
2001.
Optimal rules for the sequential selection of monotone subsequences of maximum expected length.
Stochastic Processes and their Applications,
Vol. 96,
Issue. 2,
p.
313.
Stanke, Mario
2004.
Sequential selection of random vectors under a sum constraint.
Journal of Applied Probability,
Vol. 41,
Issue. 01,
p.
131.
Bruss, F. Thomas
and
Delbaen, Freddy
2004.
A central limit theorem for the optimal selection process for monotone subsequences of maximum expected length.
Stochastic Processes and their Applications,
Vol. 114,
Issue. 2,
p.
287.
Arlotto, Alessandro
Gans, Noah
and
Steele, J. Michael
2014.
Markov Decision Problems Where Means Bound Variances.
Operations Research,
Vol. 62,
Issue. 4,
p.
864.
Feng, Tianke
and
Hartman, Joseph C.
2015.
The dynamic and stochastic knapsack Problem with homogeneous‐sized items and postponement options.
Naval Research Logistics (NRL),
Vol. 62,
Issue. 4,
p.
267.
Bruss, F. Thomas
and
Duerinckx, Mitia
2015.
Resource dependent branching processes and the envelope of societies.
The Annals of Applied Probability,
Vol. 25,
Issue. 1,
Peng, Peichao
and
Steele, J.
2016.
Sequential selection of a monotone subsequence from a random permutation.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 11,
p.
4973.
Goldenshluger, Alexander
Malinovsky, Yaakov
and
Zeevi, Assaf
2020.
A unified approach for solving sequential selection problems.
Probability Surveys,
Vol. 17,
Issue. none,
Arlotto, Alessandro
and
Xie, Xinchang
2020.
Logarithmic Regret in the Dynamic and Stochastic Knapsack Problem with Equal Rewards.
Stochastic Systems,
Vol. 10,
Issue. 2,
p.
170.
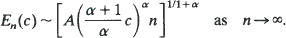 Asymptotics as c → ∞and n → ∞with c/n held fixed are derived, and connections with several closely related, well-known problems are brought out and discussed.
Asymptotics as c → ∞and n → ∞with c/n held fixed are derived, and connections with several closely related, well-known problems are brought out and discussed.



