Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-30T09:03:18.286Z Has data issue: false hasContentIssue false
  • English
  • Français

On the approximation of a ball by random polytopes

Part of: General convexity Geometric probability and stochastic geometry

Published online by Cambridge University Press:  01 July 2016

K.-H. Küfer
K.-H. Küfer*
Affiliation:
University of Kaiserslautern
*
* Postal address: Department of Mathematics, University of Kaiserslautern, Erwin-Schrödinger-Straße, Post Box 3049, D-67663 Kaiserslautern, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 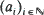be a sequence of independent and identically distributed random vectors drawn from the d-dimensional unit ball Bd and let Xn be the random polytope generated as the convex hull of a1,· ··, an. Furthermore, let Δ(Xn): = Vol (BdXn) be the volume of the part of the ball lying outside the random polytope. For uniformly distributed ai and 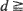2 we prove that the limiting distribution of Δ(Xn)/Ε (Δ (Xn)) for n → ∞ (satisfies a 0–1 law. In particular, we show that Var 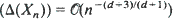for n → ∞. We provide analogous results for spherically symmetric distributions in Bd with regularly varying tail. In addition, we indicate similar results for the surface area and the number of facets of Xn.

Keywords

STOCHASTIC APPROXIMATIONCONVEX HULLVARIANCELIMITING DISTRIBUTION

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 52A22: Random convex sets and integral geometry
Type
Research Article
Information
Advances in Applied Probability , Volume 26 , Issue 4 , December 1994 , pp. 876 - 892
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bárány, I. and Larman, D. G. (1988) Convex bodies, economic cap covering, random polytopes. Mathematika 35 274–291.CrossRefGoogle Scholar
[2] Bárány, I. (1989) Intrinsic volumes and f-vectors of random polytopes. Math. Ann. 285, 671–699.CrossRefGoogle Scholar
[3] Buchta, C. (1985) Zufällige Polyeder–eine übersicht. In Zahlentheoretische Analysis. Seminar. ed. Hlawka, et al. Lecture Notes in Mathematics 1114, Springer-Verlag, New York.Google Scholar
[4] Carnal, H. (1970) Die konvexe Hülle von n rotationssymmetrisch verteilten Punkten. Z. Wahrscheinlichkeitsth. 15, 168–179.Google Scholar
[5] Dwyer, R. A. (1991) Convex hulls of samples from spherically symmetric distributions. Discrete Appl. Math. 31, 113–132.Google Scholar
[6] Groeneboom, P. (1988). Limit theorems for convex hulls. Prob. Theory Rel Fields 79, 327–368.Google Scholar
[7] Gruber, P. M. (1982) Approximation of convex bodies by polytopes. Rend. Circ. Mat. Palermo 3, 195–225.Google Scholar
[8] Hueter, I. (1992) The Convex Hull of n Random Points and its Vertex Process. Dissertation, Universität Bern.Google Scholar
[9] Müller, J. S. (1990) Approximation of a ball by random polytopes. J. Approximation Theory 63, 198–209.CrossRefGoogle Scholar
[10] Raynaud, H. (1970) Sur le comportement asymptotique de l'enveloppe convexe d'un nuage des points tirés au hazard dans. J. Appl. Prob. 7, 35–48.Google Scholar
[11] Rényi, A. and Sukanke, R. (1963) über die knovexe Hülle von n zufällig gewählten Punkten I. Z. Wahrscheinlichkeitsth. 2, 76–84.Google Scholar
[12] Schneider, R. (1988) Random approximation of convex sets. J. Microscopy 151, 211–227.CrossRefGoogle Scholar
[13] Weil, W. and Wieacker, J. A. (1993) Stochastic geometry. In Handbook of Convex Geometry, ed. Gruber, P. M. and Wills, J. M.. North-Holland, Amsterdam.Google Scholar
[14] Wendel, J. (1962) A problem in geometric probability. Math. Scand. 11, 109–111.Google Scholar
[15] Wieacker, J. A. (1978) Einige Probleme der polyedrischen Approximation. Diplomarbeit, Albert-Ludwigs-Universität Freiburg i.B.Google Scholar