Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rahimov, I.
2008.
Asymptotic distribution of the CLSE in a critical process with immigration.
Stochastic Processes and their Applications,
Vol. 118,
Issue. 10,
p.
1892.
Rahimov, I.
2008.
Asymptotically Normal Estimators for the Offspring Mean in the Branching Process with Immigration.
Communications in Statistics - Theory and Methods,
Vol. 38,
Issue. 1,
p.
13.
Rahimov, I.
2009.
Asymptotic distributions for weighted estimators of the offspring mean in a branching process.
TEST,
Vol. 18,
Issue. 3,
p.
568.
Rahimov, I.
2009.
Bootstrap of the offspring mean in the critical process with a non-stationary immigration.
Stochastic Processes and their Applications,
Vol. 119,
Issue. 11,
p.
3939.
Rahimov, Ibrahim
2010.
Workshop on Branching Processes and Their Applications.
Vol. 197,
Issue. ,
p.
121.
Ispány, Márton
and
Pap, Gyula
2010.
Workshop on Branching Processes and Their Applications.
Vol. 197,
Issue. ,
p.
135.
Rahimov, I.
2011.
Estimation of the offspring mean in a supercritical branching process with non-stationary immigration.
Statistics & Probability Letters,
Vol. 81,
Issue. 8,
p.
907.
Rahimov, I.
and
Omar, M. H.
2011.
Validity of the bootstrap in the critical process with a non-stationary immigration.
Journal of Nonparametric Statistics,
Vol. 23,
Issue. 1,
p.
1.
Rahimov, I.
2012.
Conditional Least Squares Estimators for the Offspring Mean in a Subcritical Branching Process with Immigration.
Communications in Statistics - Theory and Methods,
Vol. 41,
Issue. 12,
p.
2096.
RAHIMOV, IBRAHIM
and
YANEV, GEORGE P.
2012.
Variance Estimators in Critical Branching Processes With Non-Homogeneous Immigration.
Mathematical Population Studies,
Vol. 19,
Issue. 4,
p.
188.
Khusanbaev, Ya. M.
2013.
On the Asymptotic Behavior of a Subcritical Branching Process with Immigration.
Ukrainian Mathematical Journal,
Vol. 65,
Issue. 6,
p.
928.
Guo, Hongsong
and
Zhang, Mei
2014.
A fluctuation limit theorem for a critical branching process with dependent immigration.
Statistics & Probability Letters,
Vol. 94,
Issue. ,
p.
29.
Khusanbaev, Yakubdzhan Mukhamadzhanovich
2016.
Об асимптотике ветвящихся процессов с иммиграцией.
Дискретная математика,
Vol. 28,
Issue. 1,
p.
113.
Khusanbaev, Yakubdzhan M.
2017.
On asymptotics of branching processes with immigration.
Discrete Mathematics and Applications,
Vol. 27,
Issue. 2,
Rahimov, Ibrahim
2021.
Homogeneous Branching Processes with Non-Homogeneous Immigration.
Stochastics and Quality Control,
Vol. 36,
Issue. 2,
p.
165.
Barczy, Mátyás
Bezdány, Dániel
and
Pap, Gyula
2021.
A note on asymptotic behavior of critical Galton–Watson processes with immigration.
Involve, a Journal of Mathematics,
Vol. 14,
Issue. 5,
p.
871.
Barreto‐Souza, Wagner
and
Chan, Ngai Hang
2024.
Nearly unstable integer‐valued ARCH process and unit root testing.
Scandinavian Journal of Statistics,
Vol. 51,
Issue. 1,
p.
402.
Rahimov, I.
and
Sharipov, S.O.
2024.
On deterministic approximation for nearly critical branching processes with dependent immigration.
Statistics & Probability Letters,
Vol. 208,
Issue. ,
p.
110031.
Sharipov, Sadillo Olimjonovich
2024.
Функциональная предельная теорема для критического ветвящегося процесса со слабо зависимой иммиграцией.
Дискретная математика,
Vol. 36,
Issue. 1,
p.
136.
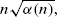 where α(n) denotes the mean number of immigrating individuals in the nth generation.
where α(n) denotes the mean number of immigrating individuals in the nth generation.



