Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-24T12:02:03.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical sponge dimensions in percolation theory

Published online by Cambridge University Press:  01 July 2016

G. R. Grimmett
G. R. Grimmett*
Affiliation:
University of Bristol
*
∗Postal address: School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, U.K.
Get access Rights & Permissions [Opens in a new window]

Abstract

In the bond percolation process on the square lattice, with 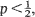let S(k) be the probability that some open path joins the longer sides of a sponge with dimensions k by a log k. There exists a positive constant α = αp such that 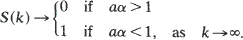Consequently, the subset of the square lattice {(x, y):0 ≦ y ≦ f(x)} which lies between the curve y = f(x) and the x-axis has the same critical probability as the square lattice itself if and only if f(x)/log x → ∞ as x → ∞.

Keywords

PERCOLATION
Type
Research Article
Information
Advances in Applied Probability , Volume 13 , Issue 2 , June 1981 , pp. 314 - 324
Copyright
Copyright © Applied Probability Trust 1981 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aizenmann, M., Delyon, F. and Souillard, B. (1980) Lower bounds on the cluster size distribution. J. Statist. Phys. 23, 267–280.CrossRefGoogle Scholar
Cox, J. T. and Grimmett, G. R. (1981) Central limit theorems for percolation models. J. Statist. Phys. CrossRefGoogle Scholar
Grimmett, G. R. (1981) On the differentiability of the number of clusters per vertex in the percolation model. J. London Math. Soc. CrossRefGoogle Scholar
Hammersley, J. M. (1962) Generalization of the fundamental theorem of subadditive functions. Proc. Camb. Phil. Soc. 58, 235–238.CrossRefGoogle Scholar
Kesten, H. (1980a) On the time constant and path length of first-passage percolation. Adv. Appl. Prob. 12, 848–863.CrossRefGoogle Scholar
Kesten, H. (1980b) The critical probability of bond percolation on the square lattice equals ½. Commun. Math. Phys. 74, 41–59.CrossRefGoogle Scholar
Kunz, H. and Souillard, B. (1978) Essential singularity in percolation problems and asymptotic behaviour of cluster size distribution. J. Statist. Phys. 19, 77–106.CrossRefGoogle Scholar
McDiarmid, C. J. H. (1980) Percolation on subsets of the square lattice. J. Appl. Prob. 17, 278–283.CrossRefGoogle Scholar
Russo, L. (1978) A note on percolation. Z. Wahrscheinlichkeitsth. 43, 39–48.CrossRefGoogle Scholar
Seymour, P. D. and Welsh, D. J. A. (1978) Percolation probabilities on the square lattice. Ann. Discrete Math. 3, 227–245.CrossRefGoogle Scholar
Smythe, R. T. and Wierman, J. C. (1978) First Passage Percolation on the Square Lattice. Lecture Notes in Mathematics 671, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Wierman, J. C. (1978) On critical probabilities in percolation theory. J. Math. Phys. 19, 1979–1982.CrossRefGoogle Scholar
Wierman, J. C. (1981) Bond percolation on honeycomb and triangular lattices. Adv. Appl. Prob. 13, 298–313.CrossRefGoogle Scholar