Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-28T14:23:51.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of stochastic processes by stochastic integrals

Published online by Cambridge University Press:  01 July 2016

B. L. S. Prakasa Rao
B. L. S. Prakasa Rao*
Affiliation:
Indian Statistical Institute, New Delhi
*
∗Postal address: Indian Statistical Institute, 7, S. J. S. Sansanwal Marg, New Delhi-110016, India.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 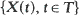be a continuous homogeneous stochastic process with independent increments. A review of the recent work on the characterization of Wiener and stable processes and connected results through stochastic integrals is presented. No proofs are given but appropriate references are mentioned.

Keywords

WIENER PROCESSSTABLE PROCESSESDOUBLE STOCHASTIC INTEGRALPROCESSES DETERMINED BY THEIR STOCHASTIC INTEGRALSCHARACTERIZATION
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 1 , March 1983 , pp. 81 - 98
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Kagan, A., Linnik, Yu. V. and Rao, C. R. (1973) Characterisation Problems in Mathematical Statistics. Wiley, New York.Google Scholar
Kannan, D. (1972a) An operator-valued stochastic integral II. Ann. Inst. H. Poincaré B 8, 9–32.Google Scholar
Kannan, D. (1972b) An operator-valued stochastic integral III. Ann. Inst. H. Poincaré B 8, 217–228.Google Scholar
Kannan, D. and Bharucha-Reid, A. T. (1971) An operator-valued stochastic integral Proc. Japanese Acad. 47, 472–476.Google Scholar
Lukacs, E. (1967) Some results in the theory of Wiener integrals. Trans. 4th Prague Conf. Inf. Theory, 29–43.Google Scholar
Lukacs, E. (1969) A characterization of stable processes. J. Appl. Prob. 6, 409–418.Google Scholar
Lukacs, E. (1970a) Characteristic Functions, 2nd edn. Griffin, London.Google Scholar
Lukacs, E. (1970b) Characterization theorems for certain stochastic processes. Rev. Internat. Statist. Inst. 38, 333–342.Google Scholar
Lukacs, E. (1975) Stochastic Convergence, 2nd edn. Academic Press, New York.Google Scholar
Lukacs, E. (1977) A stability theorem for a characterization of the Wiener process. Trans. 7th Prague Conf. 375–390.Google Scholar
Parthasarathy, K. R. (1967) Probability Measures on Metric Spaces. Academic Press, New York.Google Scholar
Prakasa Rao, B. L. S. (1968) On a characterization of symmetric stable processes with finite mean. Ann. Math. Statist. 39, 1498–1501.Google Scholar
Prakasa Rao, B. L. S. (1970) On a characterization of the Wiener process by constant regression. Ann. Math. Statist. 41, 321–325.Google Scholar
Prakasa Rao, B. L. S. (1971) Some characterization theorems for Wiener processes in a Hilbert space. Z. Wahrscheinlichkeitsth. 19, 103–116.Google Scholar
Prakasa Rao, B. L. S. (1972) Characterization of Wiener process by symmetry. Sankhya A 34, 227–234.Google Scholar
Prakasa Rao, B. L. S. (1975) Characterisation of stochastic processes determined up to shift. Theory Prob. Appl. 20, 623–626.Google Scholar
Prakasa Rao, B. L. S. (1982) On a characterisation of symmetric stable process.Google Scholar
Ramachandran, B. and Rao, C. R. (1970) Solutions of functional equations arising in some regression problems and a characterization of the Cauchy law. Sankhya A 32, 1–31.Google Scholar
Riedel, M. (1980a) Representation of the characteristic function of a stochastic integral. J. Appl. Prob. 17, 448–455.Google Scholar
Riedel, M. (1980b) Characterization of stable processes by identically distributed stochastic integrals. Adv. Appl. Prob. 12, 689–709.Google Scholar
Riedel, M. (1980c) Determination of a stochastic process by means of stochastic integrals. Teor. Veroyat. Primen. 15, 339–349.Google Scholar
Skitovich, V. P. (1956) On a characterization of Brownian motion. Theory Prob. Appl. 1, 326–328.Google Scholar
Vakhaniya, N. N. and Kandelski, N. P. (1967) A stochastic integral for operator-valued functions. Theory Prob. Appl. 12, 525–528.Google Scholar
Wang, Y. (1974) A note on homogeneous processes with independent increments. Ann. Inst. Statist. Math. 26, 356–360.CrossRefGoogle Scholar
Wang, Y. (1975) Characterization of some stochastic processes. Ann. Prob. 3, 1038–1045.Google Scholar
Zinger, A. A. and Linnik, Yu. V. (1970) Nonlinear statistics and random linear forms. Proc. Steklov Inst. Math. 111, 25–44.Google Scholar