Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-25T01:05:02.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics of First-Passage Percolation on One-Dimensional Graphs

Part of: Special processes

Published online by Cambridge University Press:  04 January 2016

Daniel Ahlberg
Daniel Ahlberg*
Affiliation:
University of Gothenburg and Chalmers University of Technology
*
∗ Current address: IMPA, Estrada Dona Castorina 110, 22460-320 Rio de Janeiro, Brazil. Email address: ahlberg@impa.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider first-passage percolation on certain one-dimensional periodic graphs, such as the 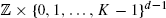nearest neighbour graph for d, K ≥ 1. We expose a regenerative structure within the first-passage process, and use this structure to show that both length and weight of minimal-weight paths present a typical one-dimensional asymptotic behaviour. Apart from a strong law of large numbers, we derive a central limit theorem, a law of the iterated logarithm, and a Donsker theorem for these quantities. In addition, we prove that the mean and variance of the length and weight of minimizing paths are monotone in the distance between their end-points, and further show how the regenerative idea can be used to couple two first-passage processes to eventually coincide. Using this coupling we derive a 0–1 law.

Keywords

First-passage percolationrenewal theoryclassical limit theorem

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60K05: Renewal theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 47 , Issue 1 , March 2015 , pp. 182 - 209
Copyright
© Applied Probability Trust 

References

Ahlberg, D. (2008). Asymptotics of first-passage percolation on 1-dimensional graphs. , University of Gothenburg.Google Scholar
Ahlberg, D. (2011). Asymptotics and dynamics in first-passage and continuum percolation. , University of Gothenburg. Available at http://gupea.ub.gu.se/handle/2077/26666.Google Scholar
Ahlberg, D. (2013). A Hsu–Robbins–Erdős strong law in first-passage percolation. Ann. Prob. To appear.Google Scholar
Athreya, K. B. and Ney, P. E. (1972). “Branching Processes. “Springer, New York.CrossRefGoogle Scholar
Benaïm, M. and Rossignol, R. (2006). “A modified Poincaré inequality and its application to first passage percolation.” Preprint. Available at http://uk.arxiv.org/abs/0602496.Google Scholar
Benjamini, I., Kalai, G. and Schramm, O. (2003). “First passage percolation has sublinear distance variance.” Ann. Prob. 31, 1970–1970.Google Scholar
Chatterjee, S. and Dey, P. S. (2013). “Central limit theorem for first-passage percolation time across thin cylinders.” Prob. Theory Relat. Fields 156, 613–663.Google Scholar
Cox, J. T. and Durrett, R. (1981). “Some limit theorems for percolation processes with necessary and sufficient conditions.” Ann. Prob. 9, 583–603.Google Scholar
Damron, M., Hanson, J. and Sosoe, P. (2013). “Sublinear variance in first-passage percolation for general distributions.“Prob. Theory Relat. Fields. To appear.Google Scholar
Durrett, R. (2010). “Probability: Theory and Examples, 4th edn. Cambridge University Press.CrossRefGoogle Scholar
Flaxman, A., Gamarnik, D. and Sorkin, G. B. (2011). “First-passage percolation on a ladder graph, and the path cost in a VCG auction.” Random Structures Algorithms 38, 350–364.CrossRefGoogle Scholar
Gouéré, J.-B. (2014). “Monotonicity in first-passage percolation.” ALEA, Lat. Am. J. Prob. Math. Stat. 11, 565–569.Google Scholar
Grimmett, G. R. and Kesten, H. (2012). “Percolation since Saint-Flour.“In Percolation Theory at Saint-Flour, Springer, Heidelberg, pp. ix–xxvii.Google Scholar
Gut, A. (2009). “Stopped Random Walks: Limit Theorems and Applications, 2nd edn. Springer, New York.Google Scholar
Hammersley, J. M. and Welsh, D. J. A. (1965). “First-passage percolation, subadditive processes, stochastic networks, and generalized renewal theory.“In Proc. Internat. Res. Semin., Statist. Lab., Univ. California, Berkeley, CA, Springer, New York, pp. 61–110.Google Scholar
Howard, C. D. (2004). “Models of first-passage percolation.“In Probability on Discrete Structures (Encyclopaedia Math. Sci. 110), Springer, Berlin, pp. 125–173.Google Scholar
Kesten, H. (1986). “Aspects of first passage percolation.“In École d'été de probabilités de Saint-Flour, XIV—1984 (Lecture Notes Math. 1180), Springer, Berlin, pp. 125–264.CrossRefGoogle Scholar
Kesten, H. (1993). “On the speed of convergence in first-passage percolation.” Ann. Appl. Prob. 3, 296–338.CrossRefGoogle Scholar
Kesten, H. and Zhang, Y. (1997). “A central limit theorem for “critical” first-passage percolation in two dimensions.” Prob. Theory Relat. Fields 107, 137–160.Google Scholar
Kingman, J. F. C. (1968). “The ergodic theory of subadditive stochastic processes.” J. R. Statist. Soc. B 30, 499–510.Google Scholar
Lindvall, T. (2002). “Lectures on the Coupling Method. “Dover, Mineola, NY.Google Scholar
Newman, C. M. and Piza, M. S. T. (1995). “Divergence of shape fluctuations in two dimensions.” Ann. Prob. 23, 977–1005.Google Scholar
Pemantle, R. and Peres, Y. (1994). “Planar first-passage percolation times are not tight.“In Probability and Phase Transition (Cambridge, 1993; NATO Adv. Sci. Inst. C Math. Phys. Sci. 420), Kluwer, Dordrecht, pp. 261–264.Google Scholar
Renlund, H. (2010). “First-passage percolation with exponential times on a ladder.” Combin. Prob. Comput. 19, 593–601.Google Scholar
Renlund, H. (2012). “First-passage percolation on ladder-like graphs with inhomogeneous exponential times.” J. Numer. Math. Stoch. 4, 79–103.Google Scholar
Richardson, D. (1973). “Random growth in a tessellation.” Proc. Camb. Philos. Soc. 74, 515–528.Google Scholar
Schlemm, E. (2009). “First-passage percolation rates on width-two stretches with exponential link weights.” Electron. Commun. Prob. 14, 424–434.Google Scholar
Schlemm, E. (2011). “On the Markov transition kernels for first passage percolation on the ladder.” J. Appl. Prob. 48, 366–388.Google Scholar
Van den Berg, J. (1983). “A counterexample to a conjecture of J. M. Hammersley and D. J. A. Welsh concerning first-passage percolation.” Adv. Appl. Prob. 15, 465–467.Google Scholar