No CrossRef data available.
Article contents
Optimal drift rate control and two-sided impulse control for a Brownian system with the long-run average criterion
Published online by Cambridge University Press: 31 July 2024
Abstract
In this paper, we consider a joint drift rate control and two-sided impulse control problem in which the system manager adjusts the drift rate as well as the instantaneous relocation for a Brownian motion, with the objective of minimizing the total average state-related cost and control cost. The system state can be negative. Assuming that instantaneous upward and downward relocations take a different cost structure, which consists of both a setup cost and a variable cost, we prove that the optimal control policy takes an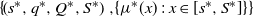 
$\left\{ {\!\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right),\!\left\{ {{\mu ^{\ast}}(x)\,:\,x \in [ {{s^{\ast}},{S^{\ast}}}]} \right\}} \right\}$ form. Specifically, the optimal impulse control policy is characterized by a quadruple 
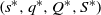$\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$, under which the system state will be immediately relocated upwardly to 
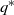${q^{\ast}}$ once it drops to 
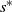${s^{\ast}}$ and be immediately relocated downwardly to 
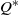${Q^{\ast}}$ once it rises to 
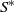${S^{\ast}}$; the optimal drift rate control policy will depend solely on the current system state, which is characterized by a function 
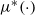${\mu ^{\ast}}\!\left( \cdot \right)$ for the system state staying in 
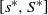$[ {{s^{\ast}},{S^{\ast}}}]$. By analyzing an associated free boundary problem consisting of an ordinary differential equation and several free boundary conditions, we obtain these optimal policy parameters and show the optimality of the proposed policy using a lower-bound approach. Finally, we investigate the effect of the system parameters on the optimal policy parameters as well as the optimal system’s long-run average cost numerically.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust
References
Adkins, W. A. and Davidson, M. G. (2012). Ordinary Differential Equations. Undergraduate Texts in Mathematics. Springer, New York.Google Scholar
Ata, B., Harrison, J. M. and Shepp, L. A. (2005). Drift rate control of a Brownian processing system. The Annals of Applied Probability 15, 1145–1160.CrossRefGoogle Scholar
Ata, B., Lee, D. and Sönmez, E. (2019). Dynamic volunteer staffing in multicrop gleaning operations. Operations Research 67, 295–314.Google Scholar
Ata, B. and Olsen, T. L. (2009). Near-optimal dynamic lead-time quotation and scheduling under convex-concave customer delay costs. Operations Research 57, 753–768.CrossRefGoogle Scholar
Ata, B. and Tongarlak, M. H. (2013). On scheduling a multiclass queue with abandonments under general delay costs. Queueing Systems 74, 65–104.CrossRefGoogle Scholar
Bather, J. A. (1966). A continuous time inventory model. Journal of Applied Probability 3, 538–549.CrossRefGoogle Scholar
Cao, P. and Yao, D. (2018). Optimal drift rate control and impulse control for a stochastic inventory/production system. SIAM Journal on Control and Optimization 56, 1856–1883.CrossRefGoogle Scholar
Chen, H., Wu, O. Q. and Yao, D. (2010). On the benefit of inventory-based dynamic pricing strategies. Production and Operations Management 19, 249–260.CrossRefGoogle Scholar
Chen, H. and Yao, D. D. (2001). Fundamentals of Queueing Networks: Performance, Asymptotics, and Optimization. Springer, New York.CrossRefGoogle Scholar
Dai, J. G. and Yao, D. (2013). Brownian inventory models with convex holding cost, part 1: average-optimal controls. Stochastic Systems 3, 442–499.CrossRefGoogle Scholar
Demarzo, P. M. and Sannikov, Y. (2006). Optimal security design and dynamic capital structure in a continuous-time agency model. Journal of Finance 61, 2681–2724.CrossRefGoogle Scholar
Fleming, W. H. and Soner, H. M. (2006). Controlled Markov Processes and Viscosity Solutions. Springer, USA.Google Scholar
Gao, X. and Huang, J. (2023). Asymptotically optimal control of make-to-stock systems. Mathematics of Operations Research.CrossRefGoogle Scholar
Ghosh, A. P. and Weerasinghe, A. P. (2007). Optimal buffer size for a stochastic processing network in heavy traffic. Queueing Systems 55, 147–159.CrossRefGoogle Scholar
Halfin, S. and Whitt, W. (1981). Heavy-traffic limits for queues with many exponential servers. Operations Research 29, 567–588.CrossRefGoogle Scholar
Harrison, J. M. and López, M. J. (1999). Heavy traffic resource pooling in parallel-server systems. Queueing Systems 33, 339–368.CrossRefGoogle Scholar
Harrison, J. M., Sellke, T. M. and Taksar, M. I. (1983). Impulse control of Brownian motion. Mathematics of Operations Research 8, 454–466.CrossRefGoogle Scholar
He, S., Yao, D. and Zhang, H. (2017). Optimal ordering policy for inventory systems with quantity-dependent setup costs. Mathematics of Operations Research 42, 979–1006.CrossRefGoogle Scholar
Hsieh, P.-F. and Sibuya, Y. (1999). Basic Theory of Ordinary Differential Equations. Universitext. Springer, New York.Google Scholar
Jack, A. and Zervos, M. (2006). Impulse and absolutely continuous ergodic control of one-dimensional Itô diffusions. In From Stochastic Calculus to Mathematical Finance: The Shiryaev Festschrift, eds. Y. Kabanov, R. Liptser, and J. Stoyanov, Springer, Berlin, pp. 295–314.CrossRefGoogle Scholar
Jack, A. and Zervos, M. (2006). Impulse control of one-dimensional Itô diffusions with an expected and a pathwise ergodic criterion. Applied Mathematics and Optimization 54, 71–93.CrossRefGoogle Scholar
Ke, T. T., Shen, Z.-J. M. and Villas-Boas, J. M. (2016). Search for information on multiple products. Management Science 62, 3576–3603.CrossRefGoogle Scholar
Koçağa, Y. L. (2017). An approximating diffusion control problem for dynamic admission and service rate control in a G/M/N+G queue. Operations Research Letters 45, 538–542.CrossRefGoogle Scholar
Kumagai, S. (1980). An implicit function theorem: Comment. Journal of Optimization Theory and Applications 31, 285–288.CrossRefGoogle Scholar
Ormeci, M., Dai, J. G. and Vande Vate, J. (2008). Impulse control of Brownian motion: the constrained average cost case. Operations Research 56, 618–629.CrossRefGoogle Scholar
Ormeci Matoglu, M. and Vande Vate, J. (2011). Drift control with changeover costs. Operations Research 59, 427–439.CrossRefGoogle Scholar
Ormeci Matoglu, M. and Vande Vate, J. (2015). Solving the drift control problem. Stochastic Systems 5, 324–371.CrossRefGoogle Scholar
Ormeci Matoglu, M., Vande Vate, J. and Yu, H. (2019). The economic average cost Brownian control problem. Advances in Applied Probability 51, 300–337.CrossRefGoogle Scholar
Rubino, M. and Ata, B. (2009). Dynamic control of a make-to-order, parallel-server system with cancellations. Operations Research 57, 94–108.CrossRefGoogle Scholar
Sun, X. and Zhu, X. (2022). Dynamic control of a make-to-order system under model uncertainty. Working Paper.Google Scholar
Vande Vate, J. H. (2021). Average cost Brownian drift control with proportional changeover costs. Stochastic Systems 11, 218–263.CrossRefGoogle Scholar
Xu, F., Yao, D. and Zhang, H. (2021). Impulse control with discontinuous setup costs: discounted cost criterion. SIAM Journal on Control and Optimization 59, 267–295.CrossRefGoogle Scholar
Yamazaki, K. (2017). Inventory control for spectrally positive Lévy demand processes. Mathematics of Operations Research 42, 212–237.CrossRefGoogle Scholar
Yao, D. (2017). Joint pricing and inventory control for a stochastic inventory system with Brownian motion demand. IISE Transactions 49, 1101–1111.CrossRefGoogle Scholar
Zhang, H. and Zhang, Q. (2012). An Optimal Inventory-Price Coordination Policy, Vol. 1, Stochastic Process, Finance and Control, Advances in Statistics, Probability and Actuarial Science, eds. S. N. Cohen, D. Madan, T. K. Siu and H. Yang, pp. 571–585.CrossRefGoogle Scholar
Zhu, J. Y. (2013). Optimal contracts with shirking. Review of Economic Studies 80, 812–839.CrossRefGoogle Scholar