No CrossRef data available.
Article contents
First displacement time of a tagged particle in a stochastic cluster in a simple exclusion process with random slow bonds
Published online by Cambridge University Press: 03 September 2019
Abstract
We consider the nearest-neighbour simple exclusion process on the one-dimensional discrete torus 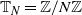 $\mathbb{T}_N=\mathbb{Z}/N\mathbb{Z}$
, with random rates
$\mathbb{T}_N=\mathbb{Z}/N\mathbb{Z}$
, with random rates 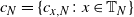 $c_N=\{c_{x,N}\colon x \in \mathbb{T}_N\}$
defined in terms of a homogeneous Poisson process on
$c_N=\{c_{x,N}\colon x \in \mathbb{T}_N\}$
defined in terms of a homogeneous Poisson process on 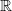 $\mathbb{R}$
with intensity
$\mathbb{R}$
with intensity 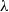 $\lambda$
. Given a realization of the Poisson process, the jump rate along the edge
$\lambda$
. Given a realization of the Poisson process, the jump rate along the edge 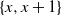 $\{x,x+1\}$
is 1 if there is not any Poisson mark in
$\{x,x+1\}$
is 1 if there is not any Poisson mark in 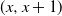 $ (x,x+1) $
; otherwise, it is
$ (x,x+1) $
; otherwise, it is 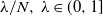 $\lambda/N,\, \lambda \in( 0,1]$
. The density profile of this process with initial measure associated to an initial profile
$\lambda/N,\, \lambda \in( 0,1]$
. The density profile of this process with initial measure associated to an initial profile 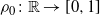 $\rho_0\colon \mathbb{R}
\rightarrow [0,1]$
, evolves as the solution of a bounded diffusion random equation. This result follows from an appropriate quenched hydrodynamic limit. If
$\rho_0\colon \mathbb{R}
\rightarrow [0,1]$
, evolves as the solution of a bounded diffusion random equation. This result follows from an appropriate quenched hydrodynamic limit. If 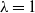 $\lambda=1$
then
$\lambda=1$
then 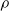 $\rho$
is discontinuous at each Poisson mark with passage through the slow bonds, otherwise the conductance at the slow bonds decreases meaning no passage through the slow bonds in the continuum. The main results are concerned with upper and lower quenched and annealed bounds of
$\rho$
is discontinuous at each Poisson mark with passage through the slow bonds, otherwise the conductance at the slow bonds decreases meaning no passage through the slow bonds in the continuum. The main results are concerned with upper and lower quenched and annealed bounds of 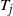 $T_j$
, where
$T_j$
, where 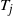 $T_j$
is the first displacement time of a tagged particle in a stochastic cluster of size j (the cluster is defined via specific macroscopic density profiles). It is possible to observe that when time t grows, then
$T_j$
is the first displacement time of a tagged particle in a stochastic cluster of size j (the cluster is defined via specific macroscopic density profiles). It is possible to observe that when time t grows, then 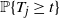 $\mathbb{P}\{T_j \geq t\}$
decays quadratically in both the upper and lower bounds, and falls as slow as the presence of more Poisson marks neighbouring the tagged particle, as expected.
$\mathbb{P}\{T_j \geq t\}$
decays quadratically in both the upper and lower bounds, and falls as slow as the presence of more Poisson marks neighbouring the tagged particle, as expected.
Keywords
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2019




