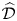 $\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
$\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
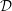 ${\mathcal{D}}$-Modules
${\mathcal{D}}$-Modules
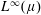 $L^{\infty }(\unicode[STIX]{x1D707})$
$L^{\infty }(\unicode[STIX]{x1D707})$
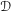 ${\mathcal{D}}$-MODULES
${\mathcal{D}}$-MODULES