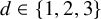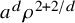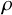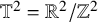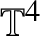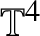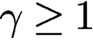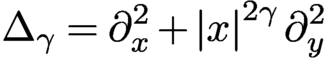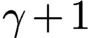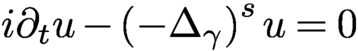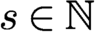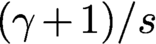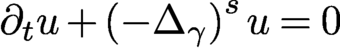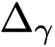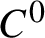41 results in 81Qxx
Dual formulation of constrained solutions of the multi-state Choquard equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Pressure of a dilute spin-polarized Fermi gas: Lower bound
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Log Calabi–Yau surfaces and Jeffrey–Kirwan residues
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 547-592
- Print publication:
- May 2024
-
- Article
-
- You have access
- HTML
- Export citation
The Spectral Gap and Low-Energy Spectrum in Mean-Field Quantum Spin Systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE METRIC OPERATORS FOR PSEUDO-HERMITIAN HAMILTONIAN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 215-228
-
- Article
-
- You have access
- HTML
- Export citation
Quantum systems at the brink: existence of bound states, critical potentials, and dimensionality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 July 2023, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal parabolic upper bound for the energy-momentum relation of a strongly coupled polaron
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 13 June 2023, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Superscars for arithmetic point scatters II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 May 2023, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stein’s method and approximating the multidimensional quantum harmonic oscillator
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 855-873
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
On Duclos–Exner’s conjecture about waveguides in strong uniform magnetic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Undecidability of the Spectral Gap
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 June 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractional interpolation inequality and radially symmetric ground states
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 937-957
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
Adiabatic theorem in the thermodynamic limit: Systems with a gap in the bulk
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 January 2022, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unconditional uniqueness for the energy-critical nonlinear Schrödinger equation on
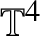 $\mathbb {T}^{4}$
$\mathbb {T}^{4}$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-adjoint extensions of bipartite Hamiltonians
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 433-447
-
- Article
- Export citation
OBSERVABILITY OF BAOUENDI–GRUSHIN-TYPE EQUATIONS THROUGH RESOLVENT ESTIMATES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 14 June 2021, pp. 541-579
- Print publication:
- March 2023
-
- Article
-
- You have access
- Export citation
Cantor spectrum for CMV and Jacobi matrices with coefficients arising from generalized skew-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2009-2027
- Print publication:
- June 2022
-
- Article
- Export citation
Asymptotic expansion of low-energy excitations for weakly interacting bosons
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 March 2021, e28
-
- Article
-
- You have access
- Open access
- Export citation
Holomorphic SCFTs with small index
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 573-601
- Print publication:
- April 2022
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation