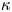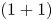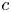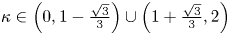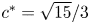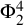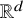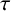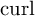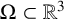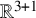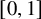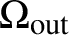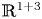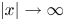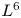108 results in 35Lxx
Travelling waves with continuous profile for hyperbolic Keller-Segel equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bifurcation of the travelling wave solutions in a perturbed (1 + 1)-dimensional dispersive long wave equation via a geometric approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-28
-
- Article
-
- You have access
- HTML
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural stability of transonic shock flows with an external force
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
A mathematical analysis of the Kakinuma model for interfacial gravity waves. Part II: justification as a shallow water approximation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-72
-
- Article
-
- You have access
- HTML
- Export citation
Dispersive and Strichartz estimates for 3D wave equation with a Laguerre potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-28
-
- Article
-
- You have access
- HTML
- Export citation
The turnpike property for mean-field optimal control problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The solvability for a nonlinear degenerate hyperbolic–parabolic coupled system arising from nematic liquid crystals
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 13 October 2023, pp. 1-68
-
- Article
-
- You have access
- HTML
- Export citation
Stability properties of multidimensional symmetric hyperbolic systems with damping, differential constraints and delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-43
-
- Article
-
- You have access
- HTML
- Export citation
EXACT SOLUTIONS OF HYPERBOLIC REACTION-DIFFUSION EQUATIONS IN TWO DIMENSIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 17 July 2023, pp. 338-354
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimates for the nonlinear viscoelastic damped wave equation on compact Lie groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 810-829
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
COMPACTNESS AND STRUCTURE OF ZERO-STATES FOR UNORIENTED AVILES–GIGA FUNCTIONALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 March 2023, pp. 941-982
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION INSIDE CYLINDRICAL CONVEX DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 304-312
- Print publication:
- April 2023
-
- Article
- Export citation
Uniqueness for a high order ill posed problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 15 July 2022, pp. 1425-1438
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The zero mass problem for Klein-Gordon equations: quadratic null interactions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse problems for nonlinear hyperbolic equations with disjoint sources and receivers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 November 2021, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYSIS OF CELL TRANSMISSION MODEL FOR TRAFFIC FLOW SIMULATION WITH APPLICATION TO NETWORK TRAFFIC
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 18 May 2021, pp. 84-99
-
- Article
- Export citation
Scattering for critical wave equations with variable coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 298-316
-
- Article
- Export citation
DRAPING WOVEN SHEETS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 07 January 2021, pp. 355-385
-
- Article
- Export citation
Global solution to a three-dimensional spherical piston problem for the relativistic Euler equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 September 2020, pp. 1-26
-
- Article
- Export citation