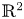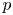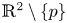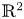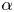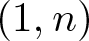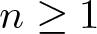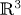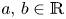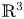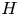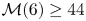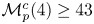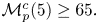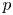98 results in 34Cxx
Binary pattern retrieval with Kuramoto-type oscillators via a least orthogonal lift of three patterns
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Emergent behaviours of a non-abelian quantum synchronisation model over the unitary group
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global centres in a class of quintic polynomial differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Limit cycles in a rotated family of generalized Liénard systems allowing for finitely many switching lines
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
Bifurcations and pattern formation in a host–parasitoid model with nonlocal effect
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
Continuous dependence of stationary distributions on parameters for stochastic predator–prey models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 February 2024, pp. 1010-1028
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Absolute concentration robustness and multistationarity in reaction networks: Conditions for coexistence
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 January 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A weakened Markus–Yamabe condition for planar polynomial differential systems of degree
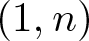 $(1,n)$
$(1,n)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1110-1118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rotating periodic solutions for p-Laplacian differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 August 2023, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Second-kind symmetric periodic orbits for planar perturbed Kepler problems and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 961-992
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Cyclicity of rigid centres on centre manifolds of three-dimensional systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 188-200
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
RECURSIVE CHARACTERISATIONS OF RANDOM MATRIX ENSEMBLES AND ASSOCIATED COMBINATORIAL OBJECTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 342-343
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Cyclicity of period annulus for a class of quadratic reversible systems with a nonrational first integral
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 09 November 2022, pp. 1706-1728
- Print publication:
- October 2023
-
- Article
- Export citation
Surfaces of prescribed linear Weingarten curvature in $\mathbb {R}^{3}$
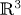
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 22 July 2022, pp. 1347-1370
- Print publication:
- August 2023
-
- Article
- Export citation
Fluctuation response patterns of network dynamics – An introduction
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 429-466
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OSCILLATION OF IMPULSIVE LINEAR DIFFERENTIAL EQUATIONS WITH DISCONTINUOUS SOLUTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 112-124
- Print publication:
- February 2023
-
- Article
- Export citation
The local cyclicity problem: Melnikov method using Lyapunov constants
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 356-375
-
- Article
- Export citation
Analytic partial-integrability of a symmetric Hopf-zero degeneracy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 April 2022, pp. 833-852
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Bloch type periodicity and applications to semi-linear differential equations in banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 326-355
-
- Article
- Export citation
Periodic solutions of p-Laplacian differential equations with jumping nonlinearity across half-eigenvalues
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 07 January 2022, pp. 307-326
- Print publication:
- February 2023
-
- Article
- Export citation