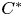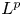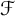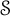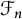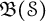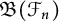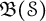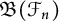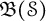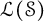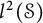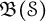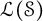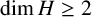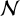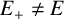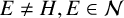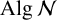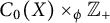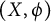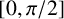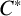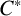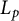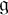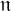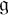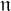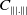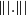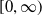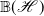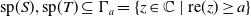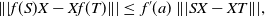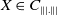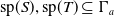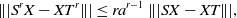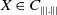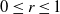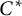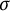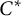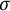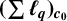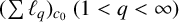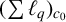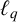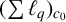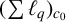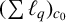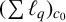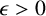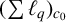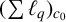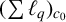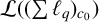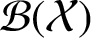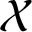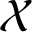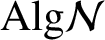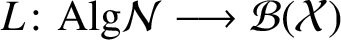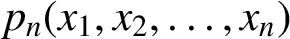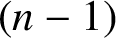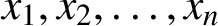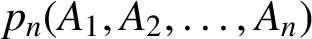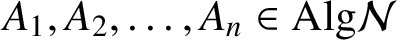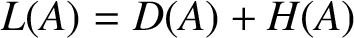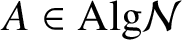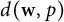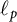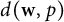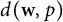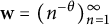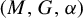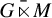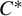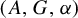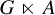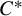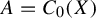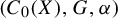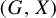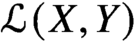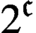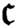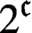71 results in 47Lxx
Topologically free actions and ideals in twisted Banach algebra crossed products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-31
-
- Article
-
- You have access
- HTML
- Export citation
Thompson’s semigroup and the first Hochschild cohomology
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
2-LOCAL ISOMETRIES OF SOME NEST ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 December 2023, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
Tensor algebras of subproduct systems and noncommutative function theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ideals with approximate unit in semicrossed products
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 September 2023, pp. 257-264
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON POSSIBLE VALUES OF THE INTERIOR ANGLE BETWEEN INTERMEDIATE SUBALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
TROTTER–KATO PRODUCT FORMULA AND AN APPROXIMATION FORMULA FOR A PROPAGATOR IN SYMMETRIC OPERATOR IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 173-174
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
A note on the column–row property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1244-1254
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CRITERION FOR HYPERSYMMETRY ON DISCRETE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 320-330
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double relative commutants in coronas of separable C*-algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 345-355
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The isomorphism problem for tensor algebras of multivariable dynamical systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 19 September 2022, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHEN IS A COMPLETION OF THE UNIVERSAL ENVELOPING ALGEBRA A BANACH PI-ALGEBRA?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 493-501
- Print publication:
- June 2023
-
- Article
- Export citation
An extension of the van Hemmen–Ando norm inequality
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 03 August 2022, pp. 121-127
- Print publication:
- January 2023
-
- Article
- Export citation
Gelfand–Naimark theorems for ordered
 $^*$-algebras
$^*$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 1272-1292
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric actions and finite approximations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2464-2470
- Print publication:
- July 2023
-
- Article
- Export citation
THE MAXIMAL IDEAL IN THE SPACE OF OPERATORS ON
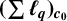 $\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
$\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 21 February 2022, pp. 340-348
- Print publication:
- October 2022
-
- Article
- Export citation
LIE-TYPE DERIVATIONS OF NEST ALGEBRAS ON BANACH SPACES AND RELATED TOPICS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 29 September 2021, pp. 391-430
- Print publication:
- June 2022
-
- Article
- Export citation
A new complemented subspace for the Lorentz sequence spaces, with an application to its lattice of closed ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 759-769
- Print publication:
- September 2022
-
- Article
- Export citation
Amenable dynamical systems over locally compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 25 June 2021, pp. 2468-2508
- Print publication:
- August 2022
-
- Article
- Export citation
Banach spaces for which the space of operators has 2𝔠 closed ideals
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 March 2021, e27
-
- Article
-
- You have access
- Open access
- Export citation