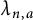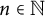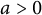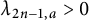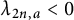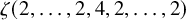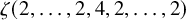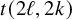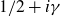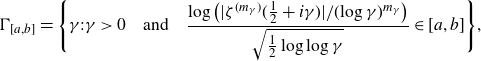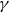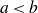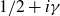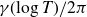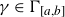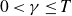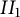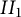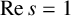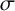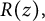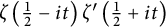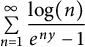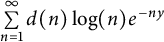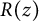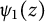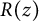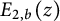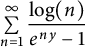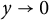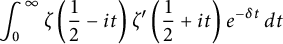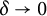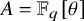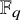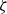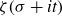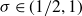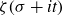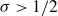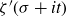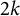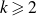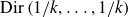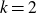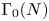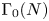203 results in 11Mxx
BOUNDS FOR MOMENTS OF QUADRATIC DIRICHLET CHARACTER SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-5
-
- Article
- Export citation
Li coefficients and the quadrilateral zeta function
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1-12
-
- Article
- Export citation
Evaluation of
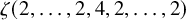 $ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
$ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The uniform distribution modulo one of certain subsequences of ordinates of zeros of the zeta function
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 01 March 2024, pp. 593-608
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The degree one Laguerre–Pólya class and the shuffle-word-embedding conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-8
-
- Article
- Export citation
Remarks on a formula of Ramanujan
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-12
-
- Article
- Export citation
BOUNDING ZETA ON THE 1-LINE UNDER THE PARTIAL RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 January 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE ZEROS OF L-FUNCTIONS ASSOCIATED TO FIXED-ORDER DIRICHLET CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 December 2023, pp. 1-10
-
- Article
- Export citation
NEW EFFECTIVE RESULTS IN THE THEORY OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 403-406
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Generalized divisor functions in arithmetic progressions: II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 28-56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Autocorrelations of characteristic polynomials for the Alternative Circular Unitary Ensemble
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 51-64
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lambert series of logarithm, the derivative of Deninger’s function
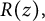 $R(z),$ and a mean value theorem for
$R(z),$ and a mean value theorem for 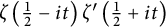 $\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
$\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1-36
-
- Article
- Export citation
Algebraic relations among Goss’s zeta values on elliptic curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spirals of Riemann’s Zeta-Function — Curvature, Denseness and Universality
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 325-338
- Print publication:
- March 2024
-
- Article
- Export citation
Shifted moments of the Riemann zeta function
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
- Export citation
An approximation formula for the shifted cubic moment of automorphic L-functions in the weight aspect
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 September 2023, pp. 1-24
-
- Article
- Export citation
SUM OF VALUES OF THE IDEAL CLASS ZETA-FUNCTION OVER NONTRIVIAL ZEROS OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 288-300
- Print publication:
- April 2024
-
- Article
- Export citation
Equivalent criterion for the grand Riemann hypothesis associated with Maass cusp forms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1-16
-
- Article
- Export citation
SHORT CHARACTER SUMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 July 2023, pp. 339-340
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation