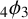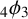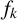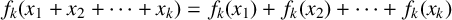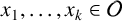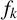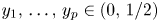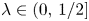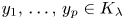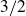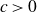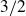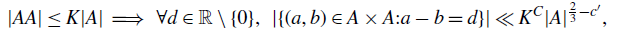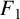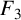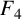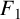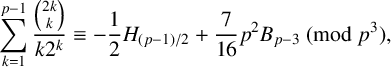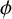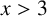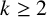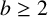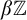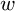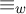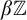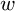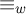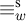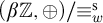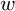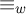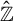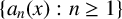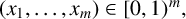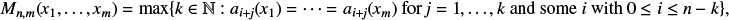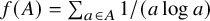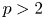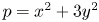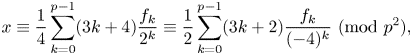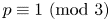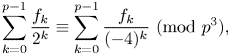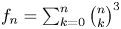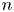188 results in 11Axx
Supercongruences involving Motzkin numbers and central trinomial coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
PRODUCTION OPTIMIZATION FOR AGENTS OF DIFFERING WORK RATES
- Part of
-
- Journal:
- The ANZIAM Journal , First View
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A PROBLEM OF PONGSRIIAM ON THE SUM OF DIVISORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
A q-SUPERCONGRUENCE ARISING FROM ANDREWS’
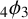 $_4\phi _3$ IDENTITY
$_4\phi _3$ IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 August 2024, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
MULTIPLICATIVE FUNCTIONS k-ADDITIVE ON GENERALISED OCTAGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
A better than
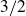 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 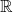 $\mathbb R$
$\mathbb R$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES
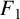 $F_1$
$F_1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
ON SOME CONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
-
- You have access
- HTML
- Export citation
Linear independence of series related to the Thue–Morse sequence along powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 822-832
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Some measure rigidity and equidistribution results for β-maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 2581-2598
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
On theorems of Fermat, Wilson, and Gegenbauer
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 12 September 2023, pp. 304-317
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 486-497
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
EVERY ARITHMETIC PROGRESSION CONTAINS INFINITELY MANY b-NIVEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 409-413
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
SELF-DIVISIBLE ULTRAFILTERS AND CONGRUENCES IN
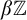 $\beta {\mathbb {Z}}$
$\beta {\mathbb {Z}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SHORTEST DISTANCE FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 186-195
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Smooth numbers with few nonzero binary digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 74-89
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
A proof of the Erdős primitive set conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 June 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation