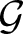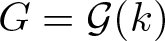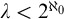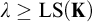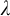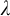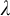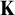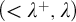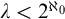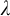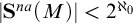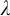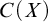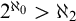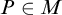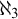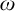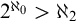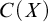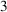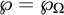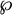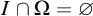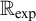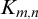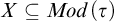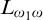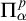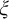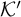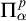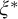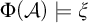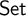261 results in 03CXX
ON GROUPS AND FIELDS DEFINABLE IN
 $1$-H-MINIMAL FIELDS
$1$-H-MINIMAL FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARTIN–SCHREIER EXTENSIONS AND COMBINATORIAL COMPLEXITY IN HENSELIAN VALUED FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 September 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Note on almost isometric ideals and local retracts in Banach and metric spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
Stereographic compactification and affine bi-Lipschitz homeomorphisms
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BUILDING MODELS IN SMALL CARDINALS IN LOCAL ABSTRACT ELEMENTARY CLASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ONE-DIMENSIONAL SUBGROUPS AND CONNECTED COMPONENTS IN NON-ABELIAN p-ADIC DEFINABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
GENERIC EXPANSIONS OF GEOMETRIC THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
COUNTING IN UNCOUNTABLY CATEGORICAL PSEUDOFINITE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
DISCONTINUOUS HOMOMORPHISMS OF
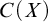 $C(X)$ WITH
$C(X)$ WITH 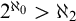 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 665-696
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
THE AMALGAMATION PROPERTY AND URYSOHN STRUCTURES IN CONTINUOUS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON GALOIS COHOMOLOGY, DEFINABILITY, AND DIFFERENTIAL ALGEBRAIC GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 496-515
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Generic Stability Independence and Treeless Theories
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONDEFINABILITY RESULTS FOR ELLIPTIC AND MODULAR FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE FRAGILITY OF INTERPOLATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS AND LIMITS OF THE SPECKER–BLATTER THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
THREE SURPRISING INSTANCES OF DIVIDING
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A LOPEZ-ESCOBAR THEOREM FOR CONTINUOUS DOMAINS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
A NEW PERSPECTIVE ON SEMI-RETRACTIONS AND THE RAMSEY PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DUALITY FOR COALGEBRAS FOR VIETORIS AND MONADICITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation