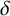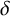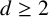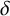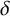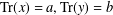14 results in 51-XX
AN INCIDENCE RESULT FOR WELL-SPACED ATOMS IN ALL DIMENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 20 February 2023, pp. 58-72
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric versions of Schwarz’s lemma for spherically convex functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1780-1799
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The pentagram map, Poncelet polygons, and commuting difference operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1084-1124
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE PRODUCT OF ELEMENTS WITH PRESCRIBED TRACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 14 May 2020, pp. 264-288
- Print publication:
- April 2022
-
- Article
- Export citation
COVERS OF GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 585-601
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
A COMBINATORIAL CHARACTERIZATION OF THE LAGRANGIAN GRASSMANNIAN LG(3,6)(
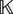 ${\mathbb{K}}$)
${\mathbb{K}}$)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 293-311
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
THEOREMS OF POINTS AND PLANES IN THREE-DIMENSIONAL PROJECTIVE SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 75-92
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
Some remarks on flocks
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
A transitive self-polar double-twenty of planes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-257
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
On Pascal ovals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-69
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
Polynomials for hyperovals of Desarguesian planes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 436-447
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Collineation groups preserving an oval in a projective place of odd order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 156-170
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Orthologic Desargues' figure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 3 / November 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-302
- Print publication:
- November 1979
-
- Article
-
- You have access
- Export citation
Special pairs of semi-bilogic and bilogic tetrahedra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 3 / November 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-308
- Print publication:
- November 1979
-
- Article
-
- You have access
- Export citation