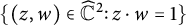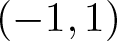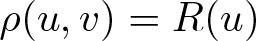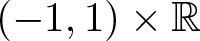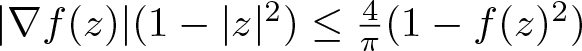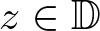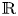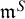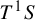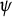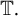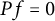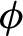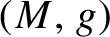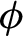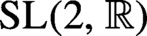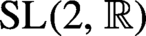68 results in 30Fxx
Différentielles quadratiques à singularités prescrites
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-65
-
- Article
- Export citation
On the ergodic theory of the real Rel foliation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1-45
-
- Article
- Export citation
Uniform spectral gap and orthogeodesic counting for strong convergence of Kleinian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 August 2023, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schwarz lemma for real harmonic functions onto surfaces with non-negative Gaussian curvature
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 516-531
-
- Article
- Export citation
Liouville property and quasi-isometries on negatively curved Riemannian surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 131-153
- Print publication:
- February 2024
-
- Article
- Export citation
Geometric filling curves on punctured surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 383-400
- Print publication:
- May 2023
-
- Article
- Export citation
The fundamental inequality for cocompact Fuchsian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 November 2022, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SINGULAR DIRECTIONS IN VEECH SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 16 September 2022, pp. 390-397
- Print publication:
- June 2023
-
- Article
- Export citation
Distribution in the unit tangent bundle of the geodesics of given type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 24 January 2022, pp. 887-903
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Circle packings, kissing reflection groups and critically fixed anti-rational maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 17 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian actions on compact nonorientable Riemann surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 634-648
- Print publication:
- September 2022
-
- Article
- Export citation
Typical properties of periodic Teichmüller geodesics: Lyapunov exponents
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 17 November 2021, pp. 556-584
- Print publication:
- February 2023
-
- Article
- Export citation
Slices of parameter space for meromorphic maps with two asymptotic values
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 99-139
- Print publication:
- January 2023
-
- Article
- Export citation
Asymptotic first boundary value problem for elliptic operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 571-581
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Ruelle’s property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 1474-1486
- Print publication:
- April 2022
-
- Article
- Export citation
Vortices over Riemann surfaces and dominated splittings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 1781-1806
- Print publication:
- May 2022
-
- Article
- Export citation
Surjective isometries of metric geometries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 828-839
- Print publication:
- December 2021
-
- Article
- Export citation
Limits of geodesic push-forwards of horocycle invariant measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 23 October 2020, pp. 2782-2804
- Print publication:
- September 2021
-
- Article
- Export citation

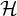
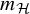
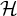
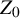
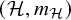
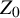
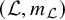
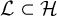
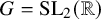
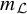
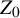
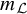
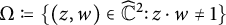 of the “complexified unit circle”
of the “complexified unit circle”