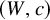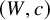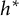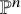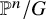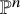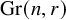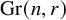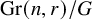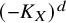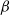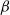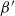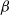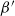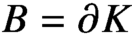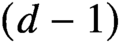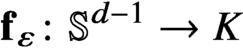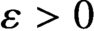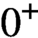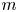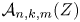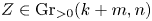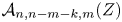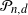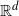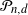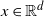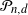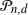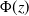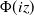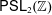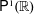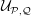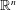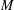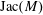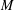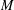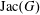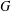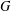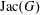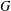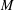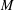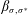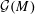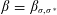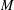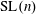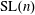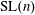81 results in 52Bxx
Polypositroids
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lattice points in slices of prisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double Schubert polynomials do have saturated Newton polytopes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remixed Eulerian numbers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 July 2023, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unwinding Toric Degenerations and Mirror Symmetry for Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 14 December 2022, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the maximum dual volume of a canonical Fano polytope
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 December 2022, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLYHEDRAL COMPLETENESS OF INTERMEDIATE LOGICS: THE NERVE CRITERION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2022, pp. 342-382
- Print publication:
- March 2024
-
- Article
- Export citation
The
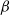 $\beta$
-Delaunay tessellation: Description of the model and geometry of typical cells
$\beta$
-Delaunay tessellation: Description of the model and geometry of typical cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1252-1290
- Print publication:
- December 2022
-
- Article
- Export citation
Spaces of Lorentzian and real stable polynomials are Euclidean balls
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 12 November 2021, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The moduli space of Harnack curves in toric surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 27 May 2021, e43
-
- Article
-
- You have access
- Open access
- Export citation
Continuous Maps from Spheres Converging to Boundaries of Convex Hulls
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 18 February 2021, e13
-
- Article
-
- You have access
- Open access
- Export citation
Plongements polyédraux tendus et nombre chromatique relatif des surfaces à bord
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1001-1013
- Print publication:
- December 2021
-
- Article
- Export citation
Parity duality for the amplituhedron
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 09 December 2020, pp. 2207-2262
- Print publication:
- November 2020
-
- Article
- Export citation
A new approach to weak convergence of random cones and polytopes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 11 August 2020, pp. 1627-1647
- Print publication:
- December 2021
-
- Article
- Export citation
Absorption probabilities for Gaussian polytopes and regular spherical simplices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 588-616
- Print publication:
- June 2020
-
- Article
- Export citation
MEASURABLE REALIZATIONS OF ABSTRACT SYSTEMS OF CONGRUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 February 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
Universal Alternating Semiregular Polytopes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 12 February 2020, pp. 572-595
- Print publication:
- April 2021
-
- Article
- Export citation
LYZ Matrices and SL(
 $n$) Contravariant Valuations on Polytopes
$n$) Contravariant Valuations on Polytopes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 18 December 2019, pp. 383-398
- Print publication:
- April 2021
-
- Article
- Export citation
GEOMETRIC BIJECTIONS FOR REGULAR MATROIDS, ZONOTOPES, AND EHRHART THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 December 2019, e45
-
- Article
-
- You have access
- Open access
- Export citation
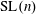 $\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
$\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 108-130
- Print publication:
- February 2021
-
- Article
- Export citation