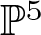 $\mathbb{P}^5$
$\mathbb{P}^5$
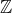 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
 $\mathcal {M}_{1,n}$ for
$\mathcal {M}_{1,n}$ for  $n=3,\dots ,10$
$n=3,\dots ,10$
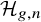 ${\mathcal {H}}_{g,n}$
${\mathcal {H}}_{g,n}$