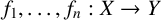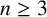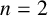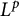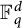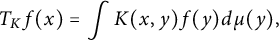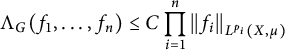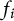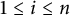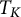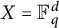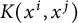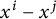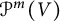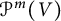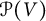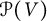41 results

Working with Network Data
- A Data Science Perspective
-
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024
Preface
-
- Book:
- A Practical Guide to Data Analysis Using R
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp xvii-xxiv
-
- Chapter
- Export citation
2 - Mathematical Terms and Notations
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 11-22
-
- Chapter
- Export citation
MULTIPLE LOOSE MAPS BETWEEN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-10
-
- Article
- Export citation
Perfect sampling of stochastic matching models with reneging
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-32
-
- Article
- Export citation
Multi-linear forms, graphs, and
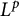 $L^p$-improving measures in
$L^p$-improving measures in 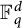 ${\Bbb F}_q^d$
${\Bbb F}_q^d$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 December 2023, pp. 1-44
-
- Article
- Export citation
Graphical methods and rings of invariants on the symmetric algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Undertaking Statistical Analysis Using Stata
-
- Book:
- Applied Regression Models in the Social Sciences
- Published online:
- 17 August 2023
- Print publication:
- 17 August 2023, pp 7-28
-
- Chapter
- Export citation
Chapter 2 - A Short History of Multimedia Sign Systems
-
- Book:
- Multimedia Comprehension
- Published online:
- 16 February 2023
- Print publication:
- 23 February 2023, pp 13-38
-
- Chapter
- Export citation
Misjudgment of interrupted time-series graphs due to serial dependence: Replication of Matyas and Greenwood (1990)
-
- Journal:
- Judgment and Decision Making / Volume 16 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 01 January 2023, pp. 687-708
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
25 - Visuals
- from Part V - Influence
-
-
- Book:
- A Critical Assessment of the Intergovernmental Panel on Climate Change
- Published online:
- 08 December 2022
- Print publication:
- 22 December 2022, pp 234-243
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Chapter 12 - Statistics and probability
- from Part 2 - Learning and teaching key mathematics content
-
-
- Book:
- Teaching Secondary Mathematics
- Published online:
- 27 October 2021
- Print publication:
- 24 September 2021, pp 301-328
-
- Chapter
- Export citation

The Hidden Language of Graphic Signs
- Cryptic Writing and Meaningful Marks
-
- Published online:
- 23 August 2021
- Print publication:
- 19 August 2021
A product form for the general stochastic matching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 449-468
- Print publication:
- June 2021
-
- Article
- Export citation
4 - Visual Models
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 62-103
-
- Chapter
- Export citation
6 - Multiple-Vertex Flat Folds: Global Properties
- from Part II - The Combinatorial Geometry of Flat Origami
-
- Book:
- Origametry
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020, pp 107-136
-
- Chapter
- Export citation
5 - Flat Vertex Folds: Local Properties
- from Part II - The Combinatorial Geometry of Flat Origami
-
- Book:
- Origametry
- Published online:
- 06 October 2020
- Print publication:
- 08 October 2020, pp 75-106
-
- Chapter
- Export citation
9 - Critical Hardy Inequalities on Manifolds and Graphs
-
-
- Book:
- Analysis and Geometry on Graphs and Manifolds
- Published online:
- 14 August 2020
- Print publication:
- 20 August 2020, pp 172-202
-
- Chapter
- Export citation

Analysis and Geometry on Graphs and Manifolds
-
- Published online:
- 14 August 2020
- Print publication:
- 20 August 2020
5 - Visualizing Data, Dynamics, and Risk
- from Section 2 - Structuring Intelligence
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 08 May 2020
- Print publication:
- 28 May 2020, pp 142-196
-
- Chapter
- Export citation