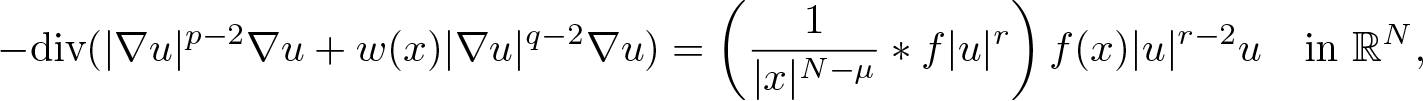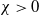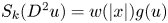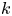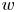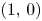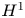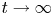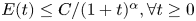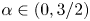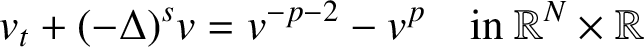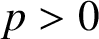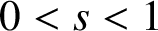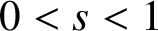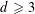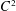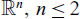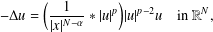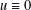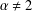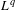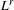45 results
Blowup of cylindrically symmetric solutions for biharmonic NLS
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
Stable solutions to double phase problems involving a nonlocal term
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1119-1141
-
- Article
-
- You have access
- HTML
- Export citation
Generalised solution to a 2D parabolic-parabolic chemotaxis system for urban crime: Global existence and large-time behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 409-429
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability properties of multidimensional symmetric hyperbolic systems with damping, differential constraints and delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-43
-
- Article
-
- You have access
- HTML
- Export citation
Some results for semi-stable radial solutions of k-Hessian equations with weight on ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 1751-1776
- Print publication:
- October 2023
-
- Article
- Export citation
Existence and stability of singular patterns in a fractional Ginzburg–Landau equation with a mean field
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1242-1268
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability and exponential decay for magnetohydrodynamic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 853-880
- Print publication:
- June 2023
-
- Article
- Export citation
Corrigendum: Dynamics of a susceptible—infected—susceptible epidemic reaction—diffusion model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 718-720
- Print publication:
- April 2023
-
- Article
-
- You have access
- HTML
- Export citation
Decay of weak solutions to Vlasov equation coupled with a shear thickening fluid
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 167-176
- Print publication:
- February 2023
-
- Article
- Export citation
UNIFORM LOWER BOUND AND LIOUVILLE TYPE THEOREM FOR FRACTIONAL LICHNEROWICZ EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 21 April 2021, pp. 484-492
- Print publication:
- December 2021
-
- Article
- Export citation
Dynamics of an infection age-space structured cholera model with Neumann boundary condition
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 393-422
-
- Article
- Export citation
On a repulsion Keller–Segel system with a logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 14 January 2021, pp. 153-181
-
- Article
- Export citation
Mean-field models for segregation dynamics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 111-132
-
- Article
- Export citation
GLOBAL NEARLY-PLANE-SYMMETRIC SOLUTIONS TO THE MEMBRANE EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 05 August 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation
Global and exponential attractor of the repulsive Keller–Segel model with logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 30 June 2020, pp. 599-617
-
- Article
- Export citation
STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 471-478
- Print publication:
- December 2020
-
- Article
- Export citation
A LIPSCHITZ METRIC FOR THE CAMASSA–HOLM EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 May 2020, e27
-
- Article
-
- You have access
- Open access
- Export citation
Existence of multi-travelling waves in capillary fluids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 2905-2936
- Print publication:
- December 2020
-
- Article
- Export citation
ON LOCAL ENERGY DECAY ESTIMATE OF THE OSEEN SEMIGROUP IN TWO DIMENSIONS AND ITS APPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 01 July 2019, pp. 859-891
- Print publication:
- May 2021
-
- Article
- Export citation
ON STABILITY OF PHYSICALLY REASONABLE SOLUTIONS TO THE TWO-DIMENSIONAL NAVIER–STOKES EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 16 May 2019, pp. 517-568
- Print publication:
- March 2021
-
- Article
- Export citation