7 results
Spanning
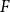 $F$-cycles in random graphs
$F$-cycles in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 833-850
-
- Article
-
- You have access
- HTML
- Export citation
Near-perfect clique-factors in sparse pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 11 December 2020, pp. 570-590
-
- Article
- Export citation
Finding tight Hamilton cycles in random hypergraphs faster
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 23 September 2020, pp. 239-257
-
- Article
- Export citation
Largest Components in Random Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 5 / September 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 741-762
-
- Article
- Export citation
SYMMETRIC AND ASYMMETRIC RAMSEY PROPERTIES IN RANDOM HYPERGRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 November 2017, e28
-
- Article
-
- You have access
- Open access
- Export citation
Minimum Degrees and Codegrees of Ramsey-Minimal 3-Uniform Hypergraphs*†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 850-869
-
- Article
- Export citation
On Colourings of Hypergraphs Without Monochromatic Fano Planes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 18 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 01 September 2009, pp. 803-818
-
- Article
- Export citation

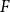
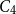
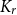
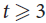
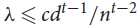
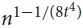
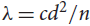
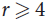
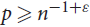
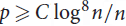
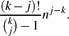
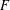
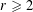
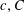
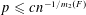
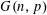
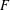
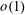
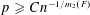
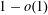
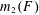
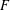
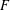
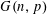
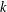
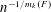
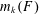
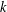
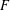
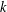
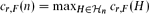 , where the maximum runs over all
, where the maximum runs over all 