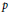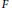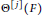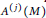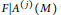5 results
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 03 March 2021, pp. 2001-2041
- Print publication:
- November 2022
-
- Article
- Export citation
Weights of the Mod p Kernels of Theta Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 2 / 01 April 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-264
- Print publication:
- 01 April 2018
-
- Article
-
- You have access
- Export citation
ON THE FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 21 October 2016, pp. 1-16
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
2 - On the basis problem for Siegel modular forms with level
-
-
- Book:
- Modular Forms on Schiermonnikoog
- Published online:
- 08 October 2009
- Print publication:
- 27 November 2008, pp 13-28
-
- Chapter
- Export citation
Siegel modular forms and theta series attached to quaternion algebras
-
- Journal:
- Nagoya Mathematical Journal / Volume 121 / March 1991
- Published online by Cambridge University Press:
- 22 January 2016, pp. 35-96
- Print publication:
- March 1991
-
- Article
-
- You have access
- Export citation