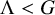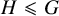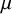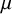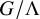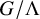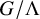1 Introduction
Originally motivated by applications to number theory, the rigidity properties of subgroup actions on a homogeneous space
![]() $X=G/\Lambda $
, where G is a real Lie group and
$X=G/\Lambda $
, where G is a real Lie group and
![]() $\Lambda <G$
a discrete subgroup, have been an active field of research over the last 50 years. Among the first striking results was Margulis’ resolution of the Oppenheim conjecture [Reference Margulis64, Reference Margulis66] via a reformulation into an orbit closure problem for the action of
$\Lambda <G$
a discrete subgroup, have been an active field of research over the last 50 years. Among the first striking results was Margulis’ resolution of the Oppenheim conjecture [Reference Margulis64, Reference Margulis66] via a reformulation into an orbit closure problem for the action of
![]() $\operatorname {\mathrm {SO}}(2,1)$
on
$\operatorname {\mathrm {SO}}(2,1)$
on
![]() $\operatorname {\mathrm {SL}}_3(\mathbb {R})/\operatorname {\mathrm {SL}}_3(\mathbb {Z})$
noticed by Raghunathan. Raghunathan had conjectured, more generally, that orbit closures for unipotent subgroups are closed orbits of larger subgroups. After more partial results by Dani, Margulis and Shah, Raghunathan’s conjecture was settled in full generality in celebrated work of Ratner [Reference Ratner81, Reference Ratner82, Reference Ratner83, Reference Ratner84].
$\operatorname {\mathrm {SL}}_3(\mathbb {R})/\operatorname {\mathrm {SL}}_3(\mathbb {Z})$
noticed by Raghunathan. Raghunathan had conjectured, more generally, that orbit closures for unipotent subgroups are closed orbits of larger subgroups. After more partial results by Dani, Margulis and Shah, Raghunathan’s conjecture was settled in full generality in celebrated work of Ratner [Reference Ratner81, Reference Ratner82, Reference Ratner83, Reference Ratner84].
In absence of unipotent elements, the dynamics of subgroup actions are harder to understand—already the case of actions on a torus
![]() $\mathbb {T}^d=\mathbb {R}^d/\mathbb {Z}^d$
by nonamenable subgroups of
$\mathbb {T}^d=\mathbb {R}^d/\mathbb {Z}^d$
by nonamenable subgroups of
![]() $\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
poses serious challenges. The very first difficulty arising in this setup is the potential lack of invariant measures. What has proved to be a fruitful approach for overcoming this issue is taking a probabilistic viewpoint of random walks and stationary measures, techniques mainly pioneered by Furstenberg starting in the 1960s [Reference Furstenberg and Kesten38, Reference Furstenberg40, Reference Furstenberg41, Reference Furstenberg42]. Using this random walks approach, Guivarc’h–Starkov [Reference Guivarc’h and Starkov44] made first contributions to understanding the action of
$\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
poses serious challenges. The very first difficulty arising in this setup is the potential lack of invariant measures. What has proved to be a fruitful approach for overcoming this issue is taking a probabilistic viewpoint of random walks and stationary measures, techniques mainly pioneered by Furstenberg starting in the 1960s [Reference Furstenberg and Kesten38, Reference Furstenberg40, Reference Furstenberg41, Reference Furstenberg42]. Using this random walks approach, Guivarc’h–Starkov [Reference Guivarc’h and Starkov44] made first contributions to understanding the action of
![]() $\Gamma <\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
on
$\Gamma <\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
on
![]() $\mathbb {T}^d$
, and Bourgain–Furman–Lindenstrauss–Mozes [Reference Bourgain, Furman, Lindenstrauss and Mozes19] proved a quantitative result which answered many remaining questions.
$\mathbb {T}^d$
, and Bourgain–Furman–Lindenstrauss–Mozes [Reference Bourgain, Furman, Lindenstrauss and Mozes19] proved a quantitative result which answered many remaining questions.
For subgroup actions on a general homogeneous space
![]() $X=G/\Lambda $
, a major breakthrough came with a series of papers by Benoist–Quint [Reference Benoist and Quint6, Reference Benoist and Quint8, Reference Benoist and Quint9, Reference Benoist and Quint10]. Applying several novel techniques, they were able to give a complete classification of stationary measures, descriptions of orbit closures and prove equidistribution statements for random walks under the assumption of semisimplicity of the Zariski closure of the acting group
$X=G/\Lambda $
, a major breakthrough came with a series of papers by Benoist–Quint [Reference Benoist and Quint6, Reference Benoist and Quint8, Reference Benoist and Quint9, Reference Benoist and Quint10]. Applying several novel techniques, they were able to give a complete classification of stationary measures, descriptions of orbit closures and prove equidistribution statements for random walks under the assumption of semisimplicity of the Zariski closure of the acting group
![]() $\Gamma $
. One crucial new ingredient in the proof of their measure classification result is the so-called ‘exponential drift’ argument (as compared to the ‘polynomial drift’ argument of Ratner), which was further developed in the seminal work of Eskin–Mirzakhani [Reference Eskin and Mirzakhani33] on stationary measures for the
$\Gamma $
. One crucial new ingredient in the proof of their measure classification result is the so-called ‘exponential drift’ argument (as compared to the ‘polynomial drift’ argument of Ratner), which was further developed in the seminal work of Eskin–Mirzakhani [Reference Eskin and Mirzakhani33] on stationary measures for the
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {R})$
-action on moduli space. Bringing back to homogeneous dynamics ideas from the setting of random walks on moduli space, Eskin–Lindenstrauss [Reference Eskin and Lindenstrauss30] have recently obtained a theorem which generalizes the measure classification results of Benoist–Quint.
$\operatorname {\mathrm {SL}}_2(\mathbb {R})$
-action on moduli space. Bringing back to homogeneous dynamics ideas from the setting of random walks on moduli space, Eskin–Lindenstrauss [Reference Eskin and Lindenstrauss30] have recently obtained a theorem which generalizes the measure classification results of Benoist–Quint.
The aim of this paper is to further advance the study of subgroup actions and random walks on homogeneous spaces, systematically dropping the assumption that the Zariski closure of the acting group
![]() $\Gamma $
is semisimple. We will introduce and study a new class of measures
$\Gamma $
is semisimple. We will introduce and study a new class of measures
![]() $\mu $
supported on a connected semisimple subgroup
$\mu $
supported on a connected semisimple subgroup
![]() $H\leqslant G$
without compact factors and with finite center that we call H-expanding measures. These are defined by an expansion condition in nontrivial irreducible finite-dimensional representations of H resembling the conclusion of the fundamental result of Furstenberg on the positivity of the top Lyapunov exponent. In particular, this class contains the Zariski dense measures underlying the work of Benoist–Quint. After deducing a measure classification result based on the progress by Eskin–Lindenstrauss [Reference Eskin and Lindenstrauss30], we will prove orbit closure descriptions, as well as recurrence and equidistribution results for the random walk on
$H\leqslant G$
without compact factors and with finite center that we call H-expanding measures. These are defined by an expansion condition in nontrivial irreducible finite-dimensional representations of H resembling the conclusion of the fundamental result of Furstenberg on the positivity of the top Lyapunov exponent. In particular, this class contains the Zariski dense measures underlying the work of Benoist–Quint. After deducing a measure classification result based on the progress by Eskin–Lindenstrauss [Reference Eskin and Lindenstrauss30], we will prove orbit closure descriptions, as well as recurrence and equidistribution results for the random walk on
![]() $G/\Lambda $
given by an H-expanding probability measure
$G/\Lambda $
given by an H-expanding probability measure
![]() $\mu $
. Finally, taking advantage of the generality of H-expanding measures, these main results will be used to also obtain new equidistribution statements for diagonalizable flows, which in turn have implications for Diophantine approximation problems on fractals.
$\mu $
. Finally, taking advantage of the generality of H-expanding measures, these main results will be used to also obtain new equidistribution statements for diagonalizable flows, which in turn have implications for Diophantine approximation problems on fractals.
To introduce the notion of H-expansion, we say that a Borel probability measure
![]() $\mu $
on
$\mu $
on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
is uniformly expanding if for every nonzero
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
is uniformly expanding if for every nonzero
![]() $v \in \mathbb {R}^d$
, we have
$v \in \mathbb {R}^d$
, we have
for
![]() $\mu ^{\mathbb {N}}$
-almost every (a.e.) sequence
$\mu ^{\mathbb {N}}$
-almost every (a.e.) sequence
![]() $(g_1,g_2,\dots )$
. A probability measure
$(g_1,g_2,\dots )$
. A probability measure
![]() $\mu $
on H is said to be H-expanding if for every finite-dimensional representation
$\mu $
on H is said to be H-expanding if for every finite-dimensional representation
![]() $(\rho ,V)$
of H without nonzero H-fixed vectors, the measure
$(\rho ,V)$
of H without nonzero H-fixed vectors, the measure
![]() $\rho _*\mu $
is uniformly expanding, where
$\rho _*\mu $
is uniformly expanding, where
![]() $\rho _*\mu $
denotes the pushforward of
$\rho _*\mu $
denotes the pushforward of
![]() $\mu $
by
$\mu $
by
![]() $\rho $
. We are going to elaborate on this definition and give nontrivially equivalent formulations in §2.
$\rho $
. We are going to elaborate on this definition and give nontrivially equivalent formulations in §2.
Ranging over all finite-dimensional representations, the H-expansion property of a probability measure
![]() $\mu $
on H is a universal condition and as such ensures validity of our results for an arbitrary embedding
$\mu $
on H is a universal condition and as such ensures validity of our results for an arbitrary embedding
![]() $H\hookrightarrow G$
and any lattice
$H\hookrightarrow G$
and any lattice
![]() $\Lambda <G$
. This universality notwithstanding, the class of H-expanding measures contains an abundance of interesting examples:
$\Lambda <G$
. This universality notwithstanding, the class of H-expanding measures contains an abundance of interesting examples:
-
○ Zariski dense measures (§3.1): If the closed subgroup
 $\Gamma _{\mu }$
of H generated by the support of
$\Gamma _{\mu }$
of H generated by the support of
 $\mu $
has Zariski dense image in
$\mu $
has Zariski dense image in
 $\operatorname {\mathrm {Ad}}(H)$
and
$\operatorname {\mathrm {Ad}}(H)$
and
 $\mu $
satisfies a moment condition, then
$\mu $
satisfies a moment condition, then
 $\mu $
is H-expanding as a consequence of Furstenberg’s theorem on positivity of the top Lyapunov exponent.
$\mu $
is H-expanding as a consequence of Furstenberg’s theorem on positivity of the top Lyapunov exponent. -
○ Measures on parabolic groups (§3.2): We give a general criterion for H-expansion of a measure
 $\mu $
on a parabolic subgroup of H and, using the notion of expanding cone introduced by the third-named author [Reference Shi92], explicitly exhibit a class of examples of such measures. For the sake of concreteness, let us mention here that, for example, our results directly imply that any probability measure on
$\mu $
on a parabolic subgroup of H and, using the notion of expanding cone introduced by the third-named author [Reference Shi92], explicitly exhibit a class of examples of such measures. For the sake of concreteness, let us mention here that, for example, our results directly imply that any probability measure on
 $H=\operatorname {\mathrm {SL}}_4(\mathbb {R})$
with support consisting of the five matrices is H-expanding.
$H=\operatorname {\mathrm {SL}}_4(\mathbb {R})$
with support consisting of the five matrices is H-expanding. $$ \begin{align*} \begin{pmatrix} 2\\ & 2\\ & & 1\\ & & & 1/4 \end{pmatrix},\, \begin{pmatrix} 2 & 1\\ 1 & 1\\ & & 1\\ & & & 1 \end{pmatrix},\, \begin{pmatrix} 1 & 1\\ 1 & 2\\ & & 1\\ & & & 1 \end{pmatrix},\, \begin{pmatrix} 1\\ & 1 & 1\\ & & 1\\ & & & 1 \end{pmatrix},\, \begin{pmatrix} 1\\ & 1\\ & & 1 & 1\\ & & & 1 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 2\\ & 2\\ & & 1\\ & & & 1/4 \end{pmatrix},\, \begin{pmatrix} 2 & 1\\ 1 & 1\\ & & 1\\ & & & 1 \end{pmatrix},\, \begin{pmatrix} 1 & 1\\ 1 & 2\\ & & 1\\ & & & 1 \end{pmatrix},\, \begin{pmatrix} 1\\ & 1 & 1\\ & & 1\\ & & & 1 \end{pmatrix},\, \begin{pmatrix} 1\\ & 1\\ & & 1 & 1\\ & & & 1 \end{pmatrix} \end{align*} $$
-
○ Epimorphic subgroups (§3.3): The closed subgroup
 $\Gamma _{\mu }$
generated by the support of
$\Gamma _{\mu }$
generated by the support of
 $\mu $
is necessarily an epimorphic subgroup of H when
$\mu $
is necessarily an epimorphic subgroup of H when
 $\mu $
is H-expanding. Conversely, thanks to the work of Bien–Borel [Reference Bien and Borel13] and its subsequent developments, we will see that many epimorphic subgroups of H support H-expanding measures. For example, any
$\mu $
is H-expanding. Conversely, thanks to the work of Bien–Borel [Reference Bien and Borel13] and its subsequent developments, we will see that many epimorphic subgroups of H support H-expanding measures. For example, any
 $\mathbb {R}$
-split simple group H admits distinguished three-dimensional epimorphic subgroups for which this is the case, showing that H-expanding measures may live on subgroups which are very small compared to H itself. See also Corollary 4.9.
$\mathbb {R}$
-split simple group H admits distinguished three-dimensional epimorphic subgroups for which this is the case, showing that H-expanding measures may live on subgroups which are very small compared to H itself. See also Corollary 4.9.
Under various weaker assumptions than H-expansion, not all of our conclusions hold in full strength. For instance, requiring uniform expansion only in the adjoint representation, homogeneity of stationary measures can fail, as an example at the end of [Reference Eskin and Lindenstrauss30, §1.2] shows. For unipotent random walks, recurrence is not always guaranteed [Reference Breuillard20, §10.2.1]. On the other hand, in the particular case of measures on parabolic subgroups, slightly weaker expansion properties were first used in the work of Simmons–Weiss [Reference Simmons and Weiss93] and subsequently in [Reference Prohaska and Sert79] to prove measure rigidity and equidistribution results in a setting corresponding to the case
![]() $H=G$
in our framework. See also Remark 1.3.
$H=G$
in our framework. See also Remark 1.3.
We next introduce the terminology necessary to state our main results. Given a continuous action of a locally compact second countable group G on a locally compact second countable metrizable space X, a probability measure
![]() $\nu $
on X is said to be
$\nu $
on X is said to be
![]() $\mu $
-stationary if
$\mu $
-stationary if
![]() $\nu =\mu *\nu $
, where the convolution is defined by
$\nu =\mu *\nu $
, where the convolution is defined by
for nonnegative Borel functions f on X. A
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\nu $
is said to be
$\nu $
is said to be
![]() $\mu $
-ergodic if it is extremal in the convex set of
$\mu $
-ergodic if it is extremal in the convex set of
![]() $\mu $
-stationary probability measures.
$\mu $
-stationary probability measures.
Now, let G be a real Lie group,
![]() $\Lambda <G$
a discrete subgroup and
$\Lambda <G$
a discrete subgroup and
![]() $X=G/\Lambda $
. A probability measure
$X=G/\Lambda $
. A probability measure
![]() $\nu $
on X is said to be homogeneous if there exists
$\nu $
on X is said to be homogeneous if there exists
![]() $x\in X$
and a closed subgroup N of G preserving
$x\in X$
and a closed subgroup N of G preserving
![]() $\nu $
such that
$\nu $
such that
![]() $\nu (Nx)=1$
. In this case, the orbit
$\nu (Nx)=1$
. In this case, the orbit
![]() $Nx$
is automatically closed and is called a homogeneous subspace of X. It is equivalent to require that
$Nx$
is automatically closed and is called a homogeneous subspace of X. It is equivalent to require that
![]() $\nu $
assigns full measure to an orbit of its stabilizer group
$\nu $
assigns full measure to an orbit of its stabilizer group
This gives a one-to-one correspondence between homogeneous measures on X and homogeneous subspaces of X. For a closed subgroup
![]() $\Gamma $
of G, a homogeneous subspace Y of X is said to be
$\Gamma $
of G, a homogeneous subspace Y of X is said to be
![]() $\Gamma $
-ergodic if
$\Gamma $
-ergodic if
![]() $\Gamma $
preserves the corresponding homogeneous probability measure
$\Gamma $
preserves the corresponding homogeneous probability measure
![]() $\nu _Y$
and the action of
$\nu _Y$
and the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $(Y,\nu _Y)$
is ergodic.
$(Y,\nu _Y)$
is ergodic.
Finally, for
![]() $g \in \operatorname {\mathrm {GL}}_d(\mathbb {R})$
we set
$g \in \operatorname {\mathrm {GL}}_d(\mathbb {R})$
we set
![]() $\operatorname {N}(g)=\max \{ \left \lVert {g} \right \rVert , \left \lVert {g^{-1}} \right \rVert \}$
for some choice of operator norm on
$\operatorname {N}(g)=\max \{ \left \lVert {g} \right \rVert , \left \lVert {g^{-1}} \right \rVert \}$
for some choice of operator norm on
![]() $\operatorname {\mathrm {Mat}}_{d\times d}(\mathbb {R})$
. A probability measure
$\operatorname {\mathrm {Mat}}_{d\times d}(\mathbb {R})$
. A probability measure
![]() $\mu $
on
$\mu $
on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
is said to have a finite first moment if
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
is said to have a finite first moment if
and to have finite exponential moments if
for
![]() $\delta>0$
sufficiently small. These definitions are independent of the choice of operator norm. We say that a probability measure
$\delta>0$
sufficiently small. These definitions are independent of the choice of operator norm. We say that a probability measure
![]() $\mu $
on a connected semisimple Lie group H with finite center has a finite first moment or finite exponential moments if its image in a finite-dimensional representation of H with finite kernel has the corresponding property. This does not depend on the choice of such a linear representation (see Lemma 2.9). Both moment conditions are automatically satisfied, for example, if
$\mu $
on a connected semisimple Lie group H with finite center has a finite first moment or finite exponential moments if its image in a finite-dimensional representation of H with finite kernel has the corresponding property. This does not depend on the choice of such a linear representation (see Lemma 2.9). Both moment conditions are automatically satisfied, for example, if
![]() $\mu $
has compact support.
$\mu $
has compact support.
1.1 Measure rigidity
We start with the classification of stationary measures. Recall that given a measure
![]() $\mu $
on H, we denote by
$\mu $
on H, we denote by
![]() $\Gamma _{\mu }$
the closed subgroup generated by the support of
$\Gamma _{\mu }$
the closed subgroup generated by the support of
![]() $\mu $
.
$\mu $
.
Theorem 1.1. Let
![]() $\Lambda $
be a discrete subgroup of a real Lie group G. Let
$\Lambda $
be a discrete subgroup of a real Lie group G. Let
![]() $H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
$H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
![]() $\mu $
be a probability measure on H that is H-expanding and has a finite first moment. Then any
$\mu $
be a probability measure on H that is H-expanding and has a finite first moment. Then any
![]() $\mu $
-ergodic
$\mu $
-ergodic
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\nu $
on
$\nu $
on
![]() $G/\Lambda $
is
$G/\Lambda $
is
![]() $\Gamma _{\mu }$
-invariant and homogeneous. Moreover, the connected component of
$\Gamma _{\mu }$
-invariant and homogeneous. Moreover, the connected component of
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
is normalized by H.
$\operatorname {\mathrm {Stab}}_G(\nu )$
is normalized by H.
Using the properties of H-expanding measures, the above theorem is deduced by an iterative application of the recent measure classification results of Eskin–Lindenstrauss [Reference Eskin and Lindenstrauss30]; see §4.1. The proof is similar to the argument Eskin–Lindenstrauss use to show that their result implies Benoist–Quint’s measure classification.
In certain cases, the last conclusion of Theorem 1.1 allows us to show that
![]() $\nu $
is actually H-invariant; see Proposition 8.2 and also the corollary below. For its statement, recall that a discrete subgroup
$\nu $
is actually H-invariant; see Proposition 8.2 and also the corollary below. For its statement, recall that a discrete subgroup
![]() $\Lambda $
is said to be a lattice in G if
$\Lambda $
is said to be a lattice in G if
![]() $X=G/\Lambda $
admits a G-invariant probability measure
$X=G/\Lambda $
admits a G-invariant probability measure
![]() $m_X$
. In this case, we refer to
$m_X$
. In this case, we refer to
![]() $m_X$
as the Haar measure on X. A lattice
$m_X$
as the Haar measure on X. A lattice
![]() $\Lambda $
in a connected semisimple Lie group G without compact factors is said to be irreducible if
$\Lambda $
in a connected semisimple Lie group G without compact factors is said to be irreducible if
![]() $\Lambda \cap S$
is not a lattice in S for every nontrivial proper connected normal subgroup S of G. Equivalently,
$\Lambda \cap S$
is not a lattice in S for every nontrivial proper connected normal subgroup S of G. Equivalently,
![]() $S\Lambda $
is dense in G for every such S.
$S\Lambda $
is dense in G for every such S.
Corollary 1.2. Let G be a connected semisimple Lie group without compact factors and with finite center, and let
![]() $\Lambda <G$
be an irreducible lattice. Let H be a connected normal subgroup of G of positive dimension, and let
$\Lambda <G$
be an irreducible lattice. Let H be a connected normal subgroup of G of positive dimension, and let
![]() $\mu $
be an H-expanding probability measure on H with finite first moment.
$\mu $
be an H-expanding probability measure on H with finite first moment.
-
(i) If
 $H\neq G$
, then the Haar measure
$H\neq G$
, then the Haar measure
 $m_X$
on
$m_X$
on
 $X=G/\Lambda $
is the unique
$X=G/\Lambda $
is the unique
 $\mu $
-stationary probability measure on X.
$\mu $
-stationary probability measure on X. -
(ii) If
 $H=G$
, then the only
$H=G$
, then the only
 $\mu $
-ergodic
$\mu $
-ergodic
 $\mu $
-stationary probability measures on X are uniform measures on finite
$\mu $
-stationary probability measures on X are uniform measures on finite
 $\Gamma _{\mu }$
-orbits and the Haar measure
$\Gamma _{\mu }$
-orbits and the Haar measure
 $m_X$
on X. Moreover,
$m_X$
on X. Moreover,
 $m_X$
is the only nonatomic
$m_X$
is the only nonatomic
 $\mu $
-stationary probability measure on X.
$\mu $
-stationary probability measure on X.
We note that finite
![]() $\Gamma _{\mu }$
-orbits do only occur when
$\Gamma _{\mu }$
-orbits do only occur when
![]() $\Gamma _{\mu }$
is virtually contained in a conjugate of
$\Gamma _{\mu }$
is virtually contained in a conjugate of
![]() $\Lambda $
. The proof of part (i) of the corollary above relies on Margulis’ arithmeticity theorem and a careful analysis of stationary measures charging an orbit of the centralizer of
$\Lambda $
. The proof of part (i) of the corollary above relies on Margulis’ arithmeticity theorem and a careful analysis of stationary measures charging an orbit of the centralizer of
![]() $\Gamma _{\mu }$
, which is carried out in §4.2. The last statement in part (ii) additionally requires countability of finite
$\Gamma _{\mu }$
, which is carried out in §4.2. The last statement in part (ii) additionally requires countability of finite
![]() $\Gamma _{\mu }$
-orbits, which follows from a general countability result for homogeneous subspaces in §5.
$\Gamma _{\mu }$
-orbits, which follows from a general countability result for homogeneous subspaces in §5.
Remark 1.3. As mentioned before, the H-expansion condition is universal so that all our results hold for an arbitrary embedding
![]() $H\hookrightarrow G$
. For a fixed Lie group G, it suffices to impose uniform expansion on
$H\hookrightarrow G$
. For a fixed Lie group G, it suffices to impose uniform expansion on
![]() $\rho _*\mu $
only for a finite collection of representations
$\rho _*\mu $
only for a finite collection of representations
![]() $(\rho ,V)$
of H (which depends on G), as the proofs show. In §4.3, we track which representations are needed in the case of measure classification; see Theorem 4.8 for the precise statement. Our countability result (Proposition 5.1) will also be phrased using only this finite collection of representations, allowing us to prove it without an assumption of compact generation (cf. [Reference Benoist and Quint10, Proposition 2.1]).
$(\rho ,V)$
of H (which depends on G), as the proofs show. In §4.3, we track which representations are needed in the case of measure classification; see Theorem 4.8 for the precise statement. Our countability result (Proposition 5.1) will also be phrased using only this finite collection of representations, allowing us to prove it without an assumption of compact generation (cf. [Reference Benoist and Quint10, Proposition 2.1]).
1.2 Recurrence and Lyapunov functions
Now, we assume in addition that
![]() $\Lambda $
is a lattice and that
$\Lambda $
is a lattice and that
![]() $\mu $
has finite exponential moments. Under certain assumptions including semisimplicity of the noncompact part of the Zariski closure of
$\mu $
has finite exponential moments. Under certain assumptions including semisimplicity of the noncompact part of the Zariski closure of
![]() $\Gamma _{\mu }$
, Eskin–Margulis [Reference Eskin and Margulis31] and later Benoist–Quint [Reference Benoist and Quint8] have shown that the random walk on
$\Gamma _{\mu }$
, Eskin–Margulis [Reference Eskin and Margulis31] and later Benoist–Quint [Reference Benoist and Quint8] have shown that the random walk on
![]() $X=G/\Lambda $
given by
$X=G/\Lambda $
given by
![]() $\mu $
satisfies strong recurrence properties. If
$\mu $
satisfies strong recurrence properties. If
![]() $\delta _x$
denotes the Dirac measure at
$\delta _x$
denotes the Dirac measure at
![]() $x\in X$
and
$x\in X$
and
![]() $\mu ^{* n} $
is the n-fold convolution power of
$\mu ^{* n} $
is the n-fold convolution power of
![]() $\mu $
, these recurrence statements take the general form that
$\mu $
, these recurrence statements take the general form that
![]() $\mu ^{*n}*\delta _x(M)$
is close to
$\mu ^{*n}*\delta _x(M)$
is close to
![]() $1$
for large n, where
$1$
for large n, where
![]() $M\subset X$
is a certain compact set. We obtain analogous results for H-expanding measures.
$M\subset X$
is a certain compact set. We obtain analogous results for H-expanding measures.
Theorem 1.4. Let
![]() $\Lambda $
be a lattice in a real Lie group G. Let
$\Lambda $
be a lattice in a real Lie group G. Let
![]() $H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
$H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
![]() $\mu $
be an H-expanding probability measure with finite exponential moments on H. Let Y be a
$\mu $
be an H-expanding probability measure with finite exponential moments on H. Let Y be a
![]() $\Gamma _{\mu }$
-ergodic homogeneous subspace of
$\Gamma _{\mu }$
-ergodic homogeneous subspace of
![]() $X=G/\Lambda $
or the empty set. Finally, let
$X=G/\Lambda $
or the empty set. Finally, let
![]() $K_L$
be any compact subset of the centralizer L of
$K_L$
be any compact subset of the centralizer L of
![]() $\Gamma _{\mu }$
in G, and set
$\Gamma _{\mu }$
in G, and set
![]() $\mathcal {N}=K_LY$
. Then for any compact subset
$\mathcal {N}=K_LY$
. Then for any compact subset
![]() $Z\subset X\setminus \mathcal {N}$
and
$Z\subset X\setminus \mathcal {N}$
and
![]() $\delta>0$
there exists a compact subset
$\delta>0$
there exists a compact subset
![]() $M_{Z,\delta }$
of
$M_{Z,\delta }$
of
![]() $X\setminus \mathcal {N}$
such that
$X\setminus \mathcal {N}$
such that
for every
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $x\in Z$
.
$x\in Z$
.
Loosely speaking, the basic case (with
![]() $Y=\emptyset $
) implies that the random walk does not spend too much time in the cusp. The general case ensures that the random walk also does not accumulate near lower-dimensional homogeneous subspaces.
$Y=\emptyset $
) implies that the random walk does not spend too much time in the cusp. The general case ensures that the random walk also does not accumulate near lower-dimensional homogeneous subspaces.
This result will be proved in §7.1 using height functions on
![]() $X=G/\Lambda $
satisfying a contraction property with respect to the averaging operator
$X=G/\Lambda $
satisfying a contraction property with respect to the averaging operator
![]() $A_{\mu }$
defined by
$A_{\mu }$
defined by
for nonnegative Borel functions f on X. Heuristically, if
![]() $\beta $
is a function on X with values in
$\beta $
is a function on X with values in
![]() $[0,\infty ]$
such that
$[0,\infty ]$
such that
for constants
![]() $a\in (0,1)$
and
$a\in (0,1)$
and
![]() $b\ge 0$
, then, with high probability, the dynamics of the random walk are driven towards the part of the space where
$b\ge 0$
, then, with high probability, the dynamics of the random walk are driven towards the part of the space where
![]() $\beta $
takes values below a certain threshold, and
$\beta $
takes values below a certain threshold, and
![]() $X_{\infty }=\beta ^{-1}(\{\infty \})$
acts as a repeller. Putting this heuristic into quantitative terms yields strong recurrence properties of the random walk away from
$X_{\infty }=\beta ^{-1}(\{\infty \})$
acts as a repeller. Putting this heuristic into quantitative terms yields strong recurrence properties of the random walk away from
![]() $X_{\infty }$
, which play a key role not only in the proof of Theorem 1.4, but also for orbit closure and equidistribution results to be described in what follows.
$X_{\infty }$
, which play a key role not only in the proof of Theorem 1.4, but also for orbit closure and equidistribution results to be described in what follows.
Ideas of this kind have a rich history in the theory of stochastic processes and dynamical systems and trace back to the work of Foster [Reference Foster35] and Lyapunov [Reference Liapounoff63] (see also [Reference Meyn and Tweedie68, §15]). In homogeneous dynamics, they first appear in Eskin–Margulis–Mozes’ work on a quantitative version of the Oppenheim conjecture [Reference Eskin, Margulis and Mozes32]. In the study of random walks on homogeneous spaces, height functions were first systematically used by Eskin–Margulis [Reference Eskin and Margulis31] to establish recurrence properties. Functions satisfying the contraction property (1.1) are therefore often referred to either as Lyapunov functions or Margulis functions.
To obtain our results, we will need to construct two types of Lyapunov functions.
-
○ Height functions with respect to the cusps (§6.1): First, corresponding to the case
 $Y=\emptyset $
in Theorem 1.4, we require a Lyapunov function
$Y=\emptyset $
in Theorem 1.4, we require a Lyapunov function
 $\beta _{\infty }$
that stays bounded on a prescribed compact subset Z of X and tends to infinity when leaving compact parts of the space into the cusps of X. Its role is to rule out escape of mass, that is, ensure that the random walk does not escape to infinity. For this case, we will show that we can use the height function constructed by Benoist–Quint [Reference Benoist and Quint8]. Indeed, as it turns out, the algebraic condition that is imposed in their paper on the Zariski closure of
$\beta _{\infty }$
that stays bounded on a prescribed compact subset Z of X and tends to infinity when leaving compact parts of the space into the cusps of X. Its role is to rule out escape of mass, that is, ensure that the random walk does not escape to infinity. For this case, we will show that we can use the height function constructed by Benoist–Quint [Reference Benoist and Quint8]. Indeed, as it turns out, the algebraic condition that is imposed in their paper on the Zariski closure of
 $\Gamma _{\mu }$
is only crucially used to ensure an expansion property in representations of H, so that the proof also goes through under our H-expansion assumption.
$\Gamma _{\mu }$
is only crucially used to ensure an expansion property in representations of H, so that the proof also goes through under our H-expansion assumption. -
○ Height functions with respect to singular subspaces (§6.2): Secondly, corresponding to the case of a lower-dimensional homogeneous subspace Y in Theorem 1.4, we also need Lyapunov functions which blow up near the singular subspace Y. These are used to ensure that random walk trajectories do not accumulate near Y when starting outside of it. Here, we give a construction inspired by the work of Eskin–Mirzakhani–Mohammadi [Reference Eskin, Mirzakhani and Mohammadi34] for random walks on moduli space. This will allow us to avoid the use of the first return cocycles and operators appearing in [Reference Benoist and Quint9, Reference Benoist and Quint10], and to obtain a height function
 $\beta _{\mathcal {N}}$
which satisfies the contraction property (1.1) with respect to
$\beta _{\mathcal {N}}$
which satisfies the contraction property (1.1) with respect to
 $A_{\mu }$
itself.
$A_{\mu }$
itself.
Remark 1.5. After finishing the first version of our article, Bénard–de Saxcé improved the Markov-chain theoretic ingredient of the proofs concerning the moment assumption. Namely, using their result [Reference Bénard and de Saxcé5, Theorem D], one can now relax the exponential moment assumption in our work (in Theorems 1.4 and 1.6) to a finite first moment assumption. Bénard–de Saxcé prove this in the particular (compared to H-expansion) setting of Benoist–Quint, using logarithmic versions of our height functions ([Reference Bénard and de Saxcé5, Theorems A,B,C]).
1.3 Orbit closures and equidistribution
Measure classification and recurrence properties at hand, the next step is the question of equidistribution of random walks with respect to a homogeneous probability measure, which, once established, yields orbit closure descriptions analogous to Ratner’s theorems in unipotent dynamics.
Let
![]() $\Gamma ^+_{\mu }$
be the closed semigroup generated by the support of
$\Gamma ^+_{\mu }$
be the closed semigroup generated by the support of
![]() $\mu $
. If
$\mu $
. If
![]() $\Gamma _{\mu }$
has Zariski dense image in
$\Gamma _{\mu }$
has Zariski dense image in
![]() $\operatorname {\mathrm {Ad}} (H)$
, then it is proved in [Reference Benoist and Quint10] that the orbit closure
$\operatorname {\mathrm {Ad}} (H)$
, then it is proved in [Reference Benoist and Quint10] that the orbit closure
![]() $\overline {\Gamma _{\mu }^+x}$
is a homogeneous subspace of X inside which the random walk equidistributes. Our next result is a generalization of this and other rigidity results for the random trajectory of points proved in [Reference Benoist and Quint10, Reference Prohaska and Sert79, Reference Simmons and Weiss93].
$\overline {\Gamma _{\mu }^+x}$
is a homogeneous subspace of X inside which the random walk equidistributes. Our next result is a generalization of this and other rigidity results for the random trajectory of points proved in [Reference Benoist and Quint10, Reference Prohaska and Sert79, Reference Simmons and Weiss93].
Theorem 1.6. Let
![]() $\Lambda $
be a lattice in a real Lie group G. Let
$\Lambda $
be a lattice in a real Lie group G. Let
![]() $H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
$H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
![]() $\mu $
be an H-expanding probability measure with finite exponential moments on H. Then for every
$\mu $
be an H-expanding probability measure with finite exponential moments on H. Then for every
![]() $x\in X=G/\Lambda $
there is a
$x\in X=G/\Lambda $
there is a
![]() $\Gamma _{\mu }$
-ergodic homogeneous subspace
$\Gamma _{\mu }$
-ergodic homogeneous subspace
![]() $Y_x\subset X$
with corresponding homogeneous probability measure
$Y_x\subset X$
with corresponding homogeneous probability measure
![]() $\nu _x$
such that the following hold:
$\nu _x$
such that the following hold:
-
(i) The orbit closure
 $\overline {\Gamma _{\mu }^+x}$
equals
$\overline {\Gamma _{\mu }^+x}$
equals
 $Y_x$
.
$Y_x$
. -
(ii) One has
 $$ \begin{align*} \lim_{n\to \infty}\frac{1}{n}\sum_{k=0}^{n-1}\mu^{*k}* \delta_x=\nu_x. \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty}\frac{1}{n}\sum_{k=0}^{n-1}\mu^{*k}* \delta_x=\nu_x. \end{align*} $$
-
(iii) For
 $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
 $(g_1, g_2 , \dots )\in H^{\mathbb {N}} $
one has
$(g_1, g_2 , \dots )\in H^{\mathbb {N}} $
one has  $$ \begin{align*} \lim_{n\to \infty}\frac{1}{n}\sum_{k=0}^{n-1}\delta_{g_k\dotsm g_1x}=\nu_x. \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty}\frac{1}{n}\sum_{k=0}^{n-1}\delta_{g_k\dotsm g_1x}=\nu_x. \end{align*} $$
In statements (ii) and (iii) of the theorem above, convergence is understood with respect to the weak* topology, where weak* convergence of a sequence of probability measures
![]() $\nu _n$
on X to a finite measure
$\nu _n$
on X to a finite measure
![]() $\nu $
on X is defined to mean that
$\nu $
on X is defined to mean that
for every compactly supported continuous test function f on X. In case the limit measure
![]() $\nu $
is a probability measure, weak* convergence
$\nu $
is a probability measure, weak* convergence
![]() $\nu _n\to \nu $
implies that equation (1.2) holds for any bounded continuous function f on X.
$\nu _n\to \nu $
implies that equation (1.2) holds for any bounded continuous function f on X.
Theorem 1.6 will be proved in §7.2. It has the nontrivial topological consequence that any infinite
![]() $\Gamma _{\mu }^+$
-orbit in X is dense in a homogeneous subspace of positive dimension. In the G-expanding case with an irreducible lattice
$\Gamma _{\mu }^+$
-orbit in X is dense in a homogeneous subspace of positive dimension. In the G-expanding case with an irreducible lattice
![]() $\Lambda <G$
, this means that every infinite
$\Lambda <G$
, this means that every infinite
![]() $\Gamma _{\mu }^+$
-orbit in
$\Gamma _{\mu }^+$
-orbit in
![]() $X=G/\Lambda $
is dense.
$X=G/\Lambda $
is dense.
Remark 1.7. Using auxiliary constructions, our results can be applied in certain cases where the connected semisimple group H is invisible. For example, they cover random walks by automorphisms on a compact nilmanifold
![]() $N/\Lambda '$
by considering
$N/\Lambda '$
by considering
![]() $G=\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))\ltimes N$
and
$G=\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))\ltimes N$
and
![]() $\Lambda =\operatorname {\mathrm {Aut}}(\Lambda ')\ltimes \Lambda '$
, where
$\Lambda =\operatorname {\mathrm {Aut}}(\Lambda ')\ltimes \Lambda '$
, where
![]() $\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))$
denotes the Zariski closure of
$\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))$
denotes the Zariski closure of
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
inside
$\operatorname {\mathrm {Aut}}(\Lambda ')$
inside
![]() $\operatorname {\mathrm {Aut}}(N)$
; see §7.4.
$\operatorname {\mathrm {Aut}}(N)$
; see §7.4.
1.4 The space of homogeneous measures
Given a closed subgroup
![]() $\Gamma $
of the Lie group G, we consider
$\Gamma $
of the Lie group G, we consider
where, as before,
![]() $X=G/\Lambda $
is the quotient of G by a lattice
$X=G/\Lambda $
is the quotient of G by a lattice
![]() $\Lambda $
. By definition, associated to each
$\Lambda $
. By definition, associated to each
![]() $Y\in \mathcal {S}(\Gamma )$
is a
$Y\in \mathcal {S}(\Gamma )$
is a
![]() $\Gamma $
-invariant and ergodic probability measure
$\Gamma $
-invariant and ergodic probability measure
![]() $\nu _Y$
with support Y. This defines an embedding of
$\nu _Y$
with support Y. This defines an embedding of
![]() $\mathcal {S}(\Gamma )$
into the space of probability measures on X, which we use to endow
$\mathcal {S}(\Gamma )$
into the space of probability measures on X, which we use to endow
![]() $\mathcal {S}(\Gamma )$
with the weak* topology. In the unipotent case, Mozes–Shah [Reference Mozes and Shah73] proved that convergence of homogeneous subspaces in this topology behaves in a very rigid way. Benoist–Quint [Reference Benoist and Quint10, §1.3] later obtained a version of this result for a subgroup
$\mathcal {S}(\Gamma )$
with the weak* topology. In the unipotent case, Mozes–Shah [Reference Mozes and Shah73] proved that convergence of homogeneous subspaces in this topology behaves in a very rigid way. Benoist–Quint [Reference Benoist and Quint10, §1.3] later obtained a version of this result for a subgroup
![]() $\Gamma $
that is Zariski dense in a semisimple group. Following their strategy, we obtain similar results in our setup.
$\Gamma $
that is Zariski dense in a semisimple group. Following their strategy, we obtain similar results in our setup.
Given a subset Z of X, let us write
![]() $\mathcal {S}_Z(\Gamma )=\{Y\in \mathcal {S}(\Gamma )\mid Y\cap Z\neq \emptyset \}$
and denote by
$\mathcal {S}_Z(\Gamma )=\{Y\in \mathcal {S}(\Gamma )\mid Y\cap Z\neq \emptyset \}$
and denote by
![]() $\delta _{\infty }$
the Dirac measure at
$\delta _{\infty }$
the Dirac measure at
![]() $\infty $
in the one-point compactification
$\infty $
in the one-point compactification
![]() $\overline {X}=X\cup \{\infty \}$
of X.
$\overline {X}=X\cup \{\infty \}$
of X.
Proposition 1.8. Retain the notation and assumptions of Theorem 1.6. Then we have:
-
(i) For every compact subset
 $Z\subset X$
,
$Z\subset X$
,
 $\mathcal {S}_Z(\Gamma _{\mu })$
is compact, and
$\mathcal {S}_Z(\Gamma _{\mu })$
is compact, and
 $\mathcal {S}_{HZ}(\Gamma _{\mu })$
is relatively compact inside
$\mathcal {S}_{HZ}(\Gamma _{\mu })$
is relatively compact inside
 $\mathcal {S}(\Gamma _{\mu })$
. Moreover, the set
$\mathcal {S}(\Gamma _{\mu })$
. Moreover, the set
 $\mathcal {S}(\Gamma _{\mu })\cup \{\delta _{\infty }\}$
is compact.
$\mathcal {S}(\Gamma _{\mu })\cup \{\delta _{\infty }\}$
is compact. -
(ii) If
 $Y_n \to Y_{\infty }$
in
$Y_n \to Y_{\infty }$
in
 $\mathcal {S}(\Gamma _{\mu })$
, then there exists a sequence
$\mathcal {S}(\Gamma _{\mu })$
, then there exists a sequence
 $l_n \in C_G(\Gamma _{\mu })$
with
$l_n \in C_G(\Gamma _{\mu })$
with
 $l_n \to e$
and
$l_n \to e$
and
 $Y_n \subset l_n Y_{\infty }$
for every
$Y_n \subset l_n Y_{\infty }$
for every
 $n\in \mathbb {N}$
large enough.
$n\in \mathbb {N}$
large enough.
This proposition is a manifestation of strong rigidity of the
![]() $\Gamma _{\mu }$
-invariant and ergodic homogeneous subspaces. For example, given a compact subset
$\Gamma _{\mu }$
-invariant and ergodic homogeneous subspaces. For example, given a compact subset
![]() $Z \subset X$
and
$Z \subset X$
and
![]() $Y_{\infty } \in \mathcal {S}(\Gamma _{\mu })$
with
$Y_{\infty } \in \mathcal {S}(\Gamma _{\mu })$
with
![]() $Z^\circ \cap Y_{\infty } \neq \emptyset $
, if for a sequence
$Z^\circ \cap Y_{\infty } \neq \emptyset $
, if for a sequence
![]() $Y_n \in \mathcal {S}(\Gamma _{\mu })$
we have
$Y_n \in \mathcal {S}(\Gamma _{\mu })$
we have
![]() $Y_n \cap Z \to Y_{\infty } \cap Z$
in the Hausdorff metric, then one can conclude that
$Y_n \cap Z \to Y_{\infty } \cap Z$
in the Hausdorff metric, then one can conclude that
![]() $Y_n \to Y_{\infty }$
in
$Y_n \to Y_{\infty }$
in
![]() $\mathcal {S}(\Gamma _{\mu })$
. In particular, the weak* topology on
$\mathcal {S}(\Gamma _{\mu })$
. In particular, the weak* topology on
![]() $\mathcal {S}(\Gamma _{\mu })$
coincides with the restriction to
$\mathcal {S}(\Gamma _{\mu })$
coincides with the restriction to
![]() $\mathcal {S}(\Gamma _{\mu })$
of the Fell topology on closed subsets of X.
$\mathcal {S}(\Gamma _{\mu })$
of the Fell topology on closed subsets of X.
Another consequence of Proposition 1.8 is the following equidistribution result for sequences of homogeneous subspaces in the case that
![]() $\Gamma _{\mu }$
has discrete centralizer in G.
$\Gamma _{\mu }$
has discrete centralizer in G.
Corollary 1.9. Retain the notation and assumptions of Theorem 1.6, and assume in addition that the centralizer
![]() $C_G(\Gamma _{\mu })$
of
$C_G(\Gamma _{\mu })$
of
![]() $\Gamma _{\mu }$
in G is discrete. Let
$\Gamma _{\mu }$
in G is discrete. Let
![]() $Y_{\infty }\in \mathcal {S}(\Gamma _{\mu })$
, and consider the set
$Y_{\infty }\in \mathcal {S}(\Gamma _{\mu })$
, and consider the set
of ergodic homogeneous subspaces of
![]() $Y_{\infty }$
. Suppose that
$Y_{\infty }$
. Suppose that
![]() $(Y_n)_n$
is a sequence in
$(Y_n)_n$
is a sequence in
![]() $\mathcal {S}(\Gamma _{\mu },Y_{\infty })$
such that for every fixed
$\mathcal {S}(\Gamma _{\mu },Y_{\infty })$
such that for every fixed
![]() $Y\in \mathcal {S}(\Gamma _{\mu },Y_{\infty })\setminus \{Y_{\infty }\}$
one has
$Y\in \mathcal {S}(\Gamma _{\mu },Y_{\infty })\setminus \{Y_{\infty }\}$
one has
![]() $Y_n\not \subset Y$
for all but finitely many n, and such that no subsequence of
$Y_n\not \subset Y$
for all but finitely many n, and such that no subsequence of
![]() $(Y_n)_n$
escapes to infinity. Then
$(Y_n)_n$
escapes to infinity. Then
![]() $Y_n\to Y_{\infty }$
in
$Y_n\to Y_{\infty }$
in
![]() $\mathcal {S}(\Gamma _{\mu })$
.
$\mathcal {S}(\Gamma _{\mu })$
.
Here, by ‘escape to infinity’ we mean weak* convergence towards the Dirac measure
![]() $\delta _{\infty }$
at infinity.
$\delta _{\infty }$
at infinity.
The proofs of both statements above will be given in §7.3.
1.5 Birkhoff genericity
We still assume that
![]() $\Lambda $
is a lattice in the Lie group G. Let
$\Lambda $
is a lattice in the Lie group G. Let
![]() $(a(t))_{t\in \mathbb {R} }$
be a one-parameter
$(a(t))_{t\in \mathbb {R} }$
be a one-parameter
![]() $\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H and
$\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H and
![]() $\nu $
a probability measure on
$\nu $
a probability measure on
![]() $X=G/\Lambda $
invariant under
$X=G/\Lambda $
invariant under
![]() $a(t)$
for every
$a(t)$
for every
![]() $t\in \mathbb {R}$
. We say that a Radon measure
$t\in \mathbb {R}$
. We say that a Radon measure
![]() $\eta $
on H is
$\eta $
on H is
![]() $a(t)$
-Birkhoff generic at
$a(t)$
-Birkhoff generic at
![]() $x\in X$
with respect to
$x\in X$
with respect to
![]() $\nu $
if
$\nu $
if
 $$ \begin{align*} \frac1T\int_0^T\delta_{a(t)hx}\mathop{}\!\mathrm{d} t\to\nu \end{align*} $$
$$ \begin{align*} \frac1T\int_0^T\delta_{a(t)hx}\mathop{}\!\mathrm{d} t\to\nu \end{align*} $$
in the weak* topology as
![]() $T\to \infty $
for
$T\to \infty $
for
![]() $\eta $
-almost every
$\eta $
-almost every
![]() $h\in H$
. It was first noticed by Simmons–Weiss [Reference Simmons and Weiss93] that, in certain situations, pathwise equidistribution of random walks as in Theorem 1.6(iii) can be used to deduce Birkhoff genericity of fractal measures
$h\in H$
. It was first noticed by Simmons–Weiss [Reference Simmons and Weiss93] that, in certain situations, pathwise equidistribution of random walks as in Theorem 1.6(iii) can be used to deduce Birkhoff genericity of fractal measures
![]() $\eta $
on unipotent subgroups of H with respect to the Haar measure on X, which has consequences in Diophantine approximation thanks to the Dani correspondence principle. Recently, more results were obtained in this direction in [Reference Prohaska and Sert79]. Both of these papers only deal with cases corresponding to
$\eta $
on unipotent subgroups of H with respect to the Haar measure on X, which has consequences in Diophantine approximation thanks to the Dani correspondence principle. Recently, more results were obtained in this direction in [Reference Prohaska and Sert79]. Both of these papers only deal with cases corresponding to
![]() $H=G$
in our setup. We are going to extend the existing results by removing this restriction. Even in the case where
$H=G$
in our setup. We are going to extend the existing results by removing this restriction. Even in the case where
![]() $H=G$
, we obtain Birkhoff genericity for more general one-parameter subgroups and fractal measures, which will also give new results on Diophantine approximation (see §1.6).
$H=G$
, we obtain Birkhoff genericity for more general one-parameter subgroups and fractal measures, which will also give new results on Diophantine approximation (see §1.6).
The one-parameter subgroups to which our results apply are required to satisfy certain expansion condition with respect to a unipotent subgroup of H. To phrase it, we use the concept of an a-expanding subgroup of H introduced in [Reference Shi91]. Namely, given an
![]() $\operatorname {\mathrm {Ad}}$
-diagonalizable element
$\operatorname {\mathrm {Ad}}$
-diagonalizable element
![]() $a\in H$
, a connected
$a\in H$
, a connected
![]() $\operatorname {\mathrm {Ad}}$
-unipotent subgroup U of H normalized by a is said to be a-expanding if for any nontrivial irreducible representation of H on a finite-dimensional real vector space V, the subspace
$\operatorname {\mathrm {Ad}}$
-unipotent subgroup U of H normalized by a is said to be a-expanding if for any nontrivial irreducible representation of H on a finite-dimensional real vector space V, the subspace
![]() $V^U$
of U-fixed vectors is expanded by a, that is,
$V^U$
of U-fixed vectors is expanded by a, that is,
![]() $\lim _{n\to \infty }a^{-n} v=0$
for any
$\lim _{n\to \infty }a^{-n} v=0$
for any
![]() $v\in V^U$
. If the projection of a to each simple factor of H is nontrivial, then certain horospherical subgroups of H are a-expanding. For example, this holds for the unstable horospherical subgroup
$v\in V^U$
. If the projection of a to each simple factor of H is nontrivial, then certain horospherical subgroups of H are a-expanding. For example, this holds for the unstable horospherical subgroup
of a; see §3.2.
Now, let U be an
![]() $a(1)$
-expanding subgroup contained in the unstable horospherical subgroup
$a(1)$
-expanding subgroup contained in the unstable horospherical subgroup
![]() $H^+_{a(1)}$
of
$H^+_{a(1)}$
of
![]() $a(1)$
. We wish to introduce a family of measures on U which are generated by random walks, in a sense to be made precise in what follows. Let
$a(1)$
. We wish to introduce a family of measures on U which are generated by random walks, in a sense to be made precise in what follows. Let
![]() $A'=\{a(t)\mid t\in \mathbb {R}\}$
, K be a maximal compact subgroup of H, and
$A'=\{a(t)\mid t\in \mathbb {R}\}$
, K be a maximal compact subgroup of H, and
![]() $K'=C_K(A')\cap N_H(U)$
. Here and hereafter,
$K'=C_K(A')\cap N_H(U)$
. Here and hereafter,
![]() $C_K(A')$
denotes the centralizer of
$C_K(A')$
denotes the centralizer of
![]() $A'$
in K and
$A'$
in K and
![]() $N_H(U)$
the normalizer of U in H. We set
$N_H(U)$
the normalizer of U in H. We set
![]() and denote by
and denote by
![]() $\lambda $
the function which associates to
$\lambda $
the function which associates to
![]() $g\in P$
the real parameter of its
$g\in P$
the real parameter of its
![]() $A'$
component in its
$A'$
component in its
![]() $K'A'U$
factorization; that is,
$K'A'U$
factorization; that is,
![]() $\lambda (g)=t \in \mathbb {R}$
for
$\lambda (g)=t \in \mathbb {R}$
for
![]() $g=k a(t) u\in K'A'U$
. Finally, given
$g=k a(t) u\in K'A'U$
. Finally, given
![]() $\omega =(g_1,g_2, \dots )\in P^{\mathbb {N}}$
and
$\omega =(g_1,g_2, \dots )\in P^{\mathbb {N}}$
and
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $k_{\omega , n} \in K'$
,
$k_{\omega , n} \in K'$
,
![]() $a_{\omega , n}\in A'$
and
$a_{\omega , n}\in A'$
and
![]() $u_{\omega , n}\in U$
be such that
$u_{\omega , n}\in U$
be such that
With this notation, we are ready to define the class of measures on U we shall be interested in.
Definition 1.10. Let
![]() $(a(t))_{t\in \mathbb {R} }\leqslant H$
be a one-parameter
$(a(t))_{t\in \mathbb {R} }\leqslant H$
be a one-parameter
![]() $\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H and U an
$\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H and U an
![]() $a(1)$
-expanding subgroup of H contained in
$a(1)$
-expanding subgroup of H contained in
![]() $H_{a(1)}^+$
. A probability measure
$H_{a(1)}^+$
. A probability measure
![]() $\eta $
on U is said to be generated by
$\eta $
on U is said to be generated by
![]() $a(1)$
-expanding random walks if there is a probability measure
$a(1)$
-expanding random walks if there is a probability measure
![]() $\mu $
on H with finite exponential moments satisfying the following properties:
$\mu $
on H with finite exponential moments satisfying the following properties:
-
(1)
 $\mu (P)=1$
and
$\mu (P)=1$
and
 $\int _P \lambda (g) \mathop {}\!\mathrm {d}\mu (g)>0$
,
$\int _P \lambda (g) \mathop {}\!\mathrm {d}\mu (g)>0$
, -
(2) the Zariski closure of the image of
 $\Gamma _{\mu }$
in
$\Gamma _{\mu }$
in
 $\operatorname {\mathrm {Ad}}(H)$
contains
$\operatorname {\mathrm {Ad}}(H)$
contains
 $\operatorname {\mathrm {Ad}}(U)$
, and
$\operatorname {\mathrm {Ad}}(U)$
, and -
(3)
 $\eta $
is equivalent to the pushforward of
$\eta $
is equivalent to the pushforward of
 $\mu ^{\mathbb {N}}$
by the map
$\mu ^{\mathbb {N}}$
by the map
 .
.
The existence of the limit in condition (3) above will be proved in Lemma 8.1. Moreover, we will see as part of our discussion in §8 that conditions (1) and (2) imply that
![]() $\mu $
is H-expanding which will allow us to employ our main measure classification and equidistribution results discussed above.
$\mu $
is H-expanding which will allow us to employ our main measure classification and equidistribution results discussed above.
For the statement of our result on Birkhoff genericity, recall that by Ratner’s theorems the orbit closure
![]() $\overline {Hx}$
is homogeneous for any
$\overline {Hx}$
is homogeneous for any
![]() $x\in X$
. We denote the homogeneous probability measure corresponding to
$x\in X$
. We denote the homogeneous probability measure corresponding to
![]() $\overline {Hx}$
by
$\overline {Hx}$
by
![]() $\nu _{ \overline {Hx}}$
.
$\nu _{ \overline {Hx}}$
.
Theorem 1.11. Let
![]() $\Lambda $
be a lattice in a real Lie group G and let
$\Lambda $
be a lattice in a real Lie group G and let
![]() $H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
$H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center. Let
![]() $(a(t))_{t\in \mathbb {R} }$
be a one-parameter
$(a(t))_{t\in \mathbb {R} }$
be a one-parameter
![]() $\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H and U an
$\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H and U an
![]() $a(1)$
-expanding subgroup of H contained in
$a(1)$
-expanding subgroup of H contained in
![]() $H_{a(1)}^+$
. Suppose that
$H_{a(1)}^+$
. Suppose that
![]() $\eta $
is a probability measure on U generated by
$\eta $
is a probability measure on U generated by
![]() $a(1)$
-expanding random walks. Then for every
$a(1)$
-expanding random walks. Then for every
![]() $x\in X$
,
$x\in X$
,
![]() $\eta $
is
$\eta $
is
![]() $a(t)$
-Birkhoff generic at x with respect to
$a(t)$
-Birkhoff generic at x with respect to
![]() $\nu _{ \overline {Hx}}$
.
$\nu _{ \overline {Hx}}$
.
Theorem 1.11 extends the main results of [Reference Shi91], which used the method of Chaika–Eskin [Reference Chaika and Eskin22] developed for the Teichmüller geodesic flow to prove Birkhoff genericity for the Haar measure on U. The same method was employed in [Reference Fraczek, Shi and Ulcigrai37] to obtain Birkhoff genericity for volume measures on curves. The proof of Theorem 1.11 will be given in §8, using the connection to random walks observed in [Reference Simmons and Weiss93].
Probability measures generated by expanding random walks include a piece of Haar measure on U and, under irreducibility conditions, self-similar measures on
![]() $\mathbb {R}^m$
as well as natural self-affine measures on Bedford–McMullen carpets. The latter example is crucial for our application to Diophantine approximation problems on fractals described next. In §9.2, we will also discuss a more general class of fractal measures covered by Definition 1.10.
$\mathbb {R}^m$
as well as natural self-affine measures on Bedford–McMullen carpets. The latter example is crucial for our application to Diophantine approximation problems on fractals described next. In §9.2, we will also discuss a more general class of fractal measures covered by Definition 1.10.
1.6 Diophantine approximation
By virtue of a correspondence principle going back to the work of Dani [Reference Dani25] and Kleinbock [Reference Kleinbock59], Theorem 1.11 on Birkhoff genericity has consequences for problems in Diophantine approximation, which we shall now describe.
Let
![]() $m \in \mathbb {N}$
be a positive integer,
$m \in \mathbb {N}$
be a positive integer,
![]() $\mathbf {v}=(v_1,\dots ,v_m)^t$
a (column) vector in
$\mathbf {v}=(v_1,\dots ,v_m)^t$
a (column) vector in
![]() $\mathbb {R}^m$
, and
$\mathbb {R}^m$
, and
![]() $\mathbf {r}=(r_1, \dots ,r_m) \in (0,1]^m$
such that
$\mathbf {r}=(r_1, \dots ,r_m) \in (0,1]^m$
such that
![]() $\sum _{i=1}^m r_i=1$
. The vector
$\sum _{i=1}^m r_i=1$
. The vector
![]() $\mathbf {v}$
is called
$\mathbf {v}$
is called
![]() $\mathbf {r}$
-badly approximable if there exists a constant
$\mathbf {r}$
-badly approximable if there exists a constant
![]() $C>0$
such that
$C>0$
such that
for every
![]() $\mathbf {p}=(p_1, \dots , p_m) \in \mathbb {Z}^m$
and
$\mathbf {p}=(p_1, \dots , p_m) \in \mathbb {Z}^m$
and
![]() $q \in \mathbb {Z}\setminus \{0\}$
. When
$q \in \mathbb {Z}\setminus \{0\}$
. When
![]() $r_i=1/m$
for every
$r_i=1/m$
for every
![]() $i=1,\dots , m$
, such a vector is simply called badly approximable. In the case
$i=1,\dots , m$
, such a vector is simply called badly approximable. In the case
![]() $m=1$
, the latter corresponds to the classical definition of a badly approximable number. It is easily seen by Dirichlet’s principle that for any vector
$m=1$
, the latter corresponds to the classical definition of a badly approximable number. It is easily seen by Dirichlet’s principle that for any vector
![]() $\mathbf {v} \in \mathbb {R}^m$
, the left-hand side of equation (1.3) is
$\mathbf {v} \in \mathbb {R}^m$
, the left-hand side of equation (1.3) is
![]() $\le 1$
for infinitely many pairs
$\le 1$
for infinitely many pairs
![]() $(\mathbf {p}, q) \in \mathbb {Z}^m \times (\mathbb {Z}\setminus \{0\})$
.
$(\mathbf {p}, q) \in \mathbb {Z}^m \times (\mathbb {Z}\setminus \{0\})$
.
The existence of badly approximable vectors was observed by Perron [Reference Perron76] a century ago. It follows from Schmidt’s results [Reference Schmidt88] that such vectors constitute a subset of
![]() $\mathbb {R}^m$
of everywhere-full Hausdorff dimension. This was strengthened in more recent works [Reference Kleinbock and Weiss55, Reference Kristensen, Thorn and Velani62] to the statement that badly approximable vectors contained in a sufficiently regular fractal
$\mathbb {R}^m$
of everywhere-full Hausdorff dimension. This was strengthened in more recent works [Reference Kleinbock and Weiss55, Reference Kristensen, Thorn and Velani62] to the statement that badly approximable vectors contained in a sufficiently regular fractal
![]() $\mathcal {K}$
form a subset of full Hausdorff dimension in
$\mathcal {K}$
form a subset of full Hausdorff dimension in
![]() $\mathcal {K}$
. For a general weight
$\mathcal {K}$
. For a general weight
![]() $\mathbf {r}$
, the results of [Reference Kleinbock and Weiss57, Reference Kristensen, Thorn and Velani62, Reference Pollington and Velani77] imply that
$\mathbf {r}$
, the results of [Reference Kleinbock and Weiss57, Reference Kristensen, Thorn and Velani62, Reference Pollington and Velani77] imply that
![]() $\mathbf {r}$
-badly approximable vectors have everywhere-full Hausdorff dimension in
$\mathbf {r}$
-badly approximable vectors have everywhere-full Hausdorff dimension in
![]() $\mathbb {R}^m$
. For
$\mathbb {R}^m$
. For
![]() $\mathbf {r}$
-badly approximable vectors on a fractal set
$\mathbf {r}$
-badly approximable vectors on a fractal set
![]() $\mathcal {K}$
, the full-dimension statement is known to hold when
$\mathcal {K}$
, the full-dimension statement is known to hold when
![]() $\mathcal {K}$
has a certain product structure (see [Reference Kleinbock and Weiss55, Theorem 8.4], [Reference Kristensen, Thorn and Velani62, Theorems 11,13]).
$\mathcal {K}$
has a certain product structure (see [Reference Kleinbock and Weiss55, Theorem 8.4], [Reference Kristensen, Thorn and Velani62, Theorems 11,13]).
The results outlined above can be summarized by saying that (
![]() $\mathbf {r}$
-)badly approximable vectors are abundant from the viewpoint of Hausdorff dimension. On the Lebesgue measure side, however, Khintchine’s theorem [Reference Khintchine54] implies that badly approximable vectors have zero Lebesgue measure. Using a generalization of Khintchine’s theorem [Reference Schmidt87], the same is seen to be true for
$\mathbf {r}$
-)badly approximable vectors are abundant from the viewpoint of Hausdorff dimension. On the Lebesgue measure side, however, Khintchine’s theorem [Reference Khintchine54] implies that badly approximable vectors have zero Lebesgue measure. Using a generalization of Khintchine’s theorem [Reference Schmidt87], the same is seen to be true for
![]() $\mathbf {r}$
-badly approximable vectors. The question whether badly approximable vectors on a given fractal
$\mathbf {r}$
-badly approximable vectors. The question whether badly approximable vectors on a given fractal
![]() $\mathcal {K}$
also form a null set with respect to a natural measure on the fractal proved to be rather more delicate. The first results in this direction are due to Einsiedler–Fishman–Shapira [Reference Einsiedler, Fishman and Shapira29], who proved that badly approximable vectors have zero Hausdorff measure on certain fractals invariant under toral endomorphisms (in case the dimension is
$\mathcal {K}$
also form a null set with respect to a natural measure on the fractal proved to be rather more delicate. The first results in this direction are due to Einsiedler–Fishman–Shapira [Reference Einsiedler, Fishman and Shapira29], who proved that badly approximable vectors have zero Hausdorff measure on certain fractals invariant under toral endomorphisms (in case the dimension is
![]() $m=1$
) or toral automorphisms (in case
$m=1$
) or toral automorphisms (in case
![]() $m=2$
). For example, their results apply to the middle-third Cantor set. This was vastly generalized by Simmons–Weiss [Reference Simmons and Weiss93], who established the same statement for general self-similar fractals satisfying a separation condition. To the best of our knowledge, for general weights
$m=2$
). For example, their results apply to the middle-third Cantor set. This was vastly generalized by Simmons–Weiss [Reference Simmons and Weiss93], who established the same statement for general self-similar fractals satisfying a separation condition. To the best of our knowledge, for general weights
![]() $\mathbf {r}$
or on fractals which are not strictly self-similar, the question of the measure of badly approximable vectors is open. Our methods allow us to make an initial contribution in this direction. For simplicity, here in the introduction we will describe only the special case of Bedford–McMullen carpets; see §9 for the discussion in full generality.
$\mathbf {r}$
or on fractals which are not strictly self-similar, the question of the measure of badly approximable vectors is open. Our methods allow us to make an initial contribution in this direction. For simplicity, here in the introduction we will describe only the special case of Bedford–McMullen carpets; see §9 for the discussion in full generality.
Bedford–McMullen carpets are two-dimensional self-affine fractals, introduced independently by Bedford [Reference Bedford2] and McMullen [Reference McMullen67], which admit a particularly simple construction. Let
![]() $a,b\ge 2$
be distinct integers and divide the unit square
$a,b\ge 2$
be distinct integers and divide the unit square
![]() $[0,1]^2$
into an
$[0,1]^2$
into an
![]() $a\times b$
-grid parallel to the coordinate axes. Choose an arbitrary subcollection S of the
$a\times b$
-grid parallel to the coordinate axes. Choose an arbitrary subcollection S of the
![]() $ab$
rectangles created and discard the remaining ones. Iteratively proceed in the same way for each of the rectangles that remain, using the same pattern S. The points remaining after infinite iteration form a Bedford–McMullen carpet
$ab$
rectangles created and discard the remaining ones. Iteratively proceed in the same way for each of the rectangles that remain, using the same pattern S. The points remaining after infinite iteration form a Bedford–McMullen carpet
![]() $\mathcal {K}$
. If
$\mathcal {K}$
. If
![]() $(c_i,d_i)_{i=1}^k$
denote the coordinates of the bottom-left corners of the rectangles kept in the first construction step and we define the affine maps
$(c_i,d_i)_{i=1}^k$
denote the coordinates of the bottom-left corners of the rectangles kept in the first construction step and we define the affine maps
![]() $\phi _i\colon \mathbb {R}^2\to \mathbb {R}^2$
by
$\phi _i\colon \mathbb {R}^2\to \mathbb {R}^2$
by
 $$ \begin{align*} \phi_i(x,y)=\begin{pmatrix}\frac1a & \\ &\frac1b\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}+\begin{pmatrix}c_i\\ d_i\end{pmatrix}, \end{align*} $$
$$ \begin{align*} \phi_i(x,y)=\begin{pmatrix}\frac1a & \\ &\frac1b\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}+\begin{pmatrix}c_i\\ d_i\end{pmatrix}, \end{align*} $$
then
![]() $\mathcal {K}$
is the unique nonempty compact subset of
$\mathcal {K}$
is the unique nonempty compact subset of
![]() $\mathbb {R}^2$
satisfying
$\mathbb {R}^2$
satisfying
![]() $\bigcup _{i=1}^k\phi _i(\mathcal {K})=\mathcal {K}$
. The Hausdorff dimension of fractals of this type was explicity calculated by Bedford and McMullen. Except for special cases, it turns out that their Hausdorff measure in the correct dimension is infinite [Reference Peres75]. However, there exists another natural measure
$\bigcup _{i=1}^k\phi _i(\mathcal {K})=\mathcal {K}$
. The Hausdorff dimension of fractals of this type was explicity calculated by Bedford and McMullen. Except for special cases, it turns out that their Hausdorff measure in the correct dimension is infinite [Reference Peres75]. However, there exists another natural measure
![]() $\nu _{\mathcal {K}}$
on
$\nu _{\mathcal {K}}$
on
![]() $\mathcal {K}$
, known as the McMullen measure: It is the unique T-invariant ergodic probability measure on
$\mathcal {K}$
, known as the McMullen measure: It is the unique T-invariant ergodic probability measure on
![]() $\mathcal {K}$
of full Hausdorff dimension, where T is the toral endomorphism corresponding to
$\mathcal {K}$
of full Hausdorff dimension, where T is the toral endomorphism corresponding to
![]() $(\begin {smallmatrix}a&\\ & b\end {smallmatrix})$
[Reference Kenyon and Peres52, Reference McMullen67]. For further background on the fractal geometry of Bedford–McMullen carpets, we refer to the survey article [Reference Fraser, Pollicott and Vaienti36].
$(\begin {smallmatrix}a&\\ & b\end {smallmatrix})$
[Reference Kenyon and Peres52, Reference McMullen67]. For further background on the fractal geometry of Bedford–McMullen carpets, we refer to the survey article [Reference Fraser, Pollicott and Vaienti36].
The following is a specialization of our Theorem 9.3 to the case of weighted badly approximable vectors on Bedford–McMullen carpets (see Corollary 9.5).
Theorem 1.12. Let
![]() $a,b$
be positive integers satisfying
$a,b$
be positive integers satisfying
![]() $\min \{a^2,b^2\}> \max \{a,b\}$
and let
$\min \{a^2,b^2\}> \max \{a,b\}$
and let
![]() $\mathcal {K}\subset \mathbb {R}^2$
be a Bedford–McMullen carpet invariant under the toral endomorphism
$\mathcal {K}\subset \mathbb {R}^2$
be a Bedford–McMullen carpet invariant under the toral endomorphism
![]() $T=(\begin {smallmatrix}a&\\&b\end {smallmatrix})$
. Suppose that
$T=(\begin {smallmatrix}a&\\&b\end {smallmatrix})$
. Suppose that
![]() $\mathcal {K}$
is not contained in any straight line. Then for the choice of weights
$\mathcal {K}$
is not contained in any straight line. Then for the choice of weights
 $$ \begin{align*} \mathbf{r}=\biggl(\frac{2\log a-\log b}{\log a+\log b},\frac{2\log b-\log a}{\log a+\log b}\biggr), \end{align*} $$
$$ \begin{align*} \mathbf{r}=\biggl(\frac{2\log a-\log b}{\log a+\log b},\frac{2\log b-\log a}{\log a+\log b}\biggr), \end{align*} $$
the set of
![]() $\mathbf {r}$
-badly approximable vectors on
$\mathbf {r}$
-badly approximable vectors on
![]() $\mathcal {K}$
has measure zero with respect to the McMullen measure
$\mathcal {K}$
has measure zero with respect to the McMullen measure
![]() $\nu _{\mathcal {K}}$
on
$\nu _{\mathcal {K}}$
on
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
The requirement above that
![]() $\mathcal {K}$
is not contained in any straight line plays the role of an irreducibility condition. It is satisfied when, in the construction of the Bedford–McMullen carpet described above, the kept rectangles in the pattern S do not all belong to a single line or column in the
$\mathcal {K}$
is not contained in any straight line plays the role of an irreducibility condition. It is satisfied when, in the construction of the Bedford–McMullen carpet described above, the kept rectangles in the pattern S do not all belong to a single line or column in the
![]() $a\times b$
-grid.
$a\times b$
-grid.
As mentioned before its statement, the above theorem will follow from a much more general result about Diophantine properties of ‘
![]() $(\mathbf {r},\mathbf {s})$
-matrix sponges’ (Theorem 9.3)—a class of fractals that we will introduce in §9.2.3. In fact, the latter result will imply a version of Theorem 1.12 for higher-dimensional analogues of Bedford–McMullen carpets, which are called ‘self-affine Sierpiński sponges’ in [Reference Kenyon and Peres52]; see Corollary 9.5.
$(\mathbf {r},\mathbf {s})$
-matrix sponges’ (Theorem 9.3)—a class of fractals that we will introduce in §9.2.3. In fact, the latter result will imply a version of Theorem 1.12 for higher-dimensional analogues of Bedford–McMullen carpets, which are called ‘self-affine Sierpiński sponges’ in [Reference Kenyon and Peres52]; see Corollary 9.5.
2 H-expansion: Definition and basic properties
We start by properly stating the definition of uniform expansion and giving alternative formulations thereof.
Definition 2.1. Let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
. A vector
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
. A vector
![]() $v\in \mathbb {R}^d$
is said to be
$v\in \mathbb {R}^d$
is said to be
![]() $\mu $
-expanded if
$\mu $
-expanded if
for
![]() $\mu ^{\mathbb {N}}$
-almost every sequence
$\mu ^{\mathbb {N}}$
-almost every sequence
![]() $(g_i)_i$
of elements of
$(g_i)_i$
of elements of
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
. The measure
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
. The measure
![]() $\mu $
is said to be uniformly expanding if every nonzero
$\mu $
is said to be uniformly expanding if every nonzero
![]() $v\in \mathbb {R}^d$
is
$v\in \mathbb {R}^d$
is
![]() $\mu $
-expanded. If equation (2.1) holds with
$\mu $
-expanded. If equation (2.1) holds with
![]() $\ge $
in place of
$\ge $
in place of
![]() $>$
for every nonzero
$>$
for every nonzero
![]() $v\in \mathbb {R}^d$
, we call
$v\in \mathbb {R}^d$
, we call
![]() $\mu $
noncontracting.
$\mu $
noncontracting.
The above definition is the most general, but it can be hard to verify in practice. The characterization in the following proposition is often simpler to check. Moreover, it will also play an important role in the height function constructions in §6. Recall that a probability measure
![]() $\mu $
on
$\mu $
on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
is said to have a finite first moment if
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
is said to have a finite first moment if
![]() $\int \log \operatorname {N}(g)\mathop {}\!\mathrm {d}\mu (g)<\infty $
, where
$\int \log \operatorname {N}(g)\mathop {}\!\mathrm {d}\mu (g)<\infty $
, where
![]() $\operatorname {N}(g)=\max \{ \left \lVert {g} \right \rVert , \left \lVert {g^{-1}} \right \rVert \}$
.
$\operatorname {N}(g)=\max \{ \left \lVert {g} \right \rVert , \left \lVert {g^{-1}} \right \rVert \}$
.
Proposition 2.2 [Reference Eskin and Lindenstrauss30, Lemma 1.5], [Reference Prohaska and Sert79, Proposition 2.4]
Let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment. Then
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment. Then
![]() $\mu $
is uniformly expanding if and only if there exists
$\mu $
is uniformly expanding if and only if there exists
![]() $N\in \mathbb {N}$
and a constant
$N\in \mathbb {N}$
and a constant
![]() $C>0$
such that for every nonzero
$C>0$
such that for every nonzero
![]() $v \in \mathbb {R}^d$
$v \in \mathbb {R}^d$
 $$ \begin{align*} \int_{\operatorname{\mathrm{GL}}_d(\mathbb{R})}\log\frac{ \left\lVert {gv} \right\rVert }{ \left\lVert {v} \right\rVert }\mathop{}\!\mathrm{d}\mu^{*N}(g)\ge C. \end{align*} $$
$$ \begin{align*} \int_{\operatorname{\mathrm{GL}}_d(\mathbb{R})}\log\frac{ \left\lVert {gv} \right\rVert }{ \left\lVert {v} \right\rVert }\mathop{}\!\mathrm{d}\mu^{*N}(g)\ge C. \end{align*} $$
Uniform expansion can also be conveniently understood in light of the following theorem of Furstenberg–Kifer and Hennion. Recall that given a probability measure
![]() $\mu $
on a Lie group G, we denote by
$\mu $
on a Lie group G, we denote by
![]() $\Gamma _{\mu }$
the closed subgroup generated by the support of
$\Gamma _{\mu }$
the closed subgroup generated by the support of
![]() $\mu $
.
$\mu $
.
Theorem 2.3 (Furstenberg–Kifer [Reference Furstenberg and Kifer39], Hennion [Reference Hennion48])
Let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment. Then there exists a partial flag
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment. Then there exists a partial flag
![]() $\mathbb {R}^d= F_1 \supset F_2 \supset \dots \supset F_k\supset F_{k+1}=\{0\}$
of
$\mathbb {R}^d= F_1 \supset F_2 \supset \dots \supset F_k\supset F_{k+1}=\{0\}$
of
![]() $\Gamma _{\mu }$
-invariant subspaces and a collection of real numbers
$\Gamma _{\mu }$
-invariant subspaces and a collection of real numbers
![]() $\beta _1(\mu )>\dots >\beta _k(\mu )$
such that for every
$\beta _1(\mu )>\dots >\beta _k(\mu )$
such that for every
![]() $v \in F_i\setminus F_{i+1}$
, we have
$v \in F_i\setminus F_{i+1}$
, we have
![]() $\mu ^{\mathbb {N}}$
-a.s.
$\mu ^{\mathbb {N}}$
-a.s.
Moreover, the
![]() $\beta _i(\mu )$
are the values of
$\beta _i(\mu )$
are the values of

that occur when
![]() $\nu $
ranges over
$\nu $
ranges over
![]() $\mu $
-ergodic
$\mu $
-ergodic
![]() $\mu $
-stationary probability measures on the projective space
$\mu $
-stationary probability measures on the projective space
![]() $\mathbb {P}(\mathbb {R}^d)$
.
$\mathbb {P}(\mathbb {R}^d)$
.
In this result, the set of exponents
![]() $\{\beta _1(\mu ),\dots ,\beta _k(\mu )\}$
is contained in the set of Lyapunov exponents of
$\{\beta _1(\mu ),\dots ,\beta _k(\mu )\}$
is contained in the set of Lyapunov exponents of
![]() $\mu $
and
$\mu $
and
![]() $\beta _1(\mu )$
coincides with the top Lyapunov exponent.
$\beta _1(\mu )$
coincides with the top Lyapunov exponent.
Uniform expansion can now be rephrased as follows.
Lemma 2.4. A probability measure
![]() $\mu $
on
$\mu $
on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment is uniformly expanding if and only if
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment is uniformly expanding if and only if
![]() $\beta _k(\mu )>0$
, where
$\beta _k(\mu )>0$
, where
![]() $\beta _k(\mu )$
is the smallest exponent appearing in Theorem 2.3.
$\beta _k(\mu )$
is the smallest exponent appearing in Theorem 2.3.
Furstenberg–Kifer’s theorem can also be used to see that, in fact, almost sure divergence is enough to get uniform expansion. It will be useful to denote by
![]() $F^{\leqslant 0}$
the largest subspace among
$F^{\leqslant 0}$
the largest subspace among
![]() $F_1,\dots ,F_{k+1}$
with nonpositive exponent.
$F_1,\dots ,F_{k+1}$
with nonpositive exponent.
Proposition 2.5. Let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment. Then
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
with finite first moment. Then
![]() $\mu $
is uniformly expanding if and only if for every nonzero
$\mu $
is uniformly expanding if and only if for every nonzero
![]() $v\in \mathbb {R}^d$
we have
$v\in \mathbb {R}^d$
we have
for
![]() $\mu ^{\mathbb {N}}$
-a.e. sequence
$\mu ^{\mathbb {N}}$
-a.e. sequence
![]() $(g_i)_i$
of elements of
$(g_i)_i$
of elements of
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
.
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
.
Proof. We only need to show that equation (2.2) implies uniform expansion. We apply Theorem 2.3 and consider the space
![]() $F^{\leqslant 0}$
defined before the statement of the proposition. This space is
$F^{\leqslant 0}$
defined before the statement of the proposition. This space is
![]() $\Gamma _{\mu }$
-invariant. If it is nonzero, its projectivization thus supports an ergodic
$\Gamma _{\mu }$
-invariant. If it is nonzero, its projectivization thus supports an ergodic
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\nu $
. Using the assumed almost sure divergence and Atkinson/Kesten’s lemma (see, e.g., [Reference Bougerol and Lacroix18, Lemma II.2.2]), it follows that
$\nu $
. Using the assumed almost sure divergence and Atkinson/Kesten’s lemma (see, e.g., [Reference Bougerol and Lacroix18, Lemma II.2.2]), it follows that
![]() $\alpha (\nu )>0$
, where
$\alpha (\nu )>0$
, where
![]() $\alpha (\nu )$
is as defined in Theorem 2.3, a contradiction.
$\alpha (\nu )$
is as defined in Theorem 2.3, a contradiction.
For later use, let us also record at this point an immediate restriction that the presence of expansion puts on
![]() $\mu $
-stationary measures on finite-dimensional vector spaces.
$\mu $
-stationary measures on finite-dimensional vector spaces.
Lemma 2.6. Let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\operatorname {\mathrm {GL}}_d(\mathbb {R})$
and E a measurable subset of
$\operatorname {\mathrm {GL}}_d(\mathbb {R})$
and E a measurable subset of
![]() $\mathbb {R}^d$
such that every
$\mathbb {R}^d$
such that every
![]() $v\in E$
is
$v\in E$
is
![]() $\mu $
-expanded. Then every
$\mu $
-expanded. Then every
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\nu $
on
$\nu $
on
![]() $\mathbb {R}^d$
satisfies
$\mathbb {R}^d$
satisfies
![]() $\nu (E)=0$
.
$\nu (E)=0$
.
In particular, if
![]() $\mu $
has a finite first moment, then any
$\mu $
has a finite first moment, then any
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\nu $
on
$\nu $
on
![]() $\mathbb {R}^d$
is supported on the Furstenberg–Kifer subspace
$\mathbb {R}^d$
is supported on the Furstenberg–Kifer subspace
![]() $F^{\leqslant 0}$
of subexponential expansion. With a similar argument for vectors that are contracted instead of expanded, one can more generally show that
$F^{\leqslant 0}$
of subexponential expansion. With a similar argument for vectors that are contracted instead of expanded, one can more generally show that
![]() $\nu ((F^{\leqslant 0}\setminus F^{<0})\cup \{0\})=1$
, where
$\nu ((F^{\leqslant 0}\setminus F^{<0})\cup \{0\})=1$
, where
![]() $F^{<0}$
is defined in a way analogous to
$F^{<0}$
is defined in a way analogous to
![]() $F^{\leqslant 0}$
.
$F^{\leqslant 0}$
.
Proof. Write
![]() $G=\operatorname {\mathrm {GL}}_d(\mathbb {R})$
and
$G=\operatorname {\mathrm {GL}}_d(\mathbb {R})$
and
![]() $V=\mathbb {R}^d$
. By [Reference Benoist and Quint11, Proposition 2.14], the forward dynamical system
$V=\mathbb {R}^d$
. By [Reference Benoist and Quint11, Proposition 2.14], the forward dynamical system
![]() $(G^{\mathbb {N}} \times V, \mu ^{\mathbb {N}} \times \nu , T^V)$
is measure preserving, where
$(G^{\mathbb {N}} \times V, \mu ^{\mathbb {N}} \times \nu , T^V)$
is measure preserving, where
Let K be a compact subset of V. Then by Poincaré recurrence applied to
![]() $G^{\mathbb {N}} \times K$
, we know that
$G^{\mathbb {N}} \times K$
, we know that
![]() $\nu (K\cap E)=0$
, and the conclusion follows.
$\nu (K\cap E)=0$
, and the conclusion follows.
Now, we come to the central concept of this article: H-expansion.
Definition 2.7. Let H be a connected semisimple Lie group with finite center and
![]() $\mu $
a probability measure on H. Given a representation
$\mu $
a probability measure on H. Given a representation
![]() $(\rho ,V)$
of H we say that
$(\rho ,V)$
of H we say that
![]() $\mu $
is uniformly expanding in
$\mu $
is uniformly expanding in
![]() $(\rho ,V)$
if
$(\rho ,V)$
if
![]() $\rho _*\mu $
is uniformly expanding. We say that
$\rho _*\mu $
is uniformly expanding. We say that
![]() $\mu $
is H-expanding if
$\mu $
is H-expanding if
![]() $\mu $
is uniformly expanding in every representation of H without nonzero H-fixed vectors, or equivalently, in every nontrivial irreducible representation of H.
$\mu $
is uniformly expanding in every representation of H without nonzero H-fixed vectors, or equivalently, in every nontrivial irreducible representation of H.
Here and everywhere else, by a ‘representation’ we always mean a continuous homomorphism into the group of invertible linear transformations of a finite-dimensional real vector space. It is well known that such representations are automatically smooth. For notational simplicity, we are going to simply write
![]() $h{\boldsymbol {\cdot }} v$
for
$h{\boldsymbol {\cdot }} v$
for
![]() $\rho (h)v$
for
$\rho (h)v$
for
![]() $h\in H$
and
$h\in H$
and
![]() $v\in V$
when the representation
$v\in V$
when the representation
![]() $(\rho ,V)$
is clear from context. In this case, we also just say that
$(\rho ,V)$
is clear from context. In this case, we also just say that
![]() $\mu $
is uniformly expanding on V to mean that
$\mu $
is uniformly expanding on V to mean that
![]() $\mu $
is uniformly expanding in
$\mu $
is uniformly expanding in
![]() $(\rho ,V)$
.
$(\rho ,V)$
.
We next recall what the moment conditions mean for a probability measure on a semisimple group that is not necessarily linear.
Definition 2.8. Let H be a connected semisimple Lie group with finite center. Let
![]() $\mu $
be a probability measure on H. Then
$\mu $
be a probability measure on H. Then
![]() $\mu $
is said to have a finite first moment (resp. finite exponential moments) if
$\mu $
is said to have a finite first moment (resp. finite exponential moments) if
![]() $\rho _*\mu $
has a finite first moment (resp. finite exponential moments) for some representation
$\rho _*\mu $
has a finite first moment (resp. finite exponential moments) for some representation
![]() $\rho $
of H with finite kernel.
$\rho $
of H with finite kernel.
Of course, these moment conditions are automatically satisfied when
![]() $\mu $
has compact support.
$\mu $
has compact support.
Lemma 2.9 [Reference Benoist and Quint11, Lemmas 10.6, 10.7]
Let H and
![]() $\mu $
be as in Definition 2.8, and suppose that
$\mu $
be as in Definition 2.8, and suppose that
![]() $\mu $
has a finite first moment (resp. finite exponential moments). Then
$\mu $
has a finite first moment (resp. finite exponential moments). Then
![]() $\rho _*\mu $
has a finite first moment (resp. finite exponential moments) for any representation
$\rho _*\mu $
has a finite first moment (resp. finite exponential moments) for any representation
![]() $\rho $
of H.
$\rho $
of H.
We remark that even though in [Reference Benoist and Quint11], the above lemma is proved for algebraic groups, the given proof also works for a connected semisimple group H with finite center. Indeed, the argument relies only on a reformulation of the moment condition into an integrability condition on the Cartan projection
![]() $\kappa \colon H\to \mathfrak {a}^+$
, which is related to representations of H by virtue of the formula
$\kappa \colon H\to \mathfrak {a}^+$
, which is related to representations of H by virtue of the formula
![]() $ \left \lVert {\rho (h)} \right \rVert =e^{\chi (\kappa (h))}$
for
$ \left \lVert {\rho (h)} \right \rVert =e^{\chi (\kappa (h))}$
for
![]() $h\in H$
, where
$h\in H$
, where
![]() $(\rho ,V)$
is an irreducible representation of H with highest weight
$(\rho ,V)$
is an irreducible representation of H with highest weight
![]() $\chi $
and
$\chi $
and
![]() $ \left \lVert {\cdot } \right \rVert $
is the operator norm associated to a Euclidean norm on V invariant under the maximal compact subgroup K of H used to define
$ \left \lVert {\cdot } \right \rVert $
is the operator norm associated to a Euclidean norm on V invariant under the maximal compact subgroup K of H used to define
![]() $\kappa $
.
$\kappa $
.
In the proposition below, we collect some first facts about H-expansion.
Proposition 2.10. Let H be a connected semisimple Lie group with finite center and
![]() $\mu $
a probability measure on H. Then:
$\mu $
a probability measure on H. Then:
-
(i) Given a representation
 $(\rho ,V)$
of H, the following are equivalent:
$(\rho ,V)$
of H, the following are equivalent:-
○ Any vector
 $v\in V$
that is not
$v\in V$
that is not
 $\rho _*\mu $
-expanded is H-fixed.
$\rho _*\mu $
-expanded is H-fixed. -
○ The measure
 $\mu $
is uniformly expanding on the quotient
$\mu $
is uniformly expanding on the quotient
 $V/V^H$
.
$V/V^H$
.
-
-
(ii) If
 $\mu $
is H-expanding, then H has no compact factors.
$\mu $
is H-expanding, then H has no compact factors. -
(iii) If
 $\mu $
is H-expanding and
$\mu $
is H-expanding and
 $\psi \colon H\to G'$
is a nontrivial continuous homomorphism into a real Lie group
$\psi \colon H\to G'$
is a nontrivial continuous homomorphism into a real Lie group
 $G'$
, then
$G'$
, then
 $H'=\psi (H)$
is a connected, closed, semisimple subgroup of
$H'=\psi (H)$
is a connected, closed, semisimple subgroup of
 $G'$
with finite center and
$G'$
with finite center and
 $\psi _*\mu $
is
$\psi _*\mu $
is
 $H'$
-expanding.
$H'$
-expanding. -
(iv) Suppose H is an almost direct product of connected normal subgroups
 $H_1$
and
$H_1$
and
 $H_2$
, and let
$H_2$
, and let
 $\mu _i$
be probability measures on
$\mu _i$
be probability measures on
 $H_i$
with finite first moments,
$H_i$
with finite first moments,
 $i=1,2$
. If
$i=1,2$
. If
 $\mu _i$
is
$\mu _i$
is
 $H_i$
-expanding for
$H_i$
-expanding for
 $i=1,2$
and
$i=1,2$
and
 $\mu $
is the pushforward of
$\mu $
is the pushforward of
 $\mu _1 \times \mu _2$
by multiplication, then
$\mu _1 \times \mu _2$
by multiplication, then
 $\mu $
is H-expanding.
$\mu $
is H-expanding.
Proof. For (i), note that by semisimplicity of H, the quotient
![]() $V/V^H$
identifies with an H-invariant complement
$V/V^H$
identifies with an H-invariant complement
![]() $V^+$
of
$V^+$
of
![]() $V^H$
in V. Thus, we only need to prove that uniform expansion of
$V^H$
in V. Thus, we only need to prove that uniform expansion of
![]() $\mu $
on
$\mu $
on
![]() $V^+$
implies the statement in the first bullet point. Let
$V^+$
implies the statement in the first bullet point. Let
![]() $p_+\colon V\to V^+$
be the projection, and take
$p_+\colon V\to V^+$
be the projection, and take
![]() $v \in V$
which is not
$v \in V$
which is not
![]() $\rho _*\mu $
-expanded. Then also
$\rho _*\mu $
-expanded. Then also
![]() $p_+(v)$
is not
$p_+(v)$
is not
![]() $\rho _*\mu $
-expanded so that uniform expansion on
$\rho _*\mu $
-expanded so that uniform expansion on
![]() $V^+$
implies
$V^+$
implies
![]() $p_+(v)=0$
. Hence, v is H-fixed.
$p_+(v)=0$
. Hence, v is H-fixed.
For (ii), suppose H has a compact factor K. Then
![]() $\mu $
cannot be uniformly expanding in the representation of H obtained by composing the projection on K with the adjoint representation of K. Thus,
$\mu $
cannot be uniformly expanding in the representation of H obtained by composing the projection on K with the adjoint representation of K. Thus,
![]() $\mu $
is not H-expanding.
$\mu $
is not H-expanding.
As H is semisimple and has finite center,
![]() $H'$
is a connected and semisimple immersed Lie subgroup of
$H'$
is a connected and semisimple immersed Lie subgroup of
![]() $G'$
with finite center in the setting of (iii). As representations of
$G'$
with finite center in the setting of (iii). As representations of
![]() $H'$
induce representations of H by precomposition with
$H'$
induce representations of H by precomposition with
![]() $\psi $
, the
$\psi $
, the
![]() $H'$
-expansion condition is immediate. It only remains to argue that
$H'$
-expansion condition is immediate. It only remains to argue that
![]() $H'$
is closed in
$H'$
is closed in
![]() $G'$
. As this is in fact a more general statement, we drop the accents and simply show that a semisimple immersed Lie subgroup H of a Lie group G must be closed when H has finite center. For this, it suffices to show that if a sequence
$G'$
. As this is in fact a more general statement, we drop the accents and simply show that a semisimple immersed Lie subgroup H of a Lie group G must be closed when H has finite center. For this, it suffices to show that if a sequence
![]() $(h_n)_n$
in H converges to the identity e in the topology of G, then this convergence holds also in the topology of H. Notice that
$(h_n)_n$
in H converges to the identity e in the topology of G, then this convergence holds also in the topology of H. Notice that
![]() $\operatorname {\mathrm {Ad}}_G(h_n)$
considered as elements of
$\operatorname {\mathrm {Ad}}_G(h_n)$
considered as elements of
![]() $\operatorname {\mathrm {Aut}}(\mathfrak h)$
converges to the identity map when
$\operatorname {\mathrm {Aut}}(\mathfrak h)$
converges to the identity map when
![]() $\operatorname {\mathrm {Aut}}(\mathfrak h)$
is endowed with the subspace topology inherited from
$\operatorname {\mathrm {Aut}}(\mathfrak h)$
is endowed with the subspace topology inherited from
![]() $\operatorname {\mathrm {Aut}}(\mathfrak g)$
. However, as linear semisimple Lie algebras are algebraic (see [Reference Hochschild49, Theorem VIII.3.2]), this subspace topology coincides with the usual topology of
$\operatorname {\mathrm {Aut}}(\mathfrak g)$
. However, as linear semisimple Lie algebras are algebraic (see [Reference Hochschild49, Theorem VIII.3.2]), this subspace topology coincides with the usual topology of
![]() $\operatorname {\mathrm {Aut}}(\mathfrak h)$
. Since near the identity,
$\operatorname {\mathrm {Aut}}(\mathfrak h)$
. Since near the identity,
![]() $\operatorname {\mathrm {Ad}}_H$
is a local isomorphism from H to
$\operatorname {\mathrm {Ad}}_H$
is a local isomorphism from H to
![]() $\operatorname {\mathrm {Aut}}(\mathfrak h)$
, we thus find a sequence
$\operatorname {\mathrm {Aut}}(\mathfrak h)$
, we thus find a sequence
![]() $(h_n')_n$
converging to e in H such that
$(h_n')_n$
converging to e in H such that
![]() $\operatorname {\mathrm {Ad}}_H(h_n)=\operatorname {\mathrm {Ad}}_H(h_n')$
for all n. This implies that
$\operatorname {\mathrm {Ad}}_H(h_n)=\operatorname {\mathrm {Ad}}_H(h_n')$
for all n. This implies that
![]() $h_n^{-1}h_n'$
is contained in the center of H and converges to e. As the center is finite, we have
$h_n^{-1}h_n'$
is contained in the center of H and converges to e. As the center is finite, we have
![]() $h_n=h_n'$
for all n large enough. We conclude that, indeed,
$h_n=h_n'$
for all n large enough. We conclude that, indeed,
![]() $h_n\to e$
as
$h_n\to e$
as
![]() $n\to \infty $
holds also in the topology of H.
$n\to \infty $
holds also in the topology of H.
Finally, to prove (iv), let
![]() $(\rho ,V)$
be a nontrivial irreducible representation of H. Since
$(\rho ,V)$
be a nontrivial irreducible representation of H. Since
![]() $H_1$
and
$H_1$
and
![]() $H_2$
commute, for every
$H_2$
commute, for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\mu ^{*n}$
is the pushforward by multiplication of
$\mu ^{*n}$
is the pushforward by multiplication of
![]() $\mu _1^{*n} \times \mu _2^{*n}$
, and the subspaces
$\mu _1^{*n} \times \mu _2^{*n}$
, and the subspaces
![]() $V^{H_i}$
of
$V^{H_i}$
of
![]() $H_i$
-fixed vectors in V are H-invariant. By irreducibility, they are trivial or all of V. It follows that one of
$H_i$
-fixed vectors in V are H-invariant. By irreducibility, they are trivial or all of V. It follows that one of
![]() $V^{H_1},V^{H_2}$
is zero. We assume without loss of generality that
$V^{H_1},V^{H_2}$
is zero. We assume without loss of generality that
![]() $V^{H_1}=\{0\}$
.
$V^{H_1}=\{0\}$
.
Note that both
![]() $\rho _*\mu _1$
and
$\rho _*\mu _1$
and
![]() $\rho _*\mu _2$
have a finite first moment by Lemma 2.9. This readily implies that
$\rho _*\mu _2$
have a finite first moment by Lemma 2.9. This readily implies that
![]() $\rho _*\mu $
has a finite first moment. By Proposition 2.2, it suffices to show that for N large enough and
$\rho _*\mu $
has a finite first moment. By Proposition 2.2, it suffices to show that for N large enough and
![]() $v\neq 0$
, the quantity
$v\neq 0$
, the quantity
 $$ \begin{align*} &\int_{H_1\times H_2}\log\frac{ \left\lVert {h_1h_2{\boldsymbol{\cdot}} v} \right\rVert }{ \left\lVert {v} \right\rVert }\mathop{}\!\mathrm{d}\mu_1^{*N}(h_1)\mathop{}\!\mathrm{d}\mu_2^{*N}(h_2)\\&=\int_{H_2}\int_{H_1}\log\frac{ \left\lVert {h_1h_2{\boldsymbol{\cdot}} v} \right\rVert }{ \left\lVert {h_2{\boldsymbol{\cdot}} v} \right\rVert }\mathop{}\!\mathrm{d}\mu_1^{*N}(h_1)\mathop{}\!\mathrm{d}\mu_2^{*N}(h_2)+\int_{H_2}\log\frac{ \left\lVert {h_2{\boldsymbol{\cdot}} v} \right\rVert }{ \left\lVert {v} \right\rVert }\mathop{}\!\mathrm{d}\mu_2^{*N}(h_2) \end{align*} $$
$$ \begin{align*} &\int_{H_1\times H_2}\log\frac{ \left\lVert {h_1h_2{\boldsymbol{\cdot}} v} \right\rVert }{ \left\lVert {v} \right\rVert }\mathop{}\!\mathrm{d}\mu_1^{*N}(h_1)\mathop{}\!\mathrm{d}\mu_2^{*N}(h_2)\\&=\int_{H_2}\int_{H_1}\log\frac{ \left\lVert {h_1h_2{\boldsymbol{\cdot}} v} \right\rVert }{ \left\lVert {h_2{\boldsymbol{\cdot}} v} \right\rVert }\mathop{}\!\mathrm{d}\mu_1^{*N}(h_1)\mathop{}\!\mathrm{d}\mu_2^{*N}(h_2)+\int_{H_2}\log\frac{ \left\lVert {h_2{\boldsymbol{\cdot}} v} \right\rVert }{ \left\lVert {v} \right\rVert }\mathop{}\!\mathrm{d}\mu_2^{*N}(h_2) \end{align*} $$
is uniformly bounded from below by some
![]() $C>0$
. As
$C>0$
. As
![]() $\rho _*\mu _1$
is uniformly expanding, Proposition 2.2 gives this lower bound for the first integral above for N large enough. By the same argument, the second term is either equal to
$\rho _*\mu _1$
is uniformly expanding, Proposition 2.2 gives this lower bound for the first integral above for N large enough. By the same argument, the second term is either equal to
![]() $0$
or also bounded below by some
$0$
or also bounded below by some
![]() $C>0$
, according to whether
$C>0$
, according to whether
![]() $V^{H_2}$
is V or
$V^{H_2}$
is V or
![]() $\{0\}$
, respectively.
$\{0\}$
, respectively.
Remark 2.11. We point out that in part (iii) of the previous proposition, if the target
![]() $G'$
of the homomorphism
$G'$
of the homomorphism
![]() $\psi $
is a real algebraic group, then the conclusion can be strengthened to the statement that the semisimple group
$\psi $
is a real algebraic group, then the conclusion can be strengthened to the statement that the semisimple group
![]() $H'=\psi (H)$
is almost algebraic, meaning that it has finite index in a real algebraic subgroup of
$H'=\psi (H)$
is almost algebraic, meaning that it has finite index in a real algebraic subgroup of
![]() $G'$
. Indeed, as already exploited in the proof above, the point is that linear semisimple Lie algebras are algebraic. In particular, this applies when
$G'$
. Indeed, as already exploited in the proof above, the point is that linear semisimple Lie algebras are algebraic. In particular, this applies when
![]() $\psi $
is a representation
$\psi $
is a representation
![]() $(\rho ,V)$
of H. This fact is useful to keep in mind.
$(\rho ,V)$
of H. This fact is useful to keep in mind.
Combining Proposition 2.10(i) with Lemma 2.6, we immediately obtain the following corollary about
![]() $\mu $
-stationary measures on vector spaces.
$\mu $
-stationary measures on vector spaces.
Corollary 2.12. Let
![]() $(\rho ,V)$
be a representation of H, and suppose that
$(\rho ,V)$
be a representation of H, and suppose that
![]() $\mu $
is uniformly expanding on
$\mu $
is uniformly expanding on
![]() $V/V^H$
. Then any
$V/V^H$
. Then any
![]() $\mu $
-stationary probability measure on V is supported on the subspace
$\mu $
-stationary probability measure on V is supported on the subspace
![]() $V^H$
of H-fixed vectors.
$V^H$
of H-fixed vectors.
3 Examples of H-expanding measures
In this section, we exhibit classes of probability measures on semisimple Lie groups that satisfy the H-expansion property.
3.1 Zariski dense measures
As already mentioned in §1, the first class of examples of H-expanding measures consists of those whose support generates a Zariski dense subgroup of H. This is the class of measures considered by Benoist–Quint [Reference Benoist and Quint6, Reference Benoist and Quint9, Reference Benoist and Quint10].
Proposition 3.1. Let H be a connected semisimple Lie group without compact factors and with finite center. Let
![]() $\mu $
be a probability measure on H with finite first moment. Suppose that
$\mu $
be a probability measure on H with finite first moment. Suppose that
![]() $\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
is Zariski dense in
$\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
is Zariski dense in
![]() $\operatorname {\mathrm {Ad}}(H)$
. Then
$\operatorname {\mathrm {Ad}}(H)$
. Then
![]() $\mu $
is H-expanding.
$\mu $
is H-expanding.
For the proof, we need the following lemma, which is used to extend the Zariski density assumption to arbitrary representations.
Lemma 3.2. Let
![]() $\Gamma $
be a subsemigroup of H and S a connected subgroup of H. Suppose that the Zariski closure of
$\Gamma $
be a subsemigroup of H and S a connected subgroup of H. Suppose that the Zariski closure of
![]() $\operatorname {\mathrm {Ad}}(\Gamma )$
contains
$\operatorname {\mathrm {Ad}}(\Gamma )$
contains
![]() $\operatorname {\mathrm {Ad}}(S)$
. Then for every representation
$\operatorname {\mathrm {Ad}}(S)$
. Then for every representation
![]() $(\rho ,V)$
of H,
$(\rho ,V)$
of H,
![]() $\rho (S)$
is contained in
$\rho (S)$
is contained in
![]() $\operatorname {\mathrm {Zcl}}(\rho (\Gamma ))$
.
$\operatorname {\mathrm {Zcl}}(\rho (\Gamma ))$
.
Proof. We consider the product representation
![]() $\rho '=\operatorname {\mathrm {Ad}}\times \rho $
. Let
$\rho '=\operatorname {\mathrm {Ad}}\times \rho $
. Let
![]() $\mathcal H'$
be the Zariski closure of
$\mathcal H'$
be the Zariski closure of
![]() $\rho '(H)$
inside
$\rho '(H)$
inside
![]() $\operatorname {\mathrm {GL}}(\mathfrak h)\times \operatorname {\mathrm {GL}}(V)$
. Then both
$\operatorname {\mathrm {GL}}(\mathfrak h)\times \operatorname {\mathrm {GL}}(V)$
. Then both
![]() $\operatorname {\mathrm {Ad}}$
and
$\operatorname {\mathrm {Ad}}$
and
![]() $\rho $
factor through
$\rho $
factor through
![]() $\mathcal H'$
. As noted in Remark 2.11,
$\mathcal H'$
. As noted in Remark 2.11,
![]() $\rho '(H)$
has finite index in
$\rho '(H)$
has finite index in
![]() $\mathcal H'$
. The same holds for the Zariski closure
$\mathcal H'$
. The same holds for the Zariski closure
![]() $\mathcal H$
of
$\mathcal H$
of
![]() $\operatorname {\mathrm {Ad}}(H)$
so that both
$\operatorname {\mathrm {Ad}}(H)$
so that both
![]() $\mathcal H$
and
$\mathcal H$
and
![]() $\mathcal H'$
are Zariski connected real algebraic groups of dimension
$\mathcal H'$
are Zariski connected real algebraic groups of dimension
![]() $\dim (H)$
. Thus, projection to the first factor of
$\dim (H)$
. Thus, projection to the first factor of
![]() $\operatorname {\mathrm {GL}}(\mathfrak h)\times \operatorname {\mathrm {GL}}(V)$
gives an isogeny
$\operatorname {\mathrm {GL}}(\mathfrak h)\times \operatorname {\mathrm {GL}}(V)$
gives an isogeny
![]() $p\colon \mathcal H'\to \mathcal H$
, and we know that
$p\colon \mathcal H'\to \mathcal H$
, and we know that
![]() $\operatorname {\mathrm {Zcl}}(\rho '(\Gamma ))$
has finite index in
$\operatorname {\mathrm {Zcl}}(\rho '(\Gamma ))$
has finite index in
![]() $p^{-1}(\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Ad}}(\Gamma )))$
. Since
$p^{-1}(\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Ad}}(\Gamma )))$
. Since
![]() $\rho '(S)$
is connected and
$\rho '(S)$
is connected and
![]() $\operatorname {\mathrm {Ad}}(S)$
is contained in
$\operatorname {\mathrm {Ad}}(S)$
is contained in
![]() $\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Ad}}(\Gamma ))$
by assumption, it follows that
$\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Ad}}(\Gamma ))$
by assumption, it follows that
![]() $\rho '(S)$
is contained in
$\rho '(S)$
is contained in
![]() $\operatorname {\mathrm {Zcl}}(\rho '(\Gamma ))$
. By projecting to the second factor, we conclude that
$\operatorname {\mathrm {Zcl}}(\rho '(\Gamma ))$
. By projecting to the second factor, we conclude that
![]() $\rho (S)$
is contained in
$\rho (S)$
is contained in
![]() $\operatorname {\mathrm {Zcl}}(\rho (\Gamma ))$
.
$\operatorname {\mathrm {Zcl}}(\rho (\Gamma ))$
.
Proof of Proposition 3.1
Let
![]() $(\rho ,V)$
be a representation of H without nonzero H-fixed vectors. By Lemma 3.2,
$(\rho ,V)$
be a representation of H without nonzero H-fixed vectors. By Lemma 3.2,
![]() $\rho (\Gamma _{\mu })$
is Zariski dense in
$\rho (\Gamma _{\mu })$
is Zariski dense in
![]() $\rho (H)$
. Now, uniform expansion in
$\rho (H)$
. Now, uniform expansion in
![]() $(\rho ,V)$
follows directly from Furstenberg’s theorem on positivity of the top Lyapunov exponent (see [Reference Furstenberg40, Theorem 8.6]). To see that the assumptions of Furstenberg’s theorem are satisfied, note that by Lemma 2.9 we know that
$(\rho ,V)$
follows directly from Furstenberg’s theorem on positivity of the top Lyapunov exponent (see [Reference Furstenberg40, Theorem 8.6]). To see that the assumptions of Furstenberg’s theorem are satisfied, note that by Lemma 2.9 we know that
![]() $\rho _*\mu $
has a finite first moment, and using Zariski density of
$\rho _*\mu $
has a finite first moment, and using Zariski density of
![]() $\rho (\Gamma _{\mu })$
together with complete reducibility one may assume that
$\rho (\Gamma _{\mu })$
together with complete reducibility one may assume that
![]() $\rho (\Gamma _{\mu })$
acts irreducibly, which implies strong irreducibility in view of Zariski connectedness of
$\rho (\Gamma _{\mu })$
acts irreducibly, which implies strong irreducibility in view of Zariski connectedness of
![]() $\rho (H)$
. Finally, since the ground field is
$\rho (H)$
. Finally, since the ground field is
![]() $\mathbb {R}$
, the fact that the Zariski closure of
$\mathbb {R}$
, the fact that the Zariski closure of
![]() $\rho (\Gamma _{\mu })$
is noncompact implies that
$\rho (\Gamma _{\mu })$
is noncompact implies that
![]() $\rho (\Gamma _{\mu })$
is not relatively compact, finishing the proof.
$\rho (\Gamma _{\mu })$
is not relatively compact, finishing the proof.
3.2 Measures on parabolic groups
Our next goal is to exhibit probability measures supported on proper parabolic subgroups of H which are H-expanding. Combining general criteria with the notion of the expanding cone, which was introduced by the third-named author in [Reference Shi92] (see also the slightly earlier work [Reference Mohammadi and Golsefidy69]) and which traces back to the works of Shah and Weiss [Reference Shah89, Reference Shah and Weiss90, Reference Weiss95], we will obtain another easy-to-verify sufficient condition for H-expansion.
We start by explaining our general setup. Let H be a connected semisimple real Lie group without compact factors and with finite center and let a be an
![]() $\operatorname {\mathrm {Ad}}$
-diagonalizable element of H. Then given a representation
$\operatorname {\mathrm {Ad}}$
-diagonalizable element of H. Then given a representation
![]() $(\rho , V)$
of H, we have a direct sum decomposition
$(\rho , V)$
of H, we have a direct sum decomposition
where
![]() $V^+_a, V^0_a, V^-_a$
are the sums of the eigenspaces of
$V^+_a, V^0_a, V^-_a$
are the sums of the eigenspaces of
![]() $\rho (a)$
with eigenvalues
$\rho (a)$
with eigenvalues
![]() $>$
,
$>$
,
![]() $=$
or
$=$
or
![]() $<1$
, respectively. Let U be a connected
$<1$
, respectively. Let U be a connected
![]() $\operatorname {\mathrm {Ad}}$
-unipotent subgroup of H normalized by a. Following [Reference Shi91], we say that U is a-expanding if for every nontrivial irreducible representation
$\operatorname {\mathrm {Ad}}$
-unipotent subgroup of H normalized by a. Following [Reference Shi91], we say that U is a-expanding if for every nontrivial irreducible representation
![]() $(\rho , V)$
of H, the subspace
$(\rho , V)$
of H, the subspace
![]() $V^U$
of U-fixed vectors is contained in
$V^U$
of U-fixed vectors is contained in
![]() $V_a^+$
. It is equivalent ([Reference Shi91, Lemma A.1]) to require that in any irreducible representation of
$V_a^+$
. It is equivalent ([Reference Shi91, Lemma A.1]) to require that in any irreducible representation of
![]() $(\rho ,V)$
of H and for any nonzero
$(\rho ,V)$
of H and for any nonzero
![]() $v\in V$
, the
$v\in V$
, the
![]() $\rho (U)$
-orbit of v is not contained in
$\rho (U)$
-orbit of v is not contained in
![]() $V^0_a \oplus V_a^-$
. For example, if a has a nontrivial projection to every simple factor of H, then the unstable horospherical subgroup
$V^0_a \oplus V_a^-$
. For example, if a has a nontrivial projection to every simple factor of H, then the unstable horospherical subgroup
![]() $H^+_a=\{ h\in H\mid \lim _{n\to \infty }a^{-n} h a^n=1_H \}$
is a-expanding ([Reference Shah89, Lemma 5.2]). In fact, it can be shown that U is a-expanding if and only if
$H^+_a=\{ h\in H\mid \lim _{n\to \infty }a^{-n} h a^n=1_H \}$
is a-expanding ([Reference Shah89, Lemma 5.2]). In fact, it can be shown that U is a-expanding if and only if
![]() $U\cap H_a^+$
is ([Reference Shi91, Lemma A.2]).
$U\cap H_a^+$
is ([Reference Shi91, Lemma A.2]).
Now, let
![]() $Q\leqslant H$
be a parabolic subgroup with maximal connected
$Q\leqslant H$
be a parabolic subgroup with maximal connected
![]() $\mathbb {R}$
-split torus A. Using the above, we will give two criteria for a measure on Q to be H-expanding. To state the first, write
$\mathbb {R}$
-split torus A. Using the above, we will give two criteria for a measure on Q to be H-expanding. To state the first, write
![]() $Q=MA_cN$
for the Langlands decomposition of Q. In particular, this means that N is the unipotent radical of Q,
$Q=MA_cN$
for the Langlands decomposition of Q. In particular, this means that N is the unipotent radical of Q,
![]() $MA_c=C_H(A_c)$
is a (reductive) Levi subgroup of Q, and
$MA_c=C_H(A_c)$
is a (reductive) Levi subgroup of Q, and
![]() $A_c$
is a maximal central connected
$A_c$
is a maximal central connected
![]() $\mathbb {R}$
-split torus in
$\mathbb {R}$
-split torus in
![]() $MA_c$
(see, e.g., [Reference Knapp60, §VII.7] for details on Langlands decomposition). We may assume that
$MA_c$
(see, e.g., [Reference Knapp60, §VII.7] for details on Langlands decomposition). We may assume that
![]() $A_c\leqslant A$
. Given a probability measure
$A_c\leqslant A$
. Given a probability measure
![]() $\mu $
on Q, by using the diffeomorphism
$\mu $
on Q, by using the diffeomorphism
![]() $Q\cong M\times A_c\times N$
given by multiplication and projecting to some of the factors, we obtain associated probability measures
$Q\cong M\times A_c\times N$
given by multiplication and projecting to some of the factors, we obtain associated probability measures
![]() $\mu _M$
,
$\mu _M$
,
![]() $\mu _{A_c}$
,
$\mu _{A_c}$
,
![]() $\mu _{MA_c}$
, etc. Finally, we denote by
$\mu _{MA_c}$
, etc. Finally, we denote by
![]() $\lambda _c\colon Q\to \mathfrak a$
the composition of the projection to
$\lambda _c\colon Q\to \mathfrak a$
the composition of the projection to
![]() $A_c$
with the logarithm map
$A_c$
with the logarithm map
![]() $\log \colon A\to \mathfrak a$
, where
$\log \colon A\to \mathfrak a$
, where
![]() $\mathfrak a$
is the Lie algebra of A.
$\mathfrak a$
is the Lie algebra of A.
Proposition 3.3 (H-expanding measures (1))
Let
![]() $\mu $
be a probability measure on H with finite first moment such that
$\mu $
be a probability measure on H with finite first moment such that
![]() $\mu (Q)=1$
for some parabolic subgroup
$\mu (Q)=1$
for some parabolic subgroup
![]() $Q=MA_cN$
of H. Denote by
$Q=MA_cN$
of H. Denote by
![]() $a_{c,\operatorname {avg}}(\mu )=\exp \bigl (\int \lambda _c(g)\mathop {}\!\mathrm {d}\mu (g)\bigr )\in A_c$
the
$a_{c,\operatorname {avg}}(\mu )=\exp \bigl (\int \lambda _c(g)\mathop {}\!\mathrm {d}\mu (g)\bigr )\in A_c$
the
![]() $A_c$
-average of
$A_c$
-average of
![]() $\mu $
. Let U be a connected Lie subgroup of N, and suppose the following:
$\mu $
. Let U be a connected Lie subgroup of N, and suppose the following:
-
(1)
 $\operatorname {\mathrm {supp}}(\mu ) \subset M A_c U\cap N_H(U)$
and the Zariski closure of
$\operatorname {\mathrm {supp}}(\mu ) \subset M A_c U\cap N_H(U)$
and the Zariski closure of
 $\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
$\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
 $\operatorname {\mathrm {Ad}}(U)$
,
$\operatorname {\mathrm {Ad}}(U)$
, -
(2) U is
 $a_{c,\operatorname {avg}}(\mu )$
-expanding, and
$a_{c,\operatorname {avg}}(\mu )$
-expanding, and -
(3)
 $\mu _M$
is noncontracting in every representation of H.
$\mu _M$
is noncontracting in every representation of H.
Then
![]() $\mu $
is H-expanding.
$\mu $
is H-expanding.
Before proceeding with the preparations for the proof of the above proposition, let us provide a few brief comments on its hypotheses.
Remark 3.4 (On the hypotheses of Proposition 3.3)
-
○ In fact, there is no freedom in the choice of U: Condition (1) implies that it needs to be the Zariski closure of the projection of
 $\Gamma _{\mu }$
to N.
$\Gamma _{\mu }$
to N. -
○ When
 $U=N$
and the parabolic group Q is absolutely proper, condition (2) can conveniently be checked using the notion of expanding cone to be discussed in §3.2.1.
$U=N$
and the parabolic group Q is absolutely proper, condition (2) can conveniently be checked using the notion of expanding cone to be discussed in §3.2.1. -
○ The noncontraction requirement on
 $\mu _M$
in condition (3) is satisfied, for instance, when the identity component of the Zariski closure of
$\mu _M$
in condition (3) is satisfied, for instance, when the identity component of the Zariski closure of
 $\operatorname {\mathrm {Ad}}(\Gamma _{\mu _M})$
is reductive with compact center (for example, the identity component of
$\operatorname {\mathrm {Ad}}(\Gamma _{\mu _M})$
is reductive with compact center (for example, the identity component of
 $\operatorname {\mathrm {Ad}}(M)$
itself). Indeed, in this case similar arguments as in the proof of Lemma 3.2 can be used to show that
$\operatorname {\mathrm {Ad}}(M)$
itself). Indeed, in this case similar arguments as in the proof of Lemma 3.2 can be used to show that
 $\Gamma _{\mu _M}$
acts completely reducibly and by transformations of determinant
$\Gamma _{\mu _M}$
acts completely reducibly and by transformations of determinant
 $\pm 1$
in every representation
$\pm 1$
in every representation
 $(\rho ,V)$
of H. Then the Lyapunov exponents of
$(\rho ,V)$
of H. Then the Lyapunov exponents of
 $\mu _M$
in any
$\mu _M$
in any
 $\Gamma _{\mu _M}$
-irreducible subspace of V sum to
$\Gamma _{\mu _M}$
-irreducible subspace of V sum to
 $0$
and one concludes using Theorem 2.3.
$0$
and one concludes using Theorem 2.3. -
○ Another useful fact for the verification of condition (3) is that the connected component
 $M^\circ $
of M is the almost direct product of its semisimple part
$M^\circ $
of M is the almost direct product of its semisimple part
 $S=[M^\circ ,M^\circ ]$
and a compact center. Provided
$S=[M^\circ ,M^\circ ]$
and a compact center. Provided
 $\mu _M$
is supported on
$\mu _M$
is supported on
 $M^\circ $
, one can thus project to the noncompact part
$M^\circ $
, one can thus project to the noncompact part
 $S^{nc}$
and is only left checking noncontraction for
$S^{nc}$
and is only left checking noncontraction for
 $\mu _{S^{nc}}$
. The latter could follow from Zariski density (Proposition 3.1), or by a recursive application of Proposition 3.3 above to
$\mu _{S^{nc}}$
. The latter could follow from Zariski density (Proposition 3.1), or by a recursive application of Proposition 3.3 above to
 $H=S^{nc}$
. In the general case, one can obtain from
$H=S^{nc}$
. In the general case, one can obtain from
 $\mu _M$
a probability measure
$\mu _M$
a probability measure
 $\mu _M^\circ $
on
$\mu _M^\circ $
on
 $M^\circ $
defined as the law of the first return to
$M^\circ $
defined as the law of the first return to
 $M^\circ $
of the random walk on M induced by
$M^\circ $
of the random walk on M induced by
 $\mu _M$
; see [Reference Benoist and Quint11, §5.2]. Using [Reference Benoist and Quint11, Proposition 5.9] and Theorem 2.3, one sees that the noncontraction property of
$\mu _M$
; see [Reference Benoist and Quint11, §5.2]. Using [Reference Benoist and Quint11, Proposition 5.9] and Theorem 2.3, one sees that the noncontraction property of
 $\mu _M^\circ $
implies that of
$\mu _M^\circ $
implies that of
 $\mu _M$
.
$\mu _M$
.
For the proof of Proposition 3.3, we require the following lemma, which reduces checking expansion to vectors fixed by some unipotent subgroup of the image of the algebraic group generated by
![]() $\operatorname {\mathrm {supp}}(\mu )$
.
$\operatorname {\mathrm {supp}}(\mu )$
.
Lemma 3.5 (A criterion for expansion)
Let V be a finite-dimensional real vector space and
![]() $\mu '$
a probability measure on
$\mu '$
a probability measure on
![]() $\operatorname {\mathrm {GL}}(V)$
with finite first moment. Denote by
$\operatorname {\mathrm {GL}}(V)$
with finite first moment. Denote by
![]() $Q'$
the Zariski closure of
$Q'$
the Zariski closure of
![]() $\Gamma _{\mu '}$
and let
$\Gamma _{\mu '}$
and let
![]() $U'$
be a unipotent subgroup of
$U'$
be a unipotent subgroup of
![]() $Q'$
. Suppose that every nonzero vector
$Q'$
. Suppose that every nonzero vector
![]() $v\in V^{U'}$
is
$v\in V^{U'}$
is
![]() $\mu '$
-expanded, where
$\mu '$
-expanded, where
![]() $V^{U'}$
denotes the subspace of
$V^{U'}$
denotes the subspace of
![]() $U'$
-fixed vectors. Then
$U'$
-fixed vectors. Then
![]() $\mu '$
is uniformly expanding.
$\mu '$
is uniformly expanding.
Proof. Let us suppose for a contradiction that
![]() $\mu '$
is not uniformly expanding. Then there exists a vector
$\mu '$
is not uniformly expanding. Then there exists a vector
![]() $v \in V\setminus \{0\}$
with
$v \in V\setminus \{0\}$
with
![]() $\liminf _{n \to \infty } \frac {1}{n}\log \left \lVert {g_n \dotsm g_1 v} \right \rVert \le 0$
for a positive measure subset of
$\liminf _{n \to \infty } \frac {1}{n}\log \left \lVert {g_n \dotsm g_1 v} \right \rVert \le 0$
for a positive measure subset of
![]() $(g_i)_i\in (Q')^{\mathbb {N}}$
with respect to
$(g_i)_i\in (Q')^{\mathbb {N}}$
with respect to
![]() $(\mu ')^{\mathbb {N}}$
. By Theorem 2.3, there exists a nontrivial
$(\mu ')^{\mathbb {N}}$
. By Theorem 2.3, there exists a nontrivial
![]() $\Gamma _{\mu '}$
-invariant subspace
$\Gamma _{\mu '}$
-invariant subspace
![]() $W\leqslant V$
such that for every
$W\leqslant V$
such that for every
![]() $w \in W$
, we have
$w \in W$
, we have
![]() $\lim _{n \to \infty } \frac {1}{n}\log \left \lVert {g_n \dotsm g_1 w} \right \rVert \le 0$
for
$\lim _{n \to \infty } \frac {1}{n}\log \left \lVert {g_n \dotsm g_1 w} \right \rVert \le 0$
for
![]() $(\mu ')^{\mathbb {N}}$
-a.e.
$(\mu ')^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in (Q')^{\mathbb {N}}$
. Since
$(g_i)_i\in (Q')^{\mathbb {N}}$
. Since
![]() $Q'$
is the Zariski closure of
$Q'$
is the Zariski closure of
![]() $\Gamma _{\mu '}$
, the subspace W is stabilized by
$\Gamma _{\mu '}$
, the subspace W is stabilized by
![]() $Q'$
and hence, by
$Q'$
and hence, by
![]() $U'$
. By the Lie–Kolchin theorem, we have
$U'$
. By the Lie–Kolchin theorem, we have
![]() $W^{U'} \neq \{0\}$
. This implies that for any nonzero
$W^{U'} \neq \{0\}$
. This implies that for any nonzero
![]() $w \in W^{U'}\leqslant V^{U'}$
, we have
$w \in W^{U'}\leqslant V^{U'}$
, we have
![]() $\lim _{n \to \infty } \frac {1}{n}\log \left \lVert {g_n \dotsm g_1 w} \right \rVert \le 0$
for
$\lim _{n \to \infty } \frac {1}{n}\log \left \lVert {g_n \dotsm g_1 w} \right \rVert \le 0$
for
![]() $(\mu ')^{\mathbb {N}}$
-a.e.
$(\mu ')^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in (Q')^{\mathbb {N}}$
, contradicting expansion on
$(g_i)_i\in (Q')^{\mathbb {N}}$
, contradicting expansion on
![]() $V^{U'}$
.
$V^{U'}$
.
Proof of Proposition 3.3
Let
![]() $(\rho ,V)$
be a nontrivial irreducible representation of H. By Lemma 2.9, the measure
$(\rho ,V)$
be a nontrivial irreducible representation of H. By Lemma 2.9, the measure
![]() $\rho _*\mu $
has a finite first moment, and Lemma 3.2 implies that
$\rho _*\mu $
has a finite first moment, and Lemma 3.2 implies that
![]() $\rho (U)$
is a unipotent subgroup of the Zariski closure of
$\rho (U)$
is a unipotent subgroup of the Zariski closure of
![]() $\rho (\Gamma _{\mu })$
. In view of Lemma 3.5, to prove uniform expansion of
$\rho (\Gamma _{\mu })$
. In view of Lemma 3.5, to prove uniform expansion of
![]() $\rho _*\mu $
it suffices to show that for every nonzero
$\rho _*\mu $
it suffices to show that for every nonzero
![]() $v \in V^U$
, we have
$v \in V^U$
, we have
for
![]() $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i \in H^{\mathbb {N}}$
. Since condition (1) implies that
$(g_i)_i \in H^{\mathbb {N}}$
. Since condition (1) implies that
![]() $\Gamma _{\mu }\subset MA_cU$
and v is U-fixed, it suffices to prove the above for
$\Gamma _{\mu }\subset MA_cU$
and v is U-fixed, it suffices to prove the above for
![]() $\mu _{MA_c}$
-a.e.
$\mu _{MA_c}$
-a.e.
![]() $(g_i)_i\in H^{\mathbb {N}}$
, where
$(g_i)_i\in H^{\mathbb {N}}$
, where
![]() $\mu _{MA_c}$
is the
$\mu _{MA_c}$
is the
![]() $MA_c$
-projection of
$MA_c$
-projection of
![]() $\mu $
. Writing
$\mu $
. Writing
![]() $g_i=m_ia_i$
for the
$g_i=m_ia_i$
for the
![]() $MA_c$
-factorization of
$MA_c$
-factorization of
![]() $g_i\in MA_c$
and using that M and
$g_i\in MA_c$
and using that M and
![]() $A_c$
commute, we see that
$A_c$
commute, we see that
The second term above is almost surely nonnegative in the limit by the assumed noncontraction property of
![]() $\mu _M$
.
$\mu _M$
.
To deal with the first term, let
![]() $\Phi (A_c,\rho )$
be the set of weights of
$\Phi (A_c,\rho )$
be the set of weights of
![]() $A_c$
for the representation
$A_c$
for the representation
![]() $(\rho ,V)$
. Let
$(\rho ,V)$
. Let
![]() $\{\chi _1,\dots ,\chi _t\}$
be the subcollection of those
$\{\chi _1,\dots ,\chi _t\}$
be the subcollection of those
![]() $\chi \in \Phi (A_c,\rho )$
with
$\chi \in \Phi (A_c,\rho )$
with
![]() $\chi (a_{c,\operatorname {avg}}(\mu ))>1$
and denote the corresponding weight spaces by
$\chi (a_{c,\operatorname {avg}}(\mu ))>1$
and denote the corresponding weight spaces by
![]() $V_1,\dots ,V_t$
. Then by the assumption on U, we have
$V_1,\dots ,V_t$
. Then by the assumption on U, we have
![]() . Since
. Since
![]() $A_c$
and M commute, W is M-invariant. Lemma 3.6 below applied to the space W and
$A_c$
and M commute, W is M-invariant. Lemma 3.6 below applied to the space W and
![]() $\mu '=\mu _{A_c}$
with
$\mu '=\mu _{A_c}$
with
![]() $v_n=m_n\dotsm m_1{\boldsymbol {\cdot }} v$
thus implies that the first term in equation (3.1) has strictly positive limit inferior
$v_n=m_n\dotsm m_1{\boldsymbol {\cdot }} v$
thus implies that the first term in equation (3.1) has strictly positive limit inferior
![]() $\mu _{MA_c}^{\mathbb {N}}$
-almost surely. This finishes the proof.
$\mu _{MA_c}^{\mathbb {N}}$
-almost surely. This finishes the proof.
Lemma 3.6. Let V be a finite-dimensional real vector space and
![]() $A'\leqslant \operatorname {\mathrm {GL}}(V)$
a closed connected diagonalizable subgroup with Lie algebra
$A'\leqslant \operatorname {\mathrm {GL}}(V)$
a closed connected diagonalizable subgroup with Lie algebra
![]() $\mathfrak a$
. Write
$\mathfrak a$
. Write
![]() $V=\bigoplus _{\chi \in \Phi (A')} V^\chi $
for the weight space decomposition of V with respect to
$V=\bigoplus _{\chi \in \Phi (A')} V^\chi $
for the weight space decomposition of V with respect to
![]() $A'$
, where
$A'$
, where
![]() $V^\chi =\{v\in V\mid av=\chi (a)v\text { for all }a\in A'\}$
and
$V^\chi =\{v\in V\mid av=\chi (a)v\text { for all }a\in A'\}$
and
![]() $\Phi (A')$
is the set of characters
$\Phi (A')$
is the set of characters
![]() $\chi $
of
$\chi $
of
![]() $A'$
such that
$A'$
such that
![]() $V^\chi \neq \{0\}$
. Let
$V^\chi \neq \{0\}$
. Let
![]() $\mu '$
be a probability measure on
$\mu '$
be a probability measure on
![]() $A'$
with finite first moment and denote
$A'$
with finite first moment and denote
![]() $a_{\operatorname {avg}}(\mu ')=\exp (\int \log (a)\mathop {}\!\mathrm {d}\mu '(a))$
. Suppose that
$a_{\operatorname {avg}}(\mu ')=\exp (\int \log (a)\mathop {}\!\mathrm {d}\mu '(a))$
. Suppose that
![]() $\chi (a_{\operatorname {avg}}(\mu '))>1$
for every
$\chi (a_{\operatorname {avg}}(\mu '))>1$
for every
![]() $\chi \in \Phi (A')$
. Then for
$\chi \in \Phi (A')$
. Then for
![]() $(\mu ')^{\mathbb {N}}$
-a.e.
$(\mu ')^{\mathbb {N}}$
-a.e.
![]() $(a_i)_i\in (A')^{\mathbb {N}}$
we have
$(a_i)_i\in (A')^{\mathbb {N}}$
we have
for every choice of nonzero vectors
![]() $v_n\in V$
.
$v_n\in V$
.
Proof. For convenience, we assume the norm
![]() $ \left \lVert {\cdot } \right \rVert $
on V is Euclidean and that the distinct weight spaces are orthogonal. Given a nonzero
$ \left \lVert {\cdot } \right \rVert $
on V is Euclidean and that the distinct weight spaces are orthogonal. Given a nonzero
![]() $v \in V$
, write
$v \in V$
, write
![]() $v=\sum _{\chi \in \Phi (A')} v^\chi (v)$
for the corresponding weight space decomposition, where
$v=\sum _{\chi \in \Phi (A')} v^\chi (v)$
for the corresponding weight space decomposition, where
![]() $v^\chi (v) \in V^\chi $
. Then for any
$v^\chi (v) \in V^\chi $
. Then for any
![]() $a_1,\dots ,a_n\in A'$
and nonzero
$a_1,\dots ,a_n\in A'$
and nonzero
![]() $v_n\in V$
we have
$v_n\in V$
we have
 $$ \begin{align*} a_n\dotsm a_1v_n =\sum_{\chi\in\Phi(A')} \chi(a_n\dotsm a_1) v^\chi(v_n). \end{align*} $$
$$ \begin{align*} a_n\dotsm a_1v_n =\sum_{\chi\in\Phi(A')} \chi(a_n\dotsm a_1) v^\chi(v_n). \end{align*} $$
Choosing for every
![]() $n\in \mathbb {N}$
a character
$n\in \mathbb {N}$
a character
![]() $\chi _n$
such that
$\chi _n$
such that
![]() $ \left \lVert {v^{\chi _n}(v_n)} \right \rVert \ge \frac {1}{\sqrt {\dim (V)}} \left \lVert {v_n} \right \rVert $
and recalling that
$ \left \lVert {v^{\chi _n}(v_n)} \right \rVert \ge \frac {1}{\sqrt {\dim (V)}} \left \lVert {v_n} \right \rVert $
and recalling that
![]() $\chi (a_{\operatorname {avg}}(\mu '))>1$
for all
$\chi (a_{\operatorname {avg}}(\mu '))>1$
for all
![]() $\chi \in \Phi (A')$
by assumption, we conclude that
$\chi \in \Phi (A')$
by assumption, we conclude that
 $$ \begin{align*} \frac1n\log\frac{ \left\lVert {a_n\dotsm a_1v_n} \right\rVert }{ \left\lVert {v_n} \right\rVert } &\ge o(1) + \frac{1}{n}\log \chi_n(a_n\dotsm a_1) \ge o(1)+\min_{\chi\in\Phi(A')}\frac{1}{n} \sum_{i=1}^n \log \chi(a_i)\\ &\overset{n\to\infty}{\longrightarrow} \min_{\chi\in\Phi(A')}\log \chi(a_{\operatorname{avg}}(\mu'))>0, \end{align*} $$
$$ \begin{align*} \frac1n\log\frac{ \left\lVert {a_n\dotsm a_1v_n} \right\rVert }{ \left\lVert {v_n} \right\rVert } &\ge o(1) + \frac{1}{n}\log \chi_n(a_n\dotsm a_1) \ge o(1)+\min_{\chi\in\Phi(A')}\frac{1}{n} \sum_{i=1}^n \log \chi(a_i)\\ &\overset{n\to\infty}{\longrightarrow} \min_{\chi\in\Phi(A')}\log \chi(a_{\operatorname{avg}}(\mu'))>0, \end{align*} $$
where the last convergence holds
![]() $(\mu ')^{\mathbb {N}}$
-almost surely by the classical law of large numbers.
$(\mu ')^{\mathbb {N}}$
-almost surely by the classical law of large numbers.
One drawback of Proposition 3.3 is that, in some sense, it requires the M- and
![]() $A_c$
-parts of
$A_c$
-parts of
![]() $\mu $
to both exhibit expansion (or at least noncontraction) individually. It would be natural to only ask the combination of both to be expanding, a behavior which should be reflected in the A-average of
$\mu $
to both exhibit expansion (or at least noncontraction) individually. It would be natural to only ask the combination of both to be expanding, a behavior which should be reflected in the A-average of
![]() $\mu $
. When
$\mu $
. When
![]() $\mu $
does not charge M in a too complicated way, we can also prove H-expansion in this case.
$\mu $
does not charge M in a too complicated way, we can also prove H-expansion in this case.
To state this second criterion, let
![]() $U\leqslant H$
be any connected
$U\leqslant H$
be any connected
![]() $\operatorname {\mathrm {Ad}}$
-unipotent subgroup. Then there exists a parabolic subgroup Q of H containing U in its unipotent radical such that also
$\operatorname {\mathrm {Ad}}$
-unipotent subgroup. Then there exists a parabolic subgroup Q of H containing U in its unipotent radical such that also
![]() $N_H(U)\leqslant Q$
[Reference Borel and Tits16]. As before, let
$N_H(U)\leqslant Q$
[Reference Borel and Tits16]. As before, let
![]() $A\leqslant Q$
be a maximal
$A\leqslant Q$
be a maximal
![]() $\mathbb {R}$
-split torus and denote by K a maximal compact subgroup of Q. Given a nontrivial subtorus
$\mathbb {R}$
-split torus and denote by K a maximal compact subgroup of Q. Given a nontrivial subtorus
![]() $A' \leqslant A$
normalizing U, set
$A' \leqslant A$
normalizing U, set
![]() $K'=C_K(A')\cap N_H(U)$
and let P be the closed subgroup
$K'=C_K(A')\cap N_H(U)$
and let P be the closed subgroup
![]() $K' A' U$
of Q. We write
$K' A' U$
of Q. We write
![]() $\lambda \colon P \to \mathfrak {a}$
for the morphism given by
$\lambda \colon P \to \mathfrak {a}$
for the morphism given by
![]() $\lambda (kau)= \log a$
.
$\lambda (kau)= \log a$
.
Proposition 3.7 (H-expanding measures (2))
Retain the notation from the paragraph above, and let
![]() $\mu $
be a probability measure on H with finite first moment such that
$\mu $
be a probability measure on H with finite first moment such that
![]() $\mu (P)=1$
. Denote by
$\mu (P)=1$
. Denote by
![]() $a_{\operatorname {avg}}(\mu )=\exp \bigl (\int \lambda (g)\mathop {}\!\mathrm {d}\mu (g)\bigr )\in A$
the A-average of
$a_{\operatorname {avg}}(\mu )=\exp \bigl (\int \lambda (g)\mathop {}\!\mathrm {d}\mu (g)\bigr )\in A$
the A-average of
![]() $\mu $
. Suppose that:
$\mu $
. Suppose that:
-
(1) The Zariski closure of
 $\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
$\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
 $\operatorname {\mathrm {Ad}}(U)$
, and
$\operatorname {\mathrm {Ad}}(U)$
, and -
(2) U is
 $a_{\operatorname {avg}}(\mu )$
-expanding.
$a_{\operatorname {avg}}(\mu )$
-expanding.
Then
![]() $\mu $
is H-expanding.
$\mu $
is H-expanding.
We emphasize that, in contrast to Proposition 3.3, here the A-average is considering also the part of the torus A inside M, if
![]() $Q=MA_cN$
is the Langlands decomposition of Q.
$Q=MA_cN$
is the Langlands decomposition of Q.
Proof. Exactly as in the proof of Proposition 3.3, given a nontrivial irreducible representation
![]() $(\rho ,V)$
of H, it suffices to prove that
$(\rho ,V)$
of H, it suffices to prove that
for
![]() $\mu _{K'A'}^{\mathbb {N}}$
-a.e.
$\mu _{K'A'}^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in H^{\mathbb {N}}$
and every
$(g_i)_i\in H^{\mathbb {N}}$
and every
![]() $v\in V^U$
, where
$v\in V^U$
, where
![]() $\mu _{K'A'}$
is the pushforward of
$\mu _{K'A'}$
is the pushforward of
![]() $\mu $
by the map
$\mu $
by the map
![]() $K'A'U\to K'A',\, kau\mapsto ka$
. As
$K'A'U\to K'A',\, kau\mapsto ka$
. As
![]() $K'$
is compact and commutes with
$K'$
is compact and commutes with
![]() $A'$
, we can ignore the
$A'$
, we can ignore the
![]() $K'$
-component and consider only
$K'$
-component and consider only
![]() $\mu _{A'}$
, defined in the analogous way. Now, the statement follows from Lemma 3.6.
$\mu _{A'}$
, defined in the analogous way. Now, the statement follows from Lemma 3.6.
3.2.1 Expanding cone
Now, we present a construction which can be used to ensure the expansion condition on U with respect to the A- or
![]() $A_c$
-average of
$A_c$
-average of
![]() $\mu $
in the criteria above (condition (2) in Propositions 3.3 and 3.7) in the case that U is the unipotent radical of an absolutely proper parabolic subgroup Q of H, where ‘absolutely proper’ means that the projection of Q to each simple factor of H is nonsurjective. As before, we let A be a maximal connected
$\mu $
in the criteria above (condition (2) in Propositions 3.3 and 3.7) in the case that U is the unipotent radical of an absolutely proper parabolic subgroup Q of H, where ‘absolutely proper’ means that the projection of Q to each simple factor of H is nonsurjective. As before, we let A be a maximal connected
![]() $\mathbb {R}$
-split torus of Q.
$\mathbb {R}$
-split torus of Q.
The expanding cone of U in A is defined to be
It is proved in [Reference Shi92, Theorem 1.2] that
![]() $A_U^+$
only depends on the Lie algebras
$A_U^+$
only depends on the Lie algebras
and
and that it can be described explicitly as follows. Let
![]() $\mathfrak a$
be the Lie algebra of A, and let
$\mathfrak a$
be the Lie algebra of A, and let
be the restricted root system of
![]() $(\mathfrak h,\mathfrak a)$
. Denote by
$(\mathfrak h,\mathfrak a)$
. Denote by
![]() $\Sigma (\mathfrak u)\subset \Sigma (\mathfrak h, \mathfrak a)$
the subset of roots whose eigenvectors lie in
$\Sigma (\mathfrak u)\subset \Sigma (\mathfrak h, \mathfrak a)$
the subset of roots whose eigenvectors lie in
![]() $\mathfrak u$
. Recall that by semisimplicity, the Killing form
$\mathfrak u$
. Recall that by semisimplicity, the Killing form
![]() $\langle \cdot , \cdot \rangle $
of
$\langle \cdot , \cdot \rangle $
of
![]() $\mathfrak h$
is positive definite on
$\mathfrak h$
is positive definite on
![]() $\mathfrak a$
. So for each
$\mathfrak a$
. So for each
![]() $\alpha \in \mathfrak a^*$
we can associate
$\alpha \in \mathfrak a^*$
we can associate
![]() $s_\alpha \in \mathfrak a$
by
$s_\alpha \in \mathfrak a$
by
![]() $\langle s_\alpha , v\rangle =\alpha ( v)$
for every
$\langle s_\alpha , v\rangle =\alpha ( v)$
for every
![]() $ v\in \mathfrak a$
. Using this isomorphism, we associate to
$ v\in \mathfrak a$
. Using this isomorphism, we associate to
![]() $\Sigma (\mathfrak u)$
the following convex cone in
$\Sigma (\mathfrak u)$
the following convex cone in
![]() $\mathfrak a$
:
$\mathfrak a$
:

The expanding cone
![]() $A_U^+$
of U is then given by
$A_U^+$
of U is then given by
![]() $A_U^+= \exp \mathfrak a^+_{\mathfrak u}$
; see [Reference Shi92, Theorem 1.2]. By abuse of language, we shall sometimes also refer to
$A_U^+= \exp \mathfrak a^+_{\mathfrak u}$
; see [Reference Shi92, Theorem 1.2]. By abuse of language, we shall sometimes also refer to
![]() $\mathfrak {a}_{\mathfrak u}^+$
as the expanding cone of U.
$\mathfrak {a}_{\mathfrak u}^+$
as the expanding cone of U.
Using these notions, we get the following immediate corollary of Proposition 3.7.
Corollary 3.8. Let U be the unipotent radical of an absolutely proper parabolic subgroup Q of H,
![]() $A\leqslant Q$
a maximal connected
$A\leqslant Q$
a maximal connected
![]() $\mathbb {R}$
-split torus and
$\mathbb {R}$
-split torus and
![]() $A'\leqslant A$
a nontrivial subtorus. Moreover, let K be a maximal compact subgroup of H,
$A'\leqslant A$
a nontrivial subtorus. Moreover, let K be a maximal compact subgroup of H,
![]() $K'=C_K(A')\cap Q$
, set
$K'=C_K(A')\cap Q$
, set
![]() $P=K'A'U$
and let
$P=K'A'U$
and let
![]() $\mu $
be a probability measure on H with finite first moment such that
$\mu $
be a probability measure on H with finite first moment such that
![]() $\mu (P)=1$
. Suppose that the Zariski closure of
$\mu (P)=1$
. Suppose that the Zariski closure of
![]() $\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
$\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
![]() $\operatorname {\mathrm {Ad}}(U)$
and that
$\operatorname {\mathrm {Ad}}(U)$
and that
![]() $\int \lambda (g)\mathop {}\!\mathrm {d}\mu (g)\in \mathfrak {a}_{\mathfrak u}^+$
. Then
$\int \lambda (g)\mathop {}\!\mathrm {d}\mu (g)\in \mathfrak {a}_{\mathfrak u}^+$
. Then
![]() $\mu $
is H-expanding.
$\mu $
is H-expanding.
3.2.2 Explicit examples
We end this subsection by giving two explicit examples where the criteria developed so far are applicable.
The first of them is the prototypical example of an expanding cone. Although simple, it turns out to be of significant importance to Diophantine approximation problems on fractals. We will take up this point and elaborate on the connection in §9.
Example 3.9. Let
![]() $H=\operatorname {\mathrm {SL}}_{m+n}(\mathbb {R})$
, and
$H=\operatorname {\mathrm {SL}}_{m+n}(\mathbb {R})$
, and
 $$ \begin{align*} Q &=\left\{ \begin{pmatrix} p_{11} & p_{12}\\ 0 & p_{22} \end{pmatrix} \in H\mid p_{11}\in \operatorname{\mathrm{GL}}_m(\mathbb{R}), p_{22}\in \operatorname{\mathrm{GL}}_n(\mathbb{R}), p_{12}\in \operatorname{\mathrm{Mat}}_{m\times n}(\mathbb{R}) \right\} ,\\ U &=\left\{ \begin{pmatrix} I_m & p_{12}\\ 0 & I_n \end{pmatrix} \in H\mid p_{12}\in \operatorname{\mathrm{Mat}}_{m\times n}(\mathbb{R}) \right\}, \end{align*} $$
$$ \begin{align*} Q &=\left\{ \begin{pmatrix} p_{11} & p_{12}\\ 0 & p_{22} \end{pmatrix} \in H\mid p_{11}\in \operatorname{\mathrm{GL}}_m(\mathbb{R}), p_{22}\in \operatorname{\mathrm{GL}}_n(\mathbb{R}), p_{12}\in \operatorname{\mathrm{Mat}}_{m\times n}(\mathbb{R}) \right\} ,\\ U &=\left\{ \begin{pmatrix} I_m & p_{12}\\ 0 & I_n \end{pmatrix} \in H\mid p_{12}\in \operatorname{\mathrm{Mat}}_{m\times n}(\mathbb{R}) \right\}, \end{align*} $$
where we denote by
![]() $I_d$
the
$I_d$
the
![]() $d\times d$
-identity matrix. The group A consists of diagonal matrices in H with positive entries, and we have
$d\times d$
-identity matrix. The group A consists of diagonal matrices in H with positive entries, and we have
(see [Reference Shi92, Example 1.1]).
For concreteness, we exemplify a class of H-expanding measures on Q: Fix a Borel subset
![]() $B_U$
of U not contained in a proper vector subspace of
$B_U$
of U not contained in a proper vector subspace of
![]() $U\cong \mathbb {R}^{mn}$
. For example,
$U\cong \mathbb {R}^{mn}$
. For example,
![]() $B_U$
can be taken to be a nondegenerate curve in U or a collection of
$B_U$
can be taken to be a nondegenerate curve in U or a collection of
![]() $k \ge mn$
points in
$k \ge mn$
points in
![]() $U \cong \mathbb {R}^{mn}$
that linearly spans U. Let
$U \cong \mathbb {R}^{mn}$
that linearly spans U. Let
![]() $\mu $
be a compactly supported probability measure on
$\mu $
be a compactly supported probability measure on
![]() $AU$
such that
$AU$
such that
-
○ its support contains an element of
 $A_U^+$
,
$A_U^+$
, -
○ the set of unipotent parts
 $u_g$
of elements
$u_g$
of elements
 $g=a_gu_g$
in
$g=a_gu_g$
in
 $\operatorname {\mathrm {supp}}(\mu )\subset AU$
contains
$\operatorname {\mathrm {supp}}(\mu )\subset AU$
contains
 $B_U$
, and
$B_U$
, and -
○ its A-average lies in the expanding cone of U, that is,
 $\int \lambda (g) \mathop {}\!\mathrm {d}\mu (g) \in \mathfrak {a}_{\mathfrak {u}}^+ $
.
$\int \lambda (g) \mathop {}\!\mathrm {d}\mu (g) \in \mathfrak {a}_{\mathfrak {u}}^+ $
.
Then
![]() $\mu $
can be seen to be H-expanding by Corollary 3.8. Indeed, as we will see in §9 on Diophantine approximation on fractals, the first two points above imply that the Zariski closure of
$\mu $
can be seen to be H-expanding by Corollary 3.8. Indeed, as we will see in §9 on Diophantine approximation on fractals, the first two points above imply that the Zariski closure of
![]() $\Gamma _{\mu }$
contains U (see the proof of Theorem 9.3).
$\Gamma _{\mu }$
contains U (see the proof of Theorem 9.3).
Note that the above example covers in particular [Reference Prohaska and Sert79, Example 2.8]. We also point out that, in Example 3.9, the assumption that
![]() $\operatorname {\mathrm {supp}}(\mu )$
contains an element of
$\operatorname {\mathrm {supp}}(\mu )$
contains an element of
![]() $A_U^+$
is not strictly necessary. The first two bullet points could be replaced by a certain ‘irreducibility condition’ of an affine action of the group generated by the support of
$A_U^+$
is not strictly necessary. The first two bullet points could be replaced by a certain ‘irreducibility condition’ of an affine action of the group generated by the support of
![]() $\mu $
(which is what we will do in §9), or, alternatively, by the assumption that the commutator group
$\mu $
(which is what we will do in §9), or, alternatively, by the assumption that the commutator group
![]() $[\Gamma _{\mu },\Gamma _{\mu }]$
is Zariski dense in U.
$[\Gamma _{\mu },\Gamma _{\mu }]$
is Zariski dense in U.
The second example is one where the reductive group M in the Langlands decomposition of Q (see the paragraph before Proposition 3.3) contributes to expansion in a nontrivial way.
Example 3.10. Let Q be the standard parabolic subgroup of
![]() $\operatorname {\mathrm {SL}}_4(\mathbb {R})$
given by
$\operatorname {\mathrm {SL}}_4(\mathbb {R})$
given by
 $$ \begin{align*} Q=\begin{pmatrix} \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ & & \ast & \ast \\ & & & \ast \end{pmatrix}\leqslant\operatorname{\mathrm{SL}}_4(\mathbb{R}). \end{align*} $$
$$ \begin{align*} Q=\begin{pmatrix} \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ & & \ast & \ast \\ & & & \ast \end{pmatrix}\leqslant\operatorname{\mathrm{SL}}_4(\mathbb{R}). \end{align*} $$
The maximal connected
![]() $\mathbb {R}$
-split torus A consists of diagonal matrices with positive entries. In the Langlands decomposition
$\mathbb {R}$
-split torus A consists of diagonal matrices with positive entries. In the Langlands decomposition
![]() $Q=MA_cN$
, we have
$Q=MA_cN$
, we have

Using the explicit description of the expanding cone in §3.2.1, one can calculate directly that the intersection of the expanding cone of
![]() $U=N$
in A with
$U=N$
in A with
![]() $A_c$
is given by
$A_c$
is given by
For
![]() $i,j \in \{1,2,3,4\}$
, let
$i,j \in \{1,2,3,4\}$
, let
![]() $u_{i,j}$
be the unipotent element whose only nonzero off-diagonal term is
$u_{i,j}$
be the unipotent element whose only nonzero off-diagonal term is
![]() $1$
at the
$1$
at the
![]() $(i,j)$
-entry. Let
$(i,j)$
-entry. Let
![]() $g=(\begin {smallmatrix} 1 & 1\\ & 1 \end {smallmatrix})$
, and consider the element s of Q given by the block diagonal matrix
$g=(\begin {smallmatrix} 1 & 1\\ & 1 \end {smallmatrix})$
, and consider the element s of Q given by the block diagonal matrix
![]() $s=(g,I_2)$
. Now, let
$s=(g,I_2)$
. Now, let
![]() $\mu $
be any compactly supported probability measure on Q whose support is given by the union of
$\mu $
be any compactly supported probability measure on Q whose support is given by the union of
![]() $\{s, s^\top , u_{2,3}, u_{3,4}\}$
and some diagonal matrices
$\{s, s^\top , u_{2,3}, u_{3,4}\}$
and some diagonal matrices
![]() $d_{\alpha , \beta }$
in Q. It is not difficult to see that
$d_{\alpha , \beta }$
in Q. It is not difficult to see that
![]() $U\leqslant \operatorname {\mathrm {Zcl}}(\Gamma _{\mu })$
and the
$U\leqslant \operatorname {\mathrm {Zcl}}(\Gamma _{\mu })$
and the
![]() $A_c$
-part
$A_c$
-part
![]() $\mu _{A_c}$
of
$\mu _{A_c}$
of
![]() $\mu $
consists of the latter diagonal matrices. Moreover, M is semisimple and the M-part of
$\mu $
consists of the latter diagonal matrices. Moreover, M is semisimple and the M-part of
![]() $\mu $
is Zariski dense in M. So, in view of Propositions 3.3 and 3.1, provided that the integral
$\mu $
is Zariski dense in M. So, in view of Propositions 3.3 and 3.1, provided that the integral
![]() $\int (\log \alpha ,\log \beta ) \mathop {}\!\mathrm {d}\mu _{A_c}(d_{\alpha ,\beta })$
is in the cone in
$\int (\log \alpha ,\log \beta ) \mathop {}\!\mathrm {d}\mu _{A_c}(d_{\alpha ,\beta })$
is in the cone in
![]() $\mathbb {R}^2$
defined by the inequalities
$\mathbb {R}^2$
defined by the inequalities
![]() $x+y<0$
and
$x+y<0$
and
![]() $y<0$
, the measure
$y<0$
, the measure
![]() $\mu $
is
$\mu $
is
![]() $\operatorname {\mathrm {SL}}_4(\mathbb {R})$
-expanding.
$\operatorname {\mathrm {SL}}_4(\mathbb {R})$
-expanding.
3.3 Split solvable epimorphic subgroups
The goal of this part is to discuss a further class of H-expanding measures. They will be supported on solvable epimorphic subgroups
![]() $F=A'U$
of semisimple real algebraic groups H, where
$F=A'U$
of semisimple real algebraic groups H, where
![]() $A'$
is a one-dimensional algebraic
$A'$
is a one-dimensional algebraic
![]() $\mathbb {R}$
-split torus and U is unipotent. The arguments rely on Proposition 3.7, ideas going back to Weiss [Reference Weiss95] and Shah–Weiss [Reference Shah and Weiss90], and the work of Bien–Borel [Reference Bien and Borel13, Reference Bien, Borel and Kollár15].
$\mathbb {R}$
-split torus and U is unipotent. The arguments rely on Proposition 3.7, ideas going back to Weiss [Reference Weiss95] and Shah–Weiss [Reference Shah and Weiss90], and the work of Bien–Borel [Reference Bien and Borel13, Reference Bien, Borel and Kollár15].
We start with a brief discussion of epimorphic subgroups, which have close connections to the notion of H-expanding measures.
3.3.1 Epimorphic subgroups
The concept of epimorphic subgroups of algebraic groups was introduced by Bien–Borel [Reference Bien and Borel13, Reference Bien and Borel14]. In [Reference Shi92], this notion was adapted to subgroups of connected semisimple Lie groups without compact factors.
Definition 3.11. A subgroup F of H is said to be epimorphic in H if for every representation of H, the vectors fixed by F are also fixed by H.
It can be shown that if H is almost algebraic in the sense of Remark 2.11 and
![]() $F\leqslant H$
is a connected Lie subgroup or a Zariski connected algebraic subgroup, it suffices to check the epimorphic property of F in real algebraic representations of H (see Proposition A.3). Consequently, in the algebraic category the above definition coincides with that of Bien–Borel. Moreover, it follows that a connected Lie subgroup F is epimorphic in H if and only if its Zariski closure
$F\leqslant H$
is a connected Lie subgroup or a Zariski connected algebraic subgroup, it suffices to check the epimorphic property of F in real algebraic representations of H (see Proposition A.3). Consequently, in the algebraic category the above definition coincides with that of Bien–Borel. Moreover, it follows that a connected Lie subgroup F is epimorphic in H if and only if its Zariski closure
![]() $\operatorname {\mathrm {Zcl}}(F)$
is.
$\operatorname {\mathrm {Zcl}}(F)$
is.
Mozes [Reference Mozes72] proved that an F-invariant probability measure on
![]() $G/\Lambda $
is already invariant under H (and thus homogeneous by Ratner’s theorem) in the case where all of
$G/\Lambda $
is already invariant under H (and thus homogeneous by Ratner’s theorem) in the case where all of
![]() $F,H,G$
are real algebraic groups. This measure rigidity result was later generalized by Shah–Weiss [Reference Shah and Weiss90, Theorem 1.8] to actions of connected epimorphic Lie subgroups which are not necessarily algebraic.
$F,H,G$
are real algebraic groups. This measure rigidity result was later generalized by Shah–Weiss [Reference Shah and Weiss90, Theorem 1.8] to actions of connected epimorphic Lie subgroups which are not necessarily algebraic.
Examples of epimorphic subgroups include parabolic subgroups of H and Zariski dense subgroups, in case H is almost algebraic. One may notice that these classes of subgroups also prominently featured in the previous parts of this section, where we gave our first examples of H-expanding measures. That this is not a coincidence becomes clear with the following observation.
Proposition 3.12. If
![]() $\mu $
is H-expanding, then the closed subgroup
$\mu $
is H-expanding, then the closed subgroup
![]() $\Gamma _{\mu }$
generated by the support of
$\Gamma _{\mu }$
generated by the support of
![]() $\mu $
is epimorphic in H.
$\mu $
is epimorphic in H.
Proof. In any given representation
![]() $(\rho ,V)$
of H, a
$(\rho ,V)$
of H, a
![]() $\Gamma _{\mu }$
-fixed vector
$\Gamma _{\mu }$
-fixed vector
![]() $v\in V$
cannot be
$v\in V$
cannot be
![]() $\rho _*\mu $
-expanded. In view of Proposition 2.10(i), it follows that v is H-fixed.
$\rho _*\mu $
-expanded. In view of Proposition 2.10(i), it follows that v is H-fixed.
On the other hand, there exist connected epimorphic subgroups of H which do not support any H-expanding probability measure.
Example 3.13. We take
![]() $H=\operatorname {\mathrm {SL}}_3(\mathbb {R})$
,
$H=\operatorname {\mathrm {SL}}_3(\mathbb {R})$
,
![]() $A'=\{\operatorname {\mathrm {diag}}(e^t, e^{-\sqrt 2 t},e^{(\sqrt 2-1)t} ) \mid t\in \mathbb {R}\}$
and U to be as in Example 3.9 for
$A'=\{\operatorname {\mathrm {diag}}(e^t, e^{-\sqrt 2 t},e^{(\sqrt 2-1)t} ) \mid t\in \mathbb {R}\}$
and U to be as in Example 3.9 for
![]() $m=2, n=1$
. The Zariski closure of
$m=2, n=1$
. The Zariski closure of
![]() $A'U$
contains
$A'U$
contains
![]() $AU$
, where
$AU$
, where
![]() $A\leqslant H$
is the diagonal subgroup with positive entries. It follows that
$A\leqslant H$
is the diagonal subgroup with positive entries. It follows that
![]() $A'U$
is an epimorphic subgroup of H, since
$A'U$
is an epimorphic subgroup of H, since
![]() $AU$
is. On the other hand,
$AU$
is. On the other hand,
![]() $A'$
has empty intersection with the expanding cone
$A'$
has empty intersection with the expanding cone
![]() $A_U^+$
which is described explicitly in Example 3.9. Therefore, for any probability measure
$A_U^+$
which is described explicitly in Example 3.9. Therefore, for any probability measure
![]() $\mu $
on
$\mu $
on
![]() $A'U$
with finite first moment, we have
$A'U$
with finite first moment, we have
where
![]() $a_{\operatorname {avg}}$
is as in Proposition 3.7. It follows from the definition of the expanding cone that there is a nontrivial irreducible representation V of H such that
$a_{\operatorname {avg}}$
is as in Proposition 3.7. It follows from the definition of the expanding cone that there is a nontrivial irreducible representation V of H such that
![]() $V^U\cap (V_a^-\oplus V_a^0) \neq \{0\}$
. Therefore,
$V^U\cap (V_a^-\oplus V_a^0) \neq \{0\}$
. Therefore,
![]() $\mu $
is not H-expanding.
$\mu $
is not H-expanding.
We point out that the phenomenon in the above example crucially depends on the one-dimensional torus
![]() $A'$
not being algebraic, as the discussion in the upcoming part will show.
$A'$
not being algebraic, as the discussion in the upcoming part will show.
3.3.2 Expanding rays in one-dimensional algebraic tori
We now state an observation (Lemma 3.14) ensuring the expansion of the unipotent part of a split solvable group with respect to its one-dimensional torus. Based on this observation, in §3.3.3 we will outline two constructions due to Bien–Borel–Kollár [Reference Bien, Borel and Kollár15], which, thanks to Proposition 3.7, yield further classes of H-expanding measures with small support on a semisimple group H.
Let H be a connected almost algebraic semisimple real Lie group without compact factors and F a connected epimorphic subgroup of H of the form
![]() $F=A'U$
, where
$F=A'U$
, where
![]() $A'$
is a connected algebraic
$A'$
is a connected algebraic
![]() $\mathbb {R}$
-split torus and U is a unipotent subgroup of H normalized by
$\mathbb {R}$
-split torus and U is a unipotent subgroup of H normalized by
![]() $A'$
. It is known that any connected algebraic epimorphic subgroup of H contains an epimorphic subgroup of this form [Reference Bien and Borel13, §10, Theorem 2].
$A'$
. It is known that any connected algebraic epimorphic subgroup of H contains an epimorphic subgroup of this form [Reference Bien and Borel13, §10, Theorem 2].
The following lemma can be proved in a similar way as Lemma 3.6 using additionally [Reference Weiss95, Lemma 1]. We omit the routine details of the proof for brevity.
Lemma 3.14. Let H and
![]() $F=A'U$
be as above and suppose that
$F=A'U$
be as above and suppose that
![]() $A'$
is one-dimensional. Then there exists a parametrization
$A'$
is one-dimensional. Then there exists a parametrization
![]() $A'=(a(t))_{t\in \mathbb {R}}$
as one-parameter subgroup such that for every representation
$A'=(a(t))_{t\in \mathbb {R}}$
as one-parameter subgroup such that for every representation
![]() $(\rho ,V)$
of H and U-fixed vector
$(\rho ,V)$
of H and U-fixed vector
![]() $v\in V^U$
, either v is H-fixed or
$v\in V^U$
, either v is H-fixed or
![]() $\lim _{t\to \infty } \left \lVert {\rho (a(t))v} \right \rVert =\infty $
. For such a parametrization, U is
$\lim _{t\to \infty } \left \lVert {\rho (a(t))v} \right \rVert =\infty $
. For such a parametrization, U is
![]() $a(t)$
-expanding in the sense of §3.2 for every
$a(t)$
-expanding in the sense of §3.2 for every
![]() $t>0$
.
$t>0$
.
3.3.3 Examples
Let H be a connected almost algebraic semisimple real Lie group, and denote its Lie algebra by
![]() $\mathfrak h$
. Let Z be a one-parameter unipotent subgroup of H and z a generator of the Lie algebra of Z. By the Jacobson–Morozov theorem z is part of an
$\mathfrak h$
. Let Z be a one-parameter unipotent subgroup of H and z a generator of the Lie algebra of Z. By the Jacobson–Morozov theorem z is part of an
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $(a,z,z_-)$
. Let
$(a,z,z_-)$
. Let
![]() $\mathfrak s$
be the Lie algebra spanned by this triple and S the corresponding connected subgroup of H. Let
$\mathfrak s$
be the Lie algebra spanned by this triple and S the corresponding connected subgroup of H. Let
![]() $A'$
be the one-parameter diagonalizable subgroup with Lie algebra spanned by a. Via the adjoint representation, write
$A'$
be the one-parameter diagonalizable subgroup with Lie algebra spanned by a. Via the adjoint representation, write
![]() $\mathfrak h$
as direct sum of the centralizer
$\mathfrak h$
as direct sum of the centralizer
![]() $\mathfrak z_o$
of
$\mathfrak z_o$
of
![]() $\mathfrak s$
and of nontrivial irreducible
$\mathfrak s$
and of nontrivial irreducible
![]() $\mathfrak s$
-submodules
$\mathfrak s$
-submodules
![]() $\mathfrak m_1=\mathfrak s,\mathfrak m_2,\dots ,\mathfrak m_k$
.
$\mathfrak m_1=\mathfrak s,\mathfrak m_2,\dots ,\mathfrak m_k$
.
Example 3.15 [Reference Bien, Borel and Kollár15, Proposition 4.5]
Retain the notation from the paragraph above, and suppose that z has nontrivial projections to each of the simple factors of
![]() $\mathfrak h$
. Let
$\mathfrak h$
. Let
![]() $z_i$
be highest weight vectors of the irreducible
$z_i$
be highest weight vectors of the irreducible
![]() $\mathfrak s$
-modules
$\mathfrak s$
-modules
![]() $\mathfrak m_i$
, with
$\mathfrak m_i$
, with
![]() $z_1=z$
. Write
$z_1=z$
. Write
![]() $\mathfrak u$
for the direct sum of their
$\mathfrak u$
for the direct sum of their
![]() $\mathbb {R}$
-spans. Denoting by U the corresponding unipotent subgroup of H, it follows that
$\mathbb {R}$
-spans. Denoting by U the corresponding unipotent subgroup of H, it follows that
![]() $F=A'U$
is a split solvable algebraic subgroup of H, which can be seen to be epimorphic in H thanks to [Reference Bien, Borel and Kollár15, Proposition 4.5]. Therefore, by virtue of Proposition 3.7, we see that any probability measure
$F=A'U$
is a split solvable algebraic subgroup of H, which can be seen to be epimorphic in H thanks to [Reference Bien, Borel and Kollár15, Proposition 4.5]. Therefore, by virtue of Proposition 3.7, we see that any probability measure
![]() $\mu $
on F whose
$\mu $
on F whose
![]() $A'$
-average lies in the expanding ray given by Lemma 3.14 is H-expanding.
$A'$
-average lies in the expanding ray given by Lemma 3.14 is H-expanding.
Example 3.16 [Reference Bien, Borel and Kollár15, §4.6]
Retain the notation from above. Suppose that H is an
![]() $\mathbb {R}$
-split simple real algebraic group and that the one-parameter unipotent subgroup Z of H contains ‘regular’ unipotent elements. For example, the generator z can be taken as sum of eigenvectors for all positive simple roots of
$\mathbb {R}$
-split simple real algebraic group and that the one-parameter unipotent subgroup Z of H contains ‘regular’ unipotent elements. For example, the generator z can be taken as sum of eigenvectors for all positive simple roots of
![]() $\mathfrak h$
. Then the subgroup S whose Lie algebra is spanned by the
$\mathfrak h$
. Then the subgroup S whose Lie algebra is spanned by the
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $(a,z,z_-)$
is a ‘principal three-dimensional subgroup’ in H. It is known that either S is properly contained in exactly one proper connected subgroup R of H, or S is maximal among proper connected subgroups of H, in which case we set
$(a,z,z_-)$
is a ‘principal three-dimensional subgroup’ in H. It is known that either S is properly contained in exactly one proper connected subgroup R of H, or S is maximal among proper connected subgroups of H, in which case we set
![]() $R=S$
. See Kostant [Reference Kostant61] for a treatment of the notions used here. Choose
$R=S$
. See Kostant [Reference Kostant61] for a treatment of the notions used here. Choose
![]() $\mathfrak m_j$
so that it does not intersect the Lie algebra
$\mathfrak m_j$
so that it does not intersect the Lie algebra
![]() $\mathfrak r$
of R, and let
$\mathfrak r$
of R, and let
![]() $Z_j$
be the subgroup of H whose Lie algebra is generated by a highest weight vector of
$Z_j$
be the subgroup of H whose Lie algebra is generated by a highest weight vector of
![]() $\mathfrak m_j$
. Then, as discussed in [Reference Bien, Borel and Kollár15, §4.6],
$\mathfrak m_j$
. Then, as discussed in [Reference Bien, Borel and Kollár15, §4.6],
![]() $F=A'ZZ_j$
is a three-dimensional split solvable algebraic epimorphic subgroup of H. Therefore, as in the previous example, three-dimensional solvable subgroups obtained by this construction support many H-expanding measures thanks to Proposition 3.7 and Lemma 3.14.
$F=A'ZZ_j$
is a three-dimensional split solvable algebraic epimorphic subgroup of H. Therefore, as in the previous example, three-dimensional solvable subgroups obtained by this construction support many H-expanding measures thanks to Proposition 3.7 and Lemma 3.14.
We end this section by mentioning an ensuing question, which was also posed to us by Barak Weiss.
Question. Let H be a semisimple real algebraic group without compact factors. Is it true that every algebraic epimorphic subgroup
![]() $F\leqslant H$
supports an H-expanding probability measure?
$F\leqslant H$
supports an H-expanding probability measure?
The answer to the above question is negative if we do not require F to be epimorphic (Proposition 3.12) or to be algebraic (Example 3.13).
On the other hand, let
![]() $F=A'U$
be an
$F=A'U$
be an
![]() $\mathbb {R}$
-split solvable epimorphic subgroup of F, where U is a unipotent group and
$\mathbb {R}$
-split solvable epimorphic subgroup of F, where U is a unipotent group and
![]() $A'$
is an
$A'$
is an
![]() $\mathbb {R}$
-split algebraic torus normalizing U. Then [Reference Bien and Borel13, §7, Lemma (iii)] provides a sufficient condition (in terms of finite-generation of a monoid generated by certain characters of
$\mathbb {R}$
-split algebraic torus normalizing U. Then [Reference Bien and Borel13, §7, Lemma (iii)] provides a sufficient condition (in terms of finite-generation of a monoid generated by certain characters of
![]() $A'$
) for F to contain an
$A'$
) for F to contain an
![]() $\mathbb {R}$
-split solvable epimorphic subgroup
$\mathbb {R}$
-split solvable epimorphic subgroup
![]() $F_0=A^{\prime }_0U$
with one-dimensional
$F_0=A^{\prime }_0U$
with one-dimensional
![]() $\mathbb {R}$
-split algebraic torus
$\mathbb {R}$
-split algebraic torus
![]() $A^{\prime }_0<A'$
. In view of Lemma 3.14, any such subgroup
$A^{\prime }_0<A'$
. In view of Lemma 3.14, any such subgroup
![]() $F_0$
supports H-expanding probability measures. However, we do not know whether the hypothesis of the aforementioned lemma of Bien–Borel is always satisfied in the context of the question above, or whether a different construction can be used to obtain H-expanding probability measures on F in case it is not.
$F_0$
supports H-expanding probability measures. However, we do not know whether the hypothesis of the aforementioned lemma of Bien–Borel is always satisfied in the context of the question above, or whether a different construction can be used to obtain H-expanding probability measures on F in case it is not.
4 Measure rigidity
This section is dedicated to the statements outlined in §1.1. In §4.1, we first prove our general measure rigidity result (Theorem 1.1), followed by a discussion of stationary measures charging an orbit of the centralizer in §4.2, which leads to the proof of Corollary 1.2. Finally, we more closely analyze, in §4.3, expansion in which representations is necessary to obtain the conclusion of Theorem 1.1. This will yield a finite criterion weaker than H-expansion for measure rigidity to hold when the ambient Lie group G is fixed.
4.1 Rigidity for expanding measures
Let
![]() $\Lambda $
be a discrete subgroup of a real Lie group G and
$\Lambda $
be a discrete subgroup of a real Lie group G and
![]() $X=G/\Lambda $
. Moreover, we let
$X=G/\Lambda $
. Moreover, we let
![]() $H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center and
$H\leqslant G$
be a connected semisimple subgroup without compact factors and with finite center and
![]() $\mu $
a probability measure on H. For the proof of Theorem 1.1, we will follow the strategy in the proof of [Reference Eskin and Lindenstrauss30, Theorem 1.3]. The argument is based on the following measure classification result of Eskin–Lindenstrauss.
$\mu $
a probability measure on H. For the proof of Theorem 1.1, we will follow the strategy in the proof of [Reference Eskin and Lindenstrauss30, Theorem 1.3]. The argument is based on the following measure classification result of Eskin–Lindenstrauss.
Definition 4.1 [Reference Eskin and Lindenstrauss30, Definition 1.6]
Let Z be a connected Lie subgroup of G. A probability measure
![]() $\mu $
on G is said to be uniformly expanding mod Z if the following hold:
$\mu $
on G is said to be uniformly expanding mod Z if the following hold:
-
(a) Z is normalized by
 $\Gamma _{\mu }$
,
$\Gamma _{\mu }$
, -
(b) the conjugation action of
 $\Gamma _{\mu }$
on Z factors through the action of a compact subgroup of
$\Gamma _{\mu }$
on Z factors through the action of a compact subgroup of
 $\operatorname {\mathrm {Aut}}(Z)$
and
$\operatorname {\mathrm {Aut}}(Z)$
and -
(c) there is a
 $\Gamma _{\mu }$
-invariant direct sum decomposition
$\Gamma _{\mu }$
-invariant direct sum decomposition
 $\mathfrak g=\operatorname {\mathrm {Lie}}(Z)\oplus V$
such that
$\mathfrak g=\operatorname {\mathrm {Lie}}(Z)\oplus V$
such that
 $\mu $
is uniformly expanding on V.
$\mu $
is uniformly expanding on V.
Theorem 4.2 (Eskin–Lindenstrauss [Reference Eskin and Lindenstrauss30, Theorem 1.7])
Let G be a real Lie group and
![]() $\Lambda <G$
a discrete subgroup. Suppose that
$\Lambda <G$
a discrete subgroup. Suppose that
![]() $\mu $
is a probability measure on G with finite first moment for which there exists a connected Lie subgroup Z of G such that
$\mu $
is a probability measure on G with finite first moment for which there exists a connected Lie subgroup Z of G such that
![]() $\mu $
is uniformly expanding mod Z. Let
$\mu $
is uniformly expanding mod Z. Let
![]() $\nu $
be any ergodic
$\nu $
be any ergodic
![]() $\mu $
-stationary probability measure on
$\mu $
-stationary probability measure on
![]() $G/\Lambda $
. Then one of the following holds:
$G/\Lambda $
. Then one of the following holds:
-
(a) There exists a closed subgroup
 $N\leqslant G$
with
$N\leqslant G$
with
 $\dim (N)>0$
, an N-homogeneous probability measure
$\dim (N)>0$
, an N-homogeneous probability measure
 $\nu _0$
on
$\nu _0$
on
 $G/\Lambda $
and a
$G/\Lambda $
and a
 $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
 $\eta $
on
$\eta $
on
 $G/N$
such that
$G/N$
such that  $$ \begin{align*} \nu=\int_{G/N}g_*\nu_0\mathop{}\!\mathrm{d}\eta(g). \end{align*} $$
$$ \begin{align*} \nu=\int_{G/N}g_*\nu_0\mathop{}\!\mathrm{d}\eta(g). \end{align*} $$
-
(b) The measure
 $\nu $
is
$\nu $
is
 $\Gamma _{\mu }$
-invariant and supported on a finite union of compact subsets of Z-orbits.
$\Gamma _{\mu }$
-invariant and supported on a finite union of compact subsets of Z-orbits.
The following two lemmas will go into the proof of Theorem 1.1.
Lemma 4.3. Suppose that
![]() $\mu $
is H-expanding. Then the Lie algebra
$\mu $
is H-expanding. Then the Lie algebra
![]() $\mathfrak g$
of G admits an H-invariant direct sum decomposition
$\mathfrak g$
of G admits an H-invariant direct sum decomposition
![]() $\mathfrak g=\mathfrak l\oplus \mathfrak v$
, where
$\mathfrak g=\mathfrak l\oplus \mathfrak v$
, where
![]() $\mathfrak l$
is the Lie algebra of the centralizer L of
$\mathfrak l$
is the Lie algebra of the centralizer L of
![]() $\Gamma _{\mu }$
in G and
$\Gamma _{\mu }$
in G and
![]() $\mathfrak v\subset \mathfrak {g}$
is a subspace on which
$\mathfrak v\subset \mathfrak {g}$
is a subspace on which
![]() $\mu $
is uniformly expanding. In particular,
$\mu $
is uniformly expanding. In particular,
![]() $\mu $
is uniformly expanding mod
$\mu $
is uniformly expanding mod
![]() $L^\circ $
in the sense of Definition 4.1.
$L^\circ $
in the sense of Definition 4.1.
Proof. Since, by Proposition 3.12,
![]() $\Gamma _{\mu }$
is epimorphic in H,
$\Gamma _{\mu }$
is epimorphic in H,
![]() $\mathfrak l$
is the space of H-fixed vectors in the adjoint representation of G. Semisimplicity thus implies the existence of an H-invariant complementary subspace
$\mathfrak l$
is the space of H-fixed vectors in the adjoint representation of G. Semisimplicity thus implies the existence of an H-invariant complementary subspace
![]() $\mathfrak v$
. Now, the claim follows directly from the definition of H-expansion.
$\mathfrak v$
. Now, the claim follows directly from the definition of H-expansion.
The second lemma concerns
![]() $\mu $
-stationary measures assigning positive mass to centralizer orbits.
$\mu $
-stationary measures assigning positive mass to centralizer orbits.
Lemma 4.4 [Reference Benoist and Quint9, Lemma 7.6]
Suppose that
![]() $\nu $
is an ergodic
$\nu $
is an ergodic
![]() $\mu $
-stationary probability measure on X such that
$\mu $
-stationary probability measure on X such that
![]() $\nu $
assigns positive mass to some L-orbit in X, where
$\nu $
assigns positive mass to some L-orbit in X, where
![]() $L=C_G(\Gamma _{\mu })$
. Let
$L=C_G(\Gamma _{\mu })$
. Let
![]() $L_0$
be any open subgroup of
$L_0$
be any open subgroup of
![]() $L\cap \operatorname {\mathrm {Stab}}_G(\nu )$
. Then
$L\cap \operatorname {\mathrm {Stab}}_G(\nu )$
. Then
![]() $\nu $
is homogeneous under the closed subgroup
$\nu $
is homogeneous under the closed subgroup
![]() $\Gamma _{\mu } L_0$
and
$\Gamma _{\mu } L_0$
and
![]() $L_0$
is open in
$L_0$
is open in
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
.
$\operatorname {\mathrm {Stab}}_G(\nu )$
.
We point out that the last claim in the statement above follows from the proof of [Reference Benoist and Quint9, Lemma 7.6], where it is shown that the support of
![]() $\nu $
is a finite union of closed
$\nu $
is a finite union of closed
![]() $L_0$
-orbits which are transitively permuted by
$L_0$
-orbits which are transitively permuted by
![]() $\Gamma _{\mu }$
. In fact, even more conclusions can be drawn in the context of this lemma; see Proposition 4.5.
$\Gamma _{\mu }$
. In fact, even more conclusions can be drawn in the context of this lemma; see Proposition 4.5.
Proof of Theorem 1.1
Our main tool is Theorem 4.2. Its assumptions are satisfied, since by Lemma 4.3,
![]() $\mu $
is uniformly expanding mod
$\mu $
is uniformly expanding mod
![]() $L^\circ $
, where L denotes the centralizer of
$L^\circ $
, where L denotes the centralizer of
![]() $\Gamma _{\mu }$
in G. If Theorem 4.2(b) holds, then by Lemma 4.4,
$\Gamma _{\mu }$
in G. If Theorem 4.2(b) holds, then by Lemma 4.4,
![]() $\nu $
is homogeneous and the connected component of
$\nu $
is homogeneous and the connected component of
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
is contained in L. By the epimorphic property of
$\operatorname {\mathrm {Stab}}_G(\nu )$
is contained in L. By the epimorphic property of
![]() $\Gamma _{\mu }$
in H from Proposition 3.12 applied to the adjoint representation of G, the connected components of
$\Gamma _{\mu }$
in H from Proposition 3.12 applied to the adjoint representation of G, the connected components of
![]() $C_G(\Gamma _{\mu })$
and
$C_G(\Gamma _{\mu })$
and
![]() $C_G(H)$
coincide. Thus, it follows that the connected component of
$C_G(H)$
coincide. Thus, it follows that the connected component of
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
is centralized by H.
$\operatorname {\mathrm {Stab}}_G(\nu )$
is centralized by H.
If Theorem 4.2(a) holds, then there exists a closed subgroup N of G with
![]() $\dim (N)>0$
, an N-homogeneous probability measure
$\dim (N)>0$
, an N-homogeneous probability measure
![]() $\nu _0$
on
$\nu _0$
on
![]() $G/\Lambda $
and a
$G/\Lambda $
and a
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\eta $
on
$\eta $
on
![]() $G/N$
such that
$G/N$
such that
We may assume that
![]() $\eta $
is
$\eta $
is
![]() $\mu $
-ergodic. Indeed, if
$\mu $
-ergodic. Indeed, if
![]() $\eta =\int _ Y \eta _y \mathop {}\!\mathrm {d} y$
is a
$\eta =\int _ Y \eta _y \mathop {}\!\mathrm {d} y$
is a
![]() $\mu $
-ergodic decomposition of
$\mu $
-ergodic decomposition of
![]() $\eta $
, then
$\eta $
, then
 $$ \begin{align*} \nu =\int_Y \biggl(\int_{G/N} g_* \nu_0 \mathop{}\!\mathrm{d} \eta_y(g)\biggr)\mathop{}\!\mathrm{d} y \end{align*} $$
$$ \begin{align*} \nu =\int_Y \biggl(\int_{G/N} g_* \nu_0 \mathop{}\!\mathrm{d} \eta_y(g)\biggr)\mathop{}\!\mathrm{d} y \end{align*} $$
is a convex decomposition of
![]() $\nu $
into
$\nu $
into
![]() $\mu $
-stationary measures. Since
$\mu $
-stationary measures. Since
![]() $\nu $
is
$\nu $
is
![]() $\mu $
-ergodic, we must have
$\mu $
-ergodic, we must have
![]() $\nu =\int _{G/N} g_* \nu _0 \mathop {}\!\mathrm {d} \eta _y(g) $
for almost every y. Thus, we can replace
$\nu =\int _{G/N} g_* \nu _0 \mathop {}\!\mathrm {d} \eta _y(g) $
for almost every y. Thus, we can replace
![]() $\eta $
by one of the
$\eta $
by one of the
![]() $\eta _y$
, if necessary. We consider N such that
$\eta _y$
, if necessary. We consider N such that
![]() $\dim (N)$
is maximal among possible representations of
$\dim (N)$
is maximal among possible representations of
![]() $\nu $
of the form (4.1).
$\nu $
of the form (4.1).
Now, consider the adjoint action of G on
![]() $S^2(\mathfrak {g}^{\wedge \dim (N)})$
, where
$S^2(\mathfrak {g}^{\wedge \dim (N)})$
, where
![]() $S^2$
denotes the symmetric square representation. Let
$S^2$
denotes the symmetric square representation. Let
![]() $\omega =v\otimes v$
, where
$\omega =v\otimes v$
, where
![]() $v\in \mathfrak {g}^{\wedge \dim (N)}$
corresponds to a basis of the Lie algebra of N. Let P be the stabilizer of
$v\in \mathfrak {g}^{\wedge \dim (N)}$
corresponds to a basis of the Lie algebra of N. Let P be the stabilizer of
![]() $\omega $
in G. Since N admits a lattice, it is unimodular so that N acts on v by
$\omega $
in G. Since N admits a lattice, it is unimodular so that N acts on v by
![]() $\pm 1$
. Thus, N fixes
$\pm 1$
. Thus, N fixes
![]() $\omega $
, that is
$\omega $
, that is
![]() $N\leqslant P$
. Let
$N\leqslant P$
. Let
![]() $\eta '$
be the pushforward of
$\eta '$
be the pushforward of
![]() $\eta $
via the natural projection map
$\eta $
via the natural projection map
![]() $G/N\to G/P$
. The measure
$G/N\to G/P$
. The measure
![]() $\eta '$
can be thought of as an ergodic
$\eta '$
can be thought of as an ergodic
![]() $\mu $
-stationary measure on
$\mu $
-stationary measure on
![]() $S^2(\mathfrak {g}^{\wedge \dim (N)})$
. By Corollary 2.12, the measure
$S^2(\mathfrak {g}^{\wedge \dim (N)})$
. By Corollary 2.12, the measure
![]() $\eta '$
must concentrate on the subspace of H-fixed vectors. Then by ergodicity,
$\eta '$
must concentrate on the subspace of H-fixed vectors. Then by ergodicity,
![]() $\eta '$
is a Dirac measure. After replacing N and P by their conjugates, we may assume without loss of generality that
$\eta '$
is a Dirac measure. After replacing N and P by their conjugates, we may assume without loss of generality that
![]() $\eta '$
is the Dirac measure on the coset P. It follows that
$\eta '$
is the Dirac measure on the coset P. It follows that
![]() $\omega $
is H-fixed. Hence,
$\omega $
is H-fixed. Hence,
![]() $H\leqslant P$
and
$H\leqslant P$
and
![]() $H\cap N^\circ $
is a normal subgroup of H. If
$H\cap N^\circ $
is a normal subgroup of H. If
![]() $H\leqslant N^\circ $
, then the action of H on
$H\leqslant N^\circ $
, then the action of H on
![]() $P/N$
is trivial, so that by ergodicity of
$P/N$
is trivial, so that by ergodicity of
![]() $\eta $
we have
$\eta $
we have
![]() $\nu =g_*\nu _0$
for an element
$\nu =g_*\nu _0$
for an element
![]() $g\in P$
with
$g\in P$
with
![]() $\operatorname {\mathrm {supp}}(\eta )=\{gN\}$
and we are done.
$\operatorname {\mathrm {supp}}(\eta )=\{gN\}$
and we are done.
So let us now assume that H is not contained in
![]() $N^\circ $
. In this case, we consider the action of
$N^\circ $
. In this case, we consider the action of
![]() $(H/(H\cap N^\circ ), \mu ') $
on
$(H/(H\cap N^\circ ), \mu ') $
on
![]() $P/N \cong (P/N^\circ )/(N/N^\circ )$
with the
$P/N \cong (P/N^\circ )/(N/N^\circ )$
with the
![]() $\mu '$
-stationary measure
$\mu '$
-stationary measure
![]() $\eta $
, where
$\eta $
, where
![]() $\mu '$
is the pushforward of
$\mu '$
is the pushforward of
![]() $\mu $
under the natural projection map
$\mu $
under the natural projection map
![]() $H\to H/(H\cap N^\circ )$
. Since
$H\to H/(H\cap N^\circ )$
. Since
![]() $\mu $
is H-expanding and H is not contained in
$\mu $
is H-expanding and H is not contained in
![]() $N^\circ $
,
$N^\circ $
,
![]() $\mu '$
is
$\mu '$
is
![]() $H/(H\cap N^\circ )$
-expanding in view of Proposition 2.10(iii). Now, in view of Lemma 4.3, we are in a position to apply Theorem 4.2 again for
$H/(H\cap N^\circ )$
-expanding in view of Proposition 2.10(iii). Now, in view of Lemma 4.3, we are in a position to apply Theorem 4.2 again for
![]() $\mu '$
. We claim that thanks to the choice of N as having maximal dimension in equation (4.1), the case (a) in Theorem 4.2 does not occur. Suppose it does. This means that there exist a closed subgroup
$\mu '$
. We claim that thanks to the choice of N as having maximal dimension in equation (4.1), the case (a) in Theorem 4.2 does not occur. Suppose it does. This means that there exist a closed subgroup
![]() $M<P/N^{\circ }$
of positive dimension, an M-homogeneous probability measure
$M<P/N^{\circ }$
of positive dimension, an M-homogeneous probability measure
![]() $\nu _0'$
on
$\nu _0'$
on
![]() $P/N$
and a
$P/N$
and a
![]() $\mu '$
-stationary probability measure
$\mu '$
-stationary probability measure
![]() $\eta '$
on
$\eta '$
on
![]() $(P/N^{\circ })/M$
such that we have
$(P/N^{\circ })/M$
such that we have
Denote by
![]() $\hat {M}$
the preimage of M under the projection
$\hat {M}$
the preimage of M under the projection
![]() $P \to P/N^{\circ }$
so that we can identify
$P \to P/N^{\circ }$
so that we can identify
![]() $(P/N^{\circ })/M$
with
$(P/N^{\circ })/M$
with
![]() $P/\hat {M}$
. By combining equations (4.1) and (4.2), we deduce that
$P/\hat {M}$
. By combining equations (4.1) and (4.2), we deduce that
 $$ \begin{align*} \nu=\int_{P/N} \int_{P/\hat{M}} (gh)_*\nu_0 \mathop{}\!\mathrm{d}\eta'(g) d\nu_0'(h)=\int_{P/\hat{M}} g_* \biggl(\int_{P/N} h_* \nu_0 \mathop{}\!\mathrm{d}\nu_0'(h)\biggr) \mathop{}\!\mathrm{d}\eta'(g). \end{align*} $$
$$ \begin{align*} \nu=\int_{P/N} \int_{P/\hat{M}} (gh)_*\nu_0 \mathop{}\!\mathrm{d}\eta'(g) d\nu_0'(h)=\int_{P/\hat{M}} g_* \biggl(\int_{P/N} h_* \nu_0 \mathop{}\!\mathrm{d}\nu_0'(h)\biggr) \mathop{}\!\mathrm{d}\eta'(g). \end{align*} $$
Now, it is easily observed that the probability measure
![]() $\Psi =\int _{P/N} h_* \nu _0 \mathop {}\!\mathrm {d}\nu _0'(h)$
on
$\Psi =\int _{P/N} h_* \nu _0 \mathop {}\!\mathrm {d}\nu _0'(h)$
on
![]() $G/\Lambda $
is
$G/\Lambda $
is
![]() $\hat {M}$
-invariant and supported on finitely many
$\hat {M}$
-invariant and supported on finitely many
![]() $\hat {M}$
-orbits. By
$\hat {M}$
-orbits. By
![]() $\mu $
-ergodicity of
$\mu $
-ergodicity of
![]() $\nu $
, for every
$\nu $
, for every
![]() $\hat {M}$
-ergodic component
$\hat {M}$
-ergodic component
![]() $\Psi _y$
of
$\Psi _y$
of
![]() $\Psi $
, we have
$\Psi $
, we have
 $$ \begin{align*}\nu=\int_{P/\hat{M}}g_*\Psi_y\mathop{}\!\mathrm{d}\eta'(g).\\[-18pt]\end{align*} $$
$$ \begin{align*}\nu=\int_{P/\hat{M}}g_*\Psi_y\mathop{}\!\mathrm{d}\eta'(g).\\[-18pt]\end{align*} $$
Take such a component
![]() $\Psi _y$
which assigns positive mass to an
$\Psi _y$
which assigns positive mass to an
![]() $\hat {M}$
-orbit. Then
$\hat {M}$
-orbit. Then
![]() $\Psi _y$
is
$\Psi _y$
is
![]() $\hat {M}$
-homogeneous and the fact that
$\hat {M}$
-homogeneous and the fact that
![]() $\dim (\hat {M})>\dim (N)$
yields a contradiction to the maximality of
$\dim (\hat {M})>\dim (N)$
yields a contradiction to the maximality of
![]() $\dim (N)$
in equation (4.1).
$\dim (N)$
in equation (4.1).
Therefore, we can conclude by case (b) of Theorem 4.2 that
![]() $\eta $
is
$\eta $
is
![]() $\Gamma _{\mu '}$
-invariant and supported on finitely many compact subsets of
$\Gamma _{\mu '}$
-invariant and supported on finitely many compact subsets of
![]() $C_{P/N^\circ }(\Gamma _{\mu '})$
-orbits. By Lemma 4.4,
$C_{P/N^\circ }(\Gamma _{\mu '})$
-orbits. By Lemma 4.4,
![]() $\eta $
is M-homogeneous for a closed subgroup
$\eta $
is M-homogeneous for a closed subgroup
![]() $M<P/N^\circ $
. In particular,
$M<P/N^\circ $
. In particular,
![]() $\eta $
can be written in the form (4.2) with
$\eta $
can be written in the form (4.2) with
![]() $\nu _0'=\eta $
and
$\nu _0'=\eta $
and
![]() $\eta '$
the Dirac mass at the identity coset, the latter being
$\eta '$
the Dirac mass at the identity coset, the latter being
![]() $\mu '$
-stationary since
$\mu '$
-stationary since
![]() $\eta $
is
$\eta $
is
![]() $\Gamma _{\mu '}$
-invariant. As we have argued above, this cannot happen if the support of
$\Gamma _{\mu '}$
-invariant. As we have argued above, this cannot happen if the support of
![]() $\eta $
has positive dimension. Thus,
$\eta $
has positive dimension. Thus,
![]() $\eta $
is a finite periodic orbit measure, and using equation (4.1) it directly follows that
$\eta $
is a finite periodic orbit measure, and using equation (4.1) it directly follows that
![]() $\nu $
is homogeneous. The connected component of
$\nu $
is homogeneous. The connected component of
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
is
$\operatorname {\mathrm {Stab}}_G(\nu )$
is
![]() $N^\circ $
, which is normalized by H, as we already established above. Hence, the proof is complete.
$N^\circ $
, which is normalized by H, as we already established above. Hence, the proof is complete.
4.2 Stationary measures charging an orbit of the centralizer
The following proposition gives additional information about the measure
![]() $\nu $
in the setting of Lemma 4.4, or more generally, in the setting of [Reference Benoist and Quint9, §7.3]. It will be used below to deduce Corollary 1.2(i) from Theorem 1.1.
$\nu $
in the setting of Lemma 4.4, or more generally, in the setting of [Reference Benoist and Quint9, §7.3]. It will be used below to deduce Corollary 1.2(i) from Theorem 1.1.
The general setting is as follows: G is a locally compact second countable group,
![]() $\Lambda $
a discrete subgroup of G,
$\Lambda $
a discrete subgroup of G,
![]() $\mu $
is a probability measure on G, L denotes the centralizer of
$\mu $
is a probability measure on G, L denotes the centralizer of
![]() $\Gamma _{\mu }$
in G, and
$\Gamma _{\mu }$
in G, and
![]() $\nu $
is a
$\nu $
is a
![]() $\mu $
-ergodic
$\mu $
-ergodic
![]() $\mu $
-stationary probability measure on
$\mu $
-stationary probability measure on
![]() $X=G/\Lambda $
assigning positive mass to some L-orbit. Finally,
$X=G/\Lambda $
assigning positive mass to some L-orbit. Finally,
![]() $L_0$
is any open subgroup of
$L_0$
is any open subgroup of
![]() $L\cap \operatorname {\mathrm {Stab}}_G(\nu )$
.
$L\cap \operatorname {\mathrm {Stab}}_G(\nu )$
.
Proposition 4.5. Retain the notation and assumptions above, and fix
![]() $x=g\Lambda \in \operatorname {\mathrm {supp}}(\nu )$
. Let
$x=g\Lambda \in \operatorname {\mathrm {supp}}(\nu )$
. Let
![]() $\nu _0$
be the restriction of
$\nu _0$
be the restriction of
![]() $\nu $
to
$\nu $
to
![]() $L_0x$
,
$L_0x$
,
![]() $\Gamma _0$
the stabilizer of
$\Gamma _0$
the stabilizer of
![]() $\nu _0$
in
$\nu _0$
in
![]() $\Gamma _{\mu }$
and
$\Gamma _{\mu }$
and
Then in addition to the conclusion of Lemma 4.4, the following holds:
-
(i)
 $\Gamma _0$
has finite index in
$\Gamma _0$
has finite index in
 $\Gamma _{\mu }$
,
$\Gamma _{\mu }$
, -
(ii)
 $\Gamma _0^L$
is a dense subgroup of
$\Gamma _0^L$
is a dense subgroup of
 $L_0$
with
$L_0$
with
 $\Gamma _0x=\Gamma _0^Lx$
and
$\Gamma _0x=\Gamma _0^Lx$
and -
(iii)
 $L_0\cap g\Lambda g^{-1}$
is a cocompact normal subgroup of
$L_0\cap g\Lambda g^{-1}$
is a cocompact normal subgroup of
 $L_0$
.
$L_0$
.
In particular,
![]() $\nu $
is compactly supported and is the unique ergodic
$\nu $
is compactly supported and is the unique ergodic
![]() $\mu $
-stationary probability measure on X assigning positive measure to
$\mu $
-stationary probability measure on X assigning positive measure to
![]() $\operatorname {\mathrm {supp}}(\nu )$
.
$\operatorname {\mathrm {supp}}(\nu )$
.
Proof. By [Reference Benoist and Quint9, Lemma 7.6] and its proof, we know that
![]() $\nu $
is the homogeneous measure on
$\nu $
is the homogeneous measure on
![]() $\Gamma _{\mu } L_0 x$
and that
$\Gamma _{\mu } L_0 x$
and that
![]() $\operatorname {\mathrm {supp}}(\nu )$
consists of finitely many closed
$\operatorname {\mathrm {supp}}(\nu )$
consists of finitely many closed
![]() $L_0$
-orbits which are transitively permuted by
$L_0$
-orbits which are transitively permuted by
![]() $\Gamma _{\mu }$
. In particular, we have
$\Gamma _{\mu }$
. In particular, we have
![]() $\nu (L_0x)>0$
. It follows that
$\nu (L_0x)>0$
. It follows that
![]() $\Gamma _0$
has finite index in
$\Gamma _0$
has finite index in
![]() $\Gamma _{\mu }$
. Moreover, since
$\Gamma _{\mu }$
. Moreover, since
![]() $\Gamma _{\mu }$
preserves
$\Gamma _{\mu }$
preserves
![]() $\nu $
and acts ergodically, the group
$\nu $
and acts ergodically, the group
![]() $\Gamma _0$
acts ergodically with respect to
$\Gamma _0$
acts ergodically with respect to
![]() $\nu _0$
. This implies that we can find
$\nu _0$
. This implies that we can find
![]() $l_0\in L_0$
such that
$l_0\in L_0$
such that
![]() $\Gamma _0 l_0 x$
is dense in
$\Gamma _0 l_0 x$
is dense in
![]() $L_0 x$
. As
$L_0 x$
. As
![]() $l_0$
commutes with
$l_0$
commutes with
![]() $\Gamma _0$
, it immediately follows that
$\Gamma _0$
, it immediately follows that
![]() $\Gamma _0x$
is dense in
$\Gamma _0x$
is dense in
![]() $L_0x$
. Since
$L_0x$
. Since
![]() $\Gamma _0^L$
is precisely defined for
$\Gamma _0^L$
is precisely defined for
![]() $\Gamma _0x=\Gamma _0^Lx$
to hold, we conclude that
$\Gamma _0x=\Gamma _0^Lx$
to hold, we conclude that
![]() $\Gamma _0^L=\Gamma _0^L(L_0\cap g\Lambda g^{-1})$
is dense in
$\Gamma _0^L=\Gamma _0^L(L_0\cap g\Lambda g^{-1})$
is dense in
![]() $L_0$
.
$L_0$
.
We next prove that
![]() $L_0\cap g\Lambda g^{-1}$
is a cocompact normal subgroup of
$L_0\cap g\Lambda g^{-1}$
is a cocompact normal subgroup of
![]() $L_0$
. Since we have already shown that
$L_0$
. Since we have already shown that
![]() $\Gamma _0^L$
is dense in
$\Gamma _0^L$
is dense in
![]() $L_0$
, it suffices to show that
$L_0$
, it suffices to show that
![]() $L_0\cap g\Lambda g^{-1}$
is normal in
$L_0\cap g\Lambda g^{-1}$
is normal in
![]() $\Gamma _0^L$
. To see this, taking an arbitrary
$\Gamma _0^L$
. To see this, taking an arbitrary
![]() $l\in \Gamma _0^L$
and choosing
$l\in \Gamma _0^L$
and choosing
![]() $h\in \Gamma _0$
with
$h\in \Gamma _0$
with
![]() $hl\in g\Lambda g^{-1}$
, we calculate
$hl\in g\Lambda g^{-1}$
, we calculate
where we used again that
![]() $\Gamma _{\mu }$
and
$\Gamma _{\mu }$
and
![]() $L_0$
commute. Since there is a finite
$L_0$
commute. Since there is a finite
![]() $L_0$
-invariant measure on the locally compact group
$L_0$
-invariant measure on the locally compact group
![]() $L_0/(L_0\cap g\Lambda g^{-1})$
, the latter must be compact.
$L_0/(L_0\cap g\Lambda g^{-1})$
, the latter must be compact.
It remains to prove the uniqueness of
![]() $\nu $
. Let
$\nu $
. Let
![]() $\nu '$
be an arbitrary ergodic
$\nu '$
be an arbitrary ergodic
![]() $\mu $
-stationary probability measure on X with
$\mu $
-stationary probability measure on X with
![]() $\nu '(\operatorname {\mathrm {supp}}(\nu ))>0$
. Take
$\nu '(\operatorname {\mathrm {supp}}(\nu ))>0$
. Take
![]() $x\in \operatorname {\mathrm {supp}}(\nu )\cap \operatorname {\mathrm {supp}}(\nu ')$
. Then by what we have shown above,
$x\in \operatorname {\mathrm {supp}}(\nu )\cap \operatorname {\mathrm {supp}}(\nu ')$
. Then by what we have shown above,
![]() $\nu '$
is homogeneous and
$\nu '$
is homogeneous and
![]() $\operatorname {\mathrm {supp}}(\nu )=\overline {\Gamma _{\mu } x}=\operatorname {\mathrm {supp}}(\nu ')$
. Hence,
$\operatorname {\mathrm {supp}}(\nu )=\overline {\Gamma _{\mu } x}=\operatorname {\mathrm {supp}}(\nu ')$
. Hence,
![]() $\nu =\nu '$
by homogeneity.
$\nu =\nu '$
by homogeneity.
Loosely speaking, the group
![]() $\Gamma _0^L$
in Proposition 4.5 consists of translations in the centralizer direction arising from the action of
$\Gamma _0^L$
in Proposition 4.5 consists of translations in the centralizer direction arising from the action of
![]() $\Gamma _0\leqslant \Gamma _{\mu }$
on the centralizer orbit under consideration. This is illustrated by the following simple example.
$\Gamma _0\leqslant \Gamma _{\mu }$
on the centralizer orbit under consideration. This is illustrated by the following simple example.
Example 4.6. Let
![]() $G=\operatorname {\mathrm {SL}}_2(\mathbb {R})\times K$
, where K is a connected compact Lie group, and let
$G=\operatorname {\mathrm {SL}}_2(\mathbb {R})\times K$
, where K is a connected compact Lie group, and let
![]() $\psi \colon \operatorname {\mathrm {SL}}_2(\mathbb {Z})\to K $
be a fixed group homomorphism with dense image. Let
$\psi \colon \operatorname {\mathrm {SL}}_2(\mathbb {Z})\to K $
be a fixed group homomorphism with dense image. Let
![]() $X=G/\Lambda $
for the lattice
$X=G/\Lambda $
for the lattice
Moreover, let
![]() $H=\operatorname {\mathrm {SL}}_2(\mathbb {R})$
, identified with the first factor of G, and choose a probability measure
$H=\operatorname {\mathrm {SL}}_2(\mathbb {R})$
, identified with the first factor of G, and choose a probability measure
![]() $\mu $
on H with
$\mu $
on H with
![]() $\Gamma _{\mu }=\operatorname {\mathrm {SL}}_2(\mathbb {Z})<H$
. Let
$\Gamma _{\mu }=\operatorname {\mathrm {SL}}_2(\mathbb {Z})<H$
. Let
![]() $\nu $
be the homogeneous measure on the K-orbit of the identity coset
$\nu $
be the homogeneous measure on the K-orbit of the identity coset
![]() $x=\Lambda $
in
$x=\Lambda $
in
![]() $G/\Lambda $
, induced by the Haar probability measure on K, where we identify K with the second factor of G. Then the action of
$G/\Lambda $
, induced by the Haar probability measure on K, where we identify K with the second factor of G. Then the action of
![]() $\gamma \in \Gamma _{\mu }$
on x is given by
$\gamma \in \Gamma _{\mu }$
on x is given by
Thus, the K-orbit of x is given by
![]() $(\Gamma _{\mu } \times K)/\Lambda $
,
$(\Gamma _{\mu } \times K)/\Lambda $
,
![]() $\nu $
is
$\nu $
is
![]() $\Gamma _{\mu }$
-invariant, and also ergodic for the
$\Gamma _{\mu }$
-invariant, and also ergodic for the
![]() $\Gamma _{\mu }$
-action since
$\Gamma _{\mu }$
-action since
![]() $\psi $
has dense image. If we set
$\psi $
has dense image. If we set
![]() $L_0=K$
, then in the notation of Proposition 4.5 we have
$L_0=K$
, then in the notation of Proposition 4.5 we have
![]() $\Gamma _0=\Gamma _{\mu }$
and
$\Gamma _0=\Gamma _{\mu }$
and
![]() $\Gamma _0^L=\psi (\Gamma _{\mu })$
, which is a dense subgroup of
$\Gamma _0^L=\psi (\Gamma _{\mu })$
, which is a dense subgroup of
![]() $L_0$
.
$L_0$
.
The key point of Corollary 1.2(i) is that we cannot have examples of the type above when X is the quotient of a semisimple group G by an irreducible lattice
![]() $\Lambda $
, such as
$\Lambda $
, such as
![]() $G/\Lambda =(\operatorname {\mathrm {SL}}_2(\mathbb {R})\times \operatorname {\mathrm {SL}}_2(\mathbb {R}))/\operatorname {\mathrm {SL}}_2(\mathbb {Z}[\sqrt {2}])$
.
$G/\Lambda =(\operatorname {\mathrm {SL}}_2(\mathbb {R})\times \operatorname {\mathrm {SL}}_2(\mathbb {R}))/\operatorname {\mathrm {SL}}_2(\mathbb {Z}[\sqrt {2}])$
.
To keep the continuity, we now proceed to the proof of Corollary 1.2, even though one part of the statement relies on the countability result for homogeneous subspaces to be established in §5. The central part of the proof makes heavy use of concepts from the theory of algebraic and arithmetic groups, in particular Margulis’ arithmeticity theorem [Reference Margulis65]. See the book by Witte Morris [Reference Witte Morris96] for a gentle introduction to this topic.
Proof of Corollary 1.2
Let
![]() $\nu $
be a
$\nu $
be a
![]() $\mu $
-ergodic
$\mu $
-ergodic
![]() $\mu $
-stationary probability measure on
$\mu $
-stationary probability measure on
![]() $X=G/\Lambda $
. By Theorem 1.1, we know that
$X=G/\Lambda $
. By Theorem 1.1, we know that
![]() $\nu $
is homogeneous and
$\nu $
is homogeneous and
![]() $\operatorname {\mathrm {Stab}}_G(\nu )^\circ $
is normalized by H. By conjugating if necessary, we may assume the identity coset
$\operatorname {\mathrm {Stab}}_G(\nu )^\circ $
is normalized by H. By conjugating if necessary, we may assume the identity coset
![]() $\Lambda $
is in the support of
$\Lambda $
is in the support of
![]() $\nu $
.
$\nu $
.
If
![]() $\operatorname {\mathrm {Stab}}_G(\nu )\cap H$
is nondiscrete, then
$\operatorname {\mathrm {Stab}}_G(\nu )\cap H$
is nondiscrete, then
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
must contain a normal subgroup of H of positive dimension. Since
$\operatorname {\mathrm {Stab}}_G(\nu )$
must contain a normal subgroup of H of positive dimension. Since
![]() $\Lambda $
is irreducible, this implies that
$\Lambda $
is irreducible, this implies that
![]() $\nu $
is G-invariant. Indeed,
$\nu $
is G-invariant. Indeed,
![]() $\operatorname {\mathrm {Stab}}_G(\nu )\Lambda $
is closed since the stabilizer intersects
$\operatorname {\mathrm {Stab}}_G(\nu )\Lambda $
is closed since the stabilizer intersects
![]() $\Lambda $
in a lattice ([Reference Raghunathan80, Theorem 1.13]), and also dense by irreducibility of
$\Lambda $
in a lattice ([Reference Raghunathan80, Theorem 1.13]), and also dense by irreducibility of
![]() $\Lambda $
if
$\Lambda $
if
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
contains a simple factor of G.
$\operatorname {\mathrm {Stab}}_G(\nu )$
contains a simple factor of G.
Let us now assume that
![]() $\operatorname {\mathrm {Stab}}_G(\nu )\cap H$
is discrete and
$\operatorname {\mathrm {Stab}}_G(\nu )\cap H$
is discrete and
![]() $H\neq G$
and use this to derive a contradiction. Since
$H\neq G$
and use this to derive a contradiction. Since
![]() $\operatorname {\mathrm {Stab}}_G(\nu )^\circ $
is normalized by H, we may view its Lie algebra as H-submodule of
$\operatorname {\mathrm {Stab}}_G(\nu )^\circ $
is normalized by H, we may view its Lie algebra as H-submodule of
![]() $\mathfrak g=\operatorname {\mathrm {Lie}}(G)$
. As every nontrivial H-isotypic component of
$\mathfrak g=\operatorname {\mathrm {Lie}}(G)$
. As every nontrivial H-isotypic component of
![]() $\mathfrak g$
is contained in
$\mathfrak g$
is contained in
![]() $\operatorname {\mathrm {Lie}}(H)$
, it follows from the discreteness assumption that we must have
$\operatorname {\mathrm {Lie}}(H)$
, it follows from the discreteness assumption that we must have
![]() $\operatorname {\mathrm {Stab}}_G(\nu )^\circ \leqslant C_G(H)\leqslant C_G(\Gamma _{\mu })$
. This puts us in the setting of Proposition 4.5, namely, the homogeneous measure
$\operatorname {\mathrm {Stab}}_G(\nu )^\circ \leqslant C_G(H)\leqslant C_G(\Gamma _{\mu })$
. This puts us in the setting of Proposition 4.5, namely, the homogeneous measure
![]() $\nu $
gives positive mass to an orbit of the centralizer L of
$\nu $
gives positive mass to an orbit of the centralizer L of
![]() $\Gamma _{\mu }$
in G. We apply this proposition with
$\Gamma _{\mu }$
in G. We apply this proposition with
![]() $x=\Lambda $
and
$x=\Lambda $
and
![]() $L_0$
the connected component of
$L_0$
the connected component of
![]() $\operatorname {\mathrm {Stab}}_G(\nu )\cap L$
and let
$\operatorname {\mathrm {Stab}}_G(\nu )\cap L$
and let
![]() $\Gamma _0$
and
$\Gamma _0$
and
![]() $\Gamma _0^L$
be as defined there. Then
$\Gamma _0^L$
be as defined there. Then
![]() $L_0\cap \Lambda $
is central by irreducibility of
$L_0\cap \Lambda $
is central by irreducibility of
![]() $\Lambda $
([Reference Raghunathan80, Corollary 5.21]), hence finite, which by part (iii) of the proposition implies that
$\Lambda $
([Reference Raghunathan80, Corollary 5.21]), hence finite, which by part (iii) of the proposition implies that
![]() $L_0$
is compact.
$L_0$
is compact.
We now invoke Margulis’ arithmeticity theorem [Reference Margulis65]. The conclusion is that we may assume that
where
![]() $\mathbf G$
is a Zariski connected absolutely simple linear algebraic group defined over a number field k,
$\mathbf G$
is a Zariski connected absolutely simple linear algebraic group defined over a number field k,
![]() $k_\sigma \in \{\mathbb {R},\mathbb {C}\}$
is the completion of
$k_\sigma \in \{\mathbb {R},\mathbb {C}\}$
is the completion of
![]() $\sigma (k)$
for a field embedding
$\sigma (k)$
for a field embedding
![]() $\sigma \colon k\to \mathbb {C}$
and S is a finite set of inequivalent such embeddings with the property that
$\sigma \colon k\to \mathbb {C}$
and S is a finite set of inequivalent such embeddings with the property that
![]() $\mathbf G^\sigma (k_\sigma )$
is noncompact if and only if
$\mathbf G^\sigma (k_\sigma )$
is noncompact if and only if
![]() $\sigma $
or
$\sigma $
or
![]() $\overline {\sigma }$
is in S. The lattice
$\overline {\sigma }$
is in S. The lattice
![]() $\Lambda $
is given as the diagonal embedding of
$\Lambda $
is given as the diagonal embedding of
![]() $\mathbf G(\mathcal {O}_k)$
in G via
$\mathbf G(\mathcal {O}_k)$
in G via
![]() $k\ni z\mapsto (\sigma (z))_{\sigma \in S}$
, where
$k\ni z\mapsto (\sigma (z))_{\sigma \in S}$
, where
![]() $\mathcal {O}_k$
is the ring of integers of k. As
$\mathcal {O}_k$
is the ring of integers of k. As
![]() $H\neq G$
is a connected normal subgroup of G of positive dimension, there is a nonempty proper subset
$H\neq G$
is a connected normal subgroup of G of positive dimension, there is a nonempty proper subset
![]() $S_1\subset S$
such that
$S_1\subset S$
such that
![]() $H =\prod _{\sigma \in S_1} \mathbf G^\sigma (k_\sigma )$
. Without loss of generality we assume that the identity embedding
$H =\prod _{\sigma \in S_1} \mathbf G^\sigma (k_\sigma )$
. Without loss of generality we assume that the identity embedding
![]() $\iota $
is contained in
$\iota $
is contained in
![]() $S_1$
. We also write
$S_1$
. We also write
![]() $S_2=S\setminus S_1$
, which is nonempty by construction. In this setup,
$S_2=S\setminus S_1$
, which is nonempty by construction. In this setup,
![]() $\Gamma _0^L$
is a dense subgroup of
$\Gamma _0^L$
is a dense subgroup of
![]() $L_0$
, which is a connected and compact subgroup contained in
$L_0$
, which is a connected and compact subgroup contained in
![]() $\prod _{\sigma \in S_2}\mathbf G^\sigma (k_\sigma )$
.
$\prod _{\sigma \in S_2}\mathbf G^\sigma (k_\sigma )$
.
The following subtlety should be noted regarding Zariski topologies: The linear algebraic group
![]() $\mathbf {G}$
naturally carries the complex Zariski topology, defined by complex polynomials in the entries of the complex matrices in
$\mathbf {G}$
naturally carries the complex Zariski topology, defined by complex polynomials in the entries of the complex matrices in
![]() $\mathbf {G}$
(similarly for the Galois conjugates
$\mathbf {G}$
(similarly for the Galois conjugates
![]() $\mathbf {G}^\sigma $
). However, in the product representation (4.3) of G, the point of view is that of real algebraic groups. This means that when
$\mathbf {G}^\sigma $
). However, in the product representation (4.3) of G, the point of view is that of real algebraic groups. This means that when
![]() $k_\sigma =\mathbb {C}$
, the group
$k_\sigma =\mathbb {C}$
, the group
![]() $\mathbf {G}^\sigma (\mathbb {C})$
has to be seen as the group of real points of the restriction of scalars
$\mathbf {G}^\sigma (\mathbb {C})$
has to be seen as the group of real points of the restriction of scalars
![]() $\operatorname {\mathrm {Res}}_{\mathbb {C}/\mathbb {R}} \mathbf G^\sigma $
with the real Zariski topology, defined by real polynomials in the real and imaginary parts of the entries of matrices in
$\operatorname {\mathrm {Res}}_{\mathbb {C}/\mathbb {R}} \mathbf G^\sigma $
with the real Zariski topology, defined by real polynomials in the real and imaginary parts of the entries of matrices in
![]() $\mathbf {G}^\sigma $
. This gives rise to the real Zariski topology on G.
$\mathbf {G}^\sigma $
. This gives rise to the real Zariski topology on G.
We also remark that in equation (4.3) and the associated product representation of H, strictly speaking, we should take the analytic identity components of the groups appearing as factors on the right-hand side. But we ignore this point for ease of notation and without loss of generality.
Relative compactness in Galois conjugates. Recall that each
![]() $\gamma _0\in \Gamma _0$
preserves the homogeneous measure on
$\gamma _0\in \Gamma _0$
preserves the homogeneous measure on
![]() $L_0x$
, so there exists
$L_0x$
, so there exists
![]() $l_0\in L_0$
such that
$l_0\in L_0$
such that
![]() $\gamma _0 x=l_0^{-1}x$
, which implies that
$\gamma _0 x=l_0^{-1}x$
, which implies that
![]() $\gamma _0 l_0 \in \Lambda $
. Let
$\gamma _0 l_0 \in \Lambda $
. Let
![]() $\Gamma _1$
be the projection of
$\Gamma _1$
be the projection of
![]() $\Gamma _0$
to
$\Gamma _0$
to
![]() $\mathbf G(k_\iota )$
(the factor corresponding to the identity embedding). Then
$\mathbf G(k_\iota )$
(the factor corresponding to the identity embedding). Then
![]() $\Gamma _0$
consists of
$\Gamma _0$
consists of
![]() $\prod _{\sigma \in S_1}\sigma (\gamma _1)$
and
$\prod _{\sigma \in S_1}\sigma (\gamma _1)$
and
![]() $\Gamma _0^L$
consists of
$\Gamma _0^L$
consists of
![]() $\prod _{\sigma \in S_2}\sigma (\gamma _1)$
for
$\prod _{\sigma \in S_2}\sigma (\gamma _1)$
for
![]() $\gamma _1\in \Gamma _1$
. So we have
$\gamma _1\in \Gamma _1$
. So we have
![]() $\Gamma _1\leqslant \mathbf {G}(\mathcal {O}_k)$
and for every
$\Gamma _1\leqslant \mathbf {G}(\mathcal {O}_k)$
and for every
![]() $\sigma \in S_2$
the group
$\sigma \in S_2$
the group
![]() $\sigma (\Gamma _1)$
(obtained by component-wise application of
$\sigma (\Gamma _1)$
(obtained by component-wise application of
![]() $\sigma $
) has compact closure. The latter conclusion holds also for
$\sigma $
) has compact closure. The latter conclusion holds also for
![]() $\sigma \notin S$
, since
$\sigma \notin S$
, since
![]() $\mathbf {G}^\sigma (k_\sigma )$
is compact in this case. So we conclude that
$\mathbf {G}^\sigma (k_\sigma )$
is compact in this case. So we conclude that
![]() $\sigma (\Gamma _1)$
is relatively compact for all embeddings
$\sigma (\Gamma _1)$
is relatively compact for all embeddings
![]() $\sigma \notin S_1$
.
$\sigma \notin S_1$
.
Zariski density properties of
![]() $\Gamma _*$
. From Proposition 3.12, it follows that the Zariski closure of
$\Gamma _*$
. From Proposition 3.12, it follows that the Zariski closure of
![]() $\Gamma _{\mu }$
is an epimorphic subgroup of H in the category of real algebraic groups (see Appendix 1 for a discussion of the epimorphic property in different categories). As
$\Gamma _{\mu }$
is an epimorphic subgroup of H in the category of real algebraic groups (see Appendix 1 for a discussion of the epimorphic property in different categories). As
![]() $\Gamma _0$
has finite index in
$\Gamma _0$
has finite index in
![]() $\Gamma _{\mu }$
, also
$\Gamma _{\mu }$
, also
![]() $\operatorname {\mathrm {Zcl}}(\Gamma _0)$
is epimorphic in H. We claim that
$\operatorname {\mathrm {Zcl}}(\Gamma _0)$
is epimorphic in H. We claim that
![]() $\operatorname {\mathrm {Zcl}}(\Gamma _0)$
is also reductive. Otherwise, its projection to one of the simple factors of H is not reductive. Without loss of generality assume that this holds for the projection to
$\operatorname {\mathrm {Zcl}}(\Gamma _0)$
is also reductive. Otherwise, its projection to one of the simple factors of H is not reductive. Without loss of generality assume that this holds for the projection to
![]() $\mathbf {G}(k_\iota )$
. This means that the Zariski closure of
$\mathbf {G}(k_\iota )$
. This means that the Zariski closure of
![]() $\Gamma _1$
(in the real Zariski topology of
$\Gamma _1$
(in the real Zariski topology of
![]() $\mathbf {G}(k_\iota )$
) has a nontrivial unipotent radical. Now, consider the Zariski closure
$\mathbf {G}(k_\iota )$
) has a nontrivial unipotent radical. Now, consider the Zariski closure
![]() $\mathbf {F}$
of
$\mathbf {F}$
of
![]() $\Gamma _1$
in the complex Zariski topology of
$\Gamma _1$
in the complex Zariski topology of
![]() $\mathbf {G}$
. Since the real Zariski topology of
$\mathbf {G}$
. Since the real Zariski topology of
![]() $\mathbf {G}(\mathbb {C})$
is finer than the complex Zariski topology of
$\mathbf {G}(\mathbb {C})$
is finer than the complex Zariski topology of
![]() $\mathbf {G}$
, also
$\mathbf {G}$
, also
![]() $\mathbf {F}$
has a nontrivial unipotent radical, that is, is not reductive. Moreover,
$\mathbf {F}$
has a nontrivial unipotent radical, that is, is not reductive. Moreover,
![]() $\mathbf {F}$
is defined over k, since
$\mathbf {F}$
is defined over k, since
![]() $\Gamma _1\leqslant \mathbf {G}(\mathcal {O}_k)$
. So the failure to be reductive carries over to the Galois conjugates of
$\Gamma _1\leqslant \mathbf {G}(\mathcal {O}_k)$
. So the failure to be reductive carries over to the Galois conjugates of
![]() $\mathbf {F}$
. Then we get a contradiction since for each
$\mathbf {F}$
. Then we get a contradiction since for each
![]() $\sigma \in S_2$
the algebraic group
$\sigma \in S_2$
the algebraic group
![]() $\mathbf {F}^\sigma $
is reductive, because it is the Zariski closure of the relatively compact group
$\mathbf {F}^\sigma $
is reductive, because it is the Zariski closure of the relatively compact group
![]() $\sigma (\Gamma _1)$
(in the complex Zariski topology). So we obtain that
$\sigma (\Gamma _1)$
(in the complex Zariski topology). So we obtain that
![]() $\operatorname {\mathrm {Zcl}}(\Gamma _0)$
is a reductive epimorphic subgroup of H, which can only happen if
$\operatorname {\mathrm {Zcl}}(\Gamma _0)$
is a reductive epimorphic subgroup of H, which can only happen if
![]() $\Gamma _0$
is Zariski dense in H. By projecting to the simple factors, we find that
$\Gamma _0$
is Zariski dense in H. By projecting to the simple factors, we find that
![]() $\sigma (\Gamma _1)$
is Zariski dense in the real Zariski topology of
$\sigma (\Gamma _1)$
is Zariski dense in the real Zariski topology of
![]() $\mathbf {G}^\sigma (k_\sigma )$
for all
$\mathbf {G}^\sigma (k_\sigma )$
for all
![]() $\sigma \in S_1$
. In particular, this implies that
$\sigma \in S_1$
. In particular, this implies that
![]() $\Gamma _1$
is Zariski dense in
$\Gamma _1$
is Zariski dense in
![]() $\mathbf {G}$
in the complex Zariski topology. This latter property can now be carried over to all Galois conjugates, showing that for every embedding
$\mathbf {G}$
in the complex Zariski topology. This latter property can now be carried over to all Galois conjugates, showing that for every embedding
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma (\Gamma _1)$
is Zariski dense in
$\sigma (\Gamma _1)$
is Zariski dense in
![]() $\mathbf {G}^\sigma $
(in the complex Zariski topology). For every embedding
$\mathbf {G}^\sigma $
(in the complex Zariski topology). For every embedding
![]() $\sigma $
, the Zariski closure of
$\sigma $
, the Zariski closure of
![]() $\sigma (\Gamma _1)$
in the real Zariski topology must therefore be
$\sigma (\Gamma _1)$
in the real Zariski topology must therefore be
![]() $\mathbf {G}^\sigma (\mathbb {C})$
or a real form of it. In particular, for every embedding with
$\mathbf {G}^\sigma (\mathbb {C})$
or a real form of it. In particular, for every embedding with
![]() $k_\sigma =\mathbb {R}$
,
$k_\sigma =\mathbb {R}$
,
![]() $\sigma (\Gamma _1)$
is Zariski dense in
$\sigma (\Gamma _1)$
is Zariski dense in
![]() $\mathbf {G}^\sigma (\mathbb {R})$
in the real Zariski topology.
$\mathbf {G}^\sigma (\mathbb {R})$
in the real Zariski topology.
A more natural field of definition. Let
![]() $k'$
be the subfield of k generated by the set
$k'$
be the subfield of k generated by the set
![]() $\operatorname {Tr}(\operatorname {\mathrm {Ad}}(\Gamma _1))$
. Then
$\operatorname {Tr}(\operatorname {\mathrm {Ad}}(\Gamma _1))$
. Then
![]() $\operatorname {\mathrm {Ad}}(\Gamma _1)$
is definable over
$\operatorname {\mathrm {Ad}}(\Gamma _1)$
is definable over
![]() $k'$
(see [Reference Margulis65, IX.1.8]). So we may and will assume that
$k'$
(see [Reference Margulis65, IX.1.8]). So we may and will assume that
![]() $\mathbf G$
is defined over
$\mathbf G$
is defined over
![]() $k'$
and
$k'$
and
![]() $\Gamma _1\leqslant \mathbf G(k')$
. The group
$\Gamma _1\leqslant \mathbf G(k')$
. The group
![]() $\operatorname {\mathrm {Res}}_{k'/\mathbb {Q}}\mathbf {G}(\mathbb {R})=\prod _{\tau \colon k'\to \mathbb {C}}\mathbf G^\tau (k^{\prime }_\tau )$
is naturally embedded in
$\operatorname {\mathrm {Res}}_{k'/\mathbb {Q}}\mathbf {G}(\mathbb {R})=\prod _{\tau \colon k'\to \mathbb {C}}\mathbf G^\tau (k^{\prime }_\tau )$
is naturally embedded in
![]() $\operatorname {\mathrm {Res}}_{k/\mathbb {Q}}\mathbf {G}(\mathbb {R})=\prod _\sigma \mathbf G^\sigma (k_\sigma )$
as a real algebraic subgroup, by identifying
$\operatorname {\mathrm {Res}}_{k/\mathbb {Q}}\mathbf {G}(\mathbb {R})=\prod _\sigma \mathbf G^\sigma (k_\sigma )$
as a real algebraic subgroup, by identifying
![]() $\mathbf {G}^\tau (k^{\prime }_\tau )$
with its diagonal embedding in
$\mathbf {G}^\tau (k^{\prime }_\tau )$
with its diagonal embedding in
![]() $\prod _{\sigma \colon \sigma |_{k'}=\tau }\mathbf {G}^\sigma (k_\sigma )$
. We deduce the following facts.
$\prod _{\sigma \colon \sigma |_{k'}=\tau }\mathbf {G}^\sigma (k_\sigma )$
. We deduce the following facts.
-
(a) We have
 $k\neq k'$
. Indeed, for
$k\neq k'$
. Indeed, for
 $\sigma \in S_2$
the group
$\sigma \in S_2$
the group
 $\mathbf {G}^\sigma (k_\sigma )$
is noncompact and
$\mathbf {G}^\sigma (k_\sigma )$
is noncompact and
 $\sigma (\Gamma _1)$
has compact closure (in the Lie group topology). In view of the Zariski density properties established in the paragraph above and using that compact groups are closed in the real Zariski topology, it follows that we must have
$\sigma (\Gamma _1)$
has compact closure (in the Lie group topology). In view of the Zariski density properties established in the paragraph above and using that compact groups are closed in the real Zariski topology, it follows that we must have
 $k_\sigma =\mathbb {C}$
, and
$k_\sigma =\mathbb {C}$
, and
 $\sigma (\Gamma _1)$
is contained in a real form of
$\sigma (\Gamma _1)$
is contained in a real form of
 $\mathbf G^\sigma (\mathbb {C})$
. The latter and the definition of
$\mathbf G^\sigma (\mathbb {C})$
. The latter and the definition of
 $k'$
(via traces in the adjoint representation) imply
$k'$
(via traces in the adjoint representation) imply
 $\sigma (k')\subset \mathbb {R}$
, which would contradict
$\sigma (k')\subset \mathbb {R}$
, which would contradict
 $k_\sigma =\mathbb {C}$
if we had
$k_\sigma =\mathbb {C}$
if we had
 $k=k'$
.
$k=k'$
. -
(b) The embeddings
 $\sigma |_{k'}$
of
$\sigma |_{k'}$
of
 $k'$
for
$k'$
for
 $\sigma \in S_1$
are pairwise distinct, since
$\sigma \in S_1$
are pairwise distinct, since
 $\Gamma _0$
is Zariski dense in H.
$\Gamma _0$
is Zariski dense in H.
Combining everything to a contradiction. In view of (a) above, the identity embedding
![]() $k'\to \mathbb {C}$
must admit a nonidentity extension
$k'\to \mathbb {C}$
must admit a nonidentity extension
![]() $\sigma \colon k\to \mathbb {C}$
. This embedding
$\sigma \colon k\to \mathbb {C}$
. This embedding
![]() $\sigma $
cannot be contained in
$\sigma $
cannot be contained in
![]() $S_1$
, since by (b) above, the elements of
$S_1$
, since by (b) above, the elements of
![]() $S_1$
have pairwise distinct restrictions to
$S_1$
have pairwise distinct restrictions to
![]() $k'$
. But
$k'$
. But
![]() $\sigma \not \in S_1$
would imply
$\sigma \not \in S_1$
would imply
![]() $\sigma (\Gamma _1 )=\Gamma _1$
is relatively compact, which is impossible since
$\sigma (\Gamma _1 )=\Gamma _1$
is relatively compact, which is impossible since
![]() $\Gamma _1$
is Zariski dense in the noncompact group
$\Gamma _1$
is Zariski dense in the noncompact group
![]() $\mathbf {G}(k_\iota )$
in the real Zariski topology. This contradiction finishes the proof of (i).
$\mathbf {G}(k_\iota )$
in the real Zariski topology. This contradiction finishes the proof of (i).
In the case
![]() $H=G$
of part (ii), the arguments at the beginning of the proof show that either
$H=G$
of part (ii), the arguments at the beginning of the proof show that either
![]() $\nu =m_X$
or
$\nu =m_X$
or
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
is discrete. In the latter case,
$\operatorname {\mathrm {Stab}}_G(\nu )$
is discrete. In the latter case,
![]() $\nu $
must be the uniform probability measure on a finite
$\nu $
must be the uniform probability measure on a finite
![]() $\Gamma _{\mu }$
-orbit (see [Reference Benoist and Quint6, Lemma 8.3]). Moreover, in this case we have that
$\Gamma _{\mu }$
-orbit (see [Reference Benoist and Quint6, Lemma 8.3]). Moreover, in this case we have that
![]() $C_G(\Gamma _{\mu })$
is discrete by the epimorphic property of
$C_G(\Gamma _{\mu })$
is discrete by the epimorphic property of
![]() $\Gamma _{\mu }$
in G from Proposition 3.12. Proposition 5.1 thus implies that there are only countably many distinct finite
$\Gamma _{\mu }$
in G from Proposition 3.12. Proposition 5.1 thus implies that there are only countably many distinct finite
![]() $\Gamma _{\mu }$
-orbits in X. Hence, if
$\Gamma _{\mu }$
-orbits in X. Hence, if
![]() $\nu $
is any nonatomic
$\nu $
is any nonatomic
![]() $\mu $
-stationary probability measure on X,
$\mu $
-stationary probability measure on X,
![]() $\nu =m_X$
follows by considering an ergodic decomposition of
$\nu =m_X$
follows by considering an ergodic decomposition of
![]() $\nu $
. This completes the proof.
$\nu $
. This completes the proof.
4.3 Expansion on Grassmannians
The H-expansion condition on
![]() $\mu $
is a universal requirement in the sense that all our results (including the measure classification theorem) hold for any embedding
$\mu $
is a universal requirement in the sense that all our results (including the measure classification theorem) hold for any embedding
![]() $H \hookrightarrow G$
and any discrete subgroup
$H \hookrightarrow G$
and any discrete subgroup
![]() $\Lambda $
in G. Having fixed
$\Lambda $
in G. Having fixed
![]() $H\leqslant G$
, however, close inspection of the proof of Theorem 1.1 reveals that it is sufficient to have uniform expansion on the quotient of each exterior power of
$H\leqslant G$
, however, close inspection of the proof of Theorem 1.1 reveals that it is sufficient to have uniform expansion on the quotient of each exterior power of
![]() $\mathfrak {g}$
by the corresponding H-fixed subspace.
$\mathfrak {g}$
by the corresponding H-fixed subspace.
Definition 4.7. Let G be a real Lie group and
![]() $H\leqslant G$
a connected semisimple subgroup with finite center. A probability measure
$H\leqslant G$
a connected semisimple subgroup with finite center. A probability measure
![]() $\mu $
on H is said to be H-expanding relative to G if
$\mu $
on H is said to be H-expanding relative to G if
![]() $\mu $
is uniformly expanding on the quotient of
$\mu $
is uniformly expanding on the quotient of
![]() $(\operatorname {\mathrm {Ad}}^{\wedge k},\mathfrak {g}^{\wedge k})$
by the corresponding H-fixed subspace for every
$(\operatorname {\mathrm {Ad}}^{\wedge k},\mathfrak {g}^{\wedge k})$
by the corresponding H-fixed subspace for every
![]() $1\le k\le \dim (G)-1$
.
$1\le k\le \dim (G)-1$
.
We remark that a related notion was previously studied by the first two authors [Reference Prohaska and Sert79].
Theorem 4.8. Let G be a real Lie group,
![]() $\Lambda \leqslant G$
a discrete subgroup and H a connected semisimple subgroup of G with finite center. Let
$\Lambda \leqslant G$
a discrete subgroup and H a connected semisimple subgroup of G with finite center. Let
![]() $\mu $
be an H-expanding probability measure relative to G with finite first moment. Then the conclusions of Theorem 1.1 hold for every ergodic
$\mu $
be an H-expanding probability measure relative to G with finite first moment. Then the conclusions of Theorem 1.1 hold for every ergodic
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\nu $
on
$\nu $
on
![]() $G/\Lambda $
.
$G/\Lambda $
.
Proof. We analyze the applications of the H-expansion property in the proof of Theorem 1.1, so we retain the notation used there.
-
○ The first application of Lemma 4.3 is possible without problems.
-
○ Next, expansion is used for the representation
 $S^2(\mathfrak {g}^{\wedge \dim (N)})$
. If
$S^2(\mathfrak {g}^{\wedge \dim (N)})$
. If
 $\dim (N)=\dim (G)$
, then the probability measure
$\dim (N)=\dim (G)$
, then the probability measure
 $\eta $
in (4.1) is finitely supported and
$\eta $
in (4.1) is finitely supported and
 $\Gamma _{\mu }$
-invariant by [Reference Benoist and Quint6, Lemma 8.3], so all claims follow. Otherwise, the measure
$\Gamma _{\mu }$
-invariant by [Reference Benoist and Quint6, Lemma 8.3], so all claims follow. Otherwise, the measure
 $\eta '$
on
$\eta '$
on
 $S^2(\mathfrak {g}^{\wedge \dim (N)})$
is supported on
$S^2(\mathfrak {g}^{\wedge \dim (N)})$
is supported on
 $\{v\otimes v\mid v\in \mathfrak {g}^{\wedge \dim (N)}\}$
by construction. Using that
$\{v\otimes v\mid v\in \mathfrak {g}^{\wedge \dim (N)}\}$
by construction. Using that
 $ \left \lVert {v\otimes v} \right \rVert = \left \lVert {v} \right \rVert ^2$
and the assumed expansion in
$ \left \lVert {v\otimes v} \right \rVert = \left \lVert {v} \right \rVert ^2$
and the assumed expansion in
 $\mathfrak {g}^{\wedge \dim (N)}$
, we can again draw the desired conclusion that
$\mathfrak {g}^{\wedge \dim (N)}$
, we can again draw the desired conclusion that
 $\eta '$
is supported on the set of H-fixed vectors.
$\eta '$
is supported on the set of H-fixed vectors. -
○ Finally, expansion is needed to reapply Theorem 4.2 in the quotient by
 $N^\circ $
. The assumption there implies that
$N^\circ $
. The assumption there implies that
 $H/(H\cap N^\circ )$
is still a semisimple group, so that
$H/(H\cap N^\circ )$
is still a semisimple group, so that
 $\dim (N)\le \dim (G)-3$
. Let
$\dim (N)\le \dim (G)-3$
. Let
 $v\in \mathfrak {g}^{\wedge \dim (N)}$
correspond to a basis of the Lie algebra
$v\in \mathfrak {g}^{\wedge \dim (N)}$
correspond to a basis of the Lie algebra
 $\mathfrak {n}$
of N. Then a norm on
$\mathfrak {n}$
of N. Then a norm on
 $\mathfrak {g}/\mathfrak {n}$
is given by
$\mathfrak {g}/\mathfrak {n}$
is given by
 $ \left \lVert {w+\mathfrak {n}} \right \rVert = \left \lVert {w\wedge v} \right \rVert $
for
$ \left \lVert {w+\mathfrak {n}} \right \rVert = \left \lVert {w\wedge v} \right \rVert $
for
 $w\in \mathfrak {g}$
. Since H fixes the vector
$w\in \mathfrak {g}$
. Since H fixes the vector
 $\omega =v\otimes v$
in
$\omega =v\otimes v$
in
 $S^2(\mathfrak {g}^{\wedge \dim (N)})$
, H acts on v by
$S^2(\mathfrak {g}^{\wedge \dim (N)})$
, H acts on v by
 $\pm 1$
. As H is connected, v is fixed by H. Thus, for every
$\pm 1$
. As H is connected, v is fixed by H. Thus, for every
 $h\in H$
and
$h\in H$
and
 $w\in \mathfrak {g}$
we have (4.4)Hence, we again obtain expansion for every vector in
$w\in \mathfrak {g}$
we have (4.4)Hence, we again obtain expansion for every vector in $$ \begin{align} \left\lVert {h{\boldsymbol{\cdot}}(w+\mathfrak{n})} \right\rVert = \left\lVert {h{\boldsymbol{\cdot}} w\wedge v} \right\rVert = \left\lVert {h{\boldsymbol{\cdot}}(w\wedge v)} \right\rVert. \end{align} $$
$$ \begin{align} \left\lVert {h{\boldsymbol{\cdot}}(w+\mathfrak{n})} \right\rVert = \left\lVert {h{\boldsymbol{\cdot}} w\wedge v} \right\rVert = \left\lVert {h{\boldsymbol{\cdot}}(w\wedge v)} \right\rVert. \end{align} $$
 $\mathfrak {g}/\mathfrak {n}$
that is not H-fixed. This justifies the application of Lemma 4.3 in the quotient.
$\mathfrak {g}/\mathfrak {n}$
that is not H-fixed. This justifies the application of Lemma 4.3 in the quotient.
Combining the above with some properties of epimorphic subgroups, we obtain the following.
Corollary 4.9. Let G be a real algebraic group,
![]() $\Lambda <G$
a lattice, and
$\Lambda <G$
a lattice, and
![]() $H\leqslant G$
a Zariski connected semisimple algebraic subgroup without compact factors. Then any Zariski connected real algebraic epimorphic subgroup
$H\leqslant G$
a Zariski connected semisimple algebraic subgroup without compact factors. Then any Zariski connected real algebraic epimorphic subgroup
![]() $F\leqslant H$
supports probability measures
$F\leqslant H$
supports probability measures
![]() $\mu $
for which the conclusions of Theorem 1.1 hold.
$\mu $
for which the conclusions of Theorem 1.1 hold.
Proof. It is known that F contains a split solvable algebraic subgroup
![]() $A'U$
, where
$A'U$
, where
![]() $A'$
is an algebraic
$A'$
is an algebraic
![]() $\mathbb {R}$
-split torus and U is unipotent and normalized by
$\mathbb {R}$
-split torus and U is unipotent and normalized by
![]() $A'$
, that is still epimorphic in H (see [Reference Bien and Borel13, §10, Theorem 2]). Thus, we may assume
$A'$
, that is still epimorphic in H (see [Reference Bien and Borel13, §10, Theorem 2]). Thus, we may assume
![]() $F=A'U$
is of this form to begin with. By [Reference Weiss95, Lemma 1] there is a nonempty open cone
$F=A'U$
is of this form to begin with. By [Reference Weiss95, Lemma 1] there is a nonempty open cone
![]() $A^{\prime }_+$
in
$A^{\prime }_+$
in
![]() $A'$
such that
$A'$
such that
![]() $\chi (a)>1$
for all
$\chi (a)>1$
for all
![]() $a\in A^{\prime }_+$
and all characters of
$a\in A^{\prime }_+$
and all characters of
![]() $A'$
having an eigenvector in one of the U-fixed subspaces
$A'$
having an eigenvector in one of the U-fixed subspaces
![]() $V_k^U$
of the finitely many representations
$V_k^U$
of the finitely many representations
![]() $V_1,\dots ,V_r$
appearing in the statement of Theorem 4.8. Then any probability measure
$V_1,\dots ,V_r$
appearing in the statement of Theorem 4.8. Then any probability measure
![]() $\mu $
on F with finite first moment whose
$\mu $
on F with finite first moment whose
![]() $A'$
-average
$A'$
-average
![]() $a_{\operatorname {avg}}(\mu )$
lies in
$a_{\operatorname {avg}}(\mu )$
lies in
![]() $A^{\prime }_+$
and for which the Zariski closure of
$A^{\prime }_+$
and for which the Zariski closure of
![]() $\Gamma _{\mu }$
contains U is uniformly expanding in all of the representations
$\Gamma _{\mu }$
contains U is uniformly expanding in all of the representations
![]() $V_k$
. Indeed, this follows directly by combining Lemma 3.5 and 3.6. Theorem 4.8 thus applies to all measures
$V_k$
. Indeed, this follows directly by combining Lemma 3.5 and 3.6. Theorem 4.8 thus applies to all measures
![]() $\mu $
satisfying these conditions.
$\mu $
satisfying these conditions.
5 Countability of homogeneous subspaces
Let
![]() $\Gamma $
be a closed subsemigroup of G and
$\Gamma $
be a closed subsemigroup of G and
![]() $\Lambda <G$
a lattice. A homogeneous subspace
$\Lambda <G$
a lattice. A homogeneous subspace
![]() $Y\subset X=G/\Lambda $
is said to be
$Y\subset X=G/\Lambda $
is said to be
![]() $\Gamma $
-invariant if
$\Gamma $
-invariant if
![]() $\Gamma $
preserves the associated homogeneous probability measure
$\Gamma $
preserves the associated homogeneous probability measure
![]() $\eta $
on Y. It is called
$\eta $
on Y. It is called
![]() $\Gamma $
-ergodic if
$\Gamma $
-ergodic if
![]() $\Gamma $
acts ergodically on
$\Gamma $
acts ergodically on
![]() $(Y,\eta )$
. Define
$(Y,\eta )$
. Define
A key input to the proof of Theorem 1.6 is countability of
![]() $\mathcal {S}(\Gamma _{\mu })$
modulo the centralizer of H. Our strategy to prove this result closely follows the approach in [Reference Benoist and Quint10], where this result is proved under the assumption that the Zariski closure of
$\mathcal {S}(\Gamma _{\mu })$
modulo the centralizer of H. Our strategy to prove this result closely follows the approach in [Reference Benoist and Quint10], where this result is proved under the assumption that the Zariski closure of
![]() $\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
is semisimple and has no compact factors. The goal of this subsection is therefore to prove the following analogue of [Reference Benoist and Quint10, Proposition 2.1].
$\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
is semisimple and has no compact factors. The goal of this subsection is therefore to prove the following analogue of [Reference Benoist and Quint10, Proposition 2.1].
Proposition 5.1. Let G be a real Lie group,
![]() $H\leqslant G$
a connected semisimple subgroup with finite center and
$H\leqslant G$
a connected semisimple subgroup with finite center and
![]() $\Gamma <H$
a subsemigroup that supports a probability measure with finite first moment that is H-expanding relative to G. Denote by L the centralizer of
$\Gamma <H$
a subsemigroup that supports a probability measure with finite first moment that is H-expanding relative to G. Denote by L the centralizer of
![]() $\Gamma $
in G. Then there exists a countable subset
$\Gamma $
in G. Then there exists a countable subset
![]() $\mathcal {Y}$
of
$\mathcal {Y}$
of
![]() $\mathcal {S}(\Gamma )$
such that
$\mathcal {S}(\Gamma )$
such that
Note that the set
![]() $\mathcal {S}(\Gamma )$
remains the same if we replace the semigroup
$\mathcal {S}(\Gamma )$
remains the same if we replace the semigroup
![]() $\Gamma $
by the closed group that it generates. Therefore, in the proof of the previous result, we can suppose that
$\Gamma $
by the closed group that it generates. Therefore, in the proof of the previous result, we can suppose that
![]() $\Gamma $
is a closed subgroup of H.
$\Gamma $
is a closed subgroup of H.
The key ingredient of the proof of this proposition is Lemma 5.3 below, which will imply countability of the closed subgroups of G that arise as the stabilizer of homogeneous subspaces in
![]() $\mathcal {S}(\Gamma )$
. To this end, we introduce the following definition, which, in view of Theorem 1.1, is the appropriate replacement of [Reference Benoist and Quint10, Definition 2.4].
$\mathcal {S}(\Gamma )$
. To this end, we introduce the following definition, which, in view of Theorem 1.1, is the appropriate replacement of [Reference Benoist and Quint10, Definition 2.4].
Definition 5.2. Let
![]() $\Delta \subset \Sigma $
be discrete subgroups of a real Lie group G. The set
$\Delta \subset \Sigma $
be discrete subgroups of a real Lie group G. The set
![]() $\mathcal {T}(G,\Delta ,\Sigma )$
is defined to be the set of closed subgroups N of G such that
$\mathcal {T}(G,\Delta ,\Sigma )$
is defined to be the set of closed subgroups N of G such that
-
(i)
 $\Sigma $
is contained in N and is a lattice in N,
$\Sigma $
is contained in N and is a lattice in N, -
(ii)
 $\Delta =\Sigma \cap N^\circ $
, where
$\Delta =\Sigma \cap N^\circ $
, where
 $N^\circ $
is the connected component of N,
$N^\circ $
is the connected component of N, -
(iii) there exist a connected semisimple Lie group
 $H_N\leqslant G$
and a subgroup
$H_N\leqslant G$
and a subgroup
 $\Gamma \leqslant H_N \cap N$
which acts ergodically on
$\Gamma \leqslant H_N \cap N$
which acts ergodically on
 $N/\Sigma $
and which supports an
$N/\Sigma $
and which supports an
 $H_N$
-expanding probability measure relative to G.
$H_N$
-expanding probability measure relative to G.
Lemma 5.3. Let G be a real Lie group and
![]() $\Delta \subset \Sigma $
finitely generated discrete subgroups of G. Then the set
$\Delta \subset \Sigma $
finitely generated discrete subgroups of G. Then the set
![]() $\mathcal {T}(G,\Delta ,\Sigma )$
is countable.
$\mathcal {T}(G,\Delta ,\Sigma )$
is countable.
The proof of this lemma requires the following strengthening of [Reference Benoist and Quint10, Lemma 2.6].
Lemma 5.4. Let G be a real Lie group,
![]() $\mathfrak {g}$
its Lie algebra and
$\mathfrak {g}$
its Lie algebra and
![]() $\Delta \subset \Sigma $
discrete subgroups of G. Let N belong to
$\Delta \subset \Sigma $
discrete subgroups of G. Let N belong to
![]() $\mathcal {T}(G,\Delta ,\Sigma )$
,
$\mathcal {T}(G,\Delta ,\Sigma )$
,
![]() $H_N$
be any connected semisimple subgroup of G as in (iii) of Definition 5.2, and let M be a unimodular Lie subgroup of G containing
$H_N$
be any connected semisimple subgroup of G as in (iii) of Definition 5.2, and let M be a unimodular Lie subgroup of G containing
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $\omega \in S^2(\mathfrak {g}^{\wedge \dim (M)})$
correspond to a basis of the Lie algebra of M. Then
$\omega \in S^2(\mathfrak {g}^{\wedge \dim (M)})$
correspond to a basis of the Lie algebra of M. Then
![]() $\omega $
is fixed by N and
$\omega $
is fixed by N and
![]() $H_N$
, and hence
$H_N$
, and hence
![]() $M^\circ $
is normalized by N and
$M^\circ $
is normalized by N and
![]() $H_N$
. In particular, this holds whenever
$H_N$
. In particular, this holds whenever
![]() $M\in \mathcal {T}(G,\Delta ,\Sigma )$
.
$M\in \mathcal {T}(G,\Delta ,\Sigma )$
.
In the statement above,
![]() $S^2(\mathfrak {g}^{\wedge \dim (M)})$
denotes the symmetric square of
$S^2(\mathfrak {g}^{\wedge \dim (M)})$
denotes the symmetric square of
![]() $\mathfrak {g}^{\wedge \dim (M)}$
. If
$\mathfrak {g}^{\wedge \dim (M)}$
. If
![]() $v\in \mathfrak {g}^{\wedge \dim (M)}$
corresponds to a basis of the Lie algebra of N, the appearing vector
$v\in \mathfrak {g}^{\wedge \dim (M)}$
corresponds to a basis of the Lie algebra of N, the appearing vector
![]() $\omega $
is given by
$\omega $
is given by
![]() $\omega =v\otimes v$
.
$\omega =v\otimes v$
.
Proof. If
![]() $\dim (M)=\dim (G)$
, then
$\dim (M)=\dim (G)$
, then
![]() $M^\circ =G^\circ $
and the statement is clear. So we assume that
$M^\circ =G^\circ $
and the statement is clear. So we assume that
![]() $\dim (M)<\dim (G)$
. Since M is unimodular and contains
$\dim (M)<\dim (G)$
. Since M is unimodular and contains
![]() $\Sigma $
, the action of
$\Sigma $
, the action of
![]() $\Sigma $
fixes
$\Sigma $
fixes
![]() $\omega $
. Therefore, the map
$\omega $
. Therefore, the map
descends to a map
![]() $N/\Sigma \to S^2(\mathfrak {g}^{\wedge \dim (M)})$
. Denote by
$N/\Sigma \to S^2(\mathfrak {g}^{\wedge \dim (M)})$
. Denote by
![]() $\eta $
the pushforward of the Haar probability measure on
$\eta $
the pushforward of the Haar probability measure on
![]() $N/\Sigma $
to
$N/\Sigma $
to
![]() $S^2(\mathfrak {g}^{\wedge \dim (M)})$
by this map, and let
$S^2(\mathfrak {g}^{\wedge \dim (M)})$
by this map, and let
![]() $\Gamma \leqslant N \cap H_N$
be as in (iii) of the definition of
$\Gamma \leqslant N \cap H_N$
be as in (iii) of the definition of
![]() $\mathcal {T}(G,\Delta ,\Sigma )$
. Then
$\mathcal {T}(G,\Delta ,\Sigma )$
. Then
![]() $\eta $
is an ergodic
$\eta $
is an ergodic
![]() $\Gamma $
-invariant probability measure supported on the set
$\Gamma $
-invariant probability measure supported on the set
![]() $\{v\otimes v\mid v\in \mathfrak {g}^{\wedge \dim (M)}\}$
. Since
$\{v\otimes v\mid v\in \mathfrak {g}^{\wedge \dim (M)}\}$
. Since
![]() $\Gamma $
supports an
$\Gamma $
supports an
![]() $H_N$
-expanding probability measure relative to G and
$H_N$
-expanding probability measure relative to G and
![]() $ \left \lVert {v\otimes v} \right \rVert = \left \lVert {v} \right \rVert ^2$
, Lemma 2.6 implies that
$ \left \lVert {v\otimes v} \right \rVert = \left \lVert {v} \right \rVert ^2$
, Lemma 2.6 implies that
![]() $\eta $
is concentrated on the subspace of
$\eta $
is concentrated on the subspace of
![]() $H_N$
-fixed vectors. The ergodicity forces
$H_N$
-fixed vectors. The ergodicity forces
![]() $\eta $
to be the Dirac mass at
$\eta $
to be the Dirac mass at
![]() $\omega $
. Hence,
$\omega $
. Hence,
![]() $\omega $
is N- and
$\omega $
is N- and
![]() $H_N$
-fixed, as required.
$H_N$
-fixed, as required.
We can now prove Lemma 5.3. The argument is basically the same as in the proof of [Reference Benoist and Quint10, Lemma 2.5], but we need to handle an additional difficulty coming from the fact that
![]() $\Gamma $
is not necessarily Zariski dense in
$\Gamma $
is not necessarily Zariski dense in
![]() $H_N$
, but only carries a probability measure that is
$H_N$
, but only carries a probability measure that is
![]() $H_N$
-expanding relative to G.
$H_N$
-expanding relative to G.
Proof of Lemma 5.3
For every
![]() $N \in \mathcal {T}(G,\Delta ,\Sigma )$
, we fix a connected semisimple group
$N \in \mathcal {T}(G,\Delta ,\Sigma )$
, we fix a connected semisimple group
![]() $H_N$
as in (iii) of Definition 5.2. Considering the closure of the group generated by the set
$H_N$
as in (iii) of Definition 5.2. Considering the closure of the group generated by the set
![]() $\bigcup _{N\in \mathcal {T}(G,\Delta ,\Sigma )}H_N N,$
we can assume that this set generates a dense subgroup of G. By Lemma 5.4,
$\bigcup _{N\in \mathcal {T}(G,\Delta ,\Sigma )}H_N N,$
we can assume that this set generates a dense subgroup of G. By Lemma 5.4,
is a normal subgroup of G. Let
![]() $\pi \colon G\to G/M$
be the natural projection map.
$\pi \colon G\to G/M$
be the natural projection map.
We will argue next that
![]() $\iota \colon N\mapsto \pi (N)$
gives an injection of
$\iota \colon N\mapsto \pi (N)$
gives an injection of
![]() $\mathcal {T}(G,\Delta ,\Sigma )\setminus \{\Sigma M\}$
into
$\mathcal {T}(G,\Delta ,\Sigma )\setminus \{\Sigma M\}$
into
![]() $\mathcal {T}(G/M,\{e\},\pi (\Sigma ))$
. First, note that
$\mathcal {T}(G/M,\{e\},\pi (\Sigma ))$
. First, note that
![]() $N\mapsto \pi (N)$
is an injective map from
$N\mapsto \pi (N)$
is an injective map from
![]() $\mathcal {T}(G,\Delta ,\Sigma )$
into the set of closed subgroups of
$\mathcal {T}(G,\Delta ,\Sigma )$
into the set of closed subgroups of
![]() $G/M$
. Since
$G/M$
. Since
![]() $\Sigma \cap M = \Delta $
is a lattice in M,
$\Sigma \cap M = \Delta $
is a lattice in M,
![]() $\Sigma M$
is closed in G by [Reference Raghunathan80, Theorem 1.13], which implies that
$\Sigma M$
is closed in G by [Reference Raghunathan80, Theorem 1.13], which implies that
![]() $\pi (\Sigma )$
is discrete. As there is an equivariant projection
$\pi (\Sigma )$
is discrete. As there is an equivariant projection
![]() $N/\Sigma \to \pi (N)/\pi (\Sigma )$
,
$N/\Sigma \to \pi (N)/\pi (\Sigma )$
,
![]() $\pi (\Sigma ) $
is a lattice in
$\pi (\Sigma ) $
is a lattice in
![]() $\pi (N)$
. If
$\pi (N)$
. If
![]() $\pi (n)\in \pi (\Sigma )$
for some
$\pi (n)\in \pi (\Sigma )$
for some
![]() $n\in N^\circ $
, then
$n\in N^\circ $
, then
![]() $n=\sigma m$
for some
$n=\sigma m$
for some
![]() $m\in M$
and
$m\in M$
and
![]() $\sigma \in \Sigma $
. Since
$\sigma \in \Sigma $
. Since
![]() $M\subset N^\circ $
, it follows that
$M\subset N^\circ $
, it follows that
![]() $\sigma \in \Sigma \cap N^\circ =\Delta \subset M$
, which proves that
$\sigma \in \Sigma \cap N^\circ =\Delta \subset M$
, which proves that
![]() $\pi (N)^\circ \cap \pi (\Sigma )=\{e\}$
is the trivial group. So we have verified conditions (i) and (ii) of Definition 5.2 for any element
$\pi (N)^\circ \cap \pi (\Sigma )=\{e\}$
is the trivial group. So we have verified conditions (i) and (ii) of Definition 5.2 for any element
![]() $\pi (N)$
in the image of
$\pi (N)$
in the image of
![]() $\iota $
. To also verify condition (iii), let
$\iota $
. To also verify condition (iii), let
![]() $H_N\leqslant G$
be the connected semisimple subgroup from condition (iii) for N and
$H_N\leqslant G$
be the connected semisimple subgroup from condition (iii) for N and
![]() $\Gamma $
a subgroup of
$\Gamma $
a subgroup of
![]() $H_N\cap N$
that acts ergodically on
$H_N\cap N$
that acts ergodically on
![]() $N/\Sigma $
and carries an
$N/\Sigma $
and carries an
![]() $H_N$
-expanding probability measure
$H_N$
-expanding probability measure
![]() $\mu $
relative to G. Then it is clear that
$\mu $
relative to G. Then it is clear that
![]() $\pi (\Gamma )$
acts ergodically on
$\pi (\Gamma )$
acts ergodically on
![]() $\pi (N)/\pi (\Sigma )$
. Now, if
$\pi (N)/\pi (\Sigma )$
. Now, if
![]() $H_N\leqslant M$
, then ergodicity of this action forces
$H_N\leqslant M$
, then ergodicity of this action forces
![]() $N=\Sigma M$
. Otherwise,
$N=\Sigma M$
. Otherwise,
![]() $\pi (H_N) $
is a connected semisimple Lie group. By Lemma 5.4 and connectedness,
$\pi (H_N) $
is a connected semisimple Lie group. By Lemma 5.4 and connectedness,
![]() $H_N$
fixes a vector
$H_N$
fixes a vector
![]() $v\in \mathfrak {g}^{\wedge \dim (M)}$
corresponding to a basis of the Lie algebra
$v\in \mathfrak {g}^{\wedge \dim (M)}$
corresponding to a basis of the Lie algebra
![]() $\mathfrak {m}$
of M. For
$\mathfrak {m}$
of M. For
![]() $1\le k\le \dim (G/M)-1$
, on
$1\le k\le \dim (G/M)-1$
, on
![]() $(\mathfrak {g}/\mathfrak {m})^{\wedge k}$
we may use a norm with the property that
$(\mathfrak {g}/\mathfrak {m})^{\wedge k}$
we may use a norm with the property that
![]() $ \left \lVert {[w]} \right \rVert = \left \lVert {w\wedge v} \right \rVert $
for every
$ \left \lVert {[w]} \right \rVert = \left \lVert {w\wedge v} \right \rVert $
for every
![]() $w\in \mathfrak {g}^{\wedge k}$
, where
$w\in \mathfrak {g}^{\wedge k}$
, where
![]() $[w]$
denotes the projection of w to
$[w]$
denotes the projection of w to
![]() $(\mathfrak {g}/\mathfrak {m})^{\wedge k}$
. Then the same calculation as in equation (4.4) shows that
$(\mathfrak {g}/\mathfrak {m})^{\wedge k}$
. Then the same calculation as in equation (4.4) shows that
![]() $\pi _*\mu $
is
$\pi _*\mu $
is
![]() $\pi (H_N)$
-expanding relative to
$\pi (H_N)$
-expanding relative to
![]() $G/M$
. So also condition (iii) of Definition 5.2 holds for
$G/M$
. So also condition (iii) of Definition 5.2 holds for
![]() $\pi (N)$
.
$\pi (N)$
.
Therefore, it suffices to prove the lemma under the assumption that
![]() $\Delta =\{e\}$
is the trivial group and that for every
$\Delta =\{e\}$
is the trivial group and that for every
![]() $N \in {\mathcal {T}(G,\{e\},\Sigma )}$
, the connected component
$N \in {\mathcal {T}(G,\{e\},\Sigma )}$
, the connected component
![]() $N^\circ $
is normal in G. In view of condition (ii), this implies that
$N^\circ $
is normal in G. In view of condition (ii), this implies that
![]() $N^\circ $
is a compact normal subgroup of G. By [Reference Benoist and Quint10, Lemma 2.7], there are only countably many such
$N^\circ $
is a compact normal subgroup of G. By [Reference Benoist and Quint10, Lemma 2.7], there are only countably many such
![]() $N^\circ $
. Similar to the first reduction step above, after fixing
$N^\circ $
. Similar to the first reduction step above, after fixing
![]() $N^\circ $
and replacing G by
$N^\circ $
and replacing G by
![]() $G/N^\circ $
and
$G/N^\circ $
and
![]() $\Sigma $
by
$\Sigma $
by
![]() $\Sigma N^\circ /N^\circ $
, we are left to show that the set
$\Sigma N^\circ /N^\circ $
, we are left to show that the set
![]() $\mathcal V(G, \Sigma )$
of discrete subgroups N containing
$\mathcal V(G, \Sigma )$
of discrete subgroups N containing
![]() $\Sigma $
as a finite index subgroup such that (iii) of Definition 5.2 holds is countable. For each
$\Sigma $
as a finite index subgroup such that (iii) of Definition 5.2 holds is countable. For each
![]() $N \in \mathcal V(G, \Sigma )$
, there is a finite index subgroup
$N \in \mathcal V(G, \Sigma )$
, there is a finite index subgroup
![]() $\Sigma '\leqslant \Sigma $
such that
$\Sigma '\leqslant \Sigma $
such that
![]() $\Sigma '$
is normal in N. Recall that by assumption
$\Sigma '$
is normal in N. Recall that by assumption
![]() $\Sigma $
is finitely generated so that it admits only finitely many homomorphisms to any fixed finite group. It follows that there are countably many such
$\Sigma $
is finitely generated so that it admits only finitely many homomorphisms to any fixed finite group. It follows that there are countably many such
![]() $\Sigma '$
. Therefore, it suffices to show that, for
$\Sigma '$
. Therefore, it suffices to show that, for
![]() $\Sigma '$
fixed, the set
$\Sigma '$
fixed, the set
![]() $\mathcal V(G, \Sigma ',\Sigma )$
of
$\mathcal V(G, \Sigma ',\Sigma )$
of
![]() $N\in \mathcal V(G, \Sigma )$
with
$N\in \mathcal V(G, \Sigma )$
with
![]() $\Sigma '$
normal in N is countable. Let S be the closed subgroup generated by
$\Sigma '$
normal in N is countable. Let S be the closed subgroup generated by
![]() $\bigcup _{N \in \mathcal V(G, \Sigma ',\Sigma )} N$
. Then
$\bigcup _{N \in \mathcal V(G, \Sigma ',\Sigma )} N$
. Then
![]() $\Sigma '$
is a discrete normal subgroup of S. For any
$\Sigma '$
is a discrete normal subgroup of S. For any
![]() $g\in \Sigma '$
, the set
$g\in \Sigma '$
, the set
![]() $\{s g s^{-1}\mid s\in S^\circ \}$
is a connected subset of
$\{s g s^{-1}\mid s\in S^\circ \}$
is a connected subset of
![]() $\Sigma '$
, so it has to be
$\Sigma '$
, so it has to be
![]() $\{ g\}$
. It follows that
$\{ g\}$
. It follows that
![]() $\Sigma '$
centralizes
$\Sigma '$
centralizes
![]() $S^\circ $
. Given
$S^\circ $
. Given
![]() $N\in \mathcal V(G, \Sigma ',\Sigma )$
, let
$N\in \mathcal V(G, \Sigma ',\Sigma )$
, let
![]() $\Gamma $
be a subgroup of
$\Gamma $
be a subgroup of
![]() $H_N \cap N$
acting ergodically on
$H_N \cap N$
acting ergodically on
![]() $N/\Sigma $
as in (iii) of Definition 5.2. By ergodicity, we have
$N/\Sigma $
as in (iii) of Definition 5.2. By ergodicity, we have
![]() $N=\Gamma \Sigma $
and since
$N=\Gamma \Sigma $
and since
![]() $\Gamma \Sigma =\Gamma (\Sigma ' \Sigma )=(\Gamma \Sigma ')\Sigma $
, N is uniquely determined by the discrete group
$\Gamma \Sigma =\Gamma (\Sigma ' \Sigma )=(\Gamma \Sigma ')\Sigma $
, N is uniquely determined by the discrete group
![]() $\Gamma \Sigma '$
. So it suffices to show that the set of subgroups
$\Gamma \Sigma '$
. So it suffices to show that the set of subgroups
![]() $\Gamma \Sigma '$
appearing in this way is countable. The finite index subgroup
$\Gamma \Sigma '$
appearing in this way is countable. The finite index subgroup
![]() $\Gamma \cap \Sigma '$
of
$\Gamma \cap \Sigma '$
of
![]() $\Gamma $
centralizes
$\Gamma $
centralizes
![]() $S^\circ $
and
$S^\circ $
and
![]() $\Gamma $
normalizes
$\Gamma $
normalizes
![]() $S^\circ $
. It follows that the conjugation action of
$S^\circ $
. It follows that the conjugation action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $S^\circ $
factors through a finite group. Now, according to (iii) of Definition 5.2, there exists a probability measure on
$S^\circ $
factors through a finite group. Now, according to (iii) of Definition 5.2, there exists a probability measure on
![]() $\Gamma $
that is
$\Gamma $
that is
![]() $H_N$
-expanding relative to G. By (i) of Proposition 2.10 applied to the adjoint representation of
$H_N$
-expanding relative to G. By (i) of Proposition 2.10 applied to the adjoint representation of
![]() $H_N$
on
$H_N$
on
![]() $\mathfrak {g}$
, we conclude that every element of the Lie algebra of S is fixed by
$\mathfrak {g}$
, we conclude that every element of the Lie algebra of S is fixed by
![]() $H_N$
. This implies that
$H_N$
. This implies that
![]() $\Gamma <H_N$
centralizes
$\Gamma <H_N$
centralizes
![]() $S^\circ $
. Therefore,
$S^\circ $
. Therefore,
![]() $\Gamma \Sigma '/\Sigma '$
is a finite subgroup of
$\Gamma \Sigma '/\Sigma '$
is a finite subgroup of
![]() $S/\Sigma '$
centralizing
$S/\Sigma '$
centralizing
![]() $S^\circ \Sigma '/\Sigma '$
. By [Reference Benoist and Quint10, Lemma 2.8], the set of compact subgroups of
$S^\circ \Sigma '/\Sigma '$
. By [Reference Benoist and Quint10, Lemma 2.8], the set of compact subgroups of
![]() $S/\Sigma '$
centralizing
$S/\Sigma '$
centralizing
![]() $S^\circ \Sigma '/\Sigma '$
is countable. This gives the required countability and hence completes the proof.
$S^\circ \Sigma '/\Sigma '$
is countable. This gives the required countability and hence completes the proof.
We also need the following version of [Reference Benoist and Quint10, Lemma 2.2].
Lemma 5.5. Let G be a real Lie group, H a connected semisimple subgroup of G and
![]() $\Gamma $
a subgroup of H that supports an H-expanding probability measure relative to G. Moreover, let L be the centralizer of
$\Gamma $
a subgroup of H that supports an H-expanding probability measure relative to G. Moreover, let L be the centralizer of
![]() $\Gamma $
in G and N a closed unimodular subgroup of G. Then the set of
$\Gamma $
in G and N a closed unimodular subgroup of G. Then the set of
![]() $\Gamma $
-fixed points in
$\Gamma $
-fixed points in
![]() $Y=G/N$
is a countable union of L-orbits.
$Y=G/N$
is a countable union of L-orbits.
Proof. It is enough to consider the case
![]() $\dim (N)<\dim (G)$
. Denote by
$\dim (N)<\dim (G)$
. Denote by
![]() $Y^\Gamma $
the set of
$Y^\Gamma $
the set of
![]() $\Gamma $
-fixed points in Y. Then it suffices to show that every L-orbit
$\Gamma $
-fixed points in Y. Then it suffices to show that every L-orbit
![]() $Ly$
in
$Ly$
in
![]() $Y^\Gamma $
is open in
$Y^\Gamma $
is open in
![]() $Y^\Gamma $
. After a conjugation, we may assume
$Y^\Gamma $
. After a conjugation, we may assume
![]() $y=eN$
is the identity coset. In particular, we then have
$y=eN$
is the identity coset. In particular, we then have
![]() $\Gamma \leqslant N$
. Let
$\Gamma \leqslant N$
. Let
![]() $\mathfrak l$
denote the Lie algebra of L. By finite-dimensionality, we can find
$\mathfrak l$
denote the Lie algebra of L. By finite-dimensionality, we can find
![]() $\gamma _1,\dots ,\gamma _r\in \Gamma $
such that
$\gamma _1,\dots ,\gamma _r\in \Gamma $
such that
In view of unimodularity of N, considering a vector in
![]() $S^2(\mathfrak {g}^{\wedge \dim (N)})$
corresponding to a basis of the Lie algebra
$S^2(\mathfrak {g}^{\wedge \dim (N)})$
corresponding to a basis of the Lie algebra
![]() $\mathfrak n$
of N and arguing as in Lemma 5.4 yields that
$\mathfrak n$
of N and arguing as in Lemma 5.4 yields that
![]() $\mathfrak n$
is H-invariant. Thanks to the expansion in the adjoint representation, it moreover follows that
$\mathfrak n$
is H-invariant. Thanks to the expansion in the adjoint representation, it moreover follows that
![]() $\mathfrak {l}$
coincides with the space of H-fixed vectors in
$\mathfrak {l}$
coincides with the space of H-fixed vectors in
![]() $\mathfrak g$
. We choose an H-invariant complement
$\mathfrak g$
. We choose an H-invariant complement
![]() $\mathfrak {v}$
of
$\mathfrak {v}$
of
![]() $\mathfrak n+\mathfrak l$
in
$\mathfrak n+\mathfrak l$
in
![]() $\mathfrak {g}$
. Then for any
$\mathfrak {g}$
. Then for any
![]() $v\in \mathfrak {v}$
sufficiently small, if
$v\in \mathfrak {v}$
sufficiently small, if
![]() $\exp (v) y$
is
$\exp (v) y$
is
![]() $\Gamma $
-fixed, then for all
$\Gamma $
-fixed, then for all
![]() $1\le i\le r$
we have
$1\le i\le r$
we have
which implies
![]() $\operatorname {\mathrm {Ad}}(\gamma _i)v=v$
and thus
$\operatorname {\mathrm {Ad}}(\gamma _i)v=v$
and thus
![]() $v\in \mathfrak l\cap \mathfrak v=\{0\}$
. This shows that
$v\in \mathfrak l\cap \mathfrak v=\{0\}$
. This shows that
![]() $Ly$
is open in
$Ly$
is open in
![]() $Y^{\Gamma }$
and hence finishes the proof that
$Y^{\Gamma }$
and hence finishes the proof that
![]() $Y^\Gamma $
is a countable union of L-orbits.
$Y^\Gamma $
is a countable union of L-orbits.
Finally, we can prove the main result of this subsection. We adapt the proof of [Reference Benoist and Quint10, Proposition 2.1] by substituting Lemmas 5.3 and 5.5 for the corresponding results, and extend it to cover semigroups that are not compactly generated.
Proof of Proposition 5.1
We first establish the statement assuming additionally that
![]() $\Gamma $
is compactly generated. Let
$\Gamma $
is compactly generated. Let
![]() $Y\in \mathcal {S}(\Gamma )$
, and denote by
$Y\in \mathcal {S}(\Gamma )$
, and denote by
![]() $G_Y$
the stabilizer of the homogeneous probability measure
$G_Y$
the stabilizer of the homogeneous probability measure
![]() $\nu $
corresponding to Y. Let
$\nu $
corresponding to Y. Let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\Gamma $
that is H-expanding relative to G. Choose
$\Gamma $
that is H-expanding relative to G. Choose
![]() $g\in G$
such that
$g\in G$
such that
![]() $g\Lambda \in Y$
and consider
$g\Lambda \in Y$
and consider
![]() $N=g^{-1}\Gamma G_Y^\circ g$
, which is a closed subgroup of G because
$N=g^{-1}\Gamma G_Y^\circ g$
, which is a closed subgroup of G because
![]() $\Gamma $
is contained in
$\Gamma $
is contained in
![]() $G_Y$
and thus normalizes
$G_Y$
and thus normalizes
![]() $G_Y^\circ $
. Now, the discrete groups
$G_Y^\circ $
. Now, the discrete groups
![]() $\Delta =N^\circ \cap \Lambda $
and
$\Delta =N^\circ \cap \Lambda $
and
![]() $\Sigma =N\cap \Lambda $
are lattices in
$\Sigma =N\cap \Lambda $
are lattices in
![]() $N^\circ $
and N, respectively. Being a lattice in a connected Lie group,
$N^\circ $
and N, respectively. Being a lattice in a connected Lie group,
![]() $\Delta $
is finitely generated (see [Reference Raghunathan80, 6.18]). As
$\Delta $
is finitely generated (see [Reference Raghunathan80, 6.18]). As
![]() $N=g^{-1}\Gamma G_Y^\circ g$
and
$N=g^{-1}\Gamma G_Y^\circ g$
and
![]() $\Gamma $
is compactly generated,
$\Gamma $
is compactly generated,
![]() $N/N^\circ $
is finitely generated. Since
$N/N^\circ $
is finitely generated. Since
![]() $\Sigma /\Delta $
has finite index in
$\Sigma /\Delta $
has finite index in
![]() $N/N^\circ $
, also
$N/N^\circ $
, also
![]() $\Sigma $
is finitely generated. As
$\Sigma $
is finitely generated. As
![]() $\Lambda $
admits only countably many finitely generated subgroups, one may assume that
$\Lambda $
admits only countably many finitely generated subgroups, one may assume that
![]() $\Delta $
and
$\Delta $
and
![]() $\Sigma $
are fixed. We claim that N belongs to
$\Sigma $
are fixed. We claim that N belongs to
![]() $\mathcal {T}(G,\Delta ,\Sigma )$
. To see this, we first record that (i) and (ii) in Definition 5.2 are immediate. Considering
$\mathcal {T}(G,\Delta ,\Sigma )$
. To see this, we first record that (i) and (ii) in Definition 5.2 are immediate. Considering
![]() $H_N=g^{-1}Hg$
, its subgroup
$H_N=g^{-1}Hg$
, its subgroup
![]() $g^{-1}\Gamma g$
and the image of
$g^{-1}\Gamma g$
and the image of
![]() $\mu $
by conjugation by
$\mu $
by conjugation by
![]() $g^{-1}$
, also (iii) is seen to hold. Consequently, we can also assume N to be fixed by virtue of Lemma 5.3. As the point
$g^{-1}$
, also (iii) is seen to hold. Consequently, we can also assume N to be fixed by virtue of Lemma 5.3. As the point
![]() $gN\in G/N$
is
$gN\in G/N$
is
![]() $\Gamma $
-invariant, by Lemma 5.5 one may further assume the L-orbit
$\Gamma $
-invariant, by Lemma 5.5 one may further assume the L-orbit
![]() $LgN\subset G/N$
is fixed. It only remains to note that for
$LgN\subset G/N$
is fixed. It only remains to note that for
![]() $l\in L$
, the orbit
$l\in L$
, the orbit
![]() $lgN\Lambda \subset X=G/\Lambda $
is precisely the translate
$lgN\Lambda \subset X=G/\Lambda $
is precisely the translate
![]() $lY$
of Y.
$lY$
of Y.
To treat the general case without the compact generation assumption, given an arbitrary probability measure
![]() $\mu '$
on
$\mu '$
on
![]() $\Gamma $
with finite first moment that is H-expanding relative to G, we consider the probability measure
$\Gamma $
with finite first moment that is H-expanding relative to G, we consider the probability measure
![]() $\mu $
given as the normalized restriction of
$\mu $
given as the normalized restriction of
![]() $\mu '$
to a sufficiently large compact ball B around the identity. By choosing B large enough, we can guarantee that the integral characterization of uniform expansion from Proposition 2.2 still holds for the finite collection of representations in Definition 4.7. In view of expansion in the adjoint representation, the connected components of
$\mu '$
to a sufficiently large compact ball B around the identity. By choosing B large enough, we can guarantee that the integral characterization of uniform expansion from Proposition 2.2 still holds for the finite collection of representations in Definition 4.7. In view of expansion in the adjoint representation, the connected components of
![]() $L=C_G(\Gamma )$
and
$L=C_G(\Gamma )$
and
![]() $L_{\mu }=C_G(\Gamma _{\mu })$
coincide. Therefore, applying the above to the compactly generated subgroup
$L_{\mu }=C_G(\Gamma _{\mu })$
coincide. Therefore, applying the above to the compactly generated subgroup
![]() $\Gamma _{\mu }$
, we can find a countable collection
$\Gamma _{\mu }$
, we can find a countable collection
![]() $\mathcal {Y}_{\mu }\subset \mathcal {S}(\Gamma _{\mu })$
such that
$\mathcal {Y}_{\mu }\subset \mathcal {S}(\Gamma _{\mu })$
such that
![]() $\mathcal {S}(\Gamma _{\mu })=\{lY_{\mu }\mid l\in L,Y_{\mu }\in \mathcal {Y}_{\mu }\}$
. We claim that
$\mathcal {S}(\Gamma _{\mu })=\{lY_{\mu }\mid l\in L,Y_{\mu }\in \mathcal {Y}_{\mu }\}$
. We claim that
![]() $\mathcal {Y}=\{\overline {\Gamma Y_{\mu }}\mid Y_{\mu }\in \mathcal {Y}_{\mu }\}\cap \mathcal {S}(\Gamma )$
satisfies the conclusion of the proposition. To see this, let
$\mathcal {Y}=\{\overline {\Gamma Y_{\mu }}\mid Y_{\mu }\in \mathcal {Y}_{\mu }\}\cap \mathcal {S}(\Gamma )$
satisfies the conclusion of the proposition. To see this, let
![]() $Y\in \mathcal {S}(\Gamma )$
be arbitrary and
$Y\in \mathcal {S}(\Gamma )$
be arbitrary and
![]() $\nu _Y$
be the associated
$\nu _Y$
be the associated
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $\Gamma $
-ergodic homogeneous measure. By Theorem 4.8, we know that every
$\Gamma $
-ergodic homogeneous measure. By Theorem 4.8, we know that every
![]() $\Gamma _{\mu }$
-ergodic component of
$\Gamma _{\mu }$
-ergodic component of
![]() $\nu _Y$
is an element of
$\nu _Y$
is an element of
![]() $\mathcal {S}(\Gamma _{\mu })$
. By Fubini’s theorem and
$\mathcal {S}(\Gamma _{\mu })$
. By Fubini’s theorem and
![]() $\Gamma $
-ergodicity of
$\Gamma $
-ergodicity of
![]() $\nu _Y$
, we can thus find
$\nu _Y$
, we can thus find
![]() $Y_{\mu }'\in \mathcal {S}(\Gamma _{\mu })$
such that almost every point
$Y_{\mu }'\in \mathcal {S}(\Gamma _{\mu })$
such that almost every point
![]() $x\in Y_{\mu }'$
with respect to the homogeneous measure on
$x\in Y_{\mu }'$
with respect to the homogeneous measure on
![]() $Y_{\mu }'$
satisfies
$Y_{\mu }'$
satisfies
![]() $Y=\overline {\Gamma x}$
. We also know that
$Y=\overline {\Gamma x}$
. We also know that
![]() $Y_{\mu }'=lY_{\mu }$
for some
$Y_{\mu }'=lY_{\mu }$
for some
![]() $Y_{\mu }\in \mathcal {Y}_{\mu }$
and
$Y_{\mu }\in \mathcal {Y}_{\mu }$
and
![]() $l\in L=C_G(\Gamma )$
. We conclude that
$l\in L=C_G(\Gamma )$
. We conclude that
![]() $Y=\overline {\Gamma Y_{\mu }'}=l\overline {\Gamma Y_{\mu }}$
, which shows that
$Y=\overline {\Gamma Y_{\mu }'}=l\overline {\Gamma Y_{\mu }}$
, which shows that
![]() $\overline {\Gamma Y_{\mu }}\in \mathcal {Y}$
and completes the proof.
$\overline {\Gamma Y_{\mu }}\in \mathcal {Y}$
and completes the proof.
6 Height functions with contraction properties
A Markov chain on a standard Borel space X is a measurable map
![]() $X\ni x\mapsto P_x$
from X to the space of Borel probability measures on X, specifying the transition probabilities at each point of X. The associated Markov operator P is defined by
$X\ni x\mapsto P_x$
from X to the space of Borel probability measures on X, specifying the transition probabilities at each point of X. The associated Markov operator P is defined by
for a nonnegative Borel function f on X and
![]() $x\in X$
. If G is a locally compact second countable group with a Borel G-action on X, then a choice of a probability measure
$x\in X$
. If G is a locally compact second countable group with a Borel G-action on X, then a choice of a probability measure
![]() $\mu $
on G induces a Markov chain on X with transition probabilities
$\mu $
on G induces a Markov chain on X with transition probabilities
![]() $P_x=\mu *\delta _x$
, which can be thought of as the formalization of the concept of the random walk on X given by
$P_x=\mu *\delta _x$
, which can be thought of as the formalization of the concept of the random walk on X given by
![]() $\mu $
. We denote the associated Markov operator by
$\mu $
. We denote the associated Markov operator by
![]() $A_{\mu }$
, which is given in this context by the explicit formula
$A_{\mu }$
, which is given in this context by the explicit formula
We also refer to
![]() $A_{\mu }$
as the averaging operator associated to
$A_{\mu }$
as the averaging operator associated to
![]() $\mu $
. See [Reference Benoist and Quint10, §3] and [Reference Benoist and Quint11, §2] for more background on Markov operators in the context of the study of random walks.
$\mu $
. See [Reference Benoist and Quint10, §3] and [Reference Benoist and Quint11, §2] for more background on Markov operators in the context of the study of random walks.
Coming back to our setting, recall that
![]() $\Lambda $
denotes a lattice in a Lie group G and H a connected semisimple subgroup of G without compact factors and with finite center, and
$\Lambda $
denotes a lattice in a Lie group G and H a connected semisimple subgroup of G without compact factors and with finite center, and
![]() $\mu $
is an H-expanding probability measure on H.
$\mu $
is an H-expanding probability measure on H.
The goal of this section is to construct height functions on
![]() $X=G/\Lambda $
that are contracted by the averaging operator
$X=G/\Lambda $
that are contracted by the averaging operator
![]() $A_{\mu }$
(also known as Lyapunov functions or sometimes Margulis functions), which will yield the recurrence properties of the random walk on X necessary for the proof of our main theorems. As already explained in §1.2, two types of height functions are required. First, one needs a height function that is proper but stays bounded on prescribed compact subsets of the space X, which prevents the random walk from escaping to infinity. Secondly, in order to ensure equidistribution towards a homogeneous measure sitting on the orbit closure, we will need to construct height functions which are unbounded near lower dimensional homogeneous subspaces. These ensure that the random walk does not accumulate near such ‘singular subspaces’, that is, does not spend too much time in their vicinity.
$A_{\mu }$
(also known as Lyapunov functions or sometimes Margulis functions), which will yield the recurrence properties of the random walk on X necessary for the proof of our main theorems. As already explained in §1.2, two types of height functions are required. First, one needs a height function that is proper but stays bounded on prescribed compact subsets of the space X, which prevents the random walk from escaping to infinity. Secondly, in order to ensure equidistribution towards a homogeneous measure sitting on the orbit closure, we will need to construct height functions which are unbounded near lower dimensional homogeneous subspaces. These ensure that the random walk does not accumulate near such ‘singular subspaces’, that is, does not spend too much time in their vicinity.
6.1 Height function with respect to the cusps
We first present the construction of the height functions responsible for ruling out escape of mass.
Theorem 6.1 (Exponential
 $\mu $
-unstability of the cusps, [Reference Benoist and Quint8])
$\mu $
-unstability of the cusps, [Reference Benoist and Quint8])
Let
![]() $\mu $
be an H-expanding probability measure with finite exponential moments. For any compact subset Z of
$\mu $
be an H-expanding probability measure with finite exponential moments. For any compact subset Z of
![]() $X=G/\Lambda $
, there exist constants
$X=G/\Lambda $
, there exist constants
![]() $m\in \mathbb {N}$
,
$m\in \mathbb {N}$
,
![]() $a \in (0,1)$
,
$a \in (0,1)$
,
![]() $b>0$
and a lower semicontinuous function
$b>0$
and a lower semicontinuous function
![]() $\beta _{\infty }\colon X\to [1, \infty ]$
uniformly bounded on Z such that for every
$\beta _{\infty }\colon X\to [1, \infty ]$
uniformly bounded on Z such that for every
![]() $x \in X$
we have
$x \in X$
we have
Moreover,
-
(i) for every
 $\ell>1$
, the set
$\ell>1$
, the set
 $\beta _{\infty }^{-1}([1,\ell ])$
is compact,
$\beta _{\infty }^{-1}([1,\ell ])$
is compact, -
(ii) the set
 $\beta _{\infty }^{-1}(\{\infty \})$
is H-invariant and
$\beta _{\infty }^{-1}(\{\infty \})$
is H-invariant and -
(iii) there exists a constant
 $\kappa>0$
such that for every
$\kappa>0$
such that for every
 $h \in H$
and
$h \in H$
and
 $x \in G/\Lambda $
we have
$x \in G/\Lambda $
we have
 $\beta _{\infty }(hx)\le \operatorname {N}(\operatorname {\mathrm {Ad}} h)^\kappa \beta _{\infty } (x)$
.
$\beta _{\infty }(hx)\le \operatorname {N}(\operatorname {\mathrm {Ad}} h)^\kappa \beta _{\infty } (x)$
.
By slight abuse of terminology, we sometimes just say that a height function is ‘proper’ when referring to property (i) above.
Let
![]() $\mathfrak {g}$
be the Lie algebra of G,
$\mathfrak {g}$
be the Lie algebra of G,
![]() $\mathfrak {r}$
the largest amenable ideal of
$\mathfrak {r}$
the largest amenable ideal of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {s}=\mathfrak {g}/\mathfrak {r}$
. A Lyapunov function as in the above theorem is constructed in [Reference Benoist and Quint8] in the case the noncompact part of the Zariski closure of the group generated by the support of the probability measure
$\mathfrak {s}=\mathfrak {g}/\mathfrak {r}$
. A Lyapunov function as in the above theorem is constructed in [Reference Benoist and Quint8] in the case the noncompact part of the Zariski closure of the group generated by the support of the probability measure
![]() $(\operatorname {\mathrm {Ad}}_{\mathfrak {s}})_*\mu $
is semisimple. However, as it turns out, this Zariski density assumption in a semisimple group without compact factors is only critically used, via Furstenberg’s result of positivity of the top Lyapunov exponent, to ensure equation (6.2) below, which is also guaranteed by our dynamical H-expansion assumption. Therefore, Benoist–Quint’s proof goes through in our setting with minor adaptations. We now explain this in more detail.
$(\operatorname {\mathrm {Ad}}_{\mathfrak {s}})_*\mu $
is semisimple. However, as it turns out, this Zariski density assumption in a semisimple group without compact factors is only critically used, via Furstenberg’s result of positivity of the top Lyapunov exponent, to ensure equation (6.2) below, which is also guaranteed by our dynamical H-expansion assumption. Therefore, Benoist–Quint’s proof goes through in our setting with minor adaptations. We now explain this in more detail.
A version of the following elementary but key lemma was already used in [Reference Eskin and Margulis31] (see also [Reference Benoist and Quint9, Lemma 6.12]). In our case, it holds true thanks to the characterization of uniform expansion expressed in Proposition 2.2.
Lemma 6.2. Let
![]() $\mu $
be an H-expanding probability measure on H with finite exponential moments and
$\mu $
be an H-expanding probability measure on H with finite exponential moments and
![]() $(\rho ,V)$
be a representation of H without nonzero H-fixed vectors. Then there exists
$(\rho ,V)$
be a representation of H without nonzero H-fixed vectors. Then there exists
![]() $\delta _0>0$
such that for every
$\delta _0>0$
such that for every
![]() $\delta \in (0,\delta _0)$
and
$\delta \in (0,\delta _0)$
and
![]() $c \in (0,1)$
, for every
$c \in (0,1)$
, for every
![]() $n \in \mathbb {N}$
large enough, we have
$n \in \mathbb {N}$
large enough, we have
 $$ \begin{align} \int_ H \frac{1}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d} \mu ^{*n}(h)\le \frac{c}{ \left\lVert {v} \right\rVert ^\delta} \end{align} $$
$$ \begin{align} \int_ H \frac{1}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d} \mu ^{*n}(h)\le \frac{c}{ \left\lVert {v} \right\rVert ^\delta} \end{align} $$
for every
![]() $v\in V\setminus \{0\}$
.
$v\in V\setminus \{0\}$
.
Proof. Using the elementary fact that for every
![]() $\varepsilon \in (0,1)$
,
$\varepsilon \in (0,1)$
,
![]() $x \in (0,\varepsilon )$
and
$x \in (0,\varepsilon )$
and
![]() $a>0$
, we have
$a>0$
, we have
![]() $a^x=1 +x \log a + (\frac {x}{\varepsilon })^2 R_a(x)$
with
$a^x=1 +x \log a + (\frac {x}{\varepsilon })^2 R_a(x)$
with
![]() $ \left \lvert {R_a(x)} \right \rvert \le e^{\varepsilon \left \lvert {\log a} \right \rvert }$
together with
$ \left \lvert {R_a(x)} \right \rvert \le e^{\varepsilon \left \lvert {\log a} \right \rvert }$
together with
![]() $ \left \lvert {\log \frac { \left \lVert {v} \right \rVert }{ \left \lVert {gv} \right \rVert }} \right \rvert \le \log \operatorname {N}(g)$
for every
$ \left \lvert {\log \frac { \left \lVert {v} \right \rVert }{ \left \lVert {gv} \right \rVert }} \right \rvert \le \log \operatorname {N}(g)$
for every
![]() $g \in \operatorname {\mathrm {GL}}(V)$
, we see that for every
$g \in \operatorname {\mathrm {GL}}(V)$
, we see that for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\varepsilon \in (0,1)$
and
$\varepsilon \in (0,1)$
and
![]() $\delta \in (0,\varepsilon )$
$\delta \in (0,\varepsilon )$
 $$ \begin{align} \int_H \frac{ \left\lVert {v} \right\rVert ^\delta}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d}\mu^{*n}(h) \le 1 + \delta \int_H \log\frac{ \left\lVert {v} \right\rVert }{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert } \mathop{}\!\mathrm{d}\mu^{*n}(h)+ \biggl(\frac{\delta}{\varepsilon}\biggr)^2 \int_H \operatorname{N}(\rho(h))^\varepsilon \mathop{}\!\mathrm{d}\mu^{*n}(h). \end{align} $$
$$ \begin{align} \int_H \frac{ \left\lVert {v} \right\rVert ^\delta}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d}\mu^{*n}(h) \le 1 + \delta \int_H \log\frac{ \left\lVert {v} \right\rVert }{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert } \mathop{}\!\mathrm{d}\mu^{*n}(h)+ \biggl(\frac{\delta}{\varepsilon}\biggr)^2 \int_H \operatorname{N}(\rho(h))^\varepsilon \mathop{}\!\mathrm{d}\mu^{*n}(h). \end{align} $$
By Proposition 2.2, there exists
![]() $N\in \mathbb {N} $
and
$N\in \mathbb {N} $
and
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $v\in V\setminus \{0\}$
, we have
$v\in V\setminus \{0\}$
, we have
Since
![]() $\rho _*\mu $
has finite exponential moments by Lemma 2.9, we can choose
$\rho _*\mu $
has finite exponential moments by Lemma 2.9, we can choose
![]() $\varepsilon _0>0$
such that
$\varepsilon _0>0$
such that
![]() $\int _H \operatorname {N}(\rho (h))^{\varepsilon _0} \mathop {}\!\mathrm {d}\mu ^{*n}(h)<\infty $
for every
$\int _H \operatorname {N}(\rho (h))^{\varepsilon _0} \mathop {}\!\mathrm {d}\mu ^{*n}(h)<\infty $
for every
![]() $n\in \mathbb {N}$
. Now, applying equation (6.3) with
$n\in \mathbb {N}$
. Now, applying equation (6.3) with
![]() $n=N$
,
$n=N$
,
![]() $\varepsilon =\varepsilon _0>0$
and using equation (6.4), we get that for every
$\varepsilon =\varepsilon _0>0$
and using equation (6.4), we get that for every
![]() $\delta>0$
smaller than some
$\delta>0$
smaller than some
![]() $\delta _0>0$
, there exists
$\delta _0>0$
, there exists
![]() $c' \in (0,1)$
such that we have
$c' \in (0,1)$
such that we have
 $$ \begin{align} \int_H \frac{1}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d} \mu ^{*N}(h)\le \frac{c'}{ \left\lVert {v} \right\rVert ^\delta} \end{align} $$
$$ \begin{align} \int_H \frac{1}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d} \mu ^{*N}(h)\le \frac{c'}{ \left\lVert {v} \right\rVert ^\delta} \end{align} $$
for every
![]() $v\in V \setminus \{0\}$
. Writing an arbitrary
$v\in V \setminus \{0\}$
. Writing an arbitrary
![]() $n \in \mathbb {N}$
as
$n \in \mathbb {N}$
as
![]() $n=m N + k$
with
$n=m N + k$
with
![]() $m,k \in \mathbb {N}$
and
$m,k \in \mathbb {N}$
and
![]() $k<N$
, using the facts that
$k<N$
, using the facts that
![]() $\mu ^{*n}=\mu ^{* m N} * \mu ^{* k}$
,
$\mu ^{*n}=\mu ^{* m N} * \mu ^{* k}$
,
![]() $\frac {1}{ \left \lVert {h{\boldsymbol {\cdot }} v} \right \rVert }\le \operatorname {N}(\rho (h)) \frac {1}{ \left \lVert {v} \right \rVert }$
and the existence of finite exponential moments, iterating equation (6.5) now yields
$\frac {1}{ \left \lVert {h{\boldsymbol {\cdot }} v} \right \rVert }\le \operatorname {N}(\rho (h)) \frac {1}{ \left \lVert {v} \right \rVert }$
and the existence of finite exponential moments, iterating equation (6.5) now yields
 $$ \begin{align*} \int_H \frac{1}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d} \mu ^{*n}(h)\le \frac{(c')^m}{ \left\lVert {v} \right\rVert ^\delta}\biggl(\int_H\operatorname{N}(\rho(h))^\delta\mathop{}\!\mathrm{d}\mu(h)\biggr)^k, \end{align*} $$
$$ \begin{align*} \int_H \frac{1}{ \left\lVert {h{\boldsymbol{\cdot}} v} \right\rVert ^\delta} \mathop{}\!\mathrm{d} \mu ^{*n}(h)\le \frac{(c')^m}{ \left\lVert {v} \right\rVert ^\delta}\biggl(\int_H\operatorname{N}(\rho(h))^\delta\mathop{}\!\mathrm{d}\mu(h)\biggr)^k, \end{align*} $$
the right-hand side of which can be made to be smaller than
![]() $c/ \left \lVert {v} \right \rVert ^\delta $
by requiring m to be large enough.
$c/ \left \lVert {v} \right \rVert ^\delta $
by requiring m to be large enough.
Proof of Theorem 6.1
We start the proof with a few general remarks on Lyapunov functions and their construction.
-
(1) It suffices to construct the function
 $\beta _{\infty }$
with values in
$\beta _{\infty }$
with values in
 $[0,\infty ]$
. Indeed, in the end one can simply add
$[0,\infty ]$
. Indeed, in the end one can simply add
 $1$
, if necessary, to ensure values in
$1$
, if necessary, to ensure values in
 $[1,\infty ]$
.
$[1,\infty ]$
. -
(2) The conclusion of the theorem is unaffected when replacing
 $\Lambda $
by a commensurable lattice
$\Lambda $
by a commensurable lattice
 $\Lambda '$
, that is, a lattice such that the intersection
$\Lambda '$
, that is, a lattice such that the intersection
 $\Lambda _0=\Lambda \cap \Lambda '$
has finite index in both
$\Lambda _0=\Lambda \cap \Lambda '$
has finite index in both
 $\Lambda $
and
$\Lambda $
and
 $\Lambda '$
. Indeed, given a Lyapunov function
$\Lambda '$
. Indeed, given a Lyapunov function
 $G/\Lambda \to [0,\infty ]$
, one can just precompose it with the projection
$G/\Lambda \to [0,\infty ]$
, one can just precompose it with the projection
 $G/\Lambda _0\to G/\Lambda $
, and, conversely, starting with a function
$G/\Lambda _0\to G/\Lambda $
, and, conversely, starting with a function
 $\beta \colon G/\Lambda _0\to [0,\infty ]$
, one can define the function
$\beta \colon G/\Lambda _0\to [0,\infty ]$
, one can define the function
 $\beta _{\infty }$
on
$\beta _{\infty }$
on
 $G/\Lambda $
by setting for
$G/\Lambda $
by setting for $$ \begin{align*} \beta_{\infty}(g\Lambda)=\sum_{\lambda\in\Lambda/\Lambda_0}\beta(g\lambda\Lambda_0) \end{align*} $$
$$ \begin{align*} \beta_{\infty}(g\Lambda)=\sum_{\lambda\in\Lambda/\Lambda_0}\beta(g\lambda\Lambda_0) \end{align*} $$
 $g\in G$
, which is easily seen to have the correct properties.
$g\in G$
, which is easily seen to have the correct properties.
-
(3) We may always assume that the lattice
 $\Lambda $
is nonuniform, that is, that
$\Lambda $
is nonuniform, that is, that
 $X=G/\Gamma $
is noncompact. For on a compact quotient, the constant function
$X=G/\Gamma $
is noncompact. For on a compact quotient, the constant function
 $1$
already has all required properties.
$1$
already has all required properties. -
(4) In the construction, we may without loss of generality replace G by any open subgroup
 $G_0$
. Indeed, X is the disjoint union of
$G_0$
. Indeed, X is the disjoint union of
 $G_0$
-orbits, and these are
$G_0$
-orbits, and these are
 $\Gamma _{\mu }$
-invariant since H is connected. Thus, one can translate a function
$\Gamma _{\mu }$
-invariant since H is connected. Thus, one can translate a function
 $\beta _{\infty }$
on
$\beta _{\infty }$
on
 $G_0/(G_0\cap \Lambda )$
to other
$G_0/(G_0\cap \Lambda )$
to other
 $G_0$
-orbits.
$G_0$
-orbits.
From now on, we assume G is connected and prove the existence of the height function
![]() $\beta _{\infty }$
with the required properties. The proof proceeds in several steps.
$\beta _{\infty }$
with the required properties. The proof proceeds in several steps.
Case 1:
![]() $G=\operatorname {\mathrm {SL}}_d(\mathbb {R})$
and
$G=\operatorname {\mathrm {SL}}_d(\mathbb {R})$
and
![]() $X=\operatorname {\mathrm {SL}}_d(\mathbb {R})/\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
. We show that the Benoist–Quint height function in [Reference Benoist and Quint8] has the required properties. We endow
$X=\operatorname {\mathrm {SL}}_d(\mathbb {R})/\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
. We show that the Benoist–Quint height function in [Reference Benoist and Quint8] has the required properties. We endow
![]() $E=\mathbb {R}^d $
with a Euclidean structure invariant by some maximal compact subgroup of H. We endow the vector space
$E=\mathbb {R}^d $
with a Euclidean structure invariant by some maximal compact subgroup of H. We endow the vector space
![]() $\bigwedge ^* E=\bigoplus _{i=0}^d \bigwedge ^i E$
with the induced Euclidean structure and use
$\bigwedge ^* E=\bigoplus _{i=0}^d \bigwedge ^i E$
with the induced Euclidean structure and use
![]() $ \left \lVert {\cdot } \right \rVert $
to denote the corresponding norm on E and on
$ \left \lVert {\cdot } \right \rVert $
to denote the corresponding norm on E and on
![]() $\bigwedge ^* E$
. For
$\bigwedge ^* E$
. For
![]() $0\le i\le d$
, we fix constants
$0\le i\le d$
, we fix constants
![]() $\delta _i=(d-i)i$
; they satisfy
$\delta _i=(d-i)i$
; they satisfy
for every
![]() $r,s,t \in \mathbb {N}$
with
$r,s,t \in \mathbb {N}$
with
![]() $s>0$
and
$s>0$
and
![]() $t>0$
.
$t>0$
.
We fix a maximal split torus A of H. Let
![]() $\mathfrak a$
and
$\mathfrak a$
and
![]() $\mathfrak h$
be the Lie algebras of A and H, respectively. Let
$\mathfrak h$
be the Lie algebras of A and H, respectively. Let
![]() $\Sigma (\mathfrak h, \mathfrak a)$
be the set of restricted roots. We fix a positive system in
$\Sigma (\mathfrak h, \mathfrak a)$
be the set of restricted roots. We fix a positive system in
![]() $\Sigma (\mathfrak h, \mathfrak a)$
. Let
$\Sigma (\mathfrak h, \mathfrak a)$
. Let
![]() $\mathcal W \subset \mathfrak a^*$
be the set of restricted weights appearing in finite-dimensional representations of H. We define a partial order on
$\mathcal W \subset \mathfrak a^*$
be the set of restricted weights appearing in finite-dimensional representations of H. We define a partial order on
![]() $\mathcal W$
by
$\mathcal W$
by
Recall that any representation of a connected semisimple real Lie group is completely reducible and each irreducible representation has a unique highest weight. We denote by
![]() $\mathcal {W}^+\subset \mathcal {W}$
the set of highest weights and let
$\mathcal {W}^+\subset \mathcal {W}$
the set of highest weights and let
![]() $\mathcal S\subset \mathcal W^+$
be the set of nonzero highest weights corresponding to the nontrivial irreducible representations of H appearing as direct summands in
$\mathcal S\subset \mathcal W^+$
be the set of nonzero highest weights corresponding to the nontrivial irreducible representations of H appearing as direct summands in
![]() $\bigwedge ^* E$
, where the representation of H on E is just the restriction of the standard representation of G. So the action of H on
$\bigwedge ^* E$
, where the representation of H on E is just the restriction of the standard representation of G. So the action of H on
![]() $\bigwedge ^*E$
decomposes into a direct sum
$\bigwedge ^*E$
decomposes into a direct sum
where
![]() $E_*^H$
is the space of H-fixed vectors in
$E_*^H$
is the space of H-fixed vectors in
![]() $\bigwedge ^* E$
and
$\bigwedge ^* E$
and
![]() $E_*^\lambda $
is the sum of all the irreducible subspaces of
$E_*^\lambda $
is the sum of all the irreducible subspaces of
![]() $\bigwedge ^* E$
with highest weight
$\bigwedge ^* E$
with highest weight
![]() $\lambda $
(i.e., the isotypic component of
$\lambda $
(i.e., the isotypic component of
![]() $\lambda $
). We fix
$\lambda $
). We fix
![]() $s_0\in \mathfrak a$
in the interior of the positive Weyl chamber and define
$s_0\in \mathfrak a$
in the interior of the positive Weyl chamber and define
![]() $\delta _\lambda = \lambda (s_0)$
for
$\delta _\lambda = \lambda (s_0)$
for
![]() $\lambda \in \mathcal {W}^+$
, so that the
$\lambda \in \mathcal {W}^+$
, so that the
![]() $\delta _\lambda $
satisfy
$\delta _\lambda $
satisfy
![]() $\lambda \le \mu $
if and only if
$\lambda \le \mu $
if and only if
![]() $\delta _\lambda \le \delta _{\mu }$
and
$\delta _\lambda \le \delta _{\mu }$
and
![]() $\delta _\lambda =0$
if and only if
$\delta _\lambda =0$
if and only if
![]() $\lambda =0$
for all
$\lambda =0$
for all
![]() $\lambda ,\mu \in \mathcal {W}^+$
. For
$\lambda ,\mu \in \mathcal {W}^+$
. For
![]() $\lambda \in \mathcal {S}$
, we use
$\lambda \in \mathcal {S}$
, we use
![]() $q_\lambda $
(resp.
$q_\lambda $
(resp.
![]() $q_0$
) to denote the H-equivariant projection from
$q_0$
) to denote the H-equivariant projection from
![]() $\bigwedge ^* E$
to
$\bigwedge ^* E$
to
![]() $E_*^\lambda $
(resp.
$E_*^\lambda $
(resp.
![]() $E_*^H$
). For any
$E_*^H$
). For any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $v\in \bigwedge ^i E$
with
$v\in \bigwedge ^i E$
with
![]() $0<i<d $
, define
$0<i<d $
, define
 $$ \begin{align*} \varphi_\varepsilon(v)=\begin{cases} \min_{\lambda\in \mathcal S} \varepsilon ^{\frac{\delta_i}{\delta_\lambda}} \left\lVert { q_\lambda(v)} \right\rVert ^{-\frac{1}{\delta_\lambda}}, & \text{if } \left\lVert {q_0(v)} \right\rVert < \varepsilon^{\delta_i}, \\ \hfill 0, & \text{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} \varphi_\varepsilon(v)=\begin{cases} \min_{\lambda\in \mathcal S} \varepsilon ^{\frac{\delta_i}{\delta_\lambda}} \left\lVert { q_\lambda(v)} \right\rVert ^{-\frac{1}{\delta_\lambda}}, & \text{if } \left\lVert {q_0(v)} \right\rVert < \varepsilon^{\delta_i}, \\ \hfill 0, & \text{otherwise}, \end{cases} \end{align*} $$
with the convention
![]() $\min \emptyset =\infty $
. Using Lemma 6.2 and H-equivariance of the projections
$\min \emptyset =\infty $
. Using Lemma 6.2 and H-equivariance of the projections
![]() $q_\lambda $
, one readily observes (cf. [Reference Benoist and Quint8, Lemma 4.3]) that for every
$q_\lambda $
, one readily observes (cf. [Reference Benoist and Quint8, Lemma 4.3]) that for every
![]() $\delta>0$
small enough, for every
$\delta>0$
small enough, for every
![]() $c\in (0,1)$
, there exists
$c\in (0,1)$
, there exists
![]() $n \in \mathbb {N}$
such that for every
$n \in \mathbb {N}$
such that for every
![]() $i=1,\dots ,d$
and
$i=1,\dots ,d$
and
![]() $v \in \bigwedge ^i E$
it holds that
$v \in \bigwedge ^i E$
it holds that
for every
![]() $\varepsilon>0$
. For every
$\varepsilon>0$
. For every
![]() $\varepsilon>0$
, let the function
$\varepsilon>0$
, let the function
![]() $\beta _{\varepsilon ,\infty }$
on
$\beta _{\varepsilon ,\infty }$
on
![]() $G/\Lambda $
be defined by
$G/\Lambda $
be defined by
where, writing
![]() $x=g\Lambda $
, the maximum is taken over all
$x=g\Lambda $
, the maximum is taken over all
![]() $0<i<d$
and nonzero
$0<i<d$
and nonzero
![]() $v\in \bigwedge ^i E$
such that
$v\in \bigwedge ^i E$
such that
![]() $v=v_1 \wedge \dots \wedge v_i$
with
$v=v_1 \wedge \dots \wedge v_i$
with
![]() for
for
![]() $j=1,\dots ,i$
(following [Reference Benoist and Quint8], such pure wedge products v will be called “x-integral monomials”).
$j=1,\dots ,i$
(following [Reference Benoist and Quint8], such pure wedge products v will be called “x-integral monomials”).
Note that by construction we have
![]() $\beta _{\varepsilon ,\infty }(x)=\infty $
if and only if there exists a nonzero H-fixed x-integral monomial
$\beta _{\varepsilon ,\infty }(x)=\infty $
if and only if there exists a nonzero H-fixed x-integral monomial
![]() $v\in \bigwedge ^i E$
whose norm is less than
$v\in \bigwedge ^i E$
whose norm is less than
![]() $\varepsilon ^{\delta _i}$
. Therefore, the set
$\varepsilon ^{\delta _i}$
. Therefore, the set
![]() $\beta _{\varepsilon ,\infty }^{-1}(\{\infty \})$
is H-invariant. Moreover, for every
$\beta _{\varepsilon ,\infty }^{-1}(\{\infty \})$
is H-invariant. Moreover, for every
![]() $\varepsilon>0$
, the function
$\varepsilon>0$
, the function
![]() $\beta _{\varepsilon ,\infty }$
is proper and lower semicontinuous (see [Reference Benoist and Quint8, Remark 5.2]). Setting
$\beta _{\varepsilon ,\infty }$
is proper and lower semicontinuous (see [Reference Benoist and Quint8, Remark 5.2]). Setting
![]() $\kappa '=\max _{\lambda \in \mathcal {S}}\delta _\lambda ^{-1}$
, it is also readily verified that for every
$\kappa '=\max _{\lambda \in \mathcal {S}}\delta _\lambda ^{-1}$
, it is also readily verified that for every
![]() $h \in H$
we have
$h \in H$
we have
![]() $\beta _{\varepsilon ,\infty }(hx) \le \operatorname {N}(h)^{d\kappa '}\beta _{\varepsilon ,\infty }(x)$
.
$\beta _{\varepsilon ,\infty }(hx) \le \operatorname {N}(h)^{d\kappa '}\beta _{\varepsilon ,\infty }(x)$
.
Now, it follows precisely in the same way as in [Reference Benoist and Quint8, Proposition 5.3], by simply replacing [Reference Benoist and Quint8, Lemma 4.3] by equation (6.8), that for every
![]() $\delta>0$
and
$\delta>0$
and
![]() $\varepsilon>0$
small enough, there exist
$\varepsilon>0$
small enough, there exist
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $a \in (0,1)$
and
$a \in (0,1)$
and
![]() $b>0$
such that
$b>0$
such that
For brevity and to avoid mere repetition, we will not reproduce this part of the proof here. We note however that this passage is the part where the crucial ‘Mother inequality’ [Reference Benoist and Quint8, §3] and the convexity assumptions (6.6) and (6.7) are used.
Finally, given a compact set Z as in the statement, by Mahler’s compactness criterion, we can choose
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\delta>0$
small enough so that the function
$\delta>0$
small enough so that the function
![]() is uniformly bounded on Z. By the discussion above, this function has all desired properties.
is uniformly bounded on Z. By the discussion above, this function has all desired properties.
Case 2: G is closed subgroup of
![]() $\operatorname {\mathrm {SL}}_d(\mathbb {R})$
and
$\operatorname {\mathrm {SL}}_d(\mathbb {R})$
and
![]() $\Lambda =G\cap \operatorname {\mathrm {SL}}_d(\mathbb {Z})$
. Then
$\Lambda =G\cap \operatorname {\mathrm {SL}}_d(\mathbb {Z})$
. Then
![]() $X=G/\Lambda $
is a closed subset of
$X=G/\Lambda $
is a closed subset of
![]() $X_0=\operatorname {\mathrm {SL}}_d(\mathbb {R})/\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
by [Reference Raghunathan80, Theorem 1.13]. Thus, we can use the height function from Case 1 above.
$X_0=\operatorname {\mathrm {SL}}_d(\mathbb {R})/\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
by [Reference Raghunathan80, Theorem 1.13]. Thus, we can use the height function from Case 1 above.
Case 3:
![]() $G=H$
is a connected real rank one simple Lie group. We assume
$G=H$
is a connected real rank one simple Lie group. We assume
![]() $X=G/\Lambda $
is noncompact. Let
$X=G/\Lambda $
is noncompact. Let
![]() $V=\bigwedge ^r \mathfrak g$
endowed with a norm
$V=\bigwedge ^r \mathfrak g$
endowed with a norm
![]() $ \left \lVert {\cdot } \right \rVert $
, where r is the dimension of the unipotent radical of a minimal parabolic subgroup of G. Let
$ \left \lVert {\cdot } \right \rVert $
, where r is the dimension of the unipotent radical of a minimal parabolic subgroup of G. Let
![]() $v_0\in V$
be a nonzero vector which corresponds to the Lie algebra of such a unipotent radical. It follows from [Reference Garland and Raghunathan43] (cf. [Reference Kleinbock and Weiss58, Proposition 3.1] and [Reference Benoist and Quint8, p. 54]) that there exist
$v_0\in V$
be a nonzero vector which corresponds to the Lie algebra of such a unipotent radical. It follows from [Reference Garland and Raghunathan43] (cf. [Reference Kleinbock and Weiss58, Proposition 3.1] and [Reference Benoist and Quint8, p. 54]) that there exist
![]() $g_1, \dots , g_r\in G$
such that for
$g_1, \dots , g_r\in G$
such that for
![]() $i=1,\dots ,r$
the vectors
$i=1,\dots ,r$
the vectors
![]() $v_i=g_i{\boldsymbol {\cdot }} v_0$
in V have the following properties:
$v_i=g_i{\boldsymbol {\cdot }} v_0$
in V have the following properties:
-
(a)
 $\Lambda v_i$
is closed and hence discrete in V for
$\Lambda v_i$
is closed and hence discrete in V for
 $1\le i\le r$
.
$1\le i\le r$
. -
(b) For any subset
 $F\subset G$
, the set
$F\subset G$
, the set
 $F\Lambda \subset G/\Lambda $
is relatively compact if and only if there exists
$F\Lambda \subset G/\Lambda $
is relatively compact if and only if there exists
 $a>0$
such that
$a>0$
such that
 $ \left \lVert {g\lambda {\boldsymbol {\cdot }} v_i} \right \rVert>a$
for any
$ \left \lVert {g\lambda {\boldsymbol {\cdot }} v_i} \right \rVert>a$
for any
 $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
,
 $g\in F$
and
$g\in F$
and
 $1\le i\le r$
.
$1\le i\le r$
. -
(c) There exists
 $a_0>0$
such that for any
$a_0>0$
such that for any
 $g\in G$
there exists at most one
$g\in G$
there exists at most one
 $v\in \bigcup _{1\le i \le r} \Lambda {\boldsymbol {\cdot }} v_i$
such that
$v\in \bigcup _{1\le i \le r} \Lambda {\boldsymbol {\cdot }} v_i$
such that
 $ \left \lVert {g{\boldsymbol {\cdot }} v} \right \rVert <a_0$
.
$ \left \lVert {g{\boldsymbol {\cdot }} v} \right \rVert <a_0$
.
Let
![]() $V' $
be the H-invariant subspace complementary to
$V' $
be the H-invariant subspace complementary to
![]() $V^H$
. In view of property (b), we know that
$V^H$
. In view of property (b), we know that
![]() $v_0\in V'$
. By Lemma 6.2, for every
$v_0\in V'$
. By Lemma 6.2, for every
![]() $\delta>0$
small enough, for every
$\delta>0$
small enough, for every
![]() $c>0$
, we have that for every
$c>0$
, we have that for every
![]() $n \in \mathbb {N}$
large enough
$n \in \mathbb {N}$
large enough
holds for all nonzero
![]() $v\in V'$
. Using properties (a)–(c) and (6.9) it is straightforward to check that
$v\in V'$
. Using properties (a)–(c) and (6.9) it is straightforward to check that
is continuous, proper and satisfies equation (6.1) when
![]() $\delta>0$
is small enough. It is also readily checked that
$\delta>0$
is small enough. It is also readily checked that
![]() $\beta _{\infty }(hx)\le \operatorname {N}(\operatorname {\mathrm {Ad}} h)^{\kappa '\delta }\beta _{\infty }(x)$
for some
$\beta _{\infty }(hx)\le \operatorname {N}(\operatorname {\mathrm {Ad}} h)^{\kappa '\delta }\beta _{\infty }(x)$
for some
![]() $\kappa '$
depending only on G.
$\kappa '$
depending only on G.
Case 4:
![]() $G=\operatorname {\mathrm {Aut}}(\mathfrak g)$
for
$G=\operatorname {\mathrm {Aut}}(\mathfrak g)$
for
![]() $\mathfrak g$
semisimple without compact ideals. In view of (4) at the begining of the proof, we may assume that G is connected. As G is of adjoint type, it is center-free. By [Reference Raghunathan80, Theorem 5.22], after replacing
$\mathfrak g$
semisimple without compact ideals. In view of (4) at the begining of the proof, we may assume that G is connected. As G is of adjoint type, it is center-free. By [Reference Raghunathan80, Theorem 5.22], after replacing
![]() $\Lambda $
by a finite index subgroup, there is a collection of semisimple factors
$\Lambda $
by a finite index subgroup, there is a collection of semisimple factors
![]() $G_i$
of G such that
$G_i$
of G such that
![]() $G=\prod _i G_i$
and
$G=\prod _i G_i$
and
![]() $\Lambda _i=G_i\cap \Lambda $
is an irreducible lattice in
$\Lambda _i=G_i\cap \Lambda $
is an irreducible lattice in
![]() $G_i$
. Then we have
$G_i$
. Then we have
![]() $G/\Lambda =\prod _i G_i/\Lambda _i$
. Thus, if we can construct functions with the desired properties on all spaces
$G/\Lambda =\prod _i G_i/\Lambda _i$
. Thus, if we can construct functions with the desired properties on all spaces
![]() $G_i/\Lambda _i$
, then their sum is a Lyapunov function on
$G_i/\Lambda _i$
, then their sum is a Lyapunov function on
![]() $X=G/\Lambda $
with the same properties (possibly with different constants). In other words, we have further reduced to the case where the lattice
$X=G/\Lambda $
with the same properties (possibly with different constants). In other words, we have further reduced to the case where the lattice
![]() $\Lambda $
in G is irreducible. We can also assume that
$\Lambda $
in G is irreducible. We can also assume that
![]() $\Lambda $
is nonuniform in view of (3) at the beginning of the proof.
$\Lambda $
is nonuniform in view of (3) at the beginning of the proof.
Case 3 handles the case of G with real rank one. Thus, we may additionally assume that the rank is at least two. Then Margulis’ arithmeticity theorem says that
![]() $\Lambda $
is arithmetic. In our setting, this implies that there is an isomorphism
$\Lambda $
is arithmetic. In our setting, this implies that there is an isomorphism
![]() $\sigma \colon G \to G'$
, where
$\sigma \colon G \to G'$
, where
![]() $G'$
is the connected component of a semisimple real algebraic subgroup of
$G'$
is the connected component of a semisimple real algebraic subgroup of
![]() $\operatorname {\mathrm {SL}}_{d'}(\mathbb {R})$
defined over
$\operatorname {\mathrm {SL}}_{d'}(\mathbb {R})$
defined over
![]() $\mathbb {Q}$
such that
$\mathbb {Q}$
such that
![]() $\sigma (\Lambda )$
and
$\sigma (\Lambda )$
and
![]() $\Lambda '=G'\cap \operatorname {\mathrm {SL}}_{d'}(\mathbb {Z})$
are commensurable (see [Reference Zimmer97, Corollary 6.1.10]). Then by Proposition 2.10(iii),
$\Lambda '=G'\cap \operatorname {\mathrm {SL}}_{d'}(\mathbb {Z})$
are commensurable (see [Reference Zimmer97, Corollary 6.1.10]). Then by Proposition 2.10(iii),
![]() $\sigma _*\mu $
is
$\sigma _*\mu $
is
![]() $\sigma (H)$
-expanding, and we conclude using Case 2 and the comment (2) on commensurability at the start of the proof.
$\sigma (H)$
-expanding, and we conclude using Case 2 and the comment (2) on commensurability at the start of the proof.
Case 5: General case. Let
![]() $\mathfrak r$
be the maximal amenable ideal of
$\mathfrak r$
be the maximal amenable ideal of
![]() $\mathfrak g$
, set
$\mathfrak g$
, set
![]() $\mathfrak s=\mathfrak g/\mathfrak r$
and
$\mathfrak s=\mathfrak g/\mathfrak r$
and
![]() $R=\ker (\operatorname {\mathrm {Ad}}_{\mathfrak s})$
. Then
$R=\ker (\operatorname {\mathrm {Ad}}_{\mathfrak s})$
. Then
![]() $\mathfrak s$
is the largest semisimple quotient of
$\mathfrak s$
is the largest semisimple quotient of
![]() $\mathfrak g$
without compact ideals and, by semisimplicity,
$\mathfrak g$
without compact ideals and, by semisimplicity,
![]() $G/R$
identifies with a finite index subgroup S of
$G/R$
identifies with a finite index subgroup S of
![]() $\operatorname {\mathrm {Aut}}(\mathfrak s)$
. From [Reference Benoist and Quint8, Lemma 6.1], we know that
$\operatorname {\mathrm {Aut}}(\mathfrak s)$
. From [Reference Benoist and Quint8, Lemma 6.1], we know that
![]() $\Lambda \cap R$
is a cocompact lattice in R and the image
$\Lambda \cap R$
is a cocompact lattice in R and the image
![]() $\Lambda _S=\operatorname {\mathrm {Ad}}_{\mathfrak s}(\Lambda )$
is a lattice in S. In particular, the projection
$\Lambda _S=\operatorname {\mathrm {Ad}}_{\mathfrak s}(\Lambda )$
is a lattice in S. In particular, the projection
![]() $G/\Lambda \to S/\Lambda _S$
is proper. Setting
$G/\Lambda \to S/\Lambda _S$
is proper. Setting
![]() $H_S=\operatorname {\mathrm {Ad}}_{\mathfrak s}(H)$
, we moreover have that
$H_S=\operatorname {\mathrm {Ad}}_{\mathfrak s}(H)$
, we moreover have that
![]() $(\operatorname {\mathrm {Ad}}_{\mathfrak s})_*\mu $
is
$(\operatorname {\mathrm {Ad}}_{\mathfrak s})_*\mu $
is
![]() $H_S$
-expanding by Proposition 2.10(iii). By Case 4 above, the theorem holds for
$H_S$
-expanding by Proposition 2.10(iii). By Case 4 above, the theorem holds for
![]() $S/\Lambda _S$
. Precomposing the obtained Lyapunov function with the projection
$S/\Lambda _S$
. Precomposing the obtained Lyapunov function with the projection
![]() $G/\Lambda \to S/\Lambda _S$
produces the desired function
$G/\Lambda \to S/\Lambda _S$
produces the desired function
![]() $\beta _{\infty }$
on X. Properties (i)–(iii) carry over from the subcases, using for the latter property that the norm in the adjoint representation controls the norms in any other representation after taking a suitable power.
$\beta _{\infty }$
on X. Properties (i)–(iii) carry over from the subcases, using for the latter property that the norm in the adjoint representation controls the norms in any other representation after taking a suitable power.
Before moving on, we make a simple remark that will be of use in the next part.
Remark 6.3. Notice that by considering a small power of
![]() $\beta _{\infty }$
, at the cost of increasing the constants
$\beta _{\infty }$
, at the cost of increasing the constants
![]() $a \in (0,1)$
and b, one can modify
$a \in (0,1)$
and b, one can modify
![]() $\kappa>0$
that satisfies property (iii) in Theorem 6.1. Indeed, given
$\kappa>0$
that satisfies property (iii) in Theorem 6.1. Indeed, given
![]() $\delta \in (0,\kappa )$
, using Jensen’s inequality, the function
$\delta \in (0,\kappa )$
, using Jensen’s inequality, the function
![]() $\beta _{\infty }^{\delta /\kappa }$
is seen to also satisfy the contraction condition (6.1) with the same
$\beta _{\infty }^{\delta /\kappa }$
is seen to also satisfy the contraction condition (6.1) with the same
![]() $m \in \mathbb {N}$
and possibly different constants
$m \in \mathbb {N}$
and possibly different constants
![]() $a \in (0,1)$
and
$a \in (0,1)$
and
![]() $b>0$
. Moreover,
$b>0$
. Moreover,
![]() $\beta _{\infty }^{\delta /\kappa }(hx) \le \operatorname {N}(\operatorname {\mathrm {Ad}} h)^\delta \beta _{\infty }^{\delta /\kappa }(x)$
.
$\beta _{\infty }^{\delta /\kappa }(hx) \le \operatorname {N}(\operatorname {\mathrm {Ad}} h)^\delta \beta _{\infty }^{\delta /\kappa }(x)$
.
6.2 Height function with respect to singular subspaces
In this section, we construct a height function with respect to a relatively compact subset of a lower-dimensional homogeneous subspace of
![]() $X=G/\Lambda $
. In contrast to the height function used in [Reference Benoist and Quint9], which satisfies a contraction property with respect to a first return Markov operator, our height function will satisfy a contraction property with respect to
$X=G/\Lambda $
. In contrast to the height function used in [Reference Benoist and Quint9], which satisfies a contraction property with respect to a first return Markov operator, our height function will satisfy a contraction property with respect to
![]() $A_{\mu }$
itself. Our construction is inspired by the work of Eskin–Mirzakhani–Mohammadi [Reference Eskin, Mirzakhani and Mohammadi34] on random walks on moduli space.
$A_{\mu }$
itself. Our construction is inspired by the work of Eskin–Mirzakhani–Mohammadi [Reference Eskin, Mirzakhani and Mohammadi34] on random walks on moduli space.
To state the main result of this subsection, we start by recalling some notation and fixing some data. Let G be a Lie group and
![]() $\Lambda < G$
a lattice. Let
$\Lambda < G$
a lattice. Let
![]() $H\leqslant G$
be a connected semisimple Lie subgroup with finite center and no compact factors. Let
$H\leqslant G$
be a connected semisimple Lie subgroup with finite center and no compact factors. Let
![]() $\mu $
be an H-expanding probability measure on H with finite exponential moments. Since
$\mu $
be an H-expanding probability measure on H with finite exponential moments. Since
![]() $\mu $
has finite exponential moments, we can fix
$\mu $
has finite exponential moments, we can fix
![]() $\delta _0\in (0,1)$
such that
$\delta _0\in (0,1)$
such that
![]() $\int _H \operatorname {N}(\operatorname {\mathrm {Ad}}(h))^{\delta _0}\mathop {}\!\mathrm {d}\mu (h)<\infty $
. Fix an arbitrary compact subset Z of
$\int _H \operatorname {N}(\operatorname {\mathrm {Ad}}(h))^{\delta _0}\mathop {}\!\mathrm {d}\mu (h)<\infty $
. Fix an arbitrary compact subset Z of
![]() $G/\Lambda $
, and let
$G/\Lambda $
, and let
![]() $\beta _{\infty }\colon G/\Lambda \to [1,\infty ]$
be the proper lower semicontinuous function given by Theorem 6.1. By passing to a small enough power, we will suppose that
$\beta _{\infty }\colon G/\Lambda \to [1,\infty ]$
be the proper lower semicontinuous function given by Theorem 6.1. By passing to a small enough power, we will suppose that
![]() $\beta _{\infty }$
satisfies
$\beta _{\infty }$
satisfies
![]() $\beta _{\infty }(hx) \le \operatorname {N}(\operatorname {\mathrm {Ad}}(h))^{\delta _0}\beta _{\infty }(x)$
for every
$\beta _{\infty }(hx) \le \operatorname {N}(\operatorname {\mathrm {Ad}}(h))^{\delta _0}\beta _{\infty }(x)$
for every
![]() $h \in H$
and
$h \in H$
and
![]() $x \in G/\Lambda $
(see Remark 6.3). Moreover, given
$x \in G/\Lambda $
(see Remark 6.3). Moreover, given
![]() $\varepsilon>0$
, we define
$\varepsilon>0$
, we define
Since
![]() $\beta _{\infty }$
is lower semicontinuous and proper,
$\beta _{\infty }$
is lower semicontinuous and proper,
![]() $X_\varepsilon $
is a compact subset of X. Here is the result we aim to prove.
$X_\varepsilon $
is a compact subset of X. Here is the result we aim to prove.
Theorem 6.4. Given
![]() $\varepsilon>0$
sufficiently small, for any sufficiently small open neighborhood O of the identity in
$\varepsilon>0$
sufficiently small, for any sufficiently small open neighborhood O of the identity in
![]() $C_G(\Gamma _{\mu })$
and for any
$C_G(\Gamma _{\mu })$
and for any
![]() $Y \in \mathcal {S}(\Gamma _{\mu })$
, there exists a height function
$Y \in \mathcal {S}(\Gamma _{\mu })$
, there exists a height function
![]() $\beta _{\mathcal N }\colon HX_\varepsilon \to [1, \infty ]$
together with constants
$\beta _{\mathcal N }\colon HX_\varepsilon \to [1, \infty ]$
together with constants
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $a_0 \in (0,1)$
and
$a_0 \in (0,1)$
and
![]() $b_0>0$
such that for any
$b_0>0$
such that for any
![]() $x\in HX_\varepsilon $
we have
$x\in HX_\varepsilon $
we have
and such that, denoting
![]() $\mathcal N=OY$
,
$\mathcal N=OY$
,
-
(i)
 $\beta _{\mathcal N }(x)=\infty $
if and only if
$\beta _{\mathcal N }(x)=\infty $
if and only if
 $x\in \mathcal N\cap HX_\varepsilon $
,
$x\in \mathcal N\cap HX_\varepsilon $
, -
(ii)
 $\beta _{\mathcal {N}}$
is bounded on compact subsets of
$\beta _{\mathcal {N}}$
is bounded on compact subsets of
 $X_\varepsilon \setminus \overline {O}Y$
,
$X_\varepsilon \setminus \overline {O}Y$
, -
(iii) for any
 $\ell \ge 1$
, the set
$\ell \ge 1$
, the set
 $\beta ^{-1}_{\mathcal N}([1, \ell ])$
is a compact subset of X.
$\beta ^{-1}_{\mathcal N}([1, \ell ])$
is a compact subset of X.
The rest of this subsection is devoted to the proof of this result, which will require two preliminary lemmas. We fix an inner product on
![]() $\mathfrak g$
, denote by
$\mathfrak g$
, denote by
![]() $ \left \lVert {\cdot } \right \rVert $
the associated operator norm on
$ \left \lVert {\cdot } \right \rVert $
the associated operator norm on
![]() $\operatorname {\mathrm {End}}(\mathfrak {g})$
, and to ease the notation, we set
$\operatorname {\mathrm {End}}(\mathfrak {g})$
, and to ease the notation, we set
where
![]() $\operatorname {\mathrm {Ad}}$
denotes the adjoint action of H on the Lie algebra
$\operatorname {\mathrm {Ad}}$
denotes the adjoint action of H on the Lie algebra
![]() $\mathfrak g$
of G.
$\mathfrak g$
of G.
Lemma 6.5. There exist constants
![]() $C\ge 1$
,
$C\ge 1$
,
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $\varepsilon _0>0$
such that for any
$\varepsilon _0>0$
such that for any
![]() $\varepsilon \in (0,\varepsilon _0)$
and any
$\varepsilon \in (0,\varepsilon _0)$
and any
![]() $x\in HX_\varepsilon $
there exists
$x\in HX_\varepsilon $
there exists
![]() $h \in \Gamma _{\mu }$
with
$h \in \Gamma _{\mu }$
with
![]() $\operatorname {N}_a(h) \le C \beta _{\infty }(x)^k$
such that
$\operatorname {N}_a(h) \le C \beta _{\infty }(x)^k$
such that
![]() $hx \in X_\varepsilon $
.
$hx \in X_\varepsilon $
.
Proof. Set
, and let a positive

be given, where
![]() $a \in (0,1)$
and
$a \in (0,1)$
and
![]() $b>0$
are the constants given by Theorem 6.1. Let
$b>0$
are the constants given by Theorem 6.1. Let
![]() $x\in HX_\varepsilon $
. Since
$x\in HX_\varepsilon $
. Since
![]() $\beta _{\infty }^{-1}(\{\infty \})$
is H-invariant, we have
$\beta _{\infty }^{-1}(\{\infty \})$
is H-invariant, we have
![]() $\beta _{\infty }(x)<\infty $
so that we may define
$\beta _{\infty }(x)<\infty $
so that we may define
![]() $n_x \ge 1$
to be the smallest integer such that
$n_x \ge 1$
to be the smallest integer such that
![]() $a^{n_x} \beta _{\infty }(x) \le 1$
. It follows that
$a^{n_x} \beta _{\infty }(x) \le 1$
. It follows that
where
![]() $m \in \mathbb {N}$
is as in Theorem 6.1.
$m \in \mathbb {N}$
is as in Theorem 6.1.
Now, decompose
![]() $\mu ^{*m n_x}$
as a sum of two nonnegative measures
$\mu ^{*m n_x}$
as a sum of two nonnegative measures
![]() $\mu _1+\mu _2$
, where
$\mu _1+\mu _2$
, where
![]() $\mu _2$
is the restriction of
$\mu _2$
is the restriction of
![]() $\mu ^{*mn_x}$
to the set
$\mu ^{*mn_x}$
to the set
![]() $\{\operatorname {N}_a(\cdot )\ge R_x\}$
for
$\{\operatorname {N}_a(\cdot )\ge R_x\}$
for
![]() $R_x= 2^{1/\delta _0}M^{m n_x/\delta _0}$
. By submultiplicativity of
$R_x= 2^{1/\delta _0}M^{m n_x/\delta _0}$
. By submultiplicativity of
![]() $N_a$
, we have
$N_a$
, we have
![]() $\int \operatorname {N}_a(h)^{\delta _0} \mathop {}\!\mathrm {d}\mu ^{*m n_x}(h) \le M^{m n_x}$
. Using this bound together with the Markov inequality, we deduce that
$\int \operatorname {N}_a(h)^{\delta _0} \mathop {}\!\mathrm {d}\mu ^{*m n_x}(h) \le M^{m n_x}$
. Using this bound together with the Markov inequality, we deduce that
![]() $\mu _2(H) \le \frac {1}{2}$
and hence
$\mu _2(H) \le \frac {1}{2}$
and hence
![]() $\mu _1(H) \ge \frac {1}{2} \ge \sqrt {\varepsilon }$
. On the other hand, we know
$\mu _1(H) \ge \frac {1}{2} \ge \sqrt {\varepsilon }$
. On the other hand, we know
Now, considering the probability measure
![]() $\hat {\mu }_1= \frac {1}{\mu _1(H)}\mu _1$
, we deduce
$\hat {\mu }_1= \frac {1}{\mu _1(H)}\mu _1$
, we deduce
![]() $A_{\hat {\mu }_1}\beta _{\infty }(x) \le \frac {1}{\varepsilon }$
. This means that there exists
$A_{\hat {\mu }_1}\beta _{\infty }(x) \le \frac {1}{\varepsilon }$
. This means that there exists
![]() $h\in \operatorname {\mathrm {supp}}(\hat {\mu }_1) \subset \Gamma _{\mu }$
such that
$h\in \operatorname {\mathrm {supp}}(\hat {\mu }_1) \subset \Gamma _{\mu }$
such that
![]() $\beta _{\infty }(hx) \le \frac {1}{\varepsilon }$
. Finally, since by construction
$\beta _{\infty }(hx) \le \frac {1}{\varepsilon }$
. Finally, since by construction
![]() $n_x \le 1+ \frac {\log \beta _{\infty }(x)}{-\log a}$
, we also obtain
$n_x \le 1+ \frac {\log \beta _{\infty }(x)}{-\log a}$
, we also obtain
This shows that the statement holds by setting
![]() $C=2^{1/\delta _0}M^{m/\delta _0}$
and
$C=2^{1/\delta _0}M^{m/\delta _0}$
and
![]() $k=m \lceil \frac {\log M}{-\delta _0 \log a} \rceil $
.
$k=m \lceil \frac {\log M}{-\delta _0 \log a} \rceil $
.
Let Y be a homogeneous space in
![]() $\mathcal {S}(\Gamma _{\mu })$
, and denote by N its stabilizer group. Recall that this means that
$\mathcal {S}(\Gamma _{\mu })$
, and denote by N its stabilizer group. Recall that this means that
![]() $N\geqslant \Gamma _{\mu }$
is a closed subgroup of G, Y is given by
$N\geqslant \Gamma _{\mu }$
is a closed subgroup of G, Y is given by
![]() $Nx$
for some
$Nx$
for some
![]() $x \in G/\Lambda $
, and there is an N-invariant probability measure on
$x \in G/\Lambda $
, and there is an N-invariant probability measure on
![]() $Nx$
which is invariant and ergodic with respect to
$Nx$
which is invariant and ergodic with respect to
![]() $\Gamma _{\mu }$
. By Theorem 1.1, the Lie algebra
$\Gamma _{\mu }$
. By Theorem 1.1, the Lie algebra
![]() $\mathfrak n$
of N is H-invariant with respect to the adjoint action. We write
$\mathfrak n$
of N is H-invariant with respect to the adjoint action. We write
![]() $\mathfrak g$
as a direct sum of
$\mathfrak g$
as a direct sum of
![]() $\operatorname {\mathrm {Ad}} (H)$
-invariant subspaces
$\operatorname {\mathrm {Ad}} (H)$
-invariant subspaces
where
![]() $\mathfrak l$
is the centralizer of
$\mathfrak l$
is the centralizer of
![]() $\mathfrak h$
and
$\mathfrak h$
and
![]() $\mathfrak v$
is a complementary H-invariant subspace of
$\mathfrak v$
is a complementary H-invariant subspace of
![]() $\mathfrak n+\mathfrak l$
. Recall that by the epimorphic property of
$\mathfrak n+\mathfrak l$
. Recall that by the epimorphic property of
![]() $\Gamma _{\mu }$
in H,
$\Gamma _{\mu }$
in H,
![]() $\mathfrak l$
is also the Lie algebra of
$\mathfrak l$
is also the Lie algebra of
![]() $C_G(\Gamma _{\mu })$
.
$C_G(\Gamma _{\mu })$
.
Lemma 6.6. With the notation of the previous paragraph, for every
![]() $Y \in \mathcal {S}(\Gamma _{\mu })$
and compact set
$Y \in \mathcal {S}(\Gamma _{\mu })$
and compact set
![]() $K\subset X=G/\Lambda $
, there exist an open neighborhood O of the identity in
$K\subset X=G/\Lambda $
, there exist an open neighborhood O of the identity in
![]() $C_G(\Gamma _{\mu })$
and
$C_G(\Gamma _{\mu })$
and
![]() $r \in (0,1)$
with the property that for any
$r \in (0,1)$
with the property that for any
![]() $x\in K$
, there is at most one
$x\in K$
, there is at most one
![]() $v\in \mathfrak v$
such that
$v\in \mathfrak v$
such that
Moreover, the set E of
![]() $x\in X$
for which
$x\in X$
for which
![]() $v\in \mathfrak v$
with equation (6.11) exists is open in X and the map
$v\in \mathfrak v$
with equation (6.11) exists is open in X and the map
![]() $E\cap K\to \mathfrak v,\,x\mapsto v$
is continuous.
$E\cap K\to \mathfrak v,\,x\mapsto v$
is continuous.
Proof. Let
![]() $K'$
be a compact neighborhood of K. In view of equation (6.10), we can choose O, r and a neighborhood U of the identity in G so that all of the following hold:
$K'$
be a compact neighborhood of K. In view of equation (6.10), we can choose O, r and a neighborhood U of the identity in G so that all of the following hold:
-
(a) we have
 $UK\subset K'$
,
$UK\subset K'$
, -
(b) the natural map
 $U \to Uy $
is injective for all
$U \to Uy $
is injective for all
 $y\in K'$
,
$y\in K'$
, -
(c) for every
 $y\in Y\cap K'$
we have
$y\in Y\cap K'$
we have
 $U y\cap Y= (U\cap N)y$
,
$U y\cap Y= (U\cap N)y$
, -
(d) the map
 $B_r(\mathfrak v)\times (U\cap ON)\to G,\,(v,g)\mapsto \exp (v)g$
is a diffeomorphism onto an open neighborhood of the identity in G, where
$B_r(\mathfrak v)\times (U\cap ON)\to G,\,(v,g)\mapsto \exp (v)g$
is a diffeomorphism onto an open neighborhood of the identity in G, where
 $B_r(\mathfrak v)$
denotes the open r-ball in
$B_r(\mathfrak v)$
denotes the open r-ball in
 $\mathfrak v$
and
$\mathfrak v$
and -
(e) we have
 $o_2^{-1}\exp (v_2) \exp (-v_1)o_1\in U$
for every
$o_2^{-1}\exp (v_2) \exp (-v_1)o_1\in U$
for every
 $v_1,v_2 \in \mathfrak {g}$
with
$v_1,v_2 \in \mathfrak {g}$
with
 $ \left \lVert {v_i} \right \rVert <r$
,
$ \left \lVert {v_i} \right \rVert <r$
,
 $i=1,2$
, and
$i=1,2$
, and
 $o_1,o_2\in O$
.
$o_1,o_2\in O$
.
Now, let
![]() $x\in K$
and
$x\in K$
and
![]() $v_1, v_2\in \mathfrak v$
satisfy equation (6.11), say
$v_1, v_2\in \mathfrak v$
satisfy equation (6.11), say
![]() $\exp (v_i)x= o_iy_i$
with
$\exp (v_i)x= o_iy_i$
with
![]() $o_i\in O$
and
$o_i\in O$
and
![]() $y_i \in Y$
for
$y_i \in Y$
for
![]() $i=1,2$
. Using properties (a) and (e), we know
$i=1,2$
. Using properties (a) and (e), we know
![]() $y_1\in K'$
. Moreover,
$y_1\in K'$
. Moreover,
![]() $y_2= o_2^{-1}\exp (v_2) \exp (-v_1) o_1y_1$
. Applying properties (b), (c) and (e), we deduce that
$y_2= o_2^{-1}\exp (v_2) \exp (-v_1) o_1y_1$
. Applying properties (b), (c) and (e), we deduce that
which means that
Using (e) once more, we see that
![]() $o_1,o_2n\in U\cap ON$
. Hence, property (d) implies that
$o_1,o_2n\in U\cap ON$
. Hence, property (d) implies that
![]() $v_1=v_2$
, giving uniqueness. Since
$v_1=v_2$
, giving uniqueness. Since
![]() $O\subset U$
, the final claims of the lemma also follows from (d).
$O\subset U$
, the final claims of the lemma also follows from (d).
Proof of Theorem 6.4
Since there is a substantial amount of relevant notation and auxiliary objects, let us start the proof by recalling the initial data. The probability measure
![]() $\mu $
on H is H-expanding with finite exponential moments, Z is a compact subset of
$\mu $
on H is H-expanding with finite exponential moments, Z is a compact subset of
![]() $X=G/\Lambda $
and
$X=G/\Lambda $
and
![]() $\beta _{\infty }\colon G/\Lambda \to [1, \infty ]$
is as given by Theorem 6.1. By the latter (and Remark 6.3), the function
$\beta _{\infty }\colon G/\Lambda \to [1, \infty ]$
is as given by Theorem 6.1. By the latter (and Remark 6.3), the function
![]() $\beta _{\infty }$
satisfies equation (6.1) with some
$\beta _{\infty }$
satisfies equation (6.1) with some
![]() $m \in \mathbb {N}$
,
$m \in \mathbb {N}$
,
![]() $a \in (0,1)$
and
$a \in (0,1)$
and
![]() $b>0$
and
$b>0$
and
![]() $\beta _{\infty }(hx) \le \operatorname {N}_a(h)^{\delta _0}\beta _{\infty }(x)$
for every
$\beta _{\infty }(hx) \le \operatorname {N}_a(h)^{\delta _0}\beta _{\infty }(x)$
for every
![]() $x \in G/\Lambda $
and
$x \in G/\Lambda $
and
![]() $h \in H$
, where
$h \in H$
, where
![]() $\delta _0\in (0,1)$
is chosen so that
$\delta _0\in (0,1)$
is chosen so that
![]() $\int _H \operatorname {N}_a(h)^{\delta _0} \mathop {}\!\mathrm {d}\mu (h)<\infty $
. Let
$\int _H \operatorname {N}_a(h)^{\delta _0} \mathop {}\!\mathrm {d}\mu (h)<\infty $
. Let
![]() $\varepsilon _0>0$
,
$\varepsilon _0>0$
,
![]() $k \in \mathbb {N}$
and
$k \in \mathbb {N}$
and
![]() $C\ge 1$
be given by Lemma 6.5, and fix
$C\ge 1$
be given by Lemma 6.5, and fix
![]() $\varepsilon \in (0,\varepsilon _0)$
. Let O be a relatively compact open neighborhood of the identity in
$\varepsilon \in (0,\varepsilon _0)$
. Let O be a relatively compact open neighborhood of the identity in
![]() $C_G(\Gamma _{\mu })$
and
$C_G(\Gamma _{\mu })$
and
![]() $r \in (0,1)$
such that the conclusion of Lemma 6.6 holds with a compact neighborhood K of
$r \in (0,1)$
such that the conclusion of Lemma 6.6 holds with a compact neighborhood K of
![]() $X_\varepsilon =\{x\in X\mid \beta _{\infty }(x)\le \varepsilon ^{-1}\}$
. Let
$X_\varepsilon =\{x\in X\mid \beta _{\infty }(x)\le \varepsilon ^{-1}\}$
. Let
![]() $Y \in \mathcal {S}(\Gamma _{\mu })$
, denote by N its stabilizer group, by
$Y \in \mathcal {S}(\Gamma _{\mu })$
, denote by N its stabilizer group, by
![]() $\mathfrak n$
its Lie algebra, and set
$\mathfrak n$
its Lie algebra, and set
![]() $\mathcal N=OY$
. Finally, let
$\mathcal N=OY$
. Finally, let
![]() $\mathfrak l$
be the Lie algebra of
$\mathfrak l$
be the Lie algebra of
![]() $C_G(\Gamma _{\mu })$
and choose an
$C_G(\Gamma _{\mu })$
and choose an
![]() $\operatorname {\mathrm {Ad}}(H)$
-invariant complementary space
$\operatorname {\mathrm {Ad}}(H)$
-invariant complementary space
![]() $\mathfrak v$
so that equation (6.10) holds.
$\mathfrak v$
so that equation (6.10) holds.
Since
![]() $\mu $
is H-expanding with finite exponential moments and
$\mu $
is H-expanding with finite exponential moments and
![]() $\mathfrak v$
has no nonzero H-fixed vectors, by Lemma 6.2 there exists
$\mathfrak v$
has no nonzero H-fixed vectors, by Lemma 6.2 there exists
such that for every
![]() $a'\in (0,1)$
we have, for all
$a'\in (0,1)$
we have, for all
![]() $n \in \mathbb {N}$
large enough,
$n \in \mathbb {N}$
large enough,
for any nonzero
![]() $v\in \mathfrak v$
. We fix such
$v\in \mathfrak v$
. We fix such
![]() $n \in \mathbb {N}$
that is a positive multiple of
$n \in \mathbb {N}$
that is a positive multiple of
![]() $m \in \mathbb {N}$
. Without loss of generality, we assume
$m \in \mathbb {N}$
. Without loss of generality, we assume
![]() $a'>a$
and let
$a'>a$
and let
![]() $\varepsilon '>0$
be such that
$\varepsilon '>0$
be such that
![]() $a'=(1+\varepsilon ')a$
. Since
$a'=(1+\varepsilon ')a$
. Since
![]() $m | n$
, (6.1) implies that
$m | n$
, (6.1) implies that
For
![]() $x\in HX_\varepsilon $
, we define
$x\in HX_\varepsilon $
, we define
Next, we claim that for every
![]() $x \in HX_\varepsilon $
, there exists at most one
$x \in HX_\varepsilon $
, there exists at most one
![]() $v\in \mathfrak v$
such that
$v\in \mathfrak v$
such that
Indeed, by Lemma 6.5, there exists
![]() $h\in \Gamma _{\mu }$
with
$h\in \Gamma _{\mu }$
with
![]() $\operatorname {N}_a(h)\le C\beta _{\infty }(x)^k$
such that
$\operatorname {N}_a(h)\le C\beta _{\infty }(x)^k$
such that
![]() $h x\in X_\varepsilon $
. Since
$h x\in X_\varepsilon $
. Since
![]() $\mathcal N$
is
$\mathcal N$
is
![]() $\Gamma _{\mu }$
-invariant, we have
$\Gamma _{\mu }$
-invariant, we have
Since
![]() $ \left \lVert {\operatorname {\mathrm {Ad}}(h)v} \right \rVert \le \operatorname {N}_a(h) \left \lVert {v} \right \rVert \le r$
, if such an
$ \left \lVert {\operatorname {\mathrm {Ad}}(h)v} \right \rVert \le \operatorname {N}_a(h) \left \lVert {v} \right \rVert \le r$
, if such an
![]() $v \in \mathfrak v$
exists, it is unique thanks to Lemma 6.6 (applied to
$v \in \mathfrak v$
exists, it is unique thanks to Lemma 6.6 (applied to
![]() $hx \in X_\varepsilon $
) and the choice of
$hx \in X_\varepsilon $
) and the choice of
![]() $r>0$
, where we are using that
$r>0$
, where we are using that
![]() $\mathfrak v$
is H-invariant.
$\mathfrak v$
is H-invariant.
Using the claim above, we may define
![]() $\alpha \colon HX_\varepsilon \to [1, \infty ]$
by
$\alpha \colon HX_\varepsilon \to [1, \infty ]$
by
 $$ \begin{align*} \alpha(x)=\begin{cases} \left\lVert {v} \right\rVert ^{-\theta}, & \text{if there exists } v\in \mathfrak v \text{ satisfying (6.5),} \\ \hfill r_x^{-\theta}, & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \alpha(x)=\begin{cases} \left\lVert {v} \right\rVert ^{-\theta}, & \text{if there exists } v\in \mathfrak v \text{ satisfying (6.5),} \\ \hfill r_x^{-\theta}, & \text{otherwise.} \end{cases} \end{align*} $$
Using the corresponding property for
![]() $\beta _{\infty }$
and the choice of
$\beta _{\infty }$
and the choice of
![]() $\theta $
in (6.12), it is readily checked that for every
$\theta $
in (6.12), it is readily checked that for every
![]() $x \in HX_\varepsilon $
and
$x \in HX_\varepsilon $
and
![]() $h \in \Gamma _{\mu }$
, we have
$h \in \Gamma _{\mu }$
, we have
![]() $\alpha (hx) \le \operatorname {N}_a(h)^{\delta _0} \alpha (x)$
. We shall show that
$\alpha (hx) \le \operatorname {N}_a(h)^{\delta _0} \alpha (x)$
. We shall show that
satisfies all requirements of the theorem.
To proceed, we start by decomposing
![]() $\mu ^{*n}$
as a sum
$\mu ^{*n}$
as a sum
![]() $\mu _1 + \mu _2$
of two nonnegative measures with
$\mu _1 + \mu _2$
of two nonnegative measures with
![]() $\mu _1$
of compact support and
$\mu _1$
of compact support and
![]() $\mu _2$
satisfying
$\mu _2$
satisfying
It follows that
Denote by D the constant
![]() $r^{-1}C M^k$
, where
$r^{-1}C M^k$
, where
![]() $M=\sup \{\operatorname {N}_a(h) \mid h \in \operatorname {\mathrm {supp}}(\mu _1) \}$
. Then
$M=\sup \{\operatorname {N}_a(h) \mid h \in \operatorname {\mathrm {supp}}(\mu _1) \}$
. Then
![]() $D>M^k\ge 1$
by choice of r, and for any element
$D>M^k\ge 1$
by choice of r, and for any element
![]() we have
we have
We are now going to establish the contraction property for
![]() $\beta _{\mathcal N}$
by distinguishing several cases based upon the size of
$\beta _{\mathcal N}$
by distinguishing several cases based upon the size of
![]() $\alpha (x)$
.
$\alpha (x)$
.
If
![]() $\alpha (x)>D^2 r_x ^{-\theta }$
, then there exists a uniquely determined
$\alpha (x)>D^2 r_x ^{-\theta }$
, then there exists a uniquely determined
![]() $v\in \mathfrak v$
so that equation (6.15) holds and
$v\in \mathfrak v$
so that equation (6.15) holds and
![]() $\alpha (x)= \left \lVert {v} \right \rVert ^{-\theta }$
. In particular,
$\alpha (x)= \left \lVert {v} \right \rVert ^{-\theta }$
. In particular,
Together with equation (6.17), the previous inequality implies that for
![]() $h \in S_{\pm }$
, we have
$h \in S_{\pm }$
, we have
Since
![]() $\exp (v) x$
belongs to the
$\exp (v) x$
belongs to the
![]() $\Gamma _{\mu }$
-invariant set
$\Gamma _{\mu }$
-invariant set
![]() $\mathcal N$
, we have
$\mathcal N$
, we have
![]() $\exp (\operatorname {\mathrm {Ad}} (h)v)hx \in \mathcal N $
. In view of equation (6.18) and the definition of
$\exp (\operatorname {\mathrm {Ad}} (h)v)hx \in \mathcal N $
. In view of equation (6.18) and the definition of
![]() $\alpha $
it follows that
$\alpha $
it follows that
![]() $\alpha (hx)= \left \lVert {\operatorname {\mathrm {Ad}}(h)v} \right \rVert ^{-\theta }$
. By equation (6.13),
$\alpha (hx)= \left \lVert {\operatorname {\mathrm {Ad}}(h)v} \right \rVert ^{-\theta }$
. By equation (6.13),
Combining with equation (6.16), we get
Together with equation (6.14), the previous inequality yields
Therefore, we proved the contraction property of
![]() $\beta _{\mathcal {N}}$
for
$\beta _{\mathcal {N}}$
for
![]() $x \in HX_\varepsilon $
satisfying
$x \in HX_\varepsilon $
satisfying
![]() $\alpha (x)> D^2r_x^{-\theta }$
.
$\alpha (x)> D^2r_x^{-\theta }$
.
Now, let
![]() $x \in HX_\varepsilon $
be such that
$x \in HX_\varepsilon $
be such that
![]() $\alpha (x) \le D^2r_x^{-\theta }$
. In this case, we have
$\alpha (x) \le D^2r_x^{-\theta }$
. In this case, we have
We claim that for any
![]() $h\in S_{\pm }$
, we have
$h\in S_{\pm }$
, we have
If not, then using equation (6.17) and the fact that
![]() $\alpha (hx) \le M\alpha (x)\le D \alpha (x)$
, we find
$\alpha (hx) \le M\alpha (x)\le D \alpha (x)$
, we find
which contradicts the first inequality in equation (6.19) since
![]() $\theta \in (0,1)$
and
$\theta \in (0,1)$
and
![]() $D>1$
. By equations (6.20) and (6.17)
$D>1$
. By equations (6.20) and (6.17)
Since
![]() $k\theta <1$
, if
$k\theta <1$
, if
![]() $\beta _{\infty }(x)$
is larger than some constant depending only on
$\beta _{\infty }(x)$
is larger than some constant depending only on
![]() $\varepsilon 'a,k\theta $
and D, we will have
$\varepsilon 'a,k\theta $
and D, we will have
In view of equation (6.19), we know that
![]() $\beta _{\infty }(x)$
is sufficiently large provided that
$\beta _{\infty }(x)$
is sufficiently large provided that
![]() $\alpha (x)$
is (depending on D). Therefore, there exists
$\alpha (x)$
is (depending on D). Therefore, there exists
![]() $b'>0$
(depending on
$b'>0$
(depending on
![]() $\varepsilon 'a, k \theta , D$
) so that if
$\varepsilon 'a, k \theta , D$
) so that if
then for any
![]() $h\in S_{\pm }$
$h\in S_{\pm }$
So in the case where (6.21) holds, combining equations (6.14), (6.16) and (6.22), we deduce
proving the required contraction property.
To treat the remaining case, suppose now that
![]() $x\in H X_\varepsilon $
and
$x\in H X_\varepsilon $
and
![]() $\alpha (x)\le \min \{b', D^2 r_x^{-\theta }\}$
. We claim that
$\alpha (x)\le \min \{b', D^2 r_x^{-\theta }\}$
. We claim that
![]() $\alpha (hx)\le D^3 b'$
for all
$\alpha (hx)\le D^3 b'$
for all
![]() $h\in S_{\pm }$
. Supposing the contrary, we would have
$h\in S_{\pm }$
. Supposing the contrary, we would have
From this, using the inequality
![]() $\alpha (hx)\le D \alpha (x)$
, it follows that
$\alpha (hx)\le D \alpha (x)$
, it follows that
a contradiction. Therefore, recalling equations (6.14) and (6.16), we obtain
 $$ \begin{align*} \int_H \beta_{\mathcal N}(h x)\mathop{}\!\mathrm{d} \mu^{*n}(h)&= \int_H \alpha(h x)\mathop{}\!\mathrm{d} \mu^{*n}(h)+ \int_H \beta_{\infty}(h x)\mathop{}\!\mathrm{d} \mu^{*n}(h) \\ &\le D^3b'+\frac{1-a'}{2}\alpha(x) +a\beta_{\infty} (x)+\frac{b}{1-a}\\ & \le \frac{1+a'}{2} \beta_{\mathcal N} (x)+D^3b'+\frac{b}{1-a}. \end{align*} $$
$$ \begin{align*} \int_H \beta_{\mathcal N}(h x)\mathop{}\!\mathrm{d} \mu^{*n}(h)&= \int_H \alpha(h x)\mathop{}\!\mathrm{d} \mu^{*n}(h)+ \int_H \beta_{\infty}(h x)\mathop{}\!\mathrm{d} \mu^{*n}(h) \\ &\le D^3b'+\frac{1-a'}{2}\alpha(x) +a\beta_{\infty} (x)+\frac{b}{1-a}\\ & \le \frac{1+a'}{2} \beta_{\mathcal N} (x)+D^3b'+\frac{b}{1-a}. \end{align*} $$
We have thus concluded the proof of the contraction property with
![]() $a_0=(1+a')/2$
and the additive constant
$a_0=(1+a')/2$
and the additive constant
![]() $b_0=D^3b'+b/(1-a)$
.
$b_0=D^3b'+b/(1-a)$
.
It remains to prove the claims (i)–(iii). Since
![]() $\beta _{\infty }$
is finite on
$\beta _{\infty }$
is finite on
![]() $HX_\varepsilon $
, (i) is directly seen to hold by definition of
$HX_\varepsilon $
, (i) is directly seen to hold by definition of
![]() $\beta _{\mathcal N}$
. Property (ii) is also immediate from the definition of
$\beta _{\mathcal N}$
. Property (ii) is also immediate from the definition of
![]() $\beta _{\mathcal {N}}$
, since
$\beta _{\mathcal {N}}$
, since
![]() $\beta _{\infty }$
is bounded on
$\beta _{\infty }$
is bounded on
![]() $X_\varepsilon $
and any compact subset not intersecting
$X_\varepsilon $
and any compact subset not intersecting
![]() $\overline {O}Y$
has positive distance to
$\overline {O}Y$
has positive distance to
![]() $\mathcal {N}$
. To prove (iii), let
$\mathcal {N}$
. To prove (iii), let
![]() $(x_j)_j$
be a sequence in
$(x_j)_j$
be a sequence in
![]() $HX_\varepsilon $
with
$HX_\varepsilon $
with
![]() $\beta _{\mathcal N }(x_j)\le \ell $
for all
$\beta _{\mathcal N }(x_j)\le \ell $
for all
![]() $j\in \mathbb {N}$
for some
$j\in \mathbb {N}$
for some
![]() $\ell \in \mathbb {R}$
. Since
$\ell \in \mathbb {R}$
. Since
![]() $\beta _{\mathcal {N}}=\beta _{\infty } + \alpha $
with
$\beta _{\mathcal {N}}=\beta _{\infty } + \alpha $
with
![]() $\alpha \ge 0$
, we also have
$\alpha \ge 0$
, we also have
![]() $\beta _{\infty }(x_j)\le \ell $
for all j. Since
$\beta _{\infty }(x_j)\le \ell $
for all j. Since
![]() $\beta _{\infty }$
is proper, we may suppose that
$\beta _{\infty }$
is proper, we may suppose that
![]() $\lim _{j \to \infty } x_j=x$
for some point
$\lim _{j \to \infty } x_j=x$
for some point
![]() $x\in X$
. We need to prove that
$x\in X$
. We need to prove that
![]() $x\in HX_\varepsilon $
and
$x\in HX_\varepsilon $
and
![]() $\beta _{\mathcal N}(x)\le \ell $
.
$\beta _{\mathcal N}(x)\le \ell $
.
We first show that
![]() $x\in HX_\varepsilon $
. It follows from Lemma 6.5 that there is a compact subset
$x\in HX_\varepsilon $
. It follows from Lemma 6.5 that there is a compact subset
![]() $K_\ell $
of
$K_\ell $
of
![]() $\Gamma _{\mu }$
such that for any
$\Gamma _{\mu }$
such that for any
![]() $j\in \mathbb {N}$
, there exists
$j\in \mathbb {N}$
, there exists
![]() $h_j\in K_\ell $
so that
$h_j\in K_\ell $
so that
![]() $h_j x_j\in X_\varepsilon $
. Since
$h_j x_j\in X_\varepsilon $
. Since
![]() $ X_\varepsilon $
is compact, by possibly passing to a subsequence, we may assume that
$ X_\varepsilon $
is compact, by possibly passing to a subsequence, we may assume that
![]() $h_j x_j$
converges to some
$h_j x_j$
converges to some
![]() $y\in X_\varepsilon $
and
$y\in X_\varepsilon $
and
![]() $h_j$
converges to some
$h_j$
converges to some
![]() $h\in \Gamma _{\mu }$
. So we have
$h\in \Gamma _{\mu }$
. So we have
which implies
![]() $x=h^{-1}y\in HX_\varepsilon $
.
$x=h^{-1}y\in HX_\varepsilon $
.
Finally, we show that
which will complete the proof in view of the lower semicontinuity of
![]() $\beta _{\infty }$
and the definition of
$\beta _{\infty }$
and the definition of
![]() $\beta _{\mathcal N}$
. First, let us pass to a subsequence so that the liminf in equation (6.23) is a limit, say
$\beta _{\mathcal N}$
. First, let us pass to a subsequence so that the liminf in equation (6.23) is a limit, say
![]() . If
. If
![]() $\alpha (x)=r_x^{-\theta }$
, then equation (6.23) follows from the definition of
$\alpha (x)=r_x^{-\theta }$
, then equation (6.23) follows from the definition of
![]() $r_x$
and lower semicontinuity of
$r_x$
and lower semicontinuity of
![]() $\beta _{\infty }$
. Suppose therefore that
$\beta _{\infty }$
. Suppose therefore that
![]() $\alpha (x)>r_x^{-\theta }$
. This implies that there exists a unique
$\alpha (x)>r_x^{-\theta }$
. This implies that there exists a unique
![]() $v \in \mathfrak v$
such that
$v \in \mathfrak v$
such that
![]() $\exp (v)x \in \mathcal {N}$
and
$\exp (v)x \in \mathcal {N}$
and
![]() $ \left \lVert {v} \right \rVert <r_x$
. Using Lemma 6.5, choose
$ \left \lVert {v} \right \rVert <r_x$
. Using Lemma 6.5, choose
![]() $h\in \Gamma _{\mu }$
with
$h\in \Gamma _{\mu }$
with
![]() $\operatorname {N}_a(h)\le C\beta _{\infty }(x)^k$
such that
$\operatorname {N}_a(h)\le C\beta _{\infty }(x)^k$
such that
![]() $hx\in X_\varepsilon $
. Then
$hx\in X_\varepsilon $
. Then
![]() $ \left \lVert {\operatorname {\mathrm {Ad}}(h)v} \right \rVert <r$
and
$ \left \lVert {\operatorname {\mathrm {Ad}}(h)v} \right \rVert <r$
and
![]() $\exp (\operatorname {\mathrm {Ad}}(h)v)hx\in \mathcal N$
. Now, since the points
$\exp (\operatorname {\mathrm {Ad}}(h)v)hx\in \mathcal N$
. Now, since the points
![]() $hx_j$
converge to
$hx_j$
converge to
![]() $hx$
, for large j they lie in the neighborhood K of
$hx$
, for large j they lie in the neighborhood K of
![]() $X_\varepsilon $
to which we applied Lemma 6.6. Thus, the last claim in this lemma imply that there exist
$X_\varepsilon $
to which we applied Lemma 6.6. Thus, the last claim in this lemma imply that there exist
![]() $v_j\in \mathfrak v$
with
$v_j\in \mathfrak v$
with
![]() $v_j\to v$
such that
$v_j\to v$
such that
![]() $\exp (v_j)x_j\in \mathcal N$
. Note that since the values
$\exp (v_j)x_j\in \mathcal N$
. Note that since the values
![]() $r_{x_j}^{-\theta }$
are contained in
$r_{x_j}^{-\theta }$
are contained in
![]() $[0,\ell ]$
, up to passing to a further subsequence, we may suppose that they converge to
$[0,\ell ]$
, up to passing to a further subsequence, we may suppose that they converge to
![]() $\alpha _2$
. Clearly,
$\alpha _2$
. Clearly,
![]() $\alpha _1 \ge \alpha _2$
. If
$\alpha _1 \ge \alpha _2$
. If
![]() $\alpha _1>\alpha _2$
, then for large j we have
$\alpha _1>\alpha _2$
, then for large j we have
![]() $\alpha (x_j)\ge \left \lVert {v_j} \right \rVert ^{-\theta }$
and it follows that equation (6.23) holds since
$\alpha (x_j)\ge \left \lVert {v_j} \right \rVert ^{-\theta }$
and it follows that equation (6.23) holds since
![]() $ \left \lVert {v_j} \right \rVert ^{-\theta }\to \left \lVert {v} \right \rVert ^{-\theta }=\alpha (x)$
. On the other hand, in case
$ \left \lVert {v_j} \right \rVert ^{-\theta }\to \left \lVert {v} \right \rVert ^{-\theta }=\alpha (x)$
. On the other hand, in case
![]() $\alpha _1=\alpha _2$
we know that for every
$\alpha _1=\alpha _2$
we know that for every
![]() $\epsilon>0$
, for
$\epsilon>0$
, for
![]() $j \in \mathbb {N}$
large enough, we have
$j \in \mathbb {N}$
large enough, we have
![]() $ \left \lVert {v_j} \right \rVert +\epsilon>r_{x_j}$
. But since
$ \left \lVert {v_j} \right \rVert +\epsilon>r_{x_j}$
. But since
![]() $v_j \to v$
and
$v_j \to v$
and
![]() $\epsilon>0$
is arbitrary, this implies that
$\epsilon>0$
is arbitrary, this implies that
![]() $\alpha (x)= \left \lVert {v} \right \rVert ^{-\theta }\le \lim _{j \to \infty } r_{x_j}^{-\theta }=\alpha _2=\alpha _1$
, as desired.
$\alpha (x)= \left \lVert {v} \right \rVert ^{-\theta }\le \lim _{j \to \infty } r_{x_j}^{-\theta }=\alpha _2=\alpha _1$
, as desired.
7 Recurrence, equidistribution, topology of homogeneous measures
Using the ingredients from §§4–6, we can now give the proofs of our results on recurrence, orbit closures, equidistribution and topology of
![]() $\mathcal {S}(\Gamma _{\mu })$
. The following lemma is used to extract the necessary information from the height functions constructed in the previous section.
$\mathcal {S}(\Gamma _{\mu })$
. The following lemma is used to extract the necessary information from the height functions constructed in the previous section.
Lemma 7.1. Let H be a locally compact
![]() $\sigma $
-compact metrizable group and X a locally compact
$\sigma $
-compact metrizable group and X a locally compact
![]() $\sigma $
-compact metrizable space endowed with a continuous H-action. Let
$\sigma $
-compact metrizable space endowed with a continuous H-action. Let
![]() $\mu $
be a Borel probability measure on H and
$\mu $
be a Borel probability measure on H and
![]() $\beta \colon X\to [1,\infty ]$
be a lower semicontinuous function such that there exist
$\beta \colon X\to [1,\infty ]$
be a lower semicontinuous function such that there exist
![]() $m\in \mathbb {N}$
,
$m\in \mathbb {N}$
,
![]() $a \in (0,1)$
and
$a \in (0,1)$
and
![]() $b>0$
such that
$b>0$
such that
for all
![]() $x\in X$
. Suppose that for every
$x\in X$
. Suppose that for every
![]() $\varepsilon>0$
the set
$\varepsilon>0$
the set
![]() $X_\varepsilon =\beta ^{-1}([0,\varepsilon ^{-1}])$
is compact and that the set
$X_\varepsilon =\beta ^{-1}([0,\varepsilon ^{-1}])$
is compact and that the set
![]() $X_{\infty }=\beta ^{-1}(\{\infty \})$
is
$X_{\infty }=\beta ^{-1}(\{\infty \})$
is
![]() $\Gamma _{\mu }$
-invariant. Then the following holds:
$\Gamma _{\mu }$
-invariant. Then the following holds:
-
(i) For any
 $\delta>0$
, there exists a compact subset
$\delta>0$
, there exists a compact subset
 $R_\delta \subset X\setminus X_{\infty }$
such that for any
$R_\delta \subset X\setminus X_{\infty }$
such that for any
 $x\in X$
with
$x\in X$
with
 $\beta (x)<\infty $
there exists
$\beta (x)<\infty $
there exists
 $n_x\in \mathbb {N}$
with
$n_x\in \mathbb {N}$
with
 $n_x=O(\log \beta (x))$
such that for every
$n_x=O(\log \beta (x))$
such that for every $$ \begin{align*} \mu^{*n}* \delta _x (R_\delta)\ge 1-\delta \end{align*} $$
$$ \begin{align*} \mu^{*n}* \delta _x (R_\delta)\ge 1-\delta \end{align*} $$
 $n\ge n_x$
.
$n\ge n_x$
.
-
(ii) For every
 $x\in X$
with
$x\in X$
with
 $\beta (x)<\infty $
, for
$\beta (x)<\infty $
, for
 $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
 $(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
, every weak* limit
$(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
, every weak* limit
 $\nu $
of the sequence
$\nu $
of the sequence
 $(\frac {1}{n}\sum _{k=0}^{n-1}\delta _{g_k\dotsm g_1x})_n$
of empirical measures satisfies
$(\frac {1}{n}\sum _{k=0}^{n-1}\delta _{g_k\dotsm g_1x})_n$
of empirical measures satisfies
 $\nu (X\setminus X_{\infty })=1$
.
$\nu (X\setminus X_{\infty })=1$
.
The techniques going into the first part of the lemma are by now standard. The second part is basically [Reference Benoist and Quint10, Proposition 3.9]. Related ideas also appear in Markov chain theory (see, e.g., [Reference Meyn and Tweedie68, Theorem 18.5.2] and the references given there). We include a brief proof for convenience.
Proof. Let
![]() $x\in X$
be such that
$x\in X$
be such that
![]() $\beta (x)<\infty $
. Iterating equation (7.1), we find for every
$\beta (x)<\infty $
. Iterating equation (7.1), we find for every
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $n\in \mathbb {N}$
$n\in \mathbb {N}$
For the proof of (i), given
![]() $\delta>0$
, we set
$\delta>0$
, we set
![]() $\varepsilon =\frac {\delta (1-a)}{2b+2}$
. Then the above estimate implies that for every
$\varepsilon =\frac {\delta (1-a)}{2b+2}$
. Then the above estimate implies that for every
![]() , we have
, we have
![]() $\mu ^{*mn}*\delta _x(X_\varepsilon )\ge 1-\delta /2$
. Moreover, we may choose a compact subset
$\mu ^{*mn}*\delta _x(X_\varepsilon )\ge 1-\delta /2$
. Moreover, we may choose a compact subset
![]() $F \subset \Gamma _{\mu }$
such that
$F \subset \Gamma _{\mu }$
such that
![]() $\mu ^{*l} (F)\ge 1-\delta /2$
for all
$\mu ^{*l} (F)\ge 1-\delta /2$
for all
![]() $0\le l<m$
. Now, setting
$0\le l<m$
. Now, setting
![]() $R_\delta $
to be the compact set
$R_\delta $
to be the compact set
![]() $FX_\varepsilon $
which, since
$FX_\varepsilon $
which, since
![]() $X \setminus X_{\infty }$
is
$X \setminus X_{\infty }$
is
![]() $\Gamma _{\mu }$
-invariant, is contained in
$\Gamma _{\mu }$
-invariant, is contained in
![]() $X\setminus X_{\infty }$
, we find
$X\setminus X_{\infty }$
, we find
for all
![]() .
.
For (ii), we appeal to [Reference Benoist and Quint10, Proposition 3.9], which implies that for
![]() $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
, for every
$(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
, for every
![]() $\delta>0$
there exists a compact subset
$\delta>0$
there exists a compact subset
![]() $K\subset X\setminus X_{\infty }$
such that
$K\subset X\setminus X_{\infty }$
such that
Moreover, by the law of large numbers, by choosing a large enough compact set
![]() $F\subset \Gamma _{\mu }$
we can ensure that for
$F\subset \Gamma _{\mu }$
we can ensure that for
![]() $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
$(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
Combining the above, it follows that for the compact subset
![]() $R=FK\subset X\setminus X_{\infty }$
we have
$R=FK\subset X\setminus X_{\infty }$
we have
for
![]() $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
, and we conclude using a version of the Portmanteau lemma.
$(g_i)_i\in \Gamma _{\mu }^{\mathbb {N}}$
, and we conclude using a version of the Portmanteau lemma.
7.1 Recurrence
We first prove our results about recurrence properties of H-expanding random walks.
Proof of Theorem 1.4
Let Z be a compact subset of
![]() $X\setminus \mathcal {N}$
, where we recall that
$X\setminus \mathcal {N}$
, where we recall that
![]() $\mathcal {N}=K_LY$
for a compact subset
$\mathcal {N}=K_LY$
for a compact subset
![]() $K_L$
of
$K_L$
of
![]() $L=C_G(\Gamma _{\mu })$
, and let
$L=C_G(\Gamma _{\mu })$
, and let
![]() $\beta _{\infty }$
be a height function coming from Theorem 6.1 such that
$\beta _{\infty }$
be a height function coming from Theorem 6.1 such that
![]() $\beta _{\infty }$
is bounded on Z, say
$\beta _{\infty }$
is bounded on Z, say
![]() $Z\subset X_\varepsilon =\{x\in X\mid \beta _{\infty }(x)\le \varepsilon ^{-1}\}$
for some
$Z\subset X_\varepsilon =\{x\in X\mid \beta _{\infty }(x)\le \varepsilon ^{-1}\}$
for some
![]() $\varepsilon>0$
. If
$\varepsilon>0$
. If
![]() $Y=\emptyset $
, we set
$Y=\emptyset $
, we set
![]() $\beta =\beta _{\infty }$
. Otherwise, we apply Theorem 6.4 to
$\beta =\beta _{\infty }$
. Otherwise, we apply Theorem 6.4 to
![]() $Y_l=lY$
for finitely many points
$Y_l=lY$
for finitely many points
![]() $l\in L$
such that the associated neighborhoods
$l\in L$
such that the associated neighborhoods
![]() $O_l$
of the identity in L coming out of the theorem satisfy
$O_l$
of the identity in L coming out of the theorem satisfy
![]() $\overline {O_l}lY\cap Z=\emptyset $
and
$\overline {O_l}lY\cap Z=\emptyset $
and
![]() $K_L\subset \bigcup _lO_ll$
. The associated height functions
$K_L\subset \bigcup _lO_ll$
. The associated height functions
![]() $\beta _l$
(extended to all of X by the value
$\beta _l$
(extended to all of X by the value
![]() $\infty $
on the complement of
$\infty $
on the complement of
![]() $HX_\varepsilon $
) take the value
$HX_\varepsilon $
) take the value
![]() $\infty $
on
$\infty $
on
![]() $O_llY$
and are bounded on Z. We set
$O_llY$
and are bounded on Z. We set
![]() $\beta =\sum _l\beta _l$
, which is a lower semicontinuous function on X with compact sublevel sets by virtue of Theorem 6.4(iii).
$\beta =\sum _l\beta _l$
, which is a lower semicontinuous function on X with compact sublevel sets by virtue of Theorem 6.4(iii).
In both cases, we now apply Lemma 7.1(i) to the height function
![]() $\beta $
. The set
$\beta $
. The set
![]() $R_\delta $
coming out of the lemma is a compact subset of
$R_\delta $
coming out of the lemma is a compact subset of
![]() $X\setminus \mathcal {N}$
such that for every
$X\setminus \mathcal {N}$
such that for every
![]() $x\in X$
with
$x\in X$
with
![]() $\beta (x)<\infty $
, for
$\beta (x)<\infty $
, for
![]() $n\ge n_x$
with
$n\ge n_x$
with
![]() $n_x=O(\log \beta (x))$
, we have
$n_x=O(\log \beta (x))$
, we have
![]() $\mu ^{*n}*\delta _x(R_\delta )\ge 1-\delta $
. Since
$\mu ^{*n}*\delta _x(R_\delta )\ge 1-\delta $
. Since
![]() $\beta $
is bounded on Z by construction, this estimate holds for all
$\beta $
is bounded on Z by construction, this estimate holds for all
![]() $n\ge n_0$
for all
$n\ge n_0$
for all
![]() $x\in Z$
. If F is a compact subset of
$x\in Z$
. If F is a compact subset of
![]() $\Gamma _{\mu }$
such that
$\Gamma _{\mu }$
such that
![]() $\mu ^{*n}(F)\ge 1-\delta $
for all
$\mu ^{*n}(F)\ge 1-\delta $
for all
![]() $0\le n<n_0$
, it follows that
$0\le n<n_0$
, it follows that
![]() $\mu ^{*n}*\delta _x(M_{Z,\delta })\ge 1-\delta $
for all
$\mu ^{*n}*\delta _x(M_{Z,\delta })\ge 1-\delta $
for all
![]() $n\ge 0$
and all
$n\ge 0$
and all
![]() $x\in Z$
for the compact subset
$x\in Z$
for the compact subset
![]() of
of
![]() $X\setminus \mathcal {N}$
, where we used for the last containment that
$X\setminus \mathcal {N}$
, where we used for the last containment that
![]() $\beta ^{-1}(\{\infty \})$
is
$\beta ^{-1}(\{\infty \})$
is
![]() $\Gamma _{\mu }$
-invariant.
$\Gamma _{\mu }$
-invariant.
Remark 7.2. For
![]() $Y=\emptyset $
, the recurrence property in Theorem 1.4 is referred to as (R1) in [Reference Benoist and Quint8, Reference Eskin and Margulis31]. In the case of a random walk given by a G-expanding probability measure on the quotient of G by an irreducible lattice, a slightly stronger, ‘uniform’ recurrence property (referred to as (R2)) can be established by using some results of [Reference Eskin and Margulis31].
$Y=\emptyset $
, the recurrence property in Theorem 1.4 is referred to as (R1) in [Reference Benoist and Quint8, Reference Eskin and Margulis31]. In the case of a random walk given by a G-expanding probability measure on the quotient of G by an irreducible lattice, a slightly stronger, ‘uniform’ recurrence property (referred to as (R2)) can be established by using some results of [Reference Eskin and Margulis31].
7.2 Orbit closures and equidistribution
The proof of Theorem 1.6 is similar to the proofs of the main results in [Reference Benoist and Quint10].
Proof of Theorem 1.6
Provided
![]() $Y_x$
contains x, part (i) is an immediate consequence of (ii). Moreover, taking a compactly supported and continuous test function, it is not hard to see that (ii) follows from (iii) by dominated convergence.
$Y_x$
contains x, part (i) is an immediate consequence of (ii). Moreover, taking a compactly supported and continuous test function, it is not hard to see that (ii) follows from (iii) by dominated convergence.
Let us thus prove (iii) with the additional property that
![]() $x\in Y_x$
. For
$x\in Y_x$
. For
![]() $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in H^{\mathbb {N}}$
, every weak* limit
$(g_i)_i\in H^{\mathbb {N}}$
, every weak* limit
![]() $\nu $
of the sequence
$\nu $
of the sequence
![]() $(\frac {1}{n}\sum _{k=0}^{n-1}\delta _{g_k\dotsm g_1x})_n$
of empirical measures is
$(\frac {1}{n}\sum _{k=0}^{n-1}\delta _{g_k\dotsm g_1x})_n$
of empirical measures is
![]() $\mu $
-stationary by the Breiman law of large numbers (see [Reference Benoist and Quint10, Corollary 3.3]). By Theorem 6.1 and Lemma 7.1(ii), for
$\mu $
-stationary by the Breiman law of large numbers (see [Reference Benoist and Quint10, Corollary 3.3]). By Theorem 6.1 and Lemma 7.1(ii), for
![]() $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
![]() $(g_i)_i\in H^{\mathbb {N}}$
every such weak* limit is a probability measure on X. We restrict to a full measure set of
$(g_i)_i\in H^{\mathbb {N}}$
every such weak* limit is a probability measure on X. We restrict to a full measure set of
![]() $(g_i)_i$
where both these conclusions hold and let
$(g_i)_i$
where both these conclusions hold and let
![]() $\nu $
be a weak* limit of the sequence of empirical measures.
$\nu $
be a weak* limit of the sequence of empirical measures.
Let
![]() $Y_0$
be a
$Y_0$
be a
![]() $\Gamma _{\mu }$
-invariant homogeneous subspace of X containing x of minimal dimension. By Theorem 1.1, every ergodic component of
$\Gamma _{\mu }$
-invariant homogeneous subspace of X containing x of minimal dimension. By Theorem 1.1, every ergodic component of
![]() $\nu $
is the homogeneous probability measure associated to an element of
$\nu $
is the homogeneous probability measure associated to an element of
Let
![]() $Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
be such that Y is not open in
$Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
be such that Y is not open in
![]() $Y_0$
. Then by minimality of
$Y_0$
. Then by minimality of
![]() $\dim (Y_0)$
, we know that
$\dim (Y_0)$
, we know that
![]() $x\notin lY$
for any
$x\notin lY$
for any
.
Let Z be an arbitrary compact subset of X, take a height function
![]() $\beta _{\infty }$
as in Theorem 6.1, and recall that
$\beta _{\infty }$
as in Theorem 6.1, and recall that
![]() $X_\varepsilon =\beta _{\infty }^{-1}([1,\varepsilon ^{-1}])$
. By Theorem 6.4, for sufficiently small
$X_\varepsilon =\beta _{\infty }^{-1}([1,\varepsilon ^{-1}])$
. By Theorem 6.4, for sufficiently small
![]() $\varepsilon>0$
, there is an open neighborhood O of the identity in L and a height function
$\varepsilon>0$
, there is an open neighborhood O of the identity in L and a height function
![]() $\beta _{\mathcal {N}}\colon HX_\varepsilon \to [1,\infty ]$
satisfying the contraction property (7.1) and such that
$\beta _{\mathcal {N}}\colon HX_\varepsilon \to [1,\infty ]$
satisfying the contraction property (7.1) and such that
-
○ for
 $x\in HX_\varepsilon $
,
$x\in HX_\varepsilon $
,
 $\beta _{\mathcal N}(x)=\infty $
if and only if
$\beta _{\mathcal N}(x)=\infty $
if and only if
 $x\in OY$
,
$x\in OY$
, -
○ for every
 $\ell \ge 1$
,
$\ell \ge 1$
,
 $\beta _{\mathcal N}^{-1}([1,\ell ])$
is a compact subset of X.
$\beta _{\mathcal N}^{-1}([1,\ell ])$
is a compact subset of X.
We extend
![]() $\beta _{\mathcal N}$
to all of X with the value
$\beta _{\mathcal N}$
to all of X with the value
![]() $\infty $
outside of
$\infty $
outside of
![]() $HX_\varepsilon $
. Then the extension satisfies the assumptions of Lemma 7.1. Write
$HX_\varepsilon $
. Then the extension satisfies the assumptions of Lemma 7.1. Write
![]() $X_{\infty ,\mathcal N}$
for the set
$X_{\infty ,\mathcal N}$
for the set
![]() $\beta _{\mathcal N}^{-1}(\{\infty \})$
so that
$\beta _{\mathcal N}^{-1}(\{\infty \})$
so that
![]() $HX_\varepsilon \cap OY\subset X_{\infty ,\mathcal N}$
. After further restricting to a full measure set of
$HX_\varepsilon \cap OY\subset X_{\infty ,\mathcal N}$
. After further restricting to a full measure set of
![]() $(g_i)_i$
so that Lemma 7.1(ii) holds, we thus find
$(g_i)_i$
so that Lemma 7.1(ii) holds, we thus find
![]() $\nu (HX_\varepsilon \cap OY)=0$
. When
$\nu (HX_\varepsilon \cap OY)=0$
. When
![]() $\varepsilon $
is small enough, this implies
$\varepsilon $
is small enough, this implies
![]() $\nu (Z\cap OY)=0$
. We repeat this process for the homogeneous subspaces
$\nu (Z\cap OY)=0$
. We repeat this process for the homogeneous subspaces
![]() $lY$
for countably many
$lY$
for countably many
![]() $l\in L$
such that the translations
$l\in L$
such that the translations
![]() $Ol$
of the associated neighborhoods O cover L. This gives
$Ol$
of the associated neighborhoods O cover L. This gives
![]() $\nu (Z\cap LY)=0$
. Repeating again for countably many compact subsets Z covering X, it follows that
$\nu (Z\cap LY)=0$
. Repeating again for countably many compact subsets Z covering X, it follows that
![]() $\nu (LY)=0$
.
$\nu (LY)=0$
.
Hence, in view of the countability statement in Proposition 5.1, we deduce that
![]() $\nu (LY)=0$
holds for every
$\nu (LY)=0$
holds for every
![]() $Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
that is not open in
$Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
that is not open in
![]() $Y_0$
(to be precise, after once more restricting to a countable intersection of full measure sets of
$Y_0$
(to be precise, after once more restricting to a countable intersection of full measure sets of
![]() $(g_i)_i\in H^{\mathbb {N}}$
, once for each Y in a countable set of representatives in equation (5.1)). It follows that each ergodic component of
$(g_i)_i\in H^{\mathbb {N}}$
, once for each Y in a countable set of representatives in equation (5.1)). It follows that each ergodic component of
![]() $\nu $
must be a homogeneous measure of some
$\nu $
must be a homogeneous measure of some
![]() $Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
that is open in
$Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
that is open in
![]() $Y_0$
. By [Reference Benoist and Quint10, Lemma 2.9], these Y are pairwise disjoint so that there are only countably many of them. This means that for some
$Y_0$
. By [Reference Benoist and Quint10, Lemma 2.9], these Y are pairwise disjoint so that there are only countably many of them. This means that for some
![]() $Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
open in
$Y\in \mathcal {S}(\Gamma _{\mu },Y_0)$
open in
![]() $Y_0$
we must have
$Y_0$
we must have
![]() $\nu (Y)>0$
. Then necessarily
$\nu (Y)>0$
. Then necessarily
![]() $x\in Y$
. By construction of
$x\in Y$
. By construction of
![]() $\nu $
and
$\nu $
and
![]() $\Gamma _{\mu }$
-invariance of Y it follows that
$\Gamma _{\mu }$
-invariance of Y it follows that
![]() $\nu (Y')=0$
for any
$\nu (Y')=0$
for any
![]() $Y'\in \mathcal {S}(\Gamma _{\mu },Y_0)$
distinct from Y. Hence, all ergodic components of
$Y'\in \mathcal {S}(\Gamma _{\mu },Y_0)$
distinct from Y. Hence, all ergodic components of
![]() $\nu $
are in fact equal to the homogeneous probability measure on Y, which finishes the proof of (iii).
$\nu $
are in fact equal to the homogeneous probability measure on Y, which finishes the proof of (iii).
Remark 7.3 (Nonaveraged convergence in law)
It is a natural question, already posed by Benoist–Quint at the end of their survey [Reference Benoist and Quint7], whether, or under what conditions, the Cesàro average in Theorem 1.6(ii) can be removed. Unfortunately, in the generality of our results, this question of convergence of
![]() $\mu ^{*n}*\delta _x$
towards
$\mu ^{*n}*\delta _x$
towards
![]() $\nu _x$
seems to be out of reach with current methods. Answers are available only in certain special cases where additional structure can be exploited. For example, in the setting of toral automorphisms, the harmonic analytic approach used by Bourgain–Furman–Lindenstrauss–Mozes [Reference Bourgain, Furman, Lindenstrauss and Mozes19] allows them to obtain the convergence of
$\nu _x$
seems to be out of reach with current methods. Answers are available only in certain special cases where additional structure can be exploited. For example, in the setting of toral automorphisms, the harmonic analytic approach used by Bourgain–Furman–Lindenstrauss–Mozes [Reference Bourgain, Furman, Lindenstrauss and Mozes19] allows them to obtain the convergence of
![]() $\mu ^{*n}*\delta _x$
together with a speed depending on Diophantine properties of the starting point x. Their approach was recently refined and generalized to some nilmanifolds in the works [Reference He and de Saxcé45, Reference He, Lakrec and Lindenstrauss46, Reference He, Lakrec, Lindenstrauss, Avila, Rassias and Sinai47] of He–de Saxcé and He–Lakrec–Lindenstrauss. Outside the realm of nilmanifolds, quantitative results on the convergence of
$\mu ^{*n}*\delta _x$
together with a speed depending on Diophantine properties of the starting point x. Their approach was recently refined and generalized to some nilmanifolds in the works [Reference He and de Saxcé45, Reference He, Lakrec and Lindenstrauss46, Reference He, Lakrec, Lindenstrauss, Avila, Rassias and Sinai47] of He–de Saxcé and He–Lakrec–Lindenstrauss. Outside the realm of nilmanifolds, quantitative results on the convergence of
![]() $\mu ^{*n}*\delta _x$
include the work of Buenger [Reference Buenger21, §3] and Khalil–Luethi [Reference Khalil and Luethi53], who consider some classes of measures supported on compact-by-solvable groups, and work of the first-named author [Reference Prohaska78] on spread-out measures.
$\mu ^{*n}*\delta _x$
include the work of Buenger [Reference Buenger21, §3] and Khalil–Luethi [Reference Khalil and Luethi53], who consider some classes of measures supported on compact-by-solvable groups, and work of the first-named author [Reference Prohaska78] on spread-out measures.
Very recently, it was observed by Bénard [Reference Bénard4] that the nonaveraged convergence can be ensured with some additional hypotheses using an old result of Foguel.
7.3 Topology of homogeneous measures
Here, we prove the Mozes–Shah type results regarding the weak* topology on the set of ergodic homogeneous subspaces of X.
Let
![]() $G,H,\Lambda ,X,\mu ,\Gamma _{\mu }$
be as in Theorem 1.6, and recall that
$G,H,\Lambda ,X,\mu ,\Gamma _{\mu }$
be as in Theorem 1.6, and recall that
![]() $\mathcal {S}(\Gamma _{\mu })$
denotes the set of all
$\mathcal {S}(\Gamma _{\mu })$
denotes the set of all
![]() $\Gamma _{\mu }$
-invariant
$\Gamma _{\mu }$
-invariant
![]() $\Gamma _{\mu }$
-ergodic homogeneous subspaces Y of X. Each element Y of
$\Gamma _{\mu }$
-ergodic homogeneous subspaces Y of X. Each element Y of
![]() $\mathcal {S}(\Gamma _{\mu })$
carries an associated
$\mathcal {S}(\Gamma _{\mu })$
carries an associated
![]() $\Gamma _{\mu }$
-invariant and ergodic homogeneous probability measure
$\Gamma _{\mu }$
-invariant and ergodic homogeneous probability measure
![]() $\nu _Y$
. Using this, we embed
$\nu _Y$
. Using this, we embed
![]() $\mathcal {S}(\Gamma _{\mu })$
into the space
$\mathcal {S}(\Gamma _{\mu })$
into the space
![]() $\mathcal {P}(X)$
of Borel probability measures on X and endow
$\mathcal {P}(X)$
of Borel probability measures on X and endow
![]() $\mathcal {S}(\Gamma _{\mu })$
with the weak* topology induced from
$\mathcal {S}(\Gamma _{\mu })$
with the weak* topology induced from
![]() $\mathcal {P}(X)$
. Also, recall that for a subset
$\mathcal {P}(X)$
. Also, recall that for a subset
![]() $Z \subset X$
, we let
$Z \subset X$
, we let
![]() $\mathcal {S}_Z(\Gamma )=\{Y \in \mathcal {S}(\Gamma ) \mid Y \cap Z \neq \emptyset \}$
.
$\mathcal {S}_Z(\Gamma )=\{Y \in \mathcal {S}(\Gamma ) \mid Y \cap Z \neq \emptyset \}$
.
The following lemma will be useful for the proof of Proposition 1.8. In the statement, given
![]() $Y\in \mathcal {S}(\Gamma _{\mu })$
, we shall say that a point
$Y\in \mathcal {S}(\Gamma _{\mu })$
, we shall say that a point
![]() $y\in Y$
is Y-generic if the conclusion of Theorem 1.6(ii) holds, that is, if
$y\in Y$
is Y-generic if the conclusion of Theorem 1.6(ii) holds, that is, if
![]() $\lim _{n\to \infty }\frac 1n\sum _{k=0}^{n-1}\mu ^{*k}*\delta _y=\nu _Y$
in the weak* topology. Note that
$\lim _{n\to \infty }\frac 1n\sum _{k=0}^{n-1}\mu ^{*k}*\delta _y=\nu _Y$
in the weak* topology. Note that
![]() $\nu _Y$
-a.e. point is Y-generic by the Chacon–Ornstein ergodic theorem.
$\nu _Y$
-a.e. point is Y-generic by the Chacon–Ornstein ergodic theorem.
Lemma 7.4. Let
![]() $(\nu _j)_j$
be a sequence of ergodic homogeneous measures associated to subspaces
$(\nu _j)_j$
be a sequence of ergodic homogeneous measures associated to subspaces
![]() $Y_j\in \mathcal {S}(\Gamma _{\mu })$
converging to a finite measure
$Y_j\in \mathcal {S}(\Gamma _{\mu })$
converging to a finite measure
![]() $\nu $
on X in the weak* topology. Let
$\nu $
on X in the weak* topology. Let
![]() $\beta $
be a height function on X satisfying the assumptions of Lemma 7.1, and denote
$\beta $
be a height function on X satisfying the assumptions of Lemma 7.1, and denote
![]() $X_{\infty }=\beta ^{-1}(\{\infty \})$
. Suppose that there is a sequence of
$X_{\infty }=\beta ^{-1}(\{\infty \})$
. Suppose that there is a sequence of
![]() $Y_j$
-generic points
$Y_j$
-generic points
![]() $y_j\in Y_j$
such that
$y_j\in Y_j$
such that
![]() $y_j\notin X_{\infty }$
for infinitely many j. Then
$y_j\notin X_{\infty }$
for infinitely many j. Then
![]() $\nu (X\setminus X_{\infty })=1$
.
$\nu (X\setminus X_{\infty })=1$
.
Proof. We may assume
![]() $y_j\notin X_{\infty }$
for all j. Let
$y_j\notin X_{\infty }$
for all j. Let
![]() $\delta>0$
. By Lemma 7.1(i), there exists a compact subset
$\delta>0$
. By Lemma 7.1(i), there exists a compact subset
![]() $R_\delta \subset X\setminus X_{\infty }$
such that
$R_\delta \subset X\setminus X_{\infty }$
such that
![]() $\mu ^{*n}*\delta _{y_j}(R_\delta )\ge 1-\delta $
for all
$\mu ^{*n}*\delta _{y_j}(R_\delta )\ge 1-\delta $
for all
![]() $n\ge n_{y_j}$
. Passing to the limit in the
$n\ge n_{y_j}$
. Passing to the limit in the
![]() $Y_j$
-genericity, this implies
$Y_j$
-genericity, this implies
![]() $\nu _j(R_\delta )\ge 1-\delta $
. Letting
$\nu _j(R_\delta )\ge 1-\delta $
. Letting
![]() $j\to \infty $
, it follows that also
$j\to \infty $
, it follows that also
![]() $\nu (R_\delta )\ge 1-\delta $
. The conclusion follows, since
$\nu (R_\delta )\ge 1-\delta $
. The conclusion follows, since
![]() $R_\delta \subset X\setminus X_{\infty }$
and
$R_\delta \subset X\setminus X_{\infty }$
and
![]() $\delta>0$
was arbitrary.
$\delta>0$
was arbitrary.
Proof of Proposition 1.8
Let us first prove (ii). Let
![]() $(\nu _j)_j$
be a sequence of ergodic homogeneous probability measures associated to subspaces
$(\nu _j)_j$
be a sequence of ergodic homogeneous probability measures associated to subspaces
![]() $Y_j$
in
$Y_j$
in
![]() $\mathcal {S}(\Gamma _{\mu })$
converging to the homogeneous measure
$\mathcal {S}(\Gamma _{\mu })$
converging to the homogeneous measure
![]() $\nu _{\infty }$
associated to
$\nu _{\infty }$
associated to
![]() $Y_{\infty }\in \mathcal {S}(\Gamma _{\mu })$
. Take a sequence of
$Y_{\infty }\in \mathcal {S}(\Gamma _{\mu })$
. Take a sequence of
![]() $Y_j$
-generic points
$Y_j$
-generic points
![]() $y_j\in Y_j$
such that
$y_j\in Y_j$
such that
![]() $Z=\overline {\{y_1,y_2,\dots \}}$
is compact. Let
$Z=\overline {\{y_1,y_2,\dots \}}$
is compact. Let
![]() $\beta _{\infty }$
be a height function from Theorem 6.1 that is finite on Z, say with
$\beta _{\infty }$
be a height function from Theorem 6.1 that is finite on Z, say with
![]() $Z\subset X_\varepsilon $
for some
$Z\subset X_\varepsilon $
for some
![]() $\varepsilon>0$
sufficiently small. Let O be a small neighborhood of the identity in
$\varepsilon>0$
sufficiently small. Let O be a small neighborhood of the identity in
![]() $L=C_G(\Gamma _{\mu })$
and
$L=C_G(\Gamma _{\mu })$
and
![]() $\beta _{\mathcal {N}}$
a height function from Theorem 6.4 taking the value
$\beta _{\mathcal {N}}$
a height function from Theorem 6.4 taking the value
![]() $\infty $
on
$\infty $
on
![]() $HX_\varepsilon \cap OY_{\infty }$
. Extending
$HX_\varepsilon \cap OY_{\infty }$
. Extending
![]() $\beta _{\mathcal {N}}$
from
$\beta _{\mathcal {N}}$
from
![]() $HX_\varepsilon $
to X using the value
$HX_\varepsilon $
to X using the value
![]() $\infty $
, we are in the setting of Lemma 7.4 and know
$\infty $
, we are in the setting of Lemma 7.4 and know
![]() $\nu _{\infty }(X_{\infty ,\mathcal {N}})=1$
, where
$\nu _{\infty }(X_{\infty ,\mathcal {N}})=1$
, where
![]() $X_{\infty ,\mathcal {N}}=\beta _{\mathcal {N}}^{-1}(\{\infty \})$
. Thus, the lemma implies
$X_{\infty ,\mathcal {N}}=\beta _{\mathcal {N}}^{-1}(\{\infty \})$
. Thus, the lemma implies
![]() $\beta _{\mathcal {N}}(y_j)=\infty $
for all large j, which means that
$\beta _{\mathcal {N}}(y_j)=\infty $
for all large j, which means that
![]() $y_j\in OY_{\infty }$
since
$y_j\in OY_{\infty }$
since
![]() $y_j\in Z\subset X_\varepsilon $
. Since O can be chosen arbitrarily small, (ii) is proved.
$y_j\in Z\subset X_\varepsilon $
. Since O can be chosen arbitrarily small, (ii) is proved.
Now, let us establish (i). Note that (ii) implies that for
![]() $Z\subset X$
compact,
$Z\subset X$
compact,
![]() $\mathcal {S}_Z(\Gamma _{\mu })$
is closed in
$\mathcal {S}_Z(\Gamma _{\mu })$
is closed in
![]() $\mathcal {S}(\Gamma _{\mu })$
. So we only have to exhibit a limit point in
$\mathcal {S}(\Gamma _{\mu })$
. So we only have to exhibit a limit point in
![]() $\mathcal {S}(\Gamma _{\mu })$
of a given sequence
$\mathcal {S}(\Gamma _{\mu })$
of a given sequence
![]() $(Y_j)_j$
in
$(Y_j)_j$
in
![]() $\mathcal {S}_Z(\Gamma _{\mu })$
. Thus, we may replace Z by a compact neighborhood and assume that the homogeneous measures
$\mathcal {S}_Z(\Gamma _{\mu })$
. Thus, we may replace Z by a compact neighborhood and assume that the homogeneous measures
![]() $\nu _j$
associated to the
$\nu _j$
associated to the
![]() $Y_j$
all satisfy
$Y_j$
all satisfy
![]() $\nu _j(Z)>0$
. Then we can find
$\nu _j(Z)>0$
. Then we can find
![]() $Y_j$
-generic points
$Y_j$
-generic points
![]() $y_j\in Z$
. Letting
$y_j\in Z$
. Letting
![]() $\beta _{\infty }$
be a height function from Theorem 6.1 that is finite on Z, say again with
$\beta _{\infty }$
be a height function from Theorem 6.1 that is finite on Z, say again with
![]() $Z\subset X_\varepsilon $
, Lemma 7.4 thus implies that any limit point
$Z\subset X_\varepsilon $
, Lemma 7.4 thus implies that any limit point
![]() $\nu $
of
$\nu $
of
![]() $(\nu _j)_j$
is a probability measure on X. Let us pass to a subsequence, and assume that
$(\nu _j)_j$
is a probability measure on X. Let us pass to a subsequence, and assume that
![]() $\nu _j\to \nu $
. Then
$\nu _j\to \nu $
. Then
![]() $\nu $
is a
$\nu $
is a
![]() $\Gamma _{\mu }$
-invariant probability measure on X. By Proposition 5.1, there exists
$\Gamma _{\mu }$
-invariant probability measure on X. By Proposition 5.1, there exists
![]() $Y\in \mathcal {S}(\Gamma _{\mu })$
and a relatively compact neighborhood O of the identity in L such that
$Y\in \mathcal {S}(\Gamma _{\mu })$
and a relatively compact neighborhood O of the identity in L such that
![]() $\nu (OY)>0$
. We suppose that the dimension of Y is minimal so that the latter holds. As in the first part of the proof, using a height function
$\nu (OY)>0$
. We suppose that the dimension of Y is minimal so that the latter holds. As in the first part of the proof, using a height function
![]() $\beta _{\mathcal {N}}$
and Lemma 7.4, this implies that
$\beta _{\mathcal {N}}$
and Lemma 7.4, this implies that
![]() $y_j\in OY$
for all large j. After passing to a subsequence, we have that
$y_j\in OY$
for all large j. After passing to a subsequence, we have that
![]() $Y_j\subset l_jY_{\infty }$
for some
$Y_j\subset l_jY_{\infty }$
for some
![]() $l_j\in C_G(\Gamma _{\mu })$
converging to the identity and
$l_j\in C_G(\Gamma _{\mu })$
converging to the identity and
![]() $Y_{\infty }=lY$
for some
$Y_{\infty }=lY$
for some
![]() $l\in C_G(\Gamma _{\mu })$
. Then all ergodic components of the limit measure
$l\in C_G(\Gamma _{\mu })$
. Then all ergodic components of the limit measure
![]() $\nu $
are homogeneous probability measures associated to some ergodic homogeneous subspace
$\nu $
are homogeneous probability measures associated to some ergodic homogeneous subspace
![]() $Y'\subset Y_{\infty }$
. If subspaces
$Y'\subset Y_{\infty }$
. If subspaces
![]() $Y'\subsetneq Y_{\infty }$
were to feature in the ergodic decomposition with positive weight, then another application of Proposition 5.1 would imply that
$Y'\subsetneq Y_{\infty }$
were to feature in the ergodic decomposition with positive weight, then another application of Proposition 5.1 would imply that
![]() $\nu (LY')>0$
for some
$\nu (LY')>0$
for some
![]() $Y'\in \mathcal {S}(\Gamma _{\mu })$
of lower dimension, contradicting the choice of Y. Hence, we have established convergence of
$Y'\in \mathcal {S}(\Gamma _{\mu })$
of lower dimension, contradicting the choice of Y. Hence, we have established convergence of
![]() $\nu _j$
to the homogeneous probability measure associated to
$\nu _j$
to the homogeneous probability measure associated to
![]() $Y_{\infty }$
, proving compactness of
$Y_{\infty }$
, proving compactness of
![]() $\mathcal {S}_Z(\Gamma _{\mu })$
.
$\mathcal {S}_Z(\Gamma _{\mu })$
.
To obtain relative compactness of
![]() $\mathcal {S}_{HZ}(\Gamma _{\mu })$
, note that by H-invariance of
$\mathcal {S}_{HZ}(\Gamma _{\mu })$
, note that by H-invariance of
![]() $\beta _{\infty }^{-1}(\{\infty \})$
for the height functions
$\beta _{\infty }^{-1}(\{\infty \})$
for the height functions
![]() $\beta _{\infty }$
coming out of Theorem 6.1, we know that
$\beta _{\infty }$
coming out of Theorem 6.1, we know that
![]() $\beta _{\infty }(x)<\infty $
for every
$\beta _{\infty }(x)<\infty $
for every
![]() $x\in HZ$
if
$x\in HZ$
if
![]() $\beta _{\infty }$
is chosen to be finite on Z. Thus, Lemma 7.1(i) implies that there exists a compact subset
$\beta _{\infty }$
is chosen to be finite on Z. Thus, Lemma 7.1(i) implies that there exists a compact subset
![]() $R_{1/2}$
of X such that
$R_{1/2}$
of X such that
![]() $\mathcal {S}_{HZ}(\Gamma _{\mu })\subset \mathcal {S}_{R_{1/2}}(\Gamma _{\mu })$
, and the latter set is compact, as shown above.
$\mathcal {S}_{HZ}(\Gamma _{\mu })\subset \mathcal {S}_{R_{1/2}}(\Gamma _{\mu })$
, and the latter set is compact, as shown above.
Finally, if a limit point of a sequence of probability measures in
![]() $\mathcal {S}(\Gamma _{\mu })\cup \{\delta _{\infty }\}$
has a point
$\mathcal {S}(\Gamma _{\mu })\cup \{\delta _{\infty }\}$
has a point
![]() $x\in X$
in its support, then a subsequence is contained in
$x\in X$
in its support, then a subsequence is contained in
![]() $\mathcal {S}_Z(\Gamma _{\mu })$
for some compact neighborhood Z of x, proving compactness of
$\mathcal {S}_Z(\Gamma _{\mu })$
for some compact neighborhood Z of x, proving compactness of
![]() $\mathcal {S}(\Gamma _{\mu })\cup \{\delta _{\infty }\}$
.
$\mathcal {S}(\Gamma _{\mu })\cup \{\delta _{\infty }\}$
.
Proof of Corollary 1.9
Clearly,
![]() $\mathcal {S}(\Gamma _{\mu },Y_{\infty })$
is closed in
$\mathcal {S}(\Gamma _{\mu },Y_{\infty })$
is closed in
![]() $\mathcal {S}(\Gamma _{\mu })$
. In view of the last statement in Proposition 1.8(i), we only have to show that the only possible limit point of
$\mathcal {S}(\Gamma _{\mu })$
. In view of the last statement in Proposition 1.8(i), we only have to show that the only possible limit point of
![]() $(Y_n)_n$
inside
$(Y_n)_n$
inside
![]() $\mathcal {S}(\Gamma _{\mu },Y_{\infty })$
is
$\mathcal {S}(\Gamma _{\mu },Y_{\infty })$
is
![]() $Y_{\infty }$
. Let Y be such a limit point. By Proposition 1.8, since
$Y_{\infty }$
. Let Y be such a limit point. By Proposition 1.8, since
![]() $C_G(\Gamma _{\mu })$
is assumed discrete, it follows that
$C_G(\Gamma _{\mu })$
is assumed discrete, it follows that
![]() $Y_n\subset Y$
for infinitely many n. By assumption, this forces
$Y_n\subset Y$
for infinitely many n. By assumption, this forces
![]() $Y=Y_{\infty }$
, and we are done.
$Y=Y_{\infty }$
, and we are done.
7.4 Application to nilmanifolds
Let
![]() $\Lambda '$
be a lattice in a connected simply connected nilpotent Lie group N and let X be the compact nilmanifold
$\Lambda '$
be a lattice in a connected simply connected nilpotent Lie group N and let X be the compact nilmanifold
![]() $N/\Lambda '$
. The automorphism group
$N/\Lambda '$
. The automorphism group
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
of
$\operatorname {\mathrm {Aut}}(\Lambda ')$
of
![]() $\Lambda '$
is defined to be the subset of automorphisms of N preserving
$\Lambda '$
is defined to be the subset of automorphisms of N preserving
![]() $\Lambda '$
. It is well known that any abstract automorphism of
$\Lambda '$
. It is well known that any abstract automorphism of
![]() $\Lambda '$
extends to an automorphism of N, therefore defines an element of
$\Lambda '$
extends to an automorphism of N, therefore defines an element of
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
(see, e.g., [Reference Raghunathan80, §II]).
$\operatorname {\mathrm {Aut}}(\Lambda ')$
(see, e.g., [Reference Raghunathan80, §II]).
A probability measure
![]() $\mu $
on
$\mu $
on
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
defines a random walk on
$\operatorname {\mathrm {Aut}}(\Lambda ')$
defines a random walk on
![]() $X=N/\Lambda '$
by nilmanifold automorphisms. Our results have the following immediate corollaries for such random walks. Under an affine submanifold of X, we understand a closed subset of X that is the translate of the image in X of a closed subgroup of N.
$X=N/\Lambda '$
by nilmanifold automorphisms. Our results have the following immediate corollaries for such random walks. Under an affine submanifold of X, we understand a closed subset of X that is the translate of the image in X of a closed subgroup of N.
Corollary 7.5. Let
![]() $X=N/\Lambda '$
be a compact nilmanifold and
$X=N/\Lambda '$
be a compact nilmanifold and
![]() $\mu $
a probability measure on
$\mu $
a probability measure on
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
with finite first moment such that the Zariski closure H of
$\operatorname {\mathrm {Aut}}(\Lambda ')$
with finite first moment such that the Zariski closure H of
![]() $\Gamma _{\mu }$
in
$\Gamma _{\mu }$
in
![]() $\operatorname {\mathrm {Aut}}(N)$
is a connected semisimple group without compact factors. Then every
$\operatorname {\mathrm {Aut}}(N)$
is a connected semisimple group without compact factors. Then every
![]() $\mu $
-ergodic
$\mu $
-ergodic
![]() $\mu $
-stationary probability measure on X is
$\mu $
-stationary probability measure on X is
![]() $\Gamma _{\mu }$
-invariant, homogeneous, and supported on a finite union of affine submanifolds.
$\Gamma _{\mu }$
-invariant, homogeneous, and supported on a finite union of affine submanifolds.
Corollary 7.6. Let
![]() $X=N/\Lambda '$
be a compact nilmanifold and
$X=N/\Lambda '$
be a compact nilmanifold and
![]() $\mu $
a probability measure on
$\mu $
a probability measure on
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
with finite exponential moments such that the Zariski closure H of
$\operatorname {\mathrm {Aut}}(\Lambda ')$
with finite exponential moments such that the Zariski closure H of
![]() $\Gamma _{\mu }$
in
$\Gamma _{\mu }$
in
![]() $\operatorname {\mathrm {Aut}}(N)$
is a connected semisimple group without compact factors. Then:
$\operatorname {\mathrm {Aut}}(N)$
is a connected semisimple group without compact factors. Then:
-
(i) Every
 $\Gamma _{\mu }$
-orbit closure in X is a finite union of affine submanifolds.
$\Gamma _{\mu }$
-orbit closure in X is a finite union of affine submanifolds. -
(ii) For every
 $x\in X$
, for
$x\in X$
, for
 $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
 $(g_1, g_2 , \dots )$
one has where
$(g_1, g_2 , \dots )$
one has where $$ \begin{align*} \lim_{n\to \infty}\frac{1}{n}\sum_{k=0}^{n-1}\delta_{g_k\dotsm g_1x}=\nu_x, \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty}\frac{1}{n}\sum_{k=0}^{n-1}\delta_{g_k\dotsm g_1x}=\nu_x, \end{align*} $$
 $\nu _x$
is the homogeneous probability measure on
$\nu _x$
is the homogeneous probability measure on
 $\overline {\Gamma _{\mu } x}$
.
$\overline {\Gamma _{\mu } x}$
.
-
(iii) The set
 $\mathcal {S}(\Gamma _{\mu })$
is compact. If
$\mathcal {S}(\Gamma _{\mu })$
is compact. If
 $Y_n\to Y_{\infty }$
in
$Y_n\to Y_{\infty }$
in
 $\mathcal {S}(\Gamma _{\mu })$
, then there exists a sequence
$\mathcal {S}(\Gamma _{\mu })$
, then there exists a sequence
 $(l_n)_n$
of
$(l_n)_n$
of
 $\Gamma _{\mu }$
-invariant elements in N converging to the identity such that
$\Gamma _{\mu }$
-invariant elements in N converging to the identity such that
 $Y_n\subset l_nY_{\infty }$
for all large n.
$Y_n\subset l_nY_{\infty }$
for all large n.
The above corollaries are slight extensions of [Reference Benoist and Quint9, Corollary 1.3] and [Reference Benoist and Quint10, Corollary 1.10], respectively, removing the assumption that the probability measure
![]() $\mu $
is finitely supported.
$\mu $
is finitely supported.
To deduce these corollaries from our general theorems, one needs to exhibit an embedding
![]() $X\hookrightarrow G/\Lambda $
into the quotient of a real Lie group G containing
$X\hookrightarrow G/\Lambda $
into the quotient of a real Lie group G containing
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
by a lattice
$\operatorname {\mathrm {Aut}}(\Lambda ')$
by a lattice
![]() $\Lambda <G$
. In the classical case of toral automorphisms, one has
$\Lambda <G$
. In the classical case of toral automorphisms, one has
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')=\operatorname {\mathrm {GL}}_d(\mathbb {Z})$
, and we may simply choose
$\operatorname {\mathrm {Aut}}(\Lambda ')=\operatorname {\mathrm {GL}}_d(\mathbb {Z})$
, and we may simply choose
![]() $G=\operatorname {\mathrm {SL}}_{d+1}(\mathbb {R})$
with its lattice
$G=\operatorname {\mathrm {SL}}_{d+1}(\mathbb {R})$
with its lattice
![]() $\Lambda =\operatorname {\mathrm {SL}}_{d+1}(\mathbb {Z})$
admitting the embedding
$\Lambda =\operatorname {\mathrm {SL}}_{d+1}(\mathbb {Z})$
admitting the embedding
![]() $X=(\operatorname {\mathrm {GL}}_d(\mathbb {Z})\ltimes \mathbb {R}^d)/(\operatorname {\mathrm {GL}}_d(\mathbb {Z})\ltimes \mathbb {Z}^d)\hookrightarrow G/\Lambda $
. More generally, we can define
$X=(\operatorname {\mathrm {GL}}_d(\mathbb {Z})\ltimes \mathbb {R}^d)/(\operatorname {\mathrm {GL}}_d(\mathbb {Z})\ltimes \mathbb {Z}^d)\hookrightarrow G/\Lambda $
. More generally, we can define
![]() $G=\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))\ltimes N$
and
$G=\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))\ltimes N$
and
![]() $\Lambda =\operatorname {\mathrm {Aut}}(\Lambda ')\ltimes \Lambda '$
, where
$\Lambda =\operatorname {\mathrm {Aut}}(\Lambda ')\ltimes \Lambda '$
, where
![]() $\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))$
denotes the Zariski closure of
$\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))$
denotes the Zariski closure of
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
inside
$\operatorname {\mathrm {Aut}}(\Lambda ')$
inside
![]() $\operatorname {\mathrm {Aut}}(N)$
. Then
$\operatorname {\mathrm {Aut}}(N)$
. Then
![]() $\Lambda $
is a lattice in G by Borel–Harish-Chandra [Reference Borel and Harish-Chandra17], since
$\Lambda $
is a lattice in G by Borel–Harish-Chandra [Reference Borel and Harish-Chandra17], since
![]() $\operatorname {\mathrm {Aut}}(\Lambda ')$
is commensurable to the subgroup of integer points of
$\operatorname {\mathrm {Aut}}(\Lambda ')$
is commensurable to the subgroup of integer points of
![]() $\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))$
for a suitable
$\operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Aut}}(\Lambda '))$
for a suitable
![]() $\mathbb {Q}$
-structure on
$\mathbb {Q}$
-structure on
![]() $\operatorname {\mathrm {Aut}}(N)$
(see [Reference Raghunathan80, Theorem 2.12] and its discussion). Hence, our results apply with
$\operatorname {\mathrm {Aut}}(N)$
(see [Reference Raghunathan80, Theorem 2.12] and its discussion). Hence, our results apply with
![]() $H=\operatorname {\mathrm {Zcl}}(\Gamma _{\mu })$
in view of Proposition 3.1.
$H=\operatorname {\mathrm {Zcl}}(\Gamma _{\mu })$
in view of Proposition 3.1.
8 Birkhoff genericity
The aim of this section is to prove Theorem 1.11. Recall that H is a connected semisimple Lie group without compact factors and with finite center,
![]() $A'=\{a(t)\mid t\in \mathbb {R}\}$
is a one-parameter
$A'=\{a(t)\mid t\in \mathbb {R}\}$
is a one-parameter
![]() $\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H, and U an
$\operatorname {\mathrm {Ad}}$
-diagonalizable subgroup of H, and U an
![]() $a(1)$
-expanding subgroup of H contained in
$a(1)$
-expanding subgroup of H contained in
![]() $H^+_{a(1)}$
. In particular, U is connected,
$H^+_{a(1)}$
. In particular, U is connected,
![]() $\operatorname {\mathrm {Ad}}$
-unipotent and normalized by
$\operatorname {\mathrm {Ad}}$
-unipotent and normalized by
![]() $A'$
. Moreover, having fixed a maximal compact subgroup K of H,
$A'$
. Moreover, having fixed a maximal compact subgroup K of H,
![]() $K'$
is defined to be the compact group
$K'$
is defined to be the compact group
![]() $C_K(A')\cap N_H(U)$
and
$C_K(A')\cap N_H(U)$
and
![]() $\mu $
is a probability measure on
$\mu $
is a probability measure on
with finite exponential moments satisfying
![]() $\int _P\lambda (g)\mathop {}\!\mathrm {d}\mu (g)>0$
, where
$\int _P\lambda (g)\mathop {}\!\mathrm {d}\mu (g)>0$
, where
![]() $\lambda $
is defined by the
$\lambda $
is defined by the
![]() $K'A'U$
-factorization
$K'A'U$
-factorization
![]() $g=ka(\lambda (g))u$
for
$g=ka(\lambda (g))u$
for
![]() $g\in P$
. Recall also that for
$g\in P$
. Recall also that for
![]() $\omega =(g_i)_i\in P^{\mathbb {N}}$
and
$\omega =(g_i)_i\in P^{\mathbb {N}}$
and
![]() $n\in \mathbb {N}$
, we write
$n\in \mathbb {N}$
, we write
for the
![]() $K'A'U$
-factorization of
$K'A'U$
-factorization of
![]() $g_n\dotsm g_1$
. All these notations and assumptions will be understood to be in place until the end of this section.
$g_n\dotsm g_1$
. All these notations and assumptions will be understood to be in place until the end of this section.
The first lemma we prove ensures that the limit in condition (3) of Definition 1.10 exists almost surely.
Lemma 8.1. For
![]() $\mu ^{\mathbb {N}}$
-almost every
$\mu ^{\mathbb {N}}$
-almost every
![]() $\omega \in P^{\mathbb {N}}$
, the sequence
$\omega \in P^{\mathbb {N}}$
, the sequence
![]() $(u_{\omega , n})_n$
converges to some
$(u_{\omega , n})_n$
converges to some
![]() $u_{\omega }\in U$
.
$u_{\omega }\in U$
.
Proof. Since U does not intersect the (finite) center of H, the restriction
![]() $\operatorname {\mathrm {Ad}}_H\colon U\to \operatorname {\mathrm {Ad}}(U)$
is a Lie group isomorphism. To prove the claimed convergence, we may thus assume that H is a linear group. Let
$\operatorname {\mathrm {Ad}}_H\colon U\to \operatorname {\mathrm {Ad}}(U)$
is a Lie group isomorphism. To prove the claimed convergence, we may thus assume that H is a linear group. Let
![]() $\omega =(g_i)_i \in P^{\mathbb {N}}$
. For
$\omega =(g_i)_i \in P^{\mathbb {N}}$
. For
![]() $n \in \mathbb {N}$
, write
$n \in \mathbb {N}$
, write
![]() $g_n=k_n a_n u_n$
its (unique) factorization into
$g_n=k_n a_n u_n$
its (unique) factorization into
![]() $K'$
,
$K'$
,
![]() $A'$
and U components. We also set
$A'$
and U components. We also set
![]() $p_n=k_n a_n$
. One readily observes that the term
$p_n=k_n a_n$
. One readily observes that the term
![]() $u_{\omega ,n}$
is equal to the product
$u_{\omega ,n}$
is equal to the product
where we use the shorthand
![]() $g^h=h^{-1}gh$
. In the product (8.1), a term
$g^h=h^{-1}gh$
. In the product (8.1), a term
![]() $u_k^{p_{k-1}\dotsm p_1}$
is equivalently expressed as
$u_k^{p_{k-1}\dotsm p_1}$
is equivalently expressed as
![]() $\exp \bigl (\operatorname {\mathrm {Ad}}((p_{k-1}\dotsm p_1)^{-1})(\log u_k)\bigr )$
. Here, the
$\exp \bigl (\operatorname {\mathrm {Ad}}((p_{k-1}\dotsm p_1)^{-1})(\log u_k)\bigr )$
. Here, the
![]() $\log $
map is well defined since U being a unipotent linear group implies that the exponential map is a diffeomorphism from
$\log $
map is well defined since U being a unipotent linear group implies that the exponential map is a diffeomorphism from
![]() $\mathfrak {u}=\operatorname {\mathrm {Lie}}(U)$
onto U. Moreover, since the Lie algebra
$\mathfrak {u}=\operatorname {\mathrm {Lie}}(U)$
onto U. Moreover, since the Lie algebra
![]() $\mathfrak {u}$
is nilpotent, we know that
$\mathfrak {u}$
is nilpotent, we know that
![]() $\exp \colon \mathfrak {u} \to U$
is given by
$\exp \colon \mathfrak {u} \to U$
is given by
![]() $v\mapsto I + vq(v)$
, where q is a polynomial map. Therefore, to show that the product (8.1) converges for
$v\mapsto I + vq(v)$
, where q is a polynomial map. Therefore, to show that the product (8.1) converges for
![]() $\mu ^{\mathbb {N}}$
-almost every
$\mu ^{\mathbb {N}}$
-almost every
![]() $\omega $
, by a general convergence criterion for infinite matrix products (see, e.g., [Reference Wedderburn94, §8.10]), it suffices to show that for
$\omega $
, by a general convergence criterion for infinite matrix products (see, e.g., [Reference Wedderburn94, §8.10]), it suffices to show that for
![]() $\mu ^{\mathbb {N}}$
-a.e.
$\mu ^{\mathbb {N}}$
-a.e.
![]() $\omega $
,
$\omega $
,
converges, where
![]() $ \left \lVert {\cdot } \right \rVert $
is an arbitrary matrix norm on
$ \left \lVert {\cdot } \right \rVert $
is an arbitrary matrix norm on
![]() $\mathfrak {u}$
. We now prove this convergence. We start by observing that for
$\mathfrak {u}$
. We now prove this convergence. We start by observing that for
![]() $u\in U$
the logarithm
$u\in U$
the logarithm
![]() $\log u$
is a polynomial in u. Hence, the random nilpotent elements
$\log u$
is a polynomial in u. Hence, the random nilpotent elements
![]() $(\log u_k)_{k \ge 1}$
are i.i.d. and their distribution has a finite first moment. By the law of large numbers, it follows that almost surely
$(\log u_k)_{k \ge 1}$
are i.i.d. and their distribution has a finite first moment. By the law of large numbers, it follows that almost surely
![]() $ \left \lVert {\log u_k} \right \rVert = o(k)$
. Almost surely, we thus obtain the bound
$ \left \lVert {\log u_k} \right \rVert = o(k)$
. Almost surely, we thus obtain the bound
 $$ \begin{align} \begin{aligned} \left\lVert {\operatorname{\mathrm{Ad}}((a_{k-1}\dotsm a_1)^{-1}) (\log u_k)} \right\rVert &\le o(k) \max_{\alpha \in \Pi} \prod_{i=1}^{k-1} \exp(-\alpha\lambda(a_i))\\ &=o(k) \max_{\alpha \in \Pi} \exp\biggl(-\alpha\sum_{i=1}^{k-1}\lambda(a_i)\biggr), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\lVert {\operatorname{\mathrm{Ad}}((a_{k-1}\dotsm a_1)^{-1}) (\log u_k)} \right\rVert &\le o(k) \max_{\alpha \in \Pi} \prod_{i=1}^{k-1} \exp(-\alpha\lambda(a_i))\\ &=o(k) \max_{\alpha \in \Pi} \exp\biggl(-\alpha\sum_{i=1}^{k-1}\lambda(a_i)\biggr), \end{aligned} \end{align} $$
where
is the finite set of real numbers corresponding to the weights of
![]() $A'$
on
$A'$
on
![]() $\mathfrak u$
. Since U is contained in
$\mathfrak u$
. Since U is contained in
![]() $H_{a(1)}^+$
, we have
$H_{a(1)}^+$
, we have
![]() $\Pi \subset (0,\infty )$
. Together with
$\Pi \subset (0,\infty )$
. Together with
![]() $\int _P \lambda (g) \mathop {}\!\mathrm {d}\mu (g)>0$
, it thus follows from the Birkhoff ergodic theorem that,
$\int _P \lambda (g) \mathop {}\!\mathrm {d}\mu (g)>0$
, it thus follows from the Birkhoff ergodic theorem that,
![]() $\mu ^{\mathbb {N}}$
-almost surely, the last term in (8.2) decays exponentially. This gives the summability claimed above and hence the lemma.
$\mu ^{\mathbb {N}}$
-almost surely, the last term in (8.2) decays exponentially. This gives the summability claimed above and hence the lemma.
Proposition 8.2. Suppose that the Zariski closure of
![]() $\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
$\operatorname {\mathrm {Ad}}(\Gamma _{\mu })$
contains
![]() $\operatorname {\mathrm {Ad}}(U)$
. Then the probability measure
$\operatorname {\mathrm {Ad}}(U)$
. Then the probability measure
![]() $\mu $
is H-expanding. For a discrete subgroup
$\mu $
is H-expanding. For a discrete subgroup
![]() $\Lambda $
of a real Lie group G containing H, any ergodic
$\Lambda $
of a real Lie group G containing H, any ergodic
![]() $\mu $
-stationary probability measure on
$\mu $
-stationary probability measure on
![]() $G/\Lambda $
is H-invariant. If
$G/\Lambda $
is H-invariant. If
![]() $\Lambda $
is a lattice in G, then the conclusion of Theorem 1.6 holds with
$\Lambda $
is a lattice in G, then the conclusion of Theorem 1.6 holds with
![]() $Y_x=\overline {Hx}$
and
$Y_x=\overline {Hx}$
and
![]() $\nu _x=\nu _{\overline {Hx}}$
.
$\nu _x=\nu _{\overline {Hx}}$
.
The following observations will be useful in the proof of the previous proposition. We denote by
![]() $A^{\prime }_+=\{a(t)\mid t>0\}$
the positive ray in
$A^{\prime }_+=\{a(t)\mid t>0\}$
the positive ray in
![]() $A'$
.
$A'$
.
Lemma 8.3. Let
![]() $\Gamma $
be a subsemigroup of P such that
$\Gamma $
be a subsemigroup of P such that
![]() $\Gamma \cap K'A^{\prime }_+U \neq \emptyset $
. Then there exists
$\Gamma \cap K'A^{\prime }_+U \neq \emptyset $
. Then there exists
![]() $u \in U$
such that
$u \in U$
such that
![]() $u \Gamma u^{-1} \cap K'A^{\prime }_+ \neq \emptyset $
.
$u \Gamma u^{-1} \cap K'A^{\prime }_+ \neq \emptyset $
.
Proof. By hypothesis there exists an element
![]() $\gamma _0 \in K'A^{\prime }_+U \cap \Gamma $
. Factorize
$\gamma _0 \in K'A^{\prime }_+U \cap \Gamma $
. Factorize
![]() $\gamma _0=p_0 u_0$
with
$\gamma _0=p_0 u_0$
with
![]() $p_0 \in K'A^{\prime }_+$
and
$p_0 \in K'A^{\prime }_+$
and
![]() $u_0 \in U$
. Endow
$u_0 \in U$
. Endow
![]() $\mathfrak {u}$
with some Euclidean structure. As in the proof of Lemma 8.1, the linear map
$\mathfrak {u}$
with some Euclidean structure. As in the proof of Lemma 8.1, the linear map
![]() $\operatorname {\mathrm {Ad}}(p_0^{-1})$
preserves the Lie algebra
$\operatorname {\mathrm {Ad}}(p_0^{-1})$
preserves the Lie algebra
![]() $\mathfrak {u}$
and any large power of it acts on
$\mathfrak {u}$
and any large power of it acts on
![]() $\mathfrak {u}$
as a contraction. Moreover, since U is connected and simply connected, as a consequence of the Baker–Campbell–Hausdorff formula (see, e.g., [Reference Corwin and Greenleaf24, §1.2]), for every
$\mathfrak {u}$
as a contraction. Moreover, since U is connected and simply connected, as a consequence of the Baker–Campbell–Hausdorff formula (see, e.g., [Reference Corwin and Greenleaf24, §1.2]), for every
![]() $u\in U$
, the map
$u\in U$
, the map
![]() $q_u\colon \mathfrak {u} \to \mathfrak {u}$
defined by
$q_u\colon \mathfrak {u} \to \mathfrak {u}$
defined by
![]() $X \mapsto \log (\exp (X)u)$
is a polynomial map whose degree depends only on U and whose coefficients depend continuously on u.
$X \mapsto \log (\exp (X)u)$
is a polynomial map whose degree depends only on U and whose coefficients depend continuously on u.
Using the same notation and reasoning as in the proof of Lemma 8.1, we observe that for every
![]() $n \ge 1$
, we have
$n \ge 1$
, we have
![]() $\gamma _0^n=p_0^n u_0^{p_0^{n-1}} \dotsm u_0^{p_0}u_0$
, with the term
$\gamma _0^n=p_0^n u_0^{p_0^{n-1}} \dotsm u_0^{p_0}u_0$
, with the term
![]() converging in U as
converging in U as
![]() $n \to \infty $
. From these facts, one deduces that there exists a ball B in
$n \to \infty $
. From these facts, one deduces that there exists a ball B in
![]() $\mathfrak {u}$
around
$\mathfrak {u}$
around
![]() $0 \in \mathfrak {u}$
such that for every
$0 \in \mathfrak {u}$
such that for every
![]() $n \in \mathbb {N}$
large enough, the continuous map
$n \in \mathbb {N}$
large enough, the continuous map
![]() $f_n\colon \mathfrak {u} \to \mathfrak {u}$
defined by
$f_n\colon \mathfrak {u} \to \mathfrak {u}$
defined by
satisfies
![]() $f_n(B) \subset B$
. It follows from the Brouwer fixed point theorem that
$f_n(B) \subset B$
. It follows from the Brouwer fixed point theorem that
![]() $f_n$
has a fixed point
$f_n$
has a fixed point
![]() $X \in \mathfrak {u}$
. We claim that
$X \in \mathfrak {u}$
. We claim that
![]() $u=\exp (X) \in U$
is the desired element. Indeed, since
$u=\exp (X) \in U$
is the desired element. Indeed, since
![]() $\exp (\operatorname {\mathrm {Ad}}(p_0^{-n})X)=p_0^{-n}\exp (X)p_0^n$
, we have
$\exp (\operatorname {\mathrm {Ad}}(p_0^{-n})X)=p_0^{-n}\exp (X)p_0^n$
, we have
![]() $p_0^{-n}up_0^nu(\gamma _0^n)=u$
and hence
$p_0^{-n}up_0^nu(\gamma _0^n)=u$
and hence
![]() $u \gamma _0^n u^{-1}= u p_0^n u(\gamma _0^n) u^{-1}=p_0^n \in K'A^{\prime }_+$
.
$u \gamma _0^n u^{-1}= u p_0^n u(\gamma _0^n) u^{-1}=p_0^n \in K'A^{\prime }_+$
.
Given
![]() $g\in P$
, we write
$g\in P$
, we write
![]() $g=k_ga_gu_g$
for its
$g=k_ga_gu_g$
for its
![]() $K'A'U$
-factorization.
$K'A'U$
-factorization.
Lemma 8.4. For a subset
![]() $C\subset P$
, let
$C\subset P$
, let
![]() $U_C=\{u_g\mid g\in C\}$
be the set of its U-parts. If the Zariski closure of
$U_C=\{u_g\mid g\in C\}$
be the set of its U-parts. If the Zariski closure of
![]() $\operatorname {\mathrm {Ad}}(C)$
contains
$\operatorname {\mathrm {Ad}}(C)$
contains
![]() $\operatorname {\mathrm {Ad}}(U)$
, then
$\operatorname {\mathrm {Ad}}(U)$
, then
![]() $\operatorname {\mathrm {Ad}}(U_C)$
is Zariski dense in
$\operatorname {\mathrm {Ad}}(U_C)$
is Zariski dense in
![]() $\operatorname {\mathrm {Ad}}(U)$
.
$\operatorname {\mathrm {Ad}}(U)$
.
Proof. Denote by Q the Zariski closure of
![]() $\operatorname {\mathrm {Ad}}(P)$
, and observe that
$\operatorname {\mathrm {Ad}}(P)$
, and observe that
![]() $\operatorname {\mathrm {Ad}}(U)$
is contained in the unipotent radical
$\operatorname {\mathrm {Ad}}(U)$
is contained in the unipotent radical
![]() $R_u(Q)$
of Q. Since
$R_u(Q)$
of Q. Since
![]() $\operatorname {\mathrm {Ad}}(K'A')$
is a linearly reductive subgroup of Q, there is a Levi factor L of Q containing
$\operatorname {\mathrm {Ad}}(K'A')$
is a linearly reductive subgroup of Q, there is a Levi factor L of Q containing
![]() $\operatorname {\mathrm {Ad}}(K'A')$
(see [Reference Hochschild49, Theorem VIII.4.3]). Then we have
$\operatorname {\mathrm {Ad}}(K'A')$
(see [Reference Hochschild49, Theorem VIII.4.3]). Then we have
![]() $Q=L\ltimes R_u(Q)$
as algebraic groups. This implies
$Q=L\ltimes R_u(Q)$
as algebraic groups. This implies
 $$ \begin{align*} \operatorname{\mathrm{Ad}}(U)\subset\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(C))\subset\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(K'A')\operatorname{\mathrm{Ad}}(U_C))=\underbrace{\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(K'A'))}_{\subset L}\underbrace{\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(U_C))}_{\subset R_u(Q)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ad}}(U)\subset\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(C))\subset\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(K'A')\operatorname{\mathrm{Ad}}(U_C))=\underbrace{\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(K'A'))}_{\subset L}\underbrace{\operatorname{\mathrm{Zcl}}(\operatorname{\mathrm{Ad}}(U_C))}_{\subset R_u(Q)}. \end{align*} $$
We conclude that
![]() $\operatorname {\mathrm {Ad}}(U)\subset \operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Ad}}(U_C))$
, which is what we needed to show.
$\operatorname {\mathrm {Ad}}(U)\subset \operatorname {\mathrm {Zcl}}(\operatorname {\mathrm {Ad}}(U_C))$
, which is what we needed to show.
Proof of Proposition 8.2
After choosing a maximal connected
![]() $\mathbb {R}$
-split torus A in H containing
$\mathbb {R}$
-split torus A in H containing
![]() $A'$
, we see that the assumptions of Proposition 3.7 are satisfied. Thus,
$A'$
, we see that the assumptions of Proposition 3.7 are satisfied. Thus,
![]() $\mu $
is H-expanding. Now, let
$\mu $
is H-expanding. Now, let
![]() $\nu $
be an ergodic
$\nu $
be an ergodic
![]() $\mu $
-stationary probability measure on
$\mu $
-stationary probability measure on
![]() $X=G/ \Lambda $
. By Theorem 1.1,
$X=G/ \Lambda $
. By Theorem 1.1,
![]() $\nu $
is
$\nu $
is
![]() $\Gamma _{\mu }$
-invariant and homogeneous, and the connected component N of
$\Gamma _{\mu }$
-invariant and homogeneous, and the connected component N of
![]() $\operatorname {\mathrm {Stab}}_G(\nu )$
is normalized by H.
$\operatorname {\mathrm {Stab}}_G(\nu )$
is normalized by H.
In order to prove the statement about H-invariance, we can assume without loss of generality that
![]() $\Gamma _{\mu }$
contains an element in
$\Gamma _{\mu }$
contains an element in
![]() $K'A^{\prime }_+$
. Indeed, suppose that the conclusion is true for such measures; call them special. Given an arbitrary measure
$K'A^{\prime }_+$
. Indeed, suppose that the conclusion is true for such measures; call them special. Given an arbitrary measure
![]() $\mu $
as in the statement, by Lemma 8.3 we can find an element
$\mu $
as in the statement, by Lemma 8.3 we can find an element
![]() $u \in U$
such that
$u \in U$
such that
![]() $(\tau _u)_* \mu $
is special, where
$(\tau _u)_* \mu $
is special, where
![]() $\tau _u$
denotes conjugation by u. The properties in Definition 1.10 are preserved by this conjugation. Then
$\tau _u$
denotes conjugation by u. The properties in Definition 1.10 are preserved by this conjugation. Then
![]() $u_* \nu $
is
$u_* \nu $
is
![]() $(\tau _u)_* \mu $
-ergodic and stationary and hence it is H-invariant. But since
$(\tau _u)_* \mu $
-ergodic and stationary and hence it is H-invariant. But since
![]() $u \in U\leqslant H$
, this implies that
$u \in U\leqslant H$
, this implies that
![]() $\nu $
itself is H-invariant.
$\nu $
itself is H-invariant.
So let us take
![]() $g_0=k_0a_0 \in \Gamma _{\mu } \cap K'A^{\prime }_+$
. Then, given an arbitrary
$g_0=k_0a_0 \in \Gamma _{\mu } \cap K'A^{\prime }_+$
. Then, given an arbitrary
![]() $g \in \Gamma _{\mu }$
written as
$g \in \Gamma _{\mu }$
written as
![]() $g=k_ga_gu_g$
in its
$g=k_ga_gu_g$
in its
![]() $K'A'U$
factorization, by considering a sequence
$K'A'U$
factorization, by considering a sequence
![]() $n_k$
such that
$n_k$
such that
![]() $k_0^{n_k} \to e$
as
$k_0^{n_k} \to e$
as
![]() $k \to \infty $
, we get that the conjugates
$k \to \infty $
, we get that the conjugates
![]() $g_0^{-n_k}g g_0^{n_k}$
converge to
$g_0^{-n_k}g g_0^{n_k}$
converge to
![]() $k_g a_g$
. This implies that
$k_g a_g$
. This implies that
![]() $k_ga_g$
and thus also
$k_ga_g$
and thus also
![]() $u_g$
belongs to
$u_g$
belongs to
![]() $\Gamma _{\mu }$
. In other words,
$\Gamma _{\mu }$
. In other words,
![]() $\Gamma _{\mu }$
contains all of its U-parts.
$\Gamma _{\mu }$
contains all of its U-parts.
We next claim that for any proper connected normal subgroup
![]() $S\leqslant H$
, there exists
$S\leqslant H$
, there exists
![]() $g\in \Gamma _{\mu }$
whose U-part
$g\in \Gamma _{\mu }$
whose U-part
![]() $u_g$
does not belong to S. To see this, by way of contradiction, let us suppose that all U-parts of elements of
$u_g$
does not belong to S. To see this, by way of contradiction, let us suppose that all U-parts of elements of
![]() $\Gamma _{\mu }$
belong to some proper normal subgroup S. Using Lemma 8.4, we deduce from this that
$\Gamma _{\mu }$
belong to some proper normal subgroup S. Using Lemma 8.4, we deduce from this that
![]() $\operatorname {\mathrm {Ad}}(U)\leqslant \operatorname {\mathrm {Ad}}(S)$
, which entails that U acts trivially in the adjoint representation of H on
$\operatorname {\mathrm {Ad}}(U)\leqslant \operatorname {\mathrm {Ad}}(S)$
, which entails that U acts trivially in the adjoint representation of H on
![]() $\mathfrak {h}/\mathfrak {s}$
. On the other hand, the image of
$\mathfrak {h}/\mathfrak {s}$
. On the other hand, the image of
![]() $a(1)$
in this representation has determinant one so that it cannot expand all elements of
$a(1)$
in this representation has determinant one so that it cannot expand all elements of
![]() $\mathfrak {h}/\mathfrak {s}$
, contradicting
$\mathfrak {h}/\mathfrak {s}$
, contradicting
![]() $a(1)$
-expansion of U.
$a(1)$
-expansion of U.
Assuming that H is not contained in N, we can apply the above with
![]() $S=(N\cap H)^\circ $
. Take
$S=(N\cap H)^\circ $
. Take
![]() $g=k_g a_g u_g \in \Gamma _{\mu }$
with
$g=k_g a_g u_g \in \Gamma _{\mu }$
with
![]() $u_g\notin (N\cap H)^\circ $
. By normality, also the U-parts of
$u_g\notin (N\cap H)^\circ $
. By normality, also the U-parts of
![]() $g_0^{-n_k}g g_0^{n_k}$
do not belong to
$g_0^{-n_k}g g_0^{n_k}$
do not belong to
![]() $(N\cap H)^\circ $
. On the other hand, as observed above, these U-parts lie in
$(N\cap H)^\circ $
. On the other hand, as observed above, these U-parts lie in
![]() $\Gamma _{\mu }\leqslant H\cap \operatorname {\mathrm {Stab}}_G(\nu )$
and converge to the identity. This is impossible, since S is the connected component of
$\Gamma _{\mu }\leqslant H\cap \operatorname {\mathrm {Stab}}_G(\nu )$
and converge to the identity. This is impossible, since S is the connected component of
![]() $ H\cap \operatorname {\mathrm {Stab}}_G(\nu )$
and hence an open subgroup of it. This contradiction shows that
$ H\cap \operatorname {\mathrm {Stab}}_G(\nu )$
and hence an open subgroup of it. This contradiction shows that
![]() $H\leqslant N$
, and hence that any ergodic
$H\leqslant N$
, and hence that any ergodic
![]() $\mu $
-stationary probability measure
$\mu $
-stationary probability measure
![]() $\nu $
is H-invariant.
$\nu $
is H-invariant.
Finally, applying the H-invariance statement to the homogeneous measure
![]() $\nu _x$
from Theorem 1.6, we see that the conclusions of that theorem hold with
$\nu _x$
from Theorem 1.6, we see that the conclusions of that theorem hold with
![]() $Y_x=\overline {Hx}$
.
$Y_x=\overline {Hx}$
.
The following elementary but key equivariance property is the final ingredient required for the proof of Theorem 1.11.
Lemma 8.5. For
![]() $\mu ^{\mathbb {N}}$
-almost every
$\mu ^{\mathbb {N}}$
-almost every
![]() $\omega =(g_i)_i \in P^{\mathbb {N}}$
and every
$\omega =(g_i)_i \in P^{\mathbb {N}}$
and every
![]() $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
where
![]() $T\colon P^{\mathbb {N}}\to P^{\mathbb {N}},(g_1,g_2,\dots )\mapsto (g_2,g_3,\dots )$
denotes the shift map.
$T\colon P^{\mathbb {N}}\to P^{\mathbb {N}},(g_1,g_2,\dots )\mapsto (g_2,g_3,\dots )$
denotes the shift map.
Proof. By Lemma 8.1, there exists a set
![]() $\Omega $
of full
$\Omega $
of full
![]() $\mu ^{\mathbb {N}}$
-measure such that for every
$\mu ^{\mathbb {N}}$
-measure such that for every
![]() $\omega \in \Omega $
, the sequence
$\omega \in \Omega $
, the sequence
![]() $u_{\omega ,n}$
converges (to the limit
$u_{\omega ,n}$
converges (to the limit
![]() $u_{\omega }$
). Replacing
$u_{\omega }$
). Replacing
![]() $\Omega $
by
$\Omega $
by
![]() $\bigcap _{i\ge 0}T^{-i}\Omega $
if necessary, we may assume that
$\bigcap _{i\ge 0}T^{-i}\Omega $
if necessary, we may assume that
![]() $T\Omega \subset \Omega $
. Let
$T\Omega \subset \Omega $
. Let
![]() $\omega =(g_i)_i \in \Omega $
and
$\omega =(g_i)_i \in \Omega $
and
![]() $n \in \mathbb {N}$
. Writing
$n \in \mathbb {N}$
. Writing
![]() $g_i=k_ia_i u_i$
in its
$g_i=k_ia_i u_i$
in its
![]() $K'A'U$
factorization, a straightforward computation shows that
$K'A'U$
factorization, a straightforward computation shows that
![]() $u_{\omega ,n}= a_1^{-1}k^{-1}_1 u_{T\omega ,n-1 } k_1a_1u_1$
. Passing to the limit as
$u_{\omega ,n}= a_1^{-1}k^{-1}_1 u_{T\omega ,n-1 } k_1a_1u_1$
. Passing to the limit as
![]() $n \to \infty $
, we obtain
$n \to \infty $
, we obtain
![]() $u_{\omega }=a_1^{-1}k^{-1}_1 u_{T\omega } g_1$
. The lemma now follows by iterating the latter equality, using that
$u_{\omega }=a_1^{-1}k^{-1}_1 u_{T\omega } g_1$
. The lemma now follows by iterating the latter equality, using that
![]() $A'$
and
$A'$
and
![]() $K'$
commute.
$K'$
commute.
Proof of Theorem 1.11
Suppose the measure
![]() $\eta $
is generated by the probability measure
$\eta $
is generated by the probability measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $P=K'A'U$
as in Definition 1.10. By Theorem 1.6 and Proposition 8.2, we know that for every
$P=K'A'U$
as in Definition 1.10. By Theorem 1.6 and Proposition 8.2, we know that for every
![]() $x\in X$
, for
$x\in X$
, for
![]() $\mu ^{\mathbb {N}}$
-almost every
$\mu ^{\mathbb {N}}$
-almost every
![]() $\omega =(g_i)_i\in P^{\mathbb {N}}$
, the sequence of points
$\omega =(g_i)_i\in P^{\mathbb {N}}$
, the sequence of points
is equidistributed with respect to
![]() $\nu =\nu _{\overline {Hx}}$
.
$\nu =\nu _{\overline {Hx}}$
.
Replacing
![]() $K'$
by a subgroup, we may assume without loss of generality that
$K'$
by a subgroup, we may assume without loss of generality that
![]() $\pi _{K'}(\Gamma _{\mu }) $
is dense in
$\pi _{K'}(\Gamma _{\mu }) $
is dense in
![]() $K'$
, where
$K'$
, where
![]() $\pi _{K'}\colon P\to K'$
is the natural projection map. So the action of
$\pi _{K'}\colon P\to K'$
is the natural projection map. So the action of
![]() $\pi _{K'}(\Gamma _{\mu })$
on
$\pi _{K'}(\Gamma _{\mu })$
on
![]() $(K', m_{K'})$
by left translation is ergodic, where
$(K', m_{K'})$
by left translation is ergodic, where
![]() $m_{K'}$
is the Haar probability measure on
$m_{K'}$
is the Haar probability measure on
![]() $K'$
. By a version of Moore’s ergodicity theorem (see [Reference Bekka and Mayer3, Theorem III.2.5(i)]) applied to the regular representation on the Hilbert space
$K'$
. By a version of Moore’s ergodicity theorem (see [Reference Bekka and Mayer3, Theorem III.2.5(i)]) applied to the regular representation on the Hilbert space
![]() $L^2_0(X,\nu )$
of square integrable functions with mean zero, the action of
$L^2_0(X,\nu )$
of square integrable functions with mean zero, the action of
![]() $\Gamma _{\mu }$
on
$\Gamma _{\mu }$
on
![]() $(X, \nu )$
is weakly mixing. Therefore, the action of
$(X, \nu )$
is weakly mixing. Therefore, the action of
![]() $\Gamma _{\mu }$
on
$\Gamma _{\mu }$
on
![]() $(X\times K' , \nu \times m_{K'})$
given by
$(X\times K' , \nu \times m_{K'})$
given by
![]() $ g(y, k)= (gy , \pi _{K'}(g)k ) $
is ergodic (cf., e.g., [Reference Schmidt86, Proposition 2.2]). Thus, it follows from [Reference Simmons and Weiss93, Corollary 5.5] that for almost every
$ g(y, k)= (gy , \pi _{K'}(g)k ) $
is ergodic (cf., e.g., [Reference Schmidt86, Proposition 2.2]). Thus, it follows from [Reference Simmons and Weiss93, Corollary 5.5] that for almost every
![]() $\omega =(g_i)_i\in P^{\mathbb {N}}$
, the sequence
$\omega =(g_i)_i\in P^{\mathbb {N}}$
, the sequence
is equidistributed with respect to
![]() $\nu \times m_{K'}$
. Next, applying [Reference Simmons and Weiss93, Proposition 5.1], this can be upgraded to almost sure equidistribution of
$\nu \times m_{K'}$
. Next, applying [Reference Simmons and Weiss93, Proposition 5.1], this can be upgraded to almost sure equidistribution of
with respect to
![]() $\nu \times m_{K'}\times \mu ^{\mathbb {N}}$
, where
$\nu \times m_{K'}\times \mu ^{\mathbb {N}}$
, where
![]() $T\colon P^{\mathbb {N}}\to P^{\mathbb {N}}$
denotes the shift map. We caution here that when the support of
$T\colon P^{\mathbb {N}}\to P^{\mathbb {N}}$
denotes the shift map. We caution here that when the support of
![]() $\mu $
is noncompact, the above equidistribution takes place in a non-locally compact space so that the class of test functions to consider is that of bounded continuous functions. The proof of [Reference Simmons and Weiss93, Proposition 5.1], however, only needs minor amending to accommodate this issue; see [Reference Prohaska and Sert79, Lemma 3.9] and the short discussion before its proof. Applying the map
$\mu $
is noncompact, the above equidistribution takes place in a non-locally compact space so that the class of test functions to consider is that of bounded continuous functions. The proof of [Reference Simmons and Weiss93, Proposition 5.1], however, only needs minor amending to accommodate this issue; see [Reference Prohaska and Sert79, Lemma 3.9] and the short discussion before its proof. Applying the map
![]() $\omega =(g_1,g_2,\dots )\mapsto (u_{\omega },g_1)$
to the equidistribution in equation (8.3), we conclude that, for almost every
$\omega =(g_1,g_2,\dots )\mapsto (u_{\omega },g_1)$
to the equidistribution in equation (8.3), we conclude that, for almost every
![]() $\omega =(g_i)_i\in P^{\mathbb {N}}$
, the sequence
$\omega =(g_i)_i\in P^{\mathbb {N}}$
, the sequence
is equidistributed with respect to
![]() $\nu \times m_{K'} \times \tilde {\eta }$
, where
$\nu \times m_{K'} \times \tilde {\eta }$
, where
![]() $\tilde {\eta }$
is a probability measure on
$\tilde {\eta }$
is a probability measure on
![]() $U\times P$
that projects to
$U\times P$
that projects to
![]() $\mu $
in the second coordinate. Again, some caution is needed at this step, since
$\mu $
in the second coordinate. Again, some caution is needed at this step, since
![]() $\omega \mapsto u_{\omega }$
is not necessarily continuous. However, also this can be dealt with by considering Lusin sets and continuous extensions coming from Tietze’s theorem as in the proof of [Reference Simmons and Weiss93, Proposition 5.2].
$\omega \mapsto u_{\omega }$
is not necessarily continuous. However, also this can be dealt with by considering Lusin sets and continuous extensions coming from Tietze’s theorem as in the proof of [Reference Simmons and Weiss93, Proposition 5.2].
The rest of the proof is the same as in [Reference Simmons and Weiss93, §12]; we briefly reproduce it for the convenience of the reader. Given
![]() $f\in C_c(X)$
, one considers the bounded continuous function
$f\in C_c(X)$
, one considers the bounded continuous function
![]() $\varphi $
on
$\varphi $
on
![]() $X\times K' \times U\times P$
defined by
$X\times K' \times U\times P$
defined by
 $$ \begin{align*} \varphi(x, k, u, g)= \int_0^{\lambda(g)} f( a(t) k^{-1} ux ) \mathop{}\!\mathrm{d} t, \end{align*} $$
$$ \begin{align*} \varphi(x, k, u, g)= \int_0^{\lambda(g)} f( a(t) k^{-1} ux ) \mathop{}\!\mathrm{d} t, \end{align*} $$
where
![]() $g=k_g a(\lambda (g)) u_g$
is the decomposition according to
$g=k_g a(\lambda (g)) u_g$
is the decomposition according to
![]() $P=K'A'U$
. A direct calculation using the invariance of
$P=K'A'U$
. A direct calculation using the invariance of
![]() $\nu $
under H shows that
$\nu $
under H shows that
Suppose
![]() $\omega =(g_i)_i$
is a generic point with respect to the equidistribution of equation (8.4) for which also Lemma 8.5 holds for every n. Using only the last factor P in the equidistribution, it follows that
$\omega =(g_i)_i$
is a generic point with respect to the equidistribution of equation (8.4) for which also Lemma 8.5 holds for every n. Using only the last factor P in the equidistribution, it follows that
 $$ \begin{align} \lim_{n \to \infty} \frac{\lambda(g_{\omega,n})}{n}=\lim_{n\to\infty}\frac1n\sum_{i=1}^n \lambda(g_i) = \int_P \lambda(g) \mathop{}\!\mathrm{d}\mu(g)>0. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{\lambda(g_{\omega,n})}{n}=\lim_{n\to\infty}\frac1n\sum_{i=1}^n \lambda(g_i) = \int_P \lambda(g) \mathop{}\!\mathrm{d}\mu(g)>0. \end{align} $$
We thus obtain, by the equidistribution (8.4),
 $$ \begin{align*} \int \varphi\mathop{}\!\mathrm{d}(\nu \times m_{K'} \times \tilde{\eta})&=\lim_{n\to \infty}\frac1n\sum_{i=0}^{n-1} \varphi ( g_{\omega, i}x, k_{\omega, i}, u_{T^i\omega}, g_{i+1} )\\ &=\lim_{n \to \infty} \frac1n \sum_{i=0}^{n-1} \int_0^{\lambda(g_{i+1})} f(a(t) k_{\omega,i}^{-1}u_{T^i \omega}g_{\omega,i}x)\mathop{}\!\mathrm{d} t \\ &=\lim_{n \to \infty} \frac1n \sum_{i=0}^{n-1} \int_0^{\lambda(g_{i+1})} f(a(t) a_{\omega,i}u_{\omega} x)\mathop{}\!\mathrm{d} t\\ &=\lim_{n\to \infty}\frac1n \sum_{i=0}^{n-1} \int_{\lambda(g_{\omega,i})}^{\lambda(g_{\omega,i+1})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t\\ &= \lim_{n\to \infty}\frac{\lambda(g_{\omega,n})}{n} \frac{1}{\lambda(g_{\omega,n})}\int_0^{\lambda(g_{\omega,n})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t\\ &= \int _P \lambda(g) \mathop{}\!\mathrm{d} \mu(g) \lim_{n\to \infty}\frac{1}{\lambda(g_{\omega,n})}\int_0^{\lambda(g_{\omega,n})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t, \end{align*} $$
$$ \begin{align*} \int \varphi\mathop{}\!\mathrm{d}(\nu \times m_{K'} \times \tilde{\eta})&=\lim_{n\to \infty}\frac1n\sum_{i=0}^{n-1} \varphi ( g_{\omega, i}x, k_{\omega, i}, u_{T^i\omega}, g_{i+1} )\\ &=\lim_{n \to \infty} \frac1n \sum_{i=0}^{n-1} \int_0^{\lambda(g_{i+1})} f(a(t) k_{\omega,i}^{-1}u_{T^i \omega}g_{\omega,i}x)\mathop{}\!\mathrm{d} t \\ &=\lim_{n \to \infty} \frac1n \sum_{i=0}^{n-1} \int_0^{\lambda(g_{i+1})} f(a(t) a_{\omega,i}u_{\omega} x)\mathop{}\!\mathrm{d} t\\ &=\lim_{n\to \infty}\frac1n \sum_{i=0}^{n-1} \int_{\lambda(g_{\omega,i})}^{\lambda(g_{\omega,i+1})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t\\ &= \lim_{n\to \infty}\frac{\lambda(g_{\omega,n})}{n} \frac{1}{\lambda(g_{\omega,n})}\int_0^{\lambda(g_{\omega,n})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t\\ &= \int _P \lambda(g) \mathop{}\!\mathrm{d} \mu(g) \lim_{n\to \infty}\frac{1}{\lambda(g_{\omega,n})}\int_0^{\lambda(g_{\omega,n})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t, \end{align*} $$
where we used Lemma 8.5 in the third equality and that
![]() $\lambda (g_{\omega ,i+1})=\lambda (g_{\omega ,i})+\lambda (g_{i+1})$
in the fourth. Together with equation (8.5), this implies
$\lambda (g_{\omega ,i+1})=\lambda (g_{\omega ,i})+\lambda (g_{i+1})$
in the fourth. Together with equation (8.5), this implies
 $$ \begin{align} \lim_{n\to \infty}\frac{1}{\lambda(g_{\omega,n})}\int_0^{\lambda(g_{\omega,n})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t = \int f \mathop{}\!\mathrm{d}\nu. \end{align} $$
$$ \begin{align} \lim_{n\to \infty}\frac{1}{\lambda(g_{\omega,n})}\int_0^{\lambda(g_{\omega,n})} f(a(t) u_{\omega} x)\mathop{}\!\mathrm{d} t = \int f \mathop{}\!\mathrm{d}\nu. \end{align} $$
Finally, notice that since the random variables
![]() $\lambda (g_{\omega ,n})-\lambda (g_{\omega ,n-1})=\lambda (g_n)$
are i.i.d. with a distribution that has a finite first moment, it follows from the law of large numbers that almost surely
$\lambda (g_{\omega ,n})-\lambda (g_{\omega ,n-1})=\lambda (g_n)$
are i.i.d. with a distribution that has a finite first moment, it follows from the law of large numbers that almost surely
Now, equations (8.6), (8.7) and (8.8) together imply the Birkhoff genericity of
![]() $u_{\omega } x$
with respect to
$u_{\omega } x$
with respect to
![]() $(a(t))_{t>0}$
and
$(a(t))_{t>0}$
and
![]() $\nu $
.
$\nu $
.
9 Connections to Diophantine approximation on fractals
The goal of this section is to explain the connection between random walks and Diophantine approximation on affine fractals, prove a general result (Theorem 9.3) which will imply Theorem 1.12 on Diophantine properties of Bedford–McMullen carpets, and mention some further directions.
9.1 Weighted Diophantine approximation and Dani–Kleinbock flow
To begin with, we recall basic notions in Diophantine approximation of matrices and the connection to homogeneous dynamics.
9.1.1 Badly approximable matrices and Dirichlet improvability
Let
![]() $m,n \in \mathbb {N}$
be positive integers,
$m,n \in \mathbb {N}$
be positive integers,
![]() $\mathbf {r} =(r_1,\dots ,r_m) \in (0,1]^m$
and
$\mathbf {r} =(r_1,\dots ,r_m) \in (0,1]^m$
and
![]() $\mathbf {s} =(s_1,\dots ,s_n) \in (0,1]^n$
be such that
$\mathbf {s} =(s_1,\dots ,s_n) \in (0,1]^n$
be such that
![]() $\sum _{i=1}^m r_i=\sum _{j=1}^n s_j=1$
and
$\sum _{i=1}^m r_i=\sum _{j=1}^n s_j=1$
and
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
a matrix with rows
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
a matrix with rows
![]() $M_1,\dots ,M_m$
. Then M is called
$M_1,\dots ,M_m$
. Then M is called
![]() $(\mathbf {r},\mathbf {s})$
-badly approximable or badly approximable for the weights
$(\mathbf {r},\mathbf {s})$
-badly approximable or badly approximable for the weights
![]() $(\mathbf {r},\mathbf {s})$
if there exists a constant
$(\mathbf {r},\mathbf {s})$
if there exists a constant
![]() $C>0$
such that
$C>0$
such that
for every
![]() $(\mathbf {p}, \mathbf {q}) \in \mathbb {Z}^m\times (\mathbb {Z}^n\setminus \{0\})$
. Otherwise, M is called
$(\mathbf {p}, \mathbf {q}) \in \mathbb {Z}^m\times (\mathbb {Z}^n\setminus \{0\})$
. Otherwise, M is called
![]() $(\mathbf {r},\mathbf {s})$
-well approximable.
$(\mathbf {r},\mathbf {s})$
-well approximable.
One can see by Dirichlet’s principle, or by Blichfeldt and Minkowski’s convex body results, that for every matrix
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, there exist infinitely many pairs
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, there exist infinitely many pairs
![]() $(\mathbf {p}, \mathbf {q}) \in \mathbb {Z}^m\times (\mathbb {Z}^n\setminus \{0\})$
such that the left-hand side of (9.1) is bounded above by
$(\mathbf {p}, \mathbf {q}) \in \mathbb {Z}^m\times (\mathbb {Z}^n\setminus \{0\})$
such that the left-hand side of (9.1) is bounded above by
![]() $1$
. As a consequence of a general form of Khintchine’s theorem [Reference Schmidt87], the set of
$1$
. As a consequence of a general form of Khintchine’s theorem [Reference Schmidt87], the set of
![]() $(\mathbf {r},\mathbf {s})$
-badly approximable matrices is a Lebesgue null set. However, it has everywhere-full Hausdorff dimension; see [Reference Kleinbock and Weiss56, Corollary 4.5] and [Reference Kleinbock and Weiss57, §5.4].
$(\mathbf {r},\mathbf {s})$
-badly approximable matrices is a Lebesgue null set. However, it has everywhere-full Hausdorff dimension; see [Reference Kleinbock and Weiss56, Corollary 4.5] and [Reference Kleinbock and Weiss57, §5.4].
Given weights
![]() $(\mathbf {r}, \mathbf {s})$
, an equivalent way to express the aforementioned consequence of the Dirichlet principle is to say that for every matrix
$(\mathbf {r}, \mathbf {s})$
, an equivalent way to express the aforementioned consequence of the Dirichlet principle is to say that for every matrix
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
and for every
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
and for every
![]() $t>0$
, the following system of inequalities has a solution in
$t>0$
, the following system of inequalities has a solution in
![]() $(\mathbf {p},\mathbf {q}) \in \mathbb {Z}^m \times (\mathbb {Z}^n\setminus \{0\})$
:
$(\mathbf {p},\mathbf {q}) \in \mathbb {Z}^m \times (\mathbb {Z}^n\setminus \{0\})$
:
One says that the matrix
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is
![]() $(\mathbf {r},\mathbf {s})$
-Dirichlet improvable if there exists
$(\mathbf {r},\mathbf {s})$
-Dirichlet improvable if there exists
![]() $\varepsilon \in (0,1)$
such that for every
$\varepsilon \in (0,1)$
such that for every
![]() $t>0$
large enough, the following system of inequalities has a solution in
$t>0$
large enough, the following system of inequalities has a solution in
![]() $(\mathbf {p},\mathbf {q}) \in \mathbb {Z}^m \times (\mathbb {Z}^n\setminus \{0\})$
:
$(\mathbf {p},\mathbf {q}) \in \mathbb {Z}^m \times (\mathbb {Z}^n\setminus \{0\})$
:
In the special case where the weights
![]() $(\mathbf {r},\mathbf {s})$
are given by
$(\mathbf {r},\mathbf {s})$
are given by
![]() $(\mathbf {m}, \mathbf {n})$
—by which we mean that
$(\mathbf {m}, \mathbf {n})$
—by which we mean that
![]() $r_i=1/m$
and
$r_i=1/m$
and
![]() $s_j=1/n$
for all
$s_j=1/n$
for all
![]() $i,j$
—the notion of Dirichlet improvability was introduced and studied by Davenport–Schmidt, who showed that the set of
$i,j$
—the notion of Dirichlet improvability was introduced and studied by Davenport–Schmidt, who showed that the set of
![]() $(\mathbf {m},\mathbf {n})$
-Dirichlet improvable matrices has zero Lebesgue measure [Reference Davenport and Schmidt26] and that every
$(\mathbf {m},\mathbf {n})$
-Dirichlet improvable matrices has zero Lebesgue measure [Reference Davenport and Schmidt26] and that every
![]() $(\mathbf {m},\mathbf {n})$
-badly approximable matrix is
$(\mathbf {m},\mathbf {n})$
-badly approximable matrix is
![]() $(\mathbf {m},\mathbf {n})$
-Dirichlet improvable [Reference Davenport and Schmidt27]. The former result was generalized to arbitrary weights
$(\mathbf {m},\mathbf {n})$
-Dirichlet improvable [Reference Davenport and Schmidt27]. The former result was generalized to arbitrary weights
![]() $(\mathbf {r},\mathbf {s})$
by Kleinbock–Weiss [Reference Kleinbock and Weiss56].
$(\mathbf {r},\mathbf {s})$
by Kleinbock–Weiss [Reference Kleinbock and Weiss56].
9.1.2 Dani–Kleinbock flow
Let
![]() $G=\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
,
$G=\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
,
![]() $\Lambda =\operatorname {\mathrm {PGL}}_d(\mathbb {Z})$
, and set
$\Lambda =\operatorname {\mathrm {PGL}}_d(\mathbb {Z})$
, and set
![]() $X=G/\Lambda $
. It is easy to see that X can alternatively be written as
$X=G/\Lambda $
. It is easy to see that X can alternatively be written as
![]() $\operatorname {\mathrm {SL}}_d(\mathbb {R})/\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
, which can be identified with the space of unimodular lattices in
$\operatorname {\mathrm {SL}}_d(\mathbb {R})/\operatorname {\mathrm {SL}}_d(\mathbb {Z})$
, which can be identified with the space of unimodular lattices in
![]() $\mathbb {R}^d$
via
$\mathbb {R}^d$
via
![]() $g\operatorname {\mathrm {SL}}_d(\mathbb {Z})\leftrightarrow g\mathbb {Z}^d$
. For every
$g\operatorname {\mathrm {SL}}_d(\mathbb {Z})\leftrightarrow g\mathbb {Z}^d$
. For every
![]() $\varepsilon>0$
, we define
$\varepsilon>0$
, we define

Viewing X as space of unimodular lattices in
![]() $\mathbb {R}^d$
,
$\mathbb {R}^d$
,
![]() $K_\varepsilon $
is nothing but the subset of lattices all of whose nonzero vectors have length at least
$K_\varepsilon $
is nothing but the subset of lattices all of whose nonzero vectors have length at least
![]() $\varepsilon $
in the supremum norm. The collection of sets
$\varepsilon $
in the supremum norm. The collection of sets
![]() $K_\varepsilon $
is clearly decreasing in
$K_\varepsilon $
is clearly decreasing in
![]() $\varepsilon $
. For
$\varepsilon $
. For
![]() $\varepsilon <1$
the set
$\varepsilon <1$
the set
![]() $K_\varepsilon $
has nonempty interior, and for
$K_\varepsilon $
has nonempty interior, and for
![]() $\varepsilon>1$
one has
$\varepsilon>1$
one has
![]() $K_\varepsilon = \emptyset $
, as can be seen by Minkowski’s convex body theorem from geometry of numbers. Moreover, Mahler’s compactness criterion states that the sets
$K_\varepsilon = \emptyset $
, as can be seen by Minkowski’s convex body theorem from geometry of numbers. Moreover, Mahler’s compactness criterion states that the sets
![]() $K_\varepsilon \subset X$
for
$K_\varepsilon \subset X$
for
![]() $\varepsilon>0$
are compact and that a subset of X is relatively compact if and only if it is contained in one of the
$\varepsilon>0$
are compact and that a subset of X is relatively compact if and only if it is contained in one of the
![]() $K_\varepsilon $
.
$K_\varepsilon $
.
Now, let
![]() $d=m+n$
and denote by
$d=m+n$
and denote by
![]() $x_0$
the identity coset in
$x_0$
the identity coset in
![]() $X=G/\Lambda $
. The Dani–Kleinbock correspondence principle—observed first by Dani [Reference Dani25] and developed further, among others, by Kleinbock [Reference Kleinbock59] and later Kleinbock–Weiss [Reference Kleinbock and Weiss56]—states that, loosely speaking, the Diophantine properties of a matrix
$X=G/\Lambda $
. The Dani–Kleinbock correspondence principle—observed first by Dani [Reference Dani25] and developed further, among others, by Kleinbock [Reference Kleinbock59] and later Kleinbock–Weiss [Reference Kleinbock and Weiss56]—states that, loosely speaking, the Diophantine properties of a matrix
![]() $M\in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
are encoded in the behavior of the trajectory of
$M\in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
are encoded in the behavior of the trajectory of
![]() $u_Mx_0$
inside X under suitable one-parameter diagonal subgroups of G, where
$u_Mx_0$
inside X under suitable one-parameter diagonal subgroups of G, where
![]() . We are going to use this principle in the form of the following proposition. Given weights
. We are going to use this principle in the form of the following proposition. Given weights
![]() $(\mathbf {r}, \mathbf {s}) \in (0,1]^m \times (0,1]^n$
as before, let
$(\mathbf {r}, \mathbf {s}) \in (0,1]^m \times (0,1]^n$
as before, let
![]() $a(t)$
denote the one-parameter subgroup of G corresponding to
$a(t)$
denote the one-parameter subgroup of G corresponding to
![]() $a(1)=\operatorname {\mathrm {diag}}(e^{r_1},\dots ,e^{r_m},e^{-s_1},\dots ,e^{-s_n})$
.
$a(1)=\operatorname {\mathrm {diag}}(e^{r_1},\dots ,e^{r_m},e^{-s_1},\dots ,e^{-s_n})$
.
Proposition 9.1 (Dani–Kleinbock correspondence)
A matrix
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is
-
○ ([Reference Kleinbock59])
 $(\mathbf {r},\mathbf {s})$
-badly approximable if and only if the forward-orbit
$(\mathbf {r},\mathbf {s})$
-badly approximable if and only if the forward-orbit
 $\{a(t) u_M x_0 \mid t \ge 0\}$
is relatively compact in X, and
$\{a(t) u_M x_0 \mid t \ge 0\}$
is relatively compact in X, and -
○ ([Reference Kleinbock and Weiss56])
 $(\mathbf {r},\mathbf {s})$
-Dirichlet improvable if and only if there exists
$(\mathbf {r},\mathbf {s})$
-Dirichlet improvable if and only if there exists
 $\varepsilon \in (0,1)$
such that
$\varepsilon \in (0,1)$
such that
 $a(t) u_M x_0 \notin K_\varepsilon $
for every
$a(t) u_M x_0 \notin K_\varepsilon $
for every
 $t>0$
large enough.
$t>0$
large enough.
An obvious consequence of this proposition is that given weights
![]() $(\mathbf {r},\mathbf {s})$
, if the forward orbit
$(\mathbf {r},\mathbf {s})$
, if the forward orbit
![]() $\{a(t) u_M x_0\mid t\ge 0\}$
associated to a matrix
$\{a(t) u_M x_0\mid t\ge 0\}$
associated to a matrix
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is dense in X, then M is
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is dense in X, then M is
![]() $(\mathbf {r},\mathbf {s})$
-well approximable and not
$(\mathbf {r},\mathbf {s})$
-well approximable and not
![]() $(\mathbf {r},\mathbf {s})$
-Dirichlet improvable.
$(\mathbf {r},\mathbf {s})$
-Dirichlet improvable.
In fact, the ergodic theoretic approach that we adopt will allow us to establish the following finer Diophantine property.
Definition 9.2. Given weights
![]() $(\mathbf {r},\mathbf {s})$
and the associated one-parameter diagonal group
$(\mathbf {r},\mathbf {s})$
and the associated one-parameter diagonal group
![]() $(a(t))_{t\in \mathbb {R}}$
, a matrix
$(a(t))_{t\in \mathbb {R}}$
, a matrix
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is said to be of
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
is said to be of
![]() $(\mathbf {r},\mathbf {s})$
-generic type if the forward-orbit
$(\mathbf {r},\mathbf {s})$
-generic type if the forward-orbit
![]() $(a(t) u_M x_0)_{t> 0}$
equidistributes to the Haar measure
$(a(t) u_M x_0)_{t> 0}$
equidistributes to the Haar measure
![]() $m_X$
on X.
$m_X$
on X.
9.2 Matrix sponges and self-affine measures
Here, we briefly describe the iterated function system (IFS) construction of affine fractals and introduce the subfamily of affine fractals (matrix sponges) and self-affine measures whose Diophantine properties will be studied in the subsequent part.
9.2.1 Affine fractals
Let
![]() $\phi $
be an affine transformation of
$\phi $
be an affine transformation of
![]() $\mathbb {R}^D$
given by
$\mathbb {R}^D$
given by
![]() $\phi (x)=Ax+b$
, where
$\phi (x)=Ax+b$
, where
![]() $A \in \operatorname {\mathrm {GL}}_D(\mathbb {R})$
and
$A \in \operatorname {\mathrm {GL}}_D(\mathbb {R})$
and
![]() $b \in \mathbb {R}^D$
. It is called contracting if the operator norm of its linear part A with respect to the standard Euclidean structure of
$b \in \mathbb {R}^D$
. It is called contracting if the operator norm of its linear part A with respect to the standard Euclidean structure of
![]() $\mathbb {R}^D$
satisfies
$\mathbb {R}^D$
satisfies
![]() $ \left \lVert {A} \right \rVert <1$
. We shall refer to a finite tuple
$ \left \lVert {A} \right \rVert <1$
. We shall refer to a finite tuple
![]() $(\phi _1,\dots ,\phi _k)$
of contracting affine transformations
$(\phi _1,\dots ,\phi _k)$
of contracting affine transformations
![]() $\phi _i$
of
$\phi _i$
of
![]() $\mathbb {R}^D$
as a contracting affine IFS. Given such an IFS, there exists a unique nonempty compact subset
$\mathbb {R}^D$
as a contracting affine IFS. Given such an IFS, there exists a unique nonempty compact subset
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\mathbb {R}^D$
satisfying
$\mathbb {R}^D$
satisfying
![]() $\mathcal {K}=\bigcup _{i=1}^k \phi _i(\mathcal {K})$
, referred to as the attractor of the IFS
$\mathcal {K}=\bigcup _{i=1}^k \phi _i(\mathcal {K})$
, referred to as the attractor of the IFS
![]() $(\phi _1,\ldots ,\phi _k)$
. Putting less emphasis on the IFS,
$(\phi _1,\ldots ,\phi _k)$
. Putting less emphasis on the IFS,
![]() $\mathcal {K}$
is also called an affine fractal or self-affine set. In the particular case where all the
$\mathcal {K}$
is also called an affine fractal or self-affine set. In the particular case where all the
![]() $\phi _i$
are similarities, the attractor
$\phi _i$
are similarities, the attractor
![]() $\mathcal {K}$
is also called a self-similar set.
$\mathcal {K}$
is also called a self-similar set.
The coding map
![]() $\pi $
associated to a contracting affine IFS is the map
$\pi $
associated to a contracting affine IFS is the map
![]() $\{1,\dots ,k\}^{\mathbb {N}} \to \mathbb {R}^D$
defined by
$\{1,\dots ,k\}^{\mathbb {N}} \to \mathbb {R}^D$
defined by
for some
![]() $x \in \mathbb {R}^D$
; the limit is independent of x. The image of the coding map
$x \in \mathbb {R}^D$
; the limit is independent of x. The image of the coding map
![]() $\pi $
is precisely the affine fractal
$\pi $
is precisely the affine fractal
![]() $\mathcal {K}$
, and we have the following equivariance property with respect to the shift map T on
$\mathcal {K}$
, and we have the following equivariance property with respect to the shift map T on
![]() $\{1,\dots ,k\}^{\mathbb {N}}$
:
$\{1,\dots ,k\}^{\mathbb {N}}$
:
Our results on random walks on homogeneous spaces also allow us to study a more general situation where the IFS is not required to be finite and where one can allow contraction to only take place on average. To describe this, let I be a compact set and
![]() $I \to \operatorname {\mathrm {GL}}_D(\mathbb {R})\ltimes \mathbb {R}^D$
,
$I \to \operatorname {\mathrm {GL}}_D(\mathbb {R})\ltimes \mathbb {R}^D$
,
![]() $i \mapsto \phi _i=(A_i,b_i)$
a continuous map, where
$i \mapsto \phi _i=(A_i,b_i)$
a continuous map, where
![]() $A_i$
denotes the linear part and
$A_i$
denotes the linear part and
![]() $b_i$
the translation part of
$b_i$
the translation part of
![]() $\phi _i$
. Let
$\phi _i$
. Let
![]() $\mu $
be a probability measure on I. We shall refer to the couple
$\mu $
be a probability measure on I. We shall refer to the couple
![]() $(I,\mu )$
as a contracting-on-average affine IFS if there exists
$(I,\mu )$
as a contracting-on-average affine IFS if there exists
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
This definition does not depend on the choice of operator norm.
Using only boundedness of the translation parts, it is not hard to see that the limit
![]() $\lim _{n \to \infty } \phi _{i_1} \circ \dotsm \circ \phi _{i_n}(x)$
exists and does not depend on
$\lim _{n \to \infty } \phi _{i_1} \circ \dotsm \circ \phi _{i_n}(x)$
exists and does not depend on
![]() $x \in \mathbb {R}^D$
whenever the sequence
$x \in \mathbb {R}^D$
whenever the sequence
![]() $( \left \lVert {A_{i_1}\dotsm A_{i_n}} \right \rVert )_{n\ge 1}$
decays fast enough (e.g., exponentially). Under the contraction-on-average assumption, this holds for
$( \left \lVert {A_{i_1}\dotsm A_{i_n}} \right \rVert )_{n\ge 1}$
decays fast enough (e.g., exponentially). Under the contraction-on-average assumption, this holds for
![]() $\mu ^{\mathbb {N}}$
-almost every
$\mu ^{\mathbb {N}}$
-almost every
![]() $(i_1,i_2, \dots )$
, as one can see using submultiplicativity of the operator norm and Kingman’s subadditive ergodic theorem. In this case, we thus obtain a measurable map
$(i_1,i_2, \dots )$
, as one can see using submultiplicativity of the operator norm and Kingman’s subadditive ergodic theorem. In this case, we thus obtain a measurable map
![]() $\pi \colon I^{\mathbb {N}} \to \mathbb {R}^D$
that we shall refer to as the coding map of
$\pi \colon I^{\mathbb {N}} \to \mathbb {R}^D$
that we shall refer to as the coding map of
![]() $(I,\mu )$
. Note that the subset
$(I,\mu )$
. Note that the subset
![]() $\Omega $
of elements of
$\Omega $
of elements of
![]() $I^{\mathbb {N}}$
for which the previous limit exists satisfies
$I^{\mathbb {N}}$
for which the previous limit exists satisfies
![]() $T \Omega \subset \Omega $
and on this set the coding map
$T \Omega \subset \Omega $
and on this set the coding map
![]() $\pi $
satisfies the equivariance relation (9.3).
$\pi $
satisfies the equivariance relation (9.3).
Finally, we shall say that an IFS
![]() $(I,\mu )$
of affine maps of
$(I,\mu )$
of affine maps of
![]() $\mathbb {R}^D$
is irreducible if there does not exist a proper affine subspace W of
$\mathbb {R}^D$
is irreducible if there does not exist a proper affine subspace W of
![]() $\mathbb {R}^D$
such that
$\mathbb {R}^D$
such that
![]() $\phi _i (W)=W$
for
$\phi _i (W)=W$
for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $i \in I$
.
$i \in I$
.
9.2.2 Self-affine measures
Given a contracting-on-average affine IFS
![]() $(I,\mu )$
, the probability measure
$(I,\mu )$
, the probability measure
![]() $\nu _{\mu }=\pi _* \mu ^{\mathbb {N}}$
on
$\nu _{\mu }=\pi _* \mu ^{\mathbb {N}}$
on
![]() $\mathbb {R}^D$
is called the associated self-affine measure (or self-similar measure if the IFS comprises only similarities). It is with respect to these self-affine measures that we will study the typical Diophantine behavior of vectors in
$\mathbb {R}^D$
is called the associated self-affine measure (or self-similar measure if the IFS comprises only similarities). It is with respect to these self-affine measures that we will study the typical Diophantine behavior of vectors in
![]() $\mathbb {R}^D$
or more generally matrices in
$\mathbb {R}^D$
or more generally matrices in
![]() $\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
. The measure
$\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
. The measure
![]() $\nu _{\mu }$
is the unique stationary probability measure for the random walk on
$\nu _{\mu }$
is the unique stationary probability measure for the random walk on
![]() $\mathbb {R}^D$
given by the IFS; see [Reference Diaconis and Freedman28]. In the case of a finite IFS, that is, when
$\mathbb {R}^D$
given by the IFS; see [Reference Diaconis and Freedman28]. In the case of a finite IFS, that is, when
![]() $I=\{1,\dots ,k\}$
, this just means that
$I=\{1,\dots ,k\}$
, this just means that
![]() $\nu _{\mu }$
is the unique probability measure on
$\nu _{\mu }$
is the unique probability measure on
![]() $\mathbb {R}^D$
satisfying
$\mathbb {R}^D$
satisfying
![]() $\nu _{\mu }=\sum _{i=1}^k \mu (i)(\phi _i)_* \nu _{\mu }$
.
$\nu _{\mu }=\sum _{i=1}^k \mu (i)(\phi _i)_* \nu _{\mu }$
.
For a finite contracting IFS consisting of similarities of
![]() $\mathbb {R}^D$
, under a separation condition (see [Reference Hutchinson50]), the Hausdorff measure on the attractor
$\mathbb {R}^D$
, under a separation condition (see [Reference Hutchinson50]), the Hausdorff measure on the attractor
![]() $\mathcal {K}$
is given by a self-similar measure which is also the unique measure on
$\mathcal {K}$
is given by a self-similar measure which is also the unique measure on
![]() $\mathcal {K}$
whose pointwise dimension matches the Hausdorff dimension of the similarity fractal
$\mathcal {K}$
whose pointwise dimension matches the Hausdorff dimension of the similarity fractal
![]() $\mathcal {K}$
. For genuinely self-affine fractals, the situation is considerably more complicated (see, e.g., [Reference Barral and Feng1, Reference Käenmäki and Vilppolainen51, Reference Morris and Sert71, Reference Morris and Sert70] and the references therein). On the other hand, for the Bedford–McMullen carpets introduced in §1.6 and their higher-dimensional generalizations, there exists a unique ergodic shift-invariant probability measure on
$\mathcal {K}$
. For genuinely self-affine fractals, the situation is considerably more complicated (see, e.g., [Reference Barral and Feng1, Reference Käenmäki and Vilppolainen51, Reference Morris and Sert71, Reference Morris and Sert70] and the references therein). On the other hand, for the Bedford–McMullen carpets introduced in §1.6 and their higher-dimensional generalizations, there exists a unique ergodic shift-invariant probability measure on
![]() $\{1,\dots ,k\}^{\mathbb {N}}$
whose pushforward
$\{1,\dots ,k\}^{\mathbb {N}}$
whose pushforward
![]() $\nu $
by the coding map has full Hausdorff dimension [Reference Kenyon and Peres52]. Moreover, this measure
$\nu $
by the coding map has full Hausdorff dimension [Reference Kenyon and Peres52]. Moreover, this measure
![]() $\nu $
is self-affine. In dimension
$\nu $
is self-affine. In dimension
![]() $2$
, it was already explicitly constructed and used by McMullen [Reference McMullen67], and is referred to as the McMullen measure in the literature.
$2$
, it was already explicitly constructed and used by McMullen [Reference McMullen67], and is referred to as the McMullen measure in the literature.
9.2.3 Matrix sponges
We now describe the family of affine fractals and self-affine measures that will be of interest to us. Let
![]() $\mathbf {r}=(r_1,\dots ,r_m) \in (0,1]^m$
and
$\mathbf {r}=(r_1,\dots ,r_m) \in (0,1]^m$
and
![]() $\mathbf {s}=(s_1,\dots ,s_n) \in (0,1]^n$
be such that
$\mathbf {s}=(s_1,\dots ,s_n) \in (0,1]^n$
be such that
![]() $\sum _{i=1}^mr_i=1=\sum _{j=1}^ns_j$
. Consider the diagonalizable one-parameter groups
$\sum _{i=1}^mr_i=1=\sum _{j=1}^ns_j$
. Consider the diagonalizable one-parameter groups
![]() $A^{\prime }_{\mathbf {r}}\subset \operatorname {\mathrm {GL}}_m(\mathbb {R})$
and
$A^{\prime }_{\mathbf {r}}\subset \operatorname {\mathrm {GL}}_m(\mathbb {R})$
and
![]() $A^{\prime }_{\mathbf {s}}\subset \operatorname {\mathrm {GL}}_n(\mathbb {R})$
given by
$A^{\prime }_{\mathbf {s}}\subset \operatorname {\mathrm {GL}}_n(\mathbb {R})$
given by
![]() and
and
![]() respectively. Denote by
respectively. Denote by
![]() $K_{\mathbf {r}}$
the compact group
$K_{\mathbf {r}}$
the compact group
![]() $C_{\operatorname {\mathrm {GL}}_m(\mathbb {R})}(A^{\prime }_{\mathbf {r}}) \cap \operatorname {\mathrm {O}}_m(\mathbb {R})$
and similarly for
$C_{\operatorname {\mathrm {GL}}_m(\mathbb {R})}(A^{\prime }_{\mathbf {r}}) \cap \operatorname {\mathrm {O}}_m(\mathbb {R})$
and similarly for
![]() $K_{\mathbf {s}}$
substituting
$K_{\mathbf {s}}$
substituting
![]() $\mathbf {s}$
for
$\mathbf {s}$
for
![]() $\mathbf {r}$
and n for m.
$\mathbf {r}$
and n for m.
We identify the real vector space
![]() $\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
with
$\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
with
![]() $\mathbb {R}^{mn}$
and consider affinities
$\mathbb {R}^{mn}$
and consider affinities
![]() $\phi $
of
$\phi $
of
![]() $\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
of the type
$\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
of the type
where
![]() $B \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
,
$B \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
,
![]() $A_1\in \operatorname {\mathrm {GL}}_m(\mathbb {R})$
and
$A_1\in \operatorname {\mathrm {GL}}_m(\mathbb {R})$
and
![]() $A_2\in \operatorname {\mathrm {GL}}_n(\mathbb {R})$
. We will refer to affinities of this form as matrix affinities and use the notation
$A_2\in \operatorname {\mathrm {GL}}_n(\mathbb {R})$
. We will refer to affinities of this form as matrix affinities and use the notation
![]() $(A_1,A_2,B)$
to denote such a map. If a matrix affinity
$(A_1,A_2,B)$
to denote such a map. If a matrix affinity
![]() $\phi $
can be written as
$\phi $
can be written as
![]() $\phi =(A_1,A_2,B)$
with
$\phi =(A_1,A_2,B)$
with
![]() $A_1 \in a_{\mathbf {r}}(t) K_{\mathbf {r}}$
and
$A_1 \in a_{\mathbf {r}}(t) K_{\mathbf {r}}$
and
![]() $A_2 \in a_{\mathbf {s}}(t) K_{\mathbf {s}}$
for some
$A_2 \in a_{\mathbf {s}}(t) K_{\mathbf {s}}$
for some
![]() $t \in \mathbb {R}$
, then we call it an
$t \in \mathbb {R}$
, then we call it an
![]() $(\mathbf {r},\mathbf {s})$
-matrix sponge affinity. Given a contracting-on-average IFS
$(\mathbf {r},\mathbf {s})$
-matrix sponge affinity. Given a contracting-on-average IFS
![]() $(I,\mu )$
of
$(I,\mu )$
of
![]() $(\mathbf {r},\mathbf {s})$
-matrix sponge affinities, we call the associated attractor
$(\mathbf {r},\mathbf {s})$
-matrix sponge affinities, we call the associated attractor
![]() $\mathcal {K}$
an
$\mathcal {K}$
an
![]() $(\mathbf {r},\mathbf {s})$
-matrix sponge.
$(\mathbf {r},\mathbf {s})$
-matrix sponge.
A cautionary remark is in order about our terminology. In the literature, the terms ‘carpet’ (in dimension
![]() $2$
) or ‘sponge’ (in general dimension) are used to describe self-affine fractals associated to IFS’s whose linear parts are simultaneously diagonalizable with nontrivial (i.e., nonscalar) diagonals. However, the matrix sponge affinities that we just described also comprise many similarities of
$2$
) or ‘sponge’ (in general dimension) are used to describe self-affine fractals associated to IFS’s whose linear parts are simultaneously diagonalizable with nontrivial (i.e., nonscalar) diagonals. However, the matrix sponge affinities that we just described also comprise many similarities of
![]() $\mathbb {R}^{mn}$
. Similarities of
$\mathbb {R}^{mn}$
. Similarities of
![]() $\mathbb {R}^{mn}$
of this form are called ‘algebraic similarities’ by Simmons–Weiss [Reference Simmons and Weiss93, §8.4], which thus form a strict subclass of matrix sponge affinities. For example, specializing to
$\mathbb {R}^{mn}$
of this form are called ‘algebraic similarities’ by Simmons–Weiss [Reference Simmons and Weiss93, §8.4], which thus form a strict subclass of matrix sponge affinities. For example, specializing to
![]() $n=1$
we can record that the class of
$n=1$
we can record that the class of
![]() $(\mathbf {m},1)$
-matrix sponges contains all self-similar fractals in
$(\mathbf {m},1)$
-matrix sponges contains all self-similar fractals in
![]() $\mathbb {R}^m$
and the class of
$\mathbb {R}^m$
and the class of
![]() $(\mathbf {r},1)$
-matrix sponges contains many examples of Bedford–McMullen carpets and their higher-dimensional analogues—the self-affine Sierpiński sponges—for suitably chosen weight vectors
$(\mathbf {r},1)$
-matrix sponges contains many examples of Bedford–McMullen carpets and their higher-dimensional analogues—the self-affine Sierpiński sponges—for suitably chosen weight vectors
![]() $\mathbf {r}$
.
$\mathbf {r}$
.
9.3 Relation with random walks and consequences
Here, we first adapt the constructions of Simmons–Weiss [Reference Simmons and Weiss93] relating algebraic similarities with elements of
![]() $\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
to the more general setting of matrix affinities. Then, we state and prove the main result of this section (Theorem 9.3) on Diophantine properties of matrix sponges.
$\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
to the more general setting of matrix affinities. Then, we state and prove the main result of this section (Theorem 9.3) on Diophantine properties of matrix sponges.
9.3.1 Embedding matrix sponge affinities into
 $\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
$\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
Let
![]() $d=m+n$
. Given a matrix affinity
$d=m+n$
. Given a matrix affinity
![]() $\phi =(A_1,A_2,B)$
of
$\phi =(A_1,A_2,B)$
of
![]() $\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, where
$\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, where
![]() $A_1 \in \operatorname {\mathrm {GL}}_m(\mathbb {R})$
,
$A_1 \in \operatorname {\mathrm {GL}}_m(\mathbb {R})$
,
![]() $A_2 \in \operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
$A_2 \in \operatorname {\mathrm {GL}}_n(\mathbb {R})$
and
![]() $B \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, we consider the element
$B \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, we consider the element
![]() $\hat {A}_\phi $
of
$\hat {A}_\phi $
of
![]() $\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
corresponding to the matrix
$\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
corresponding to the matrix
 $$ \begin{align*} \hat{A}_\phi=\begin{pmatrix} A_1 & 0\\ 0 & A_2^{-1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \hat{A}_\phi=\begin{pmatrix} A_1 & 0\\ 0 & A_2^{-1} \end{pmatrix}. \end{align*} $$
The following basic relation in
![]() $\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
, which is readily verified, plays a key role in transferring the results on random walks on homogeneous spaces to the study of Diophantine properties of matrix sponges: For
$\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
, which is readily verified, plays a key role in transferring the results on random walks on homogeneous spaces to the study of Diophantine properties of matrix sponges: For
![]() $M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, we have
$M \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
, we have
where, as before,
![]() $u_M=(\begin {smallmatrix}I_m & -M \\ 0 & I_n\end {smallmatrix})$
. We set
$u_M=(\begin {smallmatrix}I_m & -M \\ 0 & I_n\end {smallmatrix})$
. We set
![]() . Given matrix affinities
. Given matrix affinities
![]() $\phi _1,\dots ,\phi _n$
, iterating equation (9.6) yields
$\phi _1,\dots ,\phi _n$
, iterating equation (9.6) yields
9.3.2 Genericity of typical points on matrix sponges
To state the following main result of this section, recall that given a contracting-on-average affine IFS
![]() $(I,\mu )$
, we denote by
$(I,\mu )$
, we denote by
![]() $\pi $
the associated coding map and by
$\pi $
the associated coding map and by
![]() $\nu _{\mu }$
the pushforward of the Bernoulli measure
$\nu _{\mu }$
the pushforward of the Bernoulli measure
![]() $\beta =\mu ^{\mathbb {N}}$
by
$\beta =\mu ^{\mathbb {N}}$
by
![]() $\pi $
.
$\pi $
.
Theorem 9.3. Let
![]() $(I,\mu )$
be an irreducible contracting-on-average IFS consisting of
$(I,\mu )$
be an irreducible contracting-on-average IFS consisting of
![]() $(\mathbf {r},\mathbf {s})$
-matrix sponge affinities. Then
$(\mathbf {r},\mathbf {s})$
-matrix sponge affinities. Then
![]() $\nu _{\mu }$
-almost every point of
$\nu _{\mu }$
-almost every point of
![]() $\mathbb {R}^{mn}$
is of
$\mathbb {R}^{mn}$
is of
![]() $(\mathbf {r},\mathbf {s})$
-generic type; in particular,
$(\mathbf {r},\mathbf {s})$
-generic type; in particular,
![]() $(\mathbf {r},\mathbf {s})$
-well approximable and not
$(\mathbf {r},\mathbf {s})$
-well approximable and not
![]() $(\mathbf {r},\mathbf {s})$
-Dirichlet improvable.
$(\mathbf {r},\mathbf {s})$
-Dirichlet improvable.
In the classical case where
![]() $(\mathbf {r},\mathbf {s})=(\mathbf {m},\mathbf {n})$
, this result corresponds to Simmons–Weiss’ [Reference Simmons and Weiss93, Theorem 8.11], which implies one of the main results of that article ([Reference Simmons and Weiss93, Theorem 1.2]). We are going to see in the proof that the contracting-on-average assumption in the theorem above amounts to asking that the
$(\mathbf {r},\mathbf {s})=(\mathbf {m},\mathbf {n})$
, this result corresponds to Simmons–Weiss’ [Reference Simmons and Weiss93, Theorem 8.11], which implies one of the main results of that article ([Reference Simmons and Weiss93, Theorem 1.2]). We are going to see in the proof that the contracting-on-average assumption in the theorem above amounts to asking that the
![]() $\mu $
-average of the t-parameters associated to the
$\mu $
-average of the t-parameters associated to the
![]() $(\mathbf {r},\mathbf {s})$
-matrix sponge affinities
$(\mathbf {r},\mathbf {s})$
-matrix sponge affinities
![]() $\phi $
in the IFS is negative. This allows for easy checking of this condition.
$\phi $
in the IFS is negative. This allows for easy checking of this condition.
Remark 9.4. The conclusion of Theorem 9.3 also holds for any measure
![]() $\tilde {\nu }_{\mu }$
obtained as pushforward of
$\tilde {\nu }_{\mu }$
obtained as pushforward of
![]() $\nu _{\mu }$
by an affine transformation of the linear space
$\nu _{\mu }$
by an affine transformation of the linear space
![]() $\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
of the form
$\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
of the form
![]() $M \mapsto \alpha M \beta +\gamma $
, where
$M \mapsto \alpha M \beta +\gamma $
, where
![]() $\alpha \in \operatorname {\mathrm {GL}}_{m}(\mathbb {R})$
commutes with the diagonal group
$\alpha \in \operatorname {\mathrm {GL}}_{m}(\mathbb {R})$
commutes with the diagonal group
![]() $A^{\prime }_{\textbf {r}}$
,
$A^{\prime }_{\textbf {r}}$
,
![]() $\beta \in \operatorname {\mathrm {GL}}_{n}(\mathbb {R})$
commutes with
$\beta \in \operatorname {\mathrm {GL}}_{n}(\mathbb {R})$
commutes with
![]() $A^{\prime }_{\textbf {s}}$
and
$A^{\prime }_{\textbf {s}}$
and
![]() $\gamma \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
. In particular, these Diophantine properties of
$\gamma \in \operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
. In particular, these Diophantine properties of
![]() $\nu _{\mu }$
are invariant under translation of
$\nu _{\mu }$
are invariant under translation of
![]() $\nu _{\mu }$
.
$\nu _{\mu }$
.
We will deduce the theorem above by combining Theorem 1.11, Dani–Kleinbock correspondence and the introduced constructions. To ease notation, we will assume from now on that I is already a set of matrix sponge affinities, with
![]() $\mu $
living thereon.
$\mu $
living thereon.
Proof of Theorem 9.3
Recall that
![]() $\mathbf {r} =(r_1,\dots ,r_m) \in (0,1]^m$
and
$\mathbf {r} =(r_1,\dots ,r_m) \in (0,1]^m$
and
![]() $\mathbf {s} =(s_1,\dots ,s_n) \in (0,1]^n$
are such that
$\mathbf {s} =(s_1,\dots ,s_n) \in (0,1]^n$
are such that
![]() $\sum _{i=1}^m r_i=1=\sum _{j=1}^n s_j$
, where m and n are positive integers. Let
$\sum _{i=1}^m r_i=1=\sum _{j=1}^n s_j$
, where m and n are positive integers. Let
![]() $d=m+n$
, and set
$d=m+n$
, and set
![]() $G=H=\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
and
$G=H=\operatorname {\mathrm {PGL}}_d(\mathbb {R})$
and
![]() $\Lambda =\operatorname {\mathrm {PGL}}_d(\mathbb {Z})$
. Moreover, we let
$\Lambda =\operatorname {\mathrm {PGL}}_d(\mathbb {Z})$
. Moreover, we let
![]() $A'=\{a(t)\mid t\in \mathbb {R}\}$
be the one-parameter diagonalizable subgroup of G containing
$A'=\{a(t)\mid t\in \mathbb {R}\}$
be the one-parameter diagonalizable subgroup of G containing
![]() $a(1)=\operatorname {\mathrm {diag}}(e^{r_1}, \dots , e^{r_m}, e^{-s_1}, \dots , e^{-s_n})$
, and denote by
$a(1)=\operatorname {\mathrm {diag}}(e^{r_1}, \dots , e^{r_m}, e^{-s_1}, \dots , e^{-s_n})$
, and denote by
![]() $A^{\prime }_+$
its positive ray
$A^{\prime }_+$
its positive ray
![]() $\{a(t) \mid t> 0 \}$
. Take U to be the unipotent subgroup of G given by the image of
$\{a(t) \mid t> 0 \}$
. Take U to be the unipotent subgroup of G given by the image of
![]() $\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
under the map
$\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R})$
under the map
![]() $M \mapsto u_M$
. It is
$M \mapsto u_M$
. It is
![]() $a(1)$
-expanding (see Example 3.9). In view of Dani–Kleinbock correspondence and Theorem 1.11, all we need to check is that the pushforward
$a(1)$
-expanding (see Example 3.9). In view of Dani–Kleinbock correspondence and Theorem 1.11, all we need to check is that the pushforward
![]() $\eta _0$
of the self-affine measure
$\eta _0$
of the self-affine measure
![]() $\nu _{\mu }$
by the map
$\nu _{\mu }$
by the map
![]() $M \mapsto u_M$
is generated by
$M \mapsto u_M$
is generated by
![]() $a(1)$
-expanding random walks in the sense of Definition 1.10.
$a(1)$
-expanding random walks in the sense of Definition 1.10.
We first define the probability measure
![]() $\mu _0$
on G. Given a matrix affinity
$\mu _0$
on G. Given a matrix affinity
![]() $\phi =(A_1,A_2,B)$
, recall the notation
$\phi =(A_1,A_2,B)$
, recall the notation
![]() $g_\phi =\hat {A}_\phi ^{-1}u_B \in \operatorname {\mathrm {PGL}}_d(\mathbb {R})$
introduced in §9.3.1. We take
$g_\phi =\hat {A}_\phi ^{-1}u_B \in \operatorname {\mathrm {PGL}}_d(\mathbb {R})$
introduced in §9.3.1. We take
the pushforward of
![]() $\mu $
by the map
$\mu $
by the map
![]() $c\colon \phi \mapsto g_\phi $
. Then it follows from our constructions that
$c\colon \phi \mapsto g_\phi $
. Then it follows from our constructions that
![]() $\mu _0(P)=1$
, where
$\mu _0(P)=1$
, where
![]() $P=K'A'U$
is defined as before Definition 1.10. Moreover, we claim that the contraction-on-average assumption implies that
$P=K'A'U$
is defined as before Definition 1.10. Moreover, we claim that the contraction-on-average assumption implies that
![]() $\int _P \lambda (g)\mathop {}\!\mathrm {d}\mu _0(g)>0$
. To see this, endow
$\int _P \lambda (g)\mathop {}\!\mathrm {d}\mu _0(g)>0$
. To see this, endow
![]() $\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R}) \cong \mathbb {R}^{mn}$
with the standard Euclidean structure and denote by
$\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R}) \cong \mathbb {R}^{mn}$
with the standard Euclidean structure and denote by
![]() $ \left \lVert {\cdot } \right \rVert $
the associated operator norm on
$ \left \lVert {\cdot } \right \rVert $
the associated operator norm on
![]() $\operatorname {\mathrm {End}}(\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R}))$
. Given an
$\operatorname {\mathrm {End}}(\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R}))$
. Given an
![]() $(\mathbf {r},\mathbf {s})$
-matrix sponge affinity
$(\mathbf {r},\mathbf {s})$
-matrix sponge affinity
![]() $\phi $
, let us denote by
$\phi $
, let us denote by
![]() $A_\phi \in \operatorname {\mathrm {End}}(\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R}))$
its linear part. By definition, we may write
$A_\phi \in \operatorname {\mathrm {End}}(\operatorname {\mathrm {Mat}}_{m \times n}(\mathbb {R}))$
its linear part. By definition, we may write
![]() $\phi =(A_1,A_2,B)$
as in equation (9.5) with
$\phi =(A_1,A_2,B)$
as in equation (9.5) with
![]() $A_1 \in a_{\mathbf {r}}(t)K_{\mathbf {r}}$
and
$A_1 \in a_{\mathbf {r}}(t)K_{\mathbf {r}}$
and
![]() $A_2 \in a_{\mathbf {s}}(t)K_{\mathbf {s}}$
for some
$A_2 \in a_{\mathbf {s}}(t)K_{\mathbf {s}}$
for some
![]() $t\in \mathbb {R}$
. Observe that by construction, the t-parameter is given by
$t\in \mathbb {R}$
. Observe that by construction, the t-parameter is given by
![]() $t=-\lambda (g_\phi )$
. This implies that
$t=-\lambda (g_\phi )$
. This implies that
where
![]() . Plugging this inequality into the contraction-on-average property (9.4) and observing that
. Plugging this inequality into the contraction-on-average property (9.4) and observing that
![]() $\lambda (g_{\phi _N\dotsm \phi _1})=\lambda (g_{\phi _N})+\dots +\lambda (g_{\phi _1})$
yields
$\lambda (g_{\phi _N\dotsm \phi _1})=\lambda (g_{\phi _N})+\dots +\lambda (g_{\phi _1})$
yields
![]() $\int _P \lambda (g)\mathop {}\!\mathrm {d}\mu _0(g)=\int \lambda (g_\phi )\mathop {}\!\mathrm {d}\mu (\phi )>0$
, hence the claim.
$\int _P \lambda (g)\mathop {}\!\mathrm {d}\mu _0(g)=\int \lambda (g_\phi )\mathop {}\!\mathrm {d}\mu (\phi )>0$
, hence the claim.
We now show that the irreducibility assumption entails that
![]() $U\leqslant \operatorname {\mathrm {Zcl}}(\Gamma _{\mu _0})$
. As in the proof of Proposition 8.2, we will first reduce to the case of special measures
$U\leqslant \operatorname {\mathrm {Zcl}}(\Gamma _{\mu _0})$
. As in the proof of Proposition 8.2, we will first reduce to the case of special measures
![]() $\mu _0$
for which
$\mu _0$
for which
![]() $\Gamma _{\mu _0}$
contains an element of
$\Gamma _{\mu _0}$
contains an element of
![]() $K'A^{\prime }_+$
. Indeed, given a general
$K'A^{\prime }_+$
. Indeed, given a general
![]() $\mu _0$
as in equation (9.8), using that
$\mu _0$
as in equation (9.8), using that
![]() $\int _P \lambda (g)\mathop {}\!\mathrm {d}\mu _0(g)>0$
and Lemma 8.3, it follows that there exists
$\int _P \lambda (g)\mathop {}\!\mathrm {d}\mu _0(g)>0$
and Lemma 8.3, it follows that there exists
![]() $u_0 \in U$
such that the pushforward by conjugation
$u_0 \in U$
such that the pushforward by conjugation
![]() $(\tau _{u_0})_* \mu _0$
is special. The closed group generated by the support of
$(\tau _{u_0})_* \mu _0$
is special. The closed group generated by the support of
![]() $(\tau _{u_0})_* \mu _0$
is
$(\tau _{u_0})_* \mu _0$
is
![]() $u_0 \Gamma _{\mu _0} u_0^{-1}$
and if the Zariski closure of this group contains U, then that of
$u_0 \Gamma _{\mu _0} u_0^{-1}$
and if the Zariski closure of this group contains U, then that of
![]() $\Gamma _{\mu _0}$
also contains U. Moreover, this conjugation corresponds to conjugating the IFS by a translation so that also irreducibility is preserved. So we now suppose that
$\Gamma _{\mu _0}$
also contains U. Moreover, this conjugation corresponds to conjugating the IFS by a translation so that also irreducibility is preserved. So we now suppose that
![]() $\mu _0$
is special. Then as in the proof of Proposition 8.2, for every
$\mu _0$
is special. Then as in the proof of Proposition 8.2, for every
![]() $g\in \Gamma _{\mu _0}$
written
$g\in \Gamma _{\mu _0}$
written
![]() $g=k_ga_gu_g$
in its
$g=k_ga_gu_g$
in its
![]() $K'A'U$
-factorization, we know that also
$K'A'U$
-factorization, we know that also
![]() $k_ga_g$
and
$k_ga_g$
and
![]() $u_g$
belong to
$u_g$
belong to
![]() $\Gamma _{\mu _0}$
. It follows that for every
$\Gamma _{\mu _0}$
. It follows that for every
![]() $g \in \Gamma _{\mu _0}$
, the one-parameter unipotent subgroup of U containing
$g \in \Gamma _{\mu _0}$
, the one-parameter unipotent subgroup of U containing
![]() $u_g$
is contained in the Zariski closure of
$u_g$
is contained in the Zariski closure of
![]() $\Gamma _{\mu _0}$
. Now, consider the connected unipotent group
$\Gamma _{\mu _0}$
. Now, consider the connected unipotent group
![]() $V=\operatorname {\mathrm {Zcl}}(\Gamma _{\mu _0}) \cap U$
and let
$V=\operatorname {\mathrm {Zcl}}(\Gamma _{\mu _0}) \cap U$
and let
![]() $W_V$
be the corresponding subspace of
$W_V$
be the corresponding subspace of
![]() $\mathbb {R}^{mn}$
under (the inverse of) the identification
$\mathbb {R}^{mn}$
under (the inverse of) the identification
![]() $M \mapsto u_M$
. We claim that the subspace
$M \mapsto u_M$
. We claim that the subspace
![]() $W_V$
is invariant by the IFS of matrix sponge affinities. Indeed, by construction, for any
$W_V$
is invariant by the IFS of matrix sponge affinities. Indeed, by construction, for any
![]() $\phi =(A_1,A_2,B)$
in the IFS, the unipotent part
$\phi =(A_1,A_2,B)$
in the IFS, the unipotent part
![]() $u_B$
of the associated element
$u_B$
of the associated element
![]() $g_\phi $
belongs to V and hence
$g_\phi $
belongs to V and hence
![]() $B \in W_V$
. Moreover, for any
$B \in W_V$
. Moreover, for any
![]() $g \in \Gamma _{\mu _0}$
, its
$g \in \Gamma _{\mu _0}$
, its
![]() $K'A'$
-component
$K'A'$
-component
![]() $k_ga_g$
normalizes V. In view of equation (9.6), this translates to the statement that for any
$k_ga_g$
normalizes V. In view of equation (9.6), this translates to the statement that for any
![]() $\phi $
of the IFS, the linear part of
$\phi $
of the IFS, the linear part of
![]() $\phi $
leaves the subspace
$\phi $
leaves the subspace
![]() $W_V$
invariant. It follows that the subspace
$W_V$
invariant. It follows that the subspace
![]() $W_V$
of
$W_V$
of
![]() $\mathbb {R}^{mn}$
is invariant by the IFS. Hence, by the irreducibility hypothesis, we have
$\mathbb {R}^{mn}$
is invariant by the IFS. Hence, by the irreducibility hypothesis, we have
![]() $W_V=\mathbb {R}^{mn}$
, or equivalently,
$W_V=\mathbb {R}^{mn}$
, or equivalently,
![]() $V=U$
.
$V=U$
.
It remains to check that the measure
![]() $\eta _0$
coincides with the image of
$\eta _0$
coincides with the image of
![]() $\mu _0^{\mathbb {N}}$
under the map
$\mu _0^{\mathbb {N}}$
under the map
![]() $\omega \mapsto u_{\omega }$
defined by Lemma 8.1. To do this, let
$\omega \mapsto u_{\omega }$
defined by Lemma 8.1. To do this, let
![]() $\omega =(g_{\phi _1},g_{\phi _2},\dots )$
. By definition of the coding map (9.2) and the map
$\omega =(g_{\phi _1},g_{\phi _2},\dots )$
. By definition of the coding map (9.2) and the map
![]() $\omega \mapsto u_{\omega }$
, it suffices to observe that for every
$\omega \mapsto u_{\omega }$
, it suffices to observe that for every
![]() $n\in \mathbb {N}$
, factorizing
$n\in \mathbb {N}$
, factorizing
![]() $g_{\phi _n} \dotsm g_{\phi _1}$
as
$g_{\phi _n} \dotsm g_{\phi _1}$
as
![]() $k_{\omega ,n}a_{\omega ,n}u_{\omega ,n}$
with
$k_{\omega ,n}a_{\omega ,n}u_{\omega ,n}$
with
![]() $k_{\omega ,n} \in K'$
,
$k_{\omega ,n} \in K'$
,
![]() $a_{\omega ,n} \in A'$
and
$a_{\omega ,n} \in A'$
and
![]() $u_{\omega ,n} \in U$
, we have
$u_{\omega ,n} \in U$
, we have
![]() $u_{\omega ,n}=u_{\phi _1\dotsm \phi _n (0)}$
; see equation (9.7). This finishes the proof.
$u_{\omega ,n}=u_{\phi _1\dotsm \phi _n (0)}$
; see equation (9.7). This finishes the proof.
Finally, we state and prove the corollary of the previous theorem regarding the higher-dimensional analogues of Bedford–McMullen carpets, which was announced at the end of §1.6. These higher-dimensional fractals are constructed by the exact analogue in
![]() $\mathbb {R}^m$
of the procedure for Bedford–McMullen carpets described before Theorem 1.12, now using pairwise distinct integers
$\mathbb {R}^m$
of the procedure for Bedford–McMullen carpets described before Theorem 1.12, now using pairwise distinct integers
![]() $a_1,\dots ,a_m\ge 2$
and a division of
$a_1,\dots ,a_m\ge 2$
and a division of
![]() $[0,1]^m$
into an
$[0,1]^m$
into an
![]() $a_1\times \dots \times a_m$
-grid. A fractal
$a_1\times \dots \times a_m$
-grid. A fractal
![]() $\mathcal {K}$
obtained in this way is called a self-affine Sierpiński sponge. Analogous to the McMullen measure on a Bedford–McMullen carpet, there exists a natural probability measure
$\mathcal {K}$
obtained in this way is called a self-affine Sierpiński sponge. Analogous to the McMullen measure on a Bedford–McMullen carpet, there exists a natural probability measure
![]() $\nu _{\mathcal {K}}$
on
$\nu _{\mathcal {K}}$
on
![]() $\mathcal {K}$
: Identifying
$\mathcal {K}$
: Identifying
![]() $[0,1]^m$
with the m-torus and denoting by T the toral endomorphism corresponding to the diagonal matrix
$[0,1]^m$
with the m-torus and denoting by T the toral endomorphism corresponding to the diagonal matrix
![]() $A=\operatorname {\mathrm {diag}}(a_1,\dots ,a_m)$
,
$A=\operatorname {\mathrm {diag}}(a_1,\dots ,a_m)$
,
![]() $\nu _{\mathcal {K}}$
is the unique T-invariant ergodic probability measure on
$\nu _{\mathcal {K}}$
is the unique T-invariant ergodic probability measure on
![]() $\mathcal {K}$
of full Hausdorff dimension (see Kenyon–Peres [Reference Kenyon and Peres52]).
$\mathcal {K}$
of full Hausdorff dimension (see Kenyon–Peres [Reference Kenyon and Peres52]).
Corollary 9.5. Let
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $a_1,\dots ,a_m\ge 2$
be pairwise distinct integers satisfying
$a_1,\dots ,a_m\ge 2$
be pairwise distinct integers satisfying
 $$ \begin{align} \frac1m\sum_{j\neq i}\log a_j< \log a_i<\frac{2}{m-1}\sum_{j\neq i}\log a_j \end{align} $$
$$ \begin{align} \frac1m\sum_{j\neq i}\log a_j< \log a_i<\frac{2}{m-1}\sum_{j\neq i}\log a_j \end{align} $$
for
![]() $i=1,\dots ,m$
. Let
$i=1,\dots ,m$
. Let
![]() $\mathcal {K}\subset \mathbb {R}^m$
be a self-affine Sierpiński sponge invariant under the toral endomorphism T corresponding to the matrix
$\mathcal {K}\subset \mathbb {R}^m$
be a self-affine Sierpiński sponge invariant under the toral endomorphism T corresponding to the matrix
![]() $A=\operatorname {\mathrm {diag}}(a_1,\dots ,a_m)$
such that
$A=\operatorname {\mathrm {diag}}(a_1,\dots ,a_m)$
such that
![]() $\mathcal {K}$
is not contained in any affine hyperplane. Then for the choice of weights
$\mathcal {K}$
is not contained in any affine hyperplane. Then for the choice of weights
 $$ \begin{align} \mathbf{r}=\biggl(\frac{m\log a_i-\sum_{j\neq i}\log a_j}{\sum_j\log a_j}\biggr)_{1\le i\le m}, \end{align} $$
$$ \begin{align} \mathbf{r}=\biggl(\frac{m\log a_i-\sum_{j\neq i}\log a_j}{\sum_j\log a_j}\biggr)_{1\le i\le m}, \end{align} $$
the set of
![]() $\mathbf {r}$
-badly approximable vectors on
$\mathbf {r}$
-badly approximable vectors on
![]() $\mathcal {K}$
has measure zero with respect to
$\mathcal {K}$
has measure zero with respect to
![]() $\nu _{\mathcal {K}}$
.
$\nu _{\mathcal {K}}$
.
This corollary directly implies Theorem 1.12.
Proof. We start by noting that
![]() $\mathcal {K}$
is the attractor of a finite contracting affine IFS
$\mathcal {K}$
is the attractor of a finite contracting affine IFS
![]() $(\phi _1,\dots ,\phi _k)$
, where
$(\phi _1,\dots ,\phi _k)$
, where
![]() $\phi _i\colon x\mapsto A^{-1}x+b_i$
with translation vectors
$\phi _i\colon x\mapsto A^{-1}x+b_i$
with translation vectors
![]() $b_i\in \prod _j\{0,\frac {1}{a_j},\dots ,\frac {a_j-1}{a_j}\}$
. If
$b_i\in \prod _j\{0,\frac {1}{a_j},\dots ,\frac {a_j-1}{a_j}\}$
. If
![]() $I=\{1,\dots ,k\}$
and
$I=\{1,\dots ,k\}$
and
![]() $\pi \colon I^{\mathbb {N}}\to \mathbb {R}^m$
denotes the associated coding map, the proof of [Reference Kenyon and Peres52, Theorem 1.2] shows that
$\pi \colon I^{\mathbb {N}}\to \mathbb {R}^m$
denotes the associated coding map, the proof of [Reference Kenyon and Peres52, Theorem 1.2] shows that
![]() $\nu _{\mathcal {K}}=\nu _{\mu }=\pi _*\mu ^{\mathbb {N}}$
for some probability measure
$\nu _{\mathcal {K}}=\nu _{\mu }=\pi _*\mu ^{\mathbb {N}}$
for some probability measure
![]() $\mu $
on I of full support. Then the assumption that
$\mu $
on I of full support. Then the assumption that
![]() $\mathcal {K}$
is not contained in any affine hyperplane implies that the IFS
$\mathcal {K}$
is not contained in any affine hyperplane implies that the IFS
![]() $(I,\mu )$
is irreducible. We wish to arrange that the
$(I,\mu )$
is irreducible. We wish to arrange that the
![]() $\phi _i$
can be seen as
$\phi _i$
can be seen as
![]() $(\mathbf {r},1)$
-matrix sponge affinities. By definition, this means that we have to write the linear part
$(\mathbf {r},1)$
-matrix sponge affinities. By definition, this means that we have to write the linear part
![]() $A^{-1}=\operatorname {\mathrm {diag}}(a_1^{-1},\dots ,a_m^{-1})$
as
$A^{-1}=\operatorname {\mathrm {diag}}(a_1^{-1},\dots ,a_m^{-1})$
as
![]() $e^ta_{\mathbf {r}}(t)$
for some
$e^ta_{\mathbf {r}}(t)$
for some
![]() $t\in \mathbb {R}$
, where
$t\in \mathbb {R}$
, where
![]() $a_{\mathbf {r}}(t)=\operatorname {\mathrm {diag}}(e^{tr_1},\dots ,e^{tr_m})$
. Solving the resulting system of equations under the constraint
$a_{\mathbf {r}}(t)=\operatorname {\mathrm {diag}}(e^{tr_1},\dots ,e^{tr_m})$
. Solving the resulting system of equations under the constraint
![]() $r_1+\dots +r_m=1$
yields the weights specified by (9.10). The condition (9.9) ensures that
$r_1+\dots +r_m=1$
yields the weights specified by (9.10). The condition (9.9) ensures that
![]() $\mathbf {r}\in (0,1)^m$
. Hence, Theorem 9.3 applies and gives the desired conclusion.
$\mathbf {r}\in (0,1)^m$
. Hence, Theorem 9.3 applies and gives the desired conclusion.
We end our discussion of Diophantine approximation by mentioning that our approach has serious limitations when trying to tackle the general problem of understanding the measure-theoretic size of badly approximable vectors or matrices—weighted or not—in general self-affine fractals. Even seemingly tractable cases—for example,
![]() $\mathbf {r}$
-badly approximable vectors on an affine fractal for which
$\mathbf {r}$
-badly approximable vectors on an affine fractal for which
![]() $\mathbf {r}$
represents the average contraction ratio—require a further understanding of diagonal flows and, frustratingly, remain open.
$\mathbf {r}$
represents the average contraction ratio—require a further understanding of diagonal flows and, frustratingly, remain open.
Appendix A Epimorphic subgroups and subalgebras
In category theory, an epimorphism is by definition a morphism
![]() $f\colon A\to B$
satisfying the right cancellation property:
$f\colon A\to B$
satisfying the right cancellation property:
![]() $g\circ f=h\circ f$
implies
$g\circ f=h\circ f$
implies
![]() $g=h$
for any two morphisms
$g=h$
for any two morphisms
![]() $g,h$
from B to another object of the category. In categories where morphisms are maps with certain properties between underlying sets, the epimorphism property is equivalent to the question whether the values on the image of f uniquely determine morphisms from B to other objects. In this case, surjective morphisms are clearly epimorphisms. In many familiar categories, the converse, that is, that only surjective morphisms can be epimorphisms, is also true. For example, this holds in the categories of
$g,h$
from B to another object of the category. In categories where morphisms are maps with certain properties between underlying sets, the epimorphism property is equivalent to the question whether the values on the image of f uniquely determine morphisms from B to other objects. In this case, surjective morphisms are clearly epimorphisms. In many familiar categories, the converse, that is, that only surjective morphisms can be epimorphisms, is also true. For example, this holds in the categories of
![]() $C^*$
-algebras, groups, finite groups, all Lie algebras over a field k, and finite-dimensional Lie algebras over a field k of positive characteristic; see [Reference Bergman12, Reference Reid85]. However, there are notable exceptions. These include the categories of finite-dimensional Lie algebras over a field of characteristic
$C^*$
-algebras, groups, finite groups, all Lie algebras over a field k, and finite-dimensional Lie algebras over a field k of positive characteristic; see [Reference Bergman12, Reference Reid85]. However, there are notable exceptions. These include the categories of finite-dimensional Lie algebras over a field of characteristic
![]() $0$
and that of algebraic groups, which are our main interest. The corresponding lines of study were initiated by Bergman [Reference Bergman12] and Bien–Borel [Reference Bien and Borel13, Reference Bien and Borel14], respectively, who proved the following.
$0$
and that of algebraic groups, which are our main interest. The corresponding lines of study were initiated by Bergman [Reference Bergman12] and Bien–Borel [Reference Bien and Borel13, Reference Bien and Borel14], respectively, who proved the following.
Proposition A.1.
-
(i) ([Reference Bergman12, Corollary 3.2]) Let
 $\mathfrak f\subset \mathfrak g$
be finite-dimensional Lie algebras over a field k. Then the inclusion
$\mathfrak f\subset \mathfrak g$
be finite-dimensional Lie algebras over a field k. Then the inclusion
 $\mathfrak f\hookrightarrow \mathfrak g$
is an epimorphism if and only if in every finite-dimensional representation of
$\mathfrak f\hookrightarrow \mathfrak g$
is an epimorphism if and only if in every finite-dimensional representation of
 $\mathfrak g$
, the subspaces annihilated by
$\mathfrak g$
, the subspaces annihilated by
 $\mathfrak f$
and
$\mathfrak f$
and
 $\mathfrak g$
coincide.
$\mathfrak g$
coincide. -
(ii) ([Reference Bien and Borel13, Theorem 1]) Let
 $\mathbf {G}$
be a Zariski connected linear algebraic group over an algebraically closed field k, and
$\mathbf {G}$
be a Zariski connected linear algebraic group over an algebraically closed field k, and
 $\mathbf {F}\leqslant \mathbf {G}$
an algebraic subgroup. Then the inclusion
$\mathbf {F}\leqslant \mathbf {G}$
an algebraic subgroup. Then the inclusion
 $\mathbf {F}\hookrightarrow \mathbf {G}$
is an epimorphism if and only if in every finite-dimensional algebraic representation of
$\mathbf {F}\hookrightarrow \mathbf {G}$
is an epimorphism if and only if in every finite-dimensional algebraic representation of
 $\mathbf {G}$
, the subspaces of
$\mathbf {G}$
, the subspaces of
 $\mathbf {F}$
- and
$\mathbf {F}$
- and
 $\mathbf {G}$
-fixed vectors coincide.
$\mathbf {G}$
-fixed vectors coincide.
We take this representation-theoretic characterization as the defining property of an epimorphic subgroup of a semisimple real Lie group.
Definition A.2.
-
(i) Let
 $\mathfrak f$
be a subalgebra of a finite-dimensional real Lie algebra
$\mathfrak f$
be a subalgebra of a finite-dimensional real Lie algebra
 $\mathfrak g$
. We say that
$\mathfrak g$
. We say that
 $\mathfrak f$
is epimorphic in
$\mathfrak f$
is epimorphic in
 $\mathfrak g$
if for any finite-dimensional real representation of
$\mathfrak g$
if for any finite-dimensional real representation of
 $\mathfrak g$
, the subspaces annihilated by
$\mathfrak g$
, the subspaces annihilated by
 $\mathfrak f$
and
$\mathfrak f$
and
 $\mathfrak g$
coincide.
$\mathfrak g$
coincide. -
(ii) Let G be a connected semisimple real Lie group. A subgroup F of G is said to be epimorphic in G if for every finite-dimensional representation of G, the vectors fixed by F are also fixed by G.
In the literature, it has been common to only introduce and study the concept of epimorphic subgroups for algebraic groups. Let us therefore check that our definition coincides with the usual one when the groups involved are algebraic.
Proposition A.3. Let G be a Zariski connected semisimple real algebraic group and F a Lie subgroup of G such that
![]() $F^\circ $
is Zariski dense in F. Suppose that F is epimorphic in G in the category of real algebraic groups, meaning that in every finite-dimensional real algebraic representation of G, the vectors fixed by F are also fixed by G. Then
$F^\circ $
is Zariski dense in F. Suppose that F is epimorphic in G in the category of real algebraic groups, meaning that in every finite-dimensional real algebraic representation of G, the vectors fixed by F are also fixed by G. Then
![]() $F^\circ $
is epimorphic in
$F^\circ $
is epimorphic in
![]() $G^\circ $
in the sense of Definition A.2.
$G^\circ $
in the sense of Definition A.2.
To be precise, by G being a real algebraic group we mean that
![]() $G=\mathbf {G}(\mathbb {R})$
is the group of real points of an underlying complex algebraic group
$G=\mathbf {G}(\mathbb {R})$
is the group of real points of an underlying complex algebraic group
![]() $\mathbf {G}$
defined over
$\mathbf {G}$
defined over
![]() $\mathbb {R}$
, and a real algebraic representation is the restriction to real points of an algebraic representation of
$\mathbb {R}$
, and a real algebraic representation is the restriction to real points of an algebraic representation of
![]() $\mathbf {G}$
defined over
$\mathbf {G}$
defined over
![]() $\mathbb {R}$
. Moreover,
$\mathbb {R}$
. Moreover,
![]() $F^\circ $
and
$F^\circ $
and
![]() $G^\circ $
denote the connected components of F and G, respectively, in the Lie group topology. It is easy to see that the converse of the proposition is also true. Finally, we remark that F is epimorphic in G in the category of real algebraic groups if and only if F is epimorphic in
$G^\circ $
denote the connected components of F and G, respectively, in the Lie group topology. It is easy to see that the converse of the proposition is also true. Finally, we remark that F is epimorphic in G in the category of real algebraic groups if and only if F is epimorphic in
![]() $\mathbf {G}$
in the category of complex algebraic groups.
$\mathbf {G}$
in the category of complex algebraic groups.
The idea of the proof of the proposition above is to pass to the Lie algebra level, where all representations are algebraic thanks to semisimplicity. The following two lemmas enable this step.
Lemma A.4. Let G be a connected semisimple Lie group and F a closed subgroup of G. If
![]() $\mathfrak f=\operatorname {\mathrm {Lie}}(F)$
is an epimorphic subalgebra of
$\mathfrak f=\operatorname {\mathrm {Lie}}(F)$
is an epimorphic subalgebra of
![]() $\mathfrak g=\operatorname {\mathrm {Lie}}(G)$
, then F is epimorphic in G.
$\mathfrak g=\operatorname {\mathrm {Lie}}(G)$
, then F is epimorphic in G.
Proof. A representation of G naturally induces a representation of its Lie algebra. A vector that is F-fixed on the Lie group level is then
![]() $\mathfrak f$
-annihilated on the Lie algebra level. Therefore, such vectors are annihilated by
$\mathfrak f$
-annihilated on the Lie algebra level. Therefore, such vectors are annihilated by
![]() $\mathfrak g$
and hence fixed by G, since G is connected.
$\mathfrak g$
and hence fixed by G, since G is connected.
Lemma A.5. Let F and G be as in Proposition A.3. Then
![]() $\mathfrak f=\operatorname {\mathrm {Lie}}(F)$
is an epimorphic subalgebra of
$\mathfrak f=\operatorname {\mathrm {Lie}}(F)$
is an epimorphic subalgebra of
![]() $\mathfrak g=\operatorname {\mathrm {Lie}}(G)$
.
$\mathfrak g=\operatorname {\mathrm {Lie}}(G)$
.
Proof. If
![]() $\mathfrak f$
is not an epimorphic subalgebra of
$\mathfrak f$
is not an epimorphic subalgebra of
![]() $\mathfrak g$
, then using complete reducibility of
$\mathfrak g$
, then using complete reducibility of
![]() $\mathfrak g$
-representations, we can find a nontrivial irreducible representation
$\mathfrak g$
-representations, we can find a nontrivial irreducible representation
![]() $\rho \colon \mathfrak g\to \mathfrak {gl}(V)$
such that the subspace
$\rho \colon \mathfrak g\to \mathfrak {gl}(V)$
such that the subspace
is nonzero. Let
![]() $\mathfrak {g}_{\mathbb {C}}$
and
$\mathfrak {g}_{\mathbb {C}}$
and
![]() $V_{\mathbb {C}}$
be the complexifications of
$V_{\mathbb {C}}$
be the complexifications of
![]() $\mathfrak g$
and V, respectively. It follows from the discussion in [Reference Onishchik74, §8] (Theorem 1 and Corollary 1) that either (1)
$\mathfrak g$
and V, respectively. It follows from the discussion in [Reference Onishchik74, §8] (Theorem 1 and Corollary 1) that either (1)
![]() $\mathfrak {g}_{\mathbb {C}}$
acts irreducibly on
$\mathfrak {g}_{\mathbb {C}}$
acts irreducibly on
![]() $V_{\mathbb {C}}$
, or (2) V has a complex structure and
$V_{\mathbb {C}}$
, or (2) V has a complex structure and
![]() $\mathfrak {g}$
acts by
$\mathfrak {g}$
acts by
![]() $\mathbb {C}$
-linear transformations. In both cases, we thus obtain an irreducible complex representation of
$\mathbb {C}$
-linear transformations. In both cases, we thus obtain an irreducible complex representation of
![]() $\mathfrak {g}_{\mathbb {C}}$
(either on
$\mathfrak {g}_{\mathbb {C}}$
(either on
![]() $V_{\mathbb {C}}$
or on V), which we denote by
$V_{\mathbb {C}}$
or on V), which we denote by
![]() $\rho _{\mathbb {C}}$
. We also set
$\rho _{\mathbb {C}}$
. We also set
![]() $k=\mathbb {R}$
in the first case and
$k=\mathbb {R}$
in the first case and
![]() $k=\mathbb {C}$
in the second, and record that since
$k=\mathbb {C}$
in the second, and record that since
![]() $\mathfrak g$
acts k-linearly, the subspace
$\mathfrak g$
acts k-linearly, the subspace
![]() $V_0$
is k-invariant.
$V_0$
is k-invariant.
We claim that there exists
![]() $n\in \mathbb {N}$
such that the tensor product representation
$n\in \mathbb {N}$
such that the tensor product representation
![]() $\rho ^{\otimes _{k} n} $
of
$\rho ^{\otimes _{k} n} $
of
![]() $\mathfrak g$
lifts to a real algebraic representation of G. Assuming the claim and using that
$\mathfrak g$
lifts to a real algebraic representation of G. Assuming the claim and using that
![]() $F^\circ $
is Zariski dense in F, we find that
$F^\circ $
is Zariski dense in F, we find that
![]() $V_0^{\otimes _ {k}n}$
is a nonzero F-fixed subspace of
$V_0^{\otimes _ {k}n}$
is a nonzero F-fixed subspace of
![]() $V^{\otimes _{k}n}$
. Since F is an epimorphic subgroup of G in the algebraic category, the space
$V^{\otimes _{k}n}$
. Since F is an epimorphic subgroup of G in the algebraic category, the space
![]() $V_0^{\otimes _ {k}n}$
is G-fixed. It follows that
$V_0^{\otimes _ {k}n}$
is G-fixed. It follows that
![]() $\mathfrak g$
annihilates
$\mathfrak g$
annihilates
![]() $V_0^{\otimes _ {k}n}$
, hence
$V_0^{\otimes _ {k}n}$
, hence
![]() $\mathfrak g$
annihilates
$\mathfrak g$
annihilates
![]() $V_0$
. This contradicts the assumption that
$V_0$
. This contradicts the assumption that
![]() $(\rho ,V)$
is a nontrivial irreducible representation, and thus establishes the statement of the lemma.
$(\rho ,V)$
is a nontrivial irreducible representation, and thus establishes the statement of the lemma.
It remains to prove the claim. Let
![]() $\mathbf {G}$
be a Zariski connected semisimple complex algebraic group defined over
$\mathbf {G}$
be a Zariski connected semisimple complex algebraic group defined over
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $G=\mathbf {G}(\mathbb {R})$
. Then
$G=\mathbf {G}(\mathbb {R})$
. Then
![]() $\mathfrak g_{\mathbb {C}}$
is the Lie algebra of
$\mathfrak g_{\mathbb {C}}$
is the Lie algebra of
![]() $\mathbf {G}$
. By [Reference Conrad, Gabber and Prasad23, Corollary A.4.11] there is a simply connected algebraic cover
$\mathbf {G}$
. By [Reference Conrad, Gabber and Prasad23, Corollary A.4.11] there is a simply connected algebraic cover
![]() $\tilde {\mathbf {G}}$
of
$\tilde {\mathbf {G}}$
of
![]() $\mathbf {G}$
defined over
$\mathbf {G}$
defined over
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
In case (1), since the representation
![]() $\rho _{\mathbb {C}}\colon \mathfrak g_{\mathbb {C}}\to \mathfrak {gl}(V_{\mathbb {C}})$
is algebraic by semisimplicity, it lifts to an irreducible algebraic representation
$\rho _{\mathbb {C}}\colon \mathfrak g_{\mathbb {C}}\to \mathfrak {gl}(V_{\mathbb {C}})$
is algebraic by semisimplicity, it lifts to an irreducible algebraic representation
![]() $\tilde {\mathbf {G}} \to \operatorname {\mathrm {GL}}(V_{\mathbb {C}})$
defined over
$\tilde {\mathbf {G}} \to \operatorname {\mathrm {GL}}(V_{\mathbb {C}})$
defined over
![]() $\mathbb {R}$
(with respect to the real structure on
$\mathbb {R}$
(with respect to the real structure on
![]() $V_{\mathbb {C}}$
given by V). The kernel
$V_{\mathbb {C}}$
given by V). The kernel
![]() $\mathbf {N}$
of the covering map
$\mathbf {N}$
of the covering map
![]() $\tilde {\mathbf {G}}\to \mathbf {G}$
is finite and central. By Schur’s lemma and irreducibility,
$\tilde {\mathbf {G}}\to \mathbf {G}$
is finite and central. By Schur’s lemma and irreducibility,
![]() $\mathbf {N}$
thus acts on
$\mathbf {N}$
thus acts on
![]() $V_{\mathbb {C}}$
by scalar multiplication by roots of unity. Therefore, there exists
$V_{\mathbb {C}}$
by scalar multiplication by roots of unity. Therefore, there exists
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $\mathbf {N}$
acts trivially on
$\mathbf {N}$
acts trivially on
![]() $V_{\mathbb {C}}^{\otimes _{\mathbb {C}} n}$
. Since the representation of
$V_{\mathbb {C}}^{\otimes _{\mathbb {C}} n}$
. Since the representation of
![]() $\tilde {\mathbf {G}}$
on
$\tilde {\mathbf {G}}$
on
![]() $V_{\mathbb {C}}^{\otimes _{\mathbb {C}} n}$
is defined over
$V_{\mathbb {C}}^{\otimes _{\mathbb {C}} n}$
is defined over
![]() $\mathbb {R}$
, we deduce that it induces a real algebraic representation of G on
$\mathbb {R}$
, we deduce that it induces a real algebraic representation of G on
![]() $V^{\otimes _{k}n}=V^{\otimes _{\mathbb {R}} n}$
.
$V^{\otimes _{k}n}=V^{\otimes _{\mathbb {R}} n}$
.
In case (2),
![]() $\rho _{\mathbb {C}}\colon \mathfrak g_{\mathbb {C}}\to \mathfrak {gl}(V)$
lifts to an irreducible algebraic representation
$\rho _{\mathbb {C}}\colon \mathfrak g_{\mathbb {C}}\to \mathfrak {gl}(V)$
lifts to an irreducible algebraic representation
![]() $\tilde {\mathbf {G}}\to \operatorname {\mathrm {GL}}(V)$
. By the same argument as in the first case, for some
$\tilde {\mathbf {G}}\to \operatorname {\mathrm {GL}}(V)$
. By the same argument as in the first case, for some
![]() $n\in \mathbb {N}$
the kernel
$n\in \mathbb {N}$
the kernel
![]() $\mathbf {N}$
of the covering map acts trivially on
$\mathbf {N}$
of the covering map acts trivially on
![]() $V^{\otimes _{\mathbb {C}} n}$
. Hence, the action of
$V^{\otimes _{\mathbb {C}} n}$
. Hence, the action of
![]() $\tilde {\mathbf {G}}$
on
$\tilde {\mathbf {G}}$
on
![]() $V^{\otimes _{k}n}=V^{\otimes _{\mathbb {C}} n}$
factors through an algebraic representation of
$V^{\otimes _{k}n}=V^{\otimes _{\mathbb {C}} n}$
factors through an algebraic representation of
![]() $\mathbf {G}$
. By restriction of scalars, we can view
$\mathbf {G}$
. By restriction of scalars, we can view
![]() $\mathbf {G}$
and
$\mathbf {G}$
and
![]() $\operatorname {\mathrm {GL}}(V^{\otimes _{\mathbb {C}} n})$
as groups of real points of algebraic groups defined over
$\operatorname {\mathrm {GL}}(V^{\otimes _{\mathbb {C}} n})$
as groups of real points of algebraic groups defined over
![]() $\mathbb {R}$
. Composing the map
$\mathbb {R}$
. Composing the map
![]() $G\to \mathbf {G}$
with the representation of
$G\to \mathbf {G}$
with the representation of
![]() $\mathbf {G}$
on
$\mathbf {G}$
on
![]() $V^{\otimes _{\mathbb {C}} n}$
we obtain the desired lift of
$V^{\otimes _{\mathbb {C}} n}$
we obtain the desired lift of
![]() $\rho ^{\otimes _{k}n}$
.
$\rho ^{\otimes _{k}n}$
.
Acknowledgments
The authors are thankful to Barak Weiss for encouraging discussions on an initial version of this article as well as for helpful bibliographical suggestions and to Manfred Einsiedler for numerous useful remarks.
Competing interest
The authors have no competing interests to declare.
Financial support
R. S. is supported by National Key Research and Development Program of China 2021YFA1003204, NSFC 12161141014 and NSF Shanghai 22ZR1406200. C. S. is supported by SNF grant 182089 and SNF Ambizione 193481.