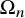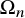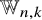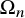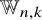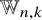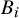1 Introduction
Let n be a positive integer. Superspace of rank n (over the ground field ![]() ${\mathbb {Q}}$) is the tensor product
${\mathbb {Q}}$) is the tensor product
of a rank n polynomial ring with a rank n exterior algebra. The ring ![]() $\Omega _n$ carries a ‘diagonal’ action of the symmetric group
$\Omega _n$ carries a ‘diagonal’ action of the symmetric group ![]() ${\mathfrak {S}}_n$ on n letters, viz.
${\mathfrak {S}}_n$ on n letters, viz.
which turns ![]() $\Omega _n$ into a bigraded
$\Omega _n$ into a bigraded ![]() ${\mathfrak {S}}_n$-module by considering x-degree and
${\mathfrak {S}}_n$-module by considering x-degree and ![]() $\theta $-degree separately.
$\theta $-degree separately.
The ring ![]() $\Omega _n$ appears in physics, where the ‘bosonic’
$\Omega _n$ appears in physics, where the ‘bosonic’ ![]() $x_i$ variables model the states of bosons and the ‘fermionic’
$x_i$ variables model the states of bosons and the ‘fermionic’ ![]() $\theta _i$ variables model the states of fermions [Reference Peskin and Schroeder22]. A number of recent papers in algebraic combinatorics consider
$\theta _i$ variables model the states of fermions [Reference Peskin and Schroeder22]. A number of recent papers in algebraic combinatorics consider ![]() ${\mathfrak {S}}_n$-modules constructed with a mix of commuting and anticommuting variables [Reference Bergeron2, Reference Billey, Rhoades and Tewari5, Reference Kroes and Rhoades17, Reference Rhoades and Wilson27, Reference Zabrocki34]. The Fields Institute Combinatorics Group made the tantalising conjecture (see [Reference Zabrocki34]) that, if
${\mathfrak {S}}_n$-modules constructed with a mix of commuting and anticommuting variables [Reference Bergeron2, Reference Billey, Rhoades and Tewari5, Reference Kroes and Rhoades17, Reference Rhoades and Wilson27, Reference Zabrocki34]. The Fields Institute Combinatorics Group made the tantalising conjecture (see [Reference Zabrocki34]) that, if ![]() $\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ denotes the ideal generated by
$\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ denotes the ideal generated by ![]() ${\mathfrak {S}}_n$-invariants with vanishing constant term, we have an
${\mathfrak {S}}_n$-invariants with vanishing constant term, we have an ![]() ${\mathfrak {S}}_n$-module isomorphism
${\mathfrak {S}}_n$-module isomorphism
where ![]() ${\mathcal {OP}}_n$ denotes the family of all ordered set partitions of
${\mathcal {OP}}_n$ denotes the family of all ordered set partitions of ![]() $[n] = \{1, \dots , n \}$ (with its natural permutation action of
$[n] = \{1, \dots , n \}$ (with its natural permutation action of ![]() ${\mathfrak {S}}_n$) and
${\mathfrak {S}}_n$) and ![]() ${\mathrm {sign}}$ is the 1-dimensional sign representation of
${\mathrm {sign}}$ is the 1-dimensional sign representation of ![]() ${\mathfrak {S}}_n$. Despite significant progress [Reference Swanson and Wallach31], the conjecture (1.3) has remained out of reach; even proving
${\mathfrak {S}}_n$. Despite significant progress [Reference Swanson and Wallach31], the conjecture (1.3) has remained out of reach; even proving ![]() $\Omega _n/ \langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle $ has the expected vector space dimension remains open.
$\Omega _n/ \langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle $ has the expected vector space dimension remains open.
The Vandermonde determinant ![]() $\delta _n \in {\mathbb {Q}}[x_1, \dots , x_n]$ is the polynomial
$\delta _n \in {\mathbb {Q}}[x_1, \dots , x_n]$ is the polynomial
where ![]() $\varepsilon _n = \sum _{w \in {\mathfrak {S}}_n} {\mathrm {sign}}(w) \cdot w \in {\mathbb {Q}}[{\mathfrak {S}}_n]$ is the antisymmetrising element of the symmetric group algebra. Given positive integers
$\varepsilon _n = \sum _{w \in {\mathfrak {S}}_n} {\mathrm {sign}}(w) \cdot w \in {\mathbb {Q}}[{\mathfrak {S}}_n]$ is the antisymmetrising element of the symmetric group algebra. Given positive integers ![]() $k \leq n$, the authors defined [Reference Rhoades and Wilson27] the following extension
$k \leq n$, the authors defined [Reference Rhoades and Wilson27] the following extension ![]() $\delta _{n,k}$ of the Vandermonde to superspace:
$\delta _{n,k}$ of the Vandermonde to superspace:
When ![]() $k = n$, we recover the classical Vandermonde:
$k = n$, we recover the classical Vandermonde: ![]() $\delta _{n,n} = \delta _n$. The
$\delta _{n,n} = \delta _n$. The ![]() $\delta _{n,k}$ may be used to build bigraded
$\delta _{n,k}$ may be used to build bigraded ![]() ${\mathfrak {S}}_n$-stable quotient rings
${\mathfrak {S}}_n$-stable quotient rings ![]() ${\mathbb {W}}_{n,k}$ of
${\mathbb {W}}_{n,k}$ of ![]() $\Omega _n$ as follows.
$\Omega _n$ as follows.
For ![]() $1 \leq i \leq n$, the partial derivative operator
$1 \leq i \leq n$, the partial derivative operator ![]() $\partial /\partial x_i$ acts naturally on the polynomial ring
$\partial /\partial x_i$ acts naturally on the polynomial ring ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$ and, by treating the
${\mathbb {Q}}[x_1, \dots , x_n]$ and, by treating the ![]() $\theta _1, \ldots , \theta _n$ as constants, on the ring
$\theta _1, \ldots , \theta _n$ as constants, on the ring ![]() $\Omega _n$. We also have a
$\Omega _n$. We also have a ![]() ${\mathbb {Q}}[x_1,\dots ,x_n]$-linear operator
${\mathbb {Q}}[x_1,\dots ,x_n]$-linear operator ![]() $\partial /\partial \theta _i$ on
$\partial /\partial \theta _i$ on ![]() $\Omega _n$ defined by
$\Omega _n$ defined by
 $$ \begin{align} \partial / \partial \theta_i: \theta_{j_1} \cdots \theta_{j_r} \mapsto \begin{cases} (-1)^{s-1} \theta_{j_1} \cdots \theta_{j_{s-1}} \theta_{j_{s+1}} \cdots \theta_{j_r} & \text{if } j_s = i \text{ for some } s, \\ 0 & \text{otherwise,} \end{cases} \end{align} $$
$$ \begin{align} \partial / \partial \theta_i: \theta_{j_1} \cdots \theta_{j_r} \mapsto \begin{cases} (-1)^{s-1} \theta_{j_1} \cdots \theta_{j_{s-1}} \theta_{j_{s+1}} \cdots \theta_{j_r} & \text{if } j_s = i \text{ for some } s, \\ 0 & \text{otherwise,} \end{cases} \end{align} $$where ![]() $1 \leq j_1, \dots , j_r \leq n$ are any distinct indices.Footnote 1 These operators satisfy the defining relations of
$1 \leq j_1, \dots , j_r \leq n$ are any distinct indices.Footnote 1 These operators satisfy the defining relations of ![]() $\Omega _n$, namely
$\Omega _n$, namely
for all ![]() $1 \leq i, j \leq n$. Given
$1 \leq i, j \leq n$. Given ![]() $f \in \Omega _n$, we, therefore, have a well-defined operator
$f \in \Omega _n$, we, therefore, have a well-defined operator ![]() $\partial f$ on
$\partial f$ on ![]() $\Omega _n$ given by replacing each
$\Omega _n$ given by replacing each ![]() $x_i$ in f with
$x_i$ in f with ![]() $\partial /\partial x_i$ and each
$\partial /\partial x_i$ and each ![]() $\theta _i$ in f with
$\theta _i$ in f with ![]() $\partial /\partial \theta _i$. This gives rise to an action, denoted
$\partial /\partial \theta _i$. This gives rise to an action, denoted ![]() $\odot $, of
$\odot $, of ![]() $\Omega _n$ on itself:
$\Omega _n$ on itself:
Definition 1.1 (Rhoades-Wilson [Reference Rhoades and Wilson27]).
Given positive integers ![]() $k \leq n$, let
$k \leq n$, let ![]() ${\mathrm {ann}} \, \delta _{n,k} \subseteq \Omega _n$ be the annihilator of the superspace Vandermonde
${\mathrm {ann}} \, \delta _{n,k} \subseteq \Omega _n$ be the annihilator of the superspace Vandermonde ![]() $\delta _{n,k}$ under the
$\delta _{n,k}$ under the ![]() $\odot $-action:
$\odot $-action:
We let ![]() ${\mathbb {W}}_{n,k}$ be the quotient of
${\mathbb {W}}_{n,k}$ be the quotient of ![]() $\Omega _n$ by this annihilator:
$\Omega _n$ by this annihilator:
When ![]() $k = n$, the ring
$k = n$, the ring ![]() ${\mathbb {W}}_{n,n}$ may be identified with the singly graded type A coinvariant ring
${\mathbb {W}}_{n,n}$ may be identified with the singly graded type A coinvariant ring
where ![]() $e_d = e_d(x_1, \dots , x_n)$ is the degree d elementary symmetric polynomial. Borel [Reference Borel4] proved that
$e_d = e_d(x_1, \dots , x_n)$ is the degree d elementary symmetric polynomial. Borel [Reference Borel4] proved that ![]() $R_n$ presents the cohomology
$R_n$ presents the cohomology ![]() $H^{\bullet }(\mathcal {F \ell }_n; {\mathbb {Q}})$ of the variety
$H^{\bullet }(\mathcal {F \ell }_n; {\mathbb {Q}})$ of the variety ![]() $\mathcal {F \ell }_n$ of complete flags in
$\mathcal {F \ell }_n$ of complete flags in ![]() ${\mathbb {C}}^n$. Since
${\mathbb {C}}^n$. Since ![]() $\mathcal {F \ell }_n$ is a smooth compact complex manifold, this means that the ring
$\mathcal {F \ell }_n$ is a smooth compact complex manifold, this means that the ring ![]() $R_n$ satisfies Poincaré Duality and the Hard Lefschetz theorem. In this paper, we provide a simple generating set (Definition 4.6, Theorem 4.12) of the ideal
$R_n$ satisfies Poincaré Duality and the Hard Lefschetz theorem. In this paper, we provide a simple generating set (Definition 4.6, Theorem 4.12) of the ideal ![]() ${\mathrm {ann}} \, \delta _{n,k}$.
${\mathrm {ann}} \, \delta _{n,k}$.
The quotient ring ![]() ${\mathbb {W}}_{n,k}$ is a bigraded
${\mathbb {W}}_{n,k}$ is a bigraded ![]() ${\mathfrak {S}}_n$-module; we let
${\mathfrak {S}}_n$-module; we let ![]() $({\mathbb {W}}_{n,k})_{i,j}$ denote its bihomogeneous piece in x-degree i and
$({\mathbb {W}}_{n,k})_{i,j}$ denote its bihomogeneous piece in x-degree i and ![]() $\theta $-degree j. In [Reference Rhoades and Wilson27], the following facts were proven about this module. Let
$\theta $-degree j. In [Reference Rhoades and Wilson27], the following facts were proven about this module. Let ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k}; q, z)$ be the bigraded Frobenius image of
${\mathrm {grFrob}}({\mathbb {W}}_{n,k}; q, z)$ be the bigraded Frobenius image of ![]() ${\mathbb {W}}_{n,k}$, with q tracking x-degree and z tracking
${\mathbb {W}}_{n,k}$, with q tracking x-degree and z tracking ![]() $\theta $-degree.
$\theta $-degree.
Theorem 1.2 (Rhoades-Wilson [Reference Rhoades and Wilson27]).
Let ![]() $k \leq n$ be positive integers, and let
$k \leq n$ be positive integers, and let ![]() $N = (n-k) \cdot (k-1) + {k \choose 2}$ and
$N = (n-k) \cdot (k-1) + {k \choose 2}$ and ![]() $M = n-k$. We have the following facts concerning the quotient
$M = n-k$. We have the following facts concerning the quotient ![]() ${\mathbb {W}}_{n,k}$.
${\mathbb {W}}_{n,k}$.
1. (Bidegree bound) The bigraded piece
 $({\mathbb {W}}_{n,k})_{i,j}$ is zero unless
$({\mathbb {W}}_{n,k})_{i,j}$ is zero unless  $0 \leq i \leq N$ and
$0 \leq i \leq N$ and  $0 \leq j \leq M$.
$0 \leq j \leq M$.2. (Superspace Poincaré Duality) The vector space
 $({\mathbb {W}}_{n,k})_{N,M} = {\mathbb {Q}}$ is 1-dimensional and spanned by
$({\mathbb {W}}_{n,k})_{N,M} = {\mathbb {Q}}$ is 1-dimensional and spanned by  $\delta _{n,k}$. For any
$\delta _{n,k}$. For any  $0 \leq i \leq N$ and
$0 \leq i \leq N$ and  $0 \leq j \leq M$, the multiplication pairing
$0 \leq j \leq M$, the multiplication pairing  $$ \begin{align*} ({\mathbb{W}}_{n,k})_{i,j} \times ({\mathbb{W}}_{n,k})_{N-i,M-j} \longrightarrow ({\mathbb{W}}_{n,k})_{N,M} = {\mathbb {Q}} \end{align*} $$
$$ \begin{align*} ({\mathbb{W}}_{n,k})_{i,j} \times ({\mathbb{W}}_{n,k})_{N-i,M-j} \longrightarrow ({\mathbb{W}}_{n,k})_{N,M} = {\mathbb {Q}} \end{align*} $$is perfect.
3. (Anticommuting degree zero) The anticommuting degree zero piece of
 ${\mathbb {W}}_{n,k}$ is isomorphic to the quotient ring (1.11)
${\mathbb {W}}_{n,k}$ is isomorphic to the quotient ring (1.11) $$ \begin{align} R_{n,k} = {\mathbb {Q}}[x_1, \dots, x_n] / \langle e_n, e_{n-1}, \dots, e_{n-k+1}, x_1^k, \dots, x_n^k \rangle , \end{align} $$
$$ \begin{align} R_{n,k} = {\mathbb {Q}}[x_1, \dots, x_n] / \langle e_n, e_{n-1}, \dots, e_{n-k+1}, x_1^k, \dots, x_n^k \rangle , \end{align} $$where
 $e_d = e_d(x_1, \dots , x_n)$ is the degree d elementary symmetric polynomial.
$e_d = e_d(x_1, \dots , x_n)$ is the degree d elementary symmetric polynomial.4. (Rotational Duality) The symmetric function
 ${\mathrm {grFrob}}({\mathbb {W}}_{n,k};q,z)$ admits the symmetry (1.12)Here,
${\mathrm {grFrob}}({\mathbb {W}}_{n,k};q,z)$ admits the symmetry (1.12)Here, $$ \begin{align} (q^N z^M) \cdot {\mathrm {grFrob}}({\mathbb{W}}_{n,k}; q^{-1}, z^{-1}) = \omega ({\mathrm {grFrob}}({\mathbb{W}}_{n,k};q,z)). \end{align} $$
$$ \begin{align} (q^N z^M) \cdot {\mathrm {grFrob}}({\mathbb{W}}_{n,k}; q^{-1}, z^{-1}) = \omega ({\mathrm {grFrob}}({\mathbb{W}}_{n,k};q,z)). \end{align} $$ $\omega $ is the involution on symmetric functions trading
$\omega $ is the involution on symmetric functions trading  $e_n$ and
$e_n$ and  $h_n$.
$h_n$.
The rings ![]() $R_{n,k}$ appearing in Theorem 1.2 (3) were introduced by Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono13] in their study of the Haglund-Remmel-Wilson Delta Conjecture [Reference Haglund, Remmel and Wilson12] (whose ‘rise formulation’ was recently proven by D’Adderio and Mellit [Reference D’Adderio and Mellit6]). Pawlowski and Rhoades [Reference Pawlowski and Rhoades21] proved that
$R_{n,k}$ appearing in Theorem 1.2 (3) were introduced by Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono13] in their study of the Haglund-Remmel-Wilson Delta Conjecture [Reference Haglund, Remmel and Wilson12] (whose ‘rise formulation’ was recently proven by D’Adderio and Mellit [Reference D’Adderio and Mellit6]). Pawlowski and Rhoades [Reference Pawlowski and Rhoades21] proved that ![]() $R_{n,k}$ presents the cohomology ring
$R_{n,k}$ presents the cohomology ring ![]() $H^{\bullet }(X_{n,k}; {\mathbb {Q}})$ of the variety
$H^{\bullet }(X_{n,k}; {\mathbb {Q}})$ of the variety ![]() $X_{n,k}$ of n-tuples
$X_{n,k}$ of n-tuples ![]() $(\ell _1, \dots , \ell _n)$ of lines in
$(\ell _1, \dots , \ell _n)$ of lines in ![]() ${\mathbb {C}}^k$ which satisfy
${\mathbb {C}}^k$ which satisfy ![]() $\ell _1 + \cdots + \ell _n = {\mathbb {C}}^k$. The variety
$\ell _1 + \cdots + \ell _n = {\mathbb {C}}^k$. The variety ![]() $X_{n,k}$ is smooth but not compact. Correspondingly, the Hilbert series of the ring
$X_{n,k}$ is smooth but not compact. Correspondingly, the Hilbert series of the ring ![]() $R_{n,k}$ is not palindromic. Theorem 1.2 (3) implies that the ‘superization’
$R_{n,k}$ is not palindromic. Theorem 1.2 (3) implies that the ‘superization’ ![]() ${\mathbb {W}}_{n,k}$ of
${\mathbb {W}}_{n,k}$ of ![]() $R_{n,k}$ satisfies a bigraded analog of Poincaré Duality. It is for this reason that our title alludes to
$R_{n,k}$ satisfies a bigraded analog of Poincaré Duality. It is for this reason that our title alludes to ![]() ${\mathbb {W}}_{n,k}$ as a ‘duality module’.
${\mathbb {W}}_{n,k}$ as a ‘duality module’.
Theorem 1.2 notwithstanding, the paper [Reference Rhoades and Wilson27] left many open questions about the nature of the bigraded ![]() ${\mathfrak {S}}_n$-modules
${\mathfrak {S}}_n$-modules ![]() ${\mathbb {W}}_{n,k}$. Indeed, the dimension of
${\mathbb {W}}_{n,k}$. Indeed, the dimension of ![]() ${\mathbb {W}}_{n,k}$ was unknown. The purpose of this paper is to elucidate the structure of the duality modules
${\mathbb {W}}_{n,k}$ was unknown. The purpose of this paper is to elucidate the structure of the duality modules ![]() ${\mathbb {W}}_{n,k}$. In order to do this, we will need the following superspace extensions of set partitions.
${\mathbb {W}}_{n,k}$. In order to do this, we will need the following superspace extensions of set partitions.
Definition 1.3. A set superpartition of ![]() $[n]$ is a set partition of
$[n]$ is a set partition of ![]() $[n]$ into nonempty sets
$[n]$ into nonempty sets ![]() $\{ B_1, \dots , B_k \}$ in which the letters
$\{ B_1, \dots , B_k \}$ in which the letters ![]() $1, \dots , n$ may be decorated with bars, and in which the minimal element
$1, \dots , n$ may be decorated with bars, and in which the minimal element ![]() $\min (B_i)$ of any block
$\min (B_i)$ of any block ![]() $B_i$ must be unbarred. An ordered set superpartition is a set superpartition
$B_i$ must be unbarred. An ordered set superpartition is a set superpartition ![]() $(B_1 \mid \cdots \mid B_k)$ equipped with a total order on its blocks.
$(B_1 \mid \cdots \mid B_k)$ equipped with a total order on its blocks.
As an example,
is a set superpartition of ![]() $[6]$ with three blocks. This set superpartition gives rise to
$[6]$ with three blocks. This set superpartition gives rise to ![]() $3!$ ordered set superpartitions, one of which is
$3!$ ordered set superpartitions, one of which is
where, by convention, we write elements in increasing order within blocks. Roughly speaking, barred letters will correspond algebraically to ![]() $\theta $-variables.
$\theta $-variables.
We define the following families of ordered set superpartitions
 $$ \begin{align*} {\mathcal{OSP}}_{n,k} &= \{ \text{all ordered set superpartitions of } [n] \text{ into } k \text{ blocks} \}, \\ {\mathcal{OSP}}_{n,k}^{(r)} &= \{ \text{all ordered set superpartitions of } [n] \text{ into } k \text{ blocks with } r \text{ barred letters} \}. \end{align*} $$
$$ \begin{align*} {\mathcal{OSP}}_{n,k} &= \{ \text{all ordered set superpartitions of } [n] \text{ into } k \text{ blocks} \}, \\ {\mathcal{OSP}}_{n,k}^{(r)} &= \{ \text{all ordered set superpartitions of } [n] \text{ into } k \text{ blocks with } r \text{ barred letters} \}. \end{align*} $$These sets are counted by
 $$ \begin{align} \left| {\mathcal{OSP}}_{n,k} \right| = 2^{n-k} \cdot k! \cdot {\mathrm {Stir}}(n,k) \quad \text{and} \quad \left| {\mathcal{OSP}}_{n,k}^{(r)} \right| = {n-k \choose r} \cdot k! \cdot {\mathrm {Stir}}(n,k), \end{align} $$
$$ \begin{align} \left| {\mathcal{OSP}}_{n,k} \right| = 2^{n-k} \cdot k! \cdot {\mathrm {Stir}}(n,k) \quad \text{and} \quad \left| {\mathcal{OSP}}_{n,k}^{(r)} \right| = {n-k \choose r} \cdot k! \cdot {\mathrm {Stir}}(n,k), \end{align} $$where ![]() ${\mathrm {Stir}}(n,k)$ is the Stirling number of the second kind counting set partitions of
${\mathrm {Stir}}(n,k)$ is the Stirling number of the second kind counting set partitions of ![]() $[n]$ into k blocks.
$[n]$ into k blocks.
The algebra of ![]() ${\mathbb {W}}_{n,k}$ is governed by the combinatorics of ordered superpartitions. More precisely, we prove the following.
${\mathbb {W}}_{n,k}$ is governed by the combinatorics of ordered superpartitions. More precisely, we prove the following.
• The ideal
 ${\mathrm {ann}} \, \delta _{n,k} \subseteq \Omega _n$ defining
${\mathrm {ann}} \, \delta _{n,k} \subseteq \Omega _n$ defining  ${\mathbb {W}}_{n,k}$ has an explicit presentation (Definition 4.6) involving elementary symmetric polynomials in partial variable sets (Theorem 4.12).
${\mathbb {W}}_{n,k}$ has an explicit presentation (Definition 4.6) involving elementary symmetric polynomials in partial variable sets (Theorem 4.12).• The vector space
 ${\mathbb {W}}_{n,k}$ has a basis indexed by
${\mathbb {W}}_{n,k}$ has a basis indexed by  ${\mathcal {OSP}}_{n,k}$ (Theorem 4.12).
${\mathcal {OSP}}_{n,k}$ (Theorem 4.12).• There are explicit statistics
 ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and  ${\mathrm {codinv}}$ on
${\mathrm {codinv}}$ on  ${\mathcal {OSP}}_{n,k}$ (see Section 3), such that the bigraded Hilbert series of
${\mathcal {OSP}}_{n,k}$ (see Section 3), such that the bigraded Hilbert series of  ${\mathbb {W}}_{n,k}$ is given by (1.14)This bigraded Hilbert series may be computed using a simple recursion (Corollary 4.13).
${\mathbb {W}}_{n,k}$ is given by (1.14)This bigraded Hilbert series may be computed using a simple recursion (Corollary 4.13). $$ \begin{align} {\mathrm {Hilb}}({\mathbb{W}}_{n,k}; q, z) = \sum_{r = 0}^{n-k} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k}^{(r)}} q^{{\mathrm {coinv}}(\sigma)} = \sum_{r = 0}^{n-k} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k}^{(r)}} q^{{\mathrm {codinv}}(\sigma)}. \end{align} $$
$$ \begin{align} {\mathrm {Hilb}}({\mathbb{W}}_{n,k}; q, z) = \sum_{r = 0}^{n-k} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k}^{(r)}} q^{{\mathrm {coinv}}(\sigma)} = \sum_{r = 0}^{n-k} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k}^{(r)}} q^{{\mathrm {codinv}}(\sigma)}. \end{align} $$• The
 $\theta $-degree pieces of
$\theta $-degree pieces of  ${\mathbb {W}}_{n,k}$ are built out of hook-shaped irreducibles. More precisely, if we regard
${\mathbb {W}}_{n,k}$ are built out of hook-shaped irreducibles. More precisely, if we regard  ${\mathbb {W}}_{n,k}$ as a singly graded module under
${\mathbb {W}}_{n,k}$ as a singly graded module under  $\theta $-degree, (1.15)where the sum is over all k-tuples
$\theta $-degree, (1.15)where the sum is over all k-tuples $$ \begin{align} {\mathrm {grFrob}}({\mathbb{W}}_{n,k}; z) = \sum_{(\lambda^{(1)}, \dots, \lambda^{(k)})} z^{n - \lambda^{(1)}_1 - \cdots - \lambda^{(k)}_1} \cdot s_{\lambda^{(1)}} \cdots s_{\lambda^{(k)}}, \end{align} $$
$$ \begin{align} {\mathrm {grFrob}}({\mathbb{W}}_{n,k}; z) = \sum_{(\lambda^{(1)}, \dots, \lambda^{(k)})} z^{n - \lambda^{(1)}_1 - \cdots - \lambda^{(k)}_1} \cdot s_{\lambda^{(1)}} \cdots s_{\lambda^{(k)}}, \end{align} $$ $(\lambda ^{(1)}, \dots , \lambda ^{(k)})$ of nonempty hook-shaped partitions which satisfy
$(\lambda ^{(1)}, \dots , \lambda ^{(k)})$ of nonempty hook-shaped partitions which satisfy  $|\lambda ^{(1)}| + \cdots + |\lambda ^{(k)}| = n$ (Corollary 5.22).
$|\lambda ^{(1)}| + \cdots + |\lambda ^{(k)}| = n$ (Corollary 5.22).• The monomial expansion of
 ${\mathrm {grFrob}}({\mathbb {W}}_{n,k};q,z)$ is a generating function for the statistics
${\mathrm {grFrob}}({\mathbb {W}}_{n,k};q,z)$ is a generating function for the statistics  ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and  ${\mathrm {codinv}}$, extended to a multiset analog of ordered set superpartitions (Theorem 5.20).
${\mathrm {codinv}}$, extended to a multiset analog of ordered set superpartitions (Theorem 5.20).
Although the ![]() ${\mathrm {codinv}}$ interpretation of
${\mathrm {codinv}}$ interpretation of ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k};q,z)$ will implicitly describe this symmetric function as a positive sum of LLT polynomials, we do not have a combinatorial interpretation for its Schur expansion and leave this as an open problem. Our results on
${\mathrm {grFrob}}({\mathbb {W}}_{n,k};q,z)$ will implicitly describe this symmetric function as a positive sum of LLT polynomials, we do not have a combinatorial interpretation for its Schur expansion and leave this as an open problem. Our results on ![]() ${\mathbb {W}}_{n,k}$-modules are ‘superizations’ of facts about the rings
${\mathbb {W}}_{n,k}$-modules are ‘superizations’ of facts about the rings ![]() $R_{n,k}$ proven in [Reference Haglund, Rhoades and Shimozono13]. Loosely speaking, ordered set partitions are replaced by ordered set superpartitions in appropriate ways. The proofs of these results will be significantly different from those of [Reference Haglund, Rhoades and Shimozono13] due to the anticommuting variables.
$R_{n,k}$ proven in [Reference Haglund, Rhoades and Shimozono13]. Loosely speaking, ordered set partitions are replaced by ordered set superpartitions in appropriate ways. The proofs of these results will be significantly different from those of [Reference Haglund, Rhoades and Shimozono13] due to the anticommuting variables.
We analyse the quotient ring ![]() ${\mathbb {W}}_{n,k}$ by considering its isomorphic harmonic subspace
${\mathbb {W}}_{n,k}$ by considering its isomorphic harmonic subspace ![]() ${\mathbb {H}}_{n,k} \subseteq \Omega _n$. This is the submodule of
${\mathbb {H}}_{n,k} \subseteq \Omega _n$. This is the submodule of ![]() $\Omega _n$ generated by
$\Omega _n$ generated by ![]() $\delta _{n,k}$ under the
$\delta _{n,k}$ under the ![]() $\odot $-action:
$\odot $-action:
Our analysis of ![]() ${\mathbb {H}}_{n,k}$ involves
${\mathbb {H}}_{n,k}$ involves
• a new total order
 $\prec $ on monomials in
$\prec $ on monomials in  $\Omega _n$ (see Section 4) used to describe
$\Omega _n$ (see Section 4) used to describe  ${\mathbb {H}}_{n,k}$ as a graded vector space, and
${\mathbb {H}}_{n,k}$ as a graded vector space, and• a new total order
 $\triangleleft $ on the components of a certain direct sum decomposition
$\triangleleft $ on the components of a certain direct sum decomposition  $\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ (both depending on an auxiliary parameter j) used to describe the graded
$\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ (both depending on an auxiliary parameter j) used to describe the graded  ${\mathfrak {S}}_n$-structure of
${\mathfrak {S}}_n$-structure of  ${\mathbb {H}}_{n,k}$ (see Section 5).
${\mathbb {H}}_{n,k}$ (see Section 5).
Roughly speaking, the orders ![]() $\prec $ and
$\prec $ and ![]() $\triangleleft $ arise from the superspace intuition that a product
$\triangleleft $ arise from the superspace intuition that a product ![]() $x_i^j \theta _i$ of an x-variable and the corresponding
$x_i^j \theta _i$ of an x-variable and the corresponding ![]() $\theta $-variable should be given a ‘negative’ exponent weight
$\theta $-variable should be given a ‘negative’ exponent weight ![]() $-j$. The order
$-j$. The order ![]() $\prec $ restricts to the lexicographical term order on monomials in
$\prec $ restricts to the lexicographical term order on monomials in ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$ but is not a term order on
${\mathbb {Q}}[x_1, \dots , x_n]$ but is not a term order on ![]() $\Omega _n$ in the sense of Gröbner theory. Indeed, the Gröbner theory of important ideals (such as the superspace coinvariant ideal) in
$\Omega _n$ in the sense of Gröbner theory. Indeed, the Gröbner theory of important ideals (such as the superspace coinvariant ideal) in ![]() $\Omega _n$ tends to be messier than that of analogous ideals in
$\Omega _n$ tends to be messier than that of analogous ideals in ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$. On the other hand, we will see in Section 4 that the
${\mathbb {Q}}[x_1, \dots , x_n]$. On the other hand, we will see in Section 4 that the ![]() $\prec $-leading terms of elements in
$\prec $-leading terms of elements in ![]() ${\mathbb {H}}_{n,k}$ correspond in a natural way to ordered set superpartitions.
${\mathbb {H}}_{n,k}$ correspond in a natural way to ordered set superpartitions.
It is our hope that the tools in this paper will prove useful in understanding other quotient rings involving ![]() $\Omega _n$, such as the superspace coinvariant ring. Indeed, the Fields Group has a conjecture (see [Reference Zabrocki34]) for the bigraded Frobenius image of
$\Omega _n$, such as the superspace coinvariant ring. Indeed, the Fields Group has a conjecture (see [Reference Zabrocki34]) for the bigraded Frobenius image of ![]() $\Omega _n/\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle $ which is equivalent (by work of [Reference Haglund, Rhoades and Shimozono13, Reference Haglund, Rhoades and Shimozono14, Reference Rhoades and Wilson27]) to
$\Omega _n/\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle $ which is equivalent (by work of [Reference Haglund, Rhoades and Shimozono13, Reference Haglund, Rhoades and Shimozono14, Reference Rhoades and Wilson27]) to
where ![]() $\{ z^{n-k} \}$ is the operator which extracts the coefficient of
$\{ z^{n-k} \}$ is the operator which extracts the coefficient of ![]() $z^{n-k}$. In our analysis of
$z^{n-k}$. In our analysis of ![]() ${\mathbb {W}}_{n,k}$, we give an explicit generating set of its defining ideal
${\mathbb {W}}_{n,k}$, we give an explicit generating set of its defining ideal ![]() ${\mathrm {ann}} \, \delta _{n,k}$. This gives rise (Proposition 6.4) to a side-by-side comparison of the
${\mathrm {ann}} \, \delta _{n,k}$. This gives rise (Proposition 6.4) to a side-by-side comparison of the ![]() $\theta $-degree
$\theta $-degree ![]() $n-k$ pieces of
$n-k$ pieces of ![]() $\Omega _n/\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle $ and
$\Omega _n/\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle $ and ![]() ${\mathbb {W}}_{n,k}$ as quotient modules with explicit relations. Hopefully, this similarity will assist in proving (1.17).
${\mathbb {W}}_{n,k}$ as quotient modules with explicit relations. Hopefully, this similarity will assist in proving (1.17).
The rest of the paper is organised as follows. In Section 2, we give background material on superspace, ![]() ${\mathfrak {S}}_n$-modules and symmetric functions. Section 3 develops combinatorics of ordered set superpartitions necessary for the algebraic study of the
${\mathfrak {S}}_n$-modules and symmetric functions. Section 3 develops combinatorics of ordered set superpartitions necessary for the algebraic study of the ![]() ${\mathbb {W}}$-modules. Section 4 uses harmonic spaces to give a monomial basis of the modules
${\mathbb {W}}$-modules. Section 4 uses harmonic spaces to give a monomial basis of the modules ![]() ${\mathbb {W}}_{n,k}$ and describe their bigraded Hilbert series. Section 5 uses skewing operators and harmonics to give a combinatorial formula for the bigraded Frobenius image of the
${\mathbb {W}}_{n,k}$ and describe their bigraded Hilbert series. Section 5 uses skewing operators and harmonics to give a combinatorial formula for the bigraded Frobenius image of the ![]() ${\mathbb {W}}$-modules. In Section 6, we conclude with some open problems.
${\mathbb {W}}$-modules. In Section 6, we conclude with some open problems.
2 Background
2.1 Alternants in superspace
Recall that if V is an ![]() ${\mathfrak {S}}_n$-module, a vector
${\mathfrak {S}}_n$-module, a vector ![]() $v \in V$ is an alternant if
$v \in V$ is an alternant if
The superspace Vandermondes ![]() $\delta _{n,k} \in \Omega _n$ are alternants used to construct the quotient rings
$\delta _{n,k} \in \Omega _n$ are alternants used to construct the quotient rings ![]() ${\mathbb {W}}_{n,k}$. In order to place
${\mathbb {W}}_{n,k}$. In order to place ![]() ${\mathbb {W}}_{n,k}$ in the proper inductive context, we will need a more general family of alternants and rings.
${\mathbb {W}}_{n,k}$ in the proper inductive context, we will need a more general family of alternants and rings.
Definition 2.1. Let ![]() $n, k, s \geq 0$ be integers. Define
$n, k, s \geq 0$ be integers. Define ![]() $\delta _{n,k,s} \in \Omega _n$ to be the element
$\delta _{n,k,s} \in \Omega _n$ to be the element
where ![]() $\varepsilon _n = \sum _{w \in {\mathfrak {S}}_n} {\mathrm {sign}}(w) \cdot w \in {\mathbb {Q}}[{\mathfrak {S}}_n]$. Let
$\varepsilon _n = \sum _{w \in {\mathfrak {S}}_n} {\mathrm {sign}}(w) \cdot w \in {\mathbb {Q}}[{\mathfrak {S}}_n]$. Let ![]() ${\mathrm {ann}} \, \delta _{n,k,s} \subseteq \Omega _n$ be the annihilator of
${\mathrm {ann}} \, \delta _{n,k,s} \subseteq \Omega _n$ be the annihilator of ![]() $\delta _{n,k,s}$, and define
$\delta _{n,k,s}$, and define ![]() ${\mathbb {W}}_{n,k,s}$ to be the quotient ring
${\mathbb {W}}_{n,k,s}$ to be the quotient ring
By convention, if ![]() $n < k$, then
$n < k$, then ![]() $\delta _{n,k,s} = 0$. In the special case
$\delta _{n,k,s} = 0$. In the special case ![]() $s = k$, we have
$s = k$, we have ![]() ${\mathbb {W}}_{n,k,k} = {\mathbb {W}}_{n,k}$. We only use the ring
${\mathbb {W}}_{n,k,k} = {\mathbb {W}}_{n,k}$. We only use the ring ![]() ${\mathbb {W}}_{n,k,s}$ in the range
${\mathbb {W}}_{n,k,s}$ in the range ![]() $k \geq s$.
$k \geq s$.
2.2 Harmonics in superspace
It will be convenient to have a model for ![]() ${\mathbb {W}}_{n,k,s}$ as a subspace rather than a quotient of
${\mathbb {W}}_{n,k,s}$ as a subspace rather than a quotient of ![]() $\Omega _n$. To this end, we define the harmonic module
$\Omega _n$. To this end, we define the harmonic module ![]() ${\mathbb {H}}_{n,k,s} \subseteq \Omega _n$ as follows.
${\mathbb {H}}_{n,k,s} \subseteq \Omega _n$ as follows.
Definition 2.2. Let ![]() $n, k, s \geq 0$, and consider
$n, k, s \geq 0$, and consider ![]() $\Omega _n$ as a module over itself by the
$\Omega _n$ as a module over itself by the ![]() $\odot $-action
$\odot $-action ![]() $f \odot g = \partial f(g)$. We define
$f \odot g = \partial f(g)$. We define ![]() ${\mathbb {H}}_{n,k,s} \subseteq \Omega _n$ to be the
${\mathbb {H}}_{n,k,s} \subseteq \Omega _n$ to be the ![]() $\Omega _n$-submodule generated by
$\Omega _n$-submodule generated by ![]() $\delta _{n,k,s}$.
$\delta _{n,k,s}$.
More explicitly, the harmonic module ![]() ${\mathbb {H}}_{n,k,s}$ is the smallest linear subspace of
${\mathbb {H}}_{n,k,s}$ is the smallest linear subspace of ![]() $\Omega _n$ containing
$\Omega _n$ containing ![]() $\delta _{n,k,s}$, which is closed under the action of the commuting partial derivatives
$\delta _{n,k,s}$, which is closed under the action of the commuting partial derivatives ![]() $\partial /\partial x_1, \dots , \partial /\partial x_n$ as well as the anticommuting partial derivatives
$\partial /\partial x_1, \dots , \partial /\partial x_n$ as well as the anticommuting partial derivatives ![]() $\partial /\partial \theta _1, \dots , \partial /\partial \theta _n$. The subspace
$\partial /\partial \theta _1, \dots , \partial /\partial \theta _n$. The subspace ![]() ${\mathbb {H}}_{n,k,s}$ is a bigraded
${\mathbb {H}}_{n,k,s}$ is a bigraded ![]() ${\mathfrak {S}}_n$-module.
${\mathfrak {S}}_n$-module.
We have a natural inclusion map ![]() ${\mathbb {H}}_{n,k,s} \hookrightarrow \Omega _n$. The composition
${\mathbb {H}}_{n,k,s} \hookrightarrow \Omega _n$. The composition
of this inclusion with the canonical projection of ![]() $\Omega _n$ onto
$\Omega _n$ onto ![]() ${\mathbb {W}}_{n,k,s}$ is an isomorphism of bigraded
${\mathbb {W}}_{n,k,s}$ is an isomorphism of bigraded ![]() ${\mathfrak {S}}_n$-modules. We make use of
${\mathfrak {S}}_n$-modules. We make use of ![]() ${\mathbb {H}}_{n,k,s}$ when we need to consider superspace elements in
${\mathbb {H}}_{n,k,s}$ when we need to consider superspace elements in ![]() $\Omega _n$ rather than cosets in
$\Omega _n$ rather than cosets in ![]() ${\mathbb {W}}_{n,k,s}$.
${\mathbb {W}}_{n,k,s}$.
2.3 Symmetric functions and  ${\mathfrak {S}}_n$-modules
${\mathfrak {S}}_n$-modules
Throughout this paper, we use the following standard q-analogs of numbers, factorials and binomial coefficients:
 $$ \begin{align} [n]_q = \frac{q^n - 1}{q - 1} = 1 + q + \cdots + q^{n-1}, \quad [n]!_q = [n]_q [n-1]_q \cdots [1]_q, \quad {n \brack k}_q = \frac{[n]!_q}{[k]!_q \cdot [n-k]!_q}.\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} [n]_q = \frac{q^n - 1}{q - 1} = 1 + q + \cdots + q^{n-1}, \quad [n]!_q = [n]_q [n-1]_q \cdots [1]_q, \quad {n \brack k}_q = \frac{[n]!_q}{[k]!_q \cdot [n-k]!_q}.\\[-16pt]\nonumber \end{align} $$ A partition ![]() $\lambda $ of
$\lambda $ of ![]() $ n$ is a weakly decreasing sequence
$ n$ is a weakly decreasing sequence ![]() $\lambda = (\lambda _1 \geq \cdots \geq \lambda _k)$ of positive integers which sum to n. We write
$\lambda = (\lambda _1 \geq \cdots \geq \lambda _k)$ of positive integers which sum to n. We write ![]() $\lambda \vdash n$ to mean that
$\lambda \vdash n$ to mean that ![]() $\lambda $ is a partition of n.
$\lambda $ is a partition of n.
Let ![]() $\Lambda = \bigoplus _{n \geq 0} \Lambda _n$ be the ring of symmetric functions in an infinite variable set
$\Lambda = \bigoplus _{n \geq 0} \Lambda _n$ be the ring of symmetric functions in an infinite variable set ![]() ${\mathbf {x}} = (x_1, x_2, \dots )$ over the ground field
${\mathbf {x}} = (x_1, x_2, \dots )$ over the ground field ![]() ${\mathbb {Q}}(q,z)$. Bases of the
${\mathbb {Q}}(q,z)$. Bases of the ![]() $n^{th}$ graded piece
$n^{th}$ graded piece ![]() $\Lambda _n$ of this ring are indexed by partitions
$\Lambda _n$ of this ring are indexed by partitions ![]() $\lambda \vdash n$. We let
$\lambda \vdash n$. We let
be the monomial, elementary, homogeneous and Schur bases of ![]() $\Lambda _n$. Given two partitions
$\Lambda _n$. Given two partitions ![]() $\lambda , \mu $ with
$\lambda , \mu $ with ![]() $\lambda _i \geq \mu _i$ for all i, we let
$\lambda _i \geq \mu _i$ for all i, we let ![]() $s_{\lambda /\mu }$ be the corresponding skew Schur function.
$s_{\lambda /\mu }$ be the corresponding skew Schur function.
A formal power series F in the variable set ![]() ${\mathbf {x}} = (x_1, x_2, \dots )$ of bounded degree is quasisymmetric if the coefficient of
${\mathbf {x}} = (x_1, x_2, \dots )$ of bounded degree is quasisymmetric if the coefficient of ![]() $x_1^{a_1} \cdots x_n^{a_n}$ equals the coefficient of
$x_1^{a_1} \cdots x_n^{a_n}$ equals the coefficient of ![]() $x_{i_1}^{a_1} \cdots x_{i_n}^{a_n}$ for any strictly increasing sequence
$x_{i_1}^{a_1} \cdots x_{i_n}^{a_n}$ for any strictly increasing sequence ![]() $i_1 < \cdots < i_n$ of indices. Given a subset
$i_1 < \cdots < i_n$ of indices. Given a subset ![]() $S \subseteq [n-1]$, the fundamental quasisymmetric function of degree n is
$S \subseteq [n-1]$, the fundamental quasisymmetric function of degree n is
 $$ \begin{align} F_{S,n} = \sum_{\substack{i_1 \leq \cdots \leq i_n \\ j \in S \, \Rightarrow \, i_j < i_{j+1}}} x_{i_1} \cdots x_{i_n}.\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} F_{S,n} = \sum_{\substack{i_1 \leq \cdots \leq i_n \\ j \in S \, \Rightarrow \, i_j < i_{j+1}}} x_{i_1} \cdots x_{i_n}.\\[-16pt]\nonumber \end{align} $$We will encounter the formal power series ![]() $F_{S,n}$ exclusively in the case where S is the inverse descent set of a permutation
$F_{S,n}$ exclusively in the case where S is the inverse descent set of a permutation ![]() $w \in {\mathfrak {S}}_n$. This is the set
$w \in {\mathfrak {S}}_n$. This is the set
We let ![]() $\langle -, - \rangle $ be the Hall inner product on
$\langle -, - \rangle $ be the Hall inner product on ![]() $\Lambda _n$ obtained by declaring the Schur functions
$\Lambda _n$ obtained by declaring the Schur functions ![]() $s_{\lambda }$ to be orthonormal. For any
$s_{\lambda }$ to be orthonormal. For any ![]() $F \in \Lambda $, we have a ‘skewing’ operator
$F \in \Lambda $, we have a ‘skewing’ operator ![]() $F^{\perp }: \Lambda \rightarrow \Lambda $ characterised by
$F^{\perp }: \Lambda \rightarrow \Lambda $ characterised by
for all ![]() $G, H \in \Lambda $. We will make use of the following fact.
$G, H \in \Lambda $. We will make use of the following fact.
Lemma 2.3. Let ![]() $F, G \in \Lambda $ be two homogeneous symmetric functions of positive degree. The following are equivalent.
$F, G \in \Lambda $ be two homogeneous symmetric functions of positive degree. The following are equivalent.
1. We have
 $F = G$.
$F = G$.2. We have
 $h_j^{\perp } F = h_j^{\perp } G$ for all
$h_j^{\perp } F = h_j^{\perp } G$ for all  $j \geq 1$.
$j \geq 1$.3. We have
 $e_j^{\perp } F = e_j^{\perp } G$ for all
$e_j^{\perp } F = e_j^{\perp } G$ for all  $j \geq 1$.
$j \geq 1$.
Lemma 2.3 follows from the fact that either of the sets ![]() $\{e_1, e_2, \dots \}$ or
$\{e_1, e_2, \dots \}$ or ![]() $\{h_1, h_2, \dots \}$ are algebraically independent generating sets of the ring
$\{h_1, h_2, \dots \}$ are algebraically independent generating sets of the ring ![]() $\Lambda $ of symmetric functions.
$\Lambda $ of symmetric functions.
Irreducible representations of ![]() ${\mathfrak {S}}_n$ are in bijective correspondence with partitions
${\mathfrak {S}}_n$ are in bijective correspondence with partitions ![]() $\lambda $ of n. If
$\lambda $ of n. If ![]() $\lambda \vdash n$ is a partition, let
$\lambda \vdash n$ is a partition, let ![]() $S^{\lambda }$ be the corresponding irreducible
$S^{\lambda }$ be the corresponding irreducible ![]() ${\mathfrak {S}}_n$-module. If V is any finite-dimensional
${\mathfrak {S}}_n$-module. If V is any finite-dimensional ![]() ${\mathfrak {S}}_n$-module, there are unique multiplicities
${\mathfrak {S}}_n$-module, there are unique multiplicities ![]() $c_{\lambda } \geq 0$, such that
$c_{\lambda } \geq 0$, such that ![]() $V \cong \bigoplus _{\lambda \vdash n} c_{\lambda } S^{\lambda }$. The Frobenius image of V is the symmetric function
$V \cong \bigoplus _{\lambda \vdash n} c_{\lambda } S^{\lambda }$. The Frobenius image of V is the symmetric function
obtained by replacing each irreducible ![]() $S^{\lambda }$ with the corresponding Schur function
$S^{\lambda }$ with the corresponding Schur function ![]() $s_{\lambda }$.
$s_{\lambda }$.
Given two positive integers ![]() $n, m$, we have the corresponding parabolic subgroup
$n, m$, we have the corresponding parabolic subgroup ![]() ${\mathfrak {S}}_n \times {\mathfrak {S}}_m \subseteq {\mathfrak {S}}_{n+m}$ obtained by permuting the first n letters and the last m letters in
${\mathfrak {S}}_n \times {\mathfrak {S}}_m \subseteq {\mathfrak {S}}_{n+m}$ obtained by permuting the first n letters and the last m letters in ![]() $[n+m]$ separately. If V is an
$[n+m]$ separately. If V is an ![]() ${\mathfrak {S}}_n$-module and W is an
${\mathfrak {S}}_n$-module and W is an ![]() ${\mathfrak {S}}_m$-module, their induction product
${\mathfrak {S}}_m$-module, their induction product ![]() $V \circ W$ is the
$V \circ W$ is the ![]() ${\mathfrak {S}}_{n+m}$-module given by
${\mathfrak {S}}_{n+m}$-module given by
Induction product and Frobenius image are related in that
Frobenius images interact with the skewing operators ![]() $h_j^{\perp }$ and
$h_j^{\perp }$ and ![]() $e_j^{\perp }$ in the following way. Let V be an
$e_j^{\perp }$ in the following way. Let V be an ![]() ${\mathfrak {S}}_n$-module, let
${\mathfrak {S}}_n$-module, let ![]() $1 \leq j \leq n$ and consider the parabolic subgroup
$1 \leq j \leq n$ and consider the parabolic subgroup ![]() ${\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j}$ of
${\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j}$ of ![]() ${\mathfrak {S}}_n$. We have the group algebra elements
${\mathfrak {S}}_n$. We have the group algebra elements ![]() $\eta _j, \varepsilon _j \in {\mathbb {Q}}[{\mathfrak {S}}_j]$
$\eta _j, \varepsilon _j \in {\mathbb {Q}}[{\mathfrak {S}}_j]$
 $$ \begin{align} \eta_j = \sum_{w \in {\mathfrak{S}}_j} w \quad \quad \quad \quad \varepsilon_j = \sum_{w \in {\mathfrak{S}}_j} {\mathrm {sign}}(w) \cdot w \end{align} $$
$$ \begin{align} \eta_j = \sum_{w \in {\mathfrak{S}}_j} w \quad \quad \quad \quad \varepsilon_j = \sum_{w \in {\mathfrak{S}}_j} {\mathrm {sign}}(w) \cdot w \end{align} $$which symmetrise and antisymmetrise in the first j letters, respectively. Since ![]() $\eta _j$ and
$\eta _j$ and ![]() $\varepsilon _j$ commute with permutations in the second parabolic factor
$\varepsilon _j$ commute with permutations in the second parabolic factor ![]() ${\mathfrak {S}}_{n-j}$, the vector spaces
${\mathfrak {S}}_{n-j}$, the vector spaces
are naturally ![]() ${\mathfrak {S}}_{n-j}$-modules. The Frobenius images of these modules are as follows.
${\mathfrak {S}}_{n-j}$-modules. The Frobenius images of these modules are as follows.
Lemma 2.4. We have ![]() ${\mathrm {Frob}}(\eta _j V) = h_j^{\perp } {\mathrm {Frob}}(V)$ and
${\mathrm {Frob}}(\eta _j V) = h_j^{\perp } {\mathrm {Frob}}(V)$ and ![]() ${\mathrm {Frob}}(\varepsilon _j V) = e_j^{\perp } {\mathrm {Frob}}(V)$.
${\mathrm {Frob}}(\varepsilon _j V) = e_j^{\perp } {\mathrm {Frob}}(V)$.
The proof of Lemma 2.4, which we omit, uses Frobenius reciprocity. Lemma 2.4 may be generalised by considering the image of V under ![]() $\sum _{w \in {\mathfrak {S}}_j} \chi ^{\mu }(w) \cdot w \in {\mathbb {Q}}[{\mathfrak {S}}_j]$, where
$\sum _{w \in {\mathfrak {S}}_j} \chi ^{\mu }(w) \cdot w \in {\mathbb {Q}}[{\mathfrak {S}}_j]$, where ![]() $\mu \vdash j$ is any partition and
$\mu \vdash j$ is any partition and ![]() $\chi ^{\mu }: {\mathfrak {S}}_j \rightarrow {\mathbb {C}}$ is the irreducible character; the effect on Frobenius images is the operator
$\chi ^{\mu }: {\mathfrak {S}}_j \rightarrow {\mathbb {C}}$ is the irreducible character; the effect on Frobenius images is the operator ![]() $s_{\mu }^{\perp }$.
$s_{\mu }^{\perp }$.
In this paper, we will consider (bi)graded vector spaces and modules. If ![]() $V = \bigoplus _{i \geq 0} V_i$ is a graded vector space with each piece
$V = \bigoplus _{i \geq 0} V_i$ is a graded vector space with each piece ![]() $V_i$ finite-dimensional, recall that its Hilbert series is given by
$V_i$ finite-dimensional, recall that its Hilbert series is given by
Similarly, if ![]() $V = \bigoplus _{i,j \geq 0} V_{i,j}$ is a bigraded vector space, we have the bigraded Hilbert series
$V = \bigoplus _{i,j \geq 0} V_{i,j}$ is a bigraded vector space, we have the bigraded Hilbert series
 $$ \begin{align} {\mathrm {Hilb}}(V; q,z) = \sum_{i,j \geq 0} \dim(V_{i,j}) \cdot q^i z^j. \end{align} $$
$$ \begin{align} {\mathrm {Hilb}}(V; q,z) = \sum_{i,j \geq 0} \dim(V_{i,j}) \cdot q^i z^j. \end{align} $$If ![]() $V = \bigoplus _{i \geq 0} V_i$ is a graded
$V = \bigoplus _{i \geq 0} V_i$ is a graded ![]() ${\mathfrak {S}}_n$-module, its graded Frobenius image is
${\mathfrak {S}}_n$-module, its graded Frobenius image is
Extending this, if ![]() $V = \bigoplus _{i,j \geq 0} V_{i,j}$ is a bigraded
$V = \bigoplus _{i,j \geq 0} V_{i,j}$ is a bigraded ![]() ${\mathfrak {S}}_n$-module, its bigraded Frobenius image is
${\mathfrak {S}}_n$-module, its bigraded Frobenius image is
 $$ \begin{align} {\mathrm {grFrob}}(V; q,z) = \sum_{i,j \geq 0} {\mathrm {Frob}}(V_{i,j}) \cdot q^i z^j. \end{align} $$
$$ \begin{align} {\mathrm {grFrob}}(V; q,z) = \sum_{i,j \geq 0} {\mathrm {Frob}}(V_{i,j}) \cdot q^i z^j. \end{align} $$2.4 Ordered set superpartitions
We will show that the duality modules ![]() ${\mathbb {W}}_{n,k}$ are governed by the combinatorics of ordered set superpartitions in
${\mathbb {W}}_{n,k}$ are governed by the combinatorics of ordered set superpartitions in ![]() ${\mathcal {OSP}}_{n,k}$. The more general modules
${\mathcal {OSP}}_{n,k}$. The more general modules ![]() ${\mathbb {W}}_{n,k,s}$ of Definition 2.1 which we will use to inductively describe the
${\mathbb {W}}_{n,k,s}$ of Definition 2.1 which we will use to inductively describe the ![]() ${\mathbb {W}}_{n,k}$ are controlled by the following more general combinatorial objects.
${\mathbb {W}}_{n,k}$ are controlled by the following more general combinatorial objects.
Definition 2.5. For ![]() $n, k, s \geq 0$, we let
$n, k, s \geq 0$, we let ![]() ${\mathcal {OSP}}_{n,k,s}$ be the family of k-tuples
${\mathcal {OSP}}_{n,k,s}$ be the family of k-tuples ![]() $(B_1 \mid \cdots \mid B_k)$ of sets of positive integers, such that
$(B_1 \mid \cdots \mid B_k)$ of sets of positive integers, such that
• we have the disjoint union decomposition
 $[n] = B_1 \sqcup \cdots \sqcup B_k$,
$[n] = B_1 \sqcup \cdots \sqcup B_k$,• the first s sets
 $B_1, \dots , B_s$ are nonempty,
$B_1, \dots , B_s$ are nonempty,• the elements of
 $B_1, \dots , B_k$ may be barred or unbarred,
$B_1, \dots , B_k$ may be barred or unbarred,• the minimal elements
 $\min B_1, \dots , \min B_s$ of the first s sets are unbarred.
$\min B_1, \dots , \min B_s$ of the first s sets are unbarred.
We denote by ![]() ${\mathcal {OSP}}_{n,k,s}^{(r)} \subseteq {\mathcal {OSP}}_{n,k,s}$ the subfamily of
${\mathcal {OSP}}_{n,k,s}^{(r)} \subseteq {\mathcal {OSP}}_{n,k,s}$ the subfamily of ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}$ with r barred elements.
$\sigma \in {\mathcal {OSP}}_{n,k,s}$ with r barred elements.
Note that, when ![]() $s=k$,
$s=k$, ![]() ${\mathcal {OSP}}_{n,k} = {\mathcal {OSP}}_{n,k,s}$. We refer to elements
${\mathcal {OSP}}_{n,k} = {\mathcal {OSP}}_{n,k,s}$. We refer to elements ![]() $\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}$ as ordered set superpartitions, despite the fact that any of the last
$\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}$ as ordered set superpartitions, despite the fact that any of the last ![]() $k-s$ sets
$k-s$ sets ![]() $B_{s+1}, \dots , B_k$ in
$B_{s+1}, \dots , B_k$ in ![]() $\sigma $ could be empty and that the minimal elements of
$\sigma $ could be empty and that the minimal elements of ![]() $B_{s+1}, \dots , B_k$ (if they exist) may be barred.
$B_{s+1}, \dots , B_k$ (if they exist) may be barred.
3 Ordered set superpartitions
3.1 The statistics  ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and  ${\mathrm {codinv}}$
${\mathrm {codinv}}$
In this section, we define two statistics on ![]() ${\mathcal {OSP}}_{n,k,s}$. The first of these is an extension of the classical inversion statistic (or rather, its complement) on permutations in
${\mathcal {OSP}}_{n,k,s}$. The first of these is an extension of the classical inversion statistic (or rather, its complement) on permutations in ![]() ${\mathfrak {S}}_n$. Given
${\mathfrak {S}}_n$. Given ![]() $\pi = \pi _1 \dots \pi _n \in {\mathfrak {S}}_n$, its coinversion code is the sequence
$\pi = \pi _1 \dots \pi _n \in {\mathfrak {S}}_n$, its coinversion code is the sequence ![]() $(c_1, \dots , c_n)$, where
$(c_1, \dots , c_n)$, where ![]() $c_i$ is the number of entries in the set
$c_i$ is the number of entries in the set ![]() $\{i+1, i+2, \dots , n \}$ which appear to the right of i in
$\{i+1, i+2, \dots , n \}$ which appear to the right of i in ![]() $\pi $. The coinversion number of
$\pi $. The coinversion number of ![]() $\pi $ is the sum
$\pi $ is the sum ![]() ${\mathrm {coinv}}(\pi ) = c_1 + \cdots + c_n$. We generalise these concepts as follows.
${\mathrm {coinv}}(\pi ) = c_1 + \cdots + c_n$. We generalise these concepts as follows.
Definition 3.1. Let ![]() $\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}$ be an ordered set superpartition. The coinversion code is the length n sequence
$\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}$ be an ordered set superpartition. The coinversion code is the length n sequence ![]() ${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$ over the alphabet
${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$ over the alphabet ![]() $\{0, 1, 2, \dots , \bar {0}, \bar {1}, \bar {2}, \dots \}$ whose
$\{0, 1, 2, \dots , \bar {0}, \bar {1}, \bar {2}, \dots \}$ whose ![]() $a^{th}$ entry
$a^{th}$ entry ![]() $c_a$ is defined as follows. Suppose that a lies in the
$c_a$ is defined as follows. Suppose that a lies in the ![]() $i^{th}$ block
$i^{th}$ block ![]() $B_i$ of
$B_i$ of ![]() $\sigma $.
$\sigma $.
• The entry
 $c_a$ is barred if and only if a is barred in
$c_a$ is barred if and only if a is barred in  $\sigma $.
$\sigma $.• If
 $a = \min B_i$ and
$a = \min B_i$ and  $i \leq s$, then
$i \leq s$, then  $$ \begin{align*} c_a = \left| \{ i+1 \leq j \leq s \,:\, \min B_j> a \} \right|. \end{align*} $$
$$ \begin{align*} c_a = \left| \{ i+1 \leq j \leq s \,:\, \min B_j> a \} \right|. \end{align*} $$• If a is barred, then
 $$ \begin{align*} c_a = \begin{cases} | \{ 1 \leq j \leq i-1 \,:\, \min B_j < a \} | & \text{if } i \leq s, \\ | \{ 1 \leq j \leq s \,:\, \min B_j < a \} | + (i-s-1) & \text{if } i> s. \end{cases} \end{align*} $$
$$ \begin{align*} c_a = \begin{cases} | \{ 1 \leq j \leq i-1 \,:\, \min B_j < a \} | & \text{if } i \leq s, \\ | \{ 1 \leq j \leq s \,:\, \min B_j < a \} | + (i-s-1) & \text{if } i> s. \end{cases} \end{align*} $$• Otherwise, we set
 $$ \begin{align*} c_a = | \{ i+1 \leq j \leq s \,:\, \min B_j> a \} | + (i-1). \end{align*} $$
$$ \begin{align*} c_a = | \{ i+1 \leq j \leq s \,:\, \min B_j> a \} | + (i-1). \end{align*} $$
The coinversion number of ![]() $\sigma $ is the sum
$\sigma $ is the sum
of the entries ![]() $(c_1, \dots , c_n)$ in
$(c_1, \dots , c_n)$ in ![]() ${\mathrm {code}}(\sigma )$.
${\mathrm {code}}(\sigma )$.
For example, consider the ordered set superpartition
The coinversion code of ![]() $\sigma $ is given by
$\sigma $ is given by
so that
Bars on the entries ![]() $c_1, \dots , c_n$ are ignored when calculating
$c_1, \dots , c_n$ are ignored when calculating ![]() ${\mathrm {coinv}}(\sigma ) = c_1 + \cdots + c_n$.
${\mathrm {coinv}}(\sigma ) = c_1 + \cdots + c_n$.
The coinversion code ![]() $(c_1, \dots , c_n)$ can be visualised by considering the column diagram notation for ordered set superpartitions. Given
$(c_1, \dots , c_n)$ can be visualised by considering the column diagram notation for ordered set superpartitions. Given ![]() $\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}$, we draw the entries of
$\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}$, we draw the entries of ![]() $B_i$ in the
$B_i$ in the ![]() $i^{th}$ column. The entries of
$i^{th}$ column. The entries of ![]() $B_i$ fill the
$B_i$ fill the ![]() $i^{th}$ column according to the following rules.
$i^{th}$ column according to the following rules.
• For
 $1 \leq i \leq k$, the barred entries of
$1 \leq i \leq k$, the barred entries of  $B_i$ start at height 1 and fill up in increasing order.
$B_i$ start at height 1 and fill up in increasing order.• For
 $1 \leq i \leq s$, the unbarred entries of
$1 \leq i \leq s$, the unbarred entries of  $B_i$ start at height 0 and fill down in increasing order.
$B_i$ start at height 0 and fill down in increasing order.• For
 $s+1 \leq i \leq k$, the unbarred entries of
$s+1 \leq i \leq k$, the unbarred entries of  $B_i$ start at height
$B_i$ start at height  $-1$ and fill down in increasing order; we also place a
$-1$ and fill down in increasing order; we also place a  $\bullet $ at height 0 in these columns.
$\bullet $ at height 0 in these columns.
In our example, the column diagram of
is given by

where the column indices are shown below and the heights of entries are shown on the left. The three ![]() $\bullet $’s at the height 0 level correspond to the fact that the blocks
$\bullet $’s at the height 0 level correspond to the fact that the blocks ![]() $B_3, B_4, B_5$ are allowed to be empty for
$B_3, B_4, B_5$ are allowed to be empty for ![]() $\sigma \in {\mathcal {OSP}}_{9,5,2}$. Given
$\sigma \in {\mathcal {OSP}}_{9,5,2}$. Given ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}$, we have the following column diagram interpretation of the
$\sigma \in {\mathcal {OSP}}_{n,k,s}$, we have the following column diagram interpretation of the ![]() $a^{th}$ letter
$a^{th}$ letter ![]() $c_a$ of
$c_a$ of ![]() ${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$.
${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$.
• If a appears at height 0, then
 $c_a$ counts the number of height zero entries to the right of a which are
$c_a$ counts the number of height zero entries to the right of a which are  $> a$.
$> a$.• If a appears at negative height in column i, then
 $c_a$ is
$c_a$ is  $i-1$, plus the number of height 0 entries to the right of a which are
$i-1$, plus the number of height 0 entries to the right of a which are  $> a$.
$> a$.• If a appears at positive height, then
 $c_a$ counts the number of height 0 entries to the left of a which are
$c_a$ counts the number of height 0 entries to the left of a which are  $< a$, plus the number of
$< a$, plus the number of  $\bullet $’s to the left of a.
$\bullet $’s to the left of a.
We will see that codes ![]() $(c_1, \dots , c_n)$ of elements
$(c_1, \dots , c_n)$ of elements ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}$ correspond to a monomial basis of the quotient ring
$\sigma \in {\mathcal {OSP}}_{n,k,s}$ correspond to a monomial basis of the quotient ring ![]() ${\mathbb {W}}_{n,k,s}$. In order to obtain the bigraded Frobenius image of
${\mathbb {W}}_{n,k,s}$. In order to obtain the bigraded Frobenius image of ![]() ${\mathbb {W}}_{n,k,s}$ in terms of
${\mathbb {W}}_{n,k,s}$ in terms of ![]() ${\mathrm {coinv}}$, we use diagrams to define a formal power series as follows.
${\mathrm {coinv}}$, we use diagrams to define a formal power series as follows.
The reading word of ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}$, denoted
$\sigma \in {\mathcal {OSP}}_{n,k,s}$, denoted ![]() ${\mathrm {read}}(\sigma )$ is the permutation in
${\mathrm {read}}(\sigma )$ is the permutation in ![]() ${\mathfrak {S}}_n$ obtained by reading the column diagram of
${\mathfrak {S}}_n$ obtained by reading the column diagram of ![]() $\sigma $ from top to bottom, and, within each row, from right to left (ignoring any bars on letters). If
$\sigma $ from top to bottom, and, within each row, from right to left (ignoring any bars on letters). If ![]() $\sigma $ is our example ordered set partition above, we have
$\sigma $ is our example ordered set partition above, we have
Definition 3.2. Let ![]() $n, k, s \geq 0$ be integers, and let
$n, k, s \geq 0$ be integers, and let ![]() $0 \leq r \leq n-s$. We define a quasisymmetric function
$0 \leq r \leq n-s$. We define a quasisymmetric function ![]() $C^{(r)}_{n,k,s}({\mathbf {x}};q)$ by the formula
$C^{(r)}_{n,k,s}({\mathbf {x}};q)$ by the formula
 $$ \begin{align} C^{(r)}_{n,k,s}({\mathbf {x}};q) = \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {coinv}}(\sigma)} \cdot F_{{\mathrm {iDes}}({\mathrm {read}}(\sigma)),n}({\mathbf {x}}). \end{align} $$
$$ \begin{align} C^{(r)}_{n,k,s}({\mathbf {x}};q) = \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {coinv}}(\sigma)} \cdot F_{{\mathrm {iDes}}({\mathrm {read}}(\sigma)),n}({\mathbf {x}}). \end{align} $$Also define a quasisymmetric function ![]() $C_{n,k,s}({\mathbf {x}};q,z)$ by
$C_{n,k,s}({\mathbf {x}};q,z)$ by
 $$ \begin{align} C_{n,k,s}({\mathbf {x}};q,z) = \sum_{r = 0}^{n-s} C^{(r)}_{n,k,s}({\mathbf {x}};q) \cdot z^r. \end{align} $$
$$ \begin{align} C_{n,k,s}({\mathbf {x}};q,z) = \sum_{r = 0}^{n-s} C^{(r)}_{n,k,s}({\mathbf {x}};q) \cdot z^r. \end{align} $$ We may avoid the use of the F’s in the definition of the C-functions by allowing repeated entries in our column diagrams. Let ![]() ${\mathcal {CT}}_{n,k,s}$ be the family of column tableaux which are all fillings of finite subsets of the infinite strip
${\mathcal {CT}}_{n,k,s}$ be the family of column tableaux which are all fillings of finite subsets of the infinite strip ![]() $[k] \times \infty $ with the alphabet
$[k] \times \infty $ with the alphabet ![]() $\{ \bullet , 1, 2, \dots , \bar {1}, \bar {2}, \dots \}$, such that
$\{ \bullet , 1, 2, \dots , \bar {1}, \bar {2}, \dots \}$, such that
• The height 0 row is filled with a sequence of s unbarred numbers, followed by a sequence of
 $k-s \bullet $’s.
$k-s \bullet $’s.• The filled cells form a contiguous sequence within each column.
• Entries at positive height are barred, while entries at negative height are unbarred.
• Unbarred numbers weakly increase going down, and barred numbers strictly increase going up.
• An unbarred number at height 0 is strictly smaller than any barred number above it.
An example column tableau ![]() $\tau \in {\mathcal {CT}}_{13, 5, 2}$ is shown below.
$\tau \in {\mathcal {CT}}_{13, 5, 2}$ is shown below.

The coinversion number ![]() ${\mathrm {coinv}}(\tau )$ extends naturally to column tableaux
${\mathrm {coinv}}(\tau )$ extends naturally to column tableaux ![]() $\tau \in {\mathcal {CT}}_{n,k,s}$: given an entry a in such a tableau, we may compute its contribution
$\tau \in {\mathcal {CT}}_{n,k,s}$: given an entry a in such a tableau, we may compute its contribution ![]() $c_a$ to
$c_a$ to ![]() ${\mathrm {coinv}}$ as before, and sum over all entries. For example, the column tableau depicted above has coinversion number
${\mathrm {coinv}}$ as before, and sum over all entries. For example, the column tableau depicted above has coinversion number
where the entries in the sum on the left are processed in reading order, that is the first value in the sum is 3 because the ![]() $\bar {4}$ in column 4 contributes 3 to the coinversion number. Let
$\bar {4}$ in column 4 contributes 3 to the coinversion number. Let ![]() ${\mathbf {x}}^{\tau } = x_1^{\alpha _1} x_2^{\alpha _2} \cdots $, where
${\mathbf {x}}^{\tau } = x_1^{\alpha _1} x_2^{\alpha _2} \cdots $, where ![]() $\alpha _i$ is the number of
$\alpha _i$ is the number of ![]() $i's$ in
$i's$ in ![]() $\tau $. In our example, we have
$\tau $. In our example, we have ![]() ${\mathbf {x}}^{\tau } = x_1^3 x_2 x_3^3 x_4^3 x_5 x_6 x_7$. The exponent sequence
${\mathbf {x}}^{\tau } = x_1^3 x_2 x_3^3 x_4^3 x_5 x_6 x_7$. The exponent sequence ![]() $\alpha = (\alpha _1, \alpha _2, \dots )$ of
$\alpha = (\alpha _1, \alpha _2, \dots )$ of ![]() ${\mathbf {x}}^{\tau }$ is called the content of
${\mathbf {x}}^{\tau }$ is called the content of ![]() $\tau $. Let
$\tau $. Let ![]() ${\mathcal {CT}}_{n,k,s}^{(r)} \subseteq {\mathcal {CT}}_{n,k,s}$ be the subfamily of column tableaux with r barred letters.
${\mathcal {CT}}_{n,k,s}^{(r)} \subseteq {\mathcal {CT}}_{n,k,s}$ be the subfamily of column tableaux with r barred letters.
Observation 3.3. The formal power series ![]() $C_{n,k,s}^{(r)}({\mathbf {x}};q)$ and
$C_{n,k,s}^{(r)}({\mathbf {x}};q)$ and ![]() $C_{n,k,s}({\mathbf {x}};q,z)$ are given by
$C_{n,k,s}({\mathbf {x}};q,z)$ are given by
 $$ \begin{align*} C_{n,k,s}^{(r)}({\mathbf {x}};q) = \sum_{\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}} q^{{\mathrm {coinv}}(\tau)} {\mathbf {x}}^{\tau} \quad \text{and} \quad C_{n,k,s}({\mathbf {x}};q,z) =\sum_{\tau \in {\mathcal {CT}}_{n,k,s}} q^{{\mathrm {coinv}}(\tau)} z^{\# \text{ of bars in } \tau} {\mathbf {x}}^{\tau}. \end{align*} $$
$$ \begin{align*} C_{n,k,s}^{(r)}({\mathbf {x}};q) = \sum_{\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}} q^{{\mathrm {coinv}}(\tau)} {\mathbf {x}}^{\tau} \quad \text{and} \quad C_{n,k,s}({\mathbf {x}};q,z) =\sum_{\tau \in {\mathcal {CT}}_{n,k,s}} q^{{\mathrm {coinv}}(\tau)} z^{\# \text{ of bars in } \tau} {\mathbf {x}}^{\tau}. \end{align*} $$ This observation follows from the definition of the fundamental quasisymmetric functions. The formulas for the C-functions in Observation 3.3 are more aesthetic but less efficient than those in Definition 3.2. It will turn out that ![]() $C_{n,k,s}({\mathbf {x}};q,z)$ is the bigraded Frobenius image
$C_{n,k,s}({\mathbf {x}};q,z)$ is the bigraded Frobenius image ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$. For reasons related to skewing recursions, the refinement
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$. For reasons related to skewing recursions, the refinement ![]() $C^{(r)}_{n,k,s}({\mathbf {x}};q)$ will be convenient to consider. At this point, it is not clear that the C-functions are even symmetric. Their symmetry (and Schur positivity) will follow from an alternative description in terms of another statistic on
$C^{(r)}_{n,k,s}({\mathbf {x}};q)$ will be convenient to consider. At this point, it is not clear that the C-functions are even symmetric. Their symmetry (and Schur positivity) will follow from an alternative description in terms of another statistic on ![]() ${\mathcal {OSP}}_{n,k,s}$.
${\mathcal {OSP}}_{n,k,s}$.
Let ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}$. We augment the column diagram of
$\sigma \in {\mathcal {OSP}}_{n,k,s}$. We augment the column diagram of ![]() $\sigma $ by placing infinitely many
$\sigma $ by placing infinitely many ![]() $+ \infty $’s below the entries in every column (we drop the
$+ \infty $’s below the entries in every column (we drop the ![]() $+$ in diagrams for the sake of compactness). Furthermore, we regard every
$+$ in diagrams for the sake of compactness). Furthermore, we regard every ![]() $\bullet $ in the column diagram as being filled with a 0. Ignoring bars, a pair of entries
$\bullet $ in the column diagram as being filled with a 0. Ignoring bars, a pair of entries ![]() $a < b$ form a diagonal coinversion pair if
$a < b$ form a diagonal coinversion pair if
• a appears to the left of and at the same height as b, or
• a appears to the right of and at height one less than b.
Schematically, these conditions have the form

for ![]() $a < b$.
$a < b$.
Definition 3.4. For ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}$, the diagonal coinversion number
$\sigma \in {\mathcal {OSP}}_{n,k,s}$, the diagonal coinversion number ![]() ${\mathrm {codinv}}(\sigma )$ is the total number of diagonal coinversion pairs in the augmented column diagram of
${\mathrm {codinv}}(\sigma )$ is the total number of diagonal coinversion pairs in the augmented column diagram of ![]() $\sigma $.
$\sigma $.
When ![]() $n=k=s$,
$n=k=s$, ![]() ${\mathrm {codinv}}$ and
${\mathrm {codinv}}$ and ![]() ${\mathrm {coinv}}$ are identical. Although these statistics clearly differ in general, it will turn out that
${\mathrm {coinv}}$ are identical. Although these statistics clearly differ in general, it will turn out that ![]() ${\mathrm {codinv}}$ is equidistributed with
${\mathrm {codinv}}$ is equidistributed with ![]() ${\mathrm {coinv}}$ on
${\mathrm {coinv}}$ on ![]() ${\mathcal {OSP}}_{n,k,s}$ and even on the subsets
${\mathcal {OSP}}_{n,k,s}$ and even on the subsets ![]() ${\mathcal {OSP}}_{n,k,s}^{(r)}$ obtained by restricting to r barred letters. In analogy with the C-functions, we define a quasisymmetric function attached to
${\mathcal {OSP}}_{n,k,s}^{(r)}$ obtained by restricting to r barred letters. In analogy with the C-functions, we define a quasisymmetric function attached to ![]() ${\mathrm {codinv}}$.
${\mathrm {codinv}}$.
Definition 3.5. Let ![]() $n, k, s \geq 0$ be integers, and let
$n, k, s \geq 0$ be integers, and let ![]() $0 \leq r \leq n-s$. Define a quasisymmetric function
$0 \leq r \leq n-s$. Define a quasisymmetric function ![]() $D^{(r)}_{n,k,s}({\mathbf {x}};q)$ by the formula
$D^{(r)}_{n,k,s}({\mathbf {x}};q)$ by the formula
 $$ \begin{align} D^{(r)}_{n,k,s}({\mathbf {x}};q) = \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {codinv}}(\sigma)} \cdot F_{{\mathrm {iDes}}({\mathrm {read}}(\sigma)),n}({\mathbf {x}}). \end{align} $$
$$ \begin{align} D^{(r)}_{n,k,s}({\mathbf {x}};q) = \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {codinv}}(\sigma)} \cdot F_{{\mathrm {iDes}}({\mathrm {read}}(\sigma)),n}({\mathbf {x}}). \end{align} $$Also define
 $$ \begin{align} D_{n,k,s}({\mathbf {x}};q,z) = \sum_{r = 0}^{n-s} D^{(r)}_{n,k,s}({\mathbf {x}};q) \cdot z^r. \end{align} $$
$$ \begin{align} D_{n,k,s}({\mathbf {x}};q,z) = \sum_{r = 0}^{n-s} D^{(r)}_{n,k,s}({\mathbf {x}};q) \cdot z^r. \end{align} $$Like the C-functions, the D-functions may be expressed in terms of infinite sums over column tableaux.
Observation 3.6. The formal power series ![]() $D_{n,k,s}^{(r)}({\mathbf {x}};q)$ and
$D_{n,k,s}^{(r)}({\mathbf {x}};q)$ and ![]() $D_{n,k,s}({\mathbf {x}};q,z)$ are given by
$D_{n,k,s}({\mathbf {x}};q,z)$ are given by
 $$ \begin{align*} D_{n,k,s}^{(r)}({\mathbf {x}};q) = \sum_{\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}} q^{{\mathrm {codinv}}(\tau)} {\mathbf {x}}^{\tau} \quad \text{and} \quad D_{n,k,s}({\mathbf {x}};q,z) = \sum_{\tau \in {\mathcal {CT}}_{n,k,s}} q^{{\mathrm {codinv}}(\tau)} z^{\# \text{ of bars in } \tau} {\mathbf {x}}^{\tau}. \end{align*} $$
$$ \begin{align*} D_{n,k,s}^{(r)}({\mathbf {x}};q) = \sum_{\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}} q^{{\mathrm {codinv}}(\tau)} {\mathbf {x}}^{\tau} \quad \text{and} \quad D_{n,k,s}({\mathbf {x}};q,z) = \sum_{\tau \in {\mathcal {CT}}_{n,k,s}} q^{{\mathrm {codinv}}(\tau)} z^{\# \text{ of bars in } \tau} {\mathbf {x}}^{\tau}. \end{align*} $$We use the theory of LLT polynomials to show that the D-functions are symmetric and Schur positive.
Proposition 3.7. The quasisymmetric functions ![]() $D_{n,k,s}^{(r)}({\mathbf {x}};q)$ and
$D_{n,k,s}^{(r)}({\mathbf {x}};q)$ and ![]() $D_{n,k,s}({\mathbf {x}};q,z)$ are symmetric and Schur positive.
$D_{n,k,s}({\mathbf {x}};q,z)$ are symmetric and Schur positive.
Proof. We prove this fact by writing ![]() $D_{n,k,s}({\mathbf {x}}; q, z)$ as a positive linear combination of LLT polynomials [Reference Lascoux, Leclerc and Thibon18]. We use the version of LLT polynomials employed by Haglund, Haiman and Loehr [Reference Haglund, Haiman and Loehr11].
$D_{n,k,s}({\mathbf {x}}; q, z)$ as a positive linear combination of LLT polynomials [Reference Lascoux, Leclerc and Thibon18]. We use the version of LLT polynomials employed by Haglund, Haiman and Loehr [Reference Haglund, Haiman and Loehr11].
A skew diagram is a set of cells in the first quadrant given by ![]() $\mu / \nu $ for some partitions
$\mu / \nu $ for some partitions ![]() $\mu \supseteq \nu $. Given a tuple
$\mu \supseteq \nu $. Given a tuple ![]() $ {\boldsymbol\lambda } = (\lambda ^{(1)}, \lambda ^{(2)}, \ldots , \lambda ^{(l)})$ of skew diagrams, the LLT polynomial indexed by
$ {\boldsymbol\lambda } = (\lambda ^{(1)}, \lambda ^{(2)}, \ldots , \lambda ^{(l)})$ of skew diagrams, the LLT polynomial indexed by ![]() ${\boldsymbol\lambda }$ is
${\boldsymbol\lambda }$ is
where the sum is over all semistandard fillings of the skew diagrams of ![]() $ {\boldsymbol\lambda }$,
$ {\boldsymbol\lambda }$, ![]() ${\mathbf {x}}^T$ is the product, where
${\mathbf {x}}^T$ is the product, where ![]() $x_i$ appears as many times as i appears in the filling T, and
$x_i$ appears as many times as i appears in the filling T, and ![]() ${\mathrm {inv}}(T)$ is the following statistic. Given a cell u with coordinates
${\mathrm {inv}}(T)$ is the following statistic. Given a cell u with coordinates ![]() $(x, y)$ in one of the skew shapes
$(x, y)$ in one of the skew shapes ![]() $\lambda ^{(i)}$, where the leftmost cell at height 0 has coordinates (0,0), the content of u is
$\lambda ^{(i)}$, where the leftmost cell at height 0 has coordinates (0,0), the content of u is ![]() $c(u) = x - y$. Then
$c(u) = x - y$. Then ![]() ${\mathrm {inv}}(T)$ is the number of pairs of cells
${\mathrm {inv}}(T)$ is the number of pairs of cells ![]() $u \in \lambda ^{(i)}$,
$u \in \lambda ^{(i)}$, ![]() $v \in \lambda ^{(j)}$ with
$v \in \lambda ^{(j)}$ with ![]() $i < j$, such that
$i < j$, such that
•
 $c(u) = c(v)$ and
$c(u) = c(v)$ and  $T(u)> T(v)$, or
$T(u)> T(v)$, or•
 $c(u) + 1 = c(v)$ and
$c(u) + 1 = c(v)$ and  $T(u) < T(v)$.
$T(u) < T(v)$.
LLT polynomials are Schur-positive symmetric functions [Reference Grojnowski and Haiman10, Reference Haglund, Haiman and Loehr11, Reference Lascoux, Leclerc and Thibon18]. We claim that we can decompose ![]() $D_{n,k,s}^{(r)}({\mathbf {x}};q)$ into LLT polynomials:
$D_{n,k,s}^{(r)}({\mathbf {x}};q)$ into LLT polynomials:
where ![]() $\mathrm {stat}$ is a fixed statistic depending on
$\mathrm {stat}$ is a fixed statistic depending on ![]() $ {\boldsymbol\lambda }$ and the sum is over all tuples of skew diagrams
$ {\boldsymbol\lambda }$ and the sum is over all tuples of skew diagrams ![]() $ {\boldsymbol\lambda } = (\lambda ^{(1)}, \ldots , \lambda ^{(k)})$ satisfying
$ {\boldsymbol\lambda } = (\lambda ^{(1)}, \ldots , \lambda ^{(k)})$ satisfying
• if
 $i \leq k-s$, then
$i \leq k-s$, then  $\lambda ^{(i)} = \mu ^{(i)} / (1)$ for a hook shape
$\lambda ^{(i)} = \mu ^{(i)} / (1)$ for a hook shape  $\mu ^{(i)}$,
$\mu ^{(i)}$,• if
 $i> k-s$, then
$i> k-s$, then  $\lambda ^{(i)}$ is a single nonempty hook shape,
$\lambda ^{(i)}$ is a single nonempty hook shape,•
 $\sum _{i=1}^{k} |\lambda ^{(i)}| = n$ and
$\sum _{i=1}^{k} |\lambda ^{(i)}| = n$ and•
 $ {\boldsymbol\lambda }$ has r total cells of negative content.
$ {\boldsymbol\lambda }$ has r total cells of negative content.
We define nonnegative integer sequences ![]() $\alpha , \beta \in \mathbb {N}^{k}$ so that
$\alpha , \beta \in \mathbb {N}^{k}$ so that
•
 $\lambda ^{(i)} = (\alpha _i + 1, 1^{\beta _i}) / (1)$ for
$\lambda ^{(i)} = (\alpha _i + 1, 1^{\beta _i}) / (1)$ for  $i \leq k-s$ and
$i \leq k-s$ and•
 $\lambda ^{(i)} = (\alpha _i + 1, 1^{\beta _i})$ for
$\lambda ^{(i)} = (\alpha _i + 1, 1^{\beta _i})$ for  $i> k-s$.
$i> k-s$.
Given a specific semistandard filling T that contributes to ![]() $\mathrm {LLT}_{{\boldsymbol\lambda }}({\mathbf {x}}; q)$ for such a
$\mathrm {LLT}_{{\boldsymbol\lambda }}({\mathbf {x}}; q)$ for such a ![]() $ {\boldsymbol\lambda }$, we will create a column tableau
$ {\boldsymbol\lambda }$, we will create a column tableau ![]() $\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}$, such that
$\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}$, such that ![]() $\tau $ will have exactly
$\tau $ will have exactly ![]() $\alpha _i$ entries at negative height and
$\alpha _i$ entries at negative height and ![]() $\beta _i$ entries at positive height in column
$\beta _i$ entries at positive height in column ![]() $k-i+1$. The sequences
$k-i+1$. The sequences ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ will completely determine how many diagonal coinversions involving an
$\beta $ will completely determine how many diagonal coinversions involving an ![]() $\infty $ or a
$\infty $ or a ![]() $\bullet $, respectively, appear in
$\bullet $, respectively, appear in ![]() $\tau $. In Figure 1, there are six such diagonal coinversions involving an
$\tau $. In Figure 1, there are six such diagonal coinversions involving an ![]() $\infty $ and seven involving a
$\infty $ and seven involving a ![]() $\bullet $. In general, this number is
$\bullet $. In general, this number is
 $$ \begin{align*} \mathrm{stat}({\boldsymbol\lambda}) = \sum_{1 \leq i < j \leq k}\left( |\alpha_i - \alpha_j| - \chi(\alpha_i> \alpha_j) \right) + \sum_{i =1}^{k-s} | \{j > i: \beta_j \neq 0 \}| , \end{align*} $$
$$ \begin{align*} \mathrm{stat}({\boldsymbol\lambda}) = \sum_{1 \leq i < j \leq k}\left( |\alpha_i - \alpha_j| - \chi(\alpha_i> \alpha_j) \right) + \sum_{i =1}^{k-s} | \{j > i: \beta_j \neq 0 \}| , \end{align*} $$where ![]() $\chi (p)$ is 1 if p is true and
$\chi (p)$ is 1 if p is true and ![]() $0$ if p is false. Note that
$0$ if p is false. Note that ![]() $\mathrm {stat}( {\boldsymbol\lambda })$ can be computed from
$\mathrm {stat}( {\boldsymbol\lambda })$ can be computed from ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ only.
$\beta $ only.

Figure 1 We depict an example of the correspondence in the proof of Proposition 3.7. Each of the five skew diagrams on the left is justified so that its bottom left entry has content 0. In this example, we have ![]() $\alpha = (2, 1, 0, 2, 0)$,
$\alpha = (2, 1, 0, 2, 0)$, ![]() $\beta = (0, 2, 0, 2, 2)$ and
$\beta = (0, 2, 0, 2, 2)$ and ![]() $\mathrm {stat}( {\boldsymbol\lambda }) = 6 + 7 = 13$
$\mathrm {stat}( {\boldsymbol\lambda }) = 6 + 7 = 13$
Now, given a specific semistandard filling T of ![]() $ {\boldsymbol\lambda }$, we map the unique entry in
$ {\boldsymbol\lambda }$, we map the unique entry in ![]() $\lambda ^{(i)}$ with content j to column
$\lambda ^{(i)}$ with content j to column ![]() $k-i+1$ and row
$k-i+1$ and row ![]() $-j$ in
$-j$ in ![]() $\tau $. Every pair which contributes to
$\tau $. Every pair which contributes to ![]() ${\mathrm {inv}}(T)$ now contributes a diagonal coinversion between integers (not
${\mathrm {inv}}(T)$ now contributes a diagonal coinversion between integers (not ![]() $\bullet $ or
$\bullet $ or ![]() $\infty $) in
$\infty $) in ![]() $\tau $. In Figure 1, there are 10 such diagonal coinversions and the filling T has
$\tau $. In Figure 1, there are 10 such diagonal coinversions and the filling T has ![]() ${\mathrm {inv}}(T) = 10$. Since this map is bijective, we have the desired result.
${\mathrm {inv}}(T) = 10$. Since this map is bijective, we have the desired result.
3.2 Equality of the C- and D-functions
Our first main result states that the C-functions and D-functions coincide. This given, Proposition 3.7 implies that the C-functions are symmetric and Schur positive. We know of no direct proof of either of these facts.
Theorem 3.8. For any integers ![]() $n,k,s \geq 0$ with
$n,k,s \geq 0$ with ![]() $k \geq s$ and any
$k \geq s$ and any ![]() $0 \leq r \leq n-s$, we have the equality of formal power series
$0 \leq r \leq n-s$, we have the equality of formal power series
Consequently, we have
Our proof of Theorem 3.8 is combinatorial and uses the column tableau forms of the formal power series ![]() $C_{n,k,s}^{(r)}({\mathbf {x}};q)$ and
$C_{n,k,s}^{(r)}({\mathbf {x}};q)$ and ![]() $D_{n,k,s}^{(r)}({\mathbf {x}};q)$ in Observations 3.3 and 3.6. The idea is to consider building up a general column tableau
$D_{n,k,s}^{(r)}({\mathbf {x}};q)$ in Observations 3.3 and 3.6. The idea is to consider building up a general column tableau ![]() $\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}$ from the column tableau consisting of
$\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}$ from the column tableau consisting of ![]() $k-s$ empty columns by successively adding larger entries and showing that the statistics
$k-s$ empty columns by successively adding larger entries and showing that the statistics ![]() ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and ![]() ${\mathrm {codinv}}$ satisfy the same recursions.
${\mathrm {codinv}}$ satisfy the same recursions.
Proof. Let ![]() $\tau $ be a column tableau with k columns and
$\tau $ be a column tableau with k columns and ![]() $k-s \bullet $’s whose entries are
$k-s \bullet $’s whose entries are ![]() $< N$. We consider building a larger column tableau involving N’s from
$< N$. We consider building a larger column tableau involving N’s from ![]() $\tau $ by the following three-step process.
$\tau $ by the following three-step process.
1. Placing
 $\bar {N}$’s on top of some subset of the k columns of
$\bar {N}$’s on top of some subset of the k columns of  $\tau $.
$\tau $.2. Placing N’s at height 0 between and on either side of the s columns of
 $\tau $ without a
$\tau $ without a  $\bullet $.
$\bullet $.3. Placing N’s at negative heights below some multiset of columns of the resulting figure.
We track the behavior of ![]() ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and ![]() ${\mathrm {codinv}}$ as we perform this procedure, starting by placing the
${\mathrm {codinv}}$ as we perform this procedure, starting by placing the ![]() $\bar {N}$’s on top of columns.
$\bar {N}$’s on top of columns.
Placing a ![]() $\bar {N}$ on top of column i of
$\bar {N}$ on top of column i of ![]() $\tau $ increases the statistic
$\tau $ increases the statistic ![]() ${\mathrm {coinv}}$ by
${\mathrm {coinv}}$ by ![]() $i-1$. We reflect this fact by giving column i the barred
$i-1$. We reflect this fact by giving column i the barred ![]() ${\mathrm {coinv}}$ label of
${\mathrm {coinv}}$ label of ![]() $i-1$. The barred
$i-1$. The barred ![]() ${\mathrm {coinv}}$ labels of the column tableau are shown in bold and barred below.
${\mathrm {coinv}}$ labels of the column tableau are shown in bold and barred below.

The barred ![]() ${\mathrm {coinv}}$ labels give rise to a bijection
${\mathrm {coinv}}$ labels give rise to a bijection
 $$ \begin{align} \iota^{{\mathrm {coinv}}}_{\bar{N}}: \left\{ \begin{array}{c}k\text{-column tableaux } \tau \text{ with} \\ k-s \bullet\text{'s and all entries } < N \end{array} \right\} &\times \left\{\begin{array}{c}\text{subsets } S \text{ of} \\ \{0,1,\dots,k-1\}\end{array} \right\} \longrightarrow \notag \\ &\qquad\qquad\quad\left\{ \begin{array}{c}k\text{-column tableaux } \tau' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau' \text{ are } \leq N \text{ and}\\ \text{the only } N\text{'s in } \tau' \text{ are barred}\end{array} \right\} \end{align} $$
$$ \begin{align} \iota^{{\mathrm {coinv}}}_{\bar{N}}: \left\{ \begin{array}{c}k\text{-column tableaux } \tau \text{ with} \\ k-s \bullet\text{'s and all entries } < N \end{array} \right\} &\times \left\{\begin{array}{c}\text{subsets } S \text{ of} \\ \{0,1,\dots,k-1\}\end{array} \right\} \longrightarrow \notag \\ &\qquad\qquad\quad\left\{ \begin{array}{c}k\text{-column tableaux } \tau' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau' \text{ are } \leq N \text{ and}\\ \text{the only } N\text{'s in } \tau' \text{ are barred}\end{array} \right\} \end{align} $$by letting ![]() $\iota ^{{\mathrm {coinv}}}_{\bar {N}}(\tau ,S)$ be the tableau
$\iota ^{{\mathrm {coinv}}}_{\bar {N}}(\tau ,S)$ be the tableau ![]() $\tau '$ obtained by placing a
$\tau '$ obtained by placing a ![]() $\bar {N}$ on top of every column with barred
$\bar {N}$ on top of every column with barred ![]() ${\mathrm {coinv}}$ label in S. If
${\mathrm {coinv}}$ label in S. If ![]() $\iota ^{{\mathrm {coinv}}}_{\bar {N}}: (\tau ,S) \mapsto \tau '$, then
$\iota ^{{\mathrm {coinv}}}_{\bar {N}}: (\tau ,S) \mapsto \tau '$, then ![]() ${\mathrm {coinv}}(\tau ') = {\mathrm {coinv}}(\tau ) + \sum _{i \in S} i$.
${\mathrm {coinv}}(\tau ') = {\mathrm {coinv}}(\tau ) + \sum _{i \in S} i$.
Next, we consider the effect of ![]() $\bar {N}$ insertion on
$\bar {N}$ insertion on ![]() ${\mathrm {codinv}}$. We bijectively label the k columns of
${\mathrm {codinv}}$. We bijectively label the k columns of ![]() $\tau $ with the k barred
$\tau $ with the k barred ![]() ${\mathrm {codinv}}$ labels
${\mathrm {codinv}}$ labels ![]() $0, 1, \dots , k-1$ (in that order) in descending order of maximal height and, within columns of the same maximal height, proceeding from right to left. The barred
$0, 1, \dots , k-1$ (in that order) in descending order of maximal height and, within columns of the same maximal height, proceeding from right to left. The barred ![]() ${\mathrm {codinv}}$ labels in our example are shown below.
${\mathrm {codinv}}$ labels in our example are shown below.

The barred ![]() ${\mathrm {codinv}}$ labels give a bijection
${\mathrm {codinv}}$ labels give a bijection
 $$ \begin{align} \iota^{{\mathrm {codinv}}}_{\bar{N}}: \left\{ \begin{array}{c}k\text{-column tableaux } \tau \text{ with} \\ k-s \bullet\text{'s and all entries } < N \end{array} \right\} &\times \left\{ \begin{array}{c}\text{subsets } S \text{ of} \\ \{0,1,\dots,k-1\}\end{array} \right\} \longrightarrow \notag \\ &\qquad\qquad\quad \left\{ \begin{array}{c}k\text{-column tableaux } \tau' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau' \text{ are } \leq N \text{ and} \\ \text{the only } N\text{'s in } \tau' \text{ are barred}\end{array} \right\} , \end{align} $$
$$ \begin{align} \iota^{{\mathrm {codinv}}}_{\bar{N}}: \left\{ \begin{array}{c}k\text{-column tableaux } \tau \text{ with} \\ k-s \bullet\text{'s and all entries } < N \end{array} \right\} &\times \left\{ \begin{array}{c}\text{subsets } S \text{ of} \\ \{0,1,\dots,k-1\}\end{array} \right\} \longrightarrow \notag \\ &\qquad\qquad\quad \left\{ \begin{array}{c}k\text{-column tableaux } \tau' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau' \text{ are } \leq N \text{ and} \\ \text{the only } N\text{'s in } \tau' \text{ are barred}\end{array} \right\} , \end{align} $$where ![]() $\iota ^{{\mathrm {codinv}}}_{\bar {N}}(\tau ,S)$ is obtained from
$\iota ^{{\mathrm {codinv}}}_{\bar {N}}(\tau ,S)$ is obtained from ![]() $\tau $ by placing a
$\tau $ by placing a ![]() $\bar {N}$ on top of every column with barred
$\bar {N}$ on top of every column with barred ![]() ${\mathrm {codinv}}$ label indexed by S. If
${\mathrm {codinv}}$ label indexed by S. If ![]() $\iota ^{{\mathrm {codinv}}}_{\bar {N}}: (\tau ,S) \mapsto \tau '$, then
$\iota ^{{\mathrm {codinv}}}_{\bar {N}}: (\tau ,S) \mapsto \tau '$, then ![]() ${\mathrm {codinv}}(\tau ') = {\mathrm {codinv}}(\tau ) + \sum _{i \in S} i$.
${\mathrm {codinv}}(\tau ') = {\mathrm {codinv}}(\tau ) + \sum _{i \in S} i$.
We move on to Step 2 of our insertion procedure: creating new columns by placing N’s at height 0. A single ‘height 0 insertion map’ ![]() $\iota _0$ of this kind on column tableaux has the same effect on
$\iota _0$ of this kind on column tableaux has the same effect on ![]() ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and ![]() ${\mathrm {codinv}}$.
${\mathrm {codinv}}$.
If ![]() $\tau $ is a column tableau with s nonbullet letters at height zero, N’s can be placed (with repetition) in any of the
$\tau $ is a column tableau with s nonbullet letters at height zero, N’s can be placed (with repetition) in any of the ![]() $s+1$ places between and on either side of these nonbullet letters. This gives rise to a bijection
$s+1$ places between and on either side of these nonbullet letters. This gives rise to a bijection
 $$ \begin{align} \iota_0: \left\{ \begin{array}{c}k\text{-column tableaux } \tau' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau' \text{ are } \leq N \text{ and}\\ \text{the only } N\text{'s in } \tau' \text{ are barred}\end{array} \right\} &\times \left\{ \begin{array}{c} \text{finite multisets } S \\ \text{drawn from } \{0,1,\dots,s\} \end{array} \right\} \longrightarrow \notag \\ &\bigsqcup_{K \geq k} \left\{ \begin{array}{c}K\text{-column tableaux } \tau" \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau" \text{ are } \leq N \text{ and}\\ \text{no } N\text{'s in } \tau" \text{ have negative height}\end{array} \right\} , \end{align} $$
$$ \begin{align} \iota_0: \left\{ \begin{array}{c}k\text{-column tableaux } \tau' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau' \text{ are } \leq N \text{ and}\\ \text{the only } N\text{'s in } \tau' \text{ are barred}\end{array} \right\} &\times \left\{ \begin{array}{c} \text{finite multisets } S \\ \text{drawn from } \{0,1,\dots,s\} \end{array} \right\} \longrightarrow \notag \\ &\bigsqcup_{K \geq k} \left\{ \begin{array}{c}K\text{-column tableaux } \tau" \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau" \text{ are } \leq N \text{ and}\\ \text{no } N\text{'s in } \tau" \text{ have negative height}\end{array} \right\} , \end{align} $$where ![]() $\iota _0(\tau ',S)$ is obtained from
$\iota _0(\tau ',S)$ is obtained from ![]() $\tau '$ by inserting
$\tau '$ by inserting ![]() $m_i$ copies of N after column i of
$m_i$ copies of N after column i of ![]() $\tau $, where
$\tau $, where ![]() $m_i$ is the multiplicity of i in S. Suppose
$m_i$ is the multiplicity of i in S. Suppose ![]() $\iota _0(\tau ',S) = \tau "$. The number K of columns of
$\iota _0(\tau ',S) = \tau "$. The number K of columns of ![]() $\tau "$ is related to the number k of columns of
$\tau "$ is related to the number k of columns of ![]() $\tau '$ by
$\tau '$ by ![]() $K = k + |S|$. Furthermore, if there are b unbarred entries in
$K = k + |S|$. Furthermore, if there are b unbarred entries in ![]() $\tau '$ of negative height, we have
$\tau '$ of negative height, we have
In other words, the height zero insertion map ![]() $\iota _0$ has the same effect on
$\iota _0$ has the same effect on ![]() ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and ![]() ${\mathrm {codinv}}$.
${\mathrm {codinv}}$.
Finally, let ![]() $\tau "$ be a column tableau with K columns with entries
$\tau "$ be a column tableau with K columns with entries ![]() $\leq N$ in which there are no N’s with negative height. To perform Step 3 of our insertion process, we insert N’s at the bottom of some multiset of columns of
$\leq N$ in which there are no N’s with negative height. To perform Step 3 of our insertion process, we insert N’s at the bottom of some multiset of columns of ![]() $\tau "$. We track the effect on
$\tau "$. We track the effect on ![]() ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and ![]() ${\mathrm {codinv}}$ as before.
${\mathrm {codinv}}$ as before.
We label the columns of ![]() $\tau "$ from left-to-right with the unbarred
$\tau "$ from left-to-right with the unbarred ![]() ${\mathrm {coinv}}$ labels
${\mathrm {coinv}}$ labels ![]() $0,1, \dots , K$. An example of this labeling is shown below in bold. Since we add unbarred letters on the bottom of a tableau, we show the unbarred labels there as well.
$0,1, \dots , K$. An example of this labeling is shown below in bold. Since we add unbarred letters on the bottom of a tableau, we show the unbarred labels there as well.

The unbarred ![]() ${\mathrm {coinv}}$ labels give a bijection
${\mathrm {coinv}}$ labels give a bijection
 $$ \begin{align} \iota^{{\mathrm {coinv}}}_N: \left\{ \begin{array}{c}K\text{-column tableaux } \tau" \text{ with } k-s \bullet\text{',} \\ \text{such that all entries of } \tau" \text{ are } \leq N \text{ and}\\ \text{no } N\text{'s in } \tau" \text{ have negative height}\end{array} \right\} &\times \left\{ \begin{array}{c} \text{finite multisets } S \\ \text{drawn from } \{0,1,\dots,K-1\} \end{array} \right\} \longrightarrow \notag \\ &\left\{ \begin{array}{c} K\text{-column tableaux } \tau"' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries in } \tau"' \text{ are } \leq N \end{array} \right\} , \end{align} $$
$$ \begin{align} \iota^{{\mathrm {coinv}}}_N: \left\{ \begin{array}{c}K\text{-column tableaux } \tau" \text{ with } k-s \bullet\text{',} \\ \text{such that all entries of } \tau" \text{ are } \leq N \text{ and}\\ \text{no } N\text{'s in } \tau" \text{ have negative height}\end{array} \right\} &\times \left\{ \begin{array}{c} \text{finite multisets } S \\ \text{drawn from } \{0,1,\dots,K-1\} \end{array} \right\} \longrightarrow \notag \\ &\left\{ \begin{array}{c} K\text{-column tableaux } \tau"' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries in } \tau"' \text{ are } \leq N \end{array} \right\} , \end{align} $$where ![]() $\iota ^{{\mathrm {coinv}}}_N(\tau ",S)$ is obtained by placing
$\iota ^{{\mathrm {coinv}}}_N(\tau ",S)$ is obtained by placing ![]() $m_i$ copies of N below the column with label i, where
$m_i$ copies of N below the column with label i, where ![]() $m_i$ is the multiplicity of i in S. If
$m_i$ is the multiplicity of i in S. If ![]() $\iota ^{{\mathrm {coinv}}}_N: (\tau ",S) \mapsto \tau "'$, then
$\iota ^{{\mathrm {coinv}}}_N: (\tau ",S) \mapsto \tau "'$, then ![]() ${\mathrm {coinv}}(\tau "') = {\mathrm {coinv}}(\tau ") + \sum _{i \in S} i$.
${\mathrm {coinv}}(\tau "') = {\mathrm {coinv}}(\tau ") + \sum _{i \in S} i$.
The effect of inserting N’s at negative height on ![]() ${\mathrm {codinv}}$ may be described as follows. We label the columns of
${\mathrm {codinv}}$ may be described as follows. We label the columns of ![]() $\tau $ bijectively with the unbarred
$\tau $ bijectively with the unbarred ![]() ${\mathrm {codinv}}$ labels
${\mathrm {codinv}}$ labels ![]() $0,1,\dots ,k-1$ (in that order) starting at columns of lesser maximal depth and, within columns of the same maximal depth, proceeding from right to left. The unbarred
$0,1,\dots ,k-1$ (in that order) starting at columns of lesser maximal depth and, within columns of the same maximal depth, proceeding from right to left. The unbarred ![]() ${\mathrm {codinv}}$ labels in our example as shown below.
${\mathrm {codinv}}$ labels in our example as shown below.

The unbarred ![]() ${\mathrm {codinv}}$ labels give a bijection
${\mathrm {codinv}}$ labels give a bijection
 $$ \begin{align} \iota^{{\mathrm {codinv}}}_N: \left\{ \begin{array}{c}K\text{-column tableaux } \tau" \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau" \text{ are } \leq N \text{ and}\\ \text{no } N\text{'s in } \tau" \text{ have negative height}\end{array} \right\} &\times \left\{\begin{array}{c} \text{finite multisets } S \\ \text{drawn from } \{0,1,\dots,K-1\} \end{array} \right\} \longrightarrow \notag\\ &\left\{ \begin{array}{c} K\text{-column tableaux } \tau"' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries in } \tau"' \text{ are } \leq N \end{array} \right\} \end{align} $$
$$ \begin{align} \iota^{{\mathrm {codinv}}}_N: \left\{ \begin{array}{c}K\text{-column tableaux } \tau" \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries of } \tau" \text{ are } \leq N \text{ and}\\ \text{no } N\text{'s in } \tau" \text{ have negative height}\end{array} \right\} &\times \left\{\begin{array}{c} \text{finite multisets } S \\ \text{drawn from } \{0,1,\dots,K-1\} \end{array} \right\} \longrightarrow \notag\\ &\left\{ \begin{array}{c} K\text{-column tableaux } \tau"' \text{ with } k-s \bullet\text{'s,} \\ \text{such that all entries in } \tau"' \text{ are } \leq N \end{array} \right\} \end{align} $$as follows. Given ![]() $(\tau ",S)$, we process the entries of S in weakly increasing order and, given an entry i, we place an N at the bottom of the column with unbarred
$(\tau ",S)$, we process the entries of S in weakly increasing order and, given an entry i, we place an N at the bottom of the column with unbarred ![]() ${\mathrm {codinv}}$ label i. Recalling that we consider every unfilled cell below a column to have the label
${\mathrm {codinv}}$ label i. Recalling that we consider every unfilled cell below a column to have the label ![]() $+ \infty $ for the purpose of calculating
$+ \infty $ for the purpose of calculating ![]() ${\mathrm {codinv}}$, we see that if
${\mathrm {codinv}}$, we see that if ![]() $\iota ^{{\mathrm {codinv}}}_N: (\tau ",S) \mapsto \tau "'$, then
$\iota ^{{\mathrm {codinv}}}_N: (\tau ",S) \mapsto \tau "'$, then ![]() ${\mathrm {codinv}}(\tau "') = {\mathrm {codinv}}(\tau ") + \sum _{i \in S} i$. In summary, the
${\mathrm {codinv}}(\tau "') = {\mathrm {codinv}}(\tau ") + \sum _{i \in S} i$. In summary, the ![]() $\iota $-maps show that the C-functions and D-functions satisfy the same recursion, which establishes the theorem.
$\iota $-maps show that the C-functions and D-functions satisfy the same recursion, which establishes the theorem.
Although the D-functions are more directly seen to be symmetric and Schur positive, in order to describe a recursive formula for the action of ![]() $h_j^{\perp }$, it will be more convenient to use the C-functions instead (Lemma 3.14). This formula will involve the more refined
$h_j^{\perp }$, it will be more convenient to use the C-functions instead (Lemma 3.14). This formula will involve the more refined ![]() $C_{n,k,s}^{(r)}({\mathbf {x}};q)$ rather than their coarsened versions
$C_{n,k,s}^{(r)}({\mathbf {x}};q)$ rather than their coarsened versions ![]() $C_{n,k,s}({\mathbf {x}};q,z)$.
$C_{n,k,s}({\mathbf {x}};q,z)$.
3.3 Substaircase shuffles
Given ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}$,
$\sigma \in {\mathcal {OSP}}_{n,k,s}$, ![]() ${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$ is a length n sequence over the alphabet
${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$ is a length n sequence over the alphabet ![]() $\{0,1,2,\dots ,\bar {0},\bar {1},\bar {2},\dots \}$. In this subsection, we show that
$\{0,1,2,\dots ,\bar {0},\bar {1},\bar {2},\dots \}$. In this subsection, we show that ![]() $\sigma \mapsto {\mathrm {code}}(\sigma )$ is injective and characterise its image. We begin by defining a partial order on sequences of (potentially barred) nonnegative integers.
$\sigma \mapsto {\mathrm {code}}(\sigma )$ is injective and characterise its image. We begin by defining a partial order on sequences of (potentially barred) nonnegative integers.
Definition 3.9. ![]() $(c_1, \dots , c_n) \leq (b_1, \dots , b_n)$ if, for every i,
$(c_1, \dots , c_n) \leq (b_1, \dots , b_n)$ if, for every i, ![]() $c_i \leq b_i$ in value and that
$c_i \leq b_i$ in value and that ![]() $c_i$ is barred if and only if
$c_i$ is barred if and only if ![]() $b_i$ is barred.
$b_i$ is barred.
The image of the classical coinversion code map on permutations in ![]() ${\mathfrak {S}}_n$ is given by words
${\mathfrak {S}}_n$ is given by words ![]() $(c_1, \dots , c_n)$ which are
$(c_1, \dots , c_n)$ which are ![]() $\leq $ the ‘staircase’ word
$\leq $ the ‘staircase’ word ![]() $(n-1, n-2, \dots , 1, 0)$. For ordered set partitions of
$(n-1, n-2, \dots , 1, 0)$. For ordered set partitions of ![]() $[n]$ into k blocks with no barred letters, this result was generalised in [Reference Rhoades and Wilson26], where the appropriate notion of ‘staircase’ is given by a shuffle of two sequences. We extend these definitions to barred letters as follows.
$[n]$ into k blocks with no barred letters, this result was generalised in [Reference Rhoades and Wilson26], where the appropriate notion of ‘staircase’ is given by a shuffle of two sequences. We extend these definitions to barred letters as follows.
Recall that a shuffle of two sequences ![]() $(a_1, \dots , a_r)$ and
$(a_1, \dots , a_r)$ and ![]() $(b_1, \dots , b_s)$ is an interleaving
$(b_1, \dots , b_s)$ is an interleaving ![]() $(c_1, \dots , c_{r+s})$ of these sequences which preserves the relative order of the a’s and the b’s. The following collection
$(c_1, \dots , c_{r+s})$ of these sequences which preserves the relative order of the a’s and the b’s. The following collection ![]() ${\mathcal {SS}}^{(r)}_{n,k,s}$ of words will turn out to be the image of the map
${\mathcal {SS}}^{(r)}_{n,k,s}$ of words will turn out to be the image of the map ![]() ${\mathrm {code}}$ on
${\mathrm {code}}$ on ![]() ${\mathcal {OSP}}_{n,k,s}^{(r)}$.
${\mathcal {OSP}}_{n,k,s}^{(r)}$.
Definition 3.10. Let ![]() $n, k, s \geq 0$ be integers. For
$n, k, s \geq 0$ be integers. For ![]() $0 \leq r \leq n-s$, a staircase with r barred letters is a length n word obtained by shuffling
$0 \leq r \leq n-s$, a staircase with r barred letters is a length n word obtained by shuffling
where ![]() $r_0 + r_1 + \cdots + r_s = r$. If
$r_0 + r_1 + \cdots + r_s = r$. If ![]() $k=s$, we insist that
$k=s$, we insist that ![]() $r_0 = 0$ in the above expression. Let
$r_0 = 0$ in the above expression. Let ![]() ${\mathcal {SS}}^{(r)}_{n,k,s}$ be the family of words
${\mathcal {SS}}^{(r)}_{n,k,s}$ be the family of words ![]() $(c_1, \dots , c_n)$ which are
$(c_1, \dots , c_n)$ which are ![]() $\leq $ some staircase
$\leq $ some staircase ![]() $(b_1, \dots , b_n)$. We also let
$(b_1, \dots , b_n)$. We also let
and refer to words in ![]() ${\mathcal {SS}}_{n,k,s}$ as substaircase.
${\mathcal {SS}}_{n,k,s}$ as substaircase.
Definition 3.10 implies that
We give an example to clarify these concepts.
Example 3.11. Consider the case ![]() $n = 5, k = 3, s = 2$ and
$n = 5, k = 3, s = 2$ and ![]() $r = 2$. The staircases with r barred letters are the shuffles of any of the six words
$r = 2$. The staircases with r barred letters are the shuffles of any of the six words
with the single-letter word ![]() $(2)$. For example, if we shuffle
$(2)$. For example, if we shuffle ![]() $(2)$ into the second sequence from the left, we get the five staircases
$(2)$ into the second sequence from the left, we get the five staircases
The leftmost sequence displayed above contributes
to ![]() ${\mathcal {SS}}_{5,3,2}^{(2)}$. These are the 12 sequences which have the same bar pattern as, and are componentwise
${\mathcal {SS}}_{5,3,2}^{(2)}$. These are the 12 sequences which have the same bar pattern as, and are componentwise ![]() $\leq $ to, the staircase
$\leq $ to, the staircase ![]() $(2, \bar {0}, 1, \bar {1}, 0)$.
$(2, \bar {0}, 1, \bar {1}, 0)$.
The previous example shows that applying Definition 3.10 to obtain the set of words in ![]() ${\mathcal {SS}}_{n,k,s}$ can be involved. The following lemma gives a simple recursive definition of substaircase sequences of length n in terms of substaircase sequences of length
${\mathcal {SS}}_{n,k,s}$ can be involved. The following lemma gives a simple recursive definition of substaircase sequences of length n in terms of substaircase sequences of length ![]() $n-1$. This recursion gives an efficient way to calculate
$n-1$. This recursion gives an efficient way to calculate ![]() ${\mathcal {SS}}_{n,k,s}$ and will be useful in our algebraic analysis of
${\mathcal {SS}}_{n,k,s}$ and will be useful in our algebraic analysis of ![]() ${\mathbb {W}}_{n,k,s}$ in Section 4. It will turn out that words in
${\mathbb {W}}_{n,k,s}$ in Section 4. It will turn out that words in ![]() ${\mathcal {SS}}_{n,k,s}$ index a monomial basis of
${\mathcal {SS}}_{n,k,s}$ index a monomial basis of ![]() ${\mathbb {W}}_{n,k,s}$.
${\mathbb {W}}_{n,k,s}$.
Lemma 3.12. Let ![]() $n, k, s \geq 0$ be integers with
$n, k, s \geq 0$ be integers with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $0 \leq r \leq n-s$. The set
$0 \leq r \leq n-s$. The set ![]() ${\mathcal {SS}}_{n,k,s}^{(r)}$ has the disjoint union decomposition
${\mathcal {SS}}_{n,k,s}^{(r)}$ has the disjoint union decomposition
 $$ \begin{align} {\mathcal{SS}}_{n,k,s}^{(r)} = &\bigsqcup_{a = 0}^{k-s-1} \left\{ ( \bar{a}, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s}^{(r-1)} \right\} \, \sqcup \end{align} $$
$$ \begin{align} {\mathcal{SS}}_{n,k,s}^{(r)} = &\bigsqcup_{a = 0}^{k-s-1} \left\{ ( \bar{a}, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s}^{(r-1)} \right\} \, \sqcup \end{align} $$ $$ \begin{align} & \bigsqcup_{a = 0}^{s-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s-1}^{(r)} \right\} \, \sqcup \end{align} $$
$$ \begin{align} & \bigsqcup_{a = 0}^{s-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s-1}^{(r)} \right\} \, \sqcup \end{align} $$ $$ \begin{align} & \bigsqcup_{a = s}^{k-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s}^{(r)} \right\} ,\end{align} $$
$$ \begin{align} & \bigsqcup_{a = s}^{k-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s}^{(r)} \right\} ,\end{align} $$and the set ![]() ${\mathcal {SS}}_{n,k,s}$ has the disjoint union decomposition
${\mathcal {SS}}_{n,k,s}$ has the disjoint union decomposition
 $$ \begin{align} {\mathcal{SS}}_{n,k,s} = &\bigsqcup_{a = 0}^{k-s-1} \left\{ ( \bar{a}, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s} \right\} \, \sqcup \end{align} $$
$$ \begin{align} {\mathcal{SS}}_{n,k,s} = &\bigsqcup_{a = 0}^{k-s-1} \left\{ ( \bar{a}, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s} \right\} \, \sqcup \end{align} $$ $$ \begin{align} & \bigsqcup_{a = 0}^{s-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s-1} \right\} \, \sqcup \end{align} $$
$$ \begin{align} & \bigsqcup_{a = 0}^{s-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s-1} \right\} \, \sqcup \end{align} $$ $$ \begin{align} & \bigsqcup_{a = s}^{k-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s} \right\}. \end{align} $$
$$ \begin{align} & \bigsqcup_{a = s}^{k-1} \left\{ (a, c_2, \dots, c_n) \,:\, (c_2, \dots, c_n) \in {\mathcal{SS}}_{n-1,k,s} \right\}. \end{align} $$Proof. The second disjoint union decomposition for ![]() ${\mathcal {SS}}_{n,k,s}$ follows from the first disjoint union decomposition for
${\mathcal {SS}}_{n,k,s}$ follows from the first disjoint union decomposition for ![]() ${\mathcal {SS}}_{n,k,s}^{(r)}$ by taking the (disjoint) union over all r, so we focus on the first decomposition.
${\mathcal {SS}}_{n,k,s}^{(r)}$ by taking the (disjoint) union over all r, so we focus on the first decomposition.
Given ![]() $(c_1, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$, there exists some word
$(c_1, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$, there exists some word ![]() $(b_1, b_2, \dots , b_n)$ obtained by shuffling
$(b_1, b_2, \dots , b_n)$ obtained by shuffling
where ![]() $r_0 + r_1 + \cdots + r_s = r$ with the constant sequence
$r_0 + r_1 + \cdots + r_s = r$ with the constant sequence ![]() $(k-1)^{n-r-s}$, such that
$(k-1)^{n-r-s}$, such that ![]() $(c_1, c_2, \dots , c_n)$ has the same bar pattern as
$(c_1, c_2, \dots , c_n)$ has the same bar pattern as ![]() $(b_1, b_2, \dots , b_n)$ and
$(b_1, b_2, \dots , b_n)$ and ![]() $c_i \leq b_i$ for all i. There are three possibilities for the first entry
$c_i \leq b_i$ for all i. There are three possibilities for the first entry ![]() $c_1$.
$c_1$.
• If
 $c_1 = \bar {a}$ is barred, then we must have
$c_1 = \bar {a}$ is barred, then we must have  $r_0> 0$ and
$r_0> 0$ and  $b_1 = \overline {k-s-1}$. It follows that
$b_1 = \overline {k-s-1}$. It follows that  $0 \leq a \leq k-s-1$. Furthermore, the word
$0 \leq a \leq k-s-1$. Furthermore, the word  $(b_2, \dots , b_n)$ is a shuffle of This implies that
$(b_2, \dots , b_n)$ is a shuffle of This implies that $$ \begin{align*} ( \overline{k-s-1} )^{r_0-1} (s-1) ( \overline{k-s} )^{r_1} (s-2) ( \overline{k-s+1} )^{r_2} (s-3) \cdots 0 ( \overline{k-1} )^{r_s} \quad \text{and} \quad (k-1)^{n-r-s}. \end{align*} $$
$$ \begin{align*} ( \overline{k-s-1} )^{r_0-1} (s-1) ( \overline{k-s} )^{r_1} (s-2) ( \overline{k-s+1} )^{r_2} (s-3) \cdots 0 ( \overline{k-1} )^{r_s} \quad \text{and} \quad (k-1)^{n-r-s}. \end{align*} $$ $(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r-1)}$. Conversely, given
$(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r-1)}$. Conversely, given  $(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r-1)}$ and
$(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r-1)}$ and  $0 \leq a \leq k-s-1$, we see that
$0 \leq a \leq k-s-1$, we see that  $(\bar {a}, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ by prepending the letter
$(\bar {a}, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ by prepending the letter  $\overline {k-s-1}$ to any
$\overline {k-s-1}$ to any  $(n-1,k,s)$-staircase
$(n-1,k,s)$-staircase  $(b_2, \dots , b_n) \geq (c_2, \dots , c_n)$.
$(b_2, \dots , b_n) \geq (c_2, \dots , c_n)$.• If
 $c_1 = a$ is unbarred with
$c_1 = a$ is unbarred with  $0 \leq a \leq s - 1$, the first letter
$0 \leq a \leq s - 1$, the first letter  $b_1$ of
$b_1$ of  $(b_1, b_2, \dots , b_n)$ must also be unbarred and
$(b_1, b_2, \dots , b_n)$ must also be unbarred and  $r_0 = 0$. This means that
$r_0 = 0$. This means that  $b_1 = s-1$ or
$b_1 = s-1$ or  $k-1$. If
$k-1$. If  $k> s$ and
$k> s$ and  $b_1 = k-1$, we may interchange the
$b_1 = k-1$, we may interchange the  $b_1$ with the unique occurrence of
$b_1$ with the unique occurrence of  $s-1$ in
$s-1$ in  $(b_1, b_2, \dots , b_n)$ to get a new staircase
$(b_1, b_2, \dots , b_n)$ to get a new staircase  $(b^{\prime }_1, b^{\prime }_2, \dots , b^{\prime }_n)$ which shares the color pattern of
$(b^{\prime }_1, b^{\prime }_2, \dots , b^{\prime }_n)$ which shares the color pattern of  $(c_1, c_2, \dots , c_n)$ and satisfies
$(c_1, c_2, \dots , c_n)$ and satisfies  $c_i \leq b^{\prime }_i$ for all i. We may, therefore, assume that
$c_i \leq b^{\prime }_i$ for all i. We may, therefore, assume that  $b_1 = s-1$. This means that the sequence
$b_1 = s-1$. This means that the sequence  $(b_2, \dots , b_n)$ is a shuffle of the words and
$(b_2, \dots , b_n)$ is a shuffle of the words and $$ \begin{align*} ( \overline{k-s} )^{r_1} (s-2) ( \overline{k-s+1} )^{r_2} (s-3) \cdots 0 ( \overline{k-1} )^{r_s} \quad \text{and} \quad (k-1)^{n-r-s} \end{align*} $$
$$ \begin{align*} ( \overline{k-s} )^{r_1} (s-2) ( \overline{k-s+1} )^{r_2} (s-3) \cdots 0 ( \overline{k-1} )^{r_s} \quad \text{and} \quad (k-1)^{n-r-s} \end{align*} $$ $r_1 + r_2 + \cdots + r_s = r$. Therefore, we have
$r_1 + r_2 + \cdots + r_s = r$. Therefore, we have  $(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s-1}^{(r)}$. Conversely, given
$(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s-1}^{(r)}$. Conversely, given  $(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s-1}^{(r)}$, one sees that
$(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s-1}^{(r)}$, one sees that  $(a, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ by prepending an
$(a, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ by prepending an  $s-1$ to any
$s-1$ to any  $(n-1,k,s-1)$-staircase
$(n-1,k,s-1)$-staircase  $(b_2, \dots , b_n) \geq (c_2, \dots , c_n)$.
$(b_2, \dots , b_n) \geq (c_2, \dots , c_n)$.• Finally, if
 $c_1 = a$ is unbarred and
$c_1 = a$ is unbarred and  $c_1 \geq s$, the first letter
$c_1 \geq s$, the first letter  $b_1$ of
$b_1$ of  $(b_1, b_2, \dots , b_n)$ must be unbarred and
$(b_1, b_2, \dots , b_n)$ must be unbarred and  $\geq s$. This implies that
$\geq s$. This implies that  $b_1 = k-1$, so that
$b_1 = k-1$, so that  $s \leq a < k-1$. Furthermore, the sequence
$s \leq a < k-1$. Furthermore, the sequence  $(b_2, \dots , b_n)$ is a shuffle of the words where
$(b_2, \dots , b_n)$ is a shuffle of the words where $$ \begin{align*} ( \overline{k-s-1} )^{r_0} (s-1) ( \overline{k-s} )^{r_1} (s-2) ( \overline{k-s+1} )^{r_2} (s-3) \cdots 0 ( \overline{k-1} )^{r_s} \quad \text{and} \quad (k-1)^{n-r-s-1}, \end{align*} $$
$$ \begin{align*} ( \overline{k-s-1} )^{r_0} (s-1) ( \overline{k-s} )^{r_1} (s-2) ( \overline{k-s+1} )^{r_2} (s-3) \cdots 0 ( \overline{k-1} )^{r_s} \quad \text{and} \quad (k-1)^{n-r-s-1}, \end{align*} $$ $r_0 + r_1 + \cdots + r_s = r$. This means that
$r_0 + r_1 + \cdots + r_s = r$. This means that  $(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r)}$. Conversely, for any
$(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r)}$. Conversely, for any  $(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r)}$, we see that
$(c_2, \dots , c_n) \in {\mathcal {SS}}_{n-1,k,s}^{(r)}$, we see that  $(a, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ by prepending a
$(a, c_2, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ by prepending a  $k-1$ to any
$k-1$ to any  $(n-1,k,s)$-staircase
$(n-1,k,s)$-staircase  $(b_2, \dots , b_n) \geq (c_2, \dots , c_n)$.
$(b_2, \dots , b_n) \geq (c_2, \dots , c_n)$.
The three bullet points above show that ![]() ${\mathcal {SS}}_{n,k,s}^{(r)}$ is a union of the claimed sets of words. The disjointness of this union follows since the first letters of the words in these sets are distinct.
${\mathcal {SS}}_{n,k,s}^{(r)}$ is a union of the claimed sets of words. The disjointness of this union follows since the first letters of the words in these sets are distinct.
We are ready to state the main result of this subsection: the codes of ordered set superpartitions are precisely the substaircase words. The key idea of the proof is to invert the map ![]() ${\mathrm {code}}: \sigma \mapsto (c_1, \dots , c_n)$, sending an ordered set partition to its coinversion code. The inverse map
${\mathrm {code}}: \sigma \mapsto (c_1, \dots , c_n)$, sending an ordered set partition to its coinversion code. The inverse map ![]() $\iota : (c_1, \dots , c_n) \mapsto \sigma $ is a variant on the insertion maps in the proof of Theorem 3.8.
$\iota : (c_1, \dots , c_n) \mapsto \sigma $ is a variant on the insertion maps in the proof of Theorem 3.8.
Theorem 3.13. Let ![]() $n, k, s \geq 0$ be integers with
$n, k, s \geq 0$ be integers with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $r \leq n-k$. The coinversion code map gives a well-defined bijection
$r \leq n-k$. The coinversion code map gives a well-defined bijection
Proof. Our first task is to show that the function ![]() ${\mathrm {code}}$ is well-defined, that is that
${\mathrm {code}}$ is well-defined, that is that ![]() ${\mathrm {code}}(\sigma ) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ for any
${\mathrm {code}}(\sigma ) \in {\mathcal {SS}}_{n,k,s}^{(r)}$ for any ![]() $\sigma \in {\mathcal {OSP}}_{n,k,s}^{(r)}$. To this end, let
$\sigma \in {\mathcal {OSP}}_{n,k,s}^{(r)}$. To this end, let ![]() $\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}^{(r)}$ with
$\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,s}^{(r)}$ with ![]() ${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$. We associate a staircase
${\mathrm {code}}(\sigma ) = (c_1, \dots , c_n)$. We associate a staircase ![]() $(b_1, \dots , b_n)$ to
$(b_1, \dots , b_n)$ to ![]() $\sigma $ as follows. Write the minimal elements
$\sigma $ as follows. Write the minimal elements ![]() $\min B_1, \dots , \min B_s$ in increasing order
$\min B_1, \dots , \min B_s$ in increasing order ![]() $i_1 < \cdots < i_s$, and set
$i_1 < \cdots < i_s$, and set ![]() $b_{i_j} = s-j$ for each
$b_{i_j} = s-j$ for each ![]() $j \in \{1,\ldots ,s\}$. If
$j \in \{1,\ldots ,s\}$. If ![]() $1 \leq i \leq n$ and i is barred in
$1 \leq i \leq n$ and i is barred in ![]() $\sigma $, write
$\sigma $, write ![]() $b_i = \overline {k-s-1+m_i}$, where
$b_i = \overline {k-s-1+m_i}$, where ![]() $m_i = | \{ 1 \leq j \leq s \,:\, i_j < i \} |$. Finally, if
$m_i = | \{ 1 \leq j \leq s \,:\, i_j < i \} |$. Finally, if ![]() $1 \leq i \leq n$, i is unbarred in
$1 \leq i \leq n$, i is unbarred in ![]() $\sigma $, and i is not minimal in any of the first s blocks
$\sigma $, and i is not minimal in any of the first s blocks ![]() $B_1, \dots , B_s$, set
$B_1, \dots , B_s$, set ![]() $b_i = k-1$.
$b_i = k-1$.
As an example of these concepts, consider ![]() $\sigma = (5, 7 \mid 1 \mid 3, \bar {4}, \bar {8} \mid \varnothing \mid \bar {2}, 6) \in {\mathcal {OSP}}_{8,5,3}^{(3)}$. The associated staircase is
$\sigma = (5, 7 \mid 1 \mid 3, \bar {4}, \bar {8} \mid \varnothing \mid \bar {2}, 6) \in {\mathcal {OSP}}_{8,5,3}^{(3)}$. The associated staircase is ![]() $(b_1, \dots , b_8) = (2, \bar {2}, 1, \bar {3}, 0, 4, 4, \bar {4})$. We have
$(b_1, \dots , b_8) = (2, \bar {2}, 1, \bar {3}, 0, 4, 4, \bar {4})$. We have ![]() ${\mathrm {code}}(\sigma ) = (c_1, \dots , c_8) = (1, \bar {2}, 0, \bar {1}, 0, 4, 0, \bar {2})$, which has the same bar pattern as, and is componentwise
${\mathrm {code}}(\sigma ) = (c_1, \dots , c_8) = (1, \bar {2}, 0, \bar {1}, 0, 4, 0, \bar {2})$, which has the same bar pattern as, and is componentwise ![]() $\leq $, the sequence
$\leq $, the sequence ![]() $(b_1, \dots , b_8)$.
$(b_1, \dots , b_8)$.
By construction, b is indeed a staircase. Furthermore, ![]() $b_i$ is barred if and only if
$b_i$ is barred if and only if ![]() $c_i$ is barred. It is also the case that
$c_i$ is barred. It is also the case that ![]() $c_i \leq b_i$ for
$c_i \leq b_i$ for ![]() $1 \leq i \leq n$. One way to see this is to note that b is the unique set superpartition
$1 \leq i \leq n$. One way to see this is to note that b is the unique set superpartition ![]() $\tau $ that has the same positive-height entries, the same zero-height entries and the same negative-height entries as
$\tau $ that has the same positive-height entries, the same zero-height entries and the same negative-height entries as ![]() $\sigma $ but with its code maximised in every coordinate. We can construct
$\sigma $ but with its code maximised in every coordinate. We can construct ![]() $\tau $ by writing the zero-height entries in increasing order from left to right and placing the other entries as far right as possible. In our example, we have
$\tau $ by writing the zero-height entries in increasing order from left to right and placing the other entries as far right as possible. In our example, we have ![]() $\tau = (1 \mid 3 \mid 5 \mid \varnothing \mid \bar {2}, \bar {4}, 6, 7, \bar {8}) \in {\mathcal {OSP}}_{8,5,3}^{(3)}$.
$\tau = (1 \mid 3 \mid 5 \mid \varnothing \mid \bar {2}, \bar {4}, 6, 7, \bar {8}) \in {\mathcal {OSP}}_{8,5,3}^{(3)}$.
We leave it for the reader to verify that ![]() $(c_1, \dots , c_n)$ has the same bar pattern as
$(c_1, \dots , c_n)$ has the same bar pattern as ![]() $(b_1, \dots , b_n)$ and
$(b_1, \dots , b_n)$ and ![]() $(c_1, \dots , c_n) \leq (b_1, \dots , b_n)$ componentwise. This shows that the function
$(c_1, \dots , c_n) \leq (b_1, \dots , b_n)$ componentwise. This shows that the function ![]() ${\mathrm {code}}$ in the statement is well defined.
${\mathrm {code}}$ in the statement is well defined.
We show that ![]() ${\mathrm {code}}$ is a bijection by constructing its inverse map
${\mathrm {code}}$ is a bijection by constructing its inverse map
as follows. The map ![]() $\iota $ starts with a sequence
$\iota $ starts with a sequence ![]() $(\varnothing \mid \cdots \mid \varnothing )$ of k copies of the empty set and builds up an ordered set superpartition by insertion.
$(\varnothing \mid \cdots \mid \varnothing )$ of k copies of the empty set and builds up an ordered set superpartition by insertion.
Given a sequence ![]() $(B_1 \mid \cdots \mid B_k)$ of k possibly empty subsets of the alphabet
$(B_1 \mid \cdots \mid B_k)$ of k possibly empty subsets of the alphabet ![]() $\{1, 2, \dots , \bar {1}, \bar {2}, \dots \}$, we assign the blocks
$\{1, 2, \dots , \bar {1}, \bar {2}, \dots \}$, we assign the blocks ![]() $B_i$ the unbarred labels
$B_i$ the unbarred labels ![]() $0, 1, 2, \dots , k-1$ as follows. Moving from right to left, we assign the labels
$0, 1, 2, \dots , k-1$ as follows. Moving from right to left, we assign the labels ![]() $0, 1, \dots , j-1$ to the j empty blocks among
$0, 1, \dots , j-1$ to the j empty blocks among ![]() $B_1, \dots , B_s$. Then, moving from left to right, we assign the unlabeled blocks the labels
$B_1, \dots , B_s$. Then, moving from left to right, we assign the unlabeled blocks the labels ![]() $j, j+1, \dots , k-1$. An example of unbarred labels when
$j, j+1, \dots , k-1$. An example of unbarred labels when ![]() $k = 7$ and
$k = 7$ and ![]() $s = 4$ is as follows:
$s = 4$ is as follows:
we draw unbarred labels below their blocks. The barred labels ![]() $\bar {0}, \bar {1}, \dots $, as assigned to the blocks
$\bar {0}, \bar {1}, \dots $, as assigned to the blocks ![]() $B_i$, where either
$B_i$, where either ![]() $i> s$ or
$i> s$ or ![]() $B_i \neq \varnothing $ by moving left to right. In our example, the barred labels are
$B_i \neq \varnothing $ by moving left to right. In our example, the barred labels are
where the blocks ![]() $B_2 = B_3 = \varnothing $ do not receive a barred label because
$B_2 = B_3 = \varnothing $ do not receive a barred label because ![]() $2, 3 \leq s = 4$. Barred labels are written above their blocks.
$2, 3 \leq s = 4$. Barred labels are written above their blocks.
Let ![]() $(c_1, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$. To define
$(c_1, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$. To define ![]() $\iota (c_1, \dots , c_n)$, we start with the sequence
$\iota (c_1, \dots , c_n)$, we start with the sequence ![]() $(B_1 \mid \cdots \mid B_k) = (\varnothing \mid \cdots \mid \varnothing )$ of k empty blocks and iteratively insert i into the block with unbarred label
$(B_1 \mid \cdots \mid B_k) = (\varnothing \mid \cdots \mid \varnothing )$ of k empty blocks and iteratively insert i into the block with unbarred label ![]() $c_i$ (if
$c_i$ (if ![]() $c_i$ is unbarred) or insert
$c_i$ is unbarred) or insert ![]() $\bar {i}$ into the block with barred label
$\bar {i}$ into the block with barred label ![]() $c_i$ (if
$c_i$ (if ![]() $c_i$ is barred). For example, if
$c_i$ is barred). For example, if ![]() $(n,k,s) = (8,5,3)$ and
$(n,k,s) = (8,5,3)$ and ![]() $(c_1, \dots , c_8) = (1, \bar {2}, 0, \bar {1}, 0, 4, 0, \bar {2})$, we perform the following insertion procedure.
$(c_1, \dots , c_8) = (1, \bar {2}, 0, \bar {1}, 0, 4, 0, \bar {2})$, we perform the following insertion procedure.
 $$\begin{align*}\begin{array}{c | c | c} i & c_i & (B_1 \mid \cdots \mid B_s) \\ \hline &&\\[-9pt] 1 & 1 & (\varnothing \,_1 \mid 1 \,_2 \,^{\bar{0}} \mid \varnothing \,_0 \mid \varnothing \,_3 \,^{\bar{1}} \mid \varnothing \,_4 \,^{\bar{2}}) \\ 2 & \bar{2} & (\varnothing \,_1 \mid 1 \,_2 \,^{\bar{0}} \mid \varnothing \,_0 \mid \varnothing \,_3 \,^{\bar{1}} \mid \bar{2} \,_4 \,^{\bar{2}}) \\ 3 & 0 & (\varnothing \,_0 \mid 1 \,_1 \,^{\bar{0}} \mid 3 \,_2 \,^{\bar{1}} \mid \varnothing \,_3 \,^{\bar{2}} \mid \bar{2} \,_4 \,^{\bar{3}}) \\ 4 & \bar{1} &(\varnothing \,_0 \mid 1 \,_1 \,^{\bar{0}} \mid 3, \bar{4} \,_2 \,^{\bar{1}} \mid \varnothing \,_3 \,^{\bar{2}} \mid \bar{2} \,_4 \,^{\bar{3}}) \\ 5 & 0 &(5 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2} \,_4 \,^{\bar{4}}) \\ 6 & 4 &(5 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2}, 6 \,_4 \,^{\bar{4}}) \\ 7 & 0 &(5, 7 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2}, 6 \,_4 \,^{\bar{4}}) \\ 8 & \bar{2} &(5, 7 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4}, \bar{8} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2}, 6 \,_4 \,^{\bar{4}}) \\ \end{array}\\[-16pt] \end{align*}$$
$$\begin{align*}\begin{array}{c | c | c} i & c_i & (B_1 \mid \cdots \mid B_s) \\ \hline &&\\[-9pt] 1 & 1 & (\varnothing \,_1 \mid 1 \,_2 \,^{\bar{0}} \mid \varnothing \,_0 \mid \varnothing \,_3 \,^{\bar{1}} \mid \varnothing \,_4 \,^{\bar{2}}) \\ 2 & \bar{2} & (\varnothing \,_1 \mid 1 \,_2 \,^{\bar{0}} \mid \varnothing \,_0 \mid \varnothing \,_3 \,^{\bar{1}} \mid \bar{2} \,_4 \,^{\bar{2}}) \\ 3 & 0 & (\varnothing \,_0 \mid 1 \,_1 \,^{\bar{0}} \mid 3 \,_2 \,^{\bar{1}} \mid \varnothing \,_3 \,^{\bar{2}} \mid \bar{2} \,_4 \,^{\bar{3}}) \\ 4 & \bar{1} &(\varnothing \,_0 \mid 1 \,_1 \,^{\bar{0}} \mid 3, \bar{4} \,_2 \,^{\bar{1}} \mid \varnothing \,_3 \,^{\bar{2}} \mid \bar{2} \,_4 \,^{\bar{3}}) \\ 5 & 0 &(5 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2} \,_4 \,^{\bar{4}}) \\ 6 & 4 &(5 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2}, 6 \,_4 \,^{\bar{4}}) \\ 7 & 0 &(5, 7 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2}, 6 \,_4 \,^{\bar{4}}) \\ 8 & \bar{2} &(5, 7 \,_0 \,^{\bar{0}} \mid 1 \,_1 \,^{\bar{1}} \mid 3, \bar{4}, \bar{8} \,_2 \,^{\bar{2}} \mid \varnothing \,_3 \,^{\bar{3}} \mid \bar{2}, 6 \,_4 \,^{\bar{4}}) \\ \end{array}\\[-16pt] \end{align*}$$The above table shows that
To verify that ![]() $\iota $ is well defined, we need to check that for any
$\iota $ is well defined, we need to check that for any ![]() $(c_1, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$, the sequence
$(c_1, \dots , c_n) \in {\mathcal {SS}}_{n,k,s}^{(r)}$, the sequence ![]() $\iota (c_1, \dots , c_n) = (B_1 \mid \cdots \mid B_k)$ of sets is a valid element of
$\iota (c_1, \dots , c_n) = (B_1 \mid \cdots \mid B_k)$ of sets is a valid element of ![]() ${\mathcal {OSP}}_{n,k,s}^{(r)}$. That is, the first s sets
${\mathcal {OSP}}_{n,k,s}^{(r)}$. That is, the first s sets ![]() $B_1, \dots , B_s$ must be nonempty. Indeed, there are s indices
$B_1, \dots , B_s$ must be nonempty. Indeed, there are s indices ![]() $1 \leq i_1 < \cdots < i_s \leq n$, such that
$1 \leq i_1 < \cdots < i_s \leq n$, such that ![]() $c_{i_1}, \dots , c_{i_s}$ are unbarred and
$c_{i_1}, \dots , c_{i_s}$ are unbarred and ![]() $c_{i_j} \leq s-j$. From the definition of our labeling, it follows that, for any j, at least j minimal elements of the nonempty sets in the list
$c_{i_j} \leq s-j$. From the definition of our labeling, it follows that, for any j, at least j minimal elements of the nonempty sets in the list ![]() $B_1, \dots , B_s$ are
$B_1, \dots , B_s$ are ![]() $\leq i_j$. Taking
$\leq i_j$. Taking ![]() $j = s$, we see that all s of the sets
$j = s$, we see that all s of the sets ![]() $B_1, \dots , B_s$ are nonempty. The fact that
$B_1, \dots , B_s$ are nonempty. The fact that ![]() ${\mathrm {code}}$ and
${\mathrm {code}}$ and ![]() $\iota $ are mutually inverse follows from the definition of our labeling.
$\iota $ are mutually inverse follows from the definition of our labeling.
3.4 Skewing formula
To show that the function ![]() $C_{n,k,s}({\mathbf {x}};q,z)$ is the bigraded Frobenius image
$C_{n,k,s}({\mathbf {x}};q,z)$ is the bigraded Frobenius image ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s}; q, z)$, we will show that the image of both of these symmetric functions under the operator
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s}; q, z)$, we will show that the image of both of these symmetric functions under the operator ![]() $h_j^{\perp }$ for
$h_j^{\perp }$ for ![]() $j \geq 1$ satisfy the same recursive formula. Lemma 2.3 will then imply that these functions coincide.
$j \geq 1$ satisfy the same recursive formula. Lemma 2.3 will then imply that these functions coincide.
We need a better understanding of the rings ![]() ${\mathbb {W}}_{n,k,s}$ before we prove an
${\mathbb {W}}_{n,k,s}$ before we prove an ![]() $h_j^{\perp }$-recursion for them, but we can prove the relevant recursion for the C-functions now (using their
$h_j^{\perp }$-recursion for them, but we can prove the relevant recursion for the C-functions now (using their ![]() ${\mathrm {coinv}}$ formulation). This recursion is stated more naturally in terms of the more refined
${\mathrm {coinv}}$ formulation). This recursion is stated more naturally in terms of the more refined ![]() $C_{n,k,s}^{(r)}({\mathbf {x}};q)$ functions rather than their coarsened versions
$C_{n,k,s}^{(r)}({\mathbf {x}};q)$ functions rather than their coarsened versions ![]() $C_{n,k,s}({\mathbf {x}};q,z)$.
$C_{n,k,s}({\mathbf {x}};q,z)$.
Lemma 3.14. Let ![]() $n, k, s \geq 0$ with
$n, k, s \geq 0$ with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $0 \leq r \leq n-s$. For any
$0 \leq r \leq n-s$. For any ![]() $j \geq 1$, we have
$j \geq 1$, we have
 $$ \begin{align} &h_j^{\perp} C_{n,k,s}^{(r)}({\mathbf {x}};q) = \notag \\ & \ \sum_{\substack{0 \leq a,b \leq j \\ a \leq r, \, b \leq s}} q^{{j-a-b \choose 2} + (s-b)a} \times {k-s-1+a+b \brack a}_q \cdot {s \brack b}_q \cdot {k-s \brack j-a-b}_q \cdot C^{(r-j+a+b)}_{n-j,k,s-b}({\mathbf {x}};q). \end{align} $$
$$ \begin{align} &h_j^{\perp} C_{n,k,s}^{(r)}({\mathbf {x}};q) = \notag \\ & \ \sum_{\substack{0 \leq a,b \leq j \\ a \leq r, \, b \leq s}} q^{{j-a-b \choose 2} + (s-b)a} \times {k-s-1+a+b \brack a}_q \cdot {s \brack b}_q \cdot {k-s \brack j-a-b}_q \cdot C^{(r-j+a+b)}_{n-j,k,s-b}({\mathbf {x}};q). \end{align} $$Proof. It is well known that the homogeneous and monomial symmetric functions are dual bases of the ring of symmetric functions. That is, we have
 $$ \begin{align} \langle h_{\lambda}, m_{\mu} \rangle = \begin{cases} 1 & \lambda = \mu \\ 0 & \lambda \neq \mu \end{cases} \end{align} $$
$$ \begin{align} \langle h_{\lambda}, m_{\mu} \rangle = \begin{cases} 1 & \lambda = \mu \\ 0 & \lambda \neq \mu \end{cases} \end{align} $$for any partitions ![]() $\lambda $ and
$\lambda $ and ![]() $\mu $. Therefore, if
$\mu $. Therefore, if ![]() $\alpha = (\alpha _1, \alpha _2, \dots )$ is any composition of n with
$\alpha = (\alpha _1, \alpha _2, \dots )$ is any composition of n with ![]() $h_{\alpha } = h_{\alpha _1} h_{\alpha _2} \cdots $, we have
$h_{\alpha } = h_{\alpha _1} h_{\alpha _2} \cdots $, we have
where the sum is over all column tableaux ![]() $\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}$ with
$\tau \in {\mathcal {CT}}_{n,k,s}^{(r)}$ with ![]() $\alpha _i$ copies of i for all i. Specialising Equation (3.25) at
$\alpha _i$ copies of i for all i. Specialising Equation (3.25) at ![]() $\alpha _1 = j$ and applying the adjoint property gives
$\alpha _1 = j$ and applying the adjoint property gives
where ![]() $\alpha ' = (\alpha _2, \alpha _3, \dots )$ is the composition of
$\alpha ' = (\alpha _2, \alpha _3, \dots )$ is the composition of ![]() $n-j$ obtained by removing
$n-j$ obtained by removing ![]() $\alpha _1$ from
$\alpha _1$ from ![]() $\alpha $ and the right-hand sides of Equations (3.25) and (3.26) are the same. The strategy is to show that the right-hand sides of Equations (3.23) and (3.26) coincide. This will be achieved combinatorially with a procedure which inserts j new smallest entries in a column tableau. Our insertion process will be somewhat more involved than the similar procedure in the proof of Theorem 3.8, where we inserted new largest entries instead. Fix nonnegative integers j, a and b satisfying
$\alpha $ and the right-hand sides of Equations (3.25) and (3.26) are the same. The strategy is to show that the right-hand sides of Equations (3.23) and (3.26) coincide. This will be achieved combinatorially with a procedure which inserts j new smallest entries in a column tableau. Our insertion process will be somewhat more involved than the similar procedure in the proof of Theorem 3.8, where we inserted new largest entries instead. Fix nonnegative integers j, a and b satisfying ![]() $0 \leq a, b \leq j$,
$0 \leq a, b \leq j$, ![]() $a \leq r$ and
$a \leq r$ and ![]() $b \leq s$. Consider a column tableau
$b \leq s$. Consider a column tableau ![]() $\sigma \in {\mathcal {CT}}_{n-j,k,s-b}^{(r-j+a+b)}$. We increment by 1 every entry in
$\sigma \in {\mathcal {CT}}_{n-j,k,s-b}^{(r-j+a+b)}$. We increment by 1 every entry in ![]() $\sigma $ to obtain another filling
$\sigma $ to obtain another filling ![]() $\tau \in {\mathcal {CT}}_{n-j,k,s-b}^{(r-j+a+b)}$. We will, in total, introduce j 1’s and
$\tau \in {\mathcal {CT}}_{n-j,k,s-b}^{(r-j+a+b)}$. We will, in total, introduce j 1’s and ![]() $\bar {1}$’s into the tableau
$\bar {1}$’s into the tableau ![]() $\tau $. Since we must add
$\tau $. Since we must add ![]() $j-a-b$ new
$j-a-b$ new ![]() $\bar {1}$’s,
$\bar {1}$’s, ![]() $b 1$’s at height 0 and
$b 1$’s at height 0 and ![]() $j 1$’s overall to obtain a tableau in
$j 1$’s overall to obtain a tableau in ![]() ${\mathcal {CT}}_{n,k,s}^{(r)}$, we will need to add a unbarred
${\mathcal {CT}}_{n,k,s}^{(r)}$, we will need to add a unbarred ![]() $1$’s at negative heights. We begin by inserting these a negative height
$1$’s at negative heights. We begin by inserting these a negative height ![]() $1$’s.
$1$’s.
Since the unbarred entries must be weakly increasing down each column, at this stage, we can only insert a negative height 1 by placing it just below one of the ![]() $k-(s-b)$-many
$k-(s-b)$-many ![]() $\bullet $’s. If we insert such an entry into column i, it will contribute
$\bullet $’s. If we insert such an entry into column i, it will contribute ![]() $i-1$ to
$i-1$ to ![]() ${\mathrm {coinv}}$. In other words, we have a bijection
${\mathrm {coinv}}$. In other words, we have a bijection
 $$ \begin{align} &\xi_{<0}: \left\{ \tau \in {\mathcal {CT}}_{n-j,k,s-b}^{(r-j+a+b)} : \tau \text{ has no 1's} \right\} \times \notag \\ &\qquad\qquad\left\{\text{finite multisets } S \text{ of size } a \text{ drawn from } \{s-b,s-b+1,\dots,k-1\} \right\} \longrightarrow \notag \\ &\qquad\qquad\qquad\quad\left\{ \tau' \in {\mathcal {CT}}_{n-j+a,k,s-b}^{(r-j+a+b)} : \tau' \text{ has } a 1\text{'s at negative heights and no other 1's} \right\}, \end{align} $$
$$ \begin{align} &\xi_{<0}: \left\{ \tau \in {\mathcal {CT}}_{n-j,k,s-b}^{(r-j+a+b)} : \tau \text{ has no 1's} \right\} \times \notag \\ &\qquad\qquad\left\{\text{finite multisets } S \text{ of size } a \text{ drawn from } \{s-b,s-b+1,\dots,k-1\} \right\} \longrightarrow \notag \\ &\qquad\qquad\qquad\quad\left\{ \tau' \in {\mathcal {CT}}_{n-j+a,k,s-b}^{(r-j+a+b)} : \tau' \text{ has } a 1\text{'s at negative heights and no other 1's} \right\}, \end{align} $$where ![]() $\tau ' = \xi _{< 0}(\tau , S)$ is obtained by iteratively placing a 1 at height
$\tau ' = \xi _{< 0}(\tau , S)$ is obtained by iteratively placing a 1 at height ![]() $-1$ in column
$-1$ in column ![]() $i + 1$ for each occurrence of i in S. Since
$i + 1$ for each occurrence of i in S. Since ![]() ${\mathrm {coinv}}(\tau ') = {\mathrm {coinv}}(\tau ) + \sum _{i \in S} i$, this map contributes
${\mathrm {coinv}}(\tau ') = {\mathrm {coinv}}(\tau ) + \sum _{i \in S} i$, this map contributes ![]() $q^{(s-b) a} {k-s-1+a+b \brack a}_q $ to (3.26).
$q^{(s-b) a} {k-s-1+a+b \brack a}_q $ to (3.26).
Next, we insert b 1’s at height 0. This will be the most complicated part of the procedure, as we need to be careful not to violate the necessary inequalities in each column. Our map will be a bijection
 $$ \begin{align} &\xi_{0}: \left\{ \tau' \in {\mathcal {CT}}_{n-j+a,k,s-b}^{(r-j+a+b)} : \tau' \text{ has } a 1\text{'s at negative heights and no other 1's} \right\} \times \notag \\ &\qquad\qquad\qquad\left\{\text{finite multisets } S \text{ of size } b \text{ drawn from } \{0,1,\ldots,s-b\} \right\} \longrightarrow \notag \\ &\left\{ \tau" \in {\mathcal {CT}}_{n-j+a+b,k,s}^{(r-j+a+b)} : \tau" \text{ has } a 1\text{'s at negative heights, } b \text{ 1's at height 0 and no other 1's} \right\}. \end{align} $$
$$ \begin{align} &\xi_{0}: \left\{ \tau' \in {\mathcal {CT}}_{n-j+a,k,s-b}^{(r-j+a+b)} : \tau' \text{ has } a 1\text{'s at negative heights and no other 1's} \right\} \times \notag \\ &\qquad\qquad\qquad\left\{\text{finite multisets } S \text{ of size } b \text{ drawn from } \{0,1,\ldots,s-b\} \right\} \longrightarrow \notag \\ &\left\{ \tau" \in {\mathcal {CT}}_{n-j+a+b,k,s}^{(r-j+a+b)} : \tau" \text{ has } a 1\text{'s at negative heights, } b \text{ 1's at height 0 and no other 1's} \right\}. \end{align} $$Given ![]() $\tau '$ and S, we begin by simply replacing the b leftmost
$\tau '$ and S, we begin by simply replacing the b leftmost ![]() $\bullet $’s in
$\bullet $’s in ![]() $\tau '$ with 1’s. Since there are
$\tau '$ with 1’s. Since there are ![]() $k-(s-b)$ bullets and
$k-(s-b)$ bullets and ![]() $k \geq s$, this can always be done. Furthermore, since
$k \geq s$, this can always be done. Furthermore, since ![]() $\tau '$ has no
$\tau '$ has no ![]() $\bar {1}$’s, this replacement does not violate any necessary column inequalities. Suppose
$\bar {1}$’s, this replacement does not violate any necessary column inequalities. Suppose ![]() $S = \{i_1 \geq \ldots \geq i_b\}$. Initialise
$S = \{i_1 \geq \ldots \geq i_b\}$. Initialise ![]() $j=1$. For
$j=1$. For ![]() $j = 1$ to b, we repeat the following algorithm
$j = 1$ to b, we repeat the following algorithm ![]() $i_j$ times:
$i_j$ times:
1. Suppose the
 $j^{\text {th}}$ 1 at height 0 is in column
$j^{\text {th}}$ 1 at height 0 is in column  $\ell $, and let
$\ell $, and let  $m> 1$ be the height 0 entry in column
$m> 1$ be the height 0 entry in column  $\ell -1$.
$\ell -1$.2. Switch the height 0 entries in columns
 $\ell $ and
$\ell $ and  $\ell -1$.
$\ell -1$.3. Move every barred entry
 $\leq m$ in column
$\leq m$ in column  $\ell $ and every unbarred entry
$\ell $ and every unbarred entry  $< m$ in column
$< m$ in column  $\ell $ to column
$\ell $ to column  $\ell -1$ (moving entries up and down as necessary so that the diagram is justified as usual).
$\ell -1$ (moving entries up and down as necessary so that the diagram is justified as usual).
We claim that each loop of this algorithm increments coinv, yields a valid column tableau and is invertible. The latter two statements are true by construction. Clearly, each loop creates one new coinversion between the 1 at height 0 and the entry m. We check that this is the only change to the total number of coinversions.
• If u is some other height 0 entry, u has the same number of height 0 entries to its right which are
 $> u$.
$> u$.• Suppose u is at negative height. The only case that might have affected u’s contribution to coinv is if
 $u< m$ starts in column
$u< m$ starts in column  $\ell $. Then u is moved to column
$\ell $. Then u is moved to column  $\ell -1$, but, due to m, there is a new height 0 entry to the right of u that is
$\ell -1$, but, due to m, there is a new height 0 entry to the right of u that is  $> u$.
$> u$.• Suppose u is at positive height. If
 $u \leq m$, then m and u did not contribute a coinversion, so moving u to the left does not affect the total coinv. If
$u \leq m$, then m and u did not contribute a coinversion, so moving u to the left does not affect the total coinv. If  $u> m$, then
$u> m$, then  $u> 1$ and u contributes the same number of coinversions.
$u> 1$ and u contributes the same number of coinversions.
After repeating this procedure ![]() $i_j$ times for
$i_j$ times for ![]() $j = 1$ to b, we have
$j = 1$ to b, we have ![]() ${\mathrm {coinv}}(\tau ") = {\mathrm {coinv}}(\tau ') + \sum _{i \in S} i$, yielding the
${\mathrm {coinv}}(\tau ") = {\mathrm {coinv}}(\tau ') + \sum _{i \in S} i$, yielding the ![]() ${s \brack b}_q$ term in (3.14).
${s \brack b}_q$ term in (3.14).
Finally, we insert the ![]() $j-a-b \bar {1}$’s into
$j-a-b \bar {1}$’s into ![]() $\tau "$. A
$\tau "$. A ![]() $\bar {1}$ can only be placed above a
$\bar {1}$ can only be placed above a ![]() $\bullet $ in
$\bullet $ in ![]() $\tau "$, of which there are now
$\tau "$, of which there are now ![]() $k-s$, and only, at most, once in each column. Placing
$k-s$, and only, at most, once in each column. Placing ![]() $\bar {1}$ over the
$\bar {1}$ over the ![]() $i^{\text {th}} \bullet $ from the left creates
$i^{\text {th}} \bullet $ from the left creates ![]() $i-1$ new coinversions, one with each bullet strictly to the left. Therefore, we have a bijection
$i-1$ new coinversions, one with each bullet strictly to the left. Therefore, we have a bijection
 $$ \begin{align} &\xi_{>0}: \left\{ \tau" \in {\mathcal {CT}}_{n-j+a+b,k,s}^{(r-j+a+b)} : \tau" \text{ has } a \ 1\text{'s at negative heights,} b \text{ 1's at height 0 and no other 1's} \right\} \times \notag \\ &\qquad\qquad\qquad\qquad\left\{\text{finite sets } S \text{ of size } j-a-b \text{ drawn from } \{0,1,\ldots,k-s-1\} \right\} \longrightarrow \notag \\ &\qquad\qquad\left\{ \tau"' \in {\mathcal {CT}}_{n,k,s}^{(r)} : \tau"' \text{ has } a 1\text{'s at negative heights, } b \text{ 1's at height 0 } j-a-b \ \bar{1}\text{'s} \right\} \end{align} $$
$$ \begin{align} &\xi_{>0}: \left\{ \tau" \in {\mathcal {CT}}_{n-j+a+b,k,s}^{(r-j+a+b)} : \tau" \text{ has } a \ 1\text{'s at negative heights,} b \text{ 1's at height 0 and no other 1's} \right\} \times \notag \\ &\qquad\qquad\qquad\qquad\left\{\text{finite sets } S \text{ of size } j-a-b \text{ drawn from } \{0,1,\ldots,k-s-1\} \right\} \longrightarrow \notag \\ &\qquad\qquad\left\{ \tau"' \in {\mathcal {CT}}_{n,k,s}^{(r)} : \tau"' \text{ has } a 1\text{'s at negative heights, } b \text{ 1's at height 0 } j-a-b \ \bar{1}\text{'s} \right\} \end{align} $$which places a ![]() $\bar {1}$ above
$\bar {1}$ above ![]() $\bullet $ number
$\bullet $ number ![]() $i+1$ from the left for every
$i+1$ from the left for every ![]() $i \in S$. This bijection satisfies
$i \in S$. This bijection satisfies ![]() ${\mathrm {coinv}}(\tau "') = {\mathrm {coinv}}(\tau ") + \sum _{i \in S} i$ and contributes the factor
${\mathrm {coinv}}(\tau "') = {\mathrm {coinv}}(\tau ") + \sum _{i \in S} i$ and contributes the factor ![]() $q^{\binom {j-a-b}{2}} {k-s \brack j-a-b}_q$ to (3.14).
$q^{\binom {j-a-b}{2}} {k-s \brack j-a-b}_q$ to (3.14).
In Figure 2, we depict an example for ![]() $n = 18$,
$n = 18$, ![]() $k=5$,
$k=5$, ![]() $s=4$,
$s=4$, ![]() $j = 6$,
$j = 6$, ![]() $a=3$,
$a=3$, ![]() $b=2$, where we have already incremented each entry so that no 1’s or
$b=2$, where we have already incremented each entry so that no 1’s or ![]() $\bar {1}$’s appear. When applying
$\bar {1}$’s appear. When applying ![]() $\xi _{< 0}$,
$\xi _{< 0}$, ![]() $\xi _0$ and
$\xi _0$ and ![]() $\xi _{>0}$, we take
$\xi _{>0}$, we take ![]() $S = \{2,2,4\}$,
$S = \{2,2,4\}$, ![]() $\{1,2\}$ and
$\{1,2\}$ and ![]() $\{0\}$, respectively. The initial tableau has 17 coinv:
$\{0\}$, respectively. The initial tableau has 17 coinv:
• 1 at height 0, between the 3 and the 4,
•
 $1+1+3+4+4=13$ from negative height entries, all coming from the column of each of these entries and
$1+1+3+4+4=13$ from negative height entries, all coming from the column of each of these entries and• 3 from positive height entries (the 3 at height 0 with
 $\bar {6}$ and
$\bar {6}$ and  $\bar {7}$, and the
$\bar {7}$, and the  $\bar {2}$ with the
$\bar {2}$ with the  $\bullet $ to its left)
$\bullet $ to its left)
After the maps in Figure 2, the increases in coinv correspond to the sums of the elements in each S. Respectively, the coinv increases to ![]() $25 = 17 + (2+2+4)$, then
$25 = 17 + (2+2+4)$, then ![]() $28=25+(1+2)$ and then
$28=25+(1+2)$ and then ![]() $28=28 + 0$.
$28=28 + 0$.

Figure 2 We show an example of the bijections described in the proof of Lemma 3.14. We take ![]() $S = \{2,2,4\}$,
$S = \{2,2,4\}$, ![]() $\{1,2\}$ and
$\{1,2\}$ and ![]() $\{0\}$ in the three maps, respectively. On the second line, the iterations making up
$\{0\}$ in the three maps, respectively. On the second line, the iterations making up ![]() $\xi _0$ are shown in finer detail.
$\xi _0$ are shown in finer detail.
4 Quotient presentation, monomial basis and Hilbert series
4.1 The superlex order on monomials
We identify length n words over ![]() $\{0, 1, 2, \dots , \bar {0}, \bar {1}, \bar {2}, \dots \}$ with monomials in
$\{0, 1, 2, \dots , \bar {0}, \bar {1}, \bar {2}, \dots \}$ with monomials in ![]() $\Omega _n$ by
$\Omega _n$ by
Here, we adopt the shorthand notation ![]() $\theta _I = \theta _{i_1} \cdots \theta _{i_k}$, where
$\theta _I = \theta _{i_1} \cdots \theta _{i_k}$, where ![]() $I = \{i_1 < \cdots < i_k \} \subseteq [n]$. For example, inside the ring
$I = \{i_1 < \cdots < i_k \} \subseteq [n]$. For example, inside the ring ![]() $\Omega _5$ we have
$\Omega _5$ we have
We sometimes compress this expression further by using exponent notation for the ![]() $x_i$ variables, for example,
$x_i$ variables, for example,
We refer to the word ![]() $(c_1, \dots , c_n)$ as the exponent sequence of its corresponding superspace monomial in
$(c_1, \dots , c_n)$ as the exponent sequence of its corresponding superspace monomial in ![]() $\Omega _n$. The monomials corresponding to substaircase sequences will be important.
$\Omega _n$. The monomials corresponding to substaircase sequences will be important.
Definition 4.1. Let ![]() $n, k, s \geq 0$ be integers with
$n, k, s \geq 0$ be integers with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $r \leq n-s$. We let
$r \leq n-s$. We let ![]() ${\mathcal {M}}_{n,k,s}$ (respectively,
${\mathcal {M}}_{n,k,s}$ (respectively, ![]() ${\mathcal {M}}_{n,k,s}^{(r)}$) be the family of monomials in
${\mathcal {M}}_{n,k,s}^{(r)}$) be the family of monomials in ![]() $\Omega _n$ corresponding to the substaircase sequences in
$\Omega _n$ corresponding to the substaircase sequences in ![]() ${\mathcal {SS}}_{n,k,s}$ (resp.
${\mathcal {SS}}_{n,k,s}$ (resp. ![]() ${\mathcal {SS}}_{n,k,s}^{(r)}$).
${\mathcal {SS}}_{n,k,s}^{(r)}$).
Orders on words ![]() $(c_1, \dots , c_n)$ give orders on monomials in
$(c_1, \dots , c_n)$ give orders on monomials in ![]() $\Omega _n$. The following total order will be crucial in our work.
$\Omega _n$. The following total order will be crucial in our work.
Definition 4.2 (Superlex Order).
Let ![]() $a = (a_1, \dots , a_n)$ and
$a = (a_1, \dots , a_n)$ and ![]() $b = (b_1, \dots , b_n)$ be two length n words over the alphabet
$b = (b_1, \dots , b_n)$ be two length n words over the alphabet ![]() $\{0,1,2, \dots , \bar {0}, \bar {1}, \bar {2}, \dots \}$. We write
$\{0,1,2, \dots , \bar {0}, \bar {1}, \bar {2}, \dots \}$. We write ![]() $a \prec b$ if there exists an index
$a \prec b$ if there exists an index ![]() $1 \leq j \leq n$, such that
$1 \leq j \leq n$, such that
•
 $a_i = b_i$ for all
$a_i = b_i$ for all  $i < j$ and
$i < j$ and•
 $a_j < b_j$ under the order on individual letters.
$a_j < b_j$ under the order on individual letters. $$ \begin{align*} \cdots < \bar{3} < \bar{2} < \bar{1} < \bar{0} < 0 < 1 < 2 < 3 < \cdots \end{align*} $$
$$ \begin{align*} \cdots < \bar{3} < \bar{2} < \bar{1} < \bar{0} < 0 < 1 < 2 < 3 < \cdots \end{align*} $$
We say that two monomials ![]() $m, m' \in \Omega _n$ satisfy
$m, m' \in \Omega _n$ satisfy ![]() $m \prec m'$ if their exponent sequences satisfy this relation. Given any nonzero superspace element
$m \prec m'$ if their exponent sequences satisfy this relation. Given any nonzero superspace element ![]() $f \in \Omega _n$, we let
$f \in \Omega _n$, we let ![]() ${\mathrm {in}}(f)$ be the
${\mathrm {in}}(f)$ be the ![]() $\prec $-maximal superspace monomial which appears in f with nonzero coefficient.
$\prec $-maximal superspace monomial which appears in f with nonzero coefficient.
In the absence of ![]() $\theta $-variables, superspace monomials in
$\theta $-variables, superspace monomials in ![]() $\Omega _n$ reduce to classical monomials in
$\Omega _n$ reduce to classical monomials in ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$, and Definition 4.2 is the lexicographical order on monomials in this ring. The classical lex order is a monomial order in the sense of Gröbner theory:
${\mathbb {Q}}[x_1, \dots , x_n]$, and Definition 4.2 is the lexicographical order on monomials in this ring. The classical lex order is a monomial order in the sense of Gröbner theory:
• there is no infinite descending chain
 $m_1 \succ m_2 \succ m_3 \succ \cdots $ of monomials in
$m_1 \succ m_2 \succ m_3 \succ \cdots $ of monomials in  ${\mathbb {Q}}[x_1, \dots , x_n]$ (i.e.
${\mathbb {Q}}[x_1, \dots , x_n]$ (i.e.  $\prec $ is a well order on these monomials) and
$\prec $ is a well order on these monomials) and• if
 $m_1, m_2$ and
$m_1, m_2$ and  $m_3$ are monomials in
$m_3$ are monomials in  ${\mathbb {Q}}[x_1, \dots , x_n]$ with
${\mathbb {Q}}[x_1, \dots , x_n]$ with  $m_1 \prec m_2$, then
$m_1 \prec m_2$, then  $m_1 m_3 \prec m_2 m_3$.
$m_1 m_3 \prec m_2 m_3$.
Both of these properties fail when we introduce ![]() $\theta $-variables. We have
$\theta $-variables. We have ![]() $\theta _1 \succ x_1 \theta _1 \succ x_1^2 \theta _1 \succ \cdots $ and
$\theta _1 \succ x_1 \theta _1 \succ x_1^2 \theta _1 \succ \cdots $ and ![]() $x_1 \prec x_1^2$, whereas
$x_1 \prec x_1^2$, whereas ![]() $x_1 \theta _1 \succ x_1^2 \theta _1$.
$x_1 \theta _1 \succ x_1^2 \theta _1$.
Despite its failure to be a monomial order, the superlex order ![]() $\prec $ of Definition 4.2 will be important for our work. It is our belief that this relates to the inscrutable Gröbner theory of important superspace ideals, such as the superspace coinvariant ideal in [Reference Zabrocki34].
$\prec $ of Definition 4.2 will be important for our work. It is our belief that this relates to the inscrutable Gröbner theory of important superspace ideals, such as the superspace coinvariant ideal in [Reference Zabrocki34].
4.2 A dimension lower bound
Recall that ![]() ${\mathbb {H}}_{n,k,s}$ is the
${\mathbb {H}}_{n,k,s}$ is the ![]() $\Omega _n$-submodule (under the
$\Omega _n$-submodule (under the ![]() $\odot $-action) of
$\odot $-action) of ![]() $\Omega _n$ generated by the Vandermonde
$\Omega _n$ generated by the Vandermonde ![]() $\delta _{n,k,s}$. Therefore, the space
$\delta _{n,k,s}$. Therefore, the space ![]() ${\mathbb {H}}_{n,k,s}$ is spanned by elements of the form
${\mathbb {H}}_{n,k,s}$ is spanned by elements of the form ![]() $m \odot \delta _{n,k,s}$, where
$m \odot \delta _{n,k,s}$, where ![]() $m \in \Omega _n$ is a monomial.
$m \in \Omega _n$ is a monomial.
In this subsection, we derive a lower bound for the Hilbert series of ![]() ${\mathbb {H}}_{n,k,s}$ (and
${\mathbb {H}}_{n,k,s}$ (and ![]() ${\mathbb {W}}_{n,k,s}$) by showing that every substaircase monomial in
${\mathbb {W}}_{n,k,s}$) by showing that every substaircase monomial in ![]() ${\mathcal {M}}_{n,k,s}$ arises as the initial term
${\mathcal {M}}_{n,k,s}$ arises as the initial term ![]() ${\mathrm {in}}(m \odot \delta _{n,k,s})$ for some monomial
${\mathrm {in}}(m \odot \delta _{n,k,s})$ for some monomial ![]() $m \in \Omega _n$. In fact, we show that the map
$m \in \Omega _n$. In fact, we show that the map ![]() $m \mapsto {\mathrm {in}}(m \odot \delta _{n,k,s})$ is an involution on the set
$m \mapsto {\mathrm {in}}(m \odot \delta _{n,k,s})$ is an involution on the set ![]() ${\mathcal {M}}_{n,k,s}$.
${\mathcal {M}}_{n,k,s}$.
Proposition 4.3. Let ![]() $n, k, s \geq 0$ be integers with
$n, k, s \geq 0$ be integers with ![]() $k \geq s$. The map
$k \geq s$. The map
given by ![]() $\iota (m) = {\mathrm {in}}(m \odot \delta _{n,k,s})$ is a well-defined involution.
$\iota (m) = {\mathrm {in}}(m \odot \delta _{n,k,s})$ is a well-defined involution.
The well-definedness assertion in Proposition 4.3 means that ![]() $m \odot \delta _{n,k,s}$ is nonzero whenever
$m \odot \delta _{n,k,s}$ is nonzero whenever ![]() $m \in {\mathcal {M}}_{n,k,s}$ and that
$m \in {\mathcal {M}}_{n,k,s}$ and that ![]() ${\mathrm {in}}(m \odot \delta _{n,k,s}) \in {\mathcal {M}}_{n,k,s}$. We will see that for any
${\mathrm {in}}(m \odot \delta _{n,k,s}) \in {\mathcal {M}}_{n,k,s}$. We will see that for any ![]() $f \in \Omega _n$ with
$f \in \Omega _n$ with ![]() $f \odot \delta _{n,k,s} \neq 0$, we have
$f \odot \delta _{n,k,s} \neq 0$, we have ![]() ${\mathrm {in}}(f \odot \delta _{n,k,s}) \in {\mathcal {M}}_{n,k,s}$. Before we prove Proposition 4.3, it will be helpful to state an observation about
${\mathrm {in}}(f \odot \delta _{n,k,s}) \in {\mathcal {M}}_{n,k,s}$. Before we prove Proposition 4.3, it will be helpful to state an observation about ![]() $m \odot M$ for arbitrary monomials m and M in
$m \odot M$ for arbitrary monomials m and M in ![]() $\Omega _n$.
$\Omega _n$.
Observation 4.4. Suppose m and M are monomials in ![]() $\Omega _n$ with exponent sequences u and U, respectively. Let
$\Omega _n$ with exponent sequences u and U, respectively. Let ![]() $m^* = m \odot M$. Then
$m^* = m \odot M$. Then ![]() $m^*$ is nonzero if and only if
$m^*$ is nonzero if and only if
•
 $u_i \leq U_i$ after ignoring bars for every i and
$u_i \leq U_i$ after ignoring bars for every i and• if
 $u_i$ is barred, then
$u_i$ is barred, then  $U_i$ is barred.
$U_i$ is barred.
If ![]() $m^*$ is nonzero, then its exponent sequence
$m^*$ is nonzero, then its exponent sequence ![]() $u^*$ has entries given by
$u^*$ has entries given by ![]() $u_i^* = U_i - u_i$ and
$u_i^* = U_i - u_i$ and ![]() $u_i^*$ is barred if and only if
$u_i^*$ is barred if and only if ![]() $U_i$ is barred and
$U_i$ is barred and ![]() $u_i$ is not barred.
$u_i$ is not barred.
Proof of Proposition 4.3.
Fix some ![]() $m \in {\mathcal {M}}_{n,k,s}$, and let u be the exponent sequence of m. We use Algorithm 1 below to construct the exponent sequence U of the monomial M which appears in
$m \in {\mathcal {M}}_{n,k,s}$, and let u be the exponent sequence of m. We use Algorithm 1 below to construct the exponent sequence U of the monomial M which appears in ![]() $\delta _{n,k,s}$, such that
$\delta _{n,k,s}$, such that ![]() $m \odot M \doteq \iota (m)$, where
$m \odot M \doteq \iota (m)$, where ![]() $\doteq $ denotes equality up to a nonzero scalar. To begin a running example, if
$\doteq $ denotes equality up to a nonzero scalar. To begin a running example, if ![]() $n = 9$,
$n = 9$, ![]() $k = 7$,
$k = 7$, ![]() $s=4$ and
$s=4$ and ![]() $u = (\bar {1},3,0,5,2,0,\bar {2},\bar {5},0)$, Algorithm 1 returns
$u = (\bar {1},3,0,5,2,0,\bar {2},\bar {5},0)$, Algorithm 1 returns

Since u is substaircase, U is indeed a shuffle of ![]() $s-1, s-2, \ldots , 0$ and
$s-1, s-2, \ldots , 0$ and ![]() $(\overline {k-1})^{n-s}$, so M appears as a monomial in
$(\overline {k-1})^{n-s}$, so M appears as a monomial in ![]() $\delta _{n,k,s}$. We claim that M is the largest monomial in
$\delta _{n,k,s}$. We claim that M is the largest monomial in ![]() $\delta _{n,k,s}$ with respect to superlexicographic order, such that
$\delta _{n,k,s}$ with respect to superlexicographic order, such that ![]() $m \odot M \neq 0$. Suppose
$m \odot M \neq 0$. Suppose ![]() $U'$ is the exponent sequence of another monomial
$U'$ is the exponent sequence of another monomial ![]() $M'$ in
$M'$ in ![]() $ \delta _{n,k,s}$, such that
$ \delta _{n,k,s}$, such that ![]() $U' \succ U$. Then there exists an index j, such that
$U' \succ U$. Then there exists an index j, such that ![]() $U^{\prime }_i = U_i$ for all
$U^{\prime }_i = U_i$ for all ![]() $i < j$ and
$i < j$ and ![]() $U^{\prime }_j \succ U_j$. Since U and
$U^{\prime }_j \succ U_j$. Since U and ![]() $U'$ are shuffles of
$U'$ are shuffles of ![]() $s-1, s-2, \ldots , 1, 0$ with
$s-1, s-2, \ldots , 1, 0$ with ![]() $(\overline {k-1})^{n-s}$, this implies that
$(\overline {k-1})^{n-s}$, this implies that ![]() $U^{\prime }_j$ is not barred and
$U^{\prime }_j$ is not barred and ![]() $U_j = \overline {k-1}$. By lines 3 and 4 in Algorithm 1,
$U_j = \overline {k-1}$. By lines 3 and 4 in Algorithm 1, ![]() $U_j = \overline {k-1}$ implies that either
$U_j = \overline {k-1}$ implies that either ![]() $u_j$ is barred or
$u_j$ is barred or ![]() $u_j \geq L$, where
$u_j \geq L$, where
If ![]() $u_j$ is barred and
$u_j$ is barred and ![]() $U^{\prime }_j$ is unbarred,
$U^{\prime }_j$ is unbarred, ![]() $m \odot M' = 0$ by Observation 4.4. Otherwise,
$m \odot M' = 0$ by Observation 4.4. Otherwise, ![]() $u_j \geq L$ and L is strictly greater than all the potential unbarred values of
$u_j \geq L$ and L is strictly greater than all the potential unbarred values of ![]() $U^{\prime }_j$, which, again, implies
$U^{\prime }_j$, which, again, implies ![]() $m \odot M' = 0$. Therefore, M is the largest monomial in
$m \odot M' = 0$. Therefore, M is the largest monomial in ![]() $\delta _{n,k,s}$, such that
$\delta _{n,k,s}$, such that ![]() $m \odot M \neq 0$.
$m \odot M \neq 0$.
Now suppose that ![]() $M" \prec M$ is a monomial in
$M" \prec M$ is a monomial in ![]() $\delta _{n,k,s}$ and
$\delta _{n,k,s}$ and ![]() $m \odot M" \neq 0$. We aim to show that
$m \odot M" \neq 0$. We aim to show that ![]() $m \odot M" \prec m \odot M$. Suppose that
$m \odot M" \prec m \odot M$. Suppose that ![]() $U"$ is the exponent sequence of
$U"$ is the exponent sequence of ![]() $M"$ and that j is the first index at which
$M"$ and that j is the first index at which ![]() $U"$ and U differ, so
$U"$ and U differ, so ![]() $U^{\prime \prime }_j \prec U_j$. Since the only barred entry in either
$U^{\prime \prime }_j \prec U_j$. Since the only barred entry in either ![]() $U"$ or U is
$U"$ or U is ![]() $\overline {k-1}$,
$\overline {k-1}$, ![]() $U_j$ must be unbarred. By Algorithm 1,
$U_j$ must be unbarred. By Algorithm 1, ![]() $u_j$ must be unbarred, and since
$u_j$ must be unbarred, and since ![]() $m \odot M" \neq 0$, we conclude that
$m \odot M" \neq 0$, we conclude that ![]() $U_j"$ is unbarred. Since Algorithm 1 always uses the largest available unbarred entry from the set
$U_j"$ is unbarred. Since Algorithm 1 always uses the largest available unbarred entry from the set ![]() $\{s, s-1, \ldots , 0\}$ in line 7,
$\{s, s-1, \ldots , 0\}$ in line 7, ![]() $U^{\prime \prime }_j < U_j$. It follows from Observation 4.4 that the entry at index j in
$U^{\prime \prime }_j < U_j$. It follows from Observation 4.4 that the entry at index j in ![]() $m \odot M"$ is strictly less than the entry at index j in
$m \odot M"$ is strictly less than the entry at index j in ![]() $m \odot M$ and that both entries are unbarred. Hence,
$m \odot M$ and that both entries are unbarred. Hence, ![]() $m \odot M" \prec m \odot M$ and
$m \odot M" \prec m \odot M$ and
Next, we show that ![]() $\iota (m) \in {\mathcal {M}}_{n,k,s}$. Let
$\iota (m) \in {\mathcal {M}}_{n,k,s}$. Let ![]() $m^* = \iota (m)$ and
$m^* = \iota (m)$ and ![]() $u^*$ be the exponent sequence of
$u^*$ be the exponent sequence of ![]() $m^*$. In Algorithm 2, we use u and U to construct an
$m^*$. In Algorithm 2, we use u and U to construct an ![]() $(n,k,s)$-staircase v that certifies
$(n,k,s)$-staircase v that certifies ![]() $m^* \in {\mathcal {M}}_{n,k,s}$, in that for every i,
$m^* \in {\mathcal {M}}_{n,k,s}$, in that for every i, ![]() $u^*_i \leq v_i$ and
$u^*_i \leq v_i$ and ![]() $v_i$ is barred if and only if
$v_i$ is barred if and only if ![]() $u^*_i$ is barred. Continuing our running example, if
$u^*_i$ is barred. Continuing our running example, if ![]() $n=9$,
$n=9$, ![]() $k=7$,
$k=7$, ![]() $s=4$,
$s=4$, ![]() $u = (\bar {1},3,0,5,2,0,\bar {2},\bar {5},0)$ and
$u = (\bar {1},3,0,5,2,0,\bar {2},\bar {5},0)$ and ![]() $U = (\bar {6},3,2,\bar {6},\bar {6},1,\bar {6},\bar {6},0)$, we can compute
$U = (\bar {6},3,2,\bar {6},\bar {6},1,\bar {6},\bar {6},0)$, we can compute
From u and U, Algorithm 2 produces
and ![]() $u^*$ is indeed ‘below’ v. Note that, although the stage of Algorithm 2 involving the set A seems complicated, we are simply letting
$u^*$ is indeed ‘below’ v. Note that, although the stage of Algorithm 2 involving the set A seems complicated, we are simply letting ![]() $v_i$ be the unique barred entry that is allowed at that index in an
$v_i$ be the unique barred entry that is allowed at that index in an ![]() $(n,k,s)$-staircase.
$(n,k,s)$-staircase.

By construction, ![]() $v_i$ is barred if and only if
$v_i$ is barred if and only if ![]() $u^*_i$ is barred. In the first ‘if’ clause of Algorithm 2, we must have
$u^*_i$ is barred. In the first ‘if’ clause of Algorithm 2, we must have ![]() $u^*_i \leq v_i$ simply because
$u^*_i \leq v_i$ simply because ![]() $k-1$ is the largest possible entry of
$k-1$ is the largest possible entry of ![]() $u^*$. In the second such clause, if we have
$u^*$. In the second such clause, if we have ![]() $u^*_i> v_i$, since
$u^*_i> v_i$, since ![]() $u^*_i = U_i - u_i$, we must have
$u^*_i = U_i - u_i$, we must have ![]() $U_i - u_i> v_i$ and
$U_i - u_i> v_i$ and ![]() $U_i> v_i$. This is impossible, since Algorithms 1 and 2 always use the largest unused element
$U_i> v_i$. This is impossible, since Algorithms 1 and 2 always use the largest unused element ![]() $\ell $ of
$\ell $ of ![]() $\{0,1,\ldots ,s-1\}$ in line 7 of each respective algorithm. In the third such clause, we must have
$\{0,1,\ldots ,s-1\}$ in line 7 of each respective algorithm. In the third such clause, we must have ![]() $U_i = \overline {k-1}$ and
$U_i = \overline {k-1}$ and ![]() $u_i$ is not barred. If
$u_i$ is not barred. If ![]() $A = \emptyset $, then line 3 in Algorithm 1 implies
$A = \emptyset $, then line 3 in Algorithm 1 implies ![]() $u_i \geq s$. Hence,
$u_i \geq s$. Hence, ![]() $u_i^* \leq k-s-1$ and
$u_i^* \leq k-s-1$ and ![]() $u^*_i$ is barred, so
$u^*_i$ is barred, so ![]() $u^*_i$ and
$u^*_i$ and ![]() $v_i$ are both barred and
$v_i$ are both barred and ![]() $u_i^* \leq v_i$. If
$u_i^* \leq v_i$. If ![]() $A \neq \varnothing $, suppose for contradiction that
$A \neq \varnothing $, suppose for contradiction that ![]() $u^*_i> v_i$. Then
$u^*_i> v_i$. Then
 $$ \begin{align*} u^*_i = U_i - u_i &> v_i \\ k-1 - u_i &> k- \min A -1 \\ u_i &< \min A,\\[-16pt] \end{align*} $$
$$ \begin{align*} u^*_i = U_i - u_i &> v_i \\ k-1 - u_i &> k- \min A -1 \\ u_i &< \min A,\\[-16pt] \end{align*} $$so ![]() $u_i$ is an unbarred entry that is less than
$u_i$ is an unbarred entry that is less than ![]() $\min A$. Then Algorithm 1 would have used line 7 to set
$\min A$. Then Algorithm 1 would have used line 7 to set ![]() $U_i = \min A-1$, since at that stage, we would have
$U_i = \min A-1$, since at that stage, we would have ![]() $\ell> u_i$. Therefore,
$\ell> u_i$. Therefore, ![]() $m^* \in {\mathcal {M}}_{n,k,s}$.
$m^* \in {\mathcal {M}}_{n,k,s}$.
Finally, we show that ![]() $\iota $ is an involution. From the argument above, we know
$\iota $ is an involution. From the argument above, we know ![]() $\iota (m) = m^{*} \in {\mathcal {M}}_{n,k,s}$. Suppose
$\iota (m) = m^{*} \in {\mathcal {M}}_{n,k,s}$. Suppose ![]() $M^*$ is the monomial we obtain by running Algorithm 1 on
$M^*$ is the monomial we obtain by running Algorithm 1 on ![]() $m^{*}$. Then
$m^{*}$. Then ![]() $M^*$ is the monomial in
$M^*$ is the monomial in ![]() $\delta _{n,k,s}$, such that
$\delta _{n,k,s}$, such that ![]() $m^* \odot M^* \doteq \iota (m^{*})$. We claim that
$m^* \odot M^* \doteq \iota (m^{*})$. We claim that ![]() $M^* = M$. If we can show this, then we will have
$M^* = M$. If we can show this, then we will have
so ![]() $\iota (\iota (m)) = m$. In our running example, where
$\iota (\iota (m)) = m$. In our running example, where ![]() $n= 9$,
$n= 9$, ![]() $k=7$,
$k=7$, ![]() $s=4$,
$s=4$, ![]() $u = (\bar {1},3,0,5,2,0,\bar {2},\bar {5},0)$,
$u = (\bar {1},3,0,5,2,0,\bar {2},\bar {5},0)$, ![]() $U = (\bar {6},3,2,\bar {6},\bar {6},1,\bar {6},\bar {6},0)$,
$U = (\bar {6},3,2,\bar {6},\bar {6},1,\bar {6},\bar {6},0)$, ![]() $u^* = (5,0,2,\bar {1},\bar {4},1,4,1,0)$ and
$u^* = (5,0,2,\bar {1},\bar {4},1,4,1,0)$ and ![]() $v = (6,3,2,\bar {4},\bar {4},1,6,6,0)$, we get
$v = (6,3,2,\bar {4},\bar {4},1,6,6,0)$, we get
To prove that ![]() $U^* = U$ in every case, consider running Algorithm 1 on m and
$U^* = U$ in every case, consider running Algorithm 1 on m and ![]() $m^*$ in parallel. We let
$m^*$ in parallel. We let ![]() $\ell ^{*}$ be the value in the algorithm creating
$\ell ^{*}$ be the value in the algorithm creating ![]() $M^*$ corresponding to
$M^*$ corresponding to ![]() $\ell $ and let
$\ell $ and let ![]() $U^*$ be the exponent sequence of
$U^*$ be the exponent sequence of ![]() $M^*$. This process has the following loop invariants.
$M^*$. This process has the following loop invariants.
Claim. After every loop of Algorithm 1, we have ![]() $\ell ^* = \ell $ and
$\ell ^* = \ell $ and ![]() $U^*_i = U_i$.
$U^*_i = U_i$.
We prove the Claim by considering the ![]() $i^{th}$ loop of Algorithm 1 and analysing the possible values of
$i^{th}$ loop of Algorithm 1 and analysing the possible values of ![]() $u_i$.
$u_i$.
• Suppose
 $u_i$ is barred. Then
$u_i$ is barred. Then  $U_i = \overline {k-1}$ and
$U_i = \overline {k-1}$ and  $u^*_i = k-1-u_i$. Since u is substaircase,
$u^*_i = k-1-u_i$. Since u is substaircase,  $u_i \leq k - \ell -1$, so Hence,
$u_i \leq k - \ell -1$, so Hence, $$ \begin{align*} u_i^{*} = k-1-u_i \geq k-1-(k-\ell-1) = \ell. \end{align*} $$
$$ \begin{align*} u_i^{*} = k-1-u_i \geq k-1-(k-\ell-1) = \ell. \end{align*} $$ $U^*_i = \overline {k-1} = U_i$.
$U^*_i = \overline {k-1} = U_i$.• Suppose
 $u_i$ is unbarred and
$u_i$ is unbarred and  $u_i \geq \ell $. Then
$u_i \geq \ell $. Then  $U_i = \overline {k-1}$,
$U_i = \overline {k-1}$,  $u_i^{*}$ is barred and
$u_i^{*}$ is barred and  $U_i^{*} = \overline {k-1} = U_i$.
$U_i^{*} = \overline {k-1} = U_i$.• Finally, suppose
 $u_i$ is unbarred and
$u_i$ is unbarred and  $u_i < \ell $. Then we let
$u_i < \ell $. Then we let  $U_i = \ell -1$ and get Then the algorithm decrements both
$U_i = \ell -1$ and get Then the algorithm decrements both $$ \begin{align*} u^*_i = \ell - u_i - 1 = \ell^* - u_i - 1 < \ell^*. \end{align*} $$
$$ \begin{align*} u^*_i = \ell - u_i - 1 = \ell^* - u_i - 1 < \ell^*. \end{align*} $$ $\ell $ and
$\ell $ and  $\ell ^*$ and sets
$\ell ^*$ and sets  $U_i^{*} = \ell ^{*} = \ell = U_i$.
$U_i^{*} = \ell ^{*} = \ell = U_i$.
This proves the Claim and the proposition.
Proposition 4.3 gives the following lower bound on the dimension of ![]() ${\mathbb {W}}_{n,k,s}$. In Theorem 4.12, we will prove that this lower bound is tight.
${\mathbb {W}}_{n,k,s}$. In Theorem 4.12, we will prove that this lower bound is tight.
Lemma 4.5. The set ![]() ${\mathcal {M}}_{n,k,s}$ descends to a linearly independent subset of
${\mathcal {M}}_{n,k,s}$ descends to a linearly independent subset of ![]() ${\mathbb {W}}_{n,k,s}$, and we have
${\mathbb {W}}_{n,k,s}$, and we have ![]() $\dim {\mathbb {W}}_{n,k,s} = \dim {\mathbb {H}}_{n,k,s} \geq |{\mathcal {M}}_{n,k,s}| = |{\mathcal {OSP}}_{n,k,s}|$.
$\dim {\mathbb {W}}_{n,k,s} = \dim {\mathbb {H}}_{n,k,s} \geq |{\mathcal {M}}_{n,k,s}| = |{\mathcal {OSP}}_{n,k,s}|$.
Proof. Proposition 4.3 shows that ![]() $\{m \odot \delta _{n,k,s} \,:\, m \in {\mathcal {M}}_{n,k,s} \}$ is a linearly independent subset of
$\{m \odot \delta _{n,k,s} \,:\, m \in {\mathcal {M}}_{n,k,s} \}$ is a linearly independent subset of ![]() ${\mathbb {H}}_{n,k,s}$, so that
${\mathbb {H}}_{n,k,s}$, so that ![]() $\dim {\mathbb {W}}_{n,k,s} = \dim {\mathbb {H}}_{n,k,s} \geq |{\mathcal {M}}_{n,k,s}|$. The equality
$\dim {\mathbb {W}}_{n,k,s} = \dim {\mathbb {H}}_{n,k,s} \geq |{\mathcal {M}}_{n,k,s}|$. The equality ![]() $|{\mathcal {M}}_{n,k,s}| = |{\mathcal {OSP}}_{n,k,s}|$ follows from Theorem 3.13.
$|{\mathcal {M}}_{n,k,s}| = |{\mathcal {OSP}}_{n,k,s}|$ follows from Theorem 3.13.
4.3 Statement of monomial basis and quotient presentation
The goal of this section is twofold: giving an explicit generating set of the defining ideal ![]() ${\mathrm {ann}} \, \delta _{n,k,s}$ of
${\mathrm {ann}} \, \delta _{n,k,s}$ of ![]() ${\mathbb {W}}_{n,k,s}$ and proving that
${\mathbb {W}}_{n,k,s}$ and proving that ![]() ${\mathcal {M}}_{n,k,s}$ descends to a basis of
${\mathcal {M}}_{n,k,s}$ descends to a basis of ![]() ${\mathbb {W}}_{n,k,s}$. The proofs of these two results will be deeply intertwined.
${\mathbb {W}}_{n,k,s}$. The proofs of these two results will be deeply intertwined.
We begin by defining an ideal ![]() $I_{n,k,s} \subseteq \Omega _n$, which will turn out to equal
$I_{n,k,s} \subseteq \Omega _n$, which will turn out to equal ![]() ${\mathrm {ann}} \, \delta _{n,k,s}$. If
${\mathrm {ann}} \, \delta _{n,k,s}$. If ![]() $S \subseteq [n]$ and
$S \subseteq [n]$ and ![]() $d \geq 0$, we let
$d \geq 0$, we let ![]() $e_d(S)$ be the elementary symmetric polynomial of degree d in the variable set
$e_d(S)$ be the elementary symmetric polynomial of degree d in the variable set ![]() $\{ x_i \,:\, x \in S \}$. For example, we have
$\{ x_i \,:\, x \in S \}$. For example, we have ![]() $e_2(134) = x_1 x_3 + x_1 x_4 + x_3 x_4$. We adopt the convention
$e_2(134) = x_1 x_3 + x_1 x_4 + x_3 x_4$. We adopt the convention ![]() $e_d(S) = 0$ whenever
$e_d(S) = 0$ whenever ![]() $d> |S|$.
$d> |S|$.
Definition 4.6. Given integers ![]() $n, k, s \geq 0$ with
$n, k, s \geq 0$ with ![]() $k \geq s$, define
$k \geq s$, define ![]() $I_{n,k,s} \subseteq \Omega _n$ to be the ideal
$I_{n,k,s} \subseteq \Omega _n$ to be the ideal
 $$ \begin{align} I_{n,k,s} = \langle x_1^k, x_2^k, \dots, x_n^k \rangle + \langle x_1^j \theta_1 + x_2^j \theta_2 + \cdots &+ x_n^j \theta_n \,:\, j \geq k-s \rangle + \notag \\ &\langle e_d(S) \cdot \theta_T \,:\, S \sqcup T = [n], \, d> |S| - s, d > 0 \rangle. \end{align} $$
$$ \begin{align} I_{n,k,s} = \langle x_1^k, x_2^k, \dots, x_n^k \rangle + \langle x_1^j \theta_1 + x_2^j \theta_2 + \cdots &+ x_n^j \theta_n \,:\, j \geq k-s \rangle + \notag \\ &\langle e_d(S) \cdot \theta_T \,:\, S \sqcup T = [n], \, d> |S| - s, d > 0 \rangle. \end{align} $$In the third summand, the pair ![]() $(S,T)$ ranges over all disjoint union decompositions
$(S,T)$ ranges over all disjoint union decompositions ![]() $S \sqcup T$ of
$S \sqcup T$ of ![]() $[n]$.
$[n]$.
For example, suppose ![]() $(n,k,s) = (4,3,2)$. The ideal
$(n,k,s) = (4,3,2)$. The ideal ![]() $I_{4,3,2} \subseteq \Omega _4$ is generated by the variable powers
$I_{4,3,2} \subseteq \Omega _4$ is generated by the variable powers ![]() $x_1^3, x_2^3, x_3^3, x_4^3$, the elements
$x_1^3, x_2^3, x_3^3, x_4^3$, the elements ![]() $x_1^j \theta _1 + x_2^j \theta _2 + x_3^j \theta _3 + x_4^j \theta _4$, where
$x_1^j \theta _1 + x_2^j \theta _2 + x_3^j \theta _3 + x_4^j \theta _4$, where ![]() $j \geq 1$ and the polynomials
$j \geq 1$ and the polynomials
 $$ \begin{align*} e_4(1234), &e_3(1234), \\ e_3(123) &\cdot \theta_4, e_2(123) \cdot \theta_4, e_3(124) \cdot \theta_3, e_2(124) \cdot \theta_3, e_3(134) \cdot \theta_2, e_2(134) \cdot \theta_2, e_3(234) \cdot \theta_1, \\ &\qquad e_2(234) \cdot \theta_1, e_2(12) \cdot \theta_{34}, e_1(12) \cdot \theta_{34}, e_2(13) \cdot \theta_{24}, e_1(13) \cdot \theta_{24}, e_2(14) \cdot \theta_{23}, \\&\qquad e_1(14) \cdot \theta_{23}, e_2(23) \cdot \theta_{14}, e_1(23) \cdot \theta_{14}, e_2(24) \cdot \theta_{13}, e_1(24) \cdot \theta_{13}, e_2(34) \cdot \theta_{12}, \\ &\qquad\qquad\qquad\qquad\qquad e_1(34) \cdot \theta_{12}, e_1(4) \cdot \theta_{123}, \theta_{123}, e_1(3) \cdot \theta_{124}, \theta_{124}, e_1(2) \cdot \theta_{134}, \theta_{134},\\ &\qquad\qquad\qquad\qquad\qquad\qquad e_1(1) \cdot \theta_{234}, \theta_{234}. \end{align*} $$
$$ \begin{align*} e_4(1234), &e_3(1234), \\ e_3(123) &\cdot \theta_4, e_2(123) \cdot \theta_4, e_3(124) \cdot \theta_3, e_2(124) \cdot \theta_3, e_3(134) \cdot \theta_2, e_2(134) \cdot \theta_2, e_3(234) \cdot \theta_1, \\ &\qquad e_2(234) \cdot \theta_1, e_2(12) \cdot \theta_{34}, e_1(12) \cdot \theta_{34}, e_2(13) \cdot \theta_{24}, e_1(13) \cdot \theta_{24}, e_2(14) \cdot \theta_{23}, \\&\qquad e_1(14) \cdot \theta_{23}, e_2(23) \cdot \theta_{14}, e_1(23) \cdot \theta_{14}, e_2(24) \cdot \theta_{13}, e_1(24) \cdot \theta_{13}, e_2(34) \cdot \theta_{12}, \\ &\qquad\qquad\qquad\qquad\qquad e_1(34) \cdot \theta_{12}, e_1(4) \cdot \theta_{123}, \theta_{123}, e_1(3) \cdot \theta_{124}, \theta_{124}, e_1(2) \cdot \theta_{134}, \theta_{134},\\ &\qquad\qquad\qquad\qquad\qquad\qquad e_1(1) \cdot \theta_{234}, \theta_{234}. \end{align*} $$There is redundancy in this list of generators, for example, the generator ![]() $e_1(4) \cdot \theta _{123} = x_4 \cdot \theta _{123}$ is a multiple of the generator
$e_1(4) \cdot \theta _{123} = x_4 \cdot \theta _{123}$ is a multiple of the generator ![]() $\theta _{123}$.
$\theta _{123}$.
We adopt the temporary notation
for the quotient of ![]() ${\mathbb {U}}_{n,k,s}$ by
${\mathbb {U}}_{n,k,s}$ by ![]() $I_{n,k,s}$. Since
$I_{n,k,s}$. Since ![]() $I_{n,k,s}$ is
$I_{n,k,s}$ is ![]() ${\mathfrak {S}}_n$-stable and bihomogeneous, the quotient
${\mathfrak {S}}_n$-stable and bihomogeneous, the quotient ![]() ${\mathbb {U}}_{n,k,s}$ is a bigraded
${\mathbb {U}}_{n,k,s}$ is a bigraded ![]() ${\mathfrak {S}}_n$-module. It will turn out that
${\mathfrak {S}}_n$-module. It will turn out that ![]() ${\mathbb {U}}_{n,k,s}$ and
${\mathbb {U}}_{n,k,s}$ and ![]() ${\mathbb {W}}_{n,k,s}$ coincide. The following lemma shows that
${\mathbb {W}}_{n,k,s}$ coincide. The following lemma shows that ![]() ${\mathbb {W}}_{n,k,s}$ is a quotient of
${\mathbb {W}}_{n,k,s}$ is a quotient of ![]() ${\mathbb {U}}_{n,k,s}$.
${\mathbb {U}}_{n,k,s}$.
Lemma 4.7. Let ![]() $n, k, s \geq 0$ with
$n, k, s \geq 0$ with ![]() $k \geq s$. We have the containment
$k \geq s$. We have the containment ![]() $I_{n,k,s} \subseteq {\mathrm {ann}} \, \delta _{n,k,s}$.
$I_{n,k,s} \subseteq {\mathrm {ann}} \, \delta _{n,k,s}$.
Proof. For every generator g of the ideal ![]() $I_{n,k,s}$, we check that
$I_{n,k,s}$, we check that ![]() $g \odot \delta _{n,k,s} = 0$. We handle the three different kinds of generators g of
$g \odot \delta _{n,k,s} = 0$. We handle the three different kinds of generators g of ![]() $I_{n,k,s}$ separately, using
$I_{n,k,s}$ separately, using ![]() $\doteq $ for equality up to a nonzero scalar.
$\doteq $ for equality up to a nonzero scalar.
Case 1. ![]() $g = x_i^k$ for some i.
$g = x_i^k$ for some i.
Since no power of ![]() $x_i \geq k$ appears in
$x_i \geq k$ appears in
it follows that ![]() $x_i^k \odot \delta _{n,k,s} = 0$.
$x_i^k \odot \delta _{n,k,s} = 0$.
Case 2. ![]() $g = x_1^j \theta _1 + \cdots + x_n^j \theta _n$ for some
$g = x_1^j \theta _1 + \cdots + x_n^j \theta _n$ for some ![]() $j \geq k-s$.
$j \geq k-s$.
We compute
 $$ \begin{align} &\doteq \varepsilon_n \cdot \left( \sum_{i = 1}^{n-s} (-1)^{i-1} x_1^{k-1} \cdots x_i^{k-j-1} \cdots x_{n-s}^{k-1} x_{n-s+1}^{s-1} \cdots x_n^0 \times \theta_1 \cdots \widehat{\theta_i} \cdots \theta_{n-s} \right) \end{align} $$
$$ \begin{align} &\doteq \varepsilon_n \cdot \left( \sum_{i = 1}^{n-s} (-1)^{i-1} x_1^{k-1} \cdots x_i^{k-j-1} \cdots x_{n-s}^{k-1} x_{n-s+1}^{s-1} \cdots x_n^0 \times \theta_1 \cdots \widehat{\theta_i} \cdots \theta_{n-s} \right) \end{align} $$ $$ \begin{align} &= \sum_{i = 1}^{n-s} (-1)^{i-1} \varepsilon_n \cdot \left(x_1^{k-1} \cdots x_i^{k-j-1} \cdots x_{n-s}^{k-1} x_{n-s+1}^{s-1} \cdots x_n^0 \times \theta_1 \cdots \widehat{\theta_i} \cdots \theta_{n-s} \right) \end{align} $$
$$ \begin{align} &= \sum_{i = 1}^{n-s} (-1)^{i-1} \varepsilon_n \cdot \left(x_1^{k-1} \cdots x_i^{k-j-1} \cdots x_{n-s}^{k-1} x_{n-s+1}^{s-1} \cdots x_n^0 \times \theta_1 \cdots \widehat{\theta_i} \cdots \theta_{n-s} \right) \end{align} $$The first equality is the definition of ![]() $\delta _{n,k,s}$. The second equality follows because
$\delta _{n,k,s}$. The second equality follows because ![]() $g \odot (-)$ is an
$g \odot (-)$ is an ![]() ${\mathfrak {S}}_n$-invariant differential operator, and so commutes with the action of
${\mathfrak {S}}_n$-invariant differential operator, and so commutes with the action of ![]() ${\mathbb {Q}}[{\mathfrak {S}}_n]$ on
${\mathbb {Q}}[{\mathfrak {S}}_n]$ on ![]() $\Omega _n$. The third equality is the effect of applying
$\Omega _n$. The third equality is the effect of applying ![]() $g \odot (-)$ and the fourth is rearrangement. The final equality holds since the hypothesis
$g \odot (-)$ and the fourth is rearrangement. The final equality holds since the hypothesis ![]() $j \geq s$ implies
$j \geq s$ implies ![]() $k-j-1 \leq s-1$, so that
$k-j-1 \leq s-1$, so that ![]() $\varepsilon _n$ annihilates the given superspace monomial.
$\varepsilon _n$ annihilates the given superspace monomial.
Case 3. ![]() $g = e_d(S) \cdot \theta _T$ for some
$g = e_d(S) \cdot \theta _T$ for some ![]() $S \sqcup T = [n]$ with
$S \sqcup T = [n]$ with ![]() $d> |S| - s$.
$d> |S| - s$.
Let ![]() $\delta _{|S|,k,s}(S)$ denote the superspace Vandermonde
$\delta _{|S|,k,s}(S)$ denote the superspace Vandermonde ![]() $\delta _{|S|,k,s}$ defined in the set
$\delta _{|S|,k,s}$ defined in the set ![]() $\{ x_i, \theta _i \,:\, i \in S \}$ of commuting and anticommuting variables indexed by S. Applying the operator
$\{ x_i, \theta _i \,:\, i \in S \}$ of commuting and anticommuting variables indexed by S. Applying the operator ![]() $\theta _T \odot (-)$ to
$\theta _T \odot (-)$ to ![]() $\delta _{n,k,s}$, we see that
$\delta _{n,k,s}$, we see that
 $$ \begin{align} \theta_T \odot \delta_{n,k,s} \doteq \prod_{j \in T} x_j^{k-1} \times \delta_{|S|,k,s}(S). \end{align} $$
$$ \begin{align} \theta_T \odot \delta_{n,k,s} \doteq \prod_{j \in T} x_j^{k-1} \times \delta_{|S|,k,s}(S). \end{align} $$Therefore, we have
 $$ \begin{align} g \odot \delta_{n,k,s} \doteq e_d(S) \odot \left( \prod_{j \in T} x_j^{k-1} \times \delta_{|S|,k,s}(S) \right) = \prod_{j \in T} x_j^{k-1} \times \left(e_d(S) \odot \delta_{|S|,k,s}(S)\right) = 0 ,\end{align} $$
$$ \begin{align} g \odot \delta_{n,k,s} \doteq e_d(S) \odot \left( \prod_{j \in T} x_j^{k-1} \times \delta_{|S|,k,s}(S) \right) = \prod_{j \in T} x_j^{k-1} \times \left(e_d(S) \odot \delta_{|S|,k,s}(S)\right) = 0 ,\end{align} $$where the second equality follows from the disjointness of the sets S and T and the final equality is a consequence of [Reference Rhoades and Wilson27, Lemma 3.2].
4.4 The harmonic space  $I_{n,k,s}^{\perp }$
$I_{n,k,s}^{\perp }$
Throughout this section, we adopt the notation
for rank ![]() $n-1$ superspace over the commuting variables
$n-1$ superspace over the commuting variables ![]() $x_2, \dots , x_n$ and the anticommuting variables
$x_2, \dots , x_n$ and the anticommuting variables ![]() $\theta _2, \dots , \theta _n$.
$\theta _2, \dots , \theta _n$.
Lemma 4.7 gives the containment ![]() $I_{n,k,s} \subseteq {\mathrm {ann}} \, \delta _{n,k,s}$. We consider the harmonic space
$I_{n,k,s} \subseteq {\mathrm {ann}} \, \delta _{n,k,s}$. We consider the harmonic space
to the ideal ![]() $I_{n,k,s}$. The composite map
$I_{n,k,s}$. The composite map
is an isomorphism of bigraded ![]() ${\mathfrak {S}}_n$-modules. Lemma 4.7 gives the containment
${\mathfrak {S}}_n$-modules. Lemma 4.7 gives the containment ![]() $I_{n,k,s} \subseteq {\mathrm {ann}} \, \delta _{n,k,s}$, which implies
$I_{n,k,s} \subseteq {\mathrm {ann}} \, \delta _{n,k,s}$, which implies
We will see (Theorem 4.12) that these spaces coincide, but it will be convenient to work with the a priori larger space ![]() $I_{n,k,s}^{\perp }$ in this section.
$I_{n,k,s}^{\perp }$ in this section.
In order to show the containment (4.15) is in fact an equality, we bound the dimension of ![]() $I_{n,k,s}^{\perp }$ from above. To do this, we inductively show (Lemma 4.11) that the leading terms of nonzero polynomials
$I_{n,k,s}^{\perp }$ from above. To do this, we inductively show (Lemma 4.11) that the leading terms of nonzero polynomials ![]() $f \in I_{n,k,s}^{\perp }$ belong to the family
$f \in I_{n,k,s}^{\perp }$ belong to the family ![]() ${\mathcal {M}}_{n,k,s}$ of substaircase monomials. For the sake of this induction, we prove lemmata about the expansions of polynomials
${\mathcal {M}}_{n,k,s}$ of substaircase monomials. For the sake of this induction, we prove lemmata about the expansions of polynomials ![]() $f \in I_{n,k,s}^{\perp }$ in terms of the initial variables
$f \in I_{n,k,s}^{\perp }$ in terms of the initial variables ![]() $x_1$ and
$x_1$ and ![]() $\theta _1$. The first of these is a simple degree bound.
$\theta _1$. The first of these is a simple degree bound.
Lemma 4.8. Let ![]() $n, k, s \geq 0$ with
$n, k, s \geq 0$ with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $f \in I_{n,k,s}^{\perp }$. Then f may be expressed uniquely as
$f \in I_{n,k,s}^{\perp }$. Then f may be expressed uniquely as
for some elements ![]() $g_0, g_1, \dots , g_{k-1}, h_0, h_1, \dots , h_{k-1} \in \Omega _{n-1}'$.
$g_0, g_1, \dots , g_{k-1}, h_0, h_1, \dots , h_{k-1} \in \Omega _{n-1}'$.
Proof. The element ![]() $x_1^k$ is a generator of
$x_1^k$ is a generator of ![]() $I_{n,k,s}$. Since
$I_{n,k,s}$. Since ![]() $f \in I_{n,k,s}^{\perp }$, we have
$f \in I_{n,k,s}^{\perp }$, we have ![]() $x_1^k \odot f = 0$, so that no power of
$x_1^k \odot f = 0$, so that no power of ![]() $x_1 \geq k$ may appear in f.
$x_1 \geq k$ may appear in f.
By the definition of the order ![]() $\prec $ on superspace monomials, if
$\prec $ on superspace monomials, if ![]() $f \in I_{n,k,s}^{\perp }$ is nonzero and if
$f \in I_{n,k,s}^{\perp }$ is nonzero and if
as in Lemma 4.8, the ![]() $\prec $-leading term of f is given by
$\prec $-leading term of f is given by
 $$ \begin{align*} {\mathrm{in}}(f) = \begin{cases} x_1^i \cdot {\mathrm{in}}(g_i) & \text{if } g_j \neq 0 \text{ for some } j\text{, and if } i \text{ is maximal with } g_i \neq 0, \\ x_1^i \theta_1 \cdot {\mathrm{in}}(h_i )& \text{if } g_j = 0 \text{ for all } j\text{, and if } i \text{ is minimal with } h_i \neq 0. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{in}}(f) = \begin{cases} x_1^i \cdot {\mathrm{in}}(g_i) & \text{if } g_j \neq 0 \text{ for some } j\text{, and if } i \text{ is maximal with } g_i \neq 0, \\ x_1^i \theta_1 \cdot {\mathrm{in}}(h_i )& \text{if } g_j = 0 \text{ for all } j\text{, and if } i \text{ is minimal with } h_i \neq 0. \end{cases} \end{align*} $$With Lemma 3.12 in mind, we aim to relate the harmonicity of ![]() $f \in I_{n,k,s}^{\perp }$ to showing that
$f \in I_{n,k,s}^{\perp }$ to showing that ![]() $g_i$ and
$g_i$ and ![]() $h_i$ lie in appropriate harmonic spaces within
$h_i$ lie in appropriate harmonic spaces within ![]() $\Omega _{n-1}'$. Our starting point is the following vanishing result for harmonics divisible by
$\Omega _{n-1}'$. Our starting point is the following vanishing result for harmonics divisible by ![]() $\theta _1$.
$\theta _1$.
Lemma 4.9. Let ![]() $n,k,s \geq 0$ be integers with
$n,k,s \geq 0$ be integers with ![]() $k \geq s$, and suppose
$k \geq s$, and suppose ![]() $f \in I_{n,k,s}^{\perp }$ is a multiple of
$f \in I_{n,k,s}^{\perp }$ is a multiple of ![]() $\theta _1$:
$\theta _1$:
for some ![]() $h_0, h_1, \dots , h_{k-1} \in \Omega ^{\prime }_{n-1}$. We have
$h_0, h_1, \dots , h_{k-1} \in \Omega ^{\prime }_{n-1}$. We have ![]() $h_{k-s} = h_{k-s+1} = \cdots = h_{k-1} = 0$.
$h_{k-s} = h_{k-s+1} = \cdots = h_{k-1} = 0$.
The vanishing conditions in Lemma 4.9 will turn out to mirror the ‘top branches’ (3.16) and (3.19) of the disjoint union decompositions in Lemma 3.12.
Proof. The generator ![]() $x_1^{k-s} \theta _1 + x_2^{k-s} \theta _2 + \cdots + x_n^{k-s} \theta _n \in I_{n,k,s}$ annihilates f under the
$x_1^{k-s} \theta _1 + x_2^{k-s} \theta _2 + \cdots + x_n^{k-s} \theta _n \in I_{n,k,s}$ annihilates f under the ![]() $\odot $-action. This gives an equation of the form
$\odot $-action. This gives an equation of the form
where the C’s are nonzero constants. Taking the coefficients of ![]() $x_1^0, x_1^1, \dots , x_1^{s-1}$, we see that
$x_1^0, x_1^1, \dots , x_1^{s-1}$, we see that ![]() $h_{k-s} = h_{k-s+1} = \cdots = h_{k-1} = 0$.
$h_{k-s} = h_{k-s+1} = \cdots = h_{k-1} = 0$.
Lemma 4.9 may be enhanced to consider harmonics ![]() $f \in I_{n,k,s}^{\perp }$ whose decomposition contains terms
$f \in I_{n,k,s}^{\perp }$ whose decomposition contains terms ![]() $x_1^i g_i$ for only relatively low values of i.
$x_1^i g_i$ for only relatively low values of i.
Lemma 4.10. Let ![]() $n, k, s \geq 0$ be integers with
$n, k, s \geq 0$ be integers with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $f \in I^{\perp }_{n,k,s}$. Assume that
$f \in I^{\perp }_{n,k,s}$. Assume that
for some ![]() $0 \leq i \leq k-1$. Then
$0 \leq i \leq k-1$. Then ![]() $h_{k-s+i+1} = h_{k-s+i+2} = \cdots = h_{k-1} = 0$.
$h_{k-s+i+1} = h_{k-s+i+2} = \cdots = h_{k-1} = 0$.
In light of Lemma 4.8, Lemma 4.10 gives no information in the range ![]() $s \leq i \leq k$. In accordance with the ‘middle branches’ (3.17) and (3.20) of the disjoint union decompositions of Lemma 3.12, Lemma 4.10 will be useful in the range
$s \leq i \leq k$. In accordance with the ‘middle branches’ (3.17) and (3.20) of the disjoint union decompositions of Lemma 3.12, Lemma 4.10 will be useful in the range ![]() $0 \leq i \leq s-1$.
$0 \leq i \leq s-1$.
Proof. The space ![]() $I^{\perp }_{n,k,s}$ is closed under the operator
$I^{\perp }_{n,k,s}$ is closed under the operator ![]() $x_1^{i+1} \odot (-)$. Applying this operator to f, we get the harmonic polynomial
$x_1^{i+1} \odot (-)$. Applying this operator to f, we get the harmonic polynomial
where the C’s are nonzero constants. Applying Lemma 4.9 to this polynomial, we see that ![]() $h_{k-s+i+1} = h_{k-s+i+2} = \cdots = h_{k-1} = 0$.
$h_{k-s+i+1} = h_{k-s+i+2} = \cdots = h_{k-1} = 0$.
The following lemma characterises the leading terms of nonzero elements in ![]() $I^{\perp }_{n,k,s}$. The recursive description of the set
$I^{\perp }_{n,k,s}$. The recursive description of the set ![]() ${\mathcal {M}}_{n,k,s}$ of substaircase monomials given in Lemma 3.12 is crucial to its proof.
${\mathcal {M}}_{n,k,s}$ of substaircase monomials given in Lemma 3.12 is crucial to its proof.
Lemma 4.11. Let ![]() $n, k, s \geq 0$ with
$n, k, s \geq 0$ with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $f \in I^{\perp }_{n,k,s}$ be nonzero. The
$f \in I^{\perp }_{n,k,s}$ be nonzero. The ![]() $\prec $-leading term of f is a substaircase monomial, that is
$\prec $-leading term of f is a substaircase monomial, that is
Proof. We proceed by induction on n. When ![]() $n = 1$, the space
$n = 1$, the space ![]() $I^{\perp }_{1,k,s}$ and the family of monomials
$I^{\perp }_{1,k,s}$ and the family of monomials ![]() ${\mathcal {M}}_{1,k,s}$ have three flavors depending on the value of s. If
${\mathcal {M}}_{1,k,s}$ have three flavors depending on the value of s. If ![]() $s = 0$, then
$s = 0$, then
and we have ![]() $I_{1,k,0}^{\perp } = \mathrm {span} \, {\mathcal {M}}_{1,k,0}$, so the result follows. If
$I_{1,k,0}^{\perp } = \mathrm {span} \, {\mathcal {M}}_{1,k,0}$, so the result follows. If ![]() $s = 1$, then
$s = 1$, then ![]() $I_{1,k,1}^{\perp }$ is the ground field
$I_{1,k,1}^{\perp }$ is the ground field ![]() ${\mathbb {Q}}$ (independent of the value of k) and
${\mathbb {Q}}$ (independent of the value of k) and ![]() ${\mathcal {M}}_{1,k,1} = \{1\}$, so the result holds. If
${\mathcal {M}}_{1,k,1} = \{1\}$, so the result holds. If ![]() $s> 1$, then
$s> 1$, then ![]() $e_0 = 1 \in I_{1,k,s}$, so that
$e_0 = 1 \in I_{1,k,s}$, so that ![]() $I_{1,k,s} = \Omega _1$ and
$I_{1,k,s} = \Omega _1$ and ![]() $I_{1,k,s}^{\perp } = 0$; since
$I_{1,k,s}^{\perp } = 0$; since ![]() ${\mathcal {M}}_{1,k,s} = \varnothing $, the result is true in this case as well. Going forward, we let
${\mathcal {M}}_{1,k,s} = \varnothing $, the result is true in this case as well. Going forward, we let ![]() $n> 1$ and that the lemma has been established for all smaller values of n, and all values of k and s.
$n> 1$ and that the lemma has been established for all smaller values of n, and all values of k and s.
By Lemma 4.8, we may write f uniquely as
for some ![]() $g_0, g_1, \dots , g_{k-1}, h_0, h_1, \dots , h_{k-1} \in \Omega ^{\prime }_{n-1}$. Our analysis breaks up into cases depending on the vanishing properties of these elements of
$g_0, g_1, \dots , g_{k-1}, h_0, h_1, \dots , h_{k-1} \in \Omega ^{\prime }_{n-1}$. Our analysis breaks up into cases depending on the vanishing properties of these elements of ![]() $\Omega ^{\prime }_{n-1}$.
$\Omega ^{\prime }_{n-1}$.
Case 1. We have ![]() $g_0 = g_1 = \cdots = g_{k-1} = 0$.
$g_0 = g_1 = \cdots = g_{k-1} = 0$.
In this case, f is a multiple of ![]() $\theta _1$. Lemma 4.9 applies, and we may write
$\theta _1$. Lemma 4.9 applies, and we may write
for some ![]() $0 \leq i < k-s$ with
$0 \leq i < k-s$ with ![]() $h_i \neq 0$. We have
$h_i \neq 0$. We have
By (3.16) and (3.19) in Lemma 3.12, it is enough to show that ![]() $h_i \in (I^{\prime }_{n-1,k,s})^{\perp }$. Here,
$h_i \in (I^{\prime }_{n-1,k,s})^{\perp }$. Here, ![]() $I^{\prime }_{n-1,k,s} \subseteq \Omega ^{\prime }_{n-1}$ is the image of
$I^{\prime }_{n-1,k,s} \subseteq \Omega ^{\prime }_{n-1}$ is the image of ![]() $I_{n-1,k,s}$ under the map
$I_{n-1,k,s}$ under the map ![]() $x_j \mapsto x_{j+1}, \theta _j \mapsto \theta _{j+1}$. We show that each generator of
$x_j \mapsto x_{j+1}, \theta _j \mapsto \theta _{j+1}$. We show that each generator of ![]() $I_{n-1,k,s}'$ annihilates
$I_{n-1,k,s}'$ annihilates ![]() $h_i$.
$h_i$.
For ![]() $2 \leq j \leq n$, we have
$2 \leq j \leq n$, we have ![]() $x_j^k \odot f = 0$, so that
$x_j^k \odot f = 0$, so that
Taking the coefficient of ![]() $x_1^i \theta _1$ shows that
$x_1^i \theta _1$ shows that ![]() $x_j^k \odot h_i = 0$.
$x_j^k \odot h_i = 0$.
Given ![]() $d \geq k-s$, we have
$d \geq k-s$, we have ![]() $(x_1^d \theta _1 + x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot f = 0$, so that
$(x_1^d \theta _1 + x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot f = 0$, so that
 $$ \begin{align} 0 = \sum_{j = i}^{k-s-1} x_1^j \theta_1 \times (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot h_j + (\text{terms not involving } \theta_1). \end{align} $$
$$ \begin{align} 0 = \sum_{j = i}^{k-s-1} x_1^j \theta_1 \times (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot h_j + (\text{terms not involving } \theta_1). \end{align} $$Taking the coefficient of ![]() $x_1^i \theta _1$, we see that
$x_1^i \theta _1$, we see that ![]() $(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot h_j = 0$.
$(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot h_j = 0$.
Finally, let ![]() $S \sqcup T = \{2,\dots ,n\}$ be a disjoint union decomposition, and let
$S \sqcup T = \{2,\dots ,n\}$ be a disjoint union decomposition, and let ![]() $d> |S|-s$. We aim to show that
$d> |S|-s$. We aim to show that ![]() $(e_d(S) \theta _T) \odot h_i = 0$. Indeed, if we let
$(e_d(S) \theta _T) \odot h_i = 0$. Indeed, if we let ![]() $\hat {T} = T \cup \{1\}$, we have
$\hat {T} = T \cup \{1\}$, we have ![]() $(e_d(S) \theta _{\hat {T}}) \odot f = 0$ since
$(e_d(S) \theta _{\hat {T}}) \odot f = 0$ since ![]() $f \in I_{n,k,s}^{\perp }$. This means
$f \in I_{n,k,s}^{\perp }$. This means
and taking the coefficient of ![]() $x_1^i$ shows
$x_1^i$ shows ![]() $(e_d(S) \theta _T) \odot h_i = 0$.
$(e_d(S) \theta _T) \odot h_i = 0$.
The previous three paragraphs imply ![]() $h_i \in (I^{\prime }_{n-1,k,s})^{\perp }$, so Lemma 3.12 and induction on n complete the proof of Case 1.
$h_i \in (I^{\prime }_{n-1,k,s})^{\perp }$, so Lemma 3.12 and induction on n complete the proof of Case 1.
Case 2. At least one ![]() $g_j$ is nonzero, but
$g_j$ is nonzero, but ![]() $g_j = 0$ for all
$g_j = 0$ for all ![]() $j \geq s$.
$j \geq s$.
In this case, Lemma 4.10 applies, and we may write
for some ![]() $0 \leq i < s$, where
$0 \leq i < s$, where ![]() $g_i \neq 0$. We have
$g_i \neq 0$. We have
and, inspired by the ‘middle branches’ (3.17) and (3.20) of Lemma 3.12, we verify that ![]() $g_i \in (I_{n-1,k,s-1}')^{\perp }$, where the prime, again, denotes increasing variable indices by one. We check that
$g_i \in (I_{n-1,k,s-1}')^{\perp }$, where the prime, again, denotes increasing variable indices by one. We check that ![]() $g_i$ is annihilated by every generator of
$g_i$ is annihilated by every generator of ![]() $I_{n-1,k,s-1}$. The verification that
$I_{n-1,k,s-1}$. The verification that ![]() $x_j^k \odot g_i = 0$ is analogous to that in Case 1 and is omitted.
$x_j^k \odot g_i = 0$ is analogous to that in Case 1 and is omitted.
Let ![]() $d \geq k-s+1$. We aim to show that
$d \geq k-s+1$. We aim to show that ![]() $(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot g_i = 0$. Indeed, since
$(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot g_i = 0$. Indeed, since ![]() $f \in I_{n,k,s}^{\perp }$, we have
$f \in I_{n,k,s}^{\perp }$, we have
 $$ \begin{align} 0 &= (x_1^d \theta_1 + x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot f \notag \\ &= \sum_{j = 0}^i x_1^j (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot g_j + \sum_{j' = 0}^{k-s+i} x_1^{j'} \theta_1 (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot h_j + \sum_{j" = 0}^{k-s+i-d} C_{j"} x_1^{j"} h_{j" + d}, \end{align} $$
$$ \begin{align} 0 &= (x_1^d \theta_1 + x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot f \notag \\ &= \sum_{j = 0}^i x_1^j (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot g_j + \sum_{j' = 0}^{k-s+i} x_1^{j'} \theta_1 (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot h_j + \sum_{j" = 0}^{k-s+i-d} C_{j"} x_1^{j"} h_{j" + d}, \end{align} $$where the C’s are nonzero constants. Since ![]() $d \geq k-s+1$, the final sum does not involve the power
$d \geq k-s+1$, the final sum does not involve the power ![]() $x_1^i$. Taking the coefficient of
$x_1^i$. Taking the coefficient of ![]() $x_1^i$ shows that
$x_1^i$ shows that ![]() $(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot g_i = 0$.
$(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot g_i = 0$.
Finally, let ![]() $S \sqcup T = \{2, \dots , n\}$ be a disjoint union decomposition and let
$S \sqcup T = \{2, \dots , n\}$ be a disjoint union decomposition and let ![]() $d> |S| - s + 1$. We need to show
$d> |S| - s + 1$. We need to show ![]() $(e_d(S) \theta _T) \odot g_i = 0$. If we let
$(e_d(S) \theta _T) \odot g_i = 0$. If we let ![]() $\hat {S} = S \cup \{1\}$, we have the relation
$\hat {S} = S \cup \{1\}$, we have the relation
and ![]() $e_d(\hat {S}) \theta _T$ is a generator of
$e_d(\hat {S}) \theta _T$ is a generator of ![]() $I_{n,k,s}$. The equation
$I_{n,k,s}$. The equation ![]() $(e_d(\hat {S}) \theta _T) \odot f) = 0$ has the form
$(e_d(\hat {S}) \theta _T) \odot f) = 0$ has the form
 $$ \begin{align} 0 = \sum_{j = 0}^i [(e_d(S) + x_1 e_{d-1}(S)) \theta_T] \odot (x_1^j g_j) + (\text{a multiple of } \theta_1). \end{align} $$
$$ \begin{align} 0 = \sum_{j = 0}^i [(e_d(S) + x_1 e_{d-1}(S)) \theta_T] \odot (x_1^j g_j) + (\text{a multiple of } \theta_1). \end{align} $$Taking the coefficient of ![]() $x_1^i$ shows that
$x_1^i$ shows that ![]() $(e_d(S) \theta _T) \odot g_i = 0$, as required.
$(e_d(S) \theta _T) \odot g_i = 0$, as required.
The previous two paragraphs show that ![]() $g_i \in (I^{\prime }_{n-1,k,s-1})^{\perp }$. Lemma 3.12 and induction on n complete the proof of Case 2.
$g_i \in (I^{\prime }_{n-1,k,s-1})^{\perp }$. Lemma 3.12 and induction on n complete the proof of Case 2.
Case 3. At least one ![]() $g_j$ is nonzero for some
$g_j$ is nonzero for some ![]() $j \geq s$.
$j \geq s$.
We apply Lemma 4.8 to write
with ![]() $g_i \neq 0$ for some
$g_i \neq 0$ for some ![]() $i \geq s$. We verify
$i \geq s$. We verify ![]() $g_i \in (I^{\prime }_{n-1,k,s})^{\perp }$ by showing that every generator of
$g_i \in (I^{\prime }_{n-1,k,s})^{\perp }$ by showing that every generator of ![]() $I^{\prime }_{n-1,k,s}$ annihilates
$I^{\prime }_{n-1,k,s}$ annihilates ![]() $g_i$. Generators of the form
$g_i$. Generators of the form ![]() $x_j^k$ are handled as before.
$x_j^k$ are handled as before.
Let ![]() $d \geq k-s$. Since
$d \geq k-s$. Since ![]() $f \in I_{n,k,s}^{\perp }$, we have
$f \in I_{n,k,s}^{\perp }$, we have
 $$ \begin{align} &= \sum_{j = 0}^i x_1^j [ (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot g_j ] + \sum_{j' = 0}^{k-d-1} C_{j'} x_1^{j'} h_{j'+d} + (\text{a multiple of } \theta_1), \end{align} $$
$$ \begin{align} &= \sum_{j = 0}^i x_1^j [ (x_2^d \theta_2 + \cdots + x_n^d \theta_n) \odot g_j ] + \sum_{j' = 0}^{k-d-1} C_{j'} x_1^{j'} h_{j'+d} + (\text{a multiple of } \theta_1), \end{align} $$where the C’s are constants. Since ![]() $i \geq s> k-d-1$, taking the coefficient of
$i \geq s> k-d-1$, taking the coefficient of ![]() $x_1^i$ shows that
$x_1^i$ shows that ![]() $(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot g_i = 0$.
$(x_2^d \theta _2 + \cdots + x_n^d \theta _n) \odot g_i = 0$.
Finally, let ![]() $S \sqcup T = \{2, \dots , n\}$ be a disjoint union decomposition and let
$S \sqcup T = \{2, \dots , n\}$ be a disjoint union decomposition and let ![]() $d> |S| - s$. We show that
$d> |S| - s$. We show that ![]() $(e_d(S) \theta _T) \odot g_i = 0$ as follows. If we set
$(e_d(S) \theta _T) \odot g_i = 0$ as follows. If we set ![]() $\hat {S} = S \cup \{1\}$, we calculate
$\hat {S} = S \cup \{1\}$, we calculate
where the last equality used the conditions ![]() $i \geq s$ and
$i \geq s$ and ![]() $d> |S| - s$, so that
$d> |S| - s$, so that ![]() $e_{d+i}(S) = 0$. Multiplying both sides by
$e_{d+i}(S) = 0$. Multiplying both sides by ![]() $\theta _T$, we get
$\theta _T$, we get
since every term on the right-hand side is a generator of ![]() $I_{n,k,s}$. Since
$I_{n,k,s}$. Since ![]() $f \in I_{n,k,s}^{\perp }$, this means
$f \in I_{n,k,s}^{\perp }$, this means
where C is a nonzero constant. This implies that ![]() $(e_d(S) \theta _T) \odot g_i = 0$.
$(e_d(S) \theta _T) \odot g_i = 0$.
The previous arguments show that ![]() $g_i \in (I^{\prime }_{n-1,k,s})^{\perp }$. The fact that
$g_i \in (I^{\prime }_{n-1,k,s})^{\perp }$. The fact that ![]() ${\mathrm {in}}(f) = x_1^i {\mathrm {in}}(g_i)$, the ‘lower branches’ (3.18) and (3.21) of the disjoint union decompositions in Lemma 3.12 and induction on n all complete the proof of Case 3, and of the lemma.
${\mathrm {in}}(f) = x_1^i {\mathrm {in}}(g_i)$, the ‘lower branches’ (3.18) and (3.21) of the disjoint union decompositions in Lemma 3.12 and induction on n all complete the proof of Case 3, and of the lemma.
4.5 Proof of quotient presentation and monomial basis
We are ready to prove that the ideal ![]() $I_{n,k,s}$ and the annihilator
$I_{n,k,s}$ and the annihilator ![]() ${\mathrm {ann}} \, \delta _{n,k,s}$ coincide, so that
${\mathrm {ann}} \, \delta _{n,k,s}$ coincide, so that ![]() ${\mathbb {W}}_{n,k,s} = {\mathbb {U}}_{n,k,s}$, and that the substaircase monomials
${\mathbb {W}}_{n,k,s} = {\mathbb {U}}_{n,k,s}$, and that the substaircase monomials ![]() ${\mathcal {M}}_{n,k,s}$ descend to a basis of
${\mathcal {M}}_{n,k,s}$ descend to a basis of ![]() ${\mathbb {W}}_{n,k,s}$. Thanks to our lemmata, this is a quick argument.
${\mathbb {W}}_{n,k,s}$. Thanks to our lemmata, this is a quick argument.
Theorem 4.12. Let ![]() $n, k, s \geq 0$ be integers with
$n, k, s \geq 0$ be integers with ![]() $k \geq s$. The ideal
$k \geq s$. The ideal ![]() $I_{n,k,s}$ is the annihilator of the superspace Vandermonde
$I_{n,k,s}$ is the annihilator of the superspace Vandermonde ![]() $\delta _{n,k,s}$:
$\delta _{n,k,s}$:
Consequently, the quotient rings ![]() ${\mathbb {W}}_{n,k,s}$ and
${\mathbb {W}}_{n,k,s}$ and ![]() ${\mathbb {U}}_{n,k,s}$ coincide:
${\mathbb {U}}_{n,k,s}$ coincide:
Furthermore, the set ![]() ${\mathcal {M}}_{n,k,s}$ descends to a monomial basis of
${\mathcal {M}}_{n,k,s}$ descends to a monomial basis of ![]() ${\mathbb {W}}_{n,k,s}$.
${\mathbb {W}}_{n,k,s}$.
Proof. We bound the dimension of ![]() $I_{n,k,s}^{\perp }$ from above using Lemma 4.11 and an argument appearing in the work of Rhoades, Yu and Zhao [Reference Rhoades, Yu and Zhao28, Section 4.4] on harmonic spaces. Let
$I_{n,k,s}^{\perp }$ from above using Lemma 4.11 and an argument appearing in the work of Rhoades, Yu and Zhao [Reference Rhoades, Yu and Zhao28, Section 4.4] on harmonic spaces. Let ![]() $N = | {\mathcal {M}}_{n,k,s} |$ be the number of substaircase monomials. We claim that
$N = | {\mathcal {M}}_{n,k,s} |$ be the number of substaircase monomials. We claim that ![]() $\dim I_{n,k,s}^{\perp } \leq N$. Given
$\dim I_{n,k,s}^{\perp } \leq N$. Given ![]() $f_1, \dots f_N, f_{N+1} \in I_{n,k,s}^{\perp }$, we have
$f_1, \dots f_N, f_{N+1} \in I_{n,k,s}^{\perp }$, we have
for any scalars ![]() $c_1, \dots , c_N, c_{N+1} \in {\mathbb {Q}}$. We may select
$c_1, \dots , c_N, c_{N+1} \in {\mathbb {Q}}$. We may select ![]() $c_i$ not all zero so that the coefficient of m vanishes on the right-hand side of Equation (4.43) for all
$c_i$ not all zero so that the coefficient of m vanishes on the right-hand side of Equation (4.43) for all ![]() $m \in {\mathcal {M}}_{n,k,s}$. By Lemma 4.11, this forces
$m \in {\mathcal {M}}_{n,k,s}$. By Lemma 4.11, this forces ![]() $f = 0$, so that Equation (4.43) shows
$f = 0$, so that Equation (4.43) shows ![]() $\{ f_1, \dots , f_N, f_{N+1} \}$ is linearly dependent.
$\{ f_1, \dots , f_N, f_{N+1} \}$ is linearly dependent.
We have the chain of equalities
where we applied Lemma 4.7 to get that ![]() ${\mathbb {U}}_{n,k,s}$ projects onto
${\mathbb {U}}_{n,k,s}$ projects onto ![]() ${\mathbb {W}}_{n,k,s}$ and Lemma 4.5 to get
${\mathbb {W}}_{n,k,s}$ and Lemma 4.5 to get ![]() $\dim {\mathbb {W}}_{n,k,s} \geq N$. This proves that
$\dim {\mathbb {W}}_{n,k,s} \geq N$. This proves that ![]() ${\mathrm {ann}} \, \delta _{n,k,s} = I_{n,k,s}$ and
${\mathrm {ann}} \, \delta _{n,k,s} = I_{n,k,s}$ and ![]() ${\mathbb {W}}_{n,k,s} = {\mathbb {U}}_{n,k,s}$. Lemma 4.5 implies that
${\mathbb {W}}_{n,k,s} = {\mathbb {U}}_{n,k,s}$. Lemma 4.5 implies that ![]() ${\mathcal {M}}_{n,k,s}$ descends to a monomial basis of
${\mathcal {M}}_{n,k,s}$ descends to a monomial basis of ![]() ${\mathbb {W}}_{n,k,s}$.
${\mathbb {W}}_{n,k,s}$.
To illustrate Theorem 4.12, let ![]() $(n,k,s) = (3,2,2)$. The staircases in this case are
$(n,k,s) = (3,2,2)$. The staircases in this case are
so that
and Theorem 4.12 asserts that ![]() ${\mathcal {M}}_{3,2,2}$ descends to a basis of
${\mathcal {M}}_{3,2,2}$ descends to a basis of ![]() ${\mathbb {W}}_{3,2,2}$. In particular, the bigraded Hilbert series
${\mathbb {W}}_{3,2,2}$. In particular, the bigraded Hilbert series ![]() ${\mathrm {Hilb}}({\mathbb {W}}_{3,2,2}; q, z)$ is given by
${\mathrm {Hilb}}({\mathbb {W}}_{3,2,2}; q, z)$ is given by
We may display this Hilbert series as a matrix
 $$ \begin{align*} {\mathrm {Hilb}}({\mathbb{W}}_{3,2,2}; q, z) = \begin{pmatrix} 1 & 3 & 2 \\ 2 & 3 & 1 \end{pmatrix} \end{align*} $$
$$ \begin{align*} {\mathrm {Hilb}}({\mathbb{W}}_{3,2,2}; q, z) = \begin{pmatrix} 1 & 3 & 2 \\ 2 & 3 & 1 \end{pmatrix} \end{align*} $$by letting rows track ![]() $\theta $-degree and columns track x-degree. The
$\theta $-degree and columns track x-degree. The ![]() $180^{\circ }$ rotational symmetry of this matrix is guaranteed by the Rotational Duality of Theorem 1.2. The larger example
$180^{\circ }$ rotational symmetry of this matrix is guaranteed by the Rotational Duality of Theorem 1.2. The larger example
 $$ \begin{align*} {\mathrm {Hilb}}({\mathbb{W}}_{6,3,2}; q, z) = \begin{pmatrix} 1 & 6 & 21 & 50 & 90 & 125 & 134 & 105 & 55 & 15 \\ 6 & 35 & 119 & 273 & 463 & 575 & 511 & 301 & 105 & 20 \\ 15 & 84 & 274 & 580 & 853 & 853 & 580 & 274 & 84 & 15 \\ 20 & 105 & 301 & 511 & 575 & 463 & 273 & 119 & 35 & 6 \\ 15 & 55 & 105 & 134 & 125 & 90 & 50 & 21 & 6 & 1 \end{pmatrix} \end{align*} $$
$$ \begin{align*} {\mathrm {Hilb}}({\mathbb{W}}_{6,3,2}; q, z) = \begin{pmatrix} 1 & 6 & 21 & 50 & 90 & 125 & 134 & 105 & 55 & 15 \\ 6 & 35 & 119 & 273 & 463 & 575 & 511 & 301 & 105 & 20 \\ 15 & 84 & 274 & 580 & 853 & 853 & 580 & 274 & 84 & 15 \\ 20 & 105 & 301 & 511 & 575 & 463 & 273 & 119 & 35 & 6 \\ 15 & 55 & 105 & 134 & 125 & 90 & 50 & 21 & 6 & 1 \end{pmatrix} \end{align*} $$is easy to compute with the following recursion.
Corollary 4.13. Suppose ![]() $n, k, s \geq 0$ are integers with
$n, k, s \geq 0$ are integers with ![]() $k \geq s$. We have
$k \geq s$. We have
 $$ \begin{align*} {\mathrm {Hilb}}({\mathbb{W}}_{n,k,s};q,z) = \sum_{r = 0}^{n-s} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {coinv}}(\sigma)} = \sum_{r = 0}^{n-s} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {codinv}}(\sigma)}. \end{align*} $$
$$ \begin{align*} {\mathrm {Hilb}}({\mathbb{W}}_{n,k,s};q,z) = \sum_{r = 0}^{n-s} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {coinv}}(\sigma)} = \sum_{r = 0}^{n-s} z^r \cdot \sum_{\sigma \in {\mathcal{OSP}}_{n,k,s}^{(r)}} q^{{\mathrm {codinv}}(\sigma)}. \end{align*} $$This bigraded Hilbert series satisfies the recursion
Together with the initial conditions
and
 $$ \begin{align} {\mathrm {Hilb}}({\mathbb{W}}_{1,k,s}; q, z) = \begin{cases} (1 + z) \cdot [k]_q & s = 0 \\ 1 & s = 1, \end{cases} \end{align} $$
$$ \begin{align} {\mathrm {Hilb}}({\mathbb{W}}_{1,k,s}; q, z) = \begin{cases} (1 + z) \cdot [k]_q & s = 0 \\ 1 & s = 1, \end{cases} \end{align} $$Corollary 4.13 determines ![]() ${\mathrm {Hilb}}({\mathbb {W}}_{n,k,s};q,z)$ completely. It is predicted [Reference Rhoades and Wilson27, Conjecture 6.5] that the matrices
${\mathrm {Hilb}}({\mathbb {W}}_{n,k,s};q,z)$ completely. It is predicted [Reference Rhoades and Wilson27, Conjecture 6.5] that the matrices ![]() ${\mathrm {Hilb}}({\mathbb {W}}_{n,k,s};q,z)$ have unimodal rows and columns. In the case
${\mathrm {Hilb}}({\mathbb {W}}_{n,k,s};q,z)$ have unimodal rows and columns. In the case ![]() $(n,k,s) = (n,n,n)$, the ring
$(n,k,s) = (n,n,n)$, the ring ![]() ${\mathbb {W}}_{n,n,n}$ is the cohomology
${\mathbb {W}}_{n,n,n}$ is the cohomology ![]() $H^{\bullet }(\mathcal {F \ell }_n; {\mathbb {Q}})$ of the flag variety
$H^{\bullet }(\mathcal {F \ell }_n; {\mathbb {Q}})$ of the flag variety ![]() $\mathcal {F \ell }_n$ and is a consequence of the Hard Lefschetz property for this smooth and compact complex manifold. Corollary 4.13 has been used to verify this conjecture for all triples
$\mathcal {F \ell }_n$ and is a consequence of the Hard Lefschetz property for this smooth and compact complex manifold. Corollary 4.13 has been used to verify this conjecture for all triples ![]() $n \geq k \geq s$ with
$n \geq k \geq s$ with ![]() $n \leq 9$.
$n \leq 9$.
Since the composition of maps ![]() ${\mathbb {H}}_{n,k,s} \hookrightarrow \Omega _n \twoheadrightarrow {\mathbb {W}}_{n,k,s}$ is an isomorphism, any basis of the harmonic space
${\mathbb {H}}_{n,k,s} \hookrightarrow \Omega _n \twoheadrightarrow {\mathbb {W}}_{n,k,s}$ is an isomorphism, any basis of the harmonic space ![]() ${\mathbb {H}}_{n,k,s}$ descends to a basis of
${\mathbb {H}}_{n,k,s}$ descends to a basis of ![]() ${\mathbb {W}}_{n,k,s}$. A basis of
${\mathbb {W}}_{n,k,s}$. A basis of ![]() ${\mathbb {W}}_{n,k,s}$ obtained in this way is a harmonic basis. Harmonic bases of quotients of the polynomial ring
${\mathbb {W}}_{n,k,s}$ obtained in this way is a harmonic basis. Harmonic bases of quotients of the polynomial ring ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$ have received significant attention [Reference Bergeron and Garsia3, Reference Rhoades, Yu and Zhao30] and are useful because working with them does not involve computationally expensive operations with cosets. The space
${\mathbb {Q}}[x_1, \dots , x_n]$ have received significant attention [Reference Bergeron and Garsia3, Reference Rhoades, Yu and Zhao30] and are useful because working with them does not involve computationally expensive operations with cosets. The space ![]() ${\mathbb {W}}_{n,k,s}$ admits the following harmonic basis.
${\mathbb {W}}_{n,k,s}$ admits the following harmonic basis.
Corollary 4.14. Let ![]() $n, k, s \geq 0$ be integers with
$n, k, s \geq 0$ be integers with ![]() $k \geq s$. We have the following equality of subspaces of
$k \geq s$. We have the following equality of subspaces of ![]() $\Omega _n$.
$\Omega _n$.
Furthermore, the set
is a basis of ![]() ${\mathbb {H}}_{n,k,s}$, and, therefore, descends to a harmonic basis of
${\mathbb {H}}_{n,k,s}$, and, therefore, descends to a harmonic basis of ![]() ${\mathbb {W}}_{n,k,s}$.
${\mathbb {W}}_{n,k,s}$.
Proof. The equality ![]() ${\mathbb {H}}_{n,k,s} = I_{n,k,s}^{\perp }$ is immediate from Theorem 4.12. For any
${\mathbb {H}}_{n,k,s} = I_{n,k,s}^{\perp }$ is immediate from Theorem 4.12. For any ![]() $c_1, \dots , c_N \in {\mathbb {Q}}$ and any monomials
$c_1, \dots , c_N \in {\mathbb {Q}}$ and any monomials ![]() $m_1, \dots , m_N$, we have
$m_1, \dots , m_N$, we have
so that a linear dependence in the subset ![]() $\{ m_1 \odot \delta _{n,k,s}, \dots , m_N \odot \delta _{n,k,s} \}$ of
$\{ m_1 \odot \delta _{n,k,s}, \dots , m_N \odot \delta _{n,k,s} \}$ of ![]() $\Omega _n$ induces a linear dependence in
$\Omega _n$ induces a linear dependence in ![]() $\{ m_1, \dots , m_N \}$ modulo
$\{ m_1, \dots , m_N \}$ modulo ![]() ${\mathrm {ann}} \, \delta _{n,k,s}$. Theorem 4.12 implies
${\mathrm {ann}} \, \delta _{n,k,s}$. Theorem 4.12 implies ![]() $\{ m \odot \delta _{n,k,s} \,:\, m \in {\mathcal {M}}_{n,k,s} \}$ is linearly independent and a dimension count finishes the proof.
$\{ m \odot \delta _{n,k,s} \,:\, m \in {\mathcal {M}}_{n,k,s} \}$ is linearly independent and a dimension count finishes the proof.
The harmonic basis of Corollary 4.14 will be used to calculate the bigraded Frobenius image of ![]() ${\mathbb {W}}_{n,k,s}$.
${\mathbb {W}}_{n,k,s}$.
5 Frobenius image
5.1 A tensor product decomposition of  $\Omega _n$
$\Omega _n$
The goal of this section is to prove that the graded Frobenius image ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$ has the combinatorial expansion
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$ has the combinatorial expansion ![]() $C_{n,k,s}({\mathbf {x}};q,z)$. Since
$C_{n,k,s}({\mathbf {x}};q,z)$. Since ![]() ${\mathbb {W}}_{n,k,s} \cong {\mathbb {H}}_{n,k,s}$ as bigraded
${\mathbb {W}}_{n,k,s} \cong {\mathbb {H}}_{n,k,s}$ as bigraded ![]() ${\mathfrak {S}}_n$-modules, we will often use the harmonic space
${\mathfrak {S}}_n$-modules, we will often use the harmonic space ![]() ${\mathbb {H}}_{n,k,s}$ to avoid working with cosets. The combinatorial recursion of Lemma 3.14 necessitates restricting these spaces to a given
${\mathbb {H}}_{n,k,s}$ to avoid working with cosets. The combinatorial recursion of Lemma 3.14 necessitates restricting these spaces to a given ![]() $\theta $-degree.
$\theta $-degree.
Definition 5.1. Given ![]() $r \geq 0$, let
$r \geq 0$, let ![]() ${\mathbb {W}}_{n,k,s}^{(r)} \subseteq {\mathbb {W}}_{n,k,s}$ and
${\mathbb {W}}_{n,k,s}^{(r)} \subseteq {\mathbb {W}}_{n,k,s}$ and ![]() ${\mathbb {H}}_{n,k,s}^{(r)} \subseteq {\mathbb {H}}_{n,k,s}$ be the subspaces of homogeneous
${\mathbb {H}}_{n,k,s}^{(r)} \subseteq {\mathbb {H}}_{n,k,s}$ be the subspaces of homogeneous ![]() $\theta $-degree r.
$\theta $-degree r.
![]() ${\mathbb {W}}_{n,k,s}^{(r)}$ and
${\mathbb {W}}_{n,k,s}^{(r)}$ and ![]() ${\mathbb {H}}_{n,k,s}^{(r)}$ are isomorphic singly graded
${\mathbb {H}}_{n,k,s}^{(r)}$ are isomorphic singly graded ![]() ${\mathfrak {S}}_n$-modules under x-degree. Our goal is to show
${\mathfrak {S}}_n$-modules under x-degree. Our goal is to show
Lemma 2.3 allows us to prove Equation (5.1) by showing both sides satisfy the same recursion under an appropriate family of skewing operators. The combinatorial side ![]() $C_{n,k,s}^{(r)}$ was handled by Lemma 3.14; we must now consider the representation theoretic side. In order to avoid repeating hypotheses, we fix the following:
$C_{n,k,s}^{(r)}$ was handled by Lemma 3.14; we must now consider the representation theoretic side. In order to avoid repeating hypotheses, we fix the following:
Notation. For the remainder of this section, we fix integers ![]() $n \geq s \geq 0$,
$n \geq s \geq 0$, ![]() $k \geq s$,
$k \geq s$, ![]() $n-s \geq r \geq 0$ and
$n-s \geq r \geq 0$ and ![]() $1 \leq j \leq n$.
$1 \leq j \leq n$.
The group algebra ![]() ${\mathbb {Q}}[{\mathfrak {S}}_j]$ and its antisymmetrising and symmetrising elements
${\mathbb {Q}}[{\mathfrak {S}}_j]$ and its antisymmetrising and symmetrising elements ![]() $\varepsilon _j$ and
$\varepsilon _j$ and ![]() $\eta _j$ act on the first j indices of
$\eta _j$ act on the first j indices of ![]() $\Omega _n$. Given the relationship
$\Omega _n$. Given the relationship
and Lemma 3.14, we would like a recursive understanding of the ![]() ${\mathfrak {S}}_{n-j}$-modules
${\mathfrak {S}}_{n-j}$-modules ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. This will be accomplished by finding a strategic basis
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. This will be accomplished by finding a strategic basis ![]() ${\mathcal {C}}$ of
${\mathcal {C}}$ of ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ (see Definition 5.11 below).
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ (see Definition 5.11 below).
We will need to distinguish between the first j and last ![]() $n-j$ indices appearing in
$n-j$ indices appearing in ![]() $\Omega _n$. To this end, we make the tensor product identification
$\Omega _n$. To this end, we make the tensor product identification
We make use of the following simple properties of this decomposition.
Proposition 5.2. Consider the tensor product decomposition ![]() $\Omega _n = \Omega _j \otimes \Omega _{n-j}$.
$\Omega _n = \Omega _j \otimes \Omega _{n-j}$.
1. If
 $f, f' \in \Omega _j$ and
$f, f' \in \Omega _j$ and  $g, g' \in \Omega _{n-j}$ have homogeneous
$g, g' \in \Omega _{n-j}$ have homogeneous  $\theta $-degree, then
$\theta $-degree, then  $$ \begin{align*} (f \otimes g) \odot (f' \otimes g') = \pm (f \odot f') \otimes (g \odot g') ,\end{align*} $$
$$ \begin{align*} (f \otimes g) \odot (f' \otimes g') = \pm (f \odot f') \otimes (g \odot g') ,\end{align*} $$where the sign is
 $(-1)^{\theta \text {-degree of } g + \theta \text {-degree of } f'}$.
$(-1)^{\theta \text {-degree of } g + \theta \text {-degree of } f'}$.2. If
 $u \in {\mathfrak {S}}_j, v \in {\mathfrak {S}}_{n-j}, f \in \Omega _j$ and
$u \in {\mathfrak {S}}_j, v \in {\mathfrak {S}}_{n-j}, f \in \Omega _j$ and  $g \in \Omega _{n-j}$, then the action of
$g \in \Omega _{n-j}$, then the action of  $u \times v \in {\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j} \subseteq {\mathfrak {S}}_n$ on
$u \times v \in {\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j} \subseteq {\mathfrak {S}}_n$ on  $f \otimes g$ is given by
$f \otimes g$ is given by  $$ \begin{align*} (u \times v) \cdot (f \otimes g) = (u \cdot f) \otimes (v \cdot g). \end{align*} $$
$$ \begin{align*} (u \times v) \cdot (f \otimes g) = (u \cdot f) \otimes (v \cdot g). \end{align*} $$3. If
 $f \in \varepsilon _j \Omega _j$ and
$f \in \varepsilon _j \Omega _j$ and  $g \in \Omega _{n-j}$, then
$g \in \Omega _{n-j}$, then  $$ \begin{align*} (f \otimes g) \odot \delta_{n,k,s} \in \eta_j {\mathbb{H}}_{n,k,s}. \end{align*} $$
$$ \begin{align*} (f \otimes g) \odot \delta_{n,k,s} \in \eta_j {\mathbb{H}}_{n,k,s}. \end{align*} $$
Proof. Items (1) and (2) are straightforward and left to the reader. For Item (3), let ![]() $u \in {\mathfrak {S}}_j$. We calculate
$u \in {\mathfrak {S}}_j$. We calculate
The first equality uses (2), the second equality uses ![]() $f \in \varepsilon _j \Omega _j$ and
$f \in \varepsilon _j \Omega _j$ and ![]() $\delta _{n,k,s} \in \varepsilon _j \Omega _n$ and the third equality is bilinearity.
$\delta _{n,k,s} \in \varepsilon _j \Omega _n$ and the third equality is bilinearity.
Proposition 5.2 (3) gives rise to a ‘duality’ between the images of the ![]() ${\mathbb {W}}$-modules under
${\mathbb {W}}$-modules under ![]() $\varepsilon _j$ and the images of the
$\varepsilon _j$ and the images of the ![]() ${\mathbb {H}}$-modules under
${\mathbb {H}}$-modules under ![]() $\eta _j$. We state this duality as follows.
$\eta _j$. We state this duality as follows.
Proposition 5.3. Let ![]() ${\mathcal {A}} \subseteq \varepsilon _j \Omega _n$ be a subset of homogeneous
${\mathcal {A}} \subseteq \varepsilon _j \Omega _n$ be a subset of homogeneous ![]() $\theta $-degree r. Define a subset
$\theta $-degree r. Define a subset ![]() ${\mathcal {A}}^{\vee } \subseteq {\mathbb {H}}_{n,k,s}^{(n-s-r)}$ by
${\mathcal {A}}^{\vee } \subseteq {\mathbb {H}}_{n,k,s}^{(n-s-r)}$ by
1.
 ${\mathcal {A}}$ descends to a linearly independent subset of
${\mathcal {A}}$ descends to a linearly independent subset of  $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ if and only if
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ if and only if  ${\mathcal {A}}^{\vee }$ is linearly independent in
${\mathcal {A}}^{\vee }$ is linearly independent in  $\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$.
$\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$.2.
 ${\mathcal {A}}$ descends to a spanning subset of
${\mathcal {A}}$ descends to a spanning subset of  $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ if and only if
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ if and only if  ${\mathcal {A}}^{\vee }$ spans
${\mathcal {A}}^{\vee }$ spans  $\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$.
$\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$.3.
 ${\mathcal {A}}$ descends to a basis of
${\mathcal {A}}$ descends to a basis of  $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ if and only if
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ if and only if  ${\mathcal {A}}^{\vee }$ is a basis of
${\mathcal {A}}^{\vee }$ is a basis of  $\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$.
$\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$.
Proof. Proposition 5.2 (3) shows that ![]() ${\mathcal {A}}^{\vee }$ is indeed a subset of
${\mathcal {A}}^{\vee }$ is indeed a subset of ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$. The isomorphism
$\eta _j {\mathbb {H}}_{n,k,s}^{(n-s-r)}$. The isomorphism ![]() ${\mathbb {W}}_{n,k,s} = \Omega _n/ {\mathrm {ann}} \, \delta _{n,k,s} \xrightarrow {\, \, \sim \, \, } {\mathbb {H}}_{n,k,s}$ given by
${\mathbb {W}}_{n,k,s} = \Omega _n/ {\mathrm {ann}} \, \delta _{n,k,s} \xrightarrow {\, \, \sim \, \, } {\mathbb {H}}_{n,k,s}$ given by ![]() $f \mapsto f \odot \delta _{n,k,s}$ implies Items (1) through (3).
$f \mapsto f \odot \delta _{n,k,s}$ implies Items (1) through (3).
5.2 A spanning subset of  $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$
Proposition 5.3 allows us to move back and forth between the alternating subspace ![]() $\varepsilon _j {\mathbb {W}}_{n,k,s}$ and the invariant subspace
$\varepsilon _j {\mathbb {W}}_{n,k,s}$ and the invariant subspace ![]() $\eta _j {\mathbb {H}}_{n,k,s}$. The following subset
$\eta _j {\mathbb {H}}_{n,k,s}$. The following subset ![]() ${\mathcal {B}} \subseteq \varepsilon _j \Omega _n$ will turn out to descend to a basis of
${\mathcal {B}} \subseteq \varepsilon _j \Omega _n$ will turn out to descend to a basis of ![]() $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$.
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$.
Definition 5.4. Define a subset ![]() ${\mathcal {B}} \subseteq \Omega _n$ by
${\mathcal {B}} \subseteq \Omega _n$ by
 $$ \begin{align} {\mathcal{B}} = \bigsqcup_{\substack{a,b \geq 0 \\ a \leq r, \, \, b \leq s}} \bigsqcup_{{\mathbf {i}}} \left\{ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(r-a)} \right\}, \\[-9pt]\nonumber\end{align} $$
$$ \begin{align} {\mathcal{B}} = \bigsqcup_{\substack{a,b \geq 0 \\ a \leq r, \, \, b \leq s}} \bigsqcup_{{\mathbf {i}}} \left\{ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(r-a)} \right\}, \\[-9pt]\nonumber\end{align} $$where the index ![]() ${\mathbf {i}} = (i_1, \dots , i_j)$ of the inner disjoint union ranges over all length j integer sequences whose first a, next b and final
${\mathbf {i}} = (i_1, \dots , i_j)$ of the inner disjoint union ranges over all length j integer sequences whose first a, next b and final ![]() $j-a-b$ entries satisfy the conditions
$j-a-b$ entries satisfy the conditions
The subset ![]() ${\mathcal {B}} \subseteq \Omega _n$ depends on
${\mathcal {B}} \subseteq \Omega _n$ depends on ![]() $n,k,s,r$ and j, but we suppress this dependence to reduce notational clutter. We note that, since every
$n,k,s,r$ and j, but we suppress this dependence to reduce notational clutter. We note that, since every ![]() ${\mathfrak {S}}_j$-orbit consists of a unique representative
${\mathfrak {S}}_j$-orbit consists of a unique representative ![]() ${\mathbf {i}}$ that meets these conditions and the indices a and b are determined by this representative, the unions in the definition are indeed disjoint. Thanks to our tensor product notation, the monomials m appearing in Definition 5.4 are automatically elements of
${\mathbf {i}}$ that meets these conditions and the indices a and b are determined by this representative, the unions in the definition are indeed disjoint. Thanks to our tensor product notation, the monomials m appearing in Definition 5.4 are automatically elements of ![]() $\Omega _{n-j} = {\mathbb {Q}}[x_{j+1}, \dots , x_n] \otimes \wedge \{ \theta _{j+1}, \dots , \theta _n \}$. The conditions on
$\Omega _{n-j} = {\mathbb {Q}}[x_{j+1}, \dots , x_n] \otimes \wedge \{ \theta _{j+1}, \dots , \theta _n \}$. The conditions on ![]() $a, b$ and the sequences
$a, b$ and the sequences ![]() ${\mathbf {i}} = (i_1, \dots , i_j)$ appearing in Definition 5.4 may look complicated, but they combinatorially correspond to the sum and q-binomial coefficients in the skewing recursion of Lemma 3.14 satisfied by the C-functions. Algebraically, they are obtained by applying
${\mathbf {i}} = (i_1, \dots , i_j)$ appearing in Definition 5.4 may look complicated, but they combinatorially correspond to the sum and q-binomial coefficients in the skewing recursion of Lemma 3.14 satisfied by the C-functions. Algebraically, they are obtained by applying ![]() $\varepsilon _j$ to every monomial in
$\varepsilon _j$ to every monomial in ![]() ${\mathcal {M}}_{n,k,s}^{(r)}$ and removing ‘obvious’ linear dependencies.
${\mathcal {M}}_{n,k,s}^{(r)}$ and removing ‘obvious’ linear dependencies.
Lemma 5.5. The subset ![]() ${\mathcal {B}}$ of
${\mathcal {B}}$ of ![]() $\Omega _n$ descends to a spanning set of
$\Omega _n$ descends to a spanning set of ![]() $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$.
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$.
Proof. By Theorem 4.12, we know that ![]() ${\mathcal {M}}_{n,k,s}^{(r)}$ descends to a basis for
${\mathcal {M}}_{n,k,s}^{(r)}$ descends to a basis for ![]() ${\mathbb {W}}_{n,k,s}^{(r)}$. This implies that
${\mathbb {W}}_{n,k,s}^{(r)}$. This implies that
descends to a spanning set of ![]() $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$. We proceed to remove linear dependencies from the set
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$. We proceed to remove linear dependencies from the set ![]() $\varepsilon _j {\mathcal {M}}_{n,k,s}^{(r)}$.
$\varepsilon _j {\mathcal {M}}_{n,k,s}^{(r)}$.
Let ![]() $m_0 \in {\mathcal {M}}_{n,k,s}^{(r)}$. There exists a permutation
$m_0 \in {\mathcal {M}}_{n,k,s}^{(r)}$. There exists a permutation ![]() $w \in {\mathfrak {S}}_j$, such that
$w \in {\mathfrak {S}}_j$, such that ![]() $w \cdot m_0 = x_1^{i_1} \cdots x_j^{i_j} \theta _1 \cdots \theta _a \otimes m$, where
$w \cdot m_0 = x_1^{i_1} \cdots x_j^{i_j} \theta _1 \cdots \theta _a \otimes m$, where ![]() $0 \leq i_1 \leq \cdots \leq i_a \leq k-1$,
$0 \leq i_1 \leq \cdots \leq i_a \leq k-1$, ![]() $0 \leq i_{a+1} \leq \cdots \leq i_j \leq k-1$. We have
$0 \leq i_{a+1} \leq \cdots \leq i_j \leq k-1$. We have
Furthermore, the action of ![]() $\varepsilon _j$ annihilates
$\varepsilon _j$ annihilates ![]() $w \cdot m_0$ unless
$w \cdot m_0$ unless ![]() $i_{a+1} < \cdots < i_j$. It follows that
$i_{a+1} < \cdots < i_j$. It follows that ![]() $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ is spanned by
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$ is spanned by
 $$ \begin{align} \bigsqcup_{\substack{a,b \geq 0 \\ a \leq r, \, \, b \leq s}} \left\{ \varepsilon_j \cdot(x_1^{i_j} \cdots x_j^{i_1} \cdot \theta_{j-a+1} \cdots \theta_j) \otimes m \,:\, \begin{array}{c} (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \in {\mathcal{M}}_{n,k,s}^{(r)}, \\ 0 \leq i_1 \leq \cdots \leq i_a \leq k-1, \\ 0 \leq i_{a+1} < \cdots < i_{a+b} \leq s-1, \\ s \leq i_{a+b+1} < \cdots < i_j \leq k-1, \end{array} \right\} , \end{align} $$
$$ \begin{align} \bigsqcup_{\substack{a,b \geq 0 \\ a \leq r, \, \, b \leq s}} \left\{ \varepsilon_j \cdot(x_1^{i_j} \cdots x_j^{i_1} \cdot \theta_{j-a+1} \cdots \theta_j) \otimes m \,:\, \begin{array}{c} (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \in {\mathcal{M}}_{n,k,s}^{(r)}, \\ 0 \leq i_1 \leq \cdots \leq i_a \leq k-1, \\ 0 \leq i_{a+1} < \cdots < i_{a+b} \leq s-1, \\ s \leq i_{a+b+1} < \cdots < i_j \leq k-1, \end{array} \right\} , \end{align} $$where the parameter b tracks the index at which the sequence ![]() $0 \leq i_{a+1} < \cdots < i_j \leq k-1$ exceeds the value s. The ‘variable reversal’
$0 \leq i_{a+1} < \cdots < i_j \leq k-1$ exceeds the value s. The ‘variable reversal’
in (5.11) relative to the definition of ![]() ${\mathcal {B}}$ only introduces a sign upon application of
${\mathcal {B}}$ only introduces a sign upon application of ![]() $\varepsilon _j$.
$\varepsilon _j$.
For which monomials ![]() $m \in \Omega _{n-j}$ and sequences
$m \in \Omega _{n-j}$ and sequences ![]() $(i_1, \dots , i_j)$ do we have the containment
$(i_1, \dots , i_j)$ do we have the containment
The lemma is reduced to the following claim.
Claim. Given sequences ![]() $0 \leq i_1 \leq \cdots \leq i_a \leq k-1, 0 \leq i_{a+1} < \cdots < i_{a+b} \leq s-1$ and
$0 \leq i_1 \leq \cdots \leq i_a \leq k-1, 0 \leq i_{a+1} < \cdots < i_{a+b} \leq s-1$ and ![]() $s \leq i_{a+b+1} < \cdots < i_j \leq k-1$ and a monomial
$s \leq i_{a+b+1} < \cdots < i_j \leq k-1$ and a monomial ![]() $m \in \Omega _{n-j}$, we have
$m \in \Omega _{n-j}$, we have
The reason for this ‘reversal’ in (5.11) is to make the monomials in the claim divisible by staircase monomials. The claim follows from Lemma 3.12 and induction; we leave details to the reader.
5.3  ${\mathcal {B}}$ is linearly independent
${\mathcal {B}}$ is linearly independent
The goal of this technical subsection is to show that the set ![]() ${\mathcal {B}}$ in Definition 5.4 is linearly independent in
${\mathcal {B}}$ in Definition 5.4 is linearly independent in ![]() $\Omega _n$. By virtue of Lemma 5.5, this implies that
$\Omega _n$. By virtue of Lemma 5.5, this implies that ![]() ${\mathcal {B}}$ descends to a basis of
${\mathcal {B}}$ descends to a basis of ![]() $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$. To do this, we prove that
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$. To do this, we prove that
is linearly independent and apply Proposition 5.3.
We will show that ![]() ${\mathcal {B}}^{\vee }$ is linearly independent by considering a strategic basis of the space
${\mathcal {B}}^{\vee }$ is linearly independent by considering a strategic basis of the space ![]() $\eta _j \Omega _n$ and showing that the expansions of the
$\eta _j \Omega _n$ and showing that the expansions of the ![]() $f \odot \delta _{n,k,s}$ in this basis satisfy a triangularity condition. Both our basis and the triangularity condition will be defined in terms of the superlex order
$f \odot \delta _{n,k,s}$ in this basis satisfy a triangularity condition. Both our basis and the triangularity condition will be defined in terms of the superlex order ![]() $\prec $.
$\prec $.
Definition 5.6. A monomial ![]() $m \in \Omega _n$ with exponent sequence
$m \in \Omega _n$ with exponent sequence ![]() $u = (u_1, \dots , u_n)$ is j-increasing if
$u = (u_1, \dots , u_n)$ is j-increasing if ![]() $u_1 \leq \cdots \leq u_j$ under the order
$u_1 \leq \cdots \leq u_j$ under the order
on letters defining superlex order ![]() $\prec $.
$\prec $.
Each orbit of the ![]() ${\mathfrak {S}}_j$-action on the first j letters of exponent sequences
${\mathfrak {S}}_j$-action on the first j letters of exponent sequences ![]() $(u_1, \dots , u_n)$ of monomials in
$(u_1, \dots , u_n)$ of monomials in ![]() $\Omega _n$ has a unique j-increasing representative. In terms of the operator
$\Omega _n$ has a unique j-increasing representative. In terms of the operator ![]() $\eta _j$, we have the following.
$\eta _j$, we have the following.
Observation 5.7. The nonzero elements in ![]() $\{\eta _j \cdot m : m \text { is } j\text {-increasing}\}$ form a basis for
$\{\eta _j \cdot m : m \text { is } j\text {-increasing}\}$ form a basis for ![]() $\eta _j \Omega _n$.
$\eta _j \Omega _n$.
The word ‘nonzero’ is necessary in Observation 5.7. Indeed, when ![]() $n = 3$ and
$n = 3$ and ![]() $j = 2$, the word
$j = 2$, the word ![]() $(\bar {0}, \bar {0}, 0)$ is j-increasing and
$(\bar {0}, \bar {0}, 0)$ is j-increasing and ![]() $\eta _2 \cdot \theta _1 \theta _2 = 0$.
$\eta _2 \cdot \theta _1 \theta _2 = 0$.
For any ![]() $f \in {\mathcal {B}}$, the element
$f \in {\mathcal {B}}$, the element ![]() $f \odot \delta _{n,k,s} \in \eta _j \Omega _n$ may be uniquely expanded in the basis of Observation 5.7. The next definition extracts a useful ‘leading term’ of this expansion. This is a variant of the superlex order which incorporates the parameter j.
$f \odot \delta _{n,k,s} \in \eta _j \Omega _n$ may be uniquely expanded in the basis of Observation 5.7. The next definition extracts a useful ‘leading term’ of this expansion. This is a variant of the superlex order which incorporates the parameter j.
Definition 5.8. Given any nonzero ![]() $g \in \eta _j \Omega _n$, let
$g \in \eta _j \Omega _n$, let ![]() ${\mathrm {in}}_j(g)$ be the j-increasing monomial m, such that
${\mathrm {in}}_j(g)$ be the j-increasing monomial m, such that
•
 $\eta _j \cdot m$ appears in the expansion of g in the basis of Observation 5.7 with nonzero coefficient, and
$\eta _j \cdot m$ appears in the expansion of g in the basis of Observation 5.7 with nonzero coefficient, and• for any j-increasing monomial
 $m'$, such that
$m'$, such that  $\eta _j \cdot m'$ appears in this expansion with nonzero coefficient, we have
$\eta _j \cdot m'$ appears in this expansion with nonzero coefficient, we have  $m \succeq m'$.
$m \succeq m'$.
As an example of these notions, for ![]() $n=5$,
$n=5$, ![]() $k=4$,
$k=4$, ![]() $s=2$ and
$s=2$ and ![]() $j=3$, we consider the superpolynomial
$j=3$, we consider the superpolynomial ![]() $f \in {\mathcal {B}}$ given by
$f \in {\mathcal {B}}$ given by
Then
 $$ \begin{align} f \odot \delta_{5,4,2} = &-18\eta_3 \cdot (x^{00323} \theta_{45}) + 54 \eta_3 \cdot (x^{21320} \theta_{14}) + 18 \eta_3 \cdot (x^{20303} \theta_{15}) \\ \nonumber&- 54 \eta_3 \cdot (x^{20321} \theta_{14}) + 18 \eta_3 \cdot ( x^{30320} \theta_{14}) - 18 \eta_3 \cdot (x^{32300} \theta_{12}).\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} f \odot \delta_{5,4,2} = &-18\eta_3 \cdot (x^{00323} \theta_{45}) + 54 \eta_3 \cdot (x^{21320} \theta_{14}) + 18 \eta_3 \cdot (x^{20303} \theta_{15}) \\ \nonumber&- 54 \eta_3 \cdot (x^{20321} \theta_{14}) + 18 \eta_3 \cdot ( x^{30320} \theta_{14}) - 18 \eta_3 \cdot (x^{32300} \theta_{12}).\\[-9pt]\nonumber \end{align} $$We have written the terms in the final expression so that each monomial that appears is j-increasing and these monomials decrease in superlex order from left to right. Therefore
The most important property of ![]() ${\mathrm {in}}_j$ is as follows.
${\mathrm {in}}_j$ is as follows.
Lemma 5.9. The map
is injective.
Proof. We give a method for finding ![]() ${\mathrm {in}}_j(f \odot \delta _{n,k,s})$ for any
${\mathrm {in}}_j(f \odot \delta _{n,k,s})$ for any ![]() $f \in {\mathcal {B}}$. Suppose that
$f \in {\mathcal {B}}$. Suppose that
so ![]() $m \in {\mathcal {M}}_{n-j,k,s-b}^{(r-a)}$ and
$m \in {\mathcal {M}}_{n-j,k,s-b}^{(r-a)}$ and
We define a reordering ![]() $(h_1, \dots , h_j)$ of the sequence
$(h_1, \dots , h_j)$ of the sequence ![]() $(i_1, \dots , i_j)$ by
$(i_1, \dots , i_j)$ by
The sequence ![]() $(h_1, \dots , h_j)$ satisfies
$(h_1, \dots , h_j)$ satisfies
 $$ \begin{align*}s &\leq h_1 < \cdots < h_{j-a-b} \leq k-1, \ s-1 \geq h_{j-a-b+1}> \cdots > h_{j-a} \geq 0, \ k-s-1+b\\ &\geq h_{j-a+1} \geq \cdots \geq h_j \geq 0. \end{align*} $$
$$ \begin{align*}s &\leq h_1 < \cdots < h_{j-a-b} \leq k-1, \ s-1 \geq h_{j-a-b+1}> \cdots > h_{j-a} \geq 0, \ k-s-1+b\\ &\geq h_{j-a+1} \geq \cdots \geq h_j \geq 0. \end{align*} $$Furthermore, let ![]() $t = (t_1, \dots , t_n)$ be the exponent sequence of the entire monomial
$t = (t_1, \dots , t_n)$ be the exponent sequence of the entire monomial
We construct a monomial M with exponent sequence u as follows:
•
 $u_1 = \cdots = u_{j-a-b} = \overline {k-1}$,
$u_1 = \cdots = u_{j-a-b} = \overline {k-1}$,•
 $(u_{j-a-b+1}, \ldots , u_{j-a}) = (s-1, s-2, \ldots , s-b)$,
$(u_{j-a-b+1}, \ldots , u_{j-a}) = (s-1, s-2, \ldots , s-b)$,•
 $u_{j-a+1} = \cdots = u_j = \overline {k-1}$ and
$u_{j-a+1} = \cdots = u_j = \overline {k-1}$ and• For
 $p=j+1$ to n,
$p=j+1$ to n,  $u_p$ is
$u_p$ is  $\overline {k-1}$ if
$\overline {k-1}$ if  $t_p$ is barred or greater than the largest unused element of
$t_p$ is barred or greater than the largest unused element of  $\{0,1,\ldots ,s-b-1\}$. Otherwise, we let
$\{0,1,\ldots ,s-b-1\}$. Otherwise, we let  $u_p$ be the largest unused element of
$u_p$ be the largest unused element of  $\{0,1,2\ldots ,s-b-1\}$.
$\{0,1,2\ldots ,s-b-1\}$.
The last bullet point above is an instance of Algorithm 1 in the proof of Proposition 4.3. Since m is substaircase, this algorithm successfully produces a monomial M appearing in ![]() $\delta _{n,k,s}$.
$\delta _{n,k,s}$.
Claim. ![]() ${\mathrm {in}}_j(f \odot \delta _{n,k,s}) \doteq \left ( x_1^{h_1} \cdots x_j^{h_j} \theta _{1} \cdots \theta _a \otimes m \right ) \odot M.$
${\mathrm {in}}_j(f \odot \delta _{n,k,s}) \doteq \left ( x_1^{h_1} \cdots x_j^{h_j} \theta _{1} \cdots \theta _a \otimes m \right ) \odot M.$
We check this construction for the example ![]() $f =\varepsilon _3 ( x^{00110} \theta _1 ) \in {\mathcal {B}}$ given in (5.13), where
$f =\varepsilon _3 ( x^{00110} \theta _1 ) \in {\mathcal {B}}$ given in (5.13), where ![]() $n=5$,
$n=5$, ![]() $k=4$,
$k=4$, ![]() $s=2$ and
$s=2$ and ![]() $j=3$. Then
$j=3$. Then ![]() $a=1$,
$a=1$, ![]() $b=2$,
$b=2$, ![]() $t = (1,0,\bar {0},1,0)$,
$t = (1,0,\bar {0},1,0)$, ![]() $u = (1,0,\bar {3},\bar {3},\bar {3})$ and
$u = (1,0,\bar {3},\bar {3},\bar {3})$ and
which agrees with the computation of ![]() ${\mathrm {in}}_j(f \otimes \delta _{5,4,2})$ in (5.14).
${\mathrm {in}}_j(f \otimes \delta _{5,4,2})$ in (5.14).
Now we prove the claim. Let ![]() $v = (v_1, \dots , v_n)$ be the exponent sequence of the monomial
$v = (v_1, \dots , v_n)$ be the exponent sequence of the monomial ![]() $( x_1^{h_1} \cdots x_j^{h_j} \theta _{j-a+1} \cdots \theta _j \otimes m ) \odot M$ appearing in the claim. First, we check that v is indeed j-increasing. From the definitions of t and u, the first
$( x_1^{h_1} \cdots x_j^{h_j} \theta _{j-a+1} \cdots \theta _j \otimes m ) \odot M$ appearing in the claim. First, we check that v is indeed j-increasing. From the definitions of t and u, the first ![]() $j-a-b$ entries of v are all barred and
$j-a-b$ entries of v are all barred and
The next ![]() $a+b$ entries of v are all unbarred and satisfy
$a+b$ entries of v are all unbarred and satisfy
so v is j-increasing.
Let ![]() $v' = (v^{\prime }_1, \dots , v^{\prime }_n)$ be the
$v' = (v^{\prime }_1, \dots , v^{\prime }_n)$ be the ![]() $\prec $-maximal j-increasing exponent sequence whose monomial appears in
$\prec $-maximal j-increasing exponent sequence whose monomial appears in ![]() $f \odot \delta _{n,k,s}$. There are monomials appearing in f and
$f \odot \delta _{n,k,s}$. There are monomials appearing in f and ![]() $\delta _{n,k,s}$ that yield
$\delta _{n,k,s}$ that yield ![]() $v'$ under the left
$v'$ under the left ![]() $\odot $ action of f on
$\odot $ action of f on ![]() $\delta _{n,k,s}$. Denote the exponent sequences of these monomials by
$\delta _{n,k,s}$. Denote the exponent sequences of these monomials by ![]() $t' = (t^{\prime }_1, \dots , t^{\prime }_n)$ and
$t' = (t^{\prime }_1, \dots , t^{\prime }_n)$ and ![]() $u' = (u^{\prime }_1, \dots , u^{\prime }_n)$, respectively. Then
$u' = (u^{\prime }_1, \dots , u^{\prime }_n)$, respectively. Then ![]() $t'$ is obtained from t by some rearrangement of its first j entries. We show that
$t'$ is obtained from t by some rearrangement of its first j entries. We show that ![]() $v = v'$ as follows.
$v = v'$ as follows.
The sequence ![]() $(t^{\prime }_1, \dots , t^{\prime }_j)$ has
$(t^{\prime }_1, \dots , t^{\prime }_j)$ has ![]() $j-a-b$ unbarred entries
$j-a-b$ unbarred entries ![]() $> s$. Thus, the sequence
$> s$. Thus, the sequence ![]() $(v^{\prime }_1, \dots , v^{\prime }_j)$ must have at least
$(v^{\prime }_1, \dots , v^{\prime }_j)$ must have at least ![]() $j-a-b$ barred entries. Since
$j-a-b$ barred entries. Since ![]() $v'$ is j-increasing, the first
$v'$ is j-increasing, the first ![]() $j-a-b$ entries of
$j-a-b$ entries of ![]() $v'$ must be barred, which forces
$v'$ must be barred, which forces
Since ![]() $v \preceq v'$, and
$v \preceq v'$, and ![]() $v'$ is j-increasing, the barred entries
$v'$ is j-increasing, the barred entries ![]() $v^{\prime }_1, \dots , v^{\prime }_{j-a-b}$ are all
$v^{\prime }_1, \dots , v^{\prime }_{j-a-b}$ are all ![]() $< k-s$. We see that the first
$< k-s$. We see that the first ![]() $j-a-b$ entries of
$j-a-b$ entries of ![]() $t'$ are unbarred and
$t'$ are unbarred and ![]() $> s$. Since the first j entries of
$> s$. Since the first j entries of ![]() $t'$ are a rearrangement of the first j entries of t, this forces the first j entries of
$t'$ are a rearrangement of the first j entries of t, this forces the first j entries of ![]() $t'$ to be
$t'$ to be ![]() $t_1, \dots , t_{j-a-b}$ (in some order). Since
$t_1, \dots , t_{j-a-b}$ (in some order). Since ![]() $v'$ is j-increasing, we have
$v'$ is j-increasing, we have
The above paragraph forces ![]() $(t^{\prime }_{j-a-b+1}, \dots , t^{\prime }_j)$ to be a rearrangement of
$(t^{\prime }_{j-a-b+1}, \dots , t^{\prime }_j)$ to be a rearrangement of ![]() $(t_{j-a-b+1}, \dots , t_j)$. Both of these sequences contain
$(t_{j-a-b+1}, \dots , t_j)$. Both of these sequences contain
• b unbarred entries
 $< s$, all of which are unique, and
$< s$, all of which are unique, and• a barred entries, which are all
 $< k-s-1$.
$< k-s-1$.
The fact that ![]() $v'$ is the superlex maximal j-increasing exponent sequence appearing in
$v'$ is the superlex maximal j-increasing exponent sequence appearing in ![]() $f \odot \delta _{n,k,s}$ has the following consequences.
$f \odot \delta _{n,k,s}$ has the following consequences.
1. Every entry in the subsequence
 $(v^{\prime }_{j-a-b+1}, \dots , v^{\prime }_j)$ is unbarred (since
$(v^{\prime }_{j-a-b+1}, \dots , v^{\prime }_j)$ is unbarred (since  $v \preceq v'$). Consequently, the corresponding b entries of
$v \preceq v'$). Consequently, the corresponding b entries of  $u'$ are unbarred and the corresponding a entries of
$u'$ are unbarred and the corresponding a entries of  $u'$ are barred.
$u'$ are barred.2. The corresponding b entries in
 $u'$ must be
$u'$ must be  $s-1, s-2, \dots , s-b$ (in some order), and the corresponding a entries of
$s-1, s-2, \dots , s-b$ (in some order), and the corresponding a entries of  $u'$ must be
$u'$ must be  $\overline {k-1}$.
$\overline {k-1}$.3. The b entries must come before the a entries.
Items (2) and (3) above imply
and since ![]() $v'$ is j-increasing, we have
$v'$ is j-increasing, we have
We see that the three pairs of length b sequences
 $$ \begin{align*} \begin{cases} (u^{\prime}_{j-a-b+1}, \dots, u^{\prime}_{j-a}) \text{ and } (u_{j-a-b+1}, \dots, u_{j-a}), \\ (t^{\prime}_{j-a-b+1}, \dots, t^{\prime}_{j-a}) \text{ and } (t_{j-a-b+1}, \dots, t_{j-a}), \\ (v^{\prime}_{j-a-b+1}, \dots, v^{\prime}_{j-a}) \text{ and } (v_{j-a-b+1}, \dots, v_{j-a}) \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} (u^{\prime}_{j-a-b+1}, \dots, u^{\prime}_{j-a}) \text{ and } (u_{j-a-b+1}, \dots, u_{j-a}), \\ (t^{\prime}_{j-a-b+1}, \dots, t^{\prime}_{j-a}) \text{ and } (t_{j-a-b+1}, \dots, t_{j-a}), \\ (v^{\prime}_{j-a-b+1}, \dots, v^{\prime}_{j-a}) \text{ and } (v_{j-a-b+1}, \dots, v_{j-a}) \end{cases} \end{align*} $$are rearrangements of each other and ![]() $(u_{j-a-b+1}, \dots , u_{j-a}) = (s-1, s-2, \dots , s-b)$. We may apply a simultaneous permutation of
$(u_{j-a-b+1}, \dots , u_{j-a}) = (s-1, s-2, \dots , s-b)$. We may apply a simultaneous permutation of ![]() $(u^{\prime }_{j-a-b+1}, \dots , u^{\prime }_{j-a})$ and
$(u^{\prime }_{j-a-b+1}, \dots , u^{\prime }_{j-a})$ and ![]() $(t^{\prime }_{j-a-b+1}, \dots , t^{\prime }_{j-a})$ to get
$(t^{\prime }_{j-a-b+1}, \dots , t^{\prime }_{j-a})$ to get
without affecting ![]() $(v^{\prime }_{j-a-b+1}, \dots v^{\prime }_{j-a})$. Since
$(v^{\prime }_{j-a-b+1}, \dots v^{\prime }_{j-a})$. Since ![]() $v'$ is j-increasing, and the entries in
$v'$ is j-increasing, and the entries in ![]() $(t^{\prime }_{j-a-b+1}, \dots , t^{\prime }_{j-a})$ are distinct, we have
$(t^{\prime }_{j-a-b+1}, \dots , t^{\prime }_{j-a})$ are distinct, we have ![]() $t^{\prime }_{j-a-b+1}> \cdots > t^{\prime }_{j-a}$, which implies
$t^{\prime }_{j-a-b+1}> \cdots > t^{\prime }_{j-a}$, which implies
The last two paragraphs show that the first j entries of ![]() $v'$ and v coincide. The fact that the last
$v'$ and v coincide. The fact that the last ![]() $n-j$ entries of
$n-j$ entries of ![]() $v'$ and v coincide follows from an argument similar to the proof of Proposition 4.3; it is omitted here. This completes the proof of the claim.
$v'$ and v coincide follows from an argument similar to the proof of Proposition 4.3; it is omitted here. This completes the proof of the claim.
Our claim implies that ![]() ${\mathrm {in}}_j(f \odot \delta _{n,k,s})$ is the monomial associated to
${\mathrm {in}}_j(f \odot \delta _{n,k,s})$ is the monomial associated to ![]() $v = (v_1, \dots , v_n)$. We show how to recover the exponent sequence
$v = (v_1, \dots , v_n)$. We show how to recover the exponent sequence ![]() $u = (u_1, \dots , u_n)$ of the monomial M appearing in the claim. In turn, this allows us to recover
$u = (u_1, \dots , u_n)$ of the monomial M appearing in the claim. In turn, this allows us to recover ![]() $x_1^{i_1} \cdots x_j^{i_j} \theta _{1} \cdots \theta _a$ and m, such that
$x_1^{i_1} \cdots x_j^{i_j} \theta _{1} \cdots \theta _a$ and m, such that
completing the proof of the lemma.
Since ![]() $m \in {\mathcal {M}}_{n-j,k,s-b}^{(r-a)}$ and the construction of the last
$m \in {\mathcal {M}}_{n-j,k,s-b}^{(r-a)}$ and the construction of the last ![]() $n-j$ entries of u and v follows the algorithms in Proposition 4.3, that proposition proves we can recover the last
$n-j$ entries of u and v follows the algorithms in Proposition 4.3, that proposition proves we can recover the last ![]() $n-j$ entries of u and the last
$n-j$ entries of u and the last ![]() $n-j$ entries of t from the last
$n-j$ entries of t from the last ![]() $n-j$ entries of v. Since r is a global parameter and m has degree
$n-j$ entries of v. Since r is a global parameter and m has degree ![]() $r-a$ in the
$r-a$ in the ![]() $\theta _i$ variables, knowing the last
$\theta _i$ variables, knowing the last ![]() $n-j$ entries of t recovers a. This gives
$n-j$ entries of t recovers a. This gives ![]() $u_{j-a+1} = \cdots = u_j = \overline {k-1}$ and, since we know these entries of v, we recover
$u_{j-a+1} = \cdots = u_j = \overline {k-1}$ and, since we know these entries of v, we recover ![]() $t_{j-a+1}$ through
$t_{j-a+1}$ through ![]() $t_j$. By construction, v begins with
$t_j$. By construction, v begins with ![]() $j-a-b$ barred entries. Since we know j and a, we learn b. Then we know that the first
$j-a-b$ barred entries. Since we know j and a, we learn b. Then we know that the first ![]() $j-a$ entries of u are
$j-a$ entries of u are ![]() $j-a-b$ copies of
$j-a-b$ copies of ![]() $\overline {k-1}$ followed by the sequence
$\overline {k-1}$ followed by the sequence ![]() $(s-1)(s-2) \dots (s-b)$. From this information and the corresponding entries of v, we can recover
$(s-1)(s-2) \dots (s-b)$. From this information and the corresponding entries of v, we can recover ![]() $t_1$ through
$t_1$ through ![]() $t_{j-a}$. Now we know all of t. Since we know all of v, this determines all of u.
$t_{j-a}$. Now we know all of t. Since we know all of v, this determines all of u.
Finally, we put everything together to get our desired basis of ![]() $\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$.
$\varepsilon _j {\mathbb {W}}_{n,k,s}^{(r)}$.
Lemma 5.10. The subset of ![]() ${\mathcal {B}} \subseteq \Omega _n$ descends to a basis of
${\mathcal {B}} \subseteq \Omega _n$ descends to a basis of ![]() $\varepsilon _j {\mathbb {W}}^{(r)}_{n,k,s}$.
$\varepsilon _j {\mathbb {W}}^{(r)}_{n,k,s}$.
5.4 The  ${\mathcal {C}}$ basis of
${\mathcal {C}}$ basis of  $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$
Lemma 5.10 gives a basis ![]() ${\mathcal {B}}$ of
${\mathcal {B}}$ of ![]() $\varepsilon _j {\mathbb {W}}^{(r)}_{n,k,s}$. The corresponding harmonic basis is as follows.
$\varepsilon _j {\mathbb {W}}^{(r)}_{n,k,s}$. The corresponding harmonic basis is as follows.
Definition 5.11. Let ![]() ${\mathcal {C}} \subseteq \Omega _n$ be the disjoint union
${\mathcal {C}} \subseteq \Omega _n$ be the disjoint union
 $$ \begin{align} {\mathcal {C}} = \bigsqcup_{\substack{a,b \geq 0 \\ a \leq n-s-r, \, \, b \leq s}} \bigsqcup_{{\mathbf {i}}} \left\{ \left[ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)} \right\}, \end{align} $$
$$ \begin{align} {\mathcal {C}} = \bigsqcup_{\substack{a,b \geq 0 \\ a \leq n-s-r, \, \, b \leq s}} \bigsqcup_{{\mathbf {i}}} \left\{ \left[ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)} \right\}, \end{align} $$where the index ![]() ${\mathbf {i}} = (i_1, \dots , i_j)$ of the inner disjoint union ranges over all length j integer sequences whose first a, next b and final
${\mathbf {i}} = (i_1, \dots , i_j)$ of the inner disjoint union ranges over all length j integer sequences whose first a, next b and final ![]() $j-a-b$ entries satisfy the conditions
$j-a-b$ entries satisfy the conditions
The subset ![]() ${\mathcal {C}} \subseteq \Omega _n$ depends on
${\mathcal {C}} \subseteq \Omega _n$ depends on ![]() $n,k,s,r$ and j, but we suppress this dependence to avoid notational clutter.
$n,k,s,r$ and j, but we suppress this dependence to avoid notational clutter.
Definition 5.11 is formulated so that ![]() ${\mathcal {C}} \subseteq {\mathbb {H}}_{n,k,s}^{(r)}$. The following result justifies the disjointness of the unions appearing in Definition 5.11.
${\mathcal {C}} \subseteq {\mathbb {H}}_{n,k,s}^{(r)}$. The following result justifies the disjointness of the unions appearing in Definition 5.11.
Lemma 5.12. The family ![]() ${\mathcal {C}} \subseteq {\mathbb {H}}_{n,k,s}^{(r)}$ is a basis of the invariant space
${\mathcal {C}} \subseteq {\mathbb {H}}_{n,k,s}^{(r)}$ is a basis of the invariant space ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$.
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$.
Thanks to its avoidance of cosets, the ![]() ${\mathcal {C}}$ basis will be more convenient for us going forward.
${\mathcal {C}}$ basis will be more convenient for us going forward.
5.5 The  $\triangleleft $ order on bidegrees
$\triangleleft $ order on bidegrees
Our goal is to use the basis ![]() ${\mathcal {C}}$ of Lemma 5.12 to show that
${\mathcal {C}}$ of Lemma 5.12 to show that ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ is isomorphic as a graded
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ is isomorphic as a graded ![]() ${\mathfrak {S}}_{n-j}$-module to a direct sum of graded shifts of smaller
${\mathfrak {S}}_{n-j}$-module to a direct sum of graded shifts of smaller ![]() ${\mathbb {H}}$-modules in a way that matches the recursion of Lemma 3.14. To do this, we introduce a strategic direct sum decomposition of
${\mathbb {H}}$-modules in a way that matches the recursion of Lemma 3.14. To do this, we introduce a strategic direct sum decomposition of ![]() $\Omega _n = \Omega _j \otimes \Omega _{n-j}$, place a total order
$\Omega _n = \Omega _j \otimes \Omega _{n-j}$, place a total order ![]() $\triangleleft $ on the pieces of this decomposition and examine the
$\triangleleft $ on the pieces of this decomposition and examine the ![]() $\triangleleft $-lowest components of the elements in
$\triangleleft $-lowest components of the elements in ![]() ${\mathcal {C}}$.
${\mathcal {C}}$.
Our direct sum decomposition of ![]() $\Omega _n = \Omega _j \otimes \Omega _{n-j}$ is defined as follows. The second factor
$\Omega _n = \Omega _j \otimes \Omega _{n-j}$ is defined as follows. The second factor ![]() $\Omega _{n-j}$ of the tensor product
$\Omega _{n-j}$ of the tensor product ![]() $\Omega _n = \Omega _j \otimes \Omega _{n-j}$ is a bigraded algebra
$\Omega _n = \Omega _j \otimes \Omega _{n-j}$ is a bigraded algebra
where
We, therefore, have a direct sum decomposition
of the larger algebra ![]() $\Omega _n$, where we set
$\Omega _n$, where we set
In other words, the bigrading ![]() $\Omega _n(-,-)$ on
$\Omega _n(-,-)$ on ![]() $\Omega _n$ is obtained by focusing on commuting and anticommuting degree in the last
$\Omega _n$ is obtained by focusing on commuting and anticommuting degree in the last ![]() $n-j$ indices only. In particular, we have the following important observation.
$n-j$ indices only. In particular, we have the following important observation.
Observation 5.13. Although the direct sum decomposition ![]() $\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ is not stable under the action of
$\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ is not stable under the action of ![]() ${\mathfrak {S}}_n$, it is stable under the parabolic subgroup
${\mathfrak {S}}_n$, it is stable under the parabolic subgroup ![]() ${\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j}$ and the further subgroup
${\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j}$ and the further subgroup ![]() ${\mathfrak {S}}_{n-j}$.
${\mathfrak {S}}_{n-j}$.
The decomposition (5.18) will be used to study the action of ![]() ${\mathfrak {S}}_{n-j}$ on
${\mathfrak {S}}_{n-j}$ on ![]() $\Omega _n$, and, in particular, on the basis
$\Omega _n$, and, in particular, on the basis ![]() ${\mathcal {C}}$ of
${\mathcal {C}}$ of ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. We will need a nonstandard notion of ‘lowest degree component’ for elements of
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. We will need a nonstandard notion of ‘lowest degree component’ for elements of ![]() ${\mathcal {C}}$. To this end, we introduce a total order
${\mathcal {C}}$. To this end, we introduce a total order ![]() $\triangleleft $ on the summands
$\triangleleft $ on the summands ![]() $\Omega _n(p,q)$ appearing in (5.18) as follows.
$\Omega _n(p,q)$ appearing in (5.18) as follows.
Definition 5.14. Given two pairs of nonnegative integers ![]() $(p, q)$ and
$(p, q)$ and ![]() $(p', q')$, write
$(p', q')$, write ![]() $(p, q) \triangleleft (p',q')$ if
$(p, q) \triangleleft (p',q')$ if
• we have
 $q' < q$, or
$q' < q$, or• we have
 $q' = q$ and
$q' = q$ and  $p'> p$.
$p'> p$.
We also use the symbol ![]() $\triangleleft $ to denote the induced order on the summands
$\triangleleft $ to denote the induced order on the summands ![]() $\Omega _n(p,q)$ of the direct sum (5.18).
$\Omega _n(p,q)$ of the direct sum (5.18).
If there were no ![]() $\theta $-variables, Definition 5.14 would be the usual degree order induced from the second factor of the tensor decomposition
$\theta $-variables, Definition 5.14 would be the usual degree order induced from the second factor of the tensor decomposition ![]() ${\mathbb {Q}}[x_1, \dots , x_n] = {\mathbb {Q}}[x_1, \dots , x_j] \otimes {\mathbb {Q}}[x_{j+1}, \dots , x_n]$. The order
${\mathbb {Q}}[x_1, \dots , x_n] = {\mathbb {Q}}[x_1, \dots , x_j] \otimes {\mathbb {Q}}[x_{j+1}, \dots , x_n]$. The order ![]() $\triangleleft $ first compares
$\triangleleft $ first compares ![]() $\theta $-degrees in the ‘opposite’ order and breaks ties by comparing x-degrees in the classical order. This superisation of polynomial degree order should be compared with the superisation of the lexicographical term order
$\theta $-degrees in the ‘opposite’ order and breaks ties by comparing x-degrees in the classical order. This superisation of polynomial degree order should be compared with the superisation of the lexicographical term order ![]() $\prec $ in Definition 4.2 in which anticommuting variables involve a similar ‘reversal’.
$\prec $ in Definition 4.2 in which anticommuting variables involve a similar ‘reversal’.
5.6 Factoring the  $\triangleleft $-lowest components of the
$\triangleleft $-lowest components of the  ${\mathcal {C}}$ basis
${\mathcal {C}}$ basis
We consider elements in the ![]() ${\mathcal {C}}$ basis of
${\mathcal {C}}$ basis of ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ with respect to the direct sum decomposition
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ with respect to the direct sum decomposition ![]() $\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ of (5.18). While these elements are almost always inhomogeneous members of this direct sum, their
$\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ of (5.18). While these elements are almost always inhomogeneous members of this direct sum, their ![]() $\triangleleft $-lowest components have a useful recursive structure.
$\triangleleft $-lowest components have a useful recursive structure.
Lemma 5.15. Let ![]() $\left [ \varepsilon _j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta _1 \cdots \theta _a) \otimes m \right ] \odot \delta _{n,k,s} \in {\mathcal {C}}$, where
$\left [ \varepsilon _j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta _1 \cdots \theta _a) \otimes m \right ] \odot \delta _{n,k,s} \in {\mathcal {C}}$, where ![]() $m \in {\mathcal {M}}_{n-j,k,s-b}^{(n-s-r-a)}$ and the sequence
$m \in {\mathcal {M}}_{n-j,k,s-b}^{(n-s-r-a)}$ and the sequence ![]() ${\mathbf {i}} = (i_1, \dots , i_j)$ satisfies
${\mathbf {i}} = (i_1, \dots , i_j)$ satisfies
This element of ![]() ${\mathcal {C}}$ has an expansion under
${\mathcal {C}}$ has an expansion under ![]() $\triangleleft $ of the form
$\triangleleft $ of the form
where
and
The polynomial ![]() $f_{a,b,{\mathbf {i}}} \in \Omega _j$ is
$f_{a,b,{\mathbf {i}}} \in \Omega _j$ is ![]() ${\mathfrak {S}}_j$-invariant and nonzero.
${\mathfrak {S}}_j$-invariant and nonzero.
Remark 5.16. The polynomial ![]() $f_{a,b,{\mathbf {i}}}$ is bihomogeneous of x-degree
$f_{a,b,{\mathbf {i}}}$ is bihomogeneous of x-degree
 $$ \begin{align} (k-1) \cdot (j-b) + b \cdot (s-b) + {b \choose 2} - i_1 - \cdots - i_j \end{align} $$
$$ \begin{align} (k-1) \cdot (j-b) + b \cdot (s-b) + {b \choose 2} - i_1 - \cdots - i_j \end{align} $$and ![]() $\theta $-degree
$\theta $-degree ![]() $j - a - b$. The
$j - a - b$. The ![]() ${\mathfrak {S}}_j$-invariance of
${\mathfrak {S}}_j$-invariance of ![]() $f_{a,b,{\mathbf {i}}}$ is justified by Proposition 5.2. Observe that
$f_{a,b,{\mathbf {i}}}$ is justified by Proposition 5.2. Observe that ![]() $f_{a,b,{\mathbf {i}}}$ depends on
$f_{a,b,{\mathbf {i}}}$ depends on ![]() $a, b$ and
$a, b$ and ![]() ${\mathbf {i}}$ but is independent of
${\mathbf {i}}$ but is independent of ![]() $m \in {\mathcal {M}}_{n-j,k,s-b}^{(n-s-r-a)}$.
$m \in {\mathcal {M}}_{n-j,k,s-b}^{(n-s-r-a)}$.
To better understand Lemma 5.15, we analyse its statement in the case of the classical Vandermonde ![]() $\delta _n$.
$\delta _n$.
Example 5.17. In the special case ![]() $(n,k,s) = (n,n,n)$ and
$(n,k,s) = (n,n,n)$ and ![]() $j = 1$, Lemma 5.15 follows from the following expansion for the Vandermonde determinant
$j = 1$, Lemma 5.15 follows from the following expansion for the Vandermonde determinant ![]() $\delta _n$ in the variable
$\delta _n$ in the variable ![]() $x_1$:
$x_1$:
 $$ \begin{align} \delta_n = \varepsilon_n \cdot (x_1^{n-1} x_2^{n-2} \cdots x_{n-1}^1 x_n^0) = \sum_{d = 0}^{n-1} (-1)^{n-d+1} x_1^d \otimes \varepsilon_{n-1} \cdot (x_2^{n-1} \cdots x_{n-d}^{d+1} x_{n-d+1}^{d-1} \cdots x_n^0). \end{align} $$
$$ \begin{align} \delta_n = \varepsilon_n \cdot (x_1^{n-1} x_2^{n-2} \cdots x_{n-1}^1 x_n^0) = \sum_{d = 0}^{n-1} (-1)^{n-d+1} x_1^d \otimes \varepsilon_{n-1} \cdot (x_2^{n-1} \cdots x_{n-d}^{d+1} x_{n-d+1}^{d-1} \cdots x_n^0). \end{align} $$Since we have no anticommuting variables, the order ![]() $\triangleleft $ is simply the degree order on the last
$\triangleleft $ is simply the degree order on the last ![]() $n-j = n-1$ variables
$n-j = n-1$ variables ![]() $x_2, \dots , x_n$. Therefore, the
$x_2, \dots , x_n$. Therefore, the ![]() $d = n-1$ term
$d = n-1$ term
is the lowest ![]() $\triangleleft $-degree component of this expansion. The condition
$\triangleleft $-degree component of this expansion. The condition ![]() $x_1^{c_1} x_2^{c_2} \cdots x_n^{c_n} \in {\mathcal {M}}_{n,n,n}$ means that
$x_1^{c_1} x_2^{c_2} \cdots x_n^{c_n} \in {\mathcal {M}}_{n,n,n}$ means that ![]() $(c_1, c_2, \dots , c_n) \leq (n-1, n-2, \dots , 0)$ componentwise. If we set
$(c_1, c_2, \dots , c_n) \leq (n-1, n-2, \dots , 0)$ componentwise. If we set ![]() $m = x_2^{c_2} \cdots x_n^{c_n}$, applying
$m = x_2^{c_2} \cdots x_n^{c_n}$, applying ![]() $x_1^{c_1} x_2^{c_2} \cdots x_n^{c_n} = (\varepsilon _1 \cdot x_1^{c_1}) \otimes m$ to
$x_1^{c_1} x_2^{c_2} \cdots x_n^{c_n} = (\varepsilon _1 \cdot x_1^{c_1}) \otimes m$ to ![]() $\delta _n$ under the
$\delta _n$ under the ![]() $\odot $-action yields
$\odot $-action yields
where C is a nonzero constant.
Proof of Lemma 5.15. By definition, the superspace Vandermonde ![]() $\delta _{n,k,s}$ is the antisymmetrisation
$\delta _{n,k,s}$ is the antisymmetrisation
where the exponent sequences are given by ![]() $(p_1, \dots , p_n) = ( (k-1)^{n-s}, s-1, s-2, \dots , 1, 0)$ and
$(p_1, \dots , p_n) = ( (k-1)^{n-s}, s-1, s-2, \dots , 1, 0)$ and ![]() $(q_1, \dots , q_n) = (1^{n-s},0^s)$. We expand Equation (5.27) in a fashion compatible with the tensor product decomposition
$(q_1, \dots , q_n) = (1^{n-s},0^s)$. We expand Equation (5.27) in a fashion compatible with the tensor product decomposition ![]() $\Omega _n = \Omega _j \otimes \Omega _{n-j}$. For any system of right coset representatives w for
$\Omega _n = \Omega _j \otimes \Omega _{n-j}$. For any system of right coset representatives w for ![]() ${\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j}$ inside
${\mathfrak {S}}_j \times {\mathfrak {S}}_{n-j}$ inside ![]() ${\mathfrak {S}}_n$, Equation (5.27) reads
${\mathfrak {S}}_n$, Equation (5.27) reads
 $$ \begin{align} & \quad \delta_{n,k,s} = \notag \\ &\sum_{w} \pm \left[ \varepsilon_j \cdot (x_{1}^{p_{w^{-1}(1)}} \cdots x_{j}^{p_{w^{-1}(j)}} \theta_{1}^{q_{w^{-1}(1)}} \cdots \theta_{j}^{q_{w^{-1}(j)}}) \right]\notag\\&\quad \otimes \left[ \varepsilon_{n-j} \cdot (x_{j+1}^{p_{w^{-1}(j+1)}} \cdots x_n^{p_{w^{-1}(n)}} \theta_{j+1}^{q_{w^{-1}(j+1)}} \cdots \theta_n^{q_{w^{-1}(n)}}) \right], \end{align} $$
$$ \begin{align} & \quad \delta_{n,k,s} = \notag \\ &\sum_{w} \pm \left[ \varepsilon_j \cdot (x_{1}^{p_{w^{-1}(1)}} \cdots x_{j}^{p_{w^{-1}(j)}} \theta_{1}^{q_{w^{-1}(1)}} \cdots \theta_{j}^{q_{w^{-1}(j)}}) \right]\notag\\&\quad \otimes \left[ \varepsilon_{n-j} \cdot (x_{j+1}^{p_{w^{-1}(j+1)}} \cdots x_n^{p_{w^{-1}(n)}} \theta_{j+1}^{q_{w^{-1}(j+1)}} \cdots \theta_n^{q_{w^{-1}(n)}}) \right], \end{align} $$where ![]() $\pm $ is the sign of the coset representative w. Equation (5.28) is true for any system of coset representatives, but we restrict our choice somewhat in the next paragraph.
$\pm $ is the sign of the coset representative w. Equation (5.28) is true for any system of coset representatives, but we restrict our choice somewhat in the next paragraph.
Our aim is to apply the operator
to Equation (5.28) and extract the lowest term under ![]() $\triangleleft $ for which the first tensor factor does not vanish. A summand of Equation (5.28) indexed by a permutation w for which fewer than a entries in
$\triangleleft $ for which the first tensor factor does not vanish. A summand of Equation (5.28) indexed by a permutation w for which fewer than a entries in ![]() $(q_{w^{-1}(1)}, \dots , q_{w^{-1}(j)})$ equal 1 will be annihilated by the first tensor factor of the operator (5.29). We may, therefore, restrict our attention to those summands in which at least a of the entries in
$(q_{w^{-1}(1)}, \dots , q_{w^{-1}(j)})$ equal 1 will be annihilated by the first tensor factor of the operator (5.29). We may, therefore, restrict our attention to those summands in which at least a of the entries in ![]() $(q_{w^{-1}(1)}, \dots , q_{w^{-1}(j)})$ equal 1; the corresponding entries in
$(q_{w^{-1}(1)}, \dots , q_{w^{-1}(j)})$ equal 1; the corresponding entries in ![]() $(p_{w^{-1}(1)}, \dots , p_{w^{-1}(j)})$ will equal
$(p_{w^{-1}(1)}, \dots , p_{w^{-1}(j)})$ will equal ![]() $k-1$. We now assume the coset representatives w in Equation (5.28) are, such that
$k-1$. We now assume the coset representatives w in Equation (5.28) are, such that
When ![]() $k = s$, we further assume that
$k = s$, we further assume that
(this follows from the assumption on the p’s when ![]() $k> s$). There are typically many choices of coset representatives w which achieve this.
$k> s$). There are typically many choices of coset representatives w which achieve this.
We apply the operator (5.29) to each term
of Equation (5.28). In the first tensor factor, we get
The element of ![]() $\Omega _j$ in Equation (5.31) is certainly
$\Omega _j$ in Equation (5.31) is certainly ![]() ${\mathfrak {S}}_j$-invariant but can vanish for some coset representatives w.
${\mathfrak {S}}_j$-invariant but can vanish for some coset representatives w.
In order to minimise the application (5.31) of (5.29) to (5.30) under the order ![]() $\triangleleft $, we select our coset representative w in (5.31), such that
$\triangleleft $, we select our coset representative w in (5.31), such that
1. the expression (5.31) is a nonzero element of
 $\Omega _j$, and subject to this
$\Omega _j$, and subject to this2. the expression (5.31) has the smallest
 $\theta $-degree possible, and subject to this
$\theta $-degree possible, and subject to this3. the expression (5.31) has the largest x-degree possible.
For Item (1), we see that (5.31) is nonzero if and only if we have the componentwise inequalities
Subject to this, in order to satisfy Item (2), we must have
Subject to both (5.32) and (5.33), to satisfy Item (3), we must have
Said differently, Items (1)–(3) are satisfied precisely when
so that Equation (5.31) equals ![]() $f_{a,b,{\mathbf {i}}}$.
$f_{a,b,{\mathbf {i}}}$.
Let w be the unique coset representative which satisfies (5.32), (5.33) and (5.34). For this coset representative, the exponent sequence ![]() $(p_{w^{-1}(j+1)}, \dots , p_{w^{-1}(n)})$ appearing in the second tensor factor of (5.30) is a rearrangement of
$(p_{w^{-1}(j+1)}, \dots , p_{w^{-1}(n)})$ appearing in the second tensor factor of (5.30) is a rearrangement of ![]() $( (k-1)^{n-s-j+b}, s-b-1, \dots , 1, 0)$. This shows that
$( (k-1)^{n-s-j+b}, s-b-1, \dots , 1, 0)$. This shows that
for this choice of w. In summary, the application of (5.29) to ![]() $\delta _{n,k,s}$ has the form
$\delta _{n,k,s}$ has the form
 $$ \begin{align} \left\{ \left[\varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \theta_1 \cdots \theta_a) \right] \otimes m \right\} &\odot \delta_{n,k,s} \notag \\ & \ \quad = \pm f_{a,b,{\mathbf{i}}} \otimes (m \odot \delta_{n-j,k,s-b}) + \text{greater terms under } \triangleleft , \end{align} $$
$$ \begin{align} \left\{ \left[\varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \theta_1 \cdots \theta_a) \right] \otimes m \right\} &\odot \delta_{n,k,s} \notag \\ & \ \quad = \pm f_{a,b,{\mathbf{i}}} \otimes (m \odot \delta_{n-j,k,s-b}) + \text{greater terms under } \triangleleft , \end{align} $$which is what we wanted to show.
We give an example to illustrate the statement and proof of Lemma 5.15 in the presence of ![]() $\theta $-variables.
$\theta $-variables.
Example 5.18. Suppose ![]() $(n,k,s) = (7,7,4)$ so the superspace Vandermonde is
$(n,k,s) = (7,7,4)$ so the superspace Vandermonde is
We record the exponent sequence of the x-variables by ![]() $(p_1, \dots , p_7) = (6,6,6,3,2,1,0)$ and that of the
$(p_1, \dots , p_7) = (6,6,6,3,2,1,0)$ and that of the ![]() $\theta $-variables by
$\theta $-variables by ![]() $(q_1, \dots , q_7) = (1,1,1,0,0,0,0)$.
$(q_1, \dots , q_7) = (1,1,1,0,0,0,0)$.
We take ![]() $j = 3$, so that we factor superspace elements according to
$j = 3$, so that we factor superspace elements according to ![]() $\Omega _7 = \Omega _j \otimes \Omega _{n-j} = \Omega _3 \otimes \Omega _4$. For any system of right coset representatives of
$\Omega _7 = \Omega _j \otimes \Omega _{n-j} = \Omega _3 \otimes \Omega _4$. For any system of right coset representatives of ![]() ${\mathfrak {S}}_3 \times {\mathfrak {S}}_4$ in
${\mathfrak {S}}_3 \times {\mathfrak {S}}_4$ in ![]() ${\mathfrak {S}}_7$, the Vandermonde
${\mathfrak {S}}_7$, the Vandermonde ![]() $\delta _{7,7,4}$ expands as
$\delta _{7,7,4}$ expands as
 $$ \begin{align*}\delta_{7,7,4} & = \sum_{w} \pm \left[ \varepsilon_3 \cdot (x_{1}^{p_{w^{-1}(1)}} x_2^{p_{w^{-1}(2)}} x_{3}^{p_{w^{-1}(3)}} \theta_{1}^{q_{w^{-1}(1)}} \theta_2^{q_{w^{-1}(2)}} \theta_{3}^{q_{w^{-1}(3)}}) \right] \\&\quad \otimes \left[ \varepsilon_4 \cdot (x_4^{p_{w^{-1}(4)}} \cdots x_7^{p_{w^{-1}(7)}} \theta_4^{q_{w^{-1}(4)}} \cdots \theta_7^{q_{w^{-1}(7)}}) \right], \end{align*} $$
$$ \begin{align*}\delta_{7,7,4} & = \sum_{w} \pm \left[ \varepsilon_3 \cdot (x_{1}^{p_{w^{-1}(1)}} x_2^{p_{w^{-1}(2)}} x_{3}^{p_{w^{-1}(3)}} \theta_{1}^{q_{w^{-1}(1)}} \theta_2^{q_{w^{-1}(2)}} \theta_{3}^{q_{w^{-1}(3)}}) \right] \\&\quad \otimes \left[ \varepsilon_4 \cdot (x_4^{p_{w^{-1}(4)}} \cdots x_7^{p_{w^{-1}(7)}} \theta_4^{q_{w^{-1}(4)}} \cdots \theta_7^{q_{w^{-1}(7)}}) \right], \end{align*} $$where ![]() $\pm $ is the sign of the coset representative w.
$\pm $ is the sign of the coset representative w.
Let ![]() $m \in \Omega _4 \subseteq \Omega _3 \otimes \Omega _4$ be an arbitrary monomial in
$m \in \Omega _4 \subseteq \Omega _3 \otimes \Omega _4$ be an arbitrary monomial in ![]() $x_4, \dots , x_7, \theta _4, \dots , \theta _7$. We consider applying the operator
$x_4, \dots , x_7, \theta _4, \dots , \theta _7$. We consider applying the operator
to ![]() $\delta _{7,7,4}$ by applying it to each term
$\delta _{7,7,4}$ by applying it to each term
of its expansion in ![]() $\Omega _3 \otimes \Omega _4$. We choose our coset representatives w so that
$\Omega _3 \otimes \Omega _4$. We choose our coset representatives w so that
in each term.
Focusing on the first tensor factor, the evaluation
is ![]() ${\mathfrak {S}}_3$-invariant, and is nonzero if and only if we have the componentwise inequalities
${\mathfrak {S}}_3$-invariant, and is nonzero if and only if we have the componentwise inequalities
To minimise under the order ![]() $\triangleleft $ subject to these conditions, we take the unique coset representative w for which
$\triangleleft $ subject to these conditions, we take the unique coset representative w for which
For this choice of w, in the second tensor factor, we have
so that
This yields an expansion
 $$ \begin{align*} &\left\{ \left[\varepsilon_3 \cdot (x^{325} \theta_1) \right] \otimes m \right\} \odot \delta_{7,7,4} = \\ &\qquad \pm \left[ \varepsilon_3 \cdot (x^{325} \theta_1) \right] \odot \left[ \varepsilon_3 \cdot ( x^{626} \theta_{13} ) \right] \otimes [m \odot \delta_{4,7,3}] + \mathrm{greater\ terms\ under}\ \triangleleft, \end{align*} $$
$$ \begin{align*} &\left\{ \left[\varepsilon_3 \cdot (x^{325} \theta_1) \right] \otimes m \right\} \odot \delta_{7,7,4} = \\ &\qquad \pm \left[ \varepsilon_3 \cdot (x^{325} \theta_1) \right] \odot \left[ \varepsilon_3 \cdot ( x^{626} \theta_{13} ) \right] \otimes [m \odot \delta_{4,7,3}] + \mathrm{greater\ terms\ under}\ \triangleleft, \end{align*} $$where the ![]() ${\mathfrak {S}}_3$-invariant in the first tensor factor is nonzero.
${\mathfrak {S}}_3$-invariant in the first tensor factor is nonzero.
5.7 A recursion for  $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$
We are ready to state our recursion for the graded ![]() ${\mathfrak {S}}_{n-j}$-module
${\mathfrak {S}}_{n-j}$-module ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. Our crucial tools are Observation 5.13 and Lemma 5.15. Given any graded
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. Our crucial tools are Observation 5.13 and Lemma 5.15. Given any graded ![]() ${\mathfrak {S}}_{n-j}$-module
${\mathfrak {S}}_{n-j}$-module ![]() $V = \bigoplus _{i} V_{i}$ and any integer
$V = \bigoplus _{i} V_{i}$ and any integer ![]() $i_0$, let
$i_0$, let ![]() $V\{-i_0\}$ denote the same
$V\{-i_0\}$ denote the same ![]() ${\mathfrak {S}}_{n-j}$ module with degree shifted up by
${\mathfrak {S}}_{n-j}$ module with degree shifted up by ![]() $i_0$. That is, the
$i_0$. That is, the ![]() $i^{th}$ graded piece of
$i^{th}$ graded piece of ![]() $V\{-i_0\}$ is given by
$V\{-i_0\}$ is given by
Lemma 5.19. Let ![]() $n, k, s \geq 0$ with
$n, k, s \geq 0$ with ![]() $k \geq s$, and let
$k \geq s$, and let ![]() $0 \leq r \leq n-s$. Let
$0 \leq r \leq n-s$. Let ![]() $1 \leq j \leq n$. There holds an isomorphism of graded
$1 \leq j \leq n$. There holds an isomorphism of graded ![]() ${\mathfrak {S}}_{n-j}$-modules
${\mathfrak {S}}_{n-j}$-modules
 $$ \begin{align} \eta_j {\mathbb{H}}_{n,k,s}^{(r)} \cong \bigoplus_{\substack{a,b \geq 0 \\ a \leq n-s-r \\ b \leq s}} \left[ \bigoplus_{{\mathbf {i}}} {\mathbb{H}}_{n-j,k,s-b}^{(r - j + a + b)} \left\{ i_1 + \cdots + i_j - {b \choose 2} - b \cdot (s-b) - (k-1) \cdot (j-b) \right\} \right] , \end{align} $$
$$ \begin{align} \eta_j {\mathbb{H}}_{n,k,s}^{(r)} \cong \bigoplus_{\substack{a,b \geq 0 \\ a \leq n-s-r \\ b \leq s}} \left[ \bigoplus_{{\mathbf {i}}} {\mathbb{H}}_{n-j,k,s-b}^{(r - j + a + b)} \left\{ i_1 + \cdots + i_j - {b \choose 2} - b \cdot (s-b) - (k-1) \cdot (j-b) \right\} \right] , \end{align} $$where the inner direct sum is over all j-tuples ![]() ${\mathbf {i}} = (i_1, \dots , i_j)$ of nonnegative integers, such that
${\mathbf {i}} = (i_1, \dots , i_j)$ of nonnegative integers, such that
and
Equivalently, we have the symmetric function identity
 $$ \begin{align} &h_j^{\perp} {\mathrm {grFrob}}( {\mathbb{H}}_{n,k,s}^{(r)}; q) = \notag \\ &\sum_{\substack{a,b \geq 0 \\ a \leq n-s-r \\ b \leq s}} q^{ {j-a-b \choose 2} + (s-b)a} \times {k-s-1+a+b \brack a}_q \cdot {s \brack b}_q \cdot {k-s \brack j-a-b}_q \cdot {\mathrm {grFrob}}({\mathbb{H}}^{(r-j+a+b)}_{n-j,k,s-b}; q). \end{align} $$
$$ \begin{align} &h_j^{\perp} {\mathrm {grFrob}}( {\mathbb{H}}_{n,k,s}^{(r)}; q) = \notag \\ &\sum_{\substack{a,b \geq 0 \\ a \leq n-s-r \\ b \leq s}} q^{ {j-a-b \choose 2} + (s-b)a} \times {k-s-1+a+b \brack a}_q \cdot {s \brack b}_q \cdot {k-s \brack j-a-b}_q \cdot {\mathrm {grFrob}}({\mathbb{H}}^{(r-j+a+b)}_{n-j,k,s-b}; q). \end{align} $$Proof. The basis ![]() ${\mathcal {C}}$ of
${\mathcal {C}}$ of ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ in Lemma 5.12 admits a disjoint union decomposition
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$ in Lemma 5.12 admits a disjoint union decomposition
 $$ \begin{align} \bigsqcup_{\substack{a,b \geq 0 \\ a \leq n-s-r \\ b \leq s}} \bigsqcup_{{\mathbf {i}}} \left\{ \left[ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)} \right\} , \end{align} $$
$$ \begin{align} \bigsqcup_{\substack{a,b \geq 0 \\ a \leq n-s-r \\ b \leq s}} \bigsqcup_{{\mathbf {i}}} \left\{ \left[ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)} \right\} , \end{align} $$where the tuples ![]() ${\mathbf {i}} = (i_1, \dots , i_j)$ satisfy the conditions in the statement of the theorem. Lemma 5.15 shows that, for each triple
${\mathbf {i}} = (i_1, \dots , i_j)$ satisfy the conditions in the statement of the theorem. Lemma 5.15 shows that, for each triple ![]() $(a,b,{\mathbf {i}})$ indexing the disjoint union (5.41), there is a single nonzero invariant
$(a,b,{\mathbf {i}})$ indexing the disjoint union (5.41), there is a single nonzero invariant ![]() $f_{a,b,{\mathbf {i}}} \in (\Omega _j)^{{\mathfrak {S}}_j}$, such that
$f_{a,b,{\mathbf {i}}} \in (\Omega _j)^{{\mathfrak {S}}_j}$, such that
for all ![]() $m \in {\mathcal {M}}_{n-j,k,s-b}^{(n-s-r-a)}$. The sign in Equation (5.42) may depend on m but the invariant
$m \in {\mathcal {M}}_{n-j,k,s-b}^{(n-s-r-a)}$. The sign in Equation (5.42) may depend on m but the invariant ![]() $f_{a,b,{\mathbf {i}}}$ does not. The leading term
$f_{a,b,{\mathbf {i}}}$ does not. The leading term ![]() $f_{a,b,{\mathbf {i}}} \otimes (m \odot \delta _{n-j,k,s-b})$ in (5.42) lies in a single bihomogeneous piece
$f_{a,b,{\mathbf {i}}} \otimes (m \odot \delta _{n-j,k,s-b})$ in (5.42) lies in a single bihomogeneous piece
of the decomposition ![]() $\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ defining
$\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ defining ![]() $\triangleleft $.
$\triangleleft $.
The observations of the previous paragraph give rise to a filtration of ![]() $\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. For any
$\eta _j {\mathbb {H}}_{n,k,s}^{(r)}$. For any ![]() $p, q \geq 0$, we set
$p, q \geq 0$, we set
 $$ \begin{align} & \ \left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{\trianglelefteq (p,q)} = \notag \\ &\mathrm{span} \bigsqcup_{(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}})) \trianglelefteq (p,q)} \left\{\left[\varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)}\right\} , \end{align} $$
$$ \begin{align} & \ \left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{\trianglelefteq (p,q)} = \notag \\ &\mathrm{span} \bigsqcup_{(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}})) \trianglelefteq (p,q)} \left\{\left[\varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)}\right\} , \end{align} $$where ![]() $(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}}))$ is defined as in (5.43). Analogously, we define
$(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}}))$ is defined as in (5.43). Analogously, we define
 $$ \begin{align} &\left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{\triangleleft (p,q)} = \notag \\ &\mathrm{span} \bigsqcup_{(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}})) \triangleleft (p,q)} \left\{ \left[ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)} \right\} \end{align} $$
$$ \begin{align} &\left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{\triangleleft (p,q)} = \notag \\ &\mathrm{span} \bigsqcup_{(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}})) \triangleleft (p,q)} \left\{ \left[ \varepsilon_j \cdot (x_1^{i_1} \cdots x_j^{i_j} \cdot \theta_1 \cdots \theta_a) \otimes m \right] \odot \delta_{n,k,s} \,:\, m \in {\mathcal{M}}_{n-j,k,s-b}^{(n-s-r-a)} \right\} \end{align} $$and the corresponding quotient space
By Observation 5.13, the decomposition ![]() $\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ is
$\Omega _n = \bigoplus _{p,q \geq 0} \Omega _n(p,q)$ is ![]() ${\mathfrak {S}}_{n-j}$-stable. Therefore, the three vector spaces (5.44), (5.45) and (5.46) are graded
${\mathfrak {S}}_{n-j}$-stable. Therefore, the three vector spaces (5.44), (5.45) and (5.46) are graded ![]() ${\mathfrak {S}}_{n-j}$-modules under x-degree. Furthermore, we have an isomorphism
${\mathfrak {S}}_{n-j}$-modules under x-degree. Furthermore, we have an isomorphism
 $$ \begin{align} \eta_j {\mathbb{H}}_{n,k,s}^{(r)} \cong \bigoplus_{p,q \geq 0} \left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{= (p,q)}. \end{align} $$
$$ \begin{align} \eta_j {\mathbb{H}}_{n,k,s}^{(r)} \cong \bigoplus_{p,q \geq 0} \left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{= (p,q)}. \end{align} $$What does the summand ![]() $\left (\eta _j {\mathbb {H}}_{n,k,s}^{(r)} \right )_{= (p,q)}$ in (5.47) look like? The expansion (5.42) implies an isomorphism of graded
$\left (\eta _j {\mathbb {H}}_{n,k,s}^{(r)} \right )_{= (p,q)}$ in (5.47) look like? The expansion (5.42) implies an isomorphism of graded ![]() ${\mathfrak {S}}_{n-j}$-modules
${\mathfrak {S}}_{n-j}$-modules
 $$ \begin{align} \left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{= (p,q)} \cong \bigoplus_{(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}}) = (p,q)} \mathbb{V}_{a,b,{\mathbf {i}}} , \end{align} $$
$$ \begin{align} \left(\eta_j {\mathbb{H}}_{n,k,s}^{(r)} \right)_{= (p,q)} \cong \bigoplus_{(p(a,b,{\mathbf {i}}), q(a,b,{\mathbf {i}}) = (p,q)} \mathbb{V}_{a,b,{\mathbf {i}}} , \end{align} $$where
In light of Corollary 4.14, the space ![]() $\mathbb {V}_{a,b,{\mathbf {i}}}$ affords a copy of the
$\mathbb {V}_{a,b,{\mathbf {i}}}$ affords a copy of the ![]() ${\mathfrak {S}}_{n-j}$-module
${\mathfrak {S}}_{n-j}$-module ![]() ${\mathbb {H}}_{n-j,k,s-b}^{(r-j+a+b)}$ with degree shifted up by
${\mathbb {H}}_{n-j,k,s-b}^{(r-j+a+b)}$ with degree shifted up by
 $$ \begin{align} x\text{-degree of } f_{a,b,{\mathbf {i}}} = {b \choose 2} + b \cdot (s-b) + (k-1) \cdot (j-b) - i_1 - \cdots - i_j. \end{align} $$
$$ \begin{align} x\text{-degree of } f_{a,b,{\mathbf {i}}} = {b \choose 2} + b \cdot (s-b) + (k-1) \cdot (j-b) - i_1 - \cdots - i_j. \end{align} $$This completes the proof.
5.8 The  ${\mathfrak {S}}_n$-structure of
${\mathfrak {S}}_n$-structure of  ${\mathbb {W}}_{n,k,s}$
${\mathbb {W}}_{n,k,s}$
All of the pieces are in place for us to prove our combinatorial formula for ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$.
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$.
Theorem 5.20. Let ![]() $n, k \geq s \geq 0$ be integers. The bigraded Frobenius image
$n, k \geq s \geq 0$ be integers. The bigraded Frobenius image ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$ has the following combinatorial expressions in terms of the statistics
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$ has the following combinatorial expressions in terms of the statistics ![]() ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and ![]() ${\mathrm {codinv}}$.
${\mathrm {codinv}}$.
Proof. It suffices to show
for all r. Lemmas 2.3 and 2.4 reduce this task to proving
for any ![]() $j \geq 1$. By Lemmas 3.14 and 5.19, both sides of Equation (5.53) satisfy the same recursion and we are done by induction on n.
$j \geq 1$. By Lemmas 3.14 and 5.19, both sides of Equation (5.53) satisfy the same recursion and we are done by induction on n.
As an example of Theorem 5.20, let ![]() $(n,k,s) = (3,2,2)$. We list the 12 ordered set superpartitions
$(n,k,s) = (3,2,2)$. We list the 12 ordered set superpartitions ![]() $\sigma \in {\mathcal {OSP}}_{3,2,2}$ together with their coinversion numbers, reading words and inverse descent sets.
$\sigma \in {\mathcal {OSP}}_{3,2,2}$ together with their coinversion numbers, reading words and inverse descent sets.

This leads to the expression
for ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{3,2,2};q,z)$ which has Schur expansion
${\mathrm {grFrob}}({\mathbb {W}}_{3,2,2};q,z)$ which has Schur expansion
As with the bigraded Hilbert series, the bigraded Frobenius image is more attractive in matrix format
 $$ \begin{align*} {\mathrm {grFrob}}({\mathbb{W}}_{3,2,2};q,z) = \begin{pmatrix} s_3 & s_3 + s_{2,1} & s_{2,1} \\ s_{2,1} & s_{2,1} + s_{1,1,1} & s_{1,1,1} \end{pmatrix},\\[-15pt] \end{align*} $$
$$ \begin{align*} {\mathrm {grFrob}}({\mathbb{W}}_{3,2,2};q,z) = \begin{pmatrix} s_3 & s_3 + s_{2,1} & s_{2,1} \\ s_{2,1} & s_{2,1} + s_{1,1,1} & s_{1,1,1} \end{pmatrix},\\[-15pt] \end{align*} $$where the Rotational Duality of Theorem 1.2 becomes apparent.
Remark 5.21. In the case ![]() $k = s$, the family
$k = s$, the family ![]() ${\mathcal {OSP}}_{n,k,k}$ admits an involution
${\mathcal {OSP}}_{n,k,k}$ admits an involution ![]() $\iota $ sending an ordered set superpartition
$\iota $ sending an ordered set superpartition ![]() $\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,k}$ to
$\sigma = (B_1 \mid \cdots \mid B_k) \in {\mathcal {OSP}}_{n,k,k}$ to ![]() $\iota (\sigma ) = (\overline {B_k} \mid \cdots \mid \overline {B_1})$, where
$\iota (\sigma ) = (\overline {B_k} \mid \cdots \mid \overline {B_1})$, where ![]() $\overline {B_i}$ is obtained from
$\overline {B_i}$ is obtained from ![]() $B_i$ by switching the barred/unbarred status of every nonminimal element of
$B_i$ by switching the barred/unbarred status of every nonminimal element of ![]() $B_i$. It may be checked that
$B_i$. It may be checked that ![]() $\iota $ complements both the statistic
$\iota $ complements both the statistic ![]() ${\mathrm {coinv}}$ and the subset
${\mathrm {coinv}}$ and the subset ![]() ${\mathrm {iDes}}$ in the sense that
${\mathrm {iDes}}$ in the sense that
 $$ \begin{align*} &{\mathrm {coinv}}(\sigma) + {\mathrm {coinv}}(\iota(\sigma)) = {k \choose 2} + (n-k) \cdot (k-1) \quad\! \text{and} \!\quad {\mathrm {iDes}}(\mathrm{read}(\sigma)) \sqcup {\mathrm {iDes}}(\mathrm{read}(\iota(\sigma))) = [n-1]\\[-9pt] \end{align*} $$
$$ \begin{align*} &{\mathrm {coinv}}(\sigma) + {\mathrm {coinv}}(\iota(\sigma)) = {k \choose 2} + (n-k) \cdot (k-1) \quad\! \text{and} \!\quad {\mathrm {iDes}}(\mathrm{read}(\sigma)) \sqcup {\mathrm {iDes}}(\mathrm{read}(\iota(\sigma))) = [n-1]\\[-9pt] \end{align*} $$for any ![]() $\sigma \in {\mathcal {OSP}}_{n,k,k}$. The Rotational Duality statement of Theorem 1.2 is, therefore, consistent with Theorem 5.20.
$\sigma \in {\mathcal {OSP}}_{n,k,k}$. The Rotational Duality statement of Theorem 1.2 is, therefore, consistent with Theorem 5.20.
The authors do not know a combinatorial formula for the Schur expansion of ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$. On the other hand, if we consider
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$. On the other hand, if we consider ![]() ${\mathbb {W}}_{n,k,s}$ as a singly graded
${\mathbb {W}}_{n,k,s}$ as a singly graded ![]() ${\mathfrak {S}}_n$-module under
${\mathfrak {S}}_n$-module under ![]() $\theta $-degree, we have a simple formula for this Schur expansion. Recall that a partition
$\theta $-degree, we have a simple formula for this Schur expansion. Recall that a partition ![]() $\lambda $ is a hook if it has the form
$\lambda $ is a hook if it has the form ![]() $\lambda = (a,1^{m-a})$ for some a. The anticommutative graded pieces of
$\lambda = (a,1^{m-a})$ for some a. The anticommutative graded pieces of ![]() ${\mathbb {W}}_{n,k,s}$ are built out of hook shapes.
${\mathbb {W}}_{n,k,s}$ are built out of hook shapes.
Corollary 5.22. Consider ![]() ${\mathbb {W}}_{n,k,s}$ as a singly graded
${\mathbb {W}}_{n,k,s}$ as a singly graded ![]() ${\mathfrak {S}}_n$-module under
${\mathfrak {S}}_n$-module under ![]() $\theta $-degree. Then
$\theta $-degree. Then
 $$ \begin{align} {\mathrm {grFrob}}({\mathbb{W}}_{n,k,s}; z) = \sum_{(\lambda^{(1)}, \dots, \lambda^{(k)})} z^{n - \lambda^{(1)}_1 - \cdots - \lambda^{(k)}_1} \cdot s_{\lambda^{(1)}} \cdots s_{\lambda^{(s)}} \cdot s_{\lambda^{(s+1)}/(1)} \cdots s_{\lambda^{(k)}/(1)} ,\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} {\mathrm {grFrob}}({\mathbb{W}}_{n,k,s}; z) = \sum_{(\lambda^{(1)}, \dots, \lambda^{(k)})} z^{n - \lambda^{(1)}_1 - \cdots - \lambda^{(k)}_1} \cdot s_{\lambda^{(1)}} \cdots s_{\lambda^{(s)}} \cdot s_{\lambda^{(s+1)}/(1)} \cdots s_{\lambda^{(k)}/(1)} ,\\[-15pt]\nonumber \end{align} $$where ![]() $(\lambda ^{(1)}, \dots , \lambda ^{(k)})$ ranges over k-tuples of nonempty hooks with a total of
$(\lambda ^{(1)}, \dots , \lambda ^{(k)})$ ranges over k-tuples of nonempty hooks with a total of
boxes.
Observe that the skew partitions ![]() $\lambda ^{(s+1)}/(1), \dots , \lambda ^{(k)}/(1)$ indexing the last
$\lambda ^{(s+1)}/(1), \dots , \lambda ^{(k)}/(1)$ indexing the last ![]() $k-s$ factors in Corollary 5.22 can be empty and we have the factorisation
$k-s$ factors in Corollary 5.22 can be empty and we have the factorisation ![]() $s_{(a,1^{m-a})/(1)} = h_{a-1} \cdot e_{m-a}$. When
$s_{(a,1^{m-a})/(1)} = h_{a-1} \cdot e_{m-a}$. When ![]() $(n,k,s) = (4,3,2)$, Corollary 5.22 says that the piece of
$(n,k,s) = (4,3,2)$, Corollary 5.22 says that the piece of ![]() ${\mathbb {W}}_{4,3,2}$ of anticommuting degree 1 has Frobenius image
${\mathbb {W}}_{4,3,2}$ of anticommuting degree 1 has Frobenius image
Proof. We have a natural bijection between column tableaux and tuples of hook-shaped semistandard tableaux, where a ![]() $\bullet $ at height zero corresponds to a skewed-out box, viz.
$\bullet $ at height zero corresponds to a skewed-out box, viz.

Now apply Theorem 5.20.
6 Conclusion
In this paper, we gave a combinatorial formula (Theorem 5.20) for the bigraded Frobenius image ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$ of a family of quotients
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$ of a family of quotients ![]() ${\mathbb {W}}_{n,k,s}$ of the superspace ring
${\mathbb {W}}_{n,k,s}$ of the superspace ring ![]() $\Omega _n$. The following problem remains open.
$\Omega _n$. The following problem remains open.
Problem 6.1. Find the Schur expansion of ![]() ${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$.
${\mathrm {grFrob}}({\mathbb {W}}_{n,k,s};q,z)$.
A solution to Problem 6.1 would refine Corollary 5.22. We remark that symmetric functions admit the operation of superisation which has the plethystic definition ![]() $f[{\mathbf {x}}] \mapsto f[{\mathbf {x}} - \mathbf {y}]$, where
$f[{\mathbf {x}}] \mapsto f[{\mathbf {x}} - \mathbf {y}]$, where ![]() ${\mathbf {x}}$ and
${\mathbf {x}}$ and ![]() $\mathbf {y}$ are two infinite alphabets; see [Reference Novelli and Thibon20] for more details. Although superisation can be used to yield (for example) the bigraded Frobenius image of
$\mathbf {y}$ are two infinite alphabets; see [Reference Novelli and Thibon20] for more details. Although superisation can be used to yield (for example) the bigraded Frobenius image of ![]() $\Omega _n$ from that of
$\Omega _n$ from that of ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$, we do not know of a way to use superisation to solve Problem 6.1.
${\mathbb {Q}}[x_1, \dots , x_n]$, we do not know of a way to use superisation to solve Problem 6.1.
One possible way to solve Problem 6.1 would be to define a statistic on ordered set superpartitions which extends the major index statistic on permutations. In the context of ordered set partitions, two such extensions are available: ![]() ${\mathrm {maj}}$ and
${\mathrm {maj}}$ and ![]() $\mathrm {minimaj}$ [Reference Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip1, Reference Haglund, Remmel and Wilson12, Reference Remmel and Wilson23, Reference Rhoades24]. If such an extension were found, an insertion argument of Wilson [Reference Wilson33] (in the case of
$\mathrm {minimaj}$ [Reference Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip1, Reference Haglund, Remmel and Wilson12, Reference Remmel and Wilson23, Reference Rhoades24]. If such an extension were found, an insertion argument of Wilson [Reference Wilson33] (in the case of ![]() ${\mathrm {maj}}$) or the crystal techniques of Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip [Reference Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip1] (in the case of
${\mathrm {maj}}$) or the crystal techniques of Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip [Reference Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip1] (in the case of ![]() $\mathrm {minimaj}$) could perhaps be used to solve Problem 6.1.
$\mathrm {minimaj}$) could perhaps be used to solve Problem 6.1.
The substaircase basis of ![]() ${\mathbb {W}}_{n,k,s}$ of Theorem 4.12 is tied to the inversion-like statistics
${\mathbb {W}}_{n,k,s}$ of Theorem 4.12 is tied to the inversion-like statistics ![]() ${\mathrm {coinv}}$ and
${\mathrm {coinv}}$ and ![]() ${\mathrm {codinv}}$ on ordered set superpartitions. Steinberg proved [Reference Steinberg29] that the set of descent monomials
${\mathrm {codinv}}$ on ordered set superpartitions. Steinberg proved [Reference Steinberg29] that the set of descent monomials ![]() $\{ d_w \,:\, w \in {\mathfrak {S}}_n \}$ form a basis for the classical coinvariant ring
$\{ d_w \,:\, w \in {\mathfrak {S}}_n \}$ form a basis for the classical coinvariant ring ![]() ${\mathbb {Q}}[x_1, \dots , x_n]/\langle e_1, \dots , e_n \rangle $, where
${\mathbb {Q}}[x_1, \dots , x_n]/\langle e_1, \dots , e_n \rangle $, where
 $$ \begin{align} d_w = \prod_{\substack{1 \leq i \leq n-1 \\ w(i)> w(i+1)}} x_{w(1)} \cdots x_{w(i)}. \end{align} $$
$$ \begin{align} d_w = \prod_{\substack{1 \leq i \leq n-1 \\ w(i)> w(i+1)}} x_{w(1)} \cdots x_{w(i)}. \end{align} $$This basis was studied further by Garsia and Stanton [Reference Garsia and Stanton8] in the context of Stanley-Reisner theory and extended to the context of ![]() $R_{n,k}$ by Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono13].
$R_{n,k}$ by Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono13].
Problem 6.2. Define an extension of the major index statistic to ordered set superpartitions in ![]() ${\mathcal {OSP}}_{n,k,s}$ and a companion descent monomial basis of
${\mathcal {OSP}}_{n,k,s}$ and a companion descent monomial basis of ![]() ${\mathbb {W}}_{n,k,s}$.
${\mathbb {W}}_{n,k,s}$.
In the context of ![]() $R_{n,k}$, Meyer used the descent monomial basis to refine the formulas for
$R_{n,k}$, Meyer used the descent monomial basis to refine the formulas for ![]() ${\mathrm {grFrob}}(R_{n,k};q)$ of Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono13, Reference Meyer19]. This refinement matched a symmetric function arising from the crystal-theoretic machinery of Benkart et al. [Reference Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip1]. A solution to Problem 6.2 might lead to similar refinements in the
${\mathrm {grFrob}}(R_{n,k};q)$ of Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono13, Reference Meyer19]. This refinement matched a symmetric function arising from the crystal-theoretic machinery of Benkart et al. [Reference Benkart, Colmenarejo, Harris, Orellana, Panova, Schilling and Yip1]. A solution to Problem 6.2 might lead to similar refinements in the ![]() ${\mathbb {W}}$-module context.
${\mathbb {W}}$-module context.
There are several results about the anticommuting degree zero piece of ![]() ${\mathbb {W}}_{n,k}$ one could try to push to the entire module
${\mathbb {W}}_{n,k}$ one could try to push to the entire module ![]() ${\mathbb {W}}_{n,k}$. We mention a couple briefly. One could look for a Hecke action on all of superspace, extending work of Huang, Rhoades and Scrimshaw [Reference Huang, Rhoades and Scrimshaw15]. One could also hope to generalise the geometric discoveries of Pawlowski and Rhoades to the entire module
${\mathbb {W}}_{n,k}$. We mention a couple briefly. One could look for a Hecke action on all of superspace, extending work of Huang, Rhoades and Scrimshaw [Reference Huang, Rhoades and Scrimshaw15]. One could also hope to generalise the geometric discoveries of Pawlowski and Rhoades to the entire module ![]() ${\mathbb {W}}_{n,k}$ [Reference Pawlowski and Rhoades21]. In particular, it would be interesting to see if this larger module allows for the definition of a Schubert basis with nonnegative structure constants, eliminating the negative constants that can appear in [Reference Pawlowski and Rhoades21].
${\mathbb {W}}_{n,k}$ [Reference Pawlowski and Rhoades21]. In particular, it would be interesting to see if this larger module allows for the definition of a Schubert basis with nonnegative structure constants, eliminating the negative constants that can appear in [Reference Pawlowski and Rhoades21].
We close with a discussion of the superspace coinvariant problem [Reference Zabrocki34] which was a key motivation of this work. As mentioned in the Introduction, it is equivalent to the following.
Conjecture 6.3. Let ![]() $\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ be the ideal generated by
$\langle (\Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ be the ideal generated by ![]() ${\mathfrak {S}}_n$-invariants with vanishing constant term. For any k, we have
${\mathfrak {S}}_n$-invariants with vanishing constant term. For any k, we have
where q tracks x-degree and z tracks ![]() $\theta $-degree.
$\theta $-degree.
Let ![]() $k \leq n$ be positive integers, and let
$k \leq n$ be positive integers, and let ![]() $\Omega _n^{(n-k)}$ be the piece of
$\Omega _n^{(n-k)}$ be the piece of ![]() $\Omega _n$ of homogeneous
$\Omega _n$ of homogeneous ![]() $\theta $-degree
$\theta $-degree ![]() $n-k$, viewed as a free
$n-k$, viewed as a free ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$-module of rank
${\mathbb {Q}}[x_1, \dots , x_n]$-module of rank ![]() ${n \choose k}$. We define two submodules
${n \choose k}$. We define two submodules ![]() $A_{n,k}, B_{n,k} \subseteq \Omega ^{(n-k)}$ in terms of generating sets as follows. Let
$A_{n,k}, B_{n,k} \subseteq \Omega ^{(n-k)}$ in terms of generating sets as follows. Let ![]() $\mathcal {E} = \sum _{i = 1}^n \frac {\partial }{\partial x_i} \theta _i$ be the Euler operator.
$\mathcal {E} = \sum _{i = 1}^n \frac {\partial }{\partial x_i} \theta _i$ be the Euler operator.
 $$ \begin{align} B_{n,k} &= \langle e_j(S) \cdot \theta_T \,:\, j \geq 1, \, \, S \sqcup T = [n], \, \, |T| = n - k \rangle + \notag \\ &\langle \mathcal{E}(p_j) \cdot \theta_{T'} \,:\, j \geq 1, \, \, T' \subseteq [n], \, \, |T'| = n-k-1 \rangle + \langle x_i^k \cdot \theta_T \,:\, T \subseteq [n], \, \, |T| = n-k \rangle. \end{align} $$
$$ \begin{align} B_{n,k} &= \langle e_j(S) \cdot \theta_T \,:\, j \geq 1, \, \, S \sqcup T = [n], \, \, |T| = n - k \rangle + \notag \\ &\langle \mathcal{E}(p_j) \cdot \theta_{T'} \,:\, j \geq 1, \, \, T' \subseteq [n], \, \, |T'| = n-k-1 \rangle + \langle x_i^k \cdot \theta_T \,:\, T \subseteq [n], \, \, |T| = n-k \rangle. \end{align} $$ Both of the submodules ![]() $A_{n,k}, B_{n,k} \subseteq \Omega _n^{(n-k)}$ are homogeneous under the x-grading and stable under the
$A_{n,k}, B_{n,k} \subseteq \Omega _n^{(n-k)}$ are homogeneous under the x-grading and stable under the ![]() ${\mathfrak {S}}_n$-action. While their generating sets are similar, they differ as follows:
${\mathfrak {S}}_n$-action. While their generating sets are similar, they differ as follows:
• The generators
 $e_j \cdot \theta _T$ of
$e_j \cdot \theta _T$ of  $A_{n,k}$ involve elementary symmetric polynomials in the full variable set
$A_{n,k}$ involve elementary symmetric polynomials in the full variable set  $\{x_1, \dots , x_n\}$, whereas the corresponding generators
$\{x_1, \dots , x_n\}$, whereas the corresponding generators  $e_j(S) \cdot \theta _T$ of
$e_j(S) \cdot \theta _T$ of  $B_{n,k}$ involve a ‘separation of variables’ with
$B_{n,k}$ involve a ‘separation of variables’ with  $S \sqcup T = [n]$.
$S \sqcup T = [n]$.• The submodule
 $B_{n,k}$ has generators of the form
$B_{n,k}$ has generators of the form  $x_i^k \cdot \theta _T$ which are not present in
$x_i^k \cdot \theta _T$ which are not present in  $A_{n,k}$.
$A_{n,k}$.
Proposition 6.4. Let ![]() $n \geq k$ be positive integers, and let
$n \geq k$ be positive integers, and let ![]() $\langle ( \Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ be the ideal generated by
$\langle ( \Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ be the ideal generated by ![]() ${\mathfrak {S}}_n$-invariants with vanishing constant term. Also let
${\mathfrak {S}}_n$-invariants with vanishing constant term. Also let ![]() $I_{n,k} = {\mathrm {ann}} \, \delta _{n,k} \subseteq \Omega _n$ be the defining ideal of
$I_{n,k} = {\mathrm {ann}} \, \delta _{n,k} \subseteq \Omega _n$ be the defining ideal of ![]() ${\mathbb {W}}_{n,k}$. We have
${\mathbb {W}}_{n,k}$. We have
Therefore, Conjecture 6.3 is equivalent to the isomorphism of graded ![]() ${\mathfrak {S}}_n$-modules
${\mathfrak {S}}_n$-modules
Proof. The equality ![]() $\langle ( \Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \cap \Omega _n^{(n-k)} = A_{n,k}$ follows from a beautiful result of Solomon [Reference Solomon30]: the ideal
$\langle ( \Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \cap \Omega _n^{(n-k)} = A_{n,k}$ follows from a beautiful result of Solomon [Reference Solomon30]: the ideal ![]() $\langle ( \Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ is generated by
$\langle ( \Omega _n)^{{\mathfrak {S}}_n}_+ \rangle \subseteq \Omega _n$ is generated by ![]() $e_1, e_2, \dots , e_n$ together with
$e_1, e_2, \dots , e_n$ together with ![]() $\mathcal {E}(p_1), \mathcal {E}(p_2), \dots , \mathcal {E}(p_n)$. In fact, either list of polynomials
$\mathcal {E}(p_1), \mathcal {E}(p_2), \dots , \mathcal {E}(p_n)$. In fact, either list of polynomials ![]() $e_1, \dots , e_n$ and
$e_1, \dots , e_n$ and ![]() $p_1, \dots , p_n$ could be replaced by any algebraically independent set of generators of the ring
$p_1, \dots , p_n$ could be replaced by any algebraically independent set of generators of the ring ![]() ${\mathbb {Q}}[x_1, \dots , x_n]^{{\mathfrak {S}}_n}$ of symmetric polynomials and this assertion would remain true.
${\mathbb {Q}}[x_1, \dots , x_n]^{{\mathfrak {S}}_n}$ of symmetric polynomials and this assertion would remain true.
The second equality ![]() $I_{n,k} \cap \Omega _n^{(n-k)} = B_{n,k}$ may be deduced as follows. From the definition of
$I_{n,k} \cap \Omega _n^{(n-k)} = B_{n,k}$ may be deduced as follows. From the definition of ![]() $I_{n,k}$, we see that
$I_{n,k}$, we see that ![]() $I_{n,k} \cap \Omega _n^{(n-k)}$ is generated by
$I_{n,k} \cap \Omega _n^{(n-k)}$ is generated by ![]() $B_{n,k}$ together with generators of the form
$B_{n,k}$ together with generators of the form
where the union ![]() $S \cup T = [n]$ need not be disjoint. If we consider such a generator
$S \cup T = [n]$ need not be disjoint. If we consider such a generator ![]() $e_j(S) \cdot \theta _T$, we may write the set S as a disjoint union
$e_j(S) \cdot \theta _T$, we may write the set S as a disjoint union ![]() $S = S_1 \sqcup S_2$, where
$S = S_1 \sqcup S_2$, where ![]() $S_1 = S - T$ and
$S_1 = S - T$ and ![]() $S_2 = S \cap T$. The identity
$S_2 = S \cap T$. The identity
 $$ \begin{align} e_j(S) \cdot \theta_T = e_j(S_1 \sqcup S_2) \cdot \theta_T = \sum_{a + b = j} e_a(S_1) \cdot e_b(S_2) \cdot \theta_T \end{align} $$
$$ \begin{align} e_j(S) \cdot \theta_T = e_j(S_1 \sqcup S_2) \cdot \theta_T = \sum_{a + b = j} e_a(S_1) \cdot e_b(S_2) \cdot \theta_T \end{align} $$and the assumption ![]() $j> |S| - k = |S_1| + |S_2| - k$ imply that all nonvanishing terms
$j> |S| - k = |S_1| + |S_2| - k$ imply that all nonvanishing terms ![]() $e_a(S_1) \cdot e_b(S_2) \cdot \theta _T$ in this sum satisfy
$e_a(S_1) \cdot e_b(S_2) \cdot \theta _T$ in this sum satisfy ![]() $a> 0$ and are, therefore, members of
$a> 0$ and are, therefore, members of ![]() $B_{n,k}$.
$B_{n,k}$.
Proposition 6.4 gives a side-by-side comparison of the ![]() ${\mathfrak {S}}_n$-modules on either side of the conjecture (1.17) as explicit quotients of the same free
${\mathfrak {S}}_n$-modules on either side of the conjecture (1.17) as explicit quotients of the same free ![]() ${\mathbb {Q}}[x_1, \dots , x_n]$-module. The authors hope that this will help shed light on the ring of superspace coinvariants.
${\mathbb {Q}}[x_1, \dots , x_n]$-module. The authors hope that this will help shed light on the ring of superspace coinvariants.
In the case of only commuting variables, the theory of orbit harmonics (see [Reference Rhoades25] for an exposition) has been successfully applied to discover and study a variety of combinatorial quotient rings [Reference Garsia and Procesi7, Reference Griffin9, Reference Kostant16, Reference Kroes and Rhoades17, Reference Tanisaki32] including the ring ![]() $R_{n,k}$ [Reference Haglund, Rhoades and Shimozono13]. Conjecture 6.3 would ideally be attacked by extending orbit harmonics to the fermionic setting, with the ideals in Proposition 6.4 arising in quotient rings thereby. Such an extension would ideally incorporate the quotient rings in [Reference Billey, Rhoades and Tewari5, Reference Kroes and Rhoades17] which involve fermionic variables.
$R_{n,k}$ [Reference Haglund, Rhoades and Shimozono13]. Conjecture 6.3 would ideally be attacked by extending orbit harmonics to the fermionic setting, with the ideals in Proposition 6.4 arising in quotient rings thereby. Such an extension would ideally incorporate the quotient rings in [Reference Billey, Rhoades and Tewari5, Reference Kroes and Rhoades17] which involve fermionic variables.
Acknowledgments
The authors are grateful to Tianyi Yu for helpful conversations as well as anonymous referees for their helpful comments which significantly improved this paper. B. Rhoades was partially supported by National Science Foundation grant DMS-1953781.B. Rhoades and A. T. Wilson contributed equally to this project.
Conflict of Interest
The authors have no conflict of interest to declare.
Data availability statement
None.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Supplementary material
There is no supplementary material for this submission.