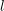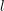1 Introduction
In its most elementary form, Bezout’s theorem states that a subset of
$\mathbb{C}^{n}$
defined by equations
$P_{1},\ldots ,P_{n}$
of respective degrees
$d_{1},\ldots ,d_{n}$
can have at most
$d_{1}\cdots d_{n}$
isolated points. Various generalizations of this statement have been proposed. For example, the Bernstein–Kushnirenko–Khovanskii theorem estimates the number of isolated points in terms of the mixed volume of the Newton polytopes
$\unicode[STIX]{x1D6E5}(P_{1}),\ldots ,\unicode[STIX]{x1D6E5}(P_{n})$
. As a consequence of the Bezout theorem and its generalizations, whenever a set defined within the algebraic category happens to be finite, one can produce effective estimates for the size of the set (which often turn out to be fairly accurate).
In this paper we consider generalizations of Bezout’s bound for systems of differential equations. The fundamental question is as follows: given a system of algebraic conditions on an
$n$
-tuple of functions and their first
$l$
derivatives, which admits finitely many solutions, can one estimate the number of solutions in terms of the degrees of the equations involved?
This question has been considered by Hrushovski and Pillay in [Reference Hrushovski and PillayHP00]. Their result, quoted in Theorem 2 below, is a powerful analog of the Bezout theorem which similarly allows one to translate qualitative finiteness results obtained using differential-algebraic and model-theoretic methods into effective estimates (two examples of a diophantine nature are discussed below).
The explicit estimate in Theorem 2 is stated in terms of slightly different algebraic data than our naive formulation of the Bezout bound, making it difficult to make a direct comparison. Nonetheless, it is clear that the Bezout bound has two advantages. First, the Bezout bound and its various generalizations are singly-exponential with respect to the ambient dimension, whereas Theorem 2 admits doubly-exponential growth. Second, assuming for example that all equations involved have degree
$d$
, the Bezout bound is a polynomial in
$d$
with exponent equal to the ambient dimension. This is the natural asymptotic for solutions of
$n$
-dimensional systems of equations, and is known of course to be optimal in the algebraic context. The bound of Theorem 2 depends polynomially on the degree as well, but the exponent can in general be much larger than the ambient dimension (indeed, exponentially large).
Our principal result is an estimate which recovers the two asymptotic properties above in the differential algebraic context. The statements are presented in §1.2, with formulations in terms of degrees and, more generally, mixed volumes of Newton polytopes.
Theorem 2 has been applied to produce effective bounds for some diophantine counting problems:
-
(i) In [Reference Hrushovski and PillayHP00] Theorem 2 was used to derive bounds on the number of transcendental lattice points on algebraic subvarieties of semi-abelian varieties. In particular, in the case of the two-dimensional torus this allowed the authors to produce doubly-exponential bounds for a counting problem due to Bombieri, improving the previous repeated-exponential bounds obtained by Buium [Reference BuiumBui95b].
-
(ii) More recently, Theorem 2 has been used in [Reference Freitag and ScanlonFS14] to derive bounds on the number of intersections between isogeny classes of elliptic curves and algebraic varieties. In particular, in the two-dimensional case this allowed the authors to produce doubly-exponential bounds for a counting problem due to Mazur.
Both of these applications follow the same principal strategy, inspired by the work of Buium [Reference BuiumBui92, Reference BuiumBui93] (see [Reference PillayPil97, Reference ScanlonSca01] for surveys). Namely, given a counting problem of a diophantine nature (over
$\mathbb{C}$
, for example) one first expands the structure by adjoining to
$\mathbb{C}$
a differential operator making it into a differentially-closed field with field of constants
$\bar{\mathbb{Q}}$
. One then writes a system of differential algebraic conditions satisfied by the solutions of the diophantine problem. Finally, one shows (and this is naturally the deeper step involving arguments specific to the problem at hand) that the system, while possibly admitting more solutions than the original diophantine problem, still admits finitely many solutions.
After carrying out the steps above, one can use Theorem 2 to produce an explicit estimate for the number of solutions of the diophantine problem. In §5 we apply our estimates to obtain refined (singly-exponential) bounds for problems (i) and (ii) above.
1.1 Setup and notation
Let
$K$
denote a differentially-closed field of characteristic zero with a derivation
$D$
, and
$K_{0}$
its field of constants. Let
$M$
denote an ambient space, which we will take to be either an affine space
$K^{n}$
or a Zariski open dense subset thereof. Denote by
$\unicode[STIX]{x1D709}$
a coordinate on
$M$
. We define the
$l$
th prolongation as
$M^{(l)}=M\times K^{nl}$
, and denote by
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}^{(0)},\unicode[STIX]{x1D709}^{(1)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
coordinates on
$M^{(l)}$
. For simplicity of notation we denote
$s:=\dim M^{(l)}=n(l+1)$
. We denote by
$\unicode[STIX]{x1D70B}_{M}:M^{(l)}\rightarrow M$
the projection onto
$M$
. If there is no ambiguity we omit
$M$
from this notation.
For any
$x\in M$
, denote by
$x^{(l)}\in M^{(l)}$
the
$l$
-jet of
$x$
, i.e. the element
$(x,\ldots ,D^{l}x)$
. We denote by
${\mathcal{J}}^{l}(M)\subset M^{(l)}$
the set of all
$l$
-jets in
$M^{(l)}$
,
$$\begin{eqnarray}{\mathcal{J}}^{l}(M):=\{x^{(l)}:x\in M\}.\end{eqnarray}$$
Let
$\unicode[STIX]{x1D6FA}^{(l)}\subset M^{(l)}$
denote a Zariski open dense subset of
$M^{(l)}$
(we include
$l$
in the notation
$\unicode[STIX]{x1D6FA}^{(l)}$
in the interest of clarity, but this is in fact an arbitrary open dense set). If we do not explicitly specify
$\unicode[STIX]{x1D6FA}^{(l)}$
then it is taken to be equal to
$M^{(l)}$
.
Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a Zariski closed set. We view
$S$
as a system of algebraic-differential conditions on
$M$
. We say that
$x\in M$
is a solution for
$S$
if
$x^{(l)}\in S$
. We define the reduction of
$S$
, denoted
${\mathcal{R}}(S)\subset S$
, to be
$$\begin{eqnarray}{\mathcal{R}}(S):=\operatorname{Clo}[{\mathcal{J}}^{l}(M)\cap S]\end{eqnarray}$$
where
$\operatorname{Clo}$
denotes Zariski closure. In other words, the reduction of
$S$
is the Zariski closure of the set of jets of the solutions of
$S$
. If
$S$
admits finitely many solutions then
${\mathcal{R}}(S)$
is the set consisting of their jets. In this case we denote the number of solutions by
${\mathcal{N}}(S)$
.
Example 1. Suppose
$M=K^{2}$
with coordinates
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
, and consider the set
$S\subset M^{(1)}$
given by the conditions
$\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}=1$
and
$\unicode[STIX]{x1D709}^{(1)}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}^{(1)}=1$
. Then
$\dim S=2$
. However, it is clear that
$S$
admits no solutions, since deriving the first condition we see that any solution must also satisfy
$\unicode[STIX]{x1D709}^{(1)}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}^{(1)}=0$
, contradicting the second condition. Thus
${\mathcal{R}}(S)=\emptyset$
.
In [Reference Hrushovski and PillayHP00], Hrushovski and Pillay considered the problem of estimating
${\mathcal{N}}(S)$
in terms of the algebraic degree of
$S$
. In particular, using differential algebraic methods, they have established the following estimate.
Theorem 2 [Reference Hrushovski and PillayHP00, Proposition 3.1].
Let
$X\subset M$
and
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be Zariski closed. Denote
$m:=\dim X$
. Denote
$T=S\cap \unicode[STIX]{x1D70B}^{-1}(X)$
and suppose that
$T$
admits finitely many solutions. Then
$$\begin{eqnarray}{\mathcal{N}}(T)\leqslant \deg (X)^{l2^{ml}}\deg (S)^{2^{ml}-1}.\end{eqnarray}$$
1.2 Statement of our results
Recall that for a Laurent polynomial
$P$
in the
$\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables (over
$K$
), its Newton polytope denoted
$\unicode[STIX]{x1D6E5}(P)$
is defined to be the convex hull of the set of exponents (of terms with non-zero coefficients) of
$P$
, viewed as a subset of
$\mathbb{R}^{s}$
. We say that
$\unicode[STIX]{x1D6E5}$
is a lattice polytope if it is obtained as the Newton polytope of some Laurent polynomial. We will denote by
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{(j)}}$
the standard simplex in the
$\unicode[STIX]{x1D709}^{(j)}$
variables, and by
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
the standard simplex in the
$\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables.
Recall that for
$s$
convex bodies
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s}$
in
$\mathbb{R}^{s}$
, their mixed volume is defined to be
$$\begin{eqnarray}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s})=\frac{\unicode[STIX]{x2202}^{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}_{1}\cdots \unicode[STIX]{x2202}\unicode[STIX]{x1D706}_{s}}\operatorname{Vol}(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D706}_{s}\unicode[STIX]{x1D6E5}_{s})|_{\unicode[STIX]{x1D706}_{1}=\cdots =\unicode[STIX]{x1D706}_{s}=0^{+}}.\end{eqnarray}$$
The mixed volume is symmetric and multilinear, and generates the volume function in the sense that
$V(\unicode[STIX]{x1D6E5},\ldots ,\unicode[STIX]{x1D6E5})=\operatorname{Vol}(\unicode[STIX]{x1D6E5})$
. In fact, these properties completely determine the mixed volume function.
The following classical Bernstein–Kushnirenko–Khovanskii (BKK) theorem relates the number of solutions of a system of polynomial equations to the mixed volume of their Newton polytopes.
Theorem 3 [Reference KušnirenkoKuš76, Reference BernsteinBer75].
Let
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s}$
be lattice polytopes in
$\mathbb{R}^{s}$
. Then for any tuple
$P_{1},\ldots ,P_{s}$
with
$\unicode[STIX]{x1D6E5}(P_{i})=\unicode[STIX]{x1D6E5}_{i}$
, the system of equations
$P_{1}=\cdots =P_{s}=0$
admits at most
$\unicode[STIX]{x1D707}$
isolated solutions in
$(K^{\ast })^{s}$
, where
$$\begin{eqnarray}\unicode[STIX]{x1D707}=s!V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s})\end{eqnarray}$$
and
$V(\cdots \,)$
denotes the mixed volume. Moreover, for a sufficiently generic choice of the tuple
$P_{i}$
the bound
$\unicode[STIX]{x1D707}$
is attained.
Remark 4. Under some mild conditions, the BKK estimate also bounds the number of zeros in
$K^{s}$
. For instance, this is true if each
$\unicode[STIX]{x1D6E5}_{i}$
is the convex hull of a finite co-ideal
$I_{i}\subset \mathbb{Z}_{{\geqslant}0}$
(since in this case one can always, after a generic translation, assume that none of the solutions lie on the coordinate axes). We will refer to such polytopes as co-ideal polytopes. The common case of the polytope of polynomials with bounded degree or multi-degree certainly satisfies this condition.
Our results can be applied either to
$(K^{\ast })^{s}$
or to
$K^{s}$
, but in the latter case we always assume that all polytopes involved are co-ideal polytopes.
Our main result is an analog of the first part of the BKK theorem. Namely, for a system of algebraic-differential conditions
$S$
admitting finitely many solution, we estimate the number of solutions in terms of a mixed volume of the Newton polytopes associated to the equations defining
$S$
. Note that our various formulations are stated in terms of the degrees/polytopes of the equations defining
$S$
, whereas Theorem 2 is stated in terms of the algebraic degree of
$S$
as a variety. The proofs of the various statements are given in §4.
Remark 5. The reader unfamiliar with the theory of Newton polytopes may wish to assume on first reading that the Newton polytopes under consideration are of the form
$d\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
(this amounts to requiring that the polynomial equations in the
$\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables have degree bounded by
$d$
). Not much will be lost by considering only this special case, where the BKK theorem reduces to the Bezout theorem. In particular, the use of the BKK theorem is not essential for obtaining the single-exponential asymptotics of the constants in all of our results.
We begin with a formulation valid for complete intersections (for a slightly more general form valid for flat limits of complete intersections, see Proposition 29).
Theorem 6. Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a complete intersection defined by polynomials with Newton polytopes
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
, and suppose that
${\mathcal{N}}(S)<\infty$
. Denote
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}:=(s+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}+\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}.\end{eqnarray}$$
Then
$$\begin{eqnarray}{\mathcal{N}}(S)\leqslant C_{s,k}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k},\unicode[STIX]{x1D6E4},\ldots ,\unicode[STIX]{x1D6E4}),\quad C_{s,k}=s!(\unicode[STIX]{x1D6FF}+2)^{\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+1)/2},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}:=s-k$
.
We note that the factor of
$s!$
in
$C_{s,k}$
is the usual factor appearing in the BKK theorem. The additional factor is an artifact of our construction and could certainly be improved somewhat.
We next present a result valid for arbitrary varieties rather than complete intersections.
Theorem 7. Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety with
${\mathcal{N}}(S)<\infty$
. Suppose that:
-
(i)
$S$
is contained in a complete intersection defined by polynomials with Newton polytopes
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
; -
(ii)
$S$
is set-theoretically cut out by equations whose Newton polytopes are contained in a polytope
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. To simplify the notation we write
$\unicode[STIX]{x1D6E5}_{j}=\unicode[STIX]{x1D6E5}$
for
$j>k$
.
Denote
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{j}:=(s+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}+\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{j}.\end{eqnarray}$$
Then
$$\begin{eqnarray}{\mathcal{N}}(S)\leqslant \mathop{\sum }_{j=k}^{s}C_{s,j}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{j},\unicode[STIX]{x1D6E4}_{j},\ldots ,\unicode[STIX]{x1D6E4}_{j}).\end{eqnarray}$$
In particular, assuming
$\unicode[STIX]{x1D6E5}_{j}\subset \unicode[STIX]{x1D6E5}$
for
$j=1,\ldots ,k$
, we have
$$\begin{eqnarray}{\mathcal{N}}(S)\leqslant E_{s,k}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k},\unicode[STIX]{x1D6E5},\ldots ,\unicode[STIX]{x1D6E5}),\quad E_{s,k}=\mathop{\sum }_{j=k}^{s}(2s)^{s-j}C_{s,k}.\end{eqnarray}$$
As an immediate consequence we obtain the following analog of the Kushnirenko theorem.
Corollary 8. Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety of top dimension
$s-k$
cut out by equations whose Newton polytopes are contained in a polytope
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. Suppose that
$S$
admits finitely many solutions. Then
$$\begin{eqnarray}{\mathcal{N}}(S)\leqslant E_{s,k}\operatorname{Vol}(\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
Proof. Let
${\mathcal{P}}$
denote the given collection of polynomials with Newton polytopes contained in
$\unicode[STIX]{x1D6E5}$
which set theoretically cut out
$S$
. We define a sequence of polynomials
$P_{1},\ldots ,P_{k}\in {\mathcal{P}}$
as follows: for
$j=1$
let
$P_{1}\in {\mathcal{P}}$
be a non-zero polynomial; for
$j<k$
and assuming
$P_{j}$
is already constructed, let
$P_{j+1}\in {\mathcal{P}}$
be any polynomial which is not identically vanishing on any component of
$\{P_{1}=\cdots =P_{j}=0\}$
. Such a polynomial must exist since otherwise a component of
$\{P_{1}=\cdots =P_{j}=0\}$
is a component of
$S$
, which is ruled out by our assumption on the dimension of
$S$
.
It follows by an easy induction that the intersection
$P_{1}=\cdots =P_{k}=0$
is a complete intersection and the claim of the theorem now follows by application of Theorem 7.◻
More generally, for systems admitting infinitely many solutions we have similar estimates for the degree of their reduction. Here the degree of an irreducible variety in
$\unicode[STIX]{x1D6FA}^{(l)}$
is defined to be the number of intersections with a generic affine-linear space of complementary dimension, and this notion is extended by linearity to arbitrary (possible mixed-dimensional) varieties. We give an analog of the second part of Theorem 7 (but the other part extends in a similar manner).
Theorem 9. Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
and suppose that:
-
(i)
$S$
is contained in a complete-intersection defined by polynomials with Newton polytopes
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
; -
(ii)
$S$
is set-theoretically cut out by equations whose Newton polytopes are contained in a polytope
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
.
Assume further that
$\unicode[STIX]{x1D6E5}_{j}\subset \unicode[STIX]{x1D6E5}$
for
$j=1,\ldots ,k$
. Then
$$\begin{eqnarray}\deg ({\mathcal{R}}(S))\leqslant (s-k+1)E_{s,k}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k},\unicode[STIX]{x1D6E5},\ldots ,\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
The proof of the following corollary is similar to that of Corollary 8.
Corollary 10. Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety of top dimension
$s-k$
cut out by equations whose Newton polytope are contained in a polytope
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. Then
$$\begin{eqnarray}\deg ({\mathcal{R}}(S))\leqslant (s-k+1)E_{s,k}\operatorname{Vol}(\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
Finally, we record a statement with a formulation more similar to that of Theorem 2. In particular, it shows that for a fixed system of differential conditions
$S$
, the number of solutions within a variety
$X$
defined by equations of degrees bounded by
$d_{X}$
grows asymptotically like
$d_{X}^{n}$
, which is the expected order of growth (even in a purely algebraic context).
Corollary 11. Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety of top dimension
$s-k$
cut out by equations of degrees at most
$d_{S}$
and
$X\subset M$
be a variety cut out by equations of degrees at most
$d_{X}\geqslant d_{S}$
. Denote
$T=S\cap \unicode[STIX]{x1D70B}^{-1}(X)$
and suppose that
$T$
admits finitely many solutions. Then
$$\begin{eqnarray}{\mathcal{N}}(T)\leqslant \frac{E_{s,k}}{s!}d_{X}^{n}d_{S}^{nl}.\end{eqnarray}$$
More generally, without the assumption that
$T$
admits finitely many solutions, we have
$$\begin{eqnarray}\deg ({\mathcal{R}}(T))\leqslant (s-k+1)\frac{E_{s,k}}{s!}d_{X}^{n}d_{S}^{nl}.\end{eqnarray}$$
Proof. We let
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{s}$
denote the polytope obtained from the polytope
$d_{S}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
by stretching each of the coordinates
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n})$
by a factor of
$d_{X}/d_{S}$
. In particular,
$\unicode[STIX]{x1D6E5}$
contains both
$d_{S}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
and
$d_{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
, i.e. it contains the Newton polytopes of the given equations for
$S$
and
$\unicode[STIX]{x1D70B}^{-1}(X)$
. It remains to note that
$$\begin{eqnarray}\operatorname{Vol}(\unicode[STIX]{x1D6E5})=(d_{X}/d_{S})^{n}d_{S}^{n(l+1)}(s!)^{-1}\end{eqnarray}$$
1.3 Elementary differential algebraic constructions
For any Zariski closed set
$V\subset M$
we define the
$l$
th prolongation
$V^{(l)}\subset M^{(l)}$
to be the Zariski closure of
$\{x^{(l)}:x\in V\}$
. The prolongation of a finite union of closed sets is clearly equal to the union of their prolongations. Moreover, by a theorem of Kolchin [Reference KolchinKol73], the prolongation of an irreducible set is itself irreducible.
The following encapsulates a key property of differentially closed fields.
Fact 12 [Reference Hrushovski and PillayHP00, Fact 3.7].
Let
$V$
denote an irreducible variety and
$W\subset V^{(1)}$
an irreducible variety which projects dominantly on
$V$
. Then for any non-empty Zariski open subset
$U\subset W$
there exists
$x\in V$
with
$x^{(1)}\in U$
.
We denote
${M^{(l)}}^{(1)}:=(M^{(l)})^{(1)}$
, and similarly for
${x^{(l)}}^{(1)}$
. We have a canonical variety
$\unicode[STIX]{x1D6EF}\subset {M^{(l)}}^{(1)}$
defined to be the Zariski closure of
$\{{x^{(l)}}^{(1)}:x\in M\}$
. It is given by the equations
${\unicode[STIX]{x1D709}^{(k)}}^{(0)}={\unicode[STIX]{x1D709}^{(k-1)}}^{(1)}$
for
$k=1,\ldots ,l$
.
Proposition 13. The points
$y\in M^{(l)}$
that satisfy
$y^{(1)}\in \unicode[STIX]{x1D6EF}$
are precisely the points of the form
$x^{(l)}$
for some
$x\in M$
.
Proof. Let
$y=(x_{0},x_{1},\ldots ,x_{l})$
with
$y^{(1)}=(y,Dy)\in \unicode[STIX]{x1D6EF}$
. It follows that
$x_{k}=Dx_{k-1}$
for
$k=1,\ldots ,l$
, so
$y=(x_{0})^{(l)}$
as claimed. The other direction is obvious.◻
Lemma 14. Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety admitting finitely many solutions. Then
$S^{(1)}\cap \unicode[STIX]{x1D6EF}$
does not project dominantly on any positive-dimensional component of
$S$
. More generally, the same holds if
${\mathcal{R}}(S)$
does not contain any component of
$S$
.
Proof. It is enough to check the case of
$S$
irreducible (and positive-dimensional). Let
$U=\unicode[STIX]{x1D6FA}^{(l)}\setminus {\mathcal{R}}(S)$
. By assumption,
$U\cap S$
is open dense in
$S$
.
Assume toward contradiction that
$S^{(1)}\cap \unicode[STIX]{x1D6EF}$
projects dominantly on
$S$
. Then some irreducible component
$W$
of this intersection projects dominantly on
$S$
as well. Thus we can apply Fact 12 to the non-empty open subset
$W\cap \unicode[STIX]{x1D70B}^{-1}(U)$
and deduce that there exists
$y\in U$
with
$y^{(1)}\in S^{(1)}\cap \unicode[STIX]{x1D6EF}$
. But by Proposition 13 such
$y$
is of the form
$z^{(l)}$
for some
$z\in M$
, and hence
$z$
is another solution of
$S$
, contradicting the definition of
$U$
.◻
1.4 Overview of the proof
1.4.1 The reduction of dimension
Let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety of positive dimension admitting finitely many solutions, and let
$\widetilde{S}:=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6FA}^{(l)}}(S^{(1)}\cap \unicode[STIX]{x1D6EF})$
. Then by Lemma 14 we have
$\dim \widetilde{S}<\dim S$
. If
$x\in M$
is any solution of
$S$
, then
$x^{(l)}\in S$
and hence
${x^{(l)}}^{(1)}\in S^{(1)}\cap \unicode[STIX]{x1D6EF}$
, so
$x^{(l)}\in \widetilde{S}$
. That is,
$x$
is also a solution of
$\widetilde{S}$
. Since
$\widetilde{S}\subset S$
we conclude that
${\mathcal{N}}(S)={\mathcal{N}}(\widetilde{S})$
.
Repeating this reduction
$s$
times, one is eventually reduced to counting the number of solutions of a zero-dimensional variety, which is certainly bounded by the number of points in the variety. This is similar to the approach employed in [Reference Hrushovski and PillayHP00]. In order to obtain good effective estimates it is thus necessary to have an effective description of
$\widetilde{S}$
in terms of
$S$
, and the key step is obtaining an effective description of
$S^{(1)}$
.
1.4.2 An approximation for the first prolongation
We now work with an arbitrary ambient space
$N$
, and the reader should keep in mind that eventually we will take this ambient space to be
$M^{(l)}$
or its open dense subset
$\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
$N$
by
$\unicode[STIX]{x1D701}$
.
If
$V\subset N$
is an effectively smooth complete intersection defined by
$k$
polynomial equations
$\{P_{j}\}$
with a given Newton polytope
$\unicode[STIX]{x1D6E5}$
, then one can explicitly write
$2k$
equations in
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}$
for
$V^{(1)}$
, with (essentially) the same Newton polytope in
$\unicode[STIX]{x1D701}$
and linear in
$\unicode[STIX]{x1D701}^{(1)}$
. However, this system of equations degenerates if
$V$
is a non-smooth intersection.
Our proof is based on the following idea. We embed
$V$
as the zero fiber
$V=X_{0}$
of a flat family
$X$
whose generic fiber is a complete intersection. Making a small perturbation, we may also assume that the generic fiber is smooth. We write the system of
$2k$
equations as above (now depending on an extra deformation parameter
$e$
), obtaining a family
$\unicode[STIX]{x1D70F}(X)$
. It turns out that the limit
$\unicode[STIX]{x1D70F}(X)_{0}$
, while not necessarily equal to
$V^{(1)}$
, still approximates it rather well: the two agree over an open dense set. To conclude, if
$V$
is a limit of a family of complete intersections of a given Newton polytope, then the same is essentially true for
$V^{(1)}$
(at least in an open dense set).
1.4.3 Conclusion
Returning now to the notation of §1.4.1, we show that if
$S$
was the limit of a family of complete intersections with a given Newton polytope, then the same is true for
$\widetilde{S}$
(with a slightly larger Newton polytope). We may now repeat the construction
$s$
times and eventually obtain the limit of a zero-dimensional variety. Of course, the number of points of such a limit is bounded by the number of points of the generic fiber, which may now be estimated with the help of the BKK theorem.
2 Smooth approximations and flat families
In this section we denote the ambient space by
$N$
and its dimension by
$n$
. The reader should keep in mind that eventually we will take this ambient space to be
$M^{(l)}$
or its open dense subset
$\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
$N$
by
$\unicode[STIX]{x1D701}$
.
2.1 The
$\unicode[STIX]{x1D70F}$
-variety associated to a flat family
Let
$V\subset N$
be given by
$$\begin{eqnarray}V=\{P_{1}=\cdots =P_{k}=0\},\quad P_{j}\in K[\unicode[STIX]{x1D701}].\end{eqnarray}$$
We define
$\unicode[STIX]{x1D70F}(V)\subset N^{(1)}$
to be
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(V):=\{(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}):P_{j}(\unicode[STIX]{x1D701})=0,(dP_{j})_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D701}^{(1)})+P_{j}^{D}(\unicode[STIX]{x1D701})=0,j=1,\ldots ,k\},\end{eqnarray}$$
where
$P^{D}$
is the polynomial obtained by applying
$D$
to each coefficient of
$P$
. It follows from the chain rule that
$V^{(1)}\subset \unicode[STIX]{x1D70F}(V)$
. Moreover, if
$V$
is effectively smooth (i.e. the differentials
$dP_{1},\ldots ,dP_{k}$
are linearly independent at every point of
$V$
) then equality holds [Reference Hrushovski and PillayHP00, Remark 3.5(3)], and in particular
$\unicode[STIX]{x1D70F}(V)$
has pure codimension
$2k$
in
$N^{(1)}$
(assuming
$V$
is non-empty).
Recall that a variety
$X\subset N\times \mathbb{A}_{K}$
is flat over
$\mathbb{A}_{K}$
if and only if every component of
$X$
projects dominantly on
$\mathbb{A}_{K}$
. For general
$X$
, we denote by
${\mathcal{F}}(X)$
the flat family obtained by removing any component which projects to a point in
$\mathbb{A}_{K}$
. For any
$\unicode[STIX]{x1D700}\in \mathbb{A}_{K}$
we denote by
$X_{\unicode[STIX]{x1D700}}$
the
$\unicode[STIX]{x1D700}$
-fiber of
$X$
.
Consider now a variety
$X\subset N\times \mathbb{A}_{K}$
given by
$$\begin{eqnarray}X={\mathcal{F}}[\{P_{1}=\cdots =P_{k}=0\}],\quad P_{j}\in K[\unicode[STIX]{x1D701},e],\end{eqnarray}$$
where
$e$
denotes a coordinate on
$\mathbb{A}_{K}$
. We say that
$X$
is a generic complete intersection if the generic fiber
$X_{\unicode[STIX]{x1D700}}$
has pure codimension
$k$
. We define
$\unicode[STIX]{x1D70F}(X)\subset N^{(1)}\times \mathbb{A}_{K}$
to be
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(X):={\mathcal{F}}[\{(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}):P_{j}(\unicode[STIX]{x1D701})=0,(dP_{j})_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D701}^{(1)})+P_{j}^{D}(\unicode[STIX]{x1D701})=0,j=1,\ldots ,k\}].\end{eqnarray}$$
For generic
$\unicode[STIX]{x1D700}\in K_{0}$
,
$\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}}$
is just
$\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}})$
. The following subsection establishes a precise sense in which
$\unicode[STIX]{x1D70F}(X)_{0}$
, obtained as the limit of these generic fibers, approximates
$(X_{0})^{(1)}$
.
2.2 Approximation of the first prolongation
In this section it will be convenient for us to assume that the field
$K$
has an analytic realization. We therefore assume that the field of constants
$K_{0}$
is a subfield of
$\mathbb{C}$
, and that all functions involved in the definition of any of the varieties we consider have been embedded in the field of meromorphic functions on the disc
$\mathbb{D}$
(this is always possible by a result of Seidenberg [Reference SeidenbergSei58, Reference SeidenbergSei69]). Thus we may consider
$K$
-varieties as analytic sets.
We begin with a simple lemma.
Lemma 15. Let
$X\subset N\times \mathbb{A}_{K}$
be a flat family, and
$x\in X_{0}$
. Then for any sequence
$\unicode[STIX]{x1D700}_{i}\in K_{0}$
with
$\unicode[STIX]{x1D700}_{i}\rightarrow 0$
, there exists a sequence of
$K$
-points
$x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
, holomorphic in a common disc and converging uniformly to
$x$
.
Proof. Intersecting with generic linear functionals vanishing at
$x$
, one can reduce the problem to the case that
$X$
is a curve. Moreover, changing coordinate
$e\rightarrow e^{\unicode[STIX]{x1D708}}$
, we may assume that the curve is irreducible, smooth and transversal to
$e$
at
$x$
in the
$K$
-sense, i.e. for generic
$t$
. We restrict the disc
$\mathbb{D}$
to make this true for every
$t$
.
Consider the intersection
$X\cap \{e=\unicode[STIX]{x1D700}_{i}\}$
. This is a zero-dimensional set, and for sufficiently small
$\unicode[STIX]{x1D700}_{i}$
contains precisely one solution
$x_{i}$
near
$x$
. All
$x_{i}$
are
$K$
-points and, moreover, are in fact defined over the field of definition of
$X$
. Therefore they may be viewed as (a priori, ramified) holomorphic functions on
$\mathbb{D}$
. But in fact
$x_{i}(t)$
is well defined for
$t\in \mathbb{D}$
, and thus no ramification can occur and the functions
$x_{i}(t)$
are holomorphic in
$\mathbb{D}$
. Finally,
$x_{i}$
converges pointwise to
$x$
by definition, and it follows by standard arguments that convergence is uniform (perhaps on a smaller disc).◻
We remark that since the Zariski topology is coarser than the analytic
$\mathbb{C}$
-topology, the converse also holds: if
$x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
is a sequence of
$K$
points holomorphic on a disc
$\mathbb{D}$
and converging uniformly to
$x\in K$
, then any Zariski closed set containing
$x_{i}$
for every
$i$
must contain
$x$
.
Proposition 16. Let
$X$
be a generic complete intersection as in (19). Then we have
$(X_{0})^{(1)}\subset \unicode[STIX]{x1D70F}(X)_{0}$
.
Proof. Since
$\unicode[STIX]{x1D70F}(X)_{0}$
is closed by definition, it is enough to prove that for every
$x\in X_{0}$
, we have
$x^{(1)}\in \unicode[STIX]{x1D70F}(X)_{0}$
. Let
$x\in X_{0}$
. Since the family
$X$
is flat, we can choose by Lemma 15 a sequence
$x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
with
$\unicode[STIX]{x1D700}_{i}\in K_{0}$
and
$\unicode[STIX]{x1D700}_{i}\rightarrow 0$
, converging uniformly to
$x$
. Then
$(x_{i})^{(1)}$
converges uniformly to
$x^{(l)}$
(in an appropriate disc). Since
$(X_{\unicode[STIX]{x1D700}_{i}})^{(1)}\subset \unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})$
and
$\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})=\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
by the remark following (20), we have
$(x_{i})^{(1)}\in \unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
. Since
$\unicode[STIX]{x1D70F}(X)$
is closed we conclude that
$x^{(l)}\in \unicode[STIX]{x1D70F}(X)_{0}$
as claimed.◻
For a variety
$V\subset N$
as in (17), we can describe
$\unicode[STIX]{x1D70F}(V)$
at effectively smooth points in terms of complex tangent spaces. Indeed, let
$x\in V$
be an effectively smooth
$K$
-point. Then
$V$
is smooth as a complex variety at
$x(t)$
for generic
$t$
and we have the equivalence
$$\begin{eqnarray}(x,v)\in \unicode[STIX]{x1D70F}(V)\;\Longleftrightarrow \;\unicode[STIX]{x2202}_{t}+v\cdot \unicode[STIX]{x2202}_{\unicode[STIX]{x1D701}}\in T_{x}V,\end{eqnarray}$$
where the right-hand side is understood to hold for generic
$t$
. In particular, if
$V$
is any variety then one can choose a system of equations such that it becomes effectively smooth at every smooth point. Thus, since we know that
$\unicode[STIX]{x1D70F}(V)$
agrees with
$V^{(1)}$
over the effectively smooth locus, we conclude that for every smooth point
$x\in V$
we also have
$$\begin{eqnarray}(x,v)\in V^{(1)}\;\Longleftrightarrow \;\unicode[STIX]{x2202}_{t}+v\cdot \unicode[STIX]{x2202}_{\unicode[STIX]{x1D701}}\in T_{x}V.\end{eqnarray}$$
The following proposition establishes a partial converse to Proposition 16.
Proposition 17. Let
$X$
be a generic complete intersection as in (19) such that the generic fiber
$X_{\unicode[STIX]{x1D700}}$
is effectively smooth. Then there is an open dense set
$U\subset X_{0}$
such that
$$\begin{eqnarray}(X_{0})^{(1)}\cap \unicode[STIX]{x1D70B}^{-1}(U)=\unicode[STIX]{x1D70F}(X)_{0}\cap \unicode[STIX]{x1D70B}^{-1}(U).\end{eqnarray}$$
Before proving this proposition, we illustrate with the following example.
Figure 1. Degeneration of
$\unicode[STIX]{x1D70F}(X)$
in Example 18.
Example 18. Consider
$X\subset \mathbb{A}_{K}^{2}\times \mathbb{A}_{K}$
given by
$y^{2}=ex$
(see Figure 1). Since the family is defined by an equation with constant coefficients,
$(X_{0})^{(1)}$
agrees with the tangent bundle of
$X_{0}$
. For generic
$\unicode[STIX]{x1D700}$
, the fiber
$X_{\unicode[STIX]{x1D700}}$
is an effectively smooth parabola, and for
$\unicode[STIX]{x1D700}$
constant
$\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}}$
agrees with the tangent bundle of this parabola.
The fiber
$\unicode[STIX]{x1D70F}(X)_{0}$
is the flat limit of
$\unicode[STIX]{x1D70F}(X)_{e}$
. Since
$\unicode[STIX]{x2202}_{y}$
is tangent to
$X_{\unicode[STIX]{x1D700}}$
at
$(x,y)=(0,0)$
for any
$\unicode[STIX]{x1D700}$
, the fiber of
$\unicode[STIX]{x1D70F}(X)_{0}$
over this point contains
$\unicode[STIX]{x2202}_{y}$
. Thus
$\unicode[STIX]{x1D70F}(X)_{0}$
is strictly larger than the tangent bundle of
$X_{0}$
. However, over any point of
$U:=X_{0}\setminus \{(0,0)\}$
, one can easily check that the limit of
$X_{\unicode[STIX]{x1D700}}$
agrees with the tangent bundle of
$X_{0}$
.
Proof of Proposition 17.
To avoid confusion, in this proof we make the convention that
$p$
denotes
$\mathbb{C}$
-points, whereas
$x$
denotes
$K$
-points.
Since the map
$e$
is flat on
$X$
(over
$K$
), it follows that for generic
$t$
there are no components of
$X$
contained in the
$e=0$
fiber. After restricting to a disc where this holds, the map
$e:X\rightarrow \mathbb{C}$
can be viewed as a flat map over
$\mathbb{C}$
. By a theorem of Hironaka [Reference HironakaHir77], there exists an analytic stratification
$\{Z_{\unicode[STIX]{x1D6FC}}\}$
of
$X_{0}$
with the following property: for any sequence of points
$p_{i}\in X$
converging to
$p\in Z_{\unicode[STIX]{x1D6FC}}$
, if
$X_{e(p_{i})}$
is smooth at
$p_{i}$
and
$T_{p_{i}}X_{e(p_{i})}$
converges to a limit
$T$
, then
$T_{p}Z_{\unicode[STIX]{x1D6FC}}\subset T$
. This is a somewhat weaker form of Thom’s
$A_{e}$
-condition, which will suffice for our purposes. We fix such a stratification, and let
$Z_{0}$
denote the (union of) top-dimensional strata.
The following observation is the key geometric idea for the proof. Let
$p_{i}\in X$
be any sequence of points converging to
$p\in Z_{0}$
with
$X_{e(p_{i})}$
smooth at
$p_{i}$
and
$v_{i}\in T_{p_{i}}X_{e(p_{i})}$
a sequence of tangent vectors converging to a vector
$v$
. Then
$v\in T_{p}X_{0}$
. Indeed, one can always pass to a subsequence such that
$T_{p_{i}}X_{e(p_{i})}$
converges to some limit
$T$
, and hence
$T_{p}Z_{0}\subset T$
. But since the dimensions of these sets agree, in fact
$T_{p}X_{0}=T_{p}Z_{0}=T$
, and in particular
$v\in T$
implies
$v\in T_{p}X_{0}$
.
We know by Proposition 16 that
$(X_{0})^{(1)}\subset \unicode[STIX]{x1D70F}(X)_{0}$
. The set of points in
$X_{0}$
such that the
$\unicode[STIX]{x1D70B}$
-fibers of these two sets are equal is
$K$
-constructible. Thus, if it does not contain an open dense set it must be contained in a closed set of strictly smaller dimension. Therefore it will suffice to establish the claim over any analytic open dense set
$U$
. We will establish it with
$U=Z_{0}$
. Thus, let
$(x,v)\in \unicode[STIX]{x1D70F}(X)_{0}$
with
$x\in Z_{0}$
, and we will prove that
$(x,v)\in (X_{0})^{(1)}$
.
Since
$\unicode[STIX]{x1D70F}(X)$
is flat by definition, we may by Lemma 15 choose a sequence
$\unicode[STIX]{x1D700}_{i}\in K_{0}$
with
$\unicode[STIX]{x1D700}_{i}\rightarrow 0$
and a sequence
$(x_{i},v_{i})\in \unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
such that
$(x_{i},v_{i})$
are defined in a common disc
$\mathbb{D}$
and converge uniformly to
$(x,v)$
. By assumption, we may take the fibers
$X_{\unicode[STIX]{x1D700}_{i}}$
to be effectively smooth. Also, by the remark following (20) we may assume that
$\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}=\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})$
. We conclude from (21) that
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}+v_{i}\cdot \unicode[STIX]{x2202}_{\unicode[STIX]{x1D701}}\in T_{x_{i}}X_{\unicode[STIX]{x1D700}_{i}}\end{eqnarray}$$
for generic
$t$
.
For
$t$
outside a countable set, each fiber
$X_{\unicode[STIX]{x1D700}_{i}}$
is effectively smooth (over
$\mathbb{C}$
) at
$x_{i}(t)$
. By the key geometric observation above it now follows that
$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}+v\cdot \unicode[STIX]{x2202}_{\unicode[STIX]{x1D701}}\in T_{x}X_{0}\end{eqnarray}$$
for generic
$t$
. Thus (22) gives
$(x,v)\in (X_{0})^{(1)}$
as claimed.◻
Corollary 19. Let
$X$
be a generic complete intersection as in (19) and suppose that the generic fiber
$X_{\unicode[STIX]{x1D700}}$
is effectively smooth. Then every component of
$(X_{0})^{(1)}$
is a component of
$\unicode[STIX]{x1D70F}(X)_{0}$
.
Proof. Indeed, if
$Z_{1},\ldots ,Z_{r}$
denote the components of
$X_{0}$
then they each have codimension
$k$
(since
$X$
is a flat family of pure codimension
$k$
), and
$Z_{i}^{(1)}$
are the components of
$(X_{0})^{(1)}$
. In particular,
$\unicode[STIX]{x1D70B}^{-1}(U)$
is dense in each
$Z_{i}^{(1)}$
(for
$U$
given in Proposition 17), and since
$\unicode[STIX]{x1D70F}(X)_{0}$
agrees with
$(X_{0})^{(1)}$
over
$\unicode[STIX]{x1D70B}^{-1}(U)$
it follows that each
$Z_{i}^{(1)}$
is also a component of
$\unicode[STIX]{x1D70F}(X)_{0}$
.◻
3 Constructions with flat families
Once again, in this section we denote the ambient space by
$N$
and its dimension by
$n$
. The reader should keep in mind that eventually we will take this ambient space to be
$M^{(l)}$
or its open dense subset
$\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
$N$
by
$\unicode[STIX]{x1D701}$
.
When speaking about the Newton polytope of a polynomial in
$K[\unicode[STIX]{x1D701},e]$
we mean the Newton polytope in the
$\unicode[STIX]{x1D701}$
variables obtained for a generic value of
$e$
.
3.1 General lemmas on perturbations and intersections in flat families
The following proposition shows that the
$0$
-fiber of a flat family is not changed if one makes a sufficiently small perturbation of the family, i.e. a perturbation of sufficiently high order in
$e$
.
Proposition 20. Let
$X\subset N\times \mathbb{A}_{K}^{2}$
be a variety, and suppose that every component of
$X$
projects dominantly on
$\mathbb{A}_{K}^{2}$
. Then the flat limit at the origin of
$X_{s,t}$
(as a variety) along
$\unicode[STIX]{x1D6E4}=\{t=0\}\subset \mathbb{A}_{K}^{2}$
is the same as the flat limit at the origin along any smooth curve
$\unicode[STIX]{x1D6E4}^{\prime }\subset \mathbb{A}_{K}^{2}$
sufficiently tangent to
$\unicode[STIX]{x1D6E4}$
.
Proof. We may assume that
$X$
is irreducible. Denote the projection to
$\mathbb{A}_{K}^{2}$
by
$\unicode[STIX]{x1D702}$
. Recall that
$N$
is an open dense subset of some projective space
$\mathbb{C}P^{S}$
. Let
$\bar{X}$
denote the closure of
$X$
in
$\mathbb{C}P^{S}\times \mathbb{A}_{K}^{2}$
, which clearly projects dominantly to
$\mathbb{A}_{K}^{2}$
as well.
Consider the map
$\unicode[STIX]{x1D6F7}$
taking a pair
$(s,t)$
to the fiber
$X_{s,t}:=\bar{X}\cap \unicode[STIX]{x1D702}^{-1}(s,t)$
with its cycle structure in the Chow variety parametrizing cycles of degree
$\deg X$
in
$\mathbb{C}P^{S}$
. This is a rational map defined over the (open dense) locus
$U=\mathbb{A}_{K}^{2}\setminus \unicode[STIX]{x1D6F4}$
such that the intersection above is proper. We have
$\operatorname{codim}\unicode[STIX]{x1D6F4}\geqslant 2$
(otherwise
$\dim \unicode[STIX]{x1D702}^{-1}(\unicode[STIX]{x1D6F4})=\dim X$
, which is ruled out by the hypotheses). Thus
$\unicode[STIX]{x1D6F7}$
is defined on both
$\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}^{\prime }$
except for possibly finitely many exceptions where they intersect
$\unicode[STIX]{x1D6F4}$
.
In projective coordinates on the Chow variety, we have
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(s,0)=s^{\unicode[STIX]{x1D708}}[\widetilde{X}]+O(s^{\unicode[STIX]{x1D708}+1}),\end{eqnarray}$$
where
$[\widetilde{X}]$
denotes the Chow form of the flat limit of
$X_{s,t}$
along
$\unicode[STIX]{x1D6E4}$
(with its cycle structure). Thus
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(s,t)=s^{\unicode[STIX]{x1D708}}[\widetilde{X}]+O(s^{\unicode[STIX]{x1D708}+1})+O(t).\end{eqnarray}$$
We see that if
$t=O(s^{\unicode[STIX]{x1D708}+1})$
along
$\unicode[STIX]{x1D6E4}^{\prime }$
then the limit of
$X_{s,t}$
along
$\unicode[STIX]{x1D6E4}^{\prime }$
is also equal to
$[\widetilde{X}]$
as a cycle. In particular, these cycles intersect
$N$
in the same set, proving the claim.◻
Remark 21. Let
$U$
denote a Zariski open subset in the space of
$n$
-tuples of polynomials with a given Newton polytope. Proposition 20 implies, in particular, that one may deform a given complete intersection family (19) to make
$P_{i}(\unicode[STIX]{x1D701},e)\in U$
for generic values of
$e$
, without changing the fiber
$X_{0}$
. Indeed, consider
$\widetilde{P}_{i}=P_{i}+sQ_{i}$
where
$Q_{i}$
denotes some tuple of polynomials from the space. Then taking
$s=e^{\unicode[STIX]{x1D708}}$
for sufficiently large
$\unicode[STIX]{x1D708}$
ensures that the families defined by
$\{P_{i}\}$
and
$\{\widetilde{P}_{i}\}$
have the same
$0$
-fiber, whereas an appropriate (generic) choice of
$Q_{i}$
ensures that
$\{\widetilde{P}_{i}\}\in U$
for generic
$e$
.
For instance, in conjunction with the Bertini theorem, this implies that one can make the generic fiber effectively smooth.
If
$X$
is a flat family and
$P\in K[\unicode[STIX]{x1D701}]$
is such that
$\{P=0\}$
intersects
$X_{0}$
properly, then the family
$Y={\mathcal{F}}\big[X\cap \{P=0\}\big]$
satisfies
$Y_{0}=X_{0}\cap \{P=0\}$
. However, if the intersection is not proper, one cannot in general predict the structure of
$Y_{0}$
. The following proposition shows that under a technical modification, one can guarantee that
$Y_{0}$
is given by the intersection between
$\{P=0\}$
and those components of
$X_{0}$
that meet it properly.
Proposition 22. Let
$X\subset N\times \mathbb{A}_{K}$
be a generic complete intersection and
$P\in K[\unicode[STIX]{x1D701}]$
. Define
$Y,\widetilde{Y}$
by
$$\begin{eqnarray}\displaystyle Y & = & \displaystyle {\mathcal{F}}[X\cap \{P=e^{1/\unicode[STIX]{x1D708}}\}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{Y} & = & \displaystyle {\mathcal{F}}[(X_{0}\times \mathbb{A}_{K})\cap \{P=e^{1/\unicode[STIX]{x1D708}}\}],\end{eqnarray}$$
where
$\unicode[STIX]{x1D708}$
is a sufficiently large natural number.
Then
$\widetilde{Y}_{0}=Y_{0}$
. In particular, if
$X_{0}=C\cup C^{\prime }$
where
$C^{\prime }$
denotes the union of components of
$X_{0}$
where
$P$
vanishes identically and
$C$
the rest, then
$Y_{0}=C\cap \{P=0\}$
.
Proof. The first part of the statement is simply Proposition 20 applied to the family
$(X\times \mathbb{A}_{K}^{s})\cap \{P=s\}$
(with
$e$
in place of
$t$
). For the second part it suffices to compute
$\widetilde{Y}_{0}$
by noting that
$\{P=e^{1/\unicode[STIX]{x1D708}}\}$
intersects
$C$
properly and does not intersect
$C^{\prime }$
at all (in the affine space).◻
Figure 2. The different families in Example 23.
We remark that the use of the ramified factor
$e^{1/\unicode[STIX]{x1D708}}$
is merely a notational convenience, to avoid reparametrizing the original family
$X$
. One could of course obtain an honest polynomial family by passing to a new deformation parameter.
Example 23. Consider
$X\subset \mathbb{C}^{2}\times \mathbb{C}$
given by
$xy=e$
, and
$P=x$
(see Figure 2). Then
$X_{0}$
has two components, the
$x$
- and
$y$
-axes. The former intersects
$\{P=0\}$
properly at the origin, whereas the latter intersects
$\{P=0\}$
non-properly.
If we consider the family
$Y={\mathcal{F}}(X\cap \{P=0\})$
we obtain
$Y_{0}=\emptyset$
. If we consider
$Y={\mathcal{F}}(X\cap \{P=e\})$
we obtain
$Y_{0}=\{(0,1)\}$
. Finally, if we consider
$Y={\mathcal{F}}(X\cap \{P=e^{\unicode[STIX]{x1D6FC}}\})$
where
$0<\unicode[STIX]{x1D6FC}<1$
, then we obtain
$Y=\{(0,0)\}$
, which is the intersection between the
$x$
-axis and
$\{P=0\}$
as predicted by Proposition 22.
3.2 Projections and reduction of dimension
We begin with a simple lemma on linear elimination of variables. Let
$P\in K[\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}]$
be a polynomial with
$\deg _{\unicode[STIX]{x1D701}^{(1)}}P\leqslant 1$
. The homogenization
$\widetilde{P}$
of
$P$
is the polynomial in one extra variable,
$\unicode[STIX]{x1D701}_{0}^{(1)},\ldots ,\unicode[STIX]{x1D701}_{n}^{(1)}$
, where the free term of
$P$
is multiplied by
$\unicode[STIX]{x1D701}_{0}^{(1)}$
.
Lemma 24. Let
$$\begin{eqnarray}P_{1},\ldots ,P_{n+1}\in K[\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}]\quad \unicode[STIX]{x1D6E5}(P_{j})\subset \unicode[STIX]{x1D6E5}_{j}\times \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}^{(1)}}\end{eqnarray}$$
and let
$\widetilde{P}_{1},\ldots ,\widetilde{P}_{n+1}$
denote their homogenization, and
$W\subset N\times \mathbb{P}_{K}^{n}$
the variety they define.
Let
$R$
denote the determinant of the
$(n+1)\times (n+1)$
matrix whose
$j$
th row is given by the
$n+1$
coefficients of
$\widetilde{P}_{j}$
, viewed as a linear form in the variables
$\unicode[STIX]{x1D701}_{0}^{(1)},\ldots ,\unicode[STIX]{x1D701}_{n}^{(1)}$
. Then
$\unicode[STIX]{x1D6E5}(R)\subset \sum _{j=1}^{n+1}\unicode[STIX]{x1D6E5}_{j}$
and
$\unicode[STIX]{x1D70B}(W)=\{R=0\}$
.
Proof. The points of
$\unicode[STIX]{x1D70B}(W)$
correspond to points
$\unicode[STIX]{x1D701}\in N$
such that the linear forms
$\widetilde{P}_{j}$
have a common kernel in
$\mathbb{P}_{K}^{n}$
– the locus of which corresponds to the zeros of the determinant
$R$
.◻
Lemma 25. Let
$$\begin{eqnarray}P_{1},\ldots ,P_{k}\in K[\unicode[STIX]{x1D701},e]\end{eqnarray}$$
and
$$\begin{eqnarray}Q_{1},\ldots ,Q_{l}\in K[\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)},e],\quad \unicode[STIX]{x1D6E5}(Q_{j})\subset \unicode[STIX]{x1D6E5}_{j}\times \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}^{(1)}},\end{eqnarray}$$
define a generic complete intersection
$X\subset N^{(1)}\times \mathbb{A}_{K}$
,
$$\begin{eqnarray}X={\mathcal{F}}[\{P_{1}=\cdots =P_{k}=Q_{1}=\cdots =Q_{l}=0\}].\end{eqnarray}$$
Denote by
$W$
the union of the components
$C$
of
$X_{0}$
such that
$\operatorname{codim}\unicode[STIX]{x1D70B}(C)>k$
. Then there exist
$R\in K[\unicode[STIX]{x1D701},e]$
and a generic complete intersection
$Y$
,
$$\begin{eqnarray}Y={\mathcal{F}}[\{P_{1}=\cdots =P_{k}=R=0\}],\quad \unicode[STIX]{x1D6E5}(R)\subset \mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6E5}_{j},\end{eqnarray}$$
such that
$\unicode[STIX]{x1D70B}(W)\subset Y_{0}$
.
Proof. We prove the claim by reverse induction on
$l$
, starting with the case
$l\geqslant n+1$
. In this case
$W=X_{0}$
. We replace
$Q_{1},\ldots ,Q_{n+1}$
by their small generic perturbation (keeping the same Newton polytope). By Proposition 20 this does not change
$X_{0}$
. We can thus assume without loss of generality that the generic fiber of
$V\subset N\times \mathbb{P}_{K}^{n}\times \mathbb{A}_{K}$
cut out by
$P_{1},\ldots ,P_{k}$
and the homogenizations of
$Q_{1},\ldots ,Q_{n+1}$
has codimension
$n+k+1$
. Applying Lemma 24 to
$Q_{1},\ldots ,Q_{n+1}$
, we thus obtain
$R$
giving a generic complete intersection (34). By construction the generic fiber
$Y_{\unicode[STIX]{x1D700}}$
contains
$\unicode[STIX]{x1D70B}(X_{\unicode[STIX]{x1D700}})$
, and it follows that
$Y_{0}$
contains
$\unicode[STIX]{x1D70B}(X_{0})$
as claimed.
We now consider the case
$l\leqslant n$
. Then for any component
$C\subset W$
, the generic fiber of
$\unicode[STIX]{x1D70B}:C\rightarrow \unicode[STIX]{x1D70B}(C)$
has dimension at least
$n+1-l\geqslant 1$
. Let
$\ell$
be a generic affine-linear form in the
$\unicode[STIX]{x1D701}^{(1)}$
variables. Then
$\{\ell =0\}$
meets
$X_{0}$
properly, and, taking
$Q_{l+1}$
to be
$\ell$
, we obtain a new family
$X^{\prime }$
such that
$$\begin{eqnarray}C^{\prime }:=C\cap \{\ell =0\}\subset X_{0}^{\prime }.\end{eqnarray}$$
Moreover,
$$\begin{eqnarray}\operatorname{Clo}[\unicode[STIX]{x1D70B}(C)]=\operatorname{Clo}[\unicode[STIX]{x1D70B}(C^{\prime })]\end{eqnarray}$$
since
$\{\ell =0\}$
meets the generic fiber of
$\unicode[STIX]{x1D70B}:C\rightarrow \unicode[STIX]{x1D70B}(C)$
. Since this is true for any component
$C\subset W$
(with sufficiently generic
$\ell$
), the claim follows by induction with the new family
$X^{\prime }$
and
$\unicode[STIX]{x1D6E5}_{l+1}=\{0\}$
.◻
The following lemma provides the main inductive step in our estimates.
Lemma 26. Let
$X\subset N\times \mathbb{A}_{K}$
given by
$$\begin{eqnarray}X={\mathcal{F}}[\{P_{1}=\cdots =P_{k}=0\}],\quad P_{j}\in K[\unicode[STIX]{x1D701},e],\unicode[STIX]{x1D6E5}(P_{j})\subset \unicode[STIX]{x1D6E5}_{j},\end{eqnarray}$$
be a generic complete intersection. Let
${\mathcal{S}}\subset N^{(1)}$
be a variety defined by equations which are affine-linear in
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}$
. Suppose that
$(X_{0})^{(1)}\cap {\mathcal{S}}$
does not project dominantly on any component of
$X_{0}$
. Then there exist
$$\begin{eqnarray}\widetilde{P}_{1},\ldots ,\widetilde{P}_{k+1}\in K[\unicode[STIX]{x1D701},e],\end{eqnarray}$$
with
$\unicode[STIX]{x1D6E5}(\widetilde{P}_{j})\subset \unicode[STIX]{x1D6E5}_{j}$
for
$j=1,\ldots ,k$
and
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(\widetilde{P}_{k+1})\subset (n-k+1)\unicode[STIX]{x1D6E4},\quad \unicode[STIX]{x1D6E4}=(n+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}}+\mathop{\sum }_{i=1}^{k}\unicode[STIX]{x1D6E5}_{j},\end{eqnarray}$$
such that
$$\begin{eqnarray}Y={\mathcal{F}}[\{\widetilde{P}_{1}=\cdots =\widetilde{P}_{k+1}=0\}]\end{eqnarray}$$
is a generic complete intersection and
$\unicode[STIX]{x1D70B}((X_{0})^{(1)}\cap {\mathcal{S}})\subset Y_{0}\subset X_{0}$
.
Proof. By Proposition 20 any sufficiently small perturbation of
$P_{1},\ldots ,P_{k}$
does not change
$X_{0}$
. We fix such a perturbation making the generic fiber of the family effectively smooth (without changing the Newton polytopes). Without loss of generality we may assume that the family
$P_{1},\ldots ,P_{k}$
is already in this form.
We let
$Z^{0}$
denote the family
$\unicode[STIX]{x1D70F}(X)$
. Recall that it is a generic complete intersection defined by the vanishing of
$P_{1},\ldots ,P_{k}$
and another set of
$k$
equations
$Q_{1},\ldots ,Q_{k}$
with
$\unicode[STIX]{x1D6E5}(Q_{j})\subset (\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}})\times \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}^{(1)}}$
. By Corollary 19 every component of
$(X_{0})^{(1)}$
is also a component of
$Z_{0}^{0}$
. Moreover, any extra components do not project dominantly on a component of
$X_{0}$
by Proposition 17.
For
$j=1,\ldots ,n-k+1$
we define
$Z^{j}$
to be the family obtained from
$Z^{j-1}$
by intersecting with a generic linear combination
$\widetilde{Q}^{j}$
of the given equations of
${\mathcal{S}}$
, using Proposition 22. We define
$R^{j},Y^{j}$
by applying Lemma 25 to
$Z^{j}$
. We have
$\unicode[STIX]{x1D6E5}(R_{j})\subset \unicode[STIX]{x1D6E4}$
. Finally, we take
$\widetilde{P}_{k+1}=R_{1}\cdots R_{n-k+1}$
which gives
$Y=Y^{1}\cup \cdots \cup Y^{n-k+1}$
.
Let
$C$
be a component of
$(X_{0})^{(1)}$
. Then it is also a component of
$Z_{0}^{0}$
. Since
$C$
projects dominantly on a component of
$X_{0}$
, it cannot be contained in
${\mathcal{S}}$
. Hence by genericity
$C^{\prime }:=C\cap \{\widetilde{Q}^{1}=0\}$
is strictly contained in
$C$
, and by Proposition 22 we have
$C^{\prime }\subset Z_{0}^{1}$
. Moreover, clearly
$C^{\prime }\cap {\mathcal{S}}=C\cap {\mathcal{S}}$
. Thus it will suffice to prove that
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(Z_{0}^{1}\cap {\mathcal{S}})\subset Y_{0}.\end{eqnarray}$$
Now let
$C$
be any component of
$Z_{0}^{1}$
. If
$\operatorname{codim}(\unicode[STIX]{x1D70B}(C))>k$
then
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(C\cap {\mathcal{S}})\subset \unicode[STIX]{x1D70B}(C)\subset Y_{0}^{1}\subset Y_{0},\end{eqnarray}$$
where the middle inclusion follows from Lemma 25. Otherwise,
$C$
projects dominantly on a component of
$X_{0}$
, so it again cannot be contained in
${\mathcal{S}}$
. Again by genericity
$C^{\prime }:=C\cap \{\widetilde{Q}^{2}=0\}$
is strictly contained in
$C$
, and by Proposition 22 we have
$C^{\prime }\subset Z_{0}^{2}$
. Moreover, clearly
$C\cap {\mathcal{S}}=C^{\prime }\cap {\mathcal{S}}$
. Thus it will suffice to prove that
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(Z_{0}^{2}\cap {\mathcal{S}})\subset Y_{0}.\end{eqnarray}$$
We repeat this process until
$Z_{0}^{n-k+1}$
. At this point every component has dimension at most
$n-k-1$
even before the
$\unicode[STIX]{x1D70B}$
projection, and thus projects to a set of codimension greater than
$k$
. As in (42) it then follows that
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(C\cap {\mathcal{S}})\subset \unicode[STIX]{x1D70B}(C)\subset Y_{0}^{n-k+1}\subset Y_{0}\end{eqnarray}$$
for every component
$C$
of
$Z_{0}^{n-k+1}$
, thus concluding the proof.◻
Remark 27. If the polytopes
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
are co-ideal polytopes (see Remark 4) then they are stable under differentiations. In this case in the definition of
$\unicode[STIX]{x1D6E4}$
in (39) one can replace
$(n+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}}$
by
$(n-k+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}}$
. For such polytopes, all of our main results remain valid with this refined definition of
$\unicode[STIX]{x1D6E4}$
.
4 Proofs of the main estimates
In this section we prove our main results on the number of isolated solutions of a differential system of equations and the degree of its reduction. Recall the notation of §1.1. In particular,
$M$
denotes our ambient space, which is a Zariski open subset of
$K^{n}$
;
$\unicode[STIX]{x1D6FA}^{(l)}$
denotes a Zariski open subset of the prolongation
$M^{(l)}$
; and
$s:=\dim \unicode[STIX]{x1D6FA}^{(l)}=n(l+1)$
. We begin with a lemma demonstrating the application of Lemma 26 to this context.
Lemma 28. Let
$X\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be a generic complete intersection family, and suppose that
$(X_{0})^{(1)}\cap \unicode[STIX]{x1D6EF}$
does not project dominantly on any component of
$X_{0}$
. Then the family
$Y$
defined by applying Lemma 26 to
$X$
with
$N=\unicode[STIX]{x1D6FA}^{(l)}$
and
${\mathcal{S}}=\unicode[STIX]{x1D6EF}$
satisfies
$X_{0}\cap {\mathcal{J}}^{l}(M)=Y_{0}\cap {\mathcal{J}}^{l}(M)$
.
Proof. Since
$Y_{0}\subset X_{0}$
, one inclusion is obvious. In the other direction, let
$x^{(l)}\in X_{0}$
. Then
${x^{(l)}}^{(1)}\in (X_{0})^{(1)}\cap \unicode[STIX]{x1D6EF}$
so by Lemma 26
$x^{(l)}=\unicode[STIX]{x1D70B}({x^{(l)}}^{(1)})\in Y_{0}$
as well.◻
We now prove our result for the case that
$S$
is a fiber
$X_{0}$
of a generic complete intersection family
$X$
. In particular, the following proposition implies (and generalizes) Theorem 6.
Proposition 29. Let
$X\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be a generic complete intersection family defined by polynomials with Newton polytopes
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
, and suppose that
$X_{0}$
admits finitely many solutions. Denote
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}=s\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}+\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}.\end{eqnarray}$$
Then
$$\begin{eqnarray}{\mathcal{N}}(X_{0})\leqslant C_{s,k}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k},\unicode[STIX]{x1D6E4},\ldots ,\unicode[STIX]{x1D6E4}),\quad C_{s,k}=s!(\unicode[STIX]{x1D6FF}+2)^{\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+1)/2},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}:=s-k$
.
Proof. Let
$X(0)=X$
. As long as
$X(j)_{0}$
has positive dimension, we define
$X(j+1)$
to be the family obtained by applying Lemma 26 to
$X(j)$
with the ambient space
$\unicode[STIX]{x1D6FA}^{(l)}$
and
$S=\unicode[STIX]{x1D6EF}$
. The lemma is applicable by application of Lemma 14, since
$X(j)_{0}$
admits finitely many solutions. We denote the extra equation obtained in this processFootnote
1
by
$R_{j+1}$
. By Lemma 28 we have
${\mathcal{N}}(X(j+1)_{0})={\mathcal{N}}(X(j)_{0})$
.
The Newton polytope of
$R_{j}$
is contained in
$(\unicode[STIX]{x1D6FF}+2)^{j}\unicode[STIX]{x1D6E4}$
, as one can see by the following simple induction:
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(R_{j})\subset (\unicode[STIX]{x1D6FF}+1)\biggl(\mathop{\sum }_{i=0}^{j-1}(\unicode[STIX]{x1D6FF}+2)^{i}\unicode[STIX]{x1D6E4}\biggr)\subset (\unicode[STIX]{x1D6FF}+1)\frac{(\unicode[STIX]{x1D6FF}+2)^{j}-1}{\unicode[STIX]{x1D6FF}+1}\unicode[STIX]{x1D6E4}\subset (\unicode[STIX]{x1D6FF}+2)^{j}\unicode[STIX]{x1D6E4}.\end{eqnarray}$$
Eventually we obtain the zero-dimensional variety
$X(\unicode[STIX]{x1D6FF})$
. From the above we conclude that
${\mathcal{N}}(X_{0})={\mathcal{N}}(X(\unicode[STIX]{x1D6FF})_{0})$
, which is certainly bounded by the number of points in
$X(\unicode[STIX]{x1D6FF})_{0}$
. Since the number of points of a flat limit is certainly bounded by the number of points of the generic fiber, we have by the BKK theorem
$$\begin{eqnarray}\displaystyle {\mathcal{N}}(X_{0}) & {\leqslant} & \displaystyle s!V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k},(\unicode[STIX]{x1D6FF}+2)^{1}\unicode[STIX]{x1D6E4},\ldots ,(\unicode[STIX]{x1D6FF}+2)^{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D6E4})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FF}+2)^{\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+1)/2}s!V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k},\unicode[STIX]{x1D6E4},\ldots ,\unicode[STIX]{x1D6E4})\end{eqnarray}$$
as claimed. ◻
We now prove our result for arbitrary varieties
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
.
Proof of Theorem 7.
Let
$X(k)\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be the (constant) family cut out by the given equations with Newton polytopes
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
.
For
$j\geqslant k$
, let
$P_{j}$
denote a generic linear combination of the given equations with Newton polytope
$\unicode[STIX]{x1D6E5}$
defining
$S$
. Define
$X(j+1)$
to be the family obtained by application of Proposition 22 to
$X(j)$
and
$P_{j}$
. Write
$X(j)_{0}=A(j)\cup B(j)$
, where
$A(j)$
denotes the union of the components of
$X(j)_{0}$
that are contained in
$S$
, and
$B(j)$
the rest.
The number of solutions of
$S$
which are contained in
$C(j)=A(j)\setminus B(j)$
is bounded by
$$\begin{eqnarray}{\mathcal{N}}(C(j))\leqslant C_{s,k}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{j},\unicode[STIX]{x1D6E4}_{j},\ldots ,\unicode[STIX]{x1D6E4}_{j}).\end{eqnarray}$$
Indeed,
$C(j)$
is the flat limit of the family
$X(j)$
in the ambient space
$\unicode[STIX]{x1D6FA}^{(l)}\setminus B(j)$
, and the bound thus follows from Proposition 29. The claim of the theorem will follow once we show that
$S=C(k)\cup \cdots \cup C(s)$
.
Let
$x\in S$
, and we will show that it belongs to some
$C(j)$
. Certainly
$x\in X(k)_{0}$
. If
$X\not \in B(k)$
, we are done. Otherwise
$x$
is contained in some component
$G\subset X(k)_{0}$
with
$G\not \subset S$
, and we may assume by genericity that
$P_{k}$
does not vanish identically on
$G$
. Then according to Proposition 22,
$X(k+1)_{0}$
contains
$G\cap \{P_{k}=0\}$
, and, in particular,
$x\in X(k+1)_{0}$
.
We continue in the same manner. The process must stop at
$j=s$
(if not before), because at this point
$X(j)_{0}$
consists of isolated points, so
$x\in X(j)_{0}$
implies
$x\in C(j)$
.◻
Finally, we prove the more general Theorem 9.
Proof of Theorem 9.
We indicate the minor changes required in the proofs of Proposition 29 and Theorem 7.
The proof of Proposition 29 carries out verbatim as long as
$X(j)_{0}$
does not have a component which is a component of
${\mathcal{R}}(S)$
. Let
$S(j)\subset {\mathcal{R}}(S)$
denote the components of codimension
$j$
. Then these are also components of
$X(j)_{0}$
, and their degrees can be bounded by the BKK theorem. We then define
$X(j+1)$
in the same way, but restricting the ambient space to
$\unicode[STIX]{x1D6FA}^{(l)}\setminus (S(1)\cup \cdots \cup S(j))$
. This insures that Lemma 26 is again applicable. It remain only to note that the degree of the remaining components of
${\mathcal{R}}(S)$
in the new ambient space is the same as the degree in the original ambient space. The proof is thus concluded by induction. The resulting bound has an extra multiplicative factor of
$s-k+1$
corresponding to the fact that we separately bound the degree in each dimension.Footnote
2
We can now carry out the proof of Theorem 7 in the same way, noting that since
$S=C(k)\cup \cdots \cup C(s)$
, any component of
${\mathcal{R}}(S)$
must be a component of
${\mathcal{R}}(C(j))$
for some
$j=k,\ldots ,s$
.◻
5 Diophantine applications
In the papers [Reference Hrushovski and PillayHP00, Reference Freitag and ScanlonFS14] the effective estimate of Theorem 2 has been used to derive estimates for some counting problems of a diophantine nature. In this section we illustrate our result by improving the estimates presented in these papers.
In this section we assume that
$K=\mathbb{C}$
, and the differentiation operator
$D$
is chosen such that the field of constants is
$k=\bar{\mathbb{Q}}$
.
5.1 Transcendental points in subvarieties of semi-abelian varieties
Recall that a semi-abelian variety is an extension of an abelian variety by a torus. Let
$A$
be a semi-abelian variety and
$\unicode[STIX]{x1D6E4}\subset A$
a subgroup of finite rational rank
$r:=\dim _{\mathbb{Q}}\unicode[STIX]{x1D6E4}\otimes \mathbb{Q}$
. Finally, let
$X$
be a subvariety of
$A$
.
In [Reference Hrushovski and PillayHP00] effective bounds are given on the number of points in the intersection
$X\cap \unicode[STIX]{x1D6E4}$
under various conditions on
$\unicode[STIX]{x1D6E4},X$
. The estimates are presented in terms of the following data. Suppose that
$A$
has dimension
$n$
and is defined over
$k$
. We assume that
$A$
is embedded as a locally closed subset of a projective space
$\mathbb{C}P^{N}$
. Let
$\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{n}$
be a basis of translation-invariant differential forms on
$A$
.
We assume that
$A$
is covered by
$t$
affine charts, and that each
$\unicode[STIX]{x1D714}_{i}$
is given in each chart by a polynomial in the local coordinates
$x_{1},\ldots ,x_{N}$
and
$dx_{1},\ldots ,dx_{n}$
. Let
$d_{A}$
be the maximal degree of the equations defining
$A$
in any of the charts, and
$d_{\unicode[STIX]{x1D714}}$
be the maximal degree of any of the polynomials defining
$\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{n}$
in any of the charts. Finally, let
$d_{X}$
denote an upper bound on the degrees of the equations defining
$X$
in any of the charts. We assume for simplicity of the formulation that
$d_{X}\geqslant d_{A}$
.
The following is a refined form of the main result of [Reference Hrushovski and PillayHP00].
Theorem 30 (Cf. [Reference Hrushovski and PillayHP00, Theorem 1.1]).
Suppose
$A,X$
are defined over
$k$
and there exist no positive-dimensional subvarieties
$X_{1},X_{2}\subset A$
such that
$X_{1}+X_{2}\subset X$
. Then
$$\begin{eqnarray}\#[(X\cap \unicode[STIX]{x1D6E4})\setminus X(k)]\leqslant F_{N,n,r}\cdot t\cdot d_{\unicode[STIX]{x1D714}}^{Nr}d_{x}^{n},\end{eqnarray}$$
where
$$\begin{eqnarray}F_{N,n,r}=\frac{E_{N(r+1),N-n}}{N(r+1)!}\binom{Nr+n}{n}d_{A}^{N-n}2^{n}.\end{eqnarray}$$
Proof. In [Reference Hrushovski and PillayHP00] it is shown that
$\unicode[STIX]{x1D6E4}$
is contained in a finite-dimensional differential algebraic subgroup
$G$
of
$A$
such that
$B:=(X\cap G)\setminus X(k)$
is finite. It is therefore enough to bound the number of points in
$B$
. Moreover, it is shown that in each of the affine charts on
$A$
, the group
$G$
can be written in the form
$$\begin{eqnarray}G=\{x:x^{(r)}\in V\},\end{eqnarray}$$
where
$V\subset (K^{N})^{(r)}$
is a variety defined by equations of degrees bounded by
$d_{\unicode[STIX]{x1D714}}$
.
We will apply Theorem 7 with parameters
$$\begin{eqnarray}\displaystyle M & = & \displaystyle K^{N},\nonumber\\ \displaystyle l & = & \displaystyle r,\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}^{(r)} & = & \displaystyle M^{(r)}\setminus \{\unicode[STIX]{x1D709}^{(1)}=0\},\nonumber\\ \displaystyle S & = & \displaystyle \unicode[STIX]{x1D6FA}^{(r)}\cap V\cap \unicode[STIX]{x1D70B}^{-1}(X).\nonumber\end{eqnarray}$$
Since
$S$
is contained in
$\unicode[STIX]{x1D70B}^{-1}(A)$
which has codimension
$N-n$
and is cut out by equations of degree at most
$d_{A}$
, we can apply Theorem 7 with
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{1}=\cdots =\unicode[STIX]{x1D6E5}_{N-n}=d_{A}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}},\quad \unicode[STIX]{x1D6E5}=d_{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}+d_{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(r)}.\end{eqnarray}$$
We note that
$\unicode[STIX]{x1D6E5}\subset \unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime }$
where
$\unicode[STIX]{x1D6E5}^{\prime }=2d_{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
and
$\unicode[STIX]{x1D6E5}^{\prime \prime }$
is the polytope of polynomials of degree
$d_{\unicode[STIX]{x1D714}}$
in
$\unicode[STIX]{x1D709}^{(1)},\ldots ,\unicode[STIX]{x1D709}^{(r)}$
.
Finally,
$S$
admits finitely many solutions, and by Theorem 7 we have
$$\begin{eqnarray}\displaystyle {\mathcal{N}}(S) & {\leqslant} & \displaystyle E_{s,N-n}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{N-n},\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime },\ldots ,\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime })\nonumber\\ \displaystyle & = & \displaystyle E_{s,N-n}\binom{s-N+n}{n}V\biggl(\underbrace{d_{A}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}}_{N-n\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}^{\prime }}_{n\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}^{\prime \prime }}_{s-N\text{ times}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle E_{s,N-n}\binom{s-N+n}{n}d_{A}^{N-n}(2d_{X})^{n}d_{\unicode[STIX]{x1D714}}^{N-n}V(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)},\ldots ,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)})\nonumber\\ \displaystyle & = & \displaystyle E_{s,N-n}\binom{s-N+n}{n}2^{n}(s!)^{-1}d_{A}^{N-n}d_{\unicode[STIX]{x1D714}}^{s-N}d_{X}^{n},\nonumber\end{eqnarray}$$
where in the second equality we expand the mixed volume by multilinearity and use the fact that the value is non-zero if and only if
$\unicode[STIX]{x1D6E5}^{\prime }$
appears exactly
$n$
times.◻
We note, in particular, that the bound of Theorem 30 is singly-exponential with respect to
$N$
and
$r$
, and has the natural asymptotic
$d_{X}^{n}$
with respect to
$d_{X}$
. We also remark that since
$A$
is smooth, the arguments of this paper could have been applied with small changes in the ambient space
$A$
rather than
$K^{N}$
, leading to somewhat better estimates.
We next present a version of Theorem 30 for a torus. This result may be seen as an analog of the Kushnirenko theorem. Similar analogs of the BKK theorem involving mixed volumes can be obtained in a similar manner.
Theorem 31. Let
$A=(\mathbb{C}^{\ast })^{n}$
and let
$X\subset A$
be defined over
$k$
by equations with Newton polytope
$\unicode[STIX]{x1D6E5}$
. Suppose that there exist no positive-dimensional subvarieties
$X_{1},X_{2}\subset A$
such that
$X_{1}+X_{2}\subset X$
. Then
$$\begin{eqnarray}\#[(X\cap \unicode[STIX]{x1D6E4})\setminus X(k)]\leqslant F_{2n,n,r}2^{n(2r+1)}\operatorname{Vol}(\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
Proof. We embed
$A$
in
$\mathbb{C}^{2n}=\mathbb{C}[x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{n}]$
with the equations
$x_{i}y_{i}=1$
. Then the invariant forms
$dx_{i}/x_{i}$
become polynomials of degree
$2$
, so
$d_{A}=d_{\unicode[STIX]{x1D714}}=2$
. The proof proceeds in a manner analogous to the proof of Theorem 30.◻
A special case with
$n=2$
in Theorem 31 is of some particular interest. It has been considered by Buium [Reference BuiumBui95b] who gave an iterated-exponential bound, answering a question posed by Bombieri. The bound was improved in [Reference Hrushovski and PillayHP00] to a doubly-exponential bound as follows.
Theorem 32 [Reference Hrushovski and PillayHP00, Corollary 1.2].
Let
$f\in \bar{\mathbb{Q}}[x,y]$
be an irreducible polynomial of degree
$d$
, whose zero locus in
$(\mathbb{C}^{\ast })^{2}$
is not a translate of a torus. Let
$\unicode[STIX]{x1D6E4}\subset \mathbb{C}^{\ast }$
be a subgroup of rational rank
$r$
. Then
$$\begin{eqnarray}\#\{(x,y)\in \unicode[STIX]{x1D6E4}^{2}:f(x,y)=0,x\not \in \bar{\mathbb{Q}}\}\leqslant d^{r2^{r}}(r+1)^{2(2^{r}+1)}.\end{eqnarray}$$
From Theorem 31 we obtain the following.
Theorem 33. Let
$f\in \bar{\mathbb{Q}}[x,y]$
be an irreducible polynomial with Newton polygon
$\unicode[STIX]{x1D6E5}$
, whose zero-locus in
$(\mathbb{C}^{\ast })^{2}$
is not a translate of a torus. Let
$\unicode[STIX]{x1D6E4}\subset \mathbb{C}^{\ast }$
be a subgroup of rational rank
$r$
. Then
$$\begin{eqnarray}\#\{(x,y)\in \unicode[STIX]{x1D6E4}^{2}:f(x,y)=0,x\not \in \bar{\mathbb{Q}}\}\leqslant F_{4,2,r}2^{4r+2}\operatorname{Vol}(\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
We note, in particular, that the bound of Theorem 32 is singly-exponential in
$r$
, and if we assume that
$\deg f=d$
then
$\operatorname{Vol}(\unicode[STIX]{x1D6E5})=d^{2}/2$
.
We also present a refined form of [Reference Hrushovski and PillayHP00, Theorem 1.1], replacing the condition on
$X$
in Theorem 31 by a condition on the lattice
$\unicode[STIX]{x1D6E4}$
. For simplicity we present the result in the context of the torus, although the proof works in general in the same way as the proof of Theorem 30.
Theorem 34. Let
$A=(\mathbb{C}^{\ast })^{n}$
and let
$X\subset A$
be defined by equations with Newton polytope
$\unicode[STIX]{x1D6E5}$
, and suppose that it does not contain a translate of a non-trivial subtorus. Suppose that
$\unicode[STIX]{x1D6E4}\cap A(k)=\{0\}$
. Then
$$\begin{eqnarray}\#(X\cap \unicode[STIX]{x1D6E4})\leqslant n(2r+1)F_{2n,n,r}2^{n(2r+1)}\operatorname{Vol}(\unicode[STIX]{x1D6E5}).\end{eqnarray}$$
Proof. In [Reference Hrushovski and PillayHP00, Lemma 6.1] it is shown that
$\unicode[STIX]{x1D6E4}$
is contained in a finite-dimensional differential algebraic subgroup
$G$
of
$(K^{\ast })^{n}$
such that
$X\cap G$
intersects only finitely many translates
$c_{1}(k^{\ast })^{n},\ldots ,c_{\unicode[STIX]{x1D708}}(k^{\ast })^{n}$
of
$(k^{\ast })^{n}$
. By the assumption on
$\unicode[STIX]{x1D6E4}$
, each such translate intersects
$\unicode[STIX]{x1D6E4}$
at most once, so it will suffice to give a bound on
$\unicode[STIX]{x1D708}$
.
We choose
$M,\unicode[STIX]{x1D6FA}^{(r)}$
as in the proof of Theorem 30 and write
$X\cap G$
as the set of solutions of a variety
$S\subset \unicode[STIX]{x1D6FA}^{(r)}$
. The logarithmic derivative
$l(x)=(Dx)/x$
takes a different value
$l(c_{j})$
on each of the translates
$c_{j}(k^{\ast })^{n}$
, so the solutions of
$S$
are contained in a union of
$\unicode[STIX]{x1D708}$
disjoint planes
$\unicode[STIX]{x1D709}^{(1)}=c_{j}\unicode[STIX]{x1D709}$
in
$\unicode[STIX]{x1D6FA}^{(r)}$
(and meets each of them). Then the same is true for the Zariski closure
${\mathcal{R}}(S)$
, and it is thus enough to bound the degree of this variety. The result now follows by Theorem 9.◻
5.2 Isogeny classes of elliptic curves
Denote by
$E_{x}$
the elliptic curve with
$j$
-invariant
$x\in \mathbb{C}$
. We write
$E_{x}\sim E_{y}$
when
$E_{x}$
is isogenous to
$E_{y}$
. We denote
$$\begin{eqnarray}\operatorname{Iso}(x)=\{y\in \mathbb{C}:E_{y}\sim E_{x}\}\end{eqnarray}$$
and more generally, for
$\bar{x}\in \mathbb{C}^{n}$
,
$$\begin{eqnarray}\operatorname{Iso}(\bar{x}):=\{\bar{y}\in \mathbb{C}^{n}:E_{x_{j}}\sim E_{y_{j}}\text{ for }j=1,\ldots ,n\}.\end{eqnarray}$$
In [Reference Freitag and ScanlonFS14] the authors, following a question of Mazur, consider the following problem: given a non-identity automorphism
$\unicode[STIX]{x1D6FC}$
of
$\mathbb{C}P^{1}$
and
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
, estimate the number of elliptic curves
$E_{\unicode[STIX]{x1D70C}}$
satisfying
$E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
$E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
. In particular, they obtain the following estimate.
Theorem 35 [Reference Freitag and ScanlonFS14, §6.1].
Assume
$\unicode[STIX]{x1D70F}$
is transcendental and set
$$\begin{eqnarray}S:=\{(z,w):w=\unicode[STIX]{x1D6FC}\cdot z\}\cap \operatorname{Iso}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}).\end{eqnarray}$$
Then the size of
$S$
, i.e. the number of elliptic curves
$E_{\unicode[STIX]{x1D70C}}$
satisfying
$E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
$E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
, is at mostFootnote
3
$2^{24}36^{7}\simeq 10^{18}$
.
The proof of this theorem, as in §5.1, is based on the introduction of a differential algebraic construction. Namely, recall that the Schwartzian operator is defined by
$$\begin{eqnarray}S(x)=\biggl(\frac{x^{\prime \prime }}{x^{\prime }}\biggr)^{\prime }-\frac{1}{2}\biggl(\frac{x^{\prime \prime }}{x^{\prime }}\biggr)^{2},\end{eqnarray}$$
where we interpret this as an operator on our differentially closed field
$\mathbb{C}$
, and write
$x^{\prime }$
as a shorthand for
$Dx$
. We introduce the differential operator
$$\begin{eqnarray}\unicode[STIX]{x1D712}(x)=S(x)+R(x)(x^{\prime })^{2},\quad R(x)=\frac{x^{2}-1968x+2654208}{2x^{2}(x-1728)^{2}},\end{eqnarray}$$
which is a third order algebraic differential operator vanishing on Klein’s j-invariant
$j$
[Reference BuiumBui95a]. Let
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
be transcendental (i.e., non-constant with respect to our chosen differential structure). By a theorem of Buium [Reference BuiumBui95a], the set
$\unicode[STIX]{x1D712}^{-1}(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F}))$
is the Kolchin closure of
$\operatorname{Iso}(\unicode[STIX]{x1D70F})$
. One may therefore attempt to study the set
$S$
in (59) by considering the (possibly larger) set
$$\begin{eqnarray}Z:=\{(z,w):w=\unicode[STIX]{x1D6FC}\cdot z\}\cap \{(z,w):\unicode[STIX]{x1D712}(z)=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D712}(w)=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F})\}.\end{eqnarray}$$
Of course, even if the set
$S$
is finite (which is not an obvious assertion), it is not clear a priori that the set
$Z$
must also be finite. However, in [Reference Freitag and ScanlonFS14, §6.1] it is proven that this is indeed the case. Since
$Z$
is a set given by differential algebraic conditions, it is thus possible to estimate its size using the methods of [Reference Hrushovski and PillayHP00], and this is carried out in [Reference Freitag and ScanlonFS14] to give Theorem 35.
We now apply our results, specifically Theorem 6, to estimate the size of
$Z$
. We begin by expressing
$Z$
as the set of solutions of a variety of differential conditions
$S$
. Let
$\unicode[STIX]{x1D6FC}\cdot z=(az+b)/(cz+d)$
. We choose
$M=\mathbb{C}^{2}$
,
$l=3$
and let
$\unicode[STIX]{x1D6FA}^{(l)}$
be the open dense subset of
$M^{(l)}$
obtained by removing the polar divisor of
$\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D709}$
(i.e.
$\{c\unicode[STIX]{x1D709}+d=0\}$
) as well as the polar divisors of
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})$
and
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D702})$
.
We write six explicit equations for
$S$
. The first is given by
$P_{1}:(c\unicode[STIX]{x1D709}+d)\unicode[STIX]{x1D702}=a\unicode[STIX]{x1D709}+b$
. We obtain the next three equations
$P_{2},P_{3},P_{4}$
by taking the first three derivatives of
$P_{1}$
with respect to
$D$
(and replacing
$D\unicode[STIX]{x1D709}$
by
$\unicode[STIX]{x1D709}^{(1)}$
, etc.). One can easily check that these equations define a complete intersection (in fact, they define the third prolongation of the graph of
$\unicode[STIX]{x1D6FC}$
: at this point it is essential that we removed the polar divisor
$c\unicode[STIX]{x1D709}+d=0$
). Clearly
$\unicode[STIX]{x1D6E5}(P_{j})\subset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}$
for
$j=1,2,3,4$
.
The next two equations
$P_{5},P_{6}$
are given by
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D702})=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F})$
respectively, where we clear out all the denominators. We have
$\unicode[STIX]{x1D6E5}(P_{5})\subset 6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}$
and
$\unicode[STIX]{x1D6E5}(P_{6})\subset 6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}$
. Since these equations are linear in
$\unicode[STIX]{x1D709}^{(3)}$
and
$\unicode[STIX]{x1D702}^{(3)}$
respectively, it is not hard to check that they are each irreducible (this was already noted in [Reference Freitag and ScanlonFS14, §5.2]). It follows that
$P_{1},\ldots ,P_{6}$
define a complete intersection. Indeed, otherwise
$P_{1},\ldots ,P_{5}$
would imply
$P_{6}$
. But
$P_{5}$
, being an equation of order 3, admits infinitely many solutions
$z$
, and for each of these
$(z,\unicode[STIX]{x1D6FC}\cdot z)$
would be a solution of
$P_{1},\ldots ,P_{5}$
and hence also of
$P_{6}$
, contradicting the fact that
$S$
has finitely many solutions.
Finally, we apply Theorem 6 to
$S$
. In computing
$\unicode[STIX]{x1D6E4}$
we also take into account Remark 27,
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}\subset [(8-6+1)+4+6](\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)})=13(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)})\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle {\mathcal{N}}(S) & {\leqslant} & \displaystyle 4^{3}\cdot 8!V\biggl(\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{4\text{ times}},6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)},6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)},\underbrace{13(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)})}_{2\text{ times}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{6}6^{2}13^{2}\cdot 8!V\biggl(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)},\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)},\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{6\text{ times}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 2^{6}6^{2}13^{2}\binom{6}{3}\cdot 8!V\biggl(\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}}_{4\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{4\text{ times}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 2^{6}6^{2}13^{2}\binom{6}{3}=2^{10}\cdot 3^{3}\cdot 13^{2}.\nonumber\end{eqnarray}$$
In conclusion, we have the following result.
Theorem 36 (Cf. Theorem 35).
Assume
$\unicode[STIX]{x1D70F}$
is transcendental. Then the number of elliptic curves
$E_{\unicode[STIX]{x1D70C}}$
satisfying
$E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
$E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
is at most
$2^{10}\cdot 3^{3}\cdot 13^{2}\simeq 5\times 10^{6}$
.
Remark 37. One could have derived a bound directly using Theorem 7 without the derivation of the extra equations
$P_{2},P_{3},P_{4}$
and the fact that the intersection with
$P_{5}$
and
$P_{6}$
is complete. We presented this more detailed approach because it gives a somewhat better estimate, and also to illustrate a computation involving mixed volumes in Theorem 6.
The computation above could certainly be improved somewhat: by using the precise Newton polytopes of
$P_{1},\ldots ,P_{6}$
; by accurately computing the resulting mixed volumes; and by following the proof of Theorem 6 where various inaccurate estimates were invariably made.
Generalizing to varieties of arbitrary dimension and degree, [Reference Freitag and ScanlonFS14] gives the following result.
Corollary 38 [Reference Freitag and ScanlonFS14, Corollary 6.9].
Let
$V\subset \mathbb{C}^{n}$
be a Zariski closed set of dimension
$m$
and
$\bar{\unicode[STIX]{x1D70F}}\in \mathbb{C}^{n}$
an
$n$
-tuple of transcendental numbers. Let
$W$
denote the Zariski closure of
$V\cap \operatorname{Iso}(\bar{\unicode[STIX]{x1D70F}})$
. Then
$W$
is a weakly-special variety, and (see footnote 3 on page 886)
$$\begin{eqnarray}\deg W\leqslant (2^{n}\deg V)^{3\cdot 2^{3m}}6^{2^{3m}-1}.\end{eqnarray}$$
We refer the reader to [Reference Freitag and ScanlonFS14] for the definition of a weakly special variety. As for the degree estimate, the proof of this corollary proceeds in a manner analogous to the proof of Theorem 35. Arguing in a manner analogous to the proof of Theorem 36 and using Theorem 9, we obtain the following result.
Corollary 39. Let
$V\subset \mathbb{C}^{n}$
be a Zariski closed set defined by equations of degree
$d$
, and
$\bar{\unicode[STIX]{x1D70F}}\in \mathbb{C}^{n}$
an
$n$
-tuple of transcendental numbers. Let
$W$
denote the Zariski closure of
$V\cap \operatorname{Iso}(\bar{\unicode[STIX]{x1D70F}})$
. Then
$\deg W\leqslant G_{n}d^{n}$
where
$G_{n}$
is an explicit constant, singly-exponential in
$n$
.
In conclusion, we remark that the estimates in terms of degrees in this section could be generalized to estimates in terms of volumes of Newton polytopes, with the proofs extending verbatim.
Acknowledgements
I would like to express my gratitude to Ehud Hrushovski for suggesting the problem studied in this paper to me and for invaluable discussions. I also wish to thank Omar Leon Sanchez for his useful suggestions during the preparation of this manuscript. Finally, I wish to thank the anonymous referee for many helpful suggestions.
