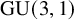1 Introduction
Let p be an odd prime number. In this paper, under some assumptions, we prove one divisibility of a two-variable Greenberg-type main conjecture for a weight ![]() $2$ newform unramified at p. The result is a key ingredient in the third author’s proof [Reference WanWan21] of the Iwasawa main conjecture, formulated by Kobayashi [Reference KobayashiKob03], for elliptic curves with supersingular reduction at p and
$2$ newform unramified at p. The result is a key ingredient in the third author’s proof [Reference WanWan21] of the Iwasawa main conjecture, formulated by Kobayashi [Reference KobayashiKob03], for elliptic curves with supersingular reduction at p and ![]() $a_p=0$, as well as in the proof of its extension to the case
$a_p=0$, as well as in the proof of its extension to the case ![]() $a_p\neq 0$ by Sprung [Reference Skinner and UrbanSpr16]. Another application of our main result is in the proof by the first and third authors [Reference Chen and HsiehCW16] of a p-converse to the theorem of Gross–Zagier and Kolyvagin for supersingular primes.
$a_p\neq 0$ by Sprung [Reference Skinner and UrbanSpr16]. Another application of our main result is in the proof by the first and third authors [Reference Chen and HsiehCW16] of a p-converse to the theorem of Gross–Zagier and Kolyvagin for supersingular primes.
Let ![]() $\pi $ be an irreducible cuspidal automorphic representation of
$\pi $ be an irreducible cuspidal automorphic representation of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$ generated by a newform of weight
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$ generated by a newform of weight ![]() $2$. Associated to
$2$. Associated to ![]() $\pi $ is a continuous two-dimensional p-adic Galois representation
$\pi $ is a continuous two-dimensional p-adic Galois representation ![]() ${\rho _{\pi }}$ of
${\rho _{\pi }}$ of ![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$ over L, a finite extension of
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$ over L, a finite extension of ![]() $\mathbb {Q}_p$. (We use the geometric convention for Galois representations. The determinant of
$\mathbb {Q}_p$. (We use the geometric convention for Galois representations. The determinant of ![]() $\rho _{\pi }$ is
$\rho _{\pi }$ is ![]() $\epsilon ^{-1}_{\mathrm {cyc}}$.) For the representation
$\epsilon ^{-1}_{\mathrm {cyc}}$.) For the representation ![]() $\rho _{\pi }$ over L, we can fix a
$\rho _{\pi }$ over L, we can fix a ![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$-stable
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$-stable ![]() $\mathcal {O}_L$-lattice
$\mathcal {O}_L$-lattice ![]() $T_{\pi }$.
$T_{\pi }$.
Take ![]() $\mathcal {K}$ to be an imaginary quadratic field in which p splits as
$\mathcal {K}$ to be an imaginary quadratic field in which p splits as ![]() $\mathfrak {p}\bar {\mathfrak {p}}$. Denote by
$\mathfrak {p}\bar {\mathfrak {p}}$. Denote by ![]() $\mathcal {K}_{\infty }$ the maximal abelian pro-p extension of
$\mathcal {K}_{\infty }$ the maximal abelian pro-p extension of ![]() $\mathcal {K}$ unramified outside p. Then the Galois group
$\mathcal {K}$ unramified outside p. Then the Galois group ![]() $\operatorname {\mathrm {Gal}}(\mathcal {K}_{\infty }/\mathcal {K})$ is isomorphic to
$\operatorname {\mathrm {Gal}}(\mathcal {K}_{\infty }/\mathcal {K})$ is isomorphic to ![]() $\mathbb {Z}^2_p$ and we denote it by
$\mathbb {Z}^2_p$ and we denote it by ![]() $\Gamma _{\mathcal {K}}$. We have the tautological character
$\Gamma _{\mathcal {K}}$. We have the tautological character
Let ![]() $\xi :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ be an algebraic Hecke character. We can associate to it a p-adic character
$\xi :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ be an algebraic Hecke character. We can associate to it a p-adic character ![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})\rightarrow \mathcal {O}^{\times }_L$, which we denote also by
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})\rightarrow \mathcal {O}^{\times }_L$, which we denote also by ![]() $\xi $.
$\xi $.
We consider the ![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})$-module
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})$-module
Define the Selmer group
 $$ \begin{align} {\mathrm{Sel}_{\pi,\mathcal{K},\xi}} = \ker \left\{ \begin{aligned} &H^1 \big(\mathcal{K},T_{\pi,\mathcal{K},\xi} \otimes_{\mathcal{O}_L [\![ \Gamma_{\mathcal{K}}]\!]} \mathcal{O}_L [\![ \Gamma_{\mathcal{K}}]\!]^{*} \big)\\ &\quad\longrightarrow \prod_{\mathfrak{v}\neq \mathfrak{p}} H^1 \big(I_{\mathfrak{v}}, T_{\pi, \mathcal{K},\xi}\otimes_{\mathcal{O}_L [\![ \Gamma_{\mathcal{K}}]\!]} \mathcal{O}_L[\![ \Gamma_{\mathcal{K}}]\!]^* \big) \end{aligned} \right\}, \end{align} $$
$$ \begin{align} {\mathrm{Sel}_{\pi,\mathcal{K},\xi}} = \ker \left\{ \begin{aligned} &H^1 \big(\mathcal{K},T_{\pi,\mathcal{K},\xi} \otimes_{\mathcal{O}_L [\![ \Gamma_{\mathcal{K}}]\!]} \mathcal{O}_L [\![ \Gamma_{\mathcal{K}}]\!]^{*} \big)\\ &\quad\longrightarrow \prod_{\mathfrak{v}\neq \mathfrak{p}} H^1 \big(I_{\mathfrak{v}}, T_{\pi, \mathcal{K},\xi}\otimes_{\mathcal{O}_L [\![ \Gamma_{\mathcal{K}}]\!]} \mathcal{O}_L[\![ \Gamma_{\mathcal{K}}]\!]^* \big) \end{aligned} \right\}, \end{align} $$with ![]() $\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]^*=\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}\left (\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!],\mathbb {Q}_p/\mathbb {Z}_p\right )$, the Pontryagin dual of
$\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]^*=\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}\left (\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!],\mathbb {Q}_p/\mathbb {Z}_p\right )$, the Pontryagin dual of ![]() $\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$. (This Selmer group has relaxed condition at
$\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$. (This Selmer group has relaxed condition at ![]() $\mathfrak {p}$ and unramified condition at
$\mathfrak {p}$ and unramified condition at ![]() $\bar {\mathfrak {p}}$.) Let
$\bar {\mathfrak {p}}$.) Let
which is well known to be a finitely generated ![]() $\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$-module. We recall the following definition of characteristic ideals.
$\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$-module. We recall the following definition of characteristic ideals.
Definition 1.0.1. For a Noetherian normal domain A and a finitely generated A-module M, we define the characteristic ideal of M as
 $$\begin{align*}{\mathrm{char}_A(M)} = \left\{x\in A \left|\begin{array}{l} \mathrm{ord}_P(x)\geq \mathrm{length}_{A_P}(M_P) \text{ for all}\\ \text{height one prime ideals } P\subset A\end{array}\right.\right\}. \end{align*}$$
$$\begin{align*}{\mathrm{char}_A(M)} = \left\{x\in A \left|\begin{array}{l} \mathrm{ord}_P(x)\geq \mathrm{length}_{A_P}(M_P) \text{ for all}\\ \text{height one prime ideals } P\subset A\end{array}\right.\right\}. \end{align*}$$ The Iwasawa–Greenberg main conjecture [Reference GreenbergGre94] predicts that the characteristic ideal of ![]() $X_{\pi ,\mathcal {K},\xi }$ is generated by the following p-adic L-function.
$X_{\pi ,\mathcal {K},\xi }$ is generated by the following p-adic L-function.
Denote by ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L$ the completion of the maximal unramified extension of
$\hat {\mathcal {O}}^{\mathrm {ur}}_L$ the completion of the maximal unramified extension of ![]() $\mathcal {O}_L$. By using the construction in [Reference Harris, Lan, Taylor and ThorneHid91], it is proved in Proposition 8.2.2 that there is a p-adic L-function
$\mathcal {O}_L$. By using the construction in [Reference Harris, Lan, Taylor and ThorneHid91], it is proved in Proposition 8.2.2 that there is a p-adic L-function
satisfying the interpolation property: For all algebraic Hecke characters ![]() $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ with p-adic avatars
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ with p-adic avatars ![]() $\tau _{p\text {-}\mathrm {adic}}$ factoring through
$\tau _{p\text {-}\mathrm {adic}}$ factoring through ![]() $\Gamma _{\mathcal {K}}$ and
$\Gamma _{\mathcal {K}}$ and ![]() $\xi \tau $ of
$\xi \tau $ of ![]() $\infty $-type
$\infty $-type ![]() $\left (k_1,k_2\right )$ with
$\left (k_1,k_2\right )$ with ![]() $k_1,k_2\in \mathbb {Z}$,
$k_1,k_2\in \mathbb {Z}$, ![]() $k_1\leq 0$,
$k_1\leq 0$, ![]() $k_2\geq 2-k_1$,
$k_2\geq 2-k_1$,
 $$ \begin{align} \begin{aligned} \mathcal{L}_{\pi,\mathcal{K},\xi}(\tau_{p\text{-}\mathrm{adic}}) =&\, \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{2(k_2-k_1)}\frac{\Gamma(k_2)\Gamma(k_2-1)}{(2\pi i)^{2k_2-1}} \cdot \gamma_p\left(\frac{3-(k_1+k_2)}{2},\pi^{\vee}_{p}\times (\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\\ &\times L^{\{\infty,p\}}\left(\frac{k_1+k_2-1}{2},\mathrm{BC}(\pi)\times\xi_0\tau_0\right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathcal{L}_{\pi,\mathcal{K},\xi}(\tau_{p\text{-}\mathrm{adic}}) =&\, \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{2(k_2-k_1)}\frac{\Gamma(k_2)\Gamma(k_2-1)}{(2\pi i)^{2k_2-1}} \cdot \gamma_p\left(\frac{3-(k_1+k_2)}{2},\pi^{\vee}_{p}\times (\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\\ &\times L^{\{\infty,p\}}\left(\frac{k_1+k_2-1}{2},\mathrm{BC}(\pi)\times\xi_0\tau_0\right), \end{aligned} \end{align} $$where ![]() $\xi _0\tau _0=\xi \tau |\cdot |^{-\frac {k_1+k_2}{2}}_{\mathbb {A}_{\mathcal {K}}}$ and
$\xi _0\tau _0=\xi \tau |\cdot |^{-\frac {k_1+k_2}{2}}_{\mathbb {A}_{\mathcal {K}}}$ and ![]() $\mathrm {BC}(\pi )$ denotes the unitary automorphic representation of
$\mathrm {BC}(\pi )$ denotes the unitary automorphic representation of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathcal {K}})$ obtained as the base change of
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathcal {K}})$ obtained as the base change of ![]() $\pi $.
$\pi $.
We are interested in the following (two-variable) Greenberg-type main conjecture.
The main result of this paper is Theorem 8.2.3, which is a partial result towards this conjecture. Like the previous works [Reference UrbanUrb01, Reference UrbanUrb06, Reference SprungSU14, Reference WanWan20] on proving Greenberg-type main conjectures for modular forms, the proof uses the congruences between Klingen Eisenstein series and cuspidal automorphic forms. The L-values in our case here are of the same type as those in [Reference WanWan20], and we also use Klingen Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,1)$ as in loc.cit. The main difference is that the modular form here is not assumed to be ordinary at p, so the standard Hida theory is not applicable.
$\operatorname {\mathrm {GU}}(3,1)$ as in loc.cit. The main difference is that the modular form here is not assumed to be ordinary at p, so the standard Hida theory is not applicable.
The key idea is to introduce the notion of semiordinary automorphic forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$. In §§2-4, we develop a Hida theory for p-adic families of (cuspidal and noncuspidal) semiordinary forms on
$\operatorname {\mathrm {GU}}(3,1)$. In §§2-4, we develop a Hida theory for p-adic families of (cuspidal and noncuspidal) semiordinary forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$ along an appropriate two-dimensional subspace of the usual three-dimensional weight space for
$\operatorname {\mathrm {GU}}(3,1)$ along an appropriate two-dimensional subspace of the usual three-dimensional weight space for ![]() $\operatorname {\mathrm {GU}}(3,1)$. The main results are stated in Theorem 2.9.1. In §5, by using the doubling method, we construct a Klingen Eisenstein family
$\operatorname {\mathrm {GU}}(3,1)$. The main results are stated in Theorem 2.9.1. In §5, by using the doubling method, we construct a Klingen Eisenstein family ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ and prove its semiordinarity. In §6, we study the degenerate Fourier–Jacobi coefficients of
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ and prove its semiordinarity. In §6, we study the degenerate Fourier–Jacobi coefficients of ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$. The analogous computations in [Reference WanWan20] assume a sufficient ramification condition (see Definition 6.30 in op.cit) which is not available in our case here, so we need a better way to do the computation at p by using the functional equations for local doubling zeta integrals. In §7, we study the nondegenerate Fourier–Jacobi coefficients of
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$. The analogous computations in [Reference WanWan20] assume a sufficient ramification condition (see Definition 6.30 in op.cit) which is not available in our case here, so we need a better way to do the computation at p by using the functional equations for local doubling zeta integrals. In §7, we study the nondegenerate Fourier–Jacobi coefficients of ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$. This part is very similar to [Reference WanWan20], and we cite many results there, but the presentation is slightly rearranged. For example, the auxiliary data for constructing the Klingen Eisenstein family are chosen at the beginning of the construction (§5.6) instead of at the end of the analysis of the nondegenerate Fourier–Jacobi coefficients, and an explanation of the strategy for analyzing the nondegenerate Fourier–Jacobi coefficients is included in §7.5. In §8, combining the results in §6 and §7, we deduce a result on the Klingen Eisenstein congruence ideal and use it as an input for the lattice construction to deduce the results on Selmer groups.
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$. This part is very similar to [Reference WanWan20], and we cite many results there, but the presentation is slightly rearranged. For example, the auxiliary data for constructing the Klingen Eisenstein family are chosen at the beginning of the construction (§5.6) instead of at the end of the analysis of the nondegenerate Fourier–Jacobi coefficients, and an explanation of the strategy for analyzing the nondegenerate Fourier–Jacobi coefficients is included in §7.5. In §8, combining the results in §6 and §7, we deduce a result on the Klingen Eisenstein congruence ideal and use it as an input for the lattice construction to deduce the results on Selmer groups.
Notation. We fix a prime ![]() $p\geq 3$ and an imaginary quadratic field
$p\geq 3$ and an imaginary quadratic field ![]() ${\mathcal {K}}$ in which p splits in
${\mathcal {K}}$ in which p splits in ![]() $\mathcal {K}$ as
$\mathcal {K}$ as ![]() $\mathfrak {p}\bar {\mathfrak {p}}$. Denote by
$\mathfrak {p}\bar {\mathfrak {p}}$. Denote by ![]() ${D_{\mathcal {K}/\mathbb {Q}}}$ the discriminant of
${D_{\mathcal {K}/\mathbb {Q}}}$ the discriminant of ![]() $\mathcal {K}/\mathbb {Q}$ and by
$\mathcal {K}/\mathbb {Q}$ and by ![]() ${\mathfrak {d}_{\mathcal {K}/\mathbb {Q}}}$ the different ideal of
${\mathfrak {d}_{\mathcal {K}/\mathbb {Q}}}$ the different ideal of ![]() $\mathcal {K}/\mathbb {Q}$. Denote by
$\mathcal {K}/\mathbb {Q}$. Denote by ![]() ${\eta _{\mathcal {K}/\mathbb {Q}}}$ the quadratic character of
${\eta _{\mathcal {K}/\mathbb {Q}}}$ the quadratic character of ![]() $\mathbb {Q}^{\times }\backslash \mathbb {A}^{\times }_{\mathbb {Q}}$ associated to
$\mathbb {Q}^{\times }\backslash \mathbb {A}^{\times }_{\mathbb {Q}}$ associated to ![]() $\mathcal {K}/\mathbb {Q}$. Denote by
$\mathcal {K}/\mathbb {Q}$. Denote by ![]() ${c}$ the nontrivial element in
${c}$ the nontrivial element in ![]() $\operatorname {\mathrm {Gal}}(\mathcal {K}/\mathbb {Q})$. For
$\operatorname {\mathrm {Gal}}(\mathcal {K}/\mathbb {Q})$. For ![]() $x\in \mathcal {K}$, denote by
$x\in \mathcal {K}$, denote by ![]() $\bar {x}$ its image under c. For a finite place v of
$\bar {x}$ its image under c. For a finite place v of ![]() $\mathbb {Q}$, we put
$\mathbb {Q}$, we put ![]() $\mathcal {K}_v=\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_v$ and
$\mathcal {K}_v=\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_v$ and ![]() $\mathcal {O}_{\mathcal {K},v}=\mathcal {O}_{\mathcal {K}}\otimes _{\mathbb {Z}}\mathbb {Z}_v$.
$\mathcal {O}_{\mathcal {K},v}=\mathcal {O}_{\mathcal {K}}\otimes _{\mathbb {Z}}\mathbb {Z}_v$.
Fix embeddings
such that the valuation of ![]() $\mathbb {Q}_p$ and
$\mathbb {Q}_p$ and ![]() $\iota _p$ induce the valuation of
$\iota _p$ induce the valuation of ![]() $\mathcal {K}$ given by
$\mathcal {K}$ given by ![]() $\mathfrak {p}$. The embedding
$\mathfrak {p}$. The embedding ![]() $\iota _p:\mathcal {K}\hookrightarrow \mathbb {Q}_p$ induces a homomorphism
$\iota _p:\mathcal {K}\hookrightarrow \mathbb {Q}_p$ induces a homomorphism ![]() ${\varrho _{\mathfrak {p}}} : \mathcal {K}_p=\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p$. We denote by
${\varrho _{\mathfrak {p}}} : \mathcal {K}_p=\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p$. We denote by ![]() ${\varrho _{\bar {\mathfrak {p}}}}:\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p$ the composition of
${\varrho _{\bar {\mathfrak {p}}}}:\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p$ the composition of ![]() $\varrho _p$ and the nontrivial element
$\varrho _p$ and the nontrivial element ![]() $c\in \operatorname {\mathrm {Gal}}(\mathcal {K}/\mathbb {Q})$. We have the isomorphism
$c\in \operatorname {\mathrm {Gal}}(\mathcal {K}/\mathbb {Q})$. We have the isomorphism
We also fix a totally imaginary element ![]() ${\delta }\in \mathcal {K}$ such that
${\delta }\in \mathcal {K}$ such that ![]() $\mathrm {Nm}(\delta )=\delta \bar {\delta }$ is a p-adic unit.
$\mathrm {Nm}(\delta )=\delta \bar {\delta }$ is a p-adic unit.
Fix the standard additive character ![]() $\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}=\bigotimes _v {\mathbf {e}_{v}} :\mathbb {Q}\backslash \mathbb {A}\rightarrow \mathbb {C}^{\times }$ with
$\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}=\bigotimes _v {\mathbf {e}_{v}} :\mathbb {Q}\backslash \mathbb {A}\rightarrow \mathbb {C}^{\times }$ with
 $$ \begin{align} \mathbf{e}_v(x)=\left\{\begin{array}{ll} e^{-2\pi i\{x\}_v}, &v\neq\infty,\\ e^{2\pi i x},&v=\infty,\end{array} \right. \end{align} $$
$$ \begin{align} \mathbf{e}_v(x)=\left\{\begin{array}{ll} e^{-2\pi i\{x\}_v}, &v\neq\infty,\\ e^{2\pi i x},&v=\infty,\end{array} \right. \end{align} $$where ![]() $\{x\}_v$ is the fractional part of x.
$\{x\}_v$ is the fractional part of x.
2 Hida theory for semiordinary forms on  $\operatorname {\mathrm {GU}}(3,1)$
$\operatorname {\mathrm {GU}}(3,1)$
In this section, we define semiordinary forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$ and state the control theorem for semiordinary families (Theorem 2.9.1). The proof of Theorem 2.9.1 is given in the following sections: 3 and 4.
$\operatorname {\mathrm {GU}}(3,1)$ and state the control theorem for semiordinary families (Theorem 2.9.1). The proof of Theorem 2.9.1 is given in the following sections: 3 and 4.
2.1 Some notation
Let ![]() $L_0$ be a free
$L_0$ be a free ![]() $\mathcal {O}_{\mathcal {K}}$-module of rank
$\mathcal {O}_{\mathcal {K}}$-module of rank ![]() $2$ with basis
$2$ with basis ![]() $\mathtt {w}_1, \mathtt {w}_2$, and we equip
$\mathtt {w}_1, \mathtt {w}_2$, and we equip ![]() $L_0\otimes _{\mathbb {Z}}\mathbb {Q}$ with a skew-Hermitian form
$L_0\otimes _{\mathbb {Z}}\mathbb {Q}$ with a skew-Hermitian form ![]() $\left <\,,\,\right>_{L_0}$ whose matrix with respect to the basis
$\left <\,,\,\right>_{L_0}$ whose matrix with respect to the basis ![]() $\mathtt {w}_1, \mathtt {w}_2$ is given by a matrix
$\mathtt {w}_1, \mathtt {w}_2$ is given by a matrix ![]() $\zeta _{0} \in \text {skew-}\operatorname {\mathrm {Her}}_2(\mathcal {O}_{\mathcal {K}})$ with
$\zeta _{0} \in \text {skew-}\operatorname {\mathrm {Her}}_2(\mathcal {O}_{\mathcal {K}})$ with ![]() $\delta \zeta _0$ positive definite. Let
$\delta \zeta _0$ positive definite. Let ![]() $X, Y$ be free
$X, Y$ be free ![]() $\mathcal {O}_{\mathcal {K}}$-modules of rank
$\mathcal {O}_{\mathcal {K}}$-modules of rank ![]() $1$ with bases
$1$ with bases ![]() $\mathtt {x}_1, \mathtt {y}_1$. Let
$\mathtt {x}_1, \mathtt {y}_1$. Let ![]() $X^{\vee }=\mathfrak {d}^{-1}_{\mathcal {K}/\mathbb {Q}}\cdot \mathtt {x}_1$ and
$X^{\vee }=\mathfrak {d}^{-1}_{\mathcal {K}/\mathbb {Q}}\cdot \mathtt {x}_1$ and ![]() $L=X^{\vee }\oplus L_0\oplus Y$. Equip
$L=X^{\vee }\oplus L_0\oplus Y$. Equip ![]() $L\otimes _{\mathbb {Z}}\mathbb {Q}$ with the skew-Hermitian form
$L\otimes _{\mathbb {Z}}\mathbb {Q}$ with the skew-Hermitian form ![]() $\left <\,,\,\right>_{L}$ whose matrix with respect to the basis
$\left <\,,\,\right>_{L}$ whose matrix with respect to the basis ![]() $\mathtt {x}_1, \mathtt {w}_1, \mathtt {w}_2, \mathtt {y}_1$ is given by
$\mathtt {x}_1, \mathtt {w}_1, \mathtt {w}_2, \mathtt {y}_1$ is given by  ${\zeta }=\begin {pmatrix}&&1\\&\zeta _0\\-1\end {pmatrix}.$
${\zeta }=\begin {pmatrix}&&1\\&\zeta _0\\-1\end {pmatrix}.$
Define the similitude unitary groups ![]() ${G'}=\operatorname {\mathrm {GU}}(2)$ and
${G'}=\operatorname {\mathrm {GU}}(2)$ and ![]() ${G}=\operatorname {\mathrm {GU}}(3,1)$ (over
${G}=\operatorname {\mathrm {GU}}(3,1)$ (over ![]() $\mathbb {Z}$) as: for all
$\mathbb {Z}$) as: for all ![]() $\mathbb {Z}$-algebra R
$\mathbb {Z}$-algebra R
 $$ \begin{align} \begin{aligned} \operatorname{\mathrm{GU}}(2)(R)&=\{(g,\nu)\in \operatorname{\mathrm{GL}}_{\mathcal{O}_{\mathcal{K}}\otimes_{\mathbb{Z}} R}(L_0\otimes_{\mathbb{Z}} R)\times R^{\times}\,:\,\left<gv_1,gv_2\right>_{L_0}=\nu\left<v_1,v_2\right>_{L_0}\},\\ \operatorname{\mathrm{GU}}(3,1)(R)&=\{(g,\nu)\in \operatorname{\mathrm{GL}}_{\mathcal{O}_{\mathcal{K}}\otimes_{\mathbb{Z}} R}(L\otimes_{\mathbb{Z}} R)\times R^{\times}\,:\,\left<gv_1,gv_2\right>_{L}=\nu\left<v_1,v_2\right>_{L}\}, \end{aligned}\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathrm{GU}}(2)(R)&=\{(g,\nu)\in \operatorname{\mathrm{GL}}_{\mathcal{O}_{\mathcal{K}}\otimes_{\mathbb{Z}} R}(L_0\otimes_{\mathbb{Z}} R)\times R^{\times}\,:\,\left<gv_1,gv_2\right>_{L_0}=\nu\left<v_1,v_2\right>_{L_0}\},\\ \operatorname{\mathrm{GU}}(3,1)(R)&=\{(g,\nu)\in \operatorname{\mathrm{GL}}_{\mathcal{O}_{\mathcal{K}}\otimes_{\mathbb{Z}} R}(L\otimes_{\mathbb{Z}} R)\times R^{\times}\,:\,\left<gv_1,gv_2\right>_{L}=\nu\left<v_1,v_2\right>_{L}\}, \end{aligned}\\[-15pt]\nonumber \end{align} $$and the unitary groups ![]() $\operatorname {\mathrm {U}}(2)$ (resp.
$\operatorname {\mathrm {U}}(2)$ (resp. ![]() $\operatorname {\mathrm {U}}(3,1)$) as the subgroup of
$\operatorname {\mathrm {U}}(3,1)$) as the subgroup of ![]() $\operatorname {\mathrm {GU}}(2)$ (resp.
$\operatorname {\mathrm {GU}}(2)$ (resp. ![]() $\operatorname {\mathrm {GU}}(3,1)$) consisting of elements with
$\operatorname {\mathrm {GU}}(3,1)$) consisting of elements with ![]() $\nu =1$.
$\nu =1$.
2.2 Shimura variety
We fix an open compact subgroup ![]() $K^p_f\subset G(\mathbb {A}^p_{\mathbb {Q},f})$, assumed throughout to be neat. Let
$K^p_f\subset G(\mathbb {A}^p_{\mathbb {Q},f})$, assumed throughout to be neat. Let ![]() $2\pi i\left <\,,\,\right>:L\times L\rightarrow \mathbb {Z}(1)$ be the alternating pairing
$2\pi i\left <\,,\,\right>:L\times L\rightarrow \mathbb {Z}(1)$ be the alternating pairing ![]() $2\pi i\cdot \mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L$ and
$2\pi i\cdot \mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L$ and ![]() $h:\mathbb {C}\rightarrow \mathrm {End}_{\mathcal {O}_{\mathcal {K}}\otimes _{\mathbb {Z}}\mathbb {R}}(L\otimes _{\mathbb {Z}}\mathbb {R})$ be the homomorphism given by
$h:\mathbb {C}\rightarrow \mathrm {End}_{\mathcal {O}_{\mathcal {K}}\otimes _{\mathbb {Z}}\mathbb {R}}(L\otimes _{\mathbb {Z}}\mathbb {R})$ be the homomorphism given by
 $$\begin{align*}h(u+iv):\left(\mathtt{x}_1,\mathtt{w}_1,\mathtt{w}_2,\mathtt{y}_1\right)\mapsto \left(\mathtt{x}_1,\mathtt{w}_1,\mathtt{w}_2,\mathtt{y}_1\right) \begin{pmatrix} 1\otimes u&&&-1\otimes v\\ &1\otimes u+\delta\otimes\frac{v}{\sqrt{\delta\bar{\delta}}}\\ &&1\otimes u+\delta\otimes\frac{v}{\sqrt{\delta\bar{\delta}}}\\ 1\otimes v&&& 1\otimes u \end{pmatrix}.\\[-15pt] \end{align*}$$
$$\begin{align*}h(u+iv):\left(\mathtt{x}_1,\mathtt{w}_1,\mathtt{w}_2,\mathtt{y}_1\right)\mapsto \left(\mathtt{x}_1,\mathtt{w}_1,\mathtt{w}_2,\mathtt{y}_1\right) \begin{pmatrix} 1\otimes u&&&-1\otimes v\\ &1\otimes u+\delta\otimes\frac{v}{\sqrt{\delta\bar{\delta}}}\\ &&1\otimes u+\delta\otimes\frac{v}{\sqrt{\delta\bar{\delta}}}\\ 1\otimes v&&& 1\otimes u \end{pmatrix}.\\[-15pt] \end{align*}$$Then the tuple ![]() $\left (\mathcal {O}_{\mathcal {K}},c,L,2\pi i\left <\,,\,\right>,h\right )$ defines a Shimura datum of polarization, endomorphism and level structure (PEL) type with reflex field
$\left (\mathcal {O}_{\mathcal {K}},c,L,2\pi i\left <\,,\,\right>,h\right )$ defines a Shimura datum of polarization, endomorphism and level structure (PEL) type with reflex field ![]() $\mathcal {K}$.
$\mathcal {K}$.
Consider the moduli problem sending every locally Noetherian connected ![]() $\mathcal {O}_{\mathcal {K},(p)}$-scheme S to the set of isomorphism classes of tuples
$\mathcal {O}_{\mathcal {K},(p)}$-scheme S to the set of isomorphism classes of tuples ![]() $(A,\lambda ,i,\alpha ^p)$ with:
$(A,\lambda ,i,\alpha ^p)$ with:
• A an abelian scheme of relative dimension
 $4$ over S;
$4$ over S;•
 $\lambda :A\rightarrow A^{\vee }$ a
$\lambda :A\rightarrow A^{\vee }$ a  $\mathbb {Z}^{\times }_{(p)}$-polarization;
$\mathbb {Z}^{\times }_{(p)}$-polarization;•
 $i:\mathcal {O}_{\mathcal {K}}\hookrightarrow \mathrm {End}_S A$ an embedding such that the induced
$i:\mathcal {O}_{\mathcal {K}}\hookrightarrow \mathrm {End}_S A$ an embedding such that the induced  $\mathcal {O}_{\mathcal {K}}$-action on
$\mathcal {O}_{\mathcal {K}}$-action on  $\operatorname {\mathrm {Lie}} A_{/S}$ satisfies the determinant condition, that is, for all
$\operatorname {\mathrm {Lie}} A_{/S}$ satisfies the determinant condition, that is, for all $$ \begin{align*} \det\left(X-i(b)|\operatorname{\mathrm{Lie}} A_{/S}\right)&=(X-b)^3(X-\bar{b})\\[-15pt] \end{align*} $$
$$ \begin{align*} \det\left(X-i(b)|\operatorname{\mathrm{Lie}} A_{/S}\right)&=(X-b)^3(X-\bar{b})\\[-15pt] \end{align*} $$ $b\in \mathcal {O}_{\mathcal {K}}$;
$b\in \mathcal {O}_{\mathcal {K}}$;•
 $\alpha ^p$ an (integral)
$\alpha ^p$ an (integral)  $K^p_f$-level structure on
$K^p_f$-level structure on  $(A, \lambda , i)$ of type
$(A, \lambda , i)$ of type  $\left (L\otimes \widehat {\mathbb {Z}}^{(p)},\mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L\right )$; that is, a
$\left (L\otimes \widehat {\mathbb {Z}}^{(p)},\mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L\right )$; that is, a  $\pi _1(S,\bar {s})$-invariant
$\pi _1(S,\bar {s})$-invariant  $K^p_f$-orbit of
$K^p_f$-orbit of  $\mathcal {O}_{\mathcal {K}}$-module isomorphisms
$\mathcal {O}_{\mathcal {K}}$-module isomorphisms  $L\otimes \widehat {\mathbb {Z}}^{(p)}\rightarrow T^{(p)}A_{\bar {s}}$, where
$L\otimes \widehat {\mathbb {Z}}^{(p)}\rightarrow T^{(p)}A_{\bar {s}}$, where  $\bar {s}$ is a geometric point of S and
$\bar {s}$ is a geometric point of S and  $T^{(p)}A_{\bar {s}}$ is the prime-to-p Tate module of
$T^{(p)}A_{\bar {s}}$ is the prime-to-p Tate module of  $A_{\bar {s}}$, together with an isomorphism
$A_{\bar {s}}$, together with an isomorphism  $\widehat {\mathbb {Z}}^{(p)}(1)\stackrel {\sim }{\rightarrow }\mathbb {G}_{m,\bar {s}}$ making the following diagram commute:
$\widehat {\mathbb {Z}}^{(p)}(1)\stackrel {\sim }{\rightarrow }\mathbb {G}_{m,\bar {s}}$ making the following diagram commute: 
(See [Reference LanLan13, Def. 1.4.1.4].)
Since ![]() $K^p_f$ is neat, the above moduli problem is represented by a smooth quasi-projective scheme
$K^p_f$ is neat, the above moduli problem is represented by a smooth quasi-projective scheme ![]() ${\mathscr {S}}$ over
${\mathscr {S}}$ over ![]() $\mathcal {O}_{\mathcal {K},(p)}$ (see [Reference LanLan13, Thm. 1.4.1.2, Cor. 7.2.3.10]).
$\mathcal {O}_{\mathcal {K},(p)}$ (see [Reference LanLan13, Thm. 1.4.1.2, Cor. 7.2.3.10]).
Denote by ![]() ${\mathscr {S}^{\mathrm {tor}}}$ the toroidal compactification of
${\mathscr {S}^{\mathrm {tor}}}$ the toroidal compactification of ![]() $\mathscr {S}$, which is a proper smooth scheme over
$\mathscr {S}$, which is a proper smooth scheme over ![]() $\mathcal {O}_{\mathcal {K},(p)}$ containing
$\mathcal {O}_{\mathcal {K},(p)}$ containing ![]() $\mathscr {S}$ as an open dense subscheme with complement being a relative Cartier divisor with normal crossings. (In our special case
$\mathscr {S}$ as an open dense subscheme with complement being a relative Cartier divisor with normal crossings. (In our special case ![]() $\operatorname {\mathrm {GU}}(3,1)$ here, there is a unique choice of the polyhedral cone decomposition for the toroidal compactification.) We denote by
$\operatorname {\mathrm {GU}}(3,1)$ here, there is a unique choice of the polyhedral cone decomposition for the toroidal compactification.) We denote by ![]() ${\mathcal {I}_{\mathscr {S}^{\mathrm {tor}}}}$ the ideal sheaf of the boundary of
${\mathcal {I}_{\mathscr {S}^{\mathrm {tor}}}}$ the ideal sheaf of the boundary of ![]() $\mathscr {S}^{\mathrm {tor}}$. By [Reference LanLan13, Thm. 6.4.1.1], the universal family
$\mathscr {S}^{\mathrm {tor}}$. By [Reference LanLan13, Thm. 6.4.1.1], the universal family ![]() $(\mathscr {A},\lambda ,i,\alpha ^p)$ over
$(\mathscr {A},\lambda ,i,\alpha ^p)$ over ![]() $\mathscr {S}$ extends to a degenerating family
$\mathscr {S}$ extends to a degenerating family ![]() $(\mathscr {G},\lambda ,i,\alpha ^p)$ over
$(\mathscr {G},\lambda ,i,\alpha ^p)$ over ![]() $\mathscr {S}^{\mathrm {tor}}$. Moreover, the base change of
$\mathscr {S}^{\mathrm {tor}}$. Moreover, the base change of ![]() $\mathscr {S}$ (resp.
$\mathscr {S}$ (resp. ![]() $\mathscr {S}^{\mathrm {tor}}$) to
$\mathscr {S}^{\mathrm {tor}}$) to ![]() $\mathcal {K}$ agrees with the Shimura variety over
$\mathcal {K}$ agrees with the Shimura variety over ![]() $\mathcal {K}$ (resp. its toroidal compactification) representing the moduli problem with full level structure at p (see [Reference LanLan15, (A.4.17), (A.4.18)]).
$\mathcal {K}$ (resp. its toroidal compactification) representing the moduli problem with full level structure at p (see [Reference LanLan15, (A.4.17), (A.4.18)]).
2.3 Hasse invariant
Set ![]() ${\underline {\omega }}:=e^*\Omega ^1_{\mathscr {G}/\mathscr {S}^{\mathrm {tor}}}$, where
${\underline {\omega }}:=e^*\Omega ^1_{\mathscr {G}/\mathscr {S}^{\mathrm {tor}}}$, where ![]() $e:\mathscr {S}^{\mathrm {tor}}\rightarrow \mathscr {G}$ is the zero section of the semiabelian scheme
$e:\mathscr {S}^{\mathrm {tor}}\rightarrow \mathscr {G}$ is the zero section of the semiabelian scheme ![]() $\mathscr {G}$ over
$\mathscr {G}$ over ![]() $\mathscr {S}^{\mathrm {tor}}$. Let
$\mathscr {S}^{\mathrm {tor}}$. Let ![]() ${\omega }$ be the line bundle
${\omega }$ be the line bundle ![]() $\det \underline {\omega }=\wedge ^{\mathrm {top}}\underline {\omega }$. The minimal compactification of
$\det \underline {\omega }=\wedge ^{\mathrm {top}}\underline {\omega }$. The minimal compactification of ![]() $\mathscr {S}$ is defined as
$\mathscr {S}$ is defined as
 $$\begin{align*}{\mathscr{S}^{\min}} =\mathrm{Proj}\Biggl(\bigoplus\limits_{k\geqslant 0}H^0(\mathscr{S}^{\mathrm{tor}},\omega^k)\Biggr). \end{align*}$$
$$\begin{align*}{\mathscr{S}^{\min}} =\mathrm{Proj}\Biggl(\bigoplus\limits_{k\geqslant 0}H^0(\mathscr{S}^{\mathrm{tor}},\omega^k)\Biggr). \end{align*}$$Let ![]() $\pi :\mathscr {S}^{\mathrm {tor}}\rightarrow \mathscr {S}^{\min }$ be the canonical projection. The push-forward
$\pi :\mathscr {S}^{\mathrm {tor}}\rightarrow \mathscr {S}^{\min }$ be the canonical projection. The push-forward ![]() $\pi _*\omega $ is an ample line bundle, and
$\pi _*\omega $ is an ample line bundle, and ![]() $\pi ^*\pi _*\omega \cong \omega $ (see [Reference LanLan13, Thm. 7.2.4.1]).
$\pi ^*\pi _*\omega \cong \omega $ (see [Reference LanLan13, Thm. 7.2.4.1]).
In the following, with a slight abuse of notation, we also denote by ![]() $\mathscr {S}^{\mathrm {tor}}$ and
$\mathscr {S}^{\mathrm {tor}}$ and ![]() $\mathscr {S}^{\min }$ their base change to
$\mathscr {S}^{\min }$ their base change to ![]() $\mathbb {Z}_p$ via the map
$\mathbb {Z}_p$ via the map ![]() $\mathcal {O}_{\mathcal {K},(p)}\rightarrow \mathbb {Z}_p$ induced by our fixed embedding
$\mathcal {O}_{\mathcal {K},(p)}\rightarrow \mathbb {Z}_p$ induced by our fixed embedding ![]() $\iota _p$, and let
$\iota _p$, and let ![]() $\mathscr {S}^{\mathrm {tor}}_{/\mathbb {F}_p}$ and
$\mathscr {S}^{\mathrm {tor}}_{/\mathbb {F}_p}$ and ![]() $\mathscr {S}^{\min }_{/\mathbb {F}_p}$ be their corresponding special fibers.
$\mathscr {S}^{\min }_{/\mathbb {F}_p}$ be their corresponding special fibers.
Let ![]() ${\mathrm {Ha}}\in H^0\left (\mathscr {S}^{\mathrm {tor}}_{/\mathbb {F}_p},\omega ^{p-1}\right )$ be the Hasse invariant defined as in [Reference LanLan18, §6.3.1]. In particular, for each geometric point
${\mathrm {Ha}}\in H^0\left (\mathscr {S}^{\mathrm {tor}}_{/\mathbb {F}_p},\omega ^{p-1}\right )$ be the Hasse invariant defined as in [Reference LanLan18, §6.3.1]. In particular, for each geometric point ![]() $\bar {s}$ of
$\bar {s}$ of ![]() $\mathscr {S}^{\mathrm {tor}}_{/\mathbb {F}_p}$, the Hasse invariant of the corresponding semiabelian scheme
$\mathscr {S}^{\mathrm {tor}}_{/\mathbb {F}_p}$, the Hasse invariant of the corresponding semiabelian scheme ![]() $\mathscr {G}_{\bar {s}}$ is nonzero if and only if the abelian part of
$\mathscr {G}_{\bar {s}}$ is nonzero if and only if the abelian part of ![]() $\mathscr {G}_{\bar {s}}$ is ordinary. Because
$\mathscr {G}_{\bar {s}}$ is ordinary. Because ![]() $\pi _*\omega $ is ample, for some
$\pi _*\omega $ is ample, for some ![]() $t_E> 0$, there exists an element in
$t_E> 0$, there exists an element in ![]() $H^0\left (\mathscr {S}^{\min },(\pi _*\omega )^{t_E(p-1)}\right )$ lifting the
$H^0\left (\mathscr {S}^{\min },(\pi _*\omega )^{t_E(p-1)}\right )$ lifting the ![]() $t_E$-th power of the push-forward of
$t_E$-th power of the push-forward of ![]() $\mathrm {Ha}$; we denote by
$\mathrm {Ha}$; we denote by ![]() ${E}$ the pullback under
${E}$ the pullback under ![]() $\pi $ of any such lift, which (because
$\pi $ of any such lift, which (because ![]() $\pi ^*\pi _*\omega \cong \omega $) defines an element
$\pi ^*\pi _*\omega \cong \omega $) defines an element ![]() $E\in H^0\left (\mathscr {S}^{\mathrm {tor}},\omega ^{t_E(p-1)}\right )$.
$E\in H^0\left (\mathscr {S}^{\mathrm {tor}},\omega ^{t_E(p-1)}\right )$.
2.4 Some groups
Before moving on, we need to introduce some more group-theoretic notations. Given a matrix ![]() $a\in \operatorname {\mathrm {GL}}_4(\mathcal {K}\otimes _{\mathbb {Q}} \mathbb {Q}_p)$, we define
$a\in \operatorname {\mathrm {GL}}_4(\mathcal {K}\otimes _{\mathbb {Q}} \mathbb {Q}_p)$, we define ![]() $a^+,a^-\in \operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$ as
$a^+,a^-\in \operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$ as
where ![]() $(\varrho _{\mathfrak {p}},\varrho _{\bar {\mathfrak {p}}}):\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p\times \mathbb {Q}_p$ are defined as in Notation, and we view an element
$(\varrho _{\mathfrak {p}},\varrho _{\bar {\mathfrak {p}}}):\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p\times \mathbb {Q}_p$ are defined as in Notation, and we view an element ![]() $g\in G(\mathbb {Q}_p)$ as a matrix inside
$g\in G(\mathbb {Q}_p)$ as a matrix inside ![]() $\operatorname {\mathrm {GL}}_4(\mathcal {K}\otimes _{\mathbb {Q}} \mathbb {Q}_p)$ via the basis
$\operatorname {\mathrm {GL}}_4(\mathcal {K}\otimes _{\mathbb {Q}} \mathbb {Q}_p)$ via the basis ![]() $(\mathtt {x}_1,\mathtt {w}_1,\mathtt {w}_2,\mathtt {y}_1)$. Then the corresponding matrices
$(\mathtt {x}_1,\mathtt {w}_1,\mathtt {w}_2,\mathtt {y}_1)$. Then the corresponding matrices ![]() $g^+,g^-\in \operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$ satisfy
$g^+,g^-\in \operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$ satisfy
In the following, we will often write ![]() $g\in G(\mathbb {Q}_p)$ as
$g\in G(\mathbb {Q}_p)$ as ![]() $(g^+,g^-)$. Note that the map
$(g^+,g^-)$. Note that the map
 $$ \begin{align} \begin{aligned} G(\mathbb{Q}_p)&\rightarrow \operatorname{\mathrm{GL}}_4(\mathbb{Q}_p)\times\mathbb{Q}^{\times}_p\\ g&\mapsto (g^+,\nu(g)) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} G(\mathbb{Q}_p)&\rightarrow \operatorname{\mathrm{GL}}_4(\mathbb{Q}_p)\times\mathbb{Q}^{\times}_p\\ g&\mapsto (g^+,\nu(g)) \end{aligned} \end{align} $$is an isomorphism.
There is a filtration ![]() ${\tt D} = \{\mathtt {D}^i\}_i$ of
${\tt D} = \{\mathtt {D}^i\}_i$ of ![]() $L\otimes _{\mathbb {Z}}\mathbb {Z}_p$ given by
$L\otimes _{\mathbb {Z}}\mathbb {Z}_p$ given by
where ![]() $X^+_p\subset X^{\vee }\otimes _{\mathbb {Z}}\mathbb {Z}_p=X\otimes _{\mathbb {Z}}\mathbb {Z}_p$ (resp.
$X^+_p\subset X^{\vee }\otimes _{\mathbb {Z}}\mathbb {Z}_p=X\otimes _{\mathbb {Z}}\mathbb {Z}_p$ (resp. ![]() $X^-_p\subset X^{\vee }\otimes _{\mathbb {Z}}\mathbb {Z}_p$,
$X^-_p\subset X^{\vee }\otimes _{\mathbb {Z}}\mathbb {Z}_p$, ![]() $L^+_{0,p}\subset L_0\otimes _{\mathbb {Z}}\mathbb {Z}_p$) is the subspace on which
$L^+_{0,p}\subset L_0\otimes _{\mathbb {Z}}\mathbb {Z}_p$) is the subspace on which ![]() $b\in \mathcal {O}_{\mathcal {K}}$ acts by
$b\in \mathcal {O}_{\mathcal {K}}$ acts by ![]() $\iota _p(b)$ (resp.
$\iota _p(b)$ (resp. ![]() $\iota _p(\bar {b})$,
$\iota _p(\bar {b})$, ![]() $\iota _p(b)$). Note that
$\iota _p(b)$). Note that ![]() $\mathtt {D}^0$ is isotropic with respect to
$\mathtt {D}^0$ is isotropic with respect to ![]() $\mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L$. For
$\mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L$. For ![]() $R=\mathbb {Z}_p$ or
$R=\mathbb {Z}_p$ or ![]() $\mathbb {Q}_p$, we put
$\mathbb {Q}_p$, we put
that is, ![]() $P_{\mathtt {D}}(R)$ is the subgroup of
$P_{\mathtt {D}}(R)$ is the subgroup of ![]() $G(R)$ stabilizing the filtration
$G(R)$ stabilizing the filtration ![]() $\mathtt {D}$ in (2.4.2). We see that
$\mathtt {D}$ in (2.4.2). We see that ![]() $P_{\mathtt {D}}^{\pm }(R):=\{g^{\pm }\colon g\in P_{\mathtt {D}}(R)\}$ are the subgroups of
$P_{\mathtt {D}}^{\pm }(R):=\{g^{\pm }\colon g\in P_{\mathtt {D}}(R)\}$ are the subgroups of ![]() $\operatorname {\mathrm {GL}}_4(R)$ given by
$\operatorname {\mathrm {GL}}_4(R)$ given by
 $$\begin{align*}P_{\mathtt{D}}^+=\left\{ \left(\begin{smallmatrix} \ast&\ast&\ast&\ast\\ \ast&\ast&\ast&\ast\\ \ast&\ast&\ast&\ast\\ &&&\ast \end{smallmatrix}\right) \right\},\quad P_{\mathtt{D}}^-=\left\{\left(\begin{smallmatrix} \ast&\ast&\ast&\ast\\ &\ast&\ast&\ast\\ &\ast&\ast&\ast\\ &\ast&\ast&\ast \end{smallmatrix}\right) \right\}. \end{align*}$$
$$\begin{align*}P_{\mathtt{D}}^+=\left\{ \left(\begin{smallmatrix} \ast&\ast&\ast&\ast\\ \ast&\ast&\ast&\ast\\ \ast&\ast&\ast&\ast\\ &&&\ast \end{smallmatrix}\right) \right\},\quad P_{\mathtt{D}}^-=\left\{\left(\begin{smallmatrix} \ast&\ast&\ast&\ast\\ &\ast&\ast&\ast\\ &\ast&\ast&\ast\\ &\ast&\ast&\ast \end{smallmatrix}\right) \right\}. \end{align*}$$Because ![]() $P_{\mathtt {D}}$ preserves both
$P_{\mathtt {D}}$ preserves both ![]() $X^+_p\oplus L^+_{0,p}$ and
$X^+_p\oplus L^+_{0,p}$ and ![]() $X^-_p$, there is a natural projection
$X^-_p$, there is a natural projection ![]() $P_{\mathtt {D}}(R)\rightarrow \operatorname {\mathrm {GL}}_3(R)\times \operatorname {\mathrm {GL}}_1(R)$ which in terms of matrices is given by
$P_{\mathtt {D}}(R)\rightarrow \operatorname {\mathrm {GL}}_3(R)\times \operatorname {\mathrm {GL}}_1(R)$ which in terms of matrices is given by
 $$ \begin{align*} g=(g^+,g^-)=\left(\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end{smallmatrix}\right) ,\left(\begin{smallmatrix}b_{11}&b_{12}&b_{13}&b_{14}\\ &b_{22}&b_{23}&b_{24}\\ &b_{32}&b_{33}&b_{34}\\ &b_{42}&a_{43}&b_{44}\end{smallmatrix}\right) \right) &\mapsto \left(\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{smallmatrix}\right) ,b_{11}\right). \end{align*} $$
$$ \begin{align*} g=(g^+,g^-)=\left(\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end{smallmatrix}\right) ,\left(\begin{smallmatrix}b_{11}&b_{12}&b_{13}&b_{14}\\ &b_{22}&b_{23}&b_{24}\\ &b_{32}&b_{33}&b_{34}\\ &b_{42}&a_{43}&b_{44}\end{smallmatrix}\right) \right) &\mapsto \left(\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{smallmatrix}\right) ,b_{11}\right). \end{align*} $$We will consider the p-level subgroups given by
 $$ \begin{align*} {K^{1}_{p,n}} &:=\left\{g\in G(\mathbb{Z}_p)\colon g^+\equiv\left(\begin{smallmatrix}\ast&\ast&\ast&\ast\\ p\ast&\ast&\ast&\ast\\ &&1&\ast\\ && &1\end{smallmatrix}\right) \quad\mod p^n\right\},\\ {K^{0}_{p,n}} &:=\left\{g\in G(\mathbb{Z}_p)\colon g^+\equiv\left(\begin{smallmatrix}\ast&\ast&\ast&\ast\\ p\ast&\ast&\ast&\ast\\ &&\ast&\ast\\ && &\ast\end{smallmatrix}\right)\quad \mod p^n\right\}, \end{align*} $$
$$ \begin{align*} {K^{1}_{p,n}} &:=\left\{g\in G(\mathbb{Z}_p)\colon g^+\equiv\left(\begin{smallmatrix}\ast&\ast&\ast&\ast\\ p\ast&\ast&\ast&\ast\\ &&1&\ast\\ && &1\end{smallmatrix}\right) \quad\mod p^n\right\},\\ {K^{0}_{p,n}} &:=\left\{g\in G(\mathbb{Z}_p)\colon g^+\equiv\left(\begin{smallmatrix}\ast&\ast&\ast&\ast\\ p\ast&\ast&\ast&\ast\\ &&\ast&\ast\\ && &\ast\end{smallmatrix}\right)\quad \mod p^n\right\}, \end{align*} $$where n is a positive integer.
2.5 Igusa towers
Let ![]() ${\mathscr {T}_{n}}$ be the ordinary locus of level
${\mathscr {T}_{n}}$ be the ordinary locus of level ![]() $K^1_{p,n}$ attached to the PEL-type Shimura data introduced in §2.2 and the filtration
$K^1_{p,n}$ attached to the PEL-type Shimura data introduced in §2.2 and the filtration ![]() $\mathtt {D}$ in (2.4.2), as constructed in [Reference LanLan18, Theorem 3.4.2.5]. By [Reference LanLan18, Prop. 3.4.6.3],
$\mathtt {D}$ in (2.4.2), as constructed in [Reference LanLan18, Theorem 3.4.2.5]. By [Reference LanLan18, Prop. 3.4.6.3], ![]() $\mathscr {T}_{n}$ is a smooth quasi-projective scheme over
$\mathscr {T}_{n}$ is a smooth quasi-projective scheme over ![]() $\mathbb {Z}_p$ representing a moduli problem for tuples
$\mathbb {Z}_p$ representing a moduli problem for tuples ![]() $(A,\lambda ,i,\alpha ^p,\alpha _p)$, where
$(A,\lambda ,i,\alpha ^p,\alpha _p)$, where ![]() $(A,\lambda ,i,\alpha ^p)$ is as in §2.2, and
$(A,\lambda ,i,\alpha ^p)$ is as in §2.2, and ![]() $\alpha _p$ is an ordinary
$\alpha _p$ is an ordinary ![]() $K^1_{p,n}$-level structure of A, that is, a
$K^1_{p,n}$-level structure of A, that is, a ![]() $K^1_{p,n}$-orbit of group scheme embeddings
$K^1_{p,n}$-orbit of group scheme embeddings ![]() $\mu _{p^n}\otimes \mathtt {D}^0\hookrightarrow A[p^n]$ with image isotropic for the
$\mu _{p^n}\otimes \mathtt {D}^0\hookrightarrow A[p^n]$ with image isotropic for the ![]() $\lambda $-Weil pairing, compatible with the
$\lambda $-Weil pairing, compatible with the ![]() $\mathcal {O}_{\mathcal {K}}$-actions on
$\mathcal {O}_{\mathcal {K}}$-actions on ![]() $\mathtt {D}^0$ and
$\mathtt {D}^0$ and ![]() $A[p^n]$ through i, as described in [Reference HidaHLTT16, §3.1.1].
$A[p^n]$ through i, as described in [Reference HidaHLTT16, §3.1.1].
Remark 2.5.1. In [Reference LanLan18, Chapter 3], the ordinary locus is defined as a normalization of the naive moduli problem introduced in [loc.cit., Def. 3.4.1.1]. In our case, because p is a good prime in the sense of [Reference LanLan18, Def. 1.1.1.6] and ![]() $\nu (K^1_{p,n})=\mathbb {Z}^{\times }_p$, this construction of the ordinary locus agrees with the moduli problem. (See [Reference HidaHLTT16, B.10] for more details.)
$\nu (K^1_{p,n})=\mathbb {Z}^{\times }_p$, this construction of the ordinary locus agrees with the moduli problem. (See [Reference HidaHLTT16, B.10] for more details.)
Let ![]() ${\mathscr {T}^{\mathrm {tor}}_n}$ be the partial toroidal compactification of the ordinary locus
${\mathscr {T}^{\mathrm {tor}}_n}$ be the partial toroidal compactification of the ordinary locus ![]() $\mathscr {T}_{n}$ ([Reference LanLan18, Thm. 5.2.1.1]); it is obtained by gluing to
$\mathscr {T}_{n}$ ([Reference LanLan18, Thm. 5.2.1.1]); it is obtained by gluing to ![]() $\mathscr {T}_{n}$ the toroidal boundary charts parameterizing degenerating families defined in [Reference LanLan18, Def. 3.4.2.0] (including an extensibility condition on the ordinary level structure). We note that, even though the generic fiber of
$\mathscr {T}_{n}$ the toroidal boundary charts parameterizing degenerating families defined in [Reference LanLan18, Def. 3.4.2.0] (including an extensibility condition on the ordinary level structure). We note that, even though the generic fiber of ![]() $\mathscr {T}_{n}$ agrees with the Shimura variety of level
$\mathscr {T}_{n}$ agrees with the Shimura variety of level ![]() $K^p_fK^1_{p,n}$ over
$K^p_fK^1_{p,n}$ over ![]() $\mathbb {Q}_p$, the generic fiber of
$\mathbb {Q}_p$, the generic fiber of ![]() $\mathscr {T}^{\mathrm {tor}}_{n}$ is in general just an open subscheme of a toroidal compactification of the Shimura variety of level
$\mathscr {T}^{\mathrm {tor}}_{n}$ is in general just an open subscheme of a toroidal compactification of the Shimura variety of level ![]() $K^p_fK^1_{p,n}$ over
$K^p_fK^1_{p,n}$ over ![]() $\mathbb {Q}_p$.
$\mathbb {Q}_p$.
Let ![]() ${\mathscr {T}^{\mathrm {tor}}_{n,m}}$ (resp.
${\mathscr {T}^{\mathrm {tor}}_{n,m}}$ (resp. ![]() ${\mathscr {S}^{\mathrm {tor}}_{m}}$) be the base change of
${\mathscr {S}^{\mathrm {tor}}_{m}}$) be the base change of ![]() $\mathscr {T}_n^{\mathrm {tor}}$ (resp.
$\mathscr {T}_n^{\mathrm {tor}}$ (resp. ![]() $\mathscr {S}^{\mathrm {tor}}_{}$) to
$\mathscr {S}^{\mathrm {tor}}_{}$) to ![]() $\mathbb {Z}/p^m\mathbb {Z}$. By [Reference LanLan18, Lem. 6.3.2.7],
$\mathbb {Z}/p^m\mathbb {Z}$. By [Reference LanLan18, Lem. 6.3.2.7], ![]() $\mathscr {S}^{\mathrm {tor}}_m[1/E]$ agrees with the ordinary locus in [Reference LanLan18, Thm. 5.2.1.1] for full level at p, and by [Reference LanLan18, Cor. 5.2.2.3] the map
$\mathscr {S}^{\mathrm {tor}}_m[1/E]$ agrees with the ordinary locus in [Reference LanLan18, Thm. 5.2.1.1] for full level at p, and by [Reference LanLan18, Cor. 5.2.2.3] the map ![]() $ \mathscr {T}^{\mathrm {tor}}_{n,m}\rightarrow \mathscr {S}^{\mathrm {tor}}_m[1/E]$ that forgets the ordinary
$ \mathscr {T}^{\mathrm {tor}}_{n,m}\rightarrow \mathscr {S}^{\mathrm {tor}}_m[1/E]$ that forgets the ordinary ![]() $K^1_{p,n}$-level structure is finite étale. Concretely, we can describe
$K^1_{p,n}$-level structure is finite étale. Concretely, we can describe ![]() $\mathscr {T}^{\mathrm {tor}}_{n,m}$ as
$\mathscr {T}^{\mathrm {tor}}_{n,m}$ as
where ![]() $P_{\mathtt {D}}(\mathbb {Z}_p)$ acts on an element
$P_{\mathtt {D}}(\mathbb {Z}_p)$ acts on an element ![]() $\alpha _p\in \underline {\operatorname {\mathrm {Isom}}}_{\mathscr {S}^{\mathrm {tor}}_m[1/E]}\left (\mu _{p^n}\otimes \mathtt {D}^0,\mathscr {G}[p^n]^{\mathrm {mult}}\right )$ by
$\alpha _p\in \underline {\operatorname {\mathrm {Isom}}}_{\mathscr {S}^{\mathrm {tor}}_m[1/E]}\left (\mu _{p^n}\otimes \mathtt {D}^0,\mathscr {G}[p^n]^{\mathrm {mult}}\right )$ by ![]() $(g\cdot \alpha _p)(v)=\alpha _p(g^{-1}v)$ for
$(g\cdot \alpha _p)(v)=\alpha _p(g^{-1}v)$ for ![]() $v\in \mathtt {D}^0$. The fiber at a geometric point
$v\in \mathtt {D}^0$. The fiber at a geometric point ![]() $\bar {s}\in \mathscr {S}^{\mathrm {tor}}_{n,m}$ parameterizes tuples
$\bar {s}\in \mathscr {S}^{\mathrm {tor}}_{n,m}$ parameterizes tuples ![]() $(\mathtt {F}^{\pm },\delta ^+_3,\delta ^-_1,\mathtt {F}^+_1[p])$, where
$(\mathtt {F}^{\pm },\delta ^+_3,\delta ^-_1,\mathtt {F}^+_1[p])$, where ![]() ${{\tt F^\pm }}$ are filtrations
${{\tt F^\pm }}$ are filtrations
 $$ \begin{align} \begin{aligned} &\mathtt{F}^+:0=\mathtt{F}^+_0\subset \mathtt{F}^+_2\subset\mathtt{F}^+_3=\mathscr{G}_{\bar{s}}[p^n]^{\mathrm{mult}+}\\ &\mathtt{F}^-:0=\mathtt{F}^-_0\subset\mathtt{F}^-_1= \mathscr{G}_{\bar{s}}[p^n]^{\mathrm{mult} -} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathtt{F}^+:0=\mathtt{F}^+_0\subset \mathtt{F}^+_2\subset\mathtt{F}^+_3=\mathscr{G}_{\bar{s}}[p^n]^{\mathrm{mult}+}\\ &\mathtt{F}^-:0=\mathtt{F}^-_0\subset\mathtt{F}^-_1= \mathscr{G}_{\bar{s}}[p^n]^{\mathrm{mult} -} \end{aligned} \end{align} $$compatible with the Weil pairing; ![]() $\delta ^+_3$ and
$\delta ^+_3$ and ![]() $\delta ^-_1$ are isomorphisms
$\delta ^-_1$ are isomorphisms
and ![]() $0\subset \mathtt {F}^+_1[p]\subset \mathtt {F}^+_2[p]$ is a two-step filtration of
$0\subset \mathtt {F}^+_1[p]\subset \mathtt {F}^+_2[p]$ is a two-step filtration of ![]() $\mathtt {F}^+_2[p]$.
$\mathtt {F}^+_2[p]$.
2.6 p-adic forms
Define the space of mod ![]() $p^m$ automorphic forms on G of level n by
$p^m$ automorphic forms on G of level n by
Letting ![]() $\mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}:=(\mathscr {T}^{\mathrm {tor}}_{n,m}\rightarrow \mathscr {S}^{\mathrm {tor}}_m[1/E])^*\mathcal {I}_{\mathscr {S}^{\mathrm {tor}}}$, we similarly define the space of mod
$\mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}:=(\mathscr {T}^{\mathrm {tor}}_{n,m}\rightarrow \mathscr {S}^{\mathrm {tor}}_m[1/E])^*\mathcal {I}_{\mathscr {S}^{\mathrm {tor}}}$, we similarly define the space of mod ![]() $p^m$ cuspidal automorphic forms on G of level n by
$p^m$ cuspidal automorphic forms on G of level n by
Passing to the limit, we obtain corresponding spaces of p-adic automorphic forms (with p-power torsion coefficients) by
Let ![]() ${T_{\mathrm {so}}}(\mathbb {Z}_p)=\mathbb {Z}_p^{\times }\times \mathbb {Z}_p^{\times }$. The map sending
${T_{\mathrm {so}}}(\mathbb {Z}_p)=\mathbb {Z}_p^{\times }\times \mathbb {Z}_p^{\times }$. The map sending ![]() $(a_1,a_2)$ to
$(a_1,a_2)$ to ![]() $g\in G(\mathbb {Z}_p)$ with
$g\in G(\mathbb {Z}_p)$ with  $g^+=\left (\begin {smallmatrix}1\\&1\\&&a_1\\&&&a^{-1}_2\end {smallmatrix}\right ) $and
$g^+=\left (\begin {smallmatrix}1\\&1\\&&a_1\\&&&a^{-1}_2\end {smallmatrix}\right ) $and ![]() $\nu (g)=1$ identifies
$\nu (g)=1$ identifies ![]() $T_{\mathrm {so}}(\mathbb {Z}/p^n)=(\mathbb {Z}/p^n\mathbb {Z})^{\times }\times (\mathbb {Z}/p^n\mathbb {Z})^{\times }$ with
$T_{\mathrm {so}}(\mathbb {Z}/p^n)=(\mathbb {Z}/p^n\mathbb {Z})^{\times }\times (\mathbb {Z}/p^n\mathbb {Z})^{\times }$ with ![]() $K^0_{p,n}/K^1_{p,n}$. Hence, the group
$K^0_{p,n}/K^1_{p,n}$. Hence, the group ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ naturally acts on
$T_{\mathrm {so}}(\mathbb {Z}_p)$ naturally acts on
making these spaces into ![]() $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-modules.
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-modules.
By a p-adic weight (for a semiordinary form) we mean a ![]() $\overline {\mathbb {Q}}_p$-valued character of
$\overline {\mathbb {Q}}_p$-valued character of ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$, that is, a pair
$T_{\mathrm {so}}(\mathbb {Z}_p)$, that is, a pair ![]() $(\tau ^+,\tau ^-)$, where
$(\tau ^+,\tau ^-)$, where ![]() $\tau ^{\pm }:\mathbb {Z}^{\times }_p\rightarrow \overline {\mathbb {Q}}^{\times }_p$ are continuous characters, and we say that a p-adic weight is arithmetic if it is of the form
$\tau ^{\pm }:\mathbb {Z}^{\times }_p\rightarrow \overline {\mathbb {Q}}^{\times }_p$ are continuous characters, and we say that a p-adic weight is arithmetic if it is of the form ![]() $(x,y)\mapsto \epsilon ^+(x)x^{t^+}\cdot \epsilon ^-(y)y^{t^-}$, where
$(x,y)\mapsto \epsilon ^+(x)x^{t^+}\cdot \epsilon ^-(y)y^{t^-}$, where ![]() $\epsilon ^{\pm }$ is of finite order and
$\epsilon ^{\pm }$ is of finite order and ![]() $t^{\pm }\in \mathbb {Z}$. If
$t^{\pm }\in \mathbb {Z}$. If ![]() $(\tau ^+,\tau ^-)$ is arithmetic, we put
$(\tau ^+,\tau ^-)$ is arithmetic, we put ![]() $\tau _{\mathrm {f}}^{\pm }:=\epsilon ^{\pm }$ and
$\tau _{\mathrm {f}}^{\pm }:=\epsilon ^{\pm }$ and ![]() $\tau _{\mathrm {alg}}^{\pm }=t^{\pm }$. Given a p-adic weight
$\tau _{\mathrm {alg}}^{\pm }=t^{\pm }$. Given a p-adic weight ![]() $(\tau ^+,\tau ^-)$, we denote by
$(\tau ^+,\tau ^-)$, we denote by ![]() $V_{n,m}[\tau ^+,\tau ^-]$ the subspace of
$V_{n,m}[\tau ^+,\tau ^-]$ the subspace of ![]() $V_{n,m}\otimes _{\mathbb {Z}_p}\mathcal {O}_{\mathbb {Q}_p(\tau ^+,\tau ^-)}$ on which
$V_{n,m}\otimes _{\mathbb {Z}_p}\mathcal {O}_{\mathbb {Q}_p(\tau ^+,\tau ^-)}$ on which ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ acts by the inverse of the character
$T_{\mathrm {so}}(\mathbb {Z}_p)$ acts by the inverse of the character ![]() $(\tau ^+,\tau ^-)$. Similarly, we define the spaces
$(\tau ^+,\tau ^-)$. Similarly, we define the spaces ![]() $V^0_{n,m}[\tau ^+,\tau ^-]$,
$V^0_{n,m}[\tau ^+,\tau ^-]$, ![]() ,
, ![]() .
.
2.7 Classical automorphic forms
The weights of classical holomorphic automorphic forms on G are indexed by tuples of integers ![]() ${\underline {t}} = (t^+_1,t^+_2,t^+_3;t^-_1)$ with
${\underline {t}} = (t^+_1,t^+_2,t^+_3;t^-_1)$ with ![]() $t^+_1\geq t^+_2\geq t^+_3$. (When
$t^+_1\geq t^+_2\geq t^+_3$. (When ![]() $t^+_3\geq -t^-_1+4$, the Archimedean component of the corresponding automorphic representation is isomorphic to a holomorphic discrete series.)
$t^+_3\geq -t^-_1+4$, the Archimedean component of the corresponding automorphic representation is isomorphic to a holomorphic discrete series.)
Let ![]() ${W_{\underline {t}}}$ be the algebraic representation of
${W_{\underline {t}}}$ be the algebraic representation of ![]() $\operatorname {\mathrm {GL}}_3\times \operatorname {\mathrm {GL}}_1$ given by
$\operatorname {\mathrm {GL}}_3\times \operatorname {\mathrm {GL}}_1$ given by
Here, for any algebra R, letting ![]() $R[\underline {x},\det \underline {x}^{-1}]$ be the polynomial ring in the variables
$R[\underline {x},\det \underline {x}^{-1}]$ be the polynomial ring in the variables ![]() $x_{ij}$ (
$x_{ij}$ (![]() $1\leq i,j\leq 3$) and
$1\leq i,j\leq 3$) and ![]() $\left (\det (x_{ij})_{1\leq i,j\leq 3}\right )^{-1}$,
$\left (\det (x_{ij})_{1\leq i,j\leq 3}\right )^{-1}$, ![]() $W_{(t^+_1,t^+_2,t^+_3)}(R)$ is the R-submodule of
$W_{(t^+_1,t^+_2,t^+_3)}(R)$ is the R-submodule of ![]() $R[\underline {x},(\det \underline {x})^{-1}]$ spanned by
$R[\underline {x},(\det \underline {x})^{-1}]$ spanned by
 $$\begin{align*}x^{a_1}_{11}x^{a_2}_{12}x^{a_3}_{13}\det\begin{pmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end{pmatrix}^{b_1}\det\begin{pmatrix}x_{11}&x_{13}\\x_{21}&x_{23}\end{pmatrix}^{b_2}\det\begin{pmatrix}x_{12}&x_{13}\\x_{22}&x_{23}\end{pmatrix}^{b_3} \det\begin{pmatrix}x_{11}&x_{12}&x_{13}\\ x_{21}&x_{22}&x_{23}\\ x_{31}&x_{32}&x_{33}\end{pmatrix}^{t^+_3},\\[-15pt] \end{align*}$$
$$\begin{align*}x^{a_1}_{11}x^{a_2}_{12}x^{a_3}_{13}\det\begin{pmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end{pmatrix}^{b_1}\det\begin{pmatrix}x_{11}&x_{13}\\x_{21}&x_{23}\end{pmatrix}^{b_2}\det\begin{pmatrix}x_{12}&x_{13}\\x_{22}&x_{23}\end{pmatrix}^{b_3} \det\begin{pmatrix}x_{11}&x_{12}&x_{13}\\ x_{21}&x_{22}&x_{23}\\ x_{31}&x_{32}&x_{33}\end{pmatrix}^{t^+_3},\\[-15pt] \end{align*}$$where ![]() $a_i,b_i\geq 0,\,a_1+a_2+a_3=t^+_1-t^+_2,\,b_1+b_2+b_3=t^+_2-t^+_3$, and
$a_i,b_i\geq 0,\,a_1+a_2+a_3=t^+_1-t^+_2,\,b_1+b_2+b_3=t^+_2-t^+_3$, and ![]() $W_{t^-_1}(R)$ is the R-submodule of
$W_{t^-_1}(R)$ is the R-submodule of ![]() $R[x,x^{-1}]$ spanned by
$R[x,x^{-1}]$ spanned by ![]() $x^{t^-_1}$.
$x^{t^-_1}$.
The groups ![]() $\operatorname {\mathrm {GL}}_3$ and
$\operatorname {\mathrm {GL}}_3$ and ![]() $\operatorname {\mathrm {GL}}_1$ act on
$\operatorname {\mathrm {GL}}_1$ act on ![]() $W_{\underline {t}}$ by right translation. One can check that the left translation of
$W_{\underline {t}}$ by right translation. One can check that the left translation of ![]() $\left (\begin {smallmatrix}a_1\\ \ast &a_2\\ \ast &\ast &a_3\end {smallmatrix}\right ) $on
$\left (\begin {smallmatrix}a_1\\ \ast &a_2\\ \ast &\ast &a_3\end {smallmatrix}\right ) $on ![]() $W_{(t^+_1,t^+_2,t^+_3)}$ is by the scalar
$W_{(t^+_1,t^+_2,t^+_3)}$ is by the scalar ![]() $a^{t^+_1}_1 a^{t^+_2}_2 a^{t^+_3}_3$; when
$a^{t^+_1}_1 a^{t^+_2}_2 a^{t^+_3}_3$; when ![]() $R=\mathbb {C}$, it is the irreducible algebraic representation of
$R=\mathbb {C}$, it is the irreducible algebraic representation of ![]() $\operatorname {\mathrm {GL}}_3(\mathbb {C})$ of highest weight
$\operatorname {\mathrm {GL}}_3(\mathbb {C})$ of highest weight ![]() $(t^+_1,t^+_2,t^+_3)$. Let
$(t^+_1,t^+_2,t^+_3)$. Let ![]() $\mathfrak {e}_{\mathrm {can}}:W_{\underline {t}}\rightarrow \mathbb {A}^1$ be the linear functional defined by the evaluation at
$\mathfrak {e}_{\mathrm {can}}:W_{\underline {t}}\rightarrow \mathbb {A}^1$ be the linear functional defined by the evaluation at ![]() $(\mathbf {1}_3,\mathbf {1}_1)$.
$(\mathbf {1}_3,\mathbf {1}_1)$.
Let ![]() $\underline {\omega }^+$ (resp.
$\underline {\omega }^+$ (resp. ![]() $\underline {\omega }^-$) be the subsheaf of
$\underline {\omega }^-$) be the subsheaf of ![]() $\underline {\omega }$ on which
$\underline {\omega }$ on which ![]() $i(b)$ acts by b (resp.
$i(b)$ acts by b (resp. ![]() $\bar {b}$) for all
$\bar {b}$) for all ![]() $b\in \mathcal {O}_{\mathcal {K}}$. Because p is unramified in
$b\in \mathcal {O}_{\mathcal {K}}$. Because p is unramified in ![]() $\mathcal {K}$,
$\mathcal {K}$, ![]() $\underline {\omega }^+$ (resp.
$\underline {\omega }^+$ (resp. ![]() $\underline {\omega }^-$) is locally free of rank
$\underline {\omega }^-$) is locally free of rank ![]() $3$ (resp. rank
$3$ (resp. rank ![]() $1$) and
$1$) and ![]() $\underline {\omega }=\underline {\omega }^+\oplus \underline {\omega }^-$.
$\underline {\omega }=\underline {\omega }^+\oplus \underline {\omega }^-$.
Set
 $$ \begin{align*} \omega^+_{(t^+_1,t^+_2,t^+_3)}&=\underline{\operatorname{\mathrm{Isom}}}_{\mathscr{S}^{\mathrm{tor}}}(\mathcal{O}^{\oplus{3}}_{\mathscr{S}^{\mathrm{tor}}},\underline{\omega}^+)\times^{\operatorname{\mathrm{GL}}_3} W_{(t^+_1,t^+_2,t^+_3)},\\ \omega^+_{t^-_1}&=\underline{\operatorname{\mathrm{Isom}}}_{\mathscr{S}^{\mathrm{tor}}}(\mathcal{O}_{\mathscr{S}^{\mathrm{tor}}},\underline{\omega}^+)\times^{\operatorname{\mathrm{GL}}_1} W_{t^-_1}\cong (\underline{\omega}^-)^{\otimes t^-_1},\\[-15pt] \end{align*} $$
$$ \begin{align*} \omega^+_{(t^+_1,t^+_2,t^+_3)}&=\underline{\operatorname{\mathrm{Isom}}}_{\mathscr{S}^{\mathrm{tor}}}(\mathcal{O}^{\oplus{3}}_{\mathscr{S}^{\mathrm{tor}}},\underline{\omega}^+)\times^{\operatorname{\mathrm{GL}}_3} W_{(t^+_1,t^+_2,t^+_3)},\\ \omega^+_{t^-_1}&=\underline{\operatorname{\mathrm{Isom}}}_{\mathscr{S}^{\mathrm{tor}}}(\mathcal{O}_{\mathscr{S}^{\mathrm{tor}}},\underline{\omega}^+)\times^{\operatorname{\mathrm{GL}}_1} W_{t^-_1}\cong (\underline{\omega}^-)^{\otimes t^-_1},\\[-15pt] \end{align*} $$and put ![]() ${\omega _{\underline {t}}}=\omega ^+_{(t^+_1,t^+_2,t^+_3)}\otimes \omega ^-_{t^-_1}$.
${\omega _{\underline {t}}}=\omega ^+_{(t^+_1,t^+_2,t^+_3)}\otimes \omega ^-_{t^-_1}$.
Letting ![]() $F/\mathbb {Q}_p$ be a finite extension containing the values of the finite-order character
$F/\mathbb {Q}_p$ be a finite extension containing the values of the finite-order character ![]() $\epsilon ^{\pm }$ of
$\epsilon ^{\pm }$ of ![]() $\mathbb {Z}^{\times }_p$, and
$\mathbb {Z}^{\times }_p$, and ![]() $S^{\mathrm {tor}}_{K^p_fK^1_{p,n}}$ be the toroidal compactification of the Shimura variety of level
$S^{\mathrm {tor}}_{K^p_fK^1_{p,n}}$ be the toroidal compactification of the Shimura variety of level ![]() $K^p_fK^1_{p,n}$ defined over
$K^p_fK^1_{p,n}$ defined over ![]() $\mathcal {K}$, we have
$\mathcal {K}$, we have
 $$\begin{align*}{M_{(0,0,t^+;t^-)}\left(K^p_fK^1_{p,n},\epsilon^+,\epsilon^-;F\right)} = \left(H^0\Big(S^{\mathrm{tor}}_{K^p_fK^1_{p,n}},\underline{\omega}_{(0,0,t^+;t^-)}\Big)\otimes_{\mathcal{K}}F\right)[\epsilon^+,\epsilon^-],\\[-15pt] \end{align*}$$
$$\begin{align*}{M_{(0,0,t^+;t^-)}\left(K^p_fK^1_{p,n},\epsilon^+,\epsilon^-;F\right)} = \left(H^0\Big(S^{\mathrm{tor}}_{K^p_fK^1_{p,n}},\underline{\omega}_{(0,0,t^+;t^-)}\Big)\otimes_{\mathcal{K}}F\right)[\epsilon^+,\epsilon^-],\\[-15pt] \end{align*}$$the space of classical automorphic forms on G of weight ![]() $(0,0,t^+;t^-)$, level
$(0,0,t^+;t^-)$, level ![]() $K^p_fK^1_{p,n}$, and nebentypus
$K^p_fK^1_{p,n}$, and nebentypus ![]() $(\epsilon ^+,\epsilon ^-)$ for the action of
$(\epsilon ^+,\epsilon ^-)$ for the action of ![]() $K^0_{p,n}/K^1_{p,n}$. Here, F is viewed as a
$K^0_{p,n}/K^1_{p,n}$. Here, F is viewed as a ![]() $\mathcal {K}$-algebra via
$\mathcal {K}$-algebra via ![]() $\mathcal {K}\stackrel {\iota _p}{\rightarrow } \mathbb {Q}_p\rightarrow F$. Similarly, we have the space of classical cuspidal automorphic forms
$\mathcal {K}\stackrel {\iota _p}{\rightarrow } \mathbb {Q}_p\rightarrow F$. Similarly, we have the space of classical cuspidal automorphic forms
 $$\begin{align*}{M^0_{(0,0,t^+;t^-)}\left(K^p_fK^1_{p,n},\epsilon^+,\epsilon^-;F\right)} =\left(H^0\Big(S^{\mathrm{tor}}_{K^p_fK^1_{p,n}},\underline{\omega}_{(0,0;t^+;t^-)}\otimes\mathcal{I}_{\mathscr{S}^{\mathrm{tor}}}\Big)\otimes_{\mathcal{K}}F\right)[\epsilon^+,\epsilon^-].\\[-15pt] \end{align*}$$
$$\begin{align*}{M^0_{(0,0,t^+;t^-)}\left(K^p_fK^1_{p,n},\epsilon^+,\epsilon^-;F\right)} =\left(H^0\Big(S^{\mathrm{tor}}_{K^p_fK^1_{p,n}},\underline{\omega}_{(0,0;t^+;t^-)}\otimes\mathcal{I}_{\mathscr{S}^{\mathrm{tor}}}\Big)\otimes_{\mathcal{K}}F\right)[\epsilon^+,\epsilon^-].\\[-15pt] \end{align*}$$There are classical embeddings

induced by the trivialization of ![]() $\underline {\omega }$ over the Igusa tower and the canonical functional
$\underline {\omega }$ over the Igusa tower and the canonical functional ![]() $\mathfrak {e}_{\mathrm {can}}$. More precisely, the trivialization of
$\mathfrak {e}_{\mathrm {can}}$. More precisely, the trivialization of ![]() $\underline {\omega }$ arises from the Hodge–Tate map
$\underline {\omega }$ arises from the Hodge–Tate map ![]() $(\mathcal {G}_{/S}[p^n]^{\mathrm {mult}})^D\otimes _{\mathbb {Z}}\mathcal {O}_S\stackrel {\sim }{\rightarrow } e^*\Omega ^1_{\mathcal {G}/S}\otimes _{\mathbb {Z}}\mathbb {Z}/p^n\mathbb {Z}$, where
$(\mathcal {G}_{/S}[p^n]^{\mathrm {mult}})^D\otimes _{\mathbb {Z}}\mathcal {O}_S\stackrel {\sim }{\rightarrow } e^*\Omega ^1_{\mathcal {G}/S}\otimes _{\mathbb {Z}}\mathbb {Z}/p^n\mathbb {Z}$, where ![]() $\mathcal {G}_{/S}$ is an ordinary semiabelian variety over S, the superscript
$\mathcal {G}_{/S}$ is an ordinary semiabelian variety over S, the superscript ![]() $^D$ denotes the Cartier dual, and
$^D$ denotes the Cartier dual, and ![]() $e:S\rightarrow \mathcal {G}$ is the zero section.
$e:S\rightarrow \mathcal {G}$ is the zero section.
Similarly, we have embeddings

2.8 The  $\mathbb {U}_p$-operator
$\mathbb {U}_p$-operator
Given a tuple ![]() $(A,\lambda ,i,\alpha ^p,\alpha _p)$ parameterized by
$(A,\lambda ,i,\alpha ^p,\alpha _p)$ parameterized by ![]() $\mathscr {T}_{n,m}$, where
$\mathscr {T}_{n,m}$, where ![]() $\alpha _p:\mu _{p^n}\otimes \mathtt {D}^0\rightarrow A[p^n]^{\mathrm {mult}}$ is an isomorphism up to
$\alpha _p:\mu _{p^n}\otimes \mathtt {D}^0\rightarrow A[p^n]^{\mathrm {mult}}$ is an isomorphism up to ![]() $K^1_{p,n}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, the corresponding filtration
$K^1_{p,n}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, the corresponding filtration ![]() $\mathtt {F^{\pm }}$ of
$\mathtt {F^{\pm }}$ of ![]() $A[p^n]^{\mathrm {mult}\pm }$ is
$A[p^n]^{\mathrm {mult}\pm }$ is
 $$ \begin{align*} \mathtt{F}^+&\colon\; 0=\mathtt{F}^+_0\subset\mathtt{F}^+_2=\{e^+_1,e^+_2\}\subset\mathtt{F}^+_3=\{e^+_1,e^+_2,e^+_3\}=A[p^n]^{\mathrm{mult}+},\\ \mathtt{F}^-&\colon\; 0=\mathtt{F}^-_0\subset\mathtt{F}^-_1=\{e^-_1\}=A[p^n]^{\mathrm{mult}-}, \end{align*} $$
$$ \begin{align*} \mathtt{F}^+&\colon\; 0=\mathtt{F}^+_0\subset\mathtt{F}^+_2=\{e^+_1,e^+_2\}\subset\mathtt{F}^+_3=\{e^+_1,e^+_2,e^+_3\}=A[p^n]^{\mathrm{mult}+},\\ \mathtt{F}^-&\colon\; 0=\mathtt{F}^-_0\subset\mathtt{F}^-_1=\{e^-_1\}=A[p^n]^{\mathrm{mult}-}, \end{align*} $$where ![]() $(e^+_1,e^+_2,e^+_3;e^-_1)=\alpha _p(\mathtt {x}^+_1,\mathtt {w}^+_1,\mathtt {w}^+_2;\mathtt {x}^-_1)$.
$(e^+_1,e^+_2,e^+_3;e^-_1)=\alpha _p(\mathtt {x}^+_1,\mathtt {w}^+_1,\mathtt {w}^+_2;\mathtt {x}^-_1)$.
Now, we define three ![]() $\mathbb {U}_p$-operators
$\mathbb {U}_p$-operators ![]() $U^+_{p,2},U^+_{p,3},U^-_{p,1}$.
$U^+_{p,2},U^+_{p,3},U^-_{p,1}$.
2.8.1  $\mathbb {U}_p$-operators on
$\mathbb {U}_p$-operators on  $V_{n,m}$
$V_{n,m}$
For ![]() $j=2,3$, let
$j=2,3$, let ![]() ${\mathscr {C}^{+}_{j,n,m}}$ denote the solution to the moduli problem classifying tuples
${\mathscr {C}^{+}_{j,n,m}}$ denote the solution to the moduli problem classifying tuples ![]() $(A,\lambda ,i,\alpha ^p,\alpha _p,C)$ with
$(A,\lambda ,i,\alpha ^p,\alpha _p,C)$ with ![]() $C\subset A[p^2]$ a Lagrangian subgroup, (that is, maximal isotropic for the
$C\subset A[p^2]$ a Lagrangian subgroup, (that is, maximal isotropic for the ![]() $\lambda $-Weil pairing) stable under the
$\lambda $-Weil pairing) stable under the ![]() $\mathcal {O}_{\mathcal {K}}$-action through i such that
$\mathcal {O}_{\mathcal {K}}$-action through i such that ![]() $A[p]=C[p]\oplus \mathtt {F}^+_j[p]$. With
$A[p]=C[p]\oplus \mathtt {F}^+_j[p]$. With ![]() $e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4$ a basis of
$e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4$ a basis of ![]() $A[p^n]$ corresponding to
$A[p^n]$ corresponding to ![]() $\alpha _p$, such a C is spanned by
$\alpha _p$, such a C is spanned by ![]() $(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n\gamma _{C,p}^{\pm }$, where for
$(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n\gamma _{C,p}^{\pm }$, where for ![]() $j=2$
$j=2$
 $$ \begin{align} \begin{aligned} \gamma^+_{C,p}&= \begin{pmatrix}1&&u_1&\ast\\&1&u_2&\ast\\&&1&\\&&&1\end{pmatrix}\begin{pmatrix}1&&&\\&1&&\\&&\frac{1}{p}&\\&&&\frac{1}{p}\end{pmatrix},\\ \gamma^-_{C,p}&= \begin{pmatrix}1\\&\iota_p(\bar{\zeta}_0)^{-1}\\&&1\end{pmatrix}\begin{pmatrix}1&\ast&&\ast\\&1\\&-u_2&1&u_1\\&&&1\end{pmatrix}\begin{pmatrix}\frac{1}{p}&&&\\&\frac{1}{p^2}&&\\&&\frac{1}{p}&\\&&&\frac{1}{p^2}\end{pmatrix}\begin{pmatrix}1\\&\iota_p(\bar{\zeta}_0)\\&&1\end{pmatrix} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \gamma^+_{C,p}&= \begin{pmatrix}1&&u_1&\ast\\&1&u_2&\ast\\&&1&\\&&&1\end{pmatrix}\begin{pmatrix}1&&&\\&1&&\\&&\frac{1}{p}&\\&&&\frac{1}{p}\end{pmatrix},\\ \gamma^-_{C,p}&= \begin{pmatrix}1\\&\iota_p(\bar{\zeta}_0)^{-1}\\&&1\end{pmatrix}\begin{pmatrix}1&\ast&&\ast\\&1\\&-u_2&1&u_1\\&&&1\end{pmatrix}\begin{pmatrix}\frac{1}{p}&&&\\&\frac{1}{p^2}&&\\&&\frac{1}{p}&\\&&&\frac{1}{p^2}\end{pmatrix}\begin{pmatrix}1\\&\iota_p(\bar{\zeta}_0)\\&&1\end{pmatrix} \end{aligned} \end{align} $$with ![]() $u_1,u_2,\ast \in \mathbb {Z}_p$, and for
$u_1,u_2,\ast \in \mathbb {Z}_p$, and for ![]() $j=3$,
$j=3$,
 $$ \begin{align} \begin{aligned} \gamma^+_{C,p}&=\begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}1&&&\\&1&&\\&&1&\\&&&\frac{1}{p}\end{pmatrix}, &\gamma^-_{C,p}&= \begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}\frac{1}{p}&&\\&\frac{1}{p^2}\\&&\frac{1}{p^2}\\&&&\frac{1}{p^2}\end{pmatrix} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \gamma^+_{C,p}&=\begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}1&&&\\&1&&\\&&1&\\&&&\frac{1}{p}\end{pmatrix}, &\gamma^-_{C,p}&= \begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}\frac{1}{p}&&\\&\frac{1}{p^2}\\&&\frac{1}{p^2}\\&&&\frac{1}{p^2}\end{pmatrix} \end{aligned} \end{align} $$with ![]() $\ast \in \mathbb {Z}_p$.
$\ast \in \mathbb {Z}_p$.
Similarly, let ![]() ${\mathscr {C}^{-}_{1,n,m}}$ be the moduli space classifying tuples
${\mathscr {C}^{-}_{1,n,m}}$ be the moduli space classifying tuples ![]() $(A,\lambda ,i,\alpha ^p,\alpha _p,C)$ with
$(A,\lambda ,i,\alpha ^p,\alpha _p,C)$ with ![]() $C\subset A[p^2]$ a Lagrange subgroup stable under the
$C\subset A[p^2]$ a Lagrange subgroup stable under the ![]() $\mathcal {O}_{\mathcal {K}}$-action through i such that
$\mathcal {O}_{\mathcal {K}}$-action through i such that ![]() $A[p]=C[p]\oplus \mathtt {F}^-_1[p]$. Then such a C is spanned by
$A[p]=C[p]\oplus \mathtt {F}^-_1[p]$. Then such a C is spanned by ![]() $(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n\gamma ^{\pm }_{C,p}$ with
$(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n\gamma ^{\pm }_{C,p}$ with
 $$ \begin{align} \begin{aligned} \gamma^+_{C,p}&=\begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}\frac{1}{p}&&&\\&\frac{1}{p}&&\\&&\frac{1}{p}&\\&&&\frac{1}{p^2}\end{pmatrix}, &\gamma^-_{C,p}&= \begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}1&&\\&\frac{1}{p}\\&&\frac{1}{p}\\&&&\frac{1}{p}\end{pmatrix}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \gamma^+_{C,p}&=\begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}\frac{1}{p}&&&\\&\frac{1}{p}&&\\&&\frac{1}{p}&\\&&&\frac{1}{p^2}\end{pmatrix}, &\gamma^-_{C,p}&= \begin{pmatrix}1&&&\ast\\&1&&\ast\\&&1&\ast\\&&&1\end{pmatrix}\begin{pmatrix}1&&\\&\frac{1}{p}\\&&\frac{1}{p}\\&&&\frac{1}{p}\end{pmatrix}. \end{aligned} \end{align} $$ For ![]() $(\bullet ,j)=(+,2),(+,3),(-,1)$, we consider the diagram
$(\bullet ,j)=(+,2),(+,3),(-,1)$, we consider the diagram

with ![]() $p_1,p_2$ the projections given by
$p_1,p_2$ the projections given by
 $$ \begin{align*} p_1:(A,\lambda,i,\alpha^p,\alpha_p,C)&\longmapsto(A,\lambda,i,\alpha^p,\alpha_p),\\ p_2:(A,\lambda,i,\alpha^p,\alpha_p,C)&\longmapsto(A',\lambda',i',(\alpha^p)',\alpha_p'), \end{align*} $$
$$ \begin{align*} p_1:(A,\lambda,i,\alpha^p,\alpha_p,C)&\longmapsto(A,\lambda,i,\alpha^p,\alpha_p),\\ p_2:(A,\lambda,i,\alpha^p,\alpha_p,C)&\longmapsto(A',\lambda',i',(\alpha^p)',\alpha_p'), \end{align*} $$where ![]() $A'=A/C$,
$A'=A/C$, ![]() $\lambda '$ is such that
$\lambda '$ is such that ![]() $\pi ^{\vee }\circ \lambda \circ \pi =p^2\lambda $ with
$\pi ^{\vee }\circ \lambda \circ \pi =p^2\lambda $ with ![]() $\pi :A\rightarrow A'$ the natural projection,
$\pi :A\rightarrow A'$ the natural projection, ![]() $i'$ is the
$i'$ is the ![]() $\mathcal {O}_{\mathcal {K}}$-action i on A descended to
$\mathcal {O}_{\mathcal {K}}$-action i on A descended to ![]() $A'$,
$A'$, ![]() $(\alpha ^{p})'=\pi \circ \alpha ^p$, and
$(\alpha ^{p})'=\pi \circ \alpha ^p$, and ![]() $\alpha _p'$ given by
$\alpha _p'$ given by ![]() $(e^{+\prime }_1,e^{+\prime }_2,e^{+\prime }_3;e^{-\prime }_1)$ defined as
$(e^{+\prime }_1,e^{+\prime }_2,e^{+\prime }_3;e^{-\prime }_1)$ defined as
 $$\begin{align*}(e^{+\prime}_1,e^{+\prime}_2,e^{+\prime}_3;e^{-\prime}_1)=\begin{cases} \pi\left((e^+_1,e^+_2,e^+_3;e^-_1)\left(\begin{smallmatrix}1&&u_1\\&1&u_2\\&&1&\\&&&1\end{smallmatrix}\right) \left(\begin{smallmatrix}1\\&1\\&&p^{-1}\\&&&p^{-1}\end{smallmatrix}\right) \right), &\bullet=+,\, j=2,\\[9pt] \pi\left((e^+_1,e^+_2, e^+_3;e^-_1)\left(\begin{smallmatrix}1\\&1\\&&1\\&&&p^{-1}\end{smallmatrix}\right) \right),&\bullet=+,\,j=3,\\[9pt] \pi\left(e^+_1,e^+_2, e^+_3;e^-_1)\left(\begin{smallmatrix}p^{-1}\\&p^{-1}\\&&p^{-1}\\&&&1\end{smallmatrix}\right) \right), &\bullet=-,\,j=1. \end{cases} \end{align*}$$
$$\begin{align*}(e^{+\prime}_1,e^{+\prime}_2,e^{+\prime}_3;e^{-\prime}_1)=\begin{cases} \pi\left((e^+_1,e^+_2,e^+_3;e^-_1)\left(\begin{smallmatrix}1&&u_1\\&1&u_2\\&&1&\\&&&1\end{smallmatrix}\right) \left(\begin{smallmatrix}1\\&1\\&&p^{-1}\\&&&p^{-1}\end{smallmatrix}\right) \right), &\bullet=+,\, j=2,\\[9pt] \pi\left((e^+_1,e^+_2, e^+_3;e^-_1)\left(\begin{smallmatrix}1\\&1\\&&1\\&&&p^{-1}\end{smallmatrix}\right) \right),&\bullet=+,\,j=3,\\[9pt] \pi\left(e^+_1,e^+_2, e^+_3;e^-_1)\left(\begin{smallmatrix}p^{-1}\\&p^{-1}\\&&p^{-1}\\&&&1\end{smallmatrix}\right) \right), &\bullet=-,\,j=1. \end{cases} \end{align*}$$One can check that if ![]() $(e^{+}_1,e^{+}_2,e^{+}_3;e^{-}_1)$ is up to
$(e^{+}_1,e^{+}_2,e^{+}_3;e^{-}_1)$ is up to ![]() $K^1_{p,n}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, then
$K^1_{p,n}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, then ![]() $(e^{+\prime }_1,e^{+\prime }_2,e^{+\prime }_3;e^{-\prime }_1)$ is well-defined up to
$(e^{+\prime }_1,e^{+\prime }_2,e^{+\prime }_3;e^{-\prime }_1)$ is well-defined up to ![]() $K^1_{p,n}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$.
$K^1_{p,n}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$.
Define
The normalization factors ![]() $p^{-j}$ and
$p^{-j}$ and ![]() $p^{-3}$ are the inverse of the pure inseparability degree of the corresponding projection
$p^{-3}$ are the inverse of the pure inseparability degree of the corresponding projection ![]() $p_1$; they are the optimal normalization to preserve integrality [Reference HidaHid02, p.71]. By computing the effect of equations (2.8.5) and (2.8.6) on Fourier–Jacobi expansions, one can check that the operators preserve
$p_1$; they are the optimal normalization to preserve integrality [Reference HidaHid02, p.71]. By computing the effect of equations (2.8.5) and (2.8.6) on Fourier–Jacobi expansions, one can check that the operators preserve ![]() $V_{n,m}$ and
$V_{n,m}$ and ![]() $V^0_{n,m}$.
$V^0_{n,m}$.
2.8.2  ${ \mathbb {U}}_p$-operators on
${ \mathbb {U}}_p$-operators on  $H^0 \left ({ \mathscr {T}}^{0,\mathrm {tor}}_{n,m}, \omega _{ \underline {t}}\right )$
$H^0 \left ({ \mathscr {T}}^{0,\mathrm {tor}}_{n,m}, \omega _{ \underline {t}}\right )$
Let ![]() $\mathscr {T}^{0,\mathrm {tor}}_{n,m}$ be the quotient of
$\mathscr {T}^{0,\mathrm {tor}}_{n,m}$ be the quotient of ![]() $\mathscr {T}^{\mathrm {tor}}_{n,m}$ by
$\mathscr {T}^{\mathrm {tor}}_{n,m}$ by ![]() $K^0_{p,n}$, which can be described as
$K^0_{p,n}$, which can be described as
Compared to ![]() $\mathscr {T}^{\mathrm {tor}}_{n,m}$, the level structure at p for
$\mathscr {T}^{\mathrm {tor}}_{n,m}$, the level structure at p for ![]() $\mathscr {T}^{0,\mathrm {tor}}_{n,m}$ forgets
$\mathscr {T}^{0,\mathrm {tor}}_{n,m}$ forgets ![]() $\delta ^+_3,\delta ^-_1$ and parameterizes
$\delta ^+_3,\delta ^-_1$ and parameterizes ![]() $(\mathtt {F}^{\pm },\mathtt {F}^+_1[p])$. We can define
$(\mathtt {F}^{\pm },\mathtt {F}^+_1[p])$. We can define ![]() $\mathbb {U}_p$-operators on
$\mathbb {U}_p$-operators on ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\right )$. In order to see that they increase the level, we need to introduce Igusa towers of more general level structure at p.
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\right )$. In order to see that they increase the level, we need to introduce Igusa towers of more general level structure at p.
Given ![]() $1\leq n_1,n_2\leq n_3\leq n_1+n_2$, define the level group
$1\leq n_1,n_2\leq n_3\leq n_1+n_2$, define the level group
 $$\begin{align*}K^0_{p,n_1,n_2,n_3}=\left\{g\in G(\mathbb{Z}_p): g^+=\left(\begin{smallmatrix} \ast & \ast & \ast & \ast\\ p\ast & \ast & \ast & \ast\\ p^{n_1}\ast & p^{n_1}\ast &\ast & \ast\\ p^{n_3}\ast & p^{n_3}\ast & p^{n_2}\ast & \ast \end{smallmatrix}\right) \right\}.\\[-9pt] \end{align*}$$
$$\begin{align*}K^0_{p,n_1,n_2,n_3}=\left\{g\in G(\mathbb{Z}_p): g^+=\left(\begin{smallmatrix} \ast & \ast & \ast & \ast\\ p\ast & \ast & \ast & \ast\\ p^{n_1}\ast & p^{n_1}\ast &\ast & \ast\\ p^{n_3}\ast & p^{n_3}\ast & p^{n_2}\ast & \ast \end{smallmatrix}\right) \right\}.\\[-9pt] \end{align*}$$Define ![]() $\mathscr {T}^0_{n_1,n_2,n_3,m}$ as the quotient of
$\mathscr {T}^0_{n_1,n_2,n_3,m}$ as the quotient of ![]() $\mathscr {T}_{n,m}$,
$\mathscr {T}_{n,m}$, ![]() $n\geq n_1,n_2,n_3$, by
$n\geq n_1,n_2,n_3$, by ![]() $K^0_{p,n_1,n_2,n_3}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, that is, the corresponding level structure at p parameterizes isomorphism
$K^0_{p,n_1,n_2,n_3}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, that is, the corresponding level structure at p parameterizes isomorphism ![]() $\alpha _p:\mu _{p^n}\otimes \mathtt {D}^0\rightarrow A[p^n]^{\mathrm {mult}}$ up to
$\alpha _p:\mu _{p^n}\otimes \mathtt {D}^0\rightarrow A[p^n]^{\mathrm {mult}}$ up to ![]() $K^0_{p,n_1,n_2,n_3}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$.
$K^0_{p,n_1,n_2,n_3}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$.
Like above, for ![]() $(\bullet ,j)=(+,2),(+,3),(-,1)$, let
$(\bullet ,j)=(+,2),(+,3),(-,1)$, let ![]() $\mathscr {C}^{0,\bullet }_{j,n_1,n_2,n_3,m}$ be the moduli space parameterizing tuples
$\mathscr {C}^{0,\bullet }_{j,n_1,n_2,n_3,m}$ be the moduli space parameterizing tuples ![]() $(A,\lambda ,i,\alpha ^p,\alpha _p,C)$ with
$(A,\lambda ,i,\alpha ^p,\alpha _p,C)$ with ![]() $C\subset A[p^2]$ a Lagrangian subgroup stable under the
$C\subset A[p^2]$ a Lagrangian subgroup stable under the ![]() $\mathcal {O}_{\mathcal {K}}$-action through i such that
$\mathcal {O}_{\mathcal {K}}$-action through i such that ![]() $A[p]=C[p]\oplus \mathtt {F}^{\bullet }_j$.
$A[p]=C[p]\oplus \mathtt {F}^{\bullet }_j$.
Consider the diagrams



where ![]() $p_1,p_2$ are defined in the same way as in the diagram (2.8.4). This time, for
$p_1,p_2$ are defined in the same way as in the diagram (2.8.4). This time, for ![]() $(e^{+}_1,e^{+}_2,e^{+}_3;,e^{-}_1)$ up to
$(e^{+}_1,e^{+}_2,e^{+}_3;,e^{-}_1)$ up to ![]() $K^0_{p,n_1,n_2,n_3}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, the
$K^0_{p,n_1,n_2,n_3}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$, the ![]() $(e^{+\prime }_1,e^{+\prime }_2,e^{+\prime }_3;,e^{-\prime }_1)$ is well defined up to
$(e^{+\prime }_1,e^{+\prime }_2,e^{+\prime }_3;,e^{-\prime }_1)$ is well defined up to ![]() $K^0_{p,n_1+1,n_2,n_3+1}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$ in case
$K^0_{p,n_1+1,n_2,n_3+1}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$ in case ![]() $\mathscr {C}^{0,+}_{2,n,m}$, and well defined up to
$\mathscr {C}^{0,+}_{2,n,m}$, and well defined up to ![]() $K^0_{p,n_1,n_2+1,n_3+1}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$ in case
$K^0_{p,n_1,n_2+1,n_3+1}\cap P_{\mathtt {D}}(\mathbb {Z}_p)$ in case ![]() $\mathscr {C}^{0,+}_{3,n,m}$ and case
$\mathscr {C}^{0,+}_{3,n,m}$ and case ![]() $\mathscr {C}^{0,-}_{1,n_1,n_2,n_3,m}$.
$\mathscr {C}^{0,-}_{1,n_1,n_2,n_3,m}$.
In order to define the ![]() $\mathbb {U}_p$-operators on the global sections of vector bundles, we also need maps
$\mathbb {U}_p$-operators on the global sections of vector bundles, we also need maps
 $$ \begin{align*} \pi^*&:H^0\left(\mathscr{C}^{0,-}_{1,n_1+1,n_2,n_3+1,m},p^*_2\omega_{\underline{t}}\right)\longrightarrow H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right)\\ \pi^*&:H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2+1,n_3+1,m},p^*_2\omega_{\underline{t}}\right)\longrightarrow H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right). \end{align*} $$
$$ \begin{align*} \pi^*&:H^0\left(\mathscr{C}^{0,-}_{1,n_1+1,n_2,n_3+1,m},p^*_2\omega_{\underline{t}}\right)\longrightarrow H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right)\\ \pi^*&:H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2+1,n_3+1,m},p^*_2\omega_{\underline{t}}\right)\longrightarrow H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right). \end{align*} $$Suppose that ![]() $\underline {\varepsilon }_A$ (resp.
$\underline {\varepsilon }_A$ (resp. ![]() $\underline {\varepsilon }_{A/C}$) is a basis of
$\underline {\varepsilon }_{A/C}$) is a basis of ![]() $\underline {\omega }_A$ (resp.
$\underline {\omega }_A$ (resp. ![]() $\underline {\omega }_{A/C}$) compatible with
$\underline {\omega }_{A/C}$) compatible with ![]() $\alpha _p$ (resp.
$\alpha _p$ (resp. ![]() $\alpha ^{\prime }_p$). We have
$\alpha ^{\prime }_p$). We have ![]() $\underline {\varepsilon }_A=(\pi ^*\underline {\omega }_{A/C})g$ with
$\underline {\varepsilon }_A=(\pi ^*\underline {\omega }_{A/C})g$ with
 $$\begin{align*}g=\begin{cases} h\left(\begin{smallmatrix}1\\&1\\&&p^{-1}\\&&&p^{-1}\end{smallmatrix}\right) h', &\bullet=+,\, j=2,\\ h\left(\begin{smallmatrix}1\\&1\\&&1\\&&&p^{-1}\end{smallmatrix}\right) h', &\bullet=+,\, j=3,\\ h\left(\begin{smallmatrix}p^{-1}\\&p^{-1}\\&&p^{-1}\\&&&1\end{smallmatrix}\right) h', &\bullet=-,\, j=1, \end{cases} \end{align*}$$
$$\begin{align*}g=\begin{cases} h\left(\begin{smallmatrix}1\\&1\\&&p^{-1}\\&&&p^{-1}\end{smallmatrix}\right) h', &\bullet=+,\, j=2,\\ h\left(\begin{smallmatrix}1\\&1\\&&1\\&&&p^{-1}\end{smallmatrix}\right) h', &\bullet=+,\, j=3,\\ h\left(\begin{smallmatrix}p^{-1}\\&p^{-1}\\&&p^{-1}\\&&&1\end{smallmatrix}\right) h', &\bullet=-,\, j=1, \end{cases} \end{align*}$$for some  $h,h'=\left (\begin {smallmatrix}\ast & p^n\ast & p^n\ast \\\ast & \ast & p\ast \\ \ast & \ast & \ast \\ &&&\ast \end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_4(\mathbb {Z}_p)$. In all the cases,
$h,h'=\left (\begin {smallmatrix}\ast & p^n\ast & p^n\ast \\\ast & \ast & p\ast \\ \ast & \ast & \ast \\ &&&\ast \end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_4(\mathbb {Z}_p)$. In all the cases, ![]() $g^{-1}$ belongs to the semigroup
$g^{-1}$ belongs to the semigroup
We make ![]() $\Delta _+$ act on
$\Delta _+$ act on ![]() $W_{\underline {t}}$ by
$W_{\underline {t}}$ by
 $$ \begin{align} \begin{aligned} &\left(h\begin{pmatrix}a_1\\&a_2\\&&a_3\end{pmatrix}h',a_4\right)\cdot q(\underline{x},y)\\ =&\,q\left(\begin{pmatrix}p^{-v_p(a_1)}\\&p^{-v_p(a_2)}\\&&p^{-v_p(a_3)}\end{pmatrix}\underline{x}h\begin{pmatrix}a_1\\&a_2\\&&a_3\end{pmatrix}h',p^{-v_p(a_4)y}a_4 \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left(h\begin{pmatrix}a_1\\&a_2\\&&a_3\end{pmatrix}h',a_4\right)\cdot q(\underline{x},y)\\ =&\,q\left(\begin{pmatrix}p^{-v_p(a_1)}\\&p^{-v_p(a_2)}\\&&p^{-v_p(a_3)}\end{pmatrix}\underline{x}h\begin{pmatrix}a_1\\&a_2\\&&a_3\end{pmatrix}h',p^{-v_p(a_4)y}a_4 \right), \end{aligned} \end{align} $$and define ![]() $\pi ^*$ as
$\pi ^*$ as
 $$ \begin{align*} \pi^*\vec{f}(A,\lambda,i,\alpha^p,\alpha_p,C,\underline{\varepsilon}_A)&=\vec{f}(A,\lambda,i,\alpha^p,\alpha_p,C,\underline{\varepsilon}_A,(\pi^*\underline{\varepsilon}_{A/C})g)\\ &=g^{-1}\cdot \vec{f}(A,\lambda,i,\alpha^p,\alpha_p,C,\underline{\varepsilon}_{A/C}). \end{align*} $$
$$ \begin{align*} \pi^*\vec{f}(A,\lambda,i,\alpha^p,\alpha_p,C,\underline{\varepsilon}_A)&=\vec{f}(A,\lambda,i,\alpha^p,\alpha_p,C,\underline{\varepsilon}_A,(\pi^*\underline{\varepsilon}_{A/C})g)\\ &=g^{-1}\cdot \vec{f}(A,\lambda,i,\alpha^p,\alpha_p,C,\underline{\varepsilon}_{A/C}). \end{align*} $$The ![]() $\mathbb {U}_p$-operators are defined as
$\mathbb {U}_p$-operators are defined as
 $$ \begin{align*} \begin{aligned} {U^{+}_{p,2}} &:H^0\left(\mathscr{T}^0_{n_1+1,n_2,n_3+1,m},\omega_{\underline{t}}\right) \stackrel{p^*_2}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{2,n_1,n_2,n_3,m},p^*_2\omega_{\underline{t}}\right)\\ &\hspace{3em}\stackrel{\pi^*}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{2,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right) \xrightarrow{p^{-2}\mathrm{Tr}\,p_1} H^0(\mathscr{T}^0_{n_1,n_2,n_3,m},\omega_{\underline{t}}),\\ {U^{+}_{p,3}} &:H^0\left(\mathscr{T}^0_{n_1,n_2+1,n_3+1,m},\omega_{\underline{t}}\right) \stackrel{p^*_2}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{3,n_1,n_2,n_3,m},p^*_2\omega_{\underline{t}}\right)\\ &\hspace{3em}\stackrel{\pi^*}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{3,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right) \xrightarrow{p^{-3}\mathrm{Tr}\,p_1} H^0(\mathscr{T}^0_{n_1,n_2,n_3,m},\omega_{\underline{t}}),\\ {U^{-}_{p,1}} &:H^0\left(\mathscr{T}^0_{n_1,n_2+1,n_3+1,m},\omega_{\underline{t}}\right) \stackrel{p^*_2}{\longrightarrow} H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_2\omega_{\underline{t}}\right)\\ &\hspace{3em}\stackrel{\pi^*}{\longrightarrow} H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right) \xrightarrow{p^{-2}\mathrm{Tr}\,p_1} H^0(\mathscr{T}^0_{n_1,n_2,n_3,m},\omega_{\underline{t}}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {U^{+}_{p,2}} &:H^0\left(\mathscr{T}^0_{n_1+1,n_2,n_3+1,m},\omega_{\underline{t}}\right) \stackrel{p^*_2}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{2,n_1,n_2,n_3,m},p^*_2\omega_{\underline{t}}\right)\\ &\hspace{3em}\stackrel{\pi^*}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{2,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right) \xrightarrow{p^{-2}\mathrm{Tr}\,p_1} H^0(\mathscr{T}^0_{n_1,n_2,n_3,m},\omega_{\underline{t}}),\\ {U^{+}_{p,3}} &:H^0\left(\mathscr{T}^0_{n_1,n_2+1,n_3+1,m},\omega_{\underline{t}}\right) \stackrel{p^*_2}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{3,n_1,n_2,n_3,m},p^*_2\omega_{\underline{t}}\right)\\ &\hspace{3em}\stackrel{\pi^*}{\longrightarrow} H^0\left(\mathscr{C}^{0,+}_{3,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right) \xrightarrow{p^{-3}\mathrm{Tr}\,p_1} H^0(\mathscr{T}^0_{n_1,n_2,n_3,m},\omega_{\underline{t}}),\\ {U^{-}_{p,1}} &:H^0\left(\mathscr{T}^0_{n_1,n_2+1,n_3+1,m},\omega_{\underline{t}}\right) \stackrel{p^*_2}{\longrightarrow} H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_2\omega_{\underline{t}}\right)\\ &\hspace{3em}\stackrel{\pi^*}{\longrightarrow} H^0\left(\mathscr{C}^{0,-}_{1,n_1,n_2,n_3,m},p^*_1\omega_{\underline{t}}\right) \xrightarrow{p^{-2}\mathrm{Tr}\,p_1} H^0(\mathscr{T}^0_{n_1,n_2,n_3,m},\omega_{\underline{t}}). \end{aligned} \end{align*} $$ Similarly as ![]() $V_{n,m}$, one can check that these
$V_{n,m}$, one can check that these ![]() $\mathbb {U}_p$-operators preserve the spaces
$\mathbb {U}_p$-operators preserve the spaces ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\right )$ and
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\right )$ and ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$. It is also easy to see that
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$. It is also easy to see that ![]() $U^+_{p,2}U^+_{p,3}U^-_{p,1}$ maps
$U^+_{p,2}U^+_{p,3}U^-_{p,1}$ maps ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\right )$ (resp.
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\right )$ (resp. ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$) into
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$) into ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n-1,m},\omega _{\underline {t}}\right )$ (resp.
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n-1,m},\omega _{\underline {t}}\right )$ (resp. ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n-1,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n-1,m}}\right )$), that is, the operator
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n-1,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n-1,m}}\right )$), that is, the operator ![]() $U^+_{p,2}U^+_{p,3}U^-_{p,1}$ increases the level.
$U^+_{p,2}U^+_{p,3}U^-_{p,1}$ increases the level.
2.8.3 Adelic  $\mathbb {U}_p$-operators
$\mathbb {U}_p$-operators
If we identify ![]() $G(\mathbb {Q}_p)$ with
$G(\mathbb {Q}_p)$ with ![]() $\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)\times \operatorname {\mathrm {GL}}_1(\mathbb {Q}_p)$ via equation (2.4.1), the
$\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)\times \operatorname {\mathrm {GL}}_1(\mathbb {Q}_p)$ via equation (2.4.1), the ![]() $\mathbb {U}_p$-operators defined above acting on classical automorphic forms on G of weight
$\mathbb {U}_p$-operators defined above acting on classical automorphic forms on G of weight ![]() $(t^+_1,t^+_2.t^+_3;t^-_1)$ correspond to the following adelic operators (up to the action of the center of
$(t^+_1,t^+_2.t^+_3;t^-_1)$ correspond to the following adelic operators (up to the action of the center of ![]() $G(\mathbb {Q}_p)$):
$G(\mathbb {Q}_p)$):
 $$ \begin{align} \begin{aligned} {U^{+}_{p,2}}:&\quad p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(1,1,0;0)\right>}\int_{N(\mathbb{Z}_p)}R \left(u\left(\begin{smallmatrix}p\\&p\\&&1\\&&&1\end{smallmatrix}\right) ,1\right)\,du; && \\ U^{+}_{p,3} :&\quad p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(1,1,1;0)\right>}\int_{N(\mathbb{Z}_p)}R \left(u\left(\begin{smallmatrix}p\\&p\\&&p\\&&&1\end{smallmatrix}\right) ,1\right)\,du; && \\ U^{-}_{p,1}:&\quad p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(0,0,0;-1)\right>}\int_{N(\mathbb{Z}_p)}R \left(u\left(\begin{smallmatrix}1\\&1\\&&1\\&&&p^{-1}\end{smallmatrix}\right) ,1\right)\,du, && \end{aligned}\\[-8pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} {U^{+}_{p,2}}:&\quad p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(1,1,0;0)\right>}\int_{N(\mathbb{Z}_p)}R \left(u\left(\begin{smallmatrix}p\\&p\\&&1\\&&&1\end{smallmatrix}\right) ,1\right)\,du; && \\ U^{+}_{p,3} :&\quad p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(1,1,1;0)\right>}\int_{N(\mathbb{Z}_p)}R \left(u\left(\begin{smallmatrix}p\\&p\\&&p\\&&&1\end{smallmatrix}\right) ,1\right)\,du; && \\ U^{-}_{p,1}:&\quad p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(0,0,0;-1)\right>}\int_{N(\mathbb{Z}_p)}R \left(u\left(\begin{smallmatrix}1\\&1\\&&1\\&&&p^{-1}\end{smallmatrix}\right) ,1\right)\,du, && \end{aligned}\\[-8pt]\nonumber \end{align} $$where  $N(\mathbb {Z}_p)=\left \{\left (\begin {smallmatrix}1&\ast & \ast & \ast \\&1&\ast & \ast \\&&1&\ast \\&&&1\end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_4(\mathbb {Z}_p)\right \}$,
$N(\mathbb {Z}_p)=\left \{\left (\begin {smallmatrix}1&\ast & \ast & \ast \\&1&\ast & \ast \\&&1&\ast \\&&&1\end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_4(\mathbb {Z}_p)\right \}$, ![]() $R(-)$ denotes the right translation, and
$R(-)$ denotes the right translation, and ![]() $2\rho _{\mathrm {c}}=(2,0,-2;0)$ is the sum of the compact positive roots of G.
$2\rho _{\mathrm {c}}=(2,0,-2;0)$ is the sum of the compact positive roots of G.
2.9 Statement of main theorem
Let ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)^{\circ }$ be the connected component of
$T_{\mathrm {so}}(\mathbb {Z}_p)^{\circ }$ be the connected component of ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ containing
$T_{\mathrm {so}}(\mathbb {Z}_p)$ containing ![]() $\mathbf {1}_2$, that is,
$\mathbf {1}_2$, that is, ![]() $T_{\mathrm {so}}(1+p\mathbb {Z}_p)$, and put
$T_{\mathrm {so}}(1+p\mathbb {Z}_p)$, and put ![]() ${\Lambda _{\mathrm {so}}} =\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)^{\circ }]\!]$.
${\Lambda _{\mathrm {so}}} =\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)^{\circ }]\!]$.
Theorem 2.9.1. The following hold:
(1) Let
 $U_p=U^+_{p,2}U^+_{p,3}U^-_{p,1}$. Then for each
$U_p=U^+_{p,2}U^+_{p,3}U^-_{p,1}$. Then for each  ,
,  $\lim \limits _{r\to \infty }(U_p)^{r!}f$ converges, and we can define the semiordinary projector as
$\lim \limits _{r\to \infty }(U_p)^{r!}f$ converges, and we can define the semiordinary projector as  ${e_{\mathrm {so}}} = \lim \limits _{r\to \infty }(U_p)^{r!}$. The
${e_{\mathrm {so}}} = \lim \limits _{r\to \infty }(U_p)^{r!}$. The  $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-modules
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-modules 
are both free of finite rank over
 $\Lambda _{\mathrm {so}}$.
$\Lambda _{\mathrm {so}}$.(2) The spaces of
 $\Lambda _{\mathrm {so}}$-families of tame level
$\Lambda _{\mathrm {so}}$-families of tame level  $K^p_f$ are defined as
$K^p_f$ are defined as 
For a given weight
 $(\tau ^+,\tau ^-)\in \operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (T_{\mathrm {so}}(\mathbb {Z}_p),F^{\times }\right )$, let
$(\tau ^+,\tau ^-)\in \operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (T_{\mathrm {so}}(\mathbb {Z}_p),F^{\times }\right )$, let  $\mathcal {P}_{\tau ^+,\tau ^-}$ be the ideal in
$\mathcal {P}_{\tau ^+,\tau ^-}$ be the ideal in  $\mathcal {O}_F[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$ generated by
$\mathcal {O}_F[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$ generated by  $\{(x,y)-\tau ^+(x)\tau ^-(y)\colon (x,y)\in T_{\mathrm {so}}(\mathbb {Z}_p)\}$. We have (2.9.1)
$\{(x,y)-\tau ^+(x)\tau ^-(y)\colon (x,y)\in T_{\mathrm {so}}(\mathbb {Z}_p)\}$. We have (2.9.1) $$ \begin{align} \begin{aligned} \mathcal{M}^0_{\mathrm{so}}\otimes_{\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]}\mathcal{O}_F[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]/\mathcal{P}_{\tau^+,\tau^-}&\stackrel{\sim}{\longrightarrow} \left(\varprojlim_{m}\varinjlim_n e_{\mathrm{so}} V^0_{n,m}\otimes_{\mathbb{Z}_p}\mathcal{O}_F\right)[\tau^+,\tau^-],\\ \mathcal{M}_{\mathrm{so}}\otimes_{\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]}\mathcal{O}_F[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]/\mathcal{P}_{\tau^+,\tau^-}&\stackrel{\sim}{\longrightarrow} \left(\varprojlim_{m}\varinjlim_n e_{\mathrm{so}} V_{n,m}\otimes_{\mathbb{Z}_p}\mathcal{O}_F\right)[\tau^+,\tau^-]. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathcal{M}^0_{\mathrm{so}}\otimes_{\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]}\mathcal{O}_F[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]/\mathcal{P}_{\tau^+,\tau^-}&\stackrel{\sim}{\longrightarrow} \left(\varprojlim_{m}\varinjlim_n e_{\mathrm{so}} V^0_{n,m}\otimes_{\mathbb{Z}_p}\mathcal{O}_F\right)[\tau^+,\tau^-],\\ \mathcal{M}_{\mathrm{so}}\otimes_{\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]}\mathcal{O}_F[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]/\mathcal{P}_{\tau^+,\tau^-}&\stackrel{\sim}{\longrightarrow} \left(\varprojlim_{m}\varinjlim_n e_{\mathrm{so}} V_{n,m}\otimes_{\mathbb{Z}_p}\mathcal{O}_F\right)[\tau^+,\tau^-]. \end{aligned} \end{align} $$The semiordinary projector preserves the spaces of classical forms, and by combining equation (2.9.1) with equation (2.7.2), we have the embeddings

where
 $t^{\pm }=\tau _{\mathrm {alg}}^{\pm }$ with
$t^{\pm }=\tau _{\mathrm {alg}}^{\pm }$ with  $(0,0, t^+; t^-)$ dominant and
$(0,0, t^+; t^-)$ dominant and  $\epsilon ^{\pm }=\tau _{\mathrm {f}}^{\pm }$.
$\epsilon ^{\pm }=\tau _{\mathrm {f}}^{\pm }$.(3) Given
 $0\geq t^+$, there exists
$0\geq t^+$, there exists  $A\geq -t^++4$ such that the above embedding for the cuspidal forms is surjective if
$A\geq -t^++4$ such that the above embedding for the cuspidal forms is surjective if  $t^-\geq A$.
$t^-\geq A$.(4) There is the following so-called fundamental exact sequence (in the study of Klingen Eisenstein congruences),
 $$\begin{align*}0\longrightarrow\mathcal{M}^0_{\mathrm{so}}\longrightarrow \mathcal{M}_{\mathrm{so}}\xrightarrow{\oplus\Phi_{g}}\bigoplus_{g}{M_{(0,0)}(K^{\prime }_{f,g};\mathbb{Z}_p)} \otimes_{\mathbb{Z}_p}\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!] \longrightarrow 0,\\[-16pt] \end{align*}$$
$$\begin{align*}0\longrightarrow\mathcal{M}^0_{\mathrm{so}}\longrightarrow \mathcal{M}_{\mathrm{so}}\xrightarrow{\oplus\Phi_{g}}\bigoplus_{g}{M_{(0,0)}(K^{\prime }_{f,g};\mathbb{Z}_p)} \otimes_{\mathbb{Z}_p}\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!] \longrightarrow 0,\\[-16pt] \end{align*}$$with g runs over
 $\big (G^{\prime }_1(\mathbb {Q})\ltimes P^{\prime }_1(\mathbb {A}^p_{\mathbb {Q},f})\big )\backslash G(\mathbb {A}^p_{\mathbb {Q},f})/K^p_f$ and
$\big (G^{\prime }_1(\mathbb {Q})\ltimes P^{\prime }_1(\mathbb {A}^p_{\mathbb {Q},f})\big )\backslash G(\mathbb {A}^p_{\mathbb {Q},f})/K^p_f$ and  $\Phi _{g}$ the Siegel operator obtained by restriction to the boundary stratum indexed by g. The level group
$\Phi _{g}$ the Siegel operator obtained by restriction to the boundary stratum indexed by g. The level group  $K^{\prime }_{f,g}=K^{\prime p}_{f,g}K^{\prime }_{p,g}\subset G'(\mathbb {A}^p_{\mathbb {Q},f})$ is defined in equation (4.4.1), and
$K^{\prime }_{f,g}=K^{\prime p}_{f,g}K^{\prime }_{p,g}\subset G'(\mathbb {A}^p_{\mathbb {Q},f})$ is defined in equation (4.4.1), and  $M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}_p)$ denotes the space of classical automorphic forms on
$M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}_p)$ denotes the space of classical automorphic forms on  $G'$ of weight
$G'$ of weight  $(0,0)$ and level
$(0,0)$ and level  $K^{\prime }_{f,g}$.
$K^{\prime }_{f,g}$.
Remark 2.9.2. In general, one can consider semiordinary families whose members have weight ![]() $\underline {t}=(t^+_1,t^+_2,t^+_3;t^-_1)$ with
$\underline {t}=(t^+_1,t^+_2,t^+_3;t^-_1)$ with ![]() $t^+_1,t^+_2$ fixed and
$t^+_1,t^+_2$ fixed and ![]() $t^+_3,t^-_1$ varying in the family. We only consider the case
$t^+_3,t^-_1$ varying in the family. We only consider the case ![]() $t^+_1=t^+_2=0$ because it suffices for proving Theorem 8.2.3, and we want to avoid having the main idea obscured by the extra complications of working with vector bundles. For the general case, instead of considering the global sections of the structure sheaf over the Igusa tower, one considers the global sections of a vector bundle
$t^+_1=t^+_2=0$ because it suffices for proving Theorem 8.2.3, and we want to avoid having the main idea obscured by the extra complications of working with vector bundles. For the general case, instead of considering the global sections of the structure sheaf over the Igusa tower, one considers the global sections of a vector bundle ![]() $\omega _{\underline {t}}$. For defining
$\omega _{\underline {t}}$. For defining ![]() (cf. §4.3) such that the quotient
(cf. §4.3) such that the quotient ![]() has a nice structure, besides the requirement of vanishing outside the strata labeled by cusp labels in
has a nice structure, besides the requirement of vanishing outside the strata labeled by cusp labels in ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, one also requires that the elements are global sections of
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, one also requires that the elements are global sections of ![]() $\omega ^{\flat }_{\underline {t}}\subset \omega _{\underline {t}}$ with
$\omega ^{\flat }_{\underline {t}}\subset \omega _{\underline {t}}$ with ![]() $\omega ^{\flat }_{\underline {t}}$ a subsheaf defined as in [Reference HsiehHsi14a, Section 4.1].
$\omega ^{\flat }_{\underline {t}}$ a subsheaf defined as in [Reference HsiehHsi14a, Section 4.1].
3 The proof of Theorem 2.9.1 for the cuspidal part
In this section, we prove Theorem 2.9.1 for cuspidal families. The results for cuspidal families will be used to deduce the results for noncuspidal families in §4.
Proposition 3.0.1 (Base change property).
Let ![]() $\mathscr {T}^{0,\mathrm {tor}}_n[1/E]$ be the open subscheme of
$\mathscr {T}^{0,\mathrm {tor}}_n[1/E]$ be the open subscheme of ![]() $\mathscr {T}^{0,\mathrm {tor}}_n$ where E, our fixed lift of Hasse invariant viewed as a section over
$\mathscr {T}^{0,\mathrm {tor}}_n$ where E, our fixed lift of Hasse invariant viewed as a section over ![]() $\mathscr {T}^{0,\mathrm {tor}}_n$, is nonvanishing. For any classical dominant weight
$\mathscr {T}^{0,\mathrm {tor}}_n$, is nonvanishing. For any classical dominant weight ![]() $\underline {t}$, the natural map
$\underline {t}$, the natural map
is an isomorphism.
Proof. Over ![]() $\mathscr {T}^{\mathrm {tor}}_n$, we have the exact sequence of sheaves
$\mathscr {T}^{\mathrm {tor}}_n$, we have the exact sequence of sheaves
By [Reference LanLan18, Thm. 8.2.1.1], ![]() $R^1_{\pi _n,*}(\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_n})=0$ (where
$R^1_{\pi _n,*}(\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_n})=0$ (where ![]() $\pi _n$ is the projection
$\pi _n$ is the projection ![]() $\pi _n:\mathscr {T}^{\mathrm {tor}}_{n}\rightarrow \mathscr {T}^{\min }_{n}$), so we have the exact sequence of sheaves
$\pi _n:\mathscr {T}^{\mathrm {tor}}_{n}\rightarrow \mathscr {T}^{\min }_{n}$), so we have the exact sequence of sheaves
over ![]() $\mathscr {T}^{\min }_{n}$. Since
$\mathscr {T}^{\min }_{n}$. Since ![]() $\mathscr {T}^{\min }_{n}[1/E]$ is affine by definition, taking global sections gives the result.
$\mathscr {T}^{\min }_{n}[1/E]$ is affine by definition, taking global sections gives the result.
Proposition 3.0.2. Let ![]() $U_p=U^+_{p,2}U^+_{p,3}U^-_{p,1}$. Let
$U_p=U^+_{p,2}U^+_{p,3}U^-_{p,1}$. Let ![]() and
and ![]() $\vec {f}\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$. Then both limits
$\vec {f}\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$. Then both limits ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ and
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ and ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}\vec {f}$ converge.
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}\vec {f}$ converge.
Proof. Consider ![]() $\tilde {\mathscr {T}}_n$, the ordinary locus of level
$\tilde {\mathscr {T}}_n$, the ordinary locus of level
 $$\begin{align*}\tilde{K}^n_{p,1}=\left\{g\subset G(\mathbb{Z}_p)\mid g^+\equiv \left(\begin{smallmatrix}1&\ast & \ast & \ast\\ &1&\ast & \ast\\&&1&\ast\\&&&1\end{smallmatrix}\right) \quad\mod p^n\right\}. \end{align*}$$
$$\begin{align*}\tilde{K}^n_{p,1}=\left\{g\subset G(\mathbb{Z}_p)\mid g^+\equiv \left(\begin{smallmatrix}1&\ast & \ast & \ast\\ &1&\ast & \ast\\&&1&\ast\\&&&1\end{smallmatrix}\right) \quad\mod p^n\right\}. \end{align*}$$ Let ![]() $\tilde {\mathscr {T}}^{\mathrm {tor}}_n$ be the partial toroidal compactification of
$\tilde {\mathscr {T}}^{\mathrm {tor}}_n$ be the partial toroidal compactification of ![]() $\tilde {\mathscr {T}}_n$, and put
$\tilde {\mathscr {T}}_n$, and put ![]() $\tilde {V}_{n,m}^0=H^0(\tilde {\mathscr {T}}^{\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\tilde {\mathscr {T}}^{\mathrm {tor}}_{n,m}})$, which contains
$\tilde {V}_{n,m}^0=H^0(\tilde {\mathscr {T}}^{\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\tilde {\mathscr {T}}^{\mathrm {tor}}_{n,m}})$, which contains ![]() $V^0_{n,m}$ as a subspace. The definition of the
$V^0_{n,m}$ as a subspace. The definition of the ![]() $\mathbb {U}_p$-operators in §2.8 can be naturally extended to
$\mathbb {U}_p$-operators in §2.8 can be naturally extended to ![]() $\tilde {V}^0_{n,m}$, so it suffices to show that
$\tilde {V}^0_{n,m}$, so it suffices to show that ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ converges for every
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ converges for every ![]() $f\in \tilde {V}^0_{n,m}$. As explained in [Reference HidaHid02],
$f\in \tilde {V}^0_{n,m}$. As explained in [Reference HidaHid02], ![]() $\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n \tilde {V}^0_{n,m}$ is p-torsion free and there is an embedding
$\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n \tilde {V}^0_{n,m}$ is p-torsion free and there is an embedding
 $$\begin{align*}\bigoplus_{\underline{t} \text{ dominant}} H^0\left(\mathscr{S}^{\mathrm{tor}},\underline{\omega}_{\underline{t}}\otimes\mathcal{I}_{\mathscr{S}^{\mathrm{tor}}}\right)\otimes\mathbb{Q} \hookrightarrow \left(\varprojlim_m\varinjlim_n \tilde{V}^0_{n,m}\right)[1/p]. \end{align*}$$
$$\begin{align*}\bigoplus_{\underline{t} \text{ dominant}} H^0\left(\mathscr{S}^{\mathrm{tor}},\underline{\omega}_{\underline{t}}\otimes\mathcal{I}_{\mathscr{S}^{\mathrm{tor}}}\right)\otimes\mathbb{Q} \hookrightarrow \left(\varprojlim_m\varinjlim_n \tilde{V}^0_{n,m}\right)[1/p]. \end{align*}$$The ![]() $\mathbb {Z}_p$-modules
$\mathbb {Z}_p$-modules ![]() $H^0\left (\mathscr {S}^{\mathrm {tor}},\underline {\omega }_{\underline {t}}\otimes \mathcal {I}_{\mathscr {S}^{\mathrm {tor}}}\right )$ are free of finite rank and stable under the action of
$H^0\left (\mathscr {S}^{\mathrm {tor}},\underline {\omega }_{\underline {t}}\otimes \mathcal {I}_{\mathscr {S}^{\mathrm {tor}}}\right )$ are free of finite rank and stable under the action of ![]() $U_p$, so the limit
$U_p$, so the limit ![]() $\lim \limits _{r\rightarrow \infty } (U_p)^{r!}$ exists on them. Since
$\lim \limits _{r\rightarrow \infty } (U_p)^{r!}$ exists on them. Since
 $$ \begin{align} \left(\bigoplus_{\underline{t} \text{ dominant}} H^0\left(\mathscr{S}^{\mathrm{tor}},\underline{\omega}_{\underline{t}}\otimes\mathcal{I}_{\mathscr{S}^{\mathrm{tor}}}\right)\otimes\mathbb{Q}\right) \cap \varprojlim_m\varinjlim_n \tilde{V}^0_{n,m} \end{align} $$
$$ \begin{align} \left(\bigoplus_{\underline{t} \text{ dominant}} H^0\left(\mathscr{S}^{\mathrm{tor}},\underline{\omega}_{\underline{t}}\otimes\mathcal{I}_{\mathscr{S}^{\mathrm{tor}}}\right)\otimes\mathbb{Q}\right) \cap \varprojlim_m\varinjlim_n \tilde{V}^0_{n,m} \end{align} $$is dense in ![]() $\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n \tilde {V}^0_{n,m}$ by [Reference HidaHid02], the convergence of
$\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n \tilde {V}^0_{n,m}$ by [Reference HidaHid02], the convergence of ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ for every
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ for every ![]() $f\in \tilde {V}^0_{n,m}$ follows.
$f\in \tilde {V}^0_{n,m}$ follows.
On the other hand, let ![]() $\vec {f}\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$. By Proposition 3.0.1,
$\vec {f}\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$. By Proposition 3.0.1, ![]() $\vec {f}$ lifts to
$\vec {f}$ lifts to
For ![]() $l\gg 0$, we have
$l\gg 0$, we have ![]() $\vec {\mathfrak {f}} E^l\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_n}\right )$, which by the Koecher principle can be viewed as an element in the finite-dimensional space
$\vec {\mathfrak {f}} E^l\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_n}\right )$, which by the Koecher principle can be viewed as an element in the finite-dimensional space ![]() $M^0_{\underline {t}+lt_E(p-1)}(K^p_fK^0_{p,n};\mathbb {Q}_p)$. Thus, the limit
$M^0_{\underline {t}+lt_E(p-1)}(K^p_fK^0_{p,n};\mathbb {Q}_p)$. Thus, the limit ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}(\vec {\mathfrak {f}} E^l)$ converges. Since
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}(\vec {\mathfrak {f}} E^l)$ converges. Since ![]() $E\equiv 1\ \ \mod p$, we have
$E\equiv 1\ \ \mod p$, we have ![]() $\vec {\mathfrak {f}} E^l\equiv \vec {f}\ \ \mod p^m$, and the convergence of
$\vec {\mathfrak {f}} E^l\equiv \vec {f}\ \ \mod p^m$, and the convergence of ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}\vec {f}$ follows.
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}\vec {f}$ follows.
Thanks to the convergence of ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}$ on
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}$ on ![]() and
and ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$, we can define the semiordinary projector on them as
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$, we can define the semiordinary projector on them as ![]() $e_{\mathrm {so}}=\lim \limits _{r\rightarrow \infty }(U_p)^{r!}$.
$e_{\mathrm {so}}=\lim \limits _{r\rightarrow \infty }(U_p)^{r!}$.
Proposition 3.0.3. For ![]() $n\geq m$ and a dominant weight
$n\geq m$ and a dominant weight ![]() $(0,0,t^+;t^-)$, the map
$(0,0,t^+;t^-)$, the map
induced by equation (2.7.1) is an isomorphism.
Proof. Given ![]() $\vec {f}$, we have
$\vec {f}$, we have

Here, C runs over the subgroups of ![]() $A[p^{4n}]$ which can be spanned as
$A[p^{4n}]$ which can be spanned as
 $$ \begin{align*} &(e^+_1,e^+_2,e^+_3,e^+_4)\cdot p^n\left(\begin{smallmatrix}1&&u_1&\ast\\&1&u_2&\ast\\ &&1&\ast\\ &&&1\end{smallmatrix}\right) \left(\begin{smallmatrix}p^{-n}&&&\\ & p^{-n}&&\\ && p^{-2n}&\\ &&& p^{-4n}\end{smallmatrix}\right) ,\\ &(e^-_1,e^-_2,e^-_3,e^-_4)\cdot p^n\left(\begin{smallmatrix}1&\ast & \ast & \ast\\ &1\\&-u_2&1&-u_1\\ &&&1\end{smallmatrix}\right) \left(\begin{smallmatrix}p^{-2n}&&\\ & p^{-5n}\\&& p^{-4n}\\&&& p^{-5n}\end{smallmatrix}\right) , \end{align*} $$
$$ \begin{align*} &(e^+_1,e^+_2,e^+_3,e^+_4)\cdot p^n\left(\begin{smallmatrix}1&&u_1&\ast\\&1&u_2&\ast\\ &&1&\ast\\ &&&1\end{smallmatrix}\right) \left(\begin{smallmatrix}p^{-n}&&&\\ & p^{-n}&&\\ && p^{-2n}&\\ &&& p^{-4n}\end{smallmatrix}\right) ,\\ &(e^-_1,e^-_2,e^-_3,e^-_4)\cdot p^n\left(\begin{smallmatrix}1&\ast & \ast & \ast\\ &1\\&-u_2&1&-u_1\\ &&&1\end{smallmatrix}\right) \left(\begin{smallmatrix}p^{-2n}&&\\ & p^{-5n}\\&& p^{-4n}\\&&& p^{-5n}\end{smallmatrix}\right) , \end{align*} $$with ![]() $e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4$ a basis of
$e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4$ a basis of ![]() $A[p^{n}]$ compatible with
$A[p^{n}]$ compatible with ![]() $\alpha _p$. For such a C,
$\alpha _p$. For such a C, ![]() $u_C=\left (\begin {smallmatrix}1&&u_1\\&1&u_2\\&&1\end {smallmatrix}\right ) $. By our definition of the
$u_C=\left (\begin {smallmatrix}1&&u_1\\&1&u_2\\&&1\end {smallmatrix}\right ) $. By our definition of the ![]() $\Delta _+$-action on
$\Delta _+$-action on ![]() $W_{\underline {t}}$ (in equation (2.8.7)), we know that if
$W_{\underline {t}}$ (in equation (2.8.7)), we know that if ![]() $w\in W_{(0,0,t^+;t^-)}$ is a vector of nonhighest weight, then
$w\in W_{(0,0,t^+;t^-)}$ is a vector of nonhighest weight, then
 $$ \begin{align*} \left(\left(\begin{smallmatrix}p^n\\ &p^n\\ &&p^{2n}\end{smallmatrix}\right) ,p^{2n}\right)\cdot w\equiv 0\quad\mod p^n. \end{align*} $$
$$ \begin{align*} \left(\left(\begin{smallmatrix}p^n\\ &p^n\\ &&p^{2n}\end{smallmatrix}\right) ,p^{2n}\right)\cdot w\equiv 0\quad\mod p^n. \end{align*} $$Therefore, from equation (3.0.2) we see that ![]() $U^n_p\vec {f}$ is actually determined by the projection of its values to the highest weight space.
$U^n_p\vec {f}$ is actually determined by the projection of its values to the highest weight space.
On one hand, this shows that the map in the statement is injective. On the other hand, given ![]() $f\in e_{\mathrm {so}} V^0_{n,m}[t^+,t^-]$, we can define
$f\in e_{\mathrm {so}} V^0_{n,m}[t^+,t^-]$, we can define ![]() $\vec {f}$ by the rule
$\vec {f}$ by the rule
where C runs over the same range as above. One can check that ![]() $\vec {f}$ satisfies
$\vec {f}$ satisfies
for  $g^+\equiv \left (\begin {smallmatrix}\ast & \ast & u_1&\ast \\ p\ast & \ast & u_2&\ast \\ &&a_1&\ast \\&&&a^{-1}_2\end {smallmatrix}\right )\quad \mod p^n$, so equation (3.0.3) defines an element in
$g^+\equiv \left (\begin {smallmatrix}\ast & \ast & u_1&\ast \\ p\ast & \ast & u_2&\ast \\ &&a_1&\ast \\&&&a^{-1}_2\end {smallmatrix}\right )\quad \mod p^n$, so equation (3.0.3) defines an element in ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{(0,0,t^+;t^-)}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )$, and it is easy to check its semiordinarity from the semiordinarity of f. The composition of equation (3.0.3) and the map in the statement is
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{(0,0,t^+;t^-)}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )$, and it is easy to check its semiordinarity from the semiordinarity of f. The composition of equation (3.0.3) and the map in the statement is ![]() $U^n_p$. Hence, the map is a bijection.
$U^n_p$. Hence, the map is a bijection.
Proposition 3.0.4. ![]() $e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )=e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{1,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{1,m}}\right )$.
$e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )=e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{1,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{1,m}}\right )$.
Proof. This follows immediately from the fact that ![]() $U_p$ maps the space
$U_p$ maps the space ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )$ into
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )$ into ![]() $H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n-1,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )$. (See §2.8.2.)
$H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n-1,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{\mathrm {tor}}_{n,m}}\right )$. (See §2.8.2.)
Proposition 3.0.5. For a fixed tame level ![]() $K^p_f$ and a fixed integer
$K^p_f$ and a fixed integer ![]() $B\geq 0$, the dimension of
$B\geq 0$, the dimension of ![]() $e_{\mathrm {so}} M^0_{\underline {t}}(K^p_fK^0_{p,1};\mathbb {Q}_p)$ is uniformly bounded for all
$e_{\mathrm {so}} M^0_{\underline {t}}(K^p_fK^0_{p,1};\mathbb {Q}_p)$ is uniformly bounded for all ![]() $t^+_1\geq t^+_2\geq t^+_3\geq -t^-_1+4$ with
$t^+_1\geq t^+_2\geq t^+_3\geq -t^-_1+4$ with ![]() $t^+_1-t^+_2\leq B$.
$t^+_1-t^+_2\leq B$.
Proof. Suppose that ![]() $\Pi $ is an irreducible cuspidal automorphic representation of
$\Pi $ is an irreducible cuspidal automorphic representation of ![]() $G(\mathbb {A}_{\mathbb {Q}})$ generated by a semiordinary form
$G(\mathbb {A}_{\mathbb {Q}})$ generated by a semiordinary form ![]() $\varphi \in e_{\mathrm {so}}M^0_{\underline {t}}\left (K^p_fK^0_{p,n};\mathbb {Q}_p\right )$ whose (generalized) eigenvalue of
$\varphi \in e_{\mathrm {so}}M^0_{\underline {t}}\left (K^p_fK^0_{p,n};\mathbb {Q}_p\right )$ whose (generalized) eigenvalue of ![]() $U^+_{p,2}$ (resp.
$U^+_{p,2}$ (resp. ![]() $U^+_{p,3}$,
$U^+_{p,3}$, ![]() $U^-_{p,1}$) is
$U^-_{p,1}$) is ![]() $\lambda ^+_2$ (resp.
$\lambda ^+_2$ (resp. ![]() $\lambda ^+_3$,
$\lambda ^+_3$, ![]() $\lambda ^-_1$). The semiordinarity condition implies that
$\lambda ^-_1$). The semiordinarity condition implies that ![]() $\lambda ^+_2,\lambda ^+_3,\lambda ^-_1$ are all p-adic units. We view
$\lambda ^+_2,\lambda ^+_3,\lambda ^-_1$ are all p-adic units. We view ![]() $\Pi _p$ as an irreducible representation of
$\Pi _p$ as an irreducible representation of ![]() $\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$ via equation (2.4.1). Let Q be the parabolic subgroup
$\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$ via equation (2.4.1). Let Q be the parabolic subgroup  $\left \lbrace \left (\begin {smallmatrix}\ast & \ast & \ast & \ast \\\ast & \ast & \ast & \ast \\&&\ast & \ast \\&&&\ast \end {smallmatrix}\right ) \right \rbrace \subset \operatorname {\mathrm {GL}}_4$ with Levi factorization
$\left \lbrace \left (\begin {smallmatrix}\ast & \ast & \ast & \ast \\\ast & \ast & \ast & \ast \\&&\ast & \ast \\&&&\ast \end {smallmatrix}\right ) \right \rbrace \subset \operatorname {\mathrm {GL}}_4$ with Levi factorization ![]() $Q=M_QN_Q$. Let
$Q=M_QN_Q$. Let
the Jacquet module of ![]() $\Pi _p$ with respect to the parabolic Q acted on by
$\Pi _p$ with respect to the parabolic Q acted on by ![]() $M_Q(\mathbb {Q}_p)\cong \operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)\times \operatorname {\mathrm {GL}}_1(\mathbb {Q}_p)\times \operatorname {\mathrm {GL}}_1(\mathbb {Q}_p)$. It follows from Jacquet’s lemma (see [Reference CasselmanCas95, Theorem 4.1.2, Proposition 4.1.4]) that
$M_Q(\mathbb {Q}_p)\cong \operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)\times \operatorname {\mathrm {GL}}_1(\mathbb {Q}_p)\times \operatorname {\mathrm {GL}}_1(\mathbb {Q}_p)$. It follows from Jacquet’s lemma (see [Reference CasselmanCas95, Theorem 4.1.2, Proposition 4.1.4]) that ![]() $\Pi ^{M_Q(\mathbb {Q}_p)\cap K^0_{p,n}}_{p,N_Q}$ equals the image under the natural projection of
$\Pi ^{M_Q(\mathbb {Q}_p)\cap K^0_{p,n}}_{p,N_Q}$ equals the image under the natural projection of
 $$ \begin{align*} &\bigcap_{r\geq 1}\left(U_{p,\mathrm{loc}}\right)^r\Pi^{K^0_{p,n}}_p, &U_{p,\mathrm{loc}}=\int_{N_Q(\mathbb{Z}_p)}\Pi_p\left(u\left(\begin{smallmatrix}p^2\\&p^2\\&&p^{\phantom{2}}\\&&&p^{-1}\end{smallmatrix}\right) \right)\,du. \end{align*} $$
$$ \begin{align*} &\bigcap_{r\geq 1}\left(U_{p,\mathrm{loc}}\right)^r\Pi^{K^0_{p,n}}_p, &U_{p,\mathrm{loc}}=\int_{N_Q(\mathbb{Z}_p)}\Pi_p\left(u\left(\begin{smallmatrix}p^2\\&p^2\\&&p^{\phantom{2}}\\&&&p^{-1}\end{smallmatrix}\right) \right)\,du. \end{align*} $$The semiordinary form ![]() $\varphi \in \Pi $ is fixed by
$\varphi \in \Pi $ is fixed by ![]() $K^0_{p,n}$ and belongs to a generalized eigenspace of
$K^0_{p,n}$ and belongs to a generalized eigenspace of ![]() $U_{p,\mathrm {loc}}$ with a nonzero eigenvalue. Thus, we deduce that
$U_{p,\mathrm {loc}}$ with a nonzero eigenvalue. Thus, we deduce that ![]() $\Pi ^{M_Q(\mathbb {Q}_p)\cap K^0_{p,n}}_{p,N_Q}\neq 0$ and
$\Pi ^{M_Q(\mathbb {Q}_p)\cap K^0_{p,n}}_{p,N_Q}\neq 0$ and ![]() $\Pi _p$ is isomorphic to a subquotient of
$\Pi _p$ is isomorphic to a subquotient of
where ![]() $\sigma $ is an irreducible smooth admissible representation of
$\sigma $ is an irreducible smooth admissible representation of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$, and
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$, and ![]() $\chi ,\chi '$ are smooth characters of
$\chi ,\chi '$ are smooth characters of ![]() $\mathbb {Q}^{\times }_p$. We have
$\mathbb {Q}^{\times }_p$. We have ![]() $M_Q(\mathbb {Q}_p)\cap K^0_{p,1}\cong K^{\prime }_{p}\times (1+p^n\mathbb {Z}_p)\times (1+p^n\mathbb {Z}_p)$ with
$M_Q(\mathbb {Q}_p)\cap K^0_{p,1}\cong K^{\prime }_{p}\times (1+p^n\mathbb {Z}_p)\times (1+p^n\mathbb {Z}_p)$ with  $K^{\prime }_{p}=\left \lbrace \begin {pmatrix}\ast & \ast \\ p\ast & \ast \end {pmatrix}\right \rbrace \subset \operatorname {\mathrm {GL}}_2(\mathbb {Z}_p)$. From
$K^{\prime }_{p}=\left \lbrace \begin {pmatrix}\ast & \ast \\ p\ast & \ast \end {pmatrix}\right \rbrace \subset \operatorname {\mathrm {GL}}_2(\mathbb {Z}_p)$. From ![]() $\Pi ^{M_Q(\mathbb {Q}_p)\cap K^0_{p,n}}_{p,N_Q}\neq 0$, we know that
$\Pi ^{M_Q(\mathbb {Q}_p)\cap K^0_{p,n}}_{p,N_Q}\neq 0$, we know that ![]() $\sigma ^{K^{\prime }_{p}}\neq 0$ ([Reference CasselmanCas95, Theorem 6.3.5]). This implies that
$\sigma ^{K^{\prime }_{p}}\neq 0$ ([Reference CasselmanCas95, Theorem 6.3.5]). This implies that ![]() $\sigma $ is not supercuspidal, and
$\sigma $ is not supercuspidal, and ![]() $\Pi _p$ is isomorphic to a subquotient of a principal series. Denote by
$\Pi _p$ is isomorphic to a subquotient of a principal series. Denote by ![]() $\alpha _1,\alpha _2,\alpha _3,\alpha _4$ the evaluations at p of the corresponding characters of
$\alpha _1,\alpha _2,\alpha _3,\alpha _4$ the evaluations at p of the corresponding characters of ![]() $\mathbb {Q}^{\times }_p$. Then, up to reordering, we have
$\mathbb {Q}^{\times }_p$. Then, up to reordering, we have
Now, in addition to ![]() $U^+_{p,2},U^+_{p,3},U^-_{p,1}$, we also consider the action of the operator
$U^+_{p,2},U^+_{p,3},U^-_{p,1}$, we also consider the action of the operator
 $$ \begin{align} U^+_{p,1}=p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(1,0,0;0)\right>}\int_{N(\mathbb{Z}_p)}R\left(u\left(\begin{smallmatrix}p\\&1\\&&1\\&&&1\end{smallmatrix}\right) ,1\right)\,du \end{align} $$
$$ \begin{align} U^+_{p,1}=p^{\left<(t^+_1,t^+_2,t^+_3;-t^-_1)+2\rho_{\mathrm{c}},(1,0,0;0)\right>}\int_{N(\mathbb{Z}_p)}R\left(u\left(\begin{smallmatrix}p\\&1\\&&1\\&&&1\end{smallmatrix}\right) ,1\right)\,du \end{align} $$on ![]() $M^0_{\underline {t}}\left (K^p_fK^0_{p,n};\mathbb {Q}_p\right )$. The operator
$M^0_{\underline {t}}\left (K^p_fK^0_{p,n};\mathbb {Q}_p\right )$. The operator ![]() $U^+_{p,1}$ has a geometric interpretation analogous to equation (2.8.5), and the above normalization makes all its eigenvalues p-integral. If
$U^+_{p,1}$ has a geometric interpretation analogous to equation (2.8.5), and the above normalization makes all its eigenvalues p-integral. If ![]() $\alpha ^{-1}_1\alpha _2\neq p^{\pm 1}$, then
$\alpha ^{-1}_1\alpha _2\neq p^{\pm 1}$, then ![]() $p^{t^+_1+\frac {1}{2}}\alpha _1$ and
$p^{t^+_1+\frac {1}{2}}\alpha _1$ and ![]() $p^{t^+_1+\frac {1}{2}}\alpha _2$ are both eigenvalues for the action of
$p^{t^+_1+\frac {1}{2}}\alpha _2$ are both eigenvalues for the action of ![]() $U^+_{p,1}$ on the holomorphic forms in
$U^+_{p,1}$ on the holomorphic forms in ![]() $\Pi $ of level
$\Pi $ of level ![]() $K^p_fK^0_{p,n}$, so
$K^p_fK^0_{p,n}$, so
By using that equation (3.0.4) is a p-adic unit and our condition ![]() $0\leq t^+_1-t^+_2\leq B$, we get
$0\leq t^+_1-t^+_2\leq B$, we get
Combining equation (3.0.8) and equation (3.0.9), we get
If ![]() $\alpha ^{-1}_1\alpha _2=p^{\pm 1}$, then equation (3.0.4) being a p-adic unit implies that
$\alpha ^{-1}_1\alpha _2=p^{\pm 1}$, then equation (3.0.4) being a p-adic unit implies that
Combining it with our condition ![]() $0\leq t^+_1-t^+_2\leq B$, we get
$0\leq t^+_1-t^+_2\leq B$, we get
Therefore, for ![]() $t^+_1\geq t^+_2\geq t^+_3\geq -t^-_1+4$,
$t^+_1\geq t^+_2\geq t^+_3\geq -t^-_1+4$, ![]() $t^+_1-t^+_2\leq B$, all the semiordinary forms in
$t^+_1-t^+_2\leq B$, all the semiordinary forms in ![]() $e_{\mathrm {so}} M^0_{\underline {t}}(K^p_fK^0_{p,1};\mathbb {Q}_p)$ have slopes
$e_{\mathrm {so}} M^0_{\underline {t}}(K^p_fK^0_{p,1};\mathbb {Q}_p)$ have slopes ![]() $\leq B$ for the
$\leq B$ for the ![]() $\mathbb {U}_p$-operator
$\mathbb {U}_p$-operator ![]() $U^+_{p,1}U^+_{p,2}U^+_{p,3}U^-_{p,1}$.
$U^+_{p,1}U^+_{p,2}U^+_{p,3}U^-_{p,1}$.
Recall that the theory of Coleman families for unitary groups (developed in [Reference BrascaBra16] as a generalization of [Reference Andreatta, Iovita and PilloniAIP15]) shows that, for every point in the weight space ![]() $\operatorname {\mathrm {Hom}}_{\mathrm {cont}}((\mathbb {Z}^{\times }_p)^4,\mathbb {C}^{\times }_p)$, there exists a neighborhood
$\operatorname {\mathrm {Hom}}_{\mathrm {cont}}((\mathbb {Z}^{\times }_p)^4,\mathbb {C}^{\times }_p)$, there exists a neighborhood ![]() $\mathcal {U}$ of that point and a projective
$\mathcal {U}$ of that point and a projective ![]() $\mathcal {A}_{\mathcal {U}}$-module of finite rank interpolating all the cuspidal overconvergent forms of weights in
$\mathcal {A}_{\mathcal {U}}$-module of finite rank interpolating all the cuspidal overconvergent forms of weights in ![]() $\mathcal {U}$ and
$\mathcal {U}$ and ![]() $U^+_{p,1}U^+_{p,2}U^+_{p,3}U^-_{p,1}$-slope
$U^+_{p,1}U^+_{p,2}U^+_{p,3}U^-_{p,1}$-slope ![]() $\leq B$ and a fixed tame level. Since all the algebraic weights
$\leq B$ and a fixed tame level. Since all the algebraic weights ![]() $\underline {t}$ are contained in a compact subset of
$\underline {t}$ are contained in a compact subset of ![]() $\operatorname {\mathrm {Hom}}_{\mathrm {cont}}((\mathbb {Z}^{\times }_p)^4,\mathbb {C}_p)$, when
$\operatorname {\mathrm {Hom}}_{\mathrm {cont}}((\mathbb {Z}^{\times }_p)^4,\mathbb {C}_p)$, when ![]() $\underline {t}$ varies among all the algebraic weights, there is a uniform bound on the dimension of the space of cuspidal overconvergent forms of weight
$\underline {t}$ varies among all the algebraic weights, there is a uniform bound on the dimension of the space of cuspidal overconvergent forms of weight ![]() $\underline {t}$ and slopes
$\underline {t}$ and slopes ![]() $\leq B$ and tame level
$\leq B$ and tame level ![]() $K^p_f$. The proposition follows.
$K^p_f$. The proposition follows.
(1)
 $\dim _{\mathbb {F}_p}\,e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{1,1},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{1,1}}\right )<\infty $.
$\dim _{\mathbb {F}_p}\,e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{1,1},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{1,1}}\right )<\infty $.(2) (Classicity) There is a canonical embedding

and for a given
 $t^+\leq 0$, there exists
$t^+\leq 0$, there exists  $A(t^+)\geq -t^++4$ such that if
$A(t^+)\geq -t^++4$ such that if  $t^-\geq A(t^+)$, then the embedding is an isomorphism.
$t^-\geq A(t^+)$, then the embedding is an isomorphism.
Proof. (1) Suppose that ![]() $\overline {f}_1,\dots ,\overline {f}_d\in e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{1,1},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{1,1}}\right )$ are linearly independent. By Proposition 3.0.1, they lift to
$\overline {f}_1,\dots ,\overline {f}_d\in e_{\mathrm {so}} H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{1,1},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{1,1}}\right )$ are linearly independent. By Proposition 3.0.1, they lift to ![]() $f_1,\dots ,f_d\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_1[1/E],\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_1}\right )$. Recall that E has scalar weight
$f_1,\dots ,f_d\in H^0\left (\mathscr {T}^{0,\mathrm {tor}}_1[1/E],\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_1}\right )$. Recall that E has scalar weight ![]() $t_E(p-1)$ and let
$t_E(p-1)$ and let ![]() $\underline {t}+lk_E(p-1)=(t^+_1+lt_E(p-1),t^+_2+lt_E(p-1),t^+_3+lt_E(p-1);t^-_1+lt_E(p-1))$. For
$\underline {t}+lk_E(p-1)=(t^+_1+lt_E(p-1),t^+_2+lt_E(p-1),t^+_3+lt_E(p-1);t^-_1+lt_E(p-1))$. For ![]() $l\gg 0$, we have
$l\gg 0$, we have
Because ![]() $E\equiv 1\ \ \mod p$, we have
$E\equiv 1\ \ \mod p$, we have ![]() $\overline {e_{\mathrm {so}}(f_jE^l)}=\overline {f}_j$, and therefore
$\overline {e_{\mathrm {so}}(f_jE^l)}=\overline {f}_j$, and therefore ![]() $e_{\mathrm {so}}(f_1E^l),\dots ,e_{\mathrm {so}}(f_dE^l)$ are linearly independent. Thus, d can be at most the bound in Proposition 3.0.5.
$e_{\mathrm {so}}(f_1E^l),\dots ,e_{\mathrm {so}}(f_dE^l)$ are linearly independent. Thus, d can be at most the bound in Proposition 3.0.5.
(2) We have ![]() $M^0_{(0,0,t^+;t^-)}\left (K_f^pK^0_{p,1};\mathbb {Q}_p\right )=H^0\left (\mathscr {T}^{0,\mathrm {tor}}_1,\omega _{(0,0,t^+;t^-)}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_1}\right )\otimes _{\iota _p}\mathbb {Q}_p$. (As mentioned above, the base change of
$M^0_{(0,0,t^+;t^-)}\left (K_f^pK^0_{p,1};\mathbb {Q}_p\right )=H^0\left (\mathscr {T}^{0,\mathrm {tor}}_1,\omega _{(0,0,t^+;t^-)}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_1}\right )\otimes _{\iota _p}\mathbb {Q}_p$. (As mentioned above, the base change of ![]() $\mathscr {T}^{0,\mathrm {tor}}_1$ to
$\mathscr {T}^{0,\mathrm {tor}}_1$ to ![]() $\mathcal {K}$ is an open subscheme of
$\mathcal {K}$ is an open subscheme of ![]() $S^{\mathrm {tor}}_{K^p_fK^0_{p,1}}$; here, we use the Koecher principle to get the equality of global sections.) The map (2.7.1) induces
$S^{\mathrm {tor}}_{K^p_fK^0_{p,1}}$; here, we use the Koecher principle to get the equality of global sections.) The map (2.7.1) induces
 $$\begin{align*}H^0\left(\mathscr{T}^{0,\mathrm{tor}}_1,\omega_{(0,0,t^+;t^-)}\otimes\mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_1}\right)\rightarrow \left(\varprojlim_m\varinjlim_n e_{\mathrm{so}}V^0_{n,m}[t^+,t^-]\right), \end{align*}$$
$$\begin{align*}H^0\left(\mathscr{T}^{0,\mathrm{tor}}_1,\omega_{(0,0,t^+;t^-)}\otimes\mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_1}\right)\rightarrow \left(\varprojlim_m\varinjlim_n e_{\mathrm{so}}V^0_{n,m}[t^+,t^-]\right), \end{align*}$$and this gives the canonical embedding in the statement.
Put ![]() $V^0_{\mathrm {so}}[t^+,t^-]=\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n e_{\mathrm {so}}V^0_{n,m}[t^+,t^-]$. Note that from Propositions 3.0.3 and 3.0.4, for
$V^0_{\mathrm {so}}[t^+,t^-]=\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n e_{\mathrm {so}}V^0_{n,m}[t^+,t^-]$. Note that from Propositions 3.0.3 and 3.0.4, for ![]() $n\geq m$, we have
$n\geq m$, we have
It follows that ![]() $V_{\mathrm {so}}^0[t^+,t^-]$ is p-torsion free, and together with Proposition 3.0.1 we get
$V_{\mathrm {so}}^0[t^+,t^-]$ is p-torsion free, and together with Proposition 3.0.1 we get
 $$ \begin{align*} \dim_{\mathbb{F}_p}V^0_{\mathrm{so}}[t^+,t^-]/pV^0_{\mathrm{so}}[t^+,t^-] &=\dim_{\mathbb{F}_p} e_{\mathrm{so}} H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1,1},\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1,1}}\right)\\ &=\dim_{\mathbb{Q}_p} e_{\mathrm{so}} H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1}[1/E],\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1}}\right)\otimes\mathbb{Q}_p. \end{align*} $$
$$ \begin{align*} \dim_{\mathbb{F}_p}V^0_{\mathrm{so}}[t^+,t^-]/pV^0_{\mathrm{so}}[t^+,t^-] &=\dim_{\mathbb{F}_p} e_{\mathrm{so}} H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1,1},\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1,1}}\right)\\ &=\dim_{\mathbb{Q}_p} e_{\mathrm{so}} H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1}[1/E],\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1}}\right)\otimes\mathbb{Q}_p. \end{align*} $$Denote this dimension by d. The above shows that ![]() $V^0_{\mathrm {so}}[t^+,t^-]$ is a free
$V^0_{\mathrm {so}}[t^+,t^-]$ is a free ![]() $\mathbb {Z}_p$-module of rank d. Thus, it suffices to show that there exists
$\mathbb {Z}_p$-module of rank d. Thus, it suffices to show that there exists ![]() $A(t^+)\geq -t^+$ such that
$A(t^+)\geq -t^+$ such that ![]() $\dim _{\mathbb {Q}_p} e_{\mathrm {so}} M^0_{(0,0,t^+;t^-)}\left (K_f^pK^0_{p,1};\mathbb {Q}_p\right ) \geq d$ for
$\dim _{\mathbb {Q}_p} e_{\mathrm {so}} M^0_{(0,0,t^+;t^-)}\left (K_f^pK^0_{p,1};\mathbb {Q}_p\right ) \geq d$ for ![]() $t^-\geq A(t^+)$. Pick an unramified Hecke character
$t^-\geq A(t^+)$. Pick an unramified Hecke character ![]() $\chi $ of
$\chi $ of ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ of
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ of ![]() $\infty $-type
$\infty $-type ![]() $(-t_E(p-1),0)$. Twisting E by the character obtained by composing
$(-t_E(p-1),0)$. Twisting E by the character obtained by composing ![]() $\chi $ with
$\chi $ with ![]() $\det :G(\mathbb {Q})\backslash G(\mathbb {A}_{\mathbb {Q}})\rightarrow \mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$, we get a holomorphic form
$\det :G(\mathbb {Q})\backslash G(\mathbb {A}_{\mathbb {Q}})\rightarrow \mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$, we get a holomorphic form ![]() $E'$ of weight
$E'$ of weight ![]() $(0,0,0;2t_E(p-1))$ with the same vanishing locus as E. Multiplying by
$(0,0,0;2t_E(p-1))$ with the same vanishing locus as E. Multiplying by ![]() $(E')^l$ and applying
$(E')^l$ and applying ![]() $e_{\mathrm {so}}$ gives an injection
$e_{\mathrm {so}}$ gives an injection
so
By the definition of d, we thus see that for each ![]() $0\leq j\leq 2t_E(p-1)-1$ there exists
$0\leq j\leq 2t_E(p-1)-1$ there exists ![]() $l_j(t^+)\geq 0$ such that
$l_j(t^+)\geq 0$ such that
Therefore, ![]() $A(t^+)=-t^++4+2t_E(p-1) (\max _j\{l_j(t^+)\}+1)$ has the required property.
$A(t^+)=-t^++4+2t_E(p-1) (\max _j\{l_j(t^+)\}+1)$ has the required property.
Theorem 3.0.7 (Vertical control theorem).
![]() is a free
is a free ![]() $\Lambda _{\mathrm {so}}$-module of finite rank.
$\Lambda _{\mathrm {so}}$-module of finite rank.
Proof. Let ![]() $\mathfrak {m}$ be a maximal ideal of
$\mathfrak {m}$ be a maximal ideal of ![]() $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$. (We know that
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$. (We know that ![]() $\mathfrak {m}\cap \Lambda _{\mathrm {so}}=(p,T^+,T^-)$, where we identify
$\mathfrak {m}\cap \Lambda _{\mathrm {so}}=(p,T^+,T^-)$, where we identify ![]() $\Lambda _{\mathrm {so}}$ with
$\Lambda _{\mathrm {so}}$ with ![]() $\mathbb {Z}_p[\![ T^+,T^-]\!]$ by identifying
$\mathbb {Z}_p[\![ T^+,T^-]\!]$ by identifying ![]() $(1+p,1)\in T_{\mathrm {so}}(\mathbb {Z}_p)$ (resp.
$(1+p,1)\in T_{\mathrm {so}}(\mathbb {Z}_p)$ (resp. ![]() $(1,1+p)\in T_{\mathrm {so}}(\mathbb {Z}_p)$ with
$(1,1+p)\in T_{\mathrm {so}}(\mathbb {Z}_p)$ with ![]() $T^+$ (resp.
$T^+$ (resp. ![]() $T^-$).) We show that
$T^-$).) We show that ![]() , the localization of
, the localization of ![]() at
at ![]() $\mathfrak {m}$, is a free
$\mathfrak {m}$, is a free ![]() $\Lambda _{\mathrm {so}}$-module of finite rank.
$\Lambda _{\mathrm {so}}$-module of finite rank.
First, we consider the quotient
, which by definition, equals
. Take ![]() $0\geq t^+\geq -t^-+4$ with
$0\geq t^+\geq -t^-+4$ with ![]() $\mathcal {P}_{t^+,t^-}\subset \mathfrak {m}$. Then
$\mathcal {P}_{t^+,t^-}\subset \mathfrak {m}$. Then

Also, Proposition 3.0.1 implies
It follows that
 $$ \begin{align*} &p\text{-torsion of }\varinjlim_m H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1,m}, \omega_{(0,0,t^+;t^-)}\otimes\mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1,m}}\right)\\ =&\, H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1}[1/E],\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1}}\right)\otimes\mathbb{Z}/p\mathbb{Z}\\ =&\, H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1,1},\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1,1}}\right), \end{align*} $$
$$ \begin{align*} &p\text{-torsion of }\varinjlim_m H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1,m}, \omega_{(0,0,t^+;t^-)}\otimes\mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1,m}}\right)\\ =&\, H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1}[1/E],\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1}}\right)\otimes\mathbb{Z}/p\mathbb{Z}\\ =&\, H^0\left(\mathscr{T}^{0,\mathrm{tor}}_{1,1},\omega_{(0,0,t^+;t^-)}\otimes \mathcal{I}_{\mathscr{T}^{0,\mathrm{tor}}_{1,1}}\right), \end{align*} $$where Proposition 3.0.1 is used again for the second equality. Thus,
By Proposition 3.0.6, we know this is finite dimensional over ![]() $\mathbb {F}_p$. Hence,
$\mathbb {F}_p$. Hence,
is finite dimensional over ![]() $\mathbb {F}_p$. Let
$\mathbb {F}_p$. Let
By Nakayama’s lemma, there exist
such that
Next, we show that ![]() $F_1,\dots ,F_d$ are
$F_1,\dots ,F_d$ are ![]() $\Lambda _{\mathrm {so}}$-linearly independent. Suppose that
$\Lambda _{\mathrm {so}}$-linearly independent. Suppose that ![]() $a_1,\dots ,a_d\in \Lambda _{\mathrm {so}}$ are such that
$a_1,\dots ,a_d\in \Lambda _{\mathrm {so}}$ are such that ![]() $a_1F_1+\cdots +a_dF_d=0$. Given any
$a_1F_1+\cdots +a_dF_d=0$. Given any ![]() $0\geq t^+\geq -t^-+4$ with
$0\geq t^+\geq -t^-+4$ with ![]() $\mathcal {P}_{t^+,t^-}\subset \mathfrak {m}$, we put
$\mathcal {P}_{t^+,t^-}\subset \mathfrak {m}$, we put
In view of Proposition 3.0.1, the ![]() $\mathbb {Z}_p$-module
$\mathbb {Z}_p$-module ![]() $\mathop {\varinjlim }\limits _m\mathop {\varinjlim }\limits _n H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$ is p-divisible, and by Proposition 3.0.3 so is
$\mathop {\varinjlim }\limits _m\mathop {\varinjlim }\limits _n H^0\left (\mathscr {T}^{0,\mathrm {tor}}_{n,m},\omega _{\underline {t}}\otimes \mathcal {I}_{\mathscr {T}^{0,\mathrm {tor}}_{n,m}}\right )$ is p-divisible, and by Proposition 3.0.3 so is
. Therefore,
is p-torsion free. On the other hand,
It follows that the ![]() $\mathbb {Z}_p$-module
$\mathbb {Z}_p$-module
is free of rank d, and therefore ![]() $a_1,\dots ,a_d\in \mathcal {P}^{\circ }_{t^+,t^-}$. Then from
$a_1,\dots ,a_d\in \mathcal {P}^{\circ }_{t^+,t^-}$. Then from ![]() $\bigcap \limits _{0\geq t^+\geq -t^-+4}\mathcal {P}^{\circ }_{t^+,t^-}=0$, we conclude that
$\bigcap \limits _{0\geq t^+\geq -t^-+4}\mathcal {P}^{\circ }_{t^+,t^-}=0$, we conclude that ![]() $a_1=\cdots =a_d=0$, and hence
$a_1=\cdots =a_d=0$, and hence
is a free ![]() $\Lambda _{\mathrm {so}}$-module of rank d.
$\Lambda _{\mathrm {so}}$-module of rank d.
This completes the proof of part (1) of Theorem 2.9.1 for cuspidal forms. For part (2), because ![]() is free over
is free over ![]() $\Lambda _{\mathrm {so}}$, letting
$\Lambda _{\mathrm {so}}$, letting ![]() $V^0_{m,\mathrm {so}}[\tau ^+,\tau ^-]=e_{\mathrm {so}} \mathop {\varinjlim }\limits _n V^0_{n,m}\otimes _{\mathbb {Z}_p}\mathcal {O}_F[\tau ^+,\tau ^-]$ we have
$V^0_{m,\mathrm {so}}[\tau ^+,\tau ^-]=e_{\mathrm {so}} \mathop {\varinjlim }\limits _n V^0_{n,m}\otimes _{\mathbb {Z}_p}\mathcal {O}_F[\tau ^+,\tau ^-]$ we have

Since the left-hand side is a free ![]() $\mathbb {Z}_p$-module (because
$\mathbb {Z}_p$-module (because ![]() $\mathcal {M}^0_{\mathrm {so}}$ is a free
$\mathcal {M}^0_{\mathrm {so}}$ is a free ![]() $\Lambda _{\mathrm {so}}$-module), we see that
$\Lambda _{\mathrm {so}}$-module), we see that ![]() $\mathop {\varinjlim }\limits _m V^0_{m,\mathrm {so}}[\tau ^+,\tau ^-])$ is p-divisible, and
$\mathop {\varinjlim }\limits _m V^0_{m,\mathrm {so}}[\tau ^+,\tau ^-])$ is p-divisible, and ![]() $V^0_{m+1,\mathrm {so}}[\tau ^+,\tau ^-]\rightarrow V^0_{m,\mathrm {so}}[\tau ^+,\tau ^-]$ is surjective, so
$V^0_{m+1,\mathrm {so}}[\tau ^+,\tau ^-]\rightarrow V^0_{m,\mathrm {so}}[\tau ^+,\tau ^-]$ is surjective, so
 $$\begin{align*}\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\varinjlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-],\mathbb{Q}_p/\mathbb{Z}_p\right)\cong \operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\varprojlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-],\mathbb{Z}_p\right)\\[-15pt] \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\varinjlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-],\mathbb{Q}_p/\mathbb{Z}_p\right)\cong \operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\varprojlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-],\mathbb{Z}_p\right)\\[-15pt] \end{align*}$$and hence
 $$ \begin{align*} (3.0.12) &=\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\varprojlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-],\mathbb{Z}_p\right),\mathbb{Z}_p\right)=\varprojlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-]\\ &=\left(\varprojlim_m \varinjlim_n e_{\mathrm{so}} V^0_{n,m}\otimes_{\mathbb{Z}_p}\mathcal{O}_F\right)[\tau^+,\tau^-],\\[-15pt] \end{align*} $$
$$ \begin{align*} (3.0.12) &=\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left(\varprojlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-],\mathbb{Z}_p\right),\mathbb{Z}_p\right)=\varprojlim_m V^0_{m,\mathrm{so}}[\tau^+,\tau^-]\\ &=\left(\varprojlim_m \varinjlim_n e_{\mathrm{so}} V^0_{n,m}\otimes_{\mathbb{Z}_p}\mathcal{O}_F\right)[\tau^+,\tau^-],\\[-15pt] \end{align*} $$concluding the proof of part (2) of Theorem 2.9.1 for cuspidal forms. Part (3) follows from Proposition 3.0.6.
4 The proof of Theorem 2.9.1 for the noncuspidal part
We apply the approach in [Reference Liu and RossoLR20] to prove the vertical control theorem for semiordinary forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$ by analyzing the quotient
$\operatorname {\mathrm {GU}}(3,1)$ by analyzing the quotient ![]() and using the vertical control theorem for cuspidal semiordinary forms on
and using the vertical control theorem for cuspidal semiordinary forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$. When studying
$\operatorname {\mathrm {GU}}(3,1)$. When studying ![]() , we introduce an auxiliary space
, we introduce an auxiliary space ![]() . One difference from loc.cit is that q-expansions are used there to reduce proving some properties for the
. One difference from loc.cit is that q-expansions are used there to reduce proving some properties for the ![]() $\mathbb {U}_p$-action on
$\mathbb {U}_p$-action on ![]() to matrix computations, but q-expansions are not available in the case of
to matrix computations, but q-expansions are not available in the case of ![]() $\operatorname {\mathrm {GU}}(3,1)$. The analogue of those properties in our case are proved in §4.5 by working with semiabelian schemes over the boundary of the partial toroidal compactification.
$\operatorname {\mathrm {GU}}(3,1)$. The analogue of those properties in our case are proved in §4.5 by working with semiabelian schemes over the boundary of the partial toroidal compactification.
4.1 Cusp labels
Following [Reference LanLan13], a cusp label is a ![]() $K_f$-orbit of triples
$K_f$-orbit of triples ![]() ${({\tt Z},\Phi ,\delta )}$, with:
${({\tt Z},\Phi ,\delta )}$, with:
•
 $\mathtt {Z}:0\subset \mathtt {Z}_{-2}\subset \mathtt {Z}_{-1}=\mathtt {Z}_{-2}^\bot \subset L\otimes \hat {\mathbb {Z}}$ a fully symplectic admissible filtration.
$\mathtt {Z}:0\subset \mathtt {Z}_{-2}\subset \mathtt {Z}_{-1}=\mathtt {Z}_{-2}^\bot \subset L\otimes \hat {\mathbb {Z}}$ a fully symplectic admissible filtration.•
 $\Phi =(\mathtt {X},\mathtt {Y},\phi ,\varphi _{-2},\varphi _0)$ a torus argument, where
$\Phi =(\mathtt {X},\mathtt {Y},\phi ,\varphi _{-2},\varphi _0)$ a torus argument, where  $\phi :\mathtt {Y}\rightarrow \mathtt {X}$ is an
$\phi :\mathtt {Y}\rightarrow \mathtt {X}$ is an  $\mathcal {O}_{\mathcal {K}}$-linear embedding of locally free
$\mathcal {O}_{\mathcal {K}}$-linear embedding of locally free  $\mathcal {O}_{\mathcal {K}}$-modules with finite cokernel, and
$\mathcal {O}_{\mathcal {K}}$-modules with finite cokernel, and  $\varphi _{-2}:\mathrm {Gr}^{\mathtt { Z}}_{-2}\stackrel {\sim }{\rightarrow }\operatorname {\mathrm {Hom}}\left (\mathtt {X}\otimes \hat {\mathbb {Z}},\hat {\mathbb {Z}}(1)\right )$ and
$\varphi _{-2}:\mathrm {Gr}^{\mathtt { Z}}_{-2}\stackrel {\sim }{\rightarrow }\operatorname {\mathrm {Hom}}\left (\mathtt {X}\otimes \hat {\mathbb {Z}},\hat {\mathbb {Z}}(1)\right )$ and  $\varphi _0:\mathrm {Gr}^{\mathtt {Z}}_0\stackrel {\sim }{\rightarrow }\mathtt {Y}\otimes \hat {\mathbb {Z}}$, with
$\varphi _0:\mathrm {Gr}^{\mathtt {Z}}_0\stackrel {\sim }{\rightarrow }\mathtt {Y}\otimes \hat {\mathbb {Z}}$, with  $\mathrm {Gr}^{\mathtt {Z}}_{-i}=\mathtt {Z}_{-i}/\mathtt {Z}_{-i-1}$, are isomorphisms such that
$\mathrm {Gr}^{\mathtt {Z}}_{-i}=\mathtt {Z}_{-i}/\mathtt {Z}_{-i-1}$, are isomorphisms such that  $\left <v,w\right>=\varphi _0(v)\Big (\phi \big (\varphi _{-2}(w)\big )\Big )$,
$\left <v,w\right>=\varphi _0(v)\Big (\phi \big (\varphi _{-2}(w)\big )\Big )$,•
 $\delta :\mathrm {Gr}^{\mathtt {Z}}=\mathrm {Gr}^{\mathtt {Z}}_{-2}\oplus \mathrm {Gr}^{\mathtt {Z}}_{-1}\oplus \mathrm {Gr}^{\mathtt {Z}}_{0}\stackrel {\sim }{\rightarrow } L\otimes \hat {\mathbb {Z}}$ is an
$\delta :\mathrm {Gr}^{\mathtt {Z}}=\mathrm {Gr}^{\mathtt {Z}}_{-2}\oplus \mathrm {Gr}^{\mathtt {Z}}_{-1}\oplus \mathrm {Gr}^{\mathtt {Z}}_{0}\stackrel {\sim }{\rightarrow } L\otimes \hat {\mathbb {Z}}$ is an  $\mathcal {O}_{\mathcal {K}}\otimes \hat {\mathbb {Z}}$-equivariant splitting.
$\mathcal {O}_{\mathcal {K}}\otimes \hat {\mathbb {Z}}$-equivariant splitting.
Following [Reference LanLan18, Def. 3.2.3.1], an ordinary cusp label of tame level ![]() $K_f^p$ is a
$K_f^p$ is a ![]() $K^p_fP_{\mathtt {D}}(\mathbb {Z}_p)$-orbit of triples
$K^p_fP_{\mathtt {D}}(\mathbb {Z}_p)$-orbit of triples ![]() $(\mathtt {Z},\Phi ,\delta )$ as above compatible with
$(\mathtt {Z},\Phi ,\delta )$ as above compatible with ![]() $\mathtt {D}$, in the sense that
$\mathtt {D}$, in the sense that
There is a unique cusp label for which ![]() $\mathtt {Z}_{-2}=0$, and in our case, all other cusp labels have
$\mathtt {Z}_{-2}=0$, and in our case, all other cusp labels have ![]() $\mathtt {Z}_{-2}$ with rank
$\mathtt {Z}_{-2}$ with rank ![]() $1$. As explained in [Reference HidaHLTT16, B.2, B.3, B.11], the latter are parametrized by a certain double coset space. To recall this, we have the filtration
$1$. As explained in [Reference HidaHLTT16, B.2, B.3, B.11], the latter are parametrized by a certain double coset space. To recall this, we have the filtration
Let ![]() ${P}\subset G$ be the parabolic subgroup preserving this filtration, and
${P}\subset G$ be the parabolic subgroup preserving this filtration, and ![]() ${P'}\subset P$ be the kernel of the natural projection
${P'}\subset P$ be the kernel of the natural projection ![]() $P\rightarrow \operatorname {\mathrm {GL}}(Y)$. Define the triple
$P\rightarrow \operatorname {\mathrm {GL}}(Y)$. Define the triple ![]() ${({\tt Z}^{(1)},\Phi ^{(1)},\delta ^{(1)})}$ as
${({\tt Z}^{(1)},\Phi ^{(1)},\delta ^{(1)})}$ as
•
 $\mathtt {Z}^{(1)}$:
$\mathtt {Z}^{(1)}$:  $\mathtt {Z}_{-2}=X^{\vee }\otimes \hat {\mathbb {Z}}$,
$\mathtt {Z}_{-2}=X^{\vee }\otimes \hat {\mathbb {Z}}$,  $\mathtt {Z}_{-1}=(X^{\vee }\oplus L_0)\otimes \hat {\mathbb {Z}}$.
$\mathtt {Z}_{-1}=(X^{\vee }\oplus L_0)\otimes \hat {\mathbb {Z}}$.•
 $\Phi ^{(1)}=(\mathtt {X}^{(1)},\mathtt {Y}^{(1)},\phi ^{(1)},\varphi ^{(1)}_{-2},\varphi ^{(1)}_0)$ with
$\Phi ^{(1)}=(\mathtt {X}^{(1)},\mathtt {Y}^{(1)},\phi ^{(1)},\varphi ^{(1)}_{-2},\varphi ^{(1)}_0)$ with  $\mathtt {X}^{(1)}=\operatorname {\mathrm {Hom}}_{\mathcal {O}_{\mathcal {K}}}\left (X^{\vee },\mathcal {O}_{\mathcal {K}}(1)\right )$,
$\mathtt {X}^{(1)}=\operatorname {\mathrm {Hom}}_{\mathcal {O}_{\mathcal {K}}}\left (X^{\vee },\mathcal {O}_{\mathcal {K}}(1)\right )$,  $\mathtt {Y}^{(1)}=Y$,
$\mathtt {Y}^{(1)}=Y$,  $\phi ^{(1)}:Y\rightarrow \operatorname {\mathrm {Hom}}_{\mathcal {O}_{\mathcal {K}}}\left (\mathfrak {d}^{-1}_{\mathcal {K}/\mathbb {Q}}\cdot \mathtt {x}_1,\mathcal {O}_{\mathcal {K}}(1)\right )$ induced by our fixed basis of
$\phi ^{(1)}:Y\rightarrow \operatorname {\mathrm {Hom}}_{\mathcal {O}_{\mathcal {K}}}\left (\mathfrak {d}^{-1}_{\mathcal {K}/\mathbb {Q}}\cdot \mathtt {x}_1,\mathcal {O}_{\mathcal {K}}(1)\right )$ induced by our fixed basis of  $\mathtt {x}_1$ and
$\mathtt {x}_1$ and  $\mathtt {y}_1$ of X and Y and the pairing
$\mathtt {y}_1$ of X and Y and the pairing  $2\pi i\cdot \mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L$,
$2\pi i\cdot \mathrm {Tr}_{\mathcal {K}/\mathbb {Q}}\circ \left <\,,\,\right>_L$,  $\varphi ^{(1)}_{-2}=2\pi \sqrt {-1}\cdot \mathrm {id}$ and
$\varphi ^{(1)}_{-2}=2\pi \sqrt {-1}\cdot \mathrm {id}$ and  $\varphi ^{(1)}_{0}=\mathrm {id}$.
$\varphi ^{(1)}_{0}=\mathrm {id}$.•
 $\delta ^{(1)}=\mathrm {id}$.
$\delta ^{(1)}=\mathrm {id}$.
Denote by ![]() $\mathtt {V}\colon 0\subset \mathtt {V}_{-2}\subset \mathtt {V}_{-1}\subset L\otimes \mathbb {Q}$ the filtration obtained as equation (4.1.1) tensored with
$\mathtt {V}\colon 0\subset \mathtt {V}_{-2}\subset \mathtt {V}_{-1}\subset L\otimes \mathbb {Q}$ the filtration obtained as equation (4.1.1) tensored with ![]() $\mathbb {Q}$. For every
$\mathbb {Q}$. For every ![]() $g\in G(\mathbb {A}_{\mathbb {Q},f})$, define
$g\in G(\mathbb {A}_{\mathbb {Q},f})$, define ![]() ${({\tt Z}^{(g)},\Phi ^{(g)},\delta ^{(g)})}$ by
${({\tt Z}^{(g)},\Phi ^{(g)},\delta ^{(g)})}$ by
•
 $\mathtt {Z}^{(g)}_j=\left (g^{-1}(\mathtt {V}_j\otimes \mathbb {A}_{\mathbb {Q},f})\right )\cap \left (L\otimes \hat {\mathbb {Z}}\right )$.
$\mathtt {Z}^{(g)}_j=\left (g^{-1}(\mathtt {V}_j\otimes \mathbb {A}_{\mathbb {Q},f})\right )\cap \left (L\otimes \hat {\mathbb {Z}}\right )$.•
 $\Phi ^{(g)}=(\mathtt {X}^{(g)},\mathtt {Y}^{(g)},\phi ^{(g)},\varphi ^{(g)}_{-2},\varphi ^{(g)}_0)$ with
$\Phi ^{(g)}=(\mathtt {X}^{(g)},\mathtt {Y}^{(g)},\phi ^{(g)},\varphi ^{(g)}_{-2},\varphi ^{(g)}_0)$ with  $(\mathtt {X}^{(g)},\mathtt {Y}^{(g)},\phi ^{(g)})=(\mathtt {X}^{(1)},\mathtt {Y}^{(1)},\phi ^{(1)})$,
$(\mathtt {X}^{(g)},\mathtt {Y}^{(g)},\phi ^{(g)})=(\mathtt {X}^{(1)},\mathtt {Y}^{(1)},\phi ^{(1)})$,  $\varphi ^{(g)}_{-2}$ (resp.
$\varphi ^{(g)}_{-2}$ (resp.  $\varphi ^{(g)}_{0}$) is the composition of
$\varphi ^{(g)}_{0}$) is the composition of  $\varphi ^{(1)}_{-2}$ (resp.
$\varphi ^{(1)}_{-2}$ (resp.  $\varphi ^{(1)}_{0}$) with
$\varphi ^{(1)}_{0}$) with  $g:\mathrm {Gr}^{\mathtt {Z}^{(g)}}_{-2}\rightarrow \mathrm {Gr}^{\mathtt {Z}}_{-2}$ (resp.
$g:\mathrm {Gr}^{\mathtt {Z}^{(g)}}_{-2}\rightarrow \mathrm {Gr}^{\mathtt {Z}}_{-2}$ (resp.  $g:\mathrm {Gr}^{\mathtt {Z}^{(g)}}_{0}\rightarrow \mathrm {Gr}^{\mathtt {Z}}_{0}$).
$g:\mathrm {Gr}^{\mathtt {Z}^{(g)}}_{0}\rightarrow \mathrm {Gr}^{\mathtt {Z}}_{0}$).•
 $\delta ^{(g)}$ is
$\delta ^{(g)}$ is  $\mathrm {Gr}^{\mathtt {Z}^{(g)}}\stackrel {\mathrm {Gr}(g)}{\rightarrow }\mathrm {Gr}^{\mathtt {Z^{(1)}}}\stackrel {\delta ^{(1)}}{\rightarrow } L\otimes \hat {\mathbb {Z}}\stackrel {g^{-1}}{\rightarrow }L\otimes \hat {\mathbb {Z}}$.
$\mathrm {Gr}^{\mathtt {Z}^{(g)}}\stackrel {\mathrm {Gr}(g)}{\rightarrow }\mathrm {Gr}^{\mathtt {Z^{(1)}}}\stackrel {\delta ^{(1)}}{\rightarrow } L\otimes \hat {\mathbb {Z}}\stackrel {g^{-1}}{\rightarrow }L\otimes \hat {\mathbb {Z}}$.
Then the map that sends g to (the cusp label represented by) ![]() $(\mathtt {Z}^{(g)},\Phi ^{(g)},\delta ^{(g)})$ sets up a bijection between the set of cusp labels with
$(\mathtt {Z}^{(g)},\Phi ^{(g)},\delta ^{(g)})$ sets up a bijection between the set of cusp labels with ![]() $\mathtt {Z}_{-2}$ rank
$\mathtt {Z}_{-2}$ rank ![]() $1$ and the double coset space
$1$ and the double coset space
(See [Reference LanLan15, Prop. A.5.9].)
Similarly, the ordinary cusp labels with ![]() $\mathtt {Z}_{-2}$ of rank
$\mathtt {Z}_{-2}$ of rank ![]() $1$ are parameterized by
$1$ are parameterized by
which is in a natural bijection with
 $$ \begin{align} \begin{aligned} &\left.\left(\operatorname{\mathrm{GL}}(X_{(p)})\ltimes (P'(\mathbb{A}^p_{\mathbb{Q},f})\times P'(\mathbb{Z}_p))\right)\middle\backslash G(\mathbb{A}^p_{\mathbb{Q},f})\times P_{\mathtt{D}}(\mathbb{Z}_p)\right/K^p_f(K^1_{p,n}\cap P_{\mathtt{D}}(\mathbb{Z}_p))\\ \cong & \,\,C(K^p_f)\times \left(U_{\mathcal{K},K^p_f}\ltimes P'(\mathbb{Z}_p)\backslash P_{\mathtt{D}}(\mathbb{Z}_p)/K^1_{p,n}\cap P_{\mathtt{D}}(\mathbb{Z}_p)\right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left.\left(\operatorname{\mathrm{GL}}(X_{(p)})\ltimes (P'(\mathbb{A}^p_{\mathbb{Q},f})\times P'(\mathbb{Z}_p))\right)\middle\backslash G(\mathbb{A}^p_{\mathbb{Q},f})\times P_{\mathtt{D}}(\mathbb{Z}_p)\right/K^p_f(K^1_{p,n}\cap P_{\mathtt{D}}(\mathbb{Z}_p))\\ \cong & \,\,C(K^p_f)\times \left(U_{\mathcal{K},K^p_f}\ltimes P'(\mathbb{Z}_p)\backslash P_{\mathtt{D}}(\mathbb{Z}_p)/K^1_{p,n}\cap P_{\mathtt{D}}(\mathbb{Z}_p)\right), \end{aligned} \end{align} $$where ![]() . By abuse of notation, we shall denote by g both elements in
. By abuse of notation, we shall denote by g both elements in ![]() $G(\mathbb {A}^p_{\mathbb {Q},f})P_{\mathtt {D}}(\mathbb {Q}_p)$ and in its quotient
$G(\mathbb {A}^p_{\mathbb {Q},f})P_{\mathtt {D}}(\mathbb {Q}_p)$ and in its quotient ![]() $C(K^p_fK^1_{p,n})_{\mathrm {ord}}$. The context should eliminate any possible confusions.
$C(K^p_fK^1_{p,n})_{\mathrm {ord}}$. The context should eliminate any possible confusions.
4.2 The formal completion along boundary strata
Let ![]() $\mathscr {Z}_{g,n}$ be the stratum associated to
$\mathscr {Z}_{g,n}$ be the stratum associated to ![]() $g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ in the partial toroidal compactification
$g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ in the partial toroidal compactification ![]() $\mathscr {T}^{\mathrm {tor}}_n$. Then we have
$\mathscr {T}^{\mathrm {tor}}_n$. Then we have
 $$\begin{align*}\mathscr{T}^{\mathrm{tor}}_n=\mathscr{T}_{n}\sqcup\bigsqcup\limits_{g\in C(K^p_fK^1_{p,n})_{\mathrm{ord}}} \mathscr{Z}_{g,n}. \end{align*}$$
$$\begin{align*}\mathscr{T}^{\mathrm{tor}}_n=\mathscr{T}_{n}\sqcup\bigsqcup\limits_{g\in C(K^p_fK^1_{p,n})_{\mathrm{ord}}} \mathscr{Z}_{g,n}. \end{align*}$$(The choice of a polyhedral cone decomposition is unique in our special case ![]() $\operatorname {\mathrm {GU}}(3,1)$ because with
$\operatorname {\mathrm {GU}}(3,1)$ because with  $\Big (\mathbf {S}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}\Big )$ defined as below and
$\Big (\mathbf {S}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}\Big )$ defined as below and ![]() $\mathbf {P}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}$ the subset of
$\mathbf {P}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}$ the subset of  $\operatorname {\mathrm {Hom}}_{\mathbb {Z}}\Big (\mathbf {S}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}},\mathbb {Z}\Big )\otimes \mathbb {R}$ consisting of positive semidefinite Hermitian forms, we have
$\operatorname {\mathrm {Hom}}_{\mathbb {Z}}\Big (\mathbf {S}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}},\mathbb {Z}\Big )\otimes \mathbb {R}$ consisting of positive semidefinite Hermitian forms, we have ![]() $\mathbf { P}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}=\mathbb {R}_{\geq 0}$.) Let
$\mathbf { P}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}=\mathbb {R}_{\geq 0}$.) Let ![]() ${\mathscr {T}^{\min }_n}$ be the partial minimal compactification of
${\mathscr {T}^{\min }_n}$ be the partial minimal compactification of ![]() $\mathscr {T}_n$ (constructed in [Reference LanLan18, Theorem 6.2.1.1]). Denoting by
$\mathscr {T}_n$ (constructed in [Reference LanLan18, Theorem 6.2.1.1]). Denoting by ![]() ${\mathscr {Y}_{g,n}}$ the stratum associated to
${\mathscr {Y}_{g,n}}$ the stratum associated to ![]() $g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ in
$g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ in ![]() $\mathscr {T}^{\min }_n$, we similarly have
$\mathscr {T}^{\min }_n$, we similarly have
 $$\begin{align*}\mathscr{T}^{\min}_n=\mathscr{T}_{n}\sqcup\bigsqcup\limits_{g\in C(K^p_fK^1_{p,n})_{\mathrm{ord}}} \mathscr{Y}_{g,n}. \end{align*}$$
$$\begin{align*}\mathscr{T}^{\min}_n=\mathscr{T}_{n}\sqcup\bigsqcup\limits_{g\in C(K^p_fK^1_{p,n})_{\mathrm{ord}}} \mathscr{Y}_{g,n}. \end{align*}$$The stratum ![]() $\mathscr {Y}_{g,n}$ can be identified with the
$\mathscr {Y}_{g,n}$ can be identified with the ![]() $0$-dimensional Shimura variety
$0$-dimensional Shimura variety ![]() ${\mathscr {S}_{G',K^{\prime }_{f,g,n}}}$, where
${\mathscr {S}_{G',K^{\prime }_{f,g,n}}}$, where
We have the following diagram:

where ![]() ${\mathscr {C}^{\mathrm {ord}}_{g,n}}\rightarrow \mathscr {S}_{G',K^{\prime }_{f,g,n}}$ is a torsor of an abelian scheme quasi-isogenous to
${\mathscr {C}^{\mathrm {ord}}_{g,n}}\rightarrow \mathscr {S}_{G',K^{\prime }_{f,g,n}}$ is a torsor of an abelian scheme quasi-isogenous to ![]() $\underline {\operatorname {\mathrm {Hom}}}_{\mathcal {O}_{\mathcal {K}}}(\mathtt {X}^{(g)},\mathcal {A})$ with
$\underline {\operatorname {\mathrm {Hom}}}_{\mathcal {O}_{\mathcal {K}}}(\mathtt {X}^{(g)},\mathcal {A})$ with ![]() $\mathcal {A}$ the universal abelian scheme over
$\mathcal {A}$ the universal abelian scheme over ![]() $\mathscr {S}_{G',K^{\prime }_{f,g,n}}$, and
$\mathscr {S}_{G',K^{\prime }_{f,g,n}}$, and ![]() $\Xi ^{\mathrm {ord}}_{g,n}\rightarrow \mathscr {C}^{\mathrm {ord}}_{g,n}$ is a torsor of the torus with character group
$\Xi ^{\mathrm {ord}}_{g,n}\rightarrow \mathscr {C}^{\mathrm {ord}}_{g,n}$ is a torsor of the torus with character group ![]() $\mathbf {S}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}$, which is a finite index subgroup of the free quotient of
$\mathbf {S}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}$, which is a finite index subgroup of the free quotient of
 $$\begin{align*}\left.\left(\frac{1}{N} \mathtt{Y}^{(g)}\otimes_{\mathbb{Z}} \mathtt{X}^{(g)}\right)\middle/ \begin{pmatrix} y\otimes\phi^{(g)}(y')-y'\otimes\phi^{(g)}(y)\\ (b\frac{1}{N}y)\otimes x-(\frac{1}{N}y\otimes (b^cx) \end{pmatrix}_{y,y'\in \mathtt{Y}^{(g)},x\in \mathtt{X}^{(g)},b\in\mathcal{O}_{\mathcal{K}}} \right. \end{align*}$$
$$\begin{align*}\left.\left(\frac{1}{N} \mathtt{Y}^{(g)}\otimes_{\mathbb{Z}} \mathtt{X}^{(g)}\right)\middle/ \begin{pmatrix} y\otimes\phi^{(g)}(y')-y'\otimes\phi^{(g)}(y)\\ (b\frac{1}{N}y)\otimes x-(\frac{1}{N}y\otimes (b^cx) \end{pmatrix}_{y,y'\in \mathtt{Y}^{(g)},x\in \mathtt{X}^{(g)},b\in\mathcal{O}_{\mathcal{K}}} \right. \end{align*}$$with N sufficiently large with respect to the level ![]() $K^p_fK^1_{p,n}$; and
$K^p_fK^1_{p,n}$; and ![]() $\Xi ^{\mathrm {ord}}_{g,n}\hookrightarrow \overline {\Xi }^{\mathrm {ord}}_{g,n}$ is the torus embedding with respect to the unique cone decomposition.
$\Xi ^{\mathrm {ord}}_{g,n}\hookrightarrow \overline {\Xi }^{\mathrm {ord}}_{g,n}$ is the torus embedding with respect to the unique cone decomposition.
Denote by ![]() ${\mathfrak {X}_{g,n}}$ the formal completion of
${\mathfrak {X}_{g,n}}$ the formal completion of ![]() $\mathscr {T}^{\mathrm {tor}}_n$ along the stratum
$\mathscr {T}^{\mathrm {tor}}_n$ along the stratum ![]() $\mathscr {Z}_{g,n}$. Then
$\mathscr {Z}_{g,n}$. Then ![]() $\mathfrak {X}_{g,n}$ is canonically isomorphic to the quotient by
$\mathfrak {X}_{g,n}$ is canonically isomorphic to the quotient by ![]() $\Gamma _g$ of the formal completion of
$\Gamma _g$ of the formal completion of ![]() $\overline {\Xi }^{\mathrm {ord}}_{g,n}$ along the boundary
$\overline {\Xi }^{\mathrm {ord}}_{g,n}$ along the boundary ![]() $\overline {\Xi }^{\mathrm {ord}}_{g,n}-\Xi ^{\mathrm {ord}}_{g,n}$. Here,
$\overline {\Xi }^{\mathrm {ord}}_{g,n}-\Xi ^{\mathrm {ord}}_{g,n}$. Here, ![]() $\Gamma _g$ is the (finite, in our case) subgroup of
$\Gamma _g$ is the (finite, in our case) subgroup of ![]() $\operatorname {\mathrm {GL}}(\mathtt {X}^{(g)})\times \operatorname {\mathrm {GL}}(\mathtt {Y}^{(g)})$ preserving
$\operatorname {\mathrm {GL}}(\mathtt {X}^{(g)})\times \operatorname {\mathrm {GL}}(\mathtt {Y}^{(g)})$ preserving ![]() $\varphi ^{(g)}_{-2}$ and
$\varphi ^{(g)}_{-2}$ and ![]() $\varphi ^{(g)}_{0}$ (as orbits).
$\varphi ^{(g)}_{0}$ (as orbits).
4.3 The subset  $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ of
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ of  $C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ and the subspace
$C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ and the subspace  of
of 
By a generic point, denoted by ![]() ${\eta }$, of the formal completion
${\eta }$, of the formal completion ![]() $\mathfrak {X}_{g,n}$, we mean a generic point of
$\mathfrak {X}_{g,n}$, we mean a generic point of ![]() $\operatorname {\mathrm {Spec}}(\Gamma (U,\mathcal {O}_U))$ with U an affine open subscheme of
$\operatorname {\mathrm {Spec}}(\Gamma (U,\mathcal {O}_U))$ with U an affine open subscheme of ![]() $\mathfrak {X}_{g,n}$. Let
$\mathfrak {X}_{g,n}$. Let ![]() $(\mathcal {G},\lambda ,i,\alpha ^p,\alpha _p)$ be the pullback to
$(\mathcal {G},\lambda ,i,\alpha ^p,\alpha _p)$ be the pullback to ![]() $\operatorname {\mathrm {Spec}}(\Gamma (U,\mathcal {O}_U))$ of the family of semiabelian varieties over
$\operatorname {\mathrm {Spec}}(\Gamma (U,\mathcal {O}_U))$ of the family of semiabelian varieties over ![]() $\mathscr {T}^{\mathrm {tor}}_n$, which is a degenerating family obtained by Mumford’s construction. Let
$\mathscr {T}^{\mathrm {tor}}_n$, which is a degenerating family obtained by Mumford’s construction. Let
be the Raynaud extension of ![]() $\mathcal {G}$. Then, for any positive integer N, the group
$\mathcal {G}$. Then, for any positive integer N, the group ![]() $\mathcal {T}[N]$ (resp.
$\mathcal {T}[N]$ (resp. ![]() $\mathcal {G}^\natural [N]$) is canonically isomorphic to a subgroup of
$\mathcal {G}^\natural [N]$) is canonically isomorphic to a subgroup of ![]() $\mathcal {G}[N]$, which we denote by
$\mathcal {G}[N]$, which we denote by ![]() ${(\mathcal {G}[N])^\mu }$ (resp.
${(\mathcal {G}[N])^\mu }$ (resp. ![]() ${(\mathcal {G}[N])^{\mathrm {f}}}$). We have
${(\mathcal {G}[N])^{\mathrm {f}}}$). We have ![]() $(\mathcal {G}[N])^\mu \subset (\mathcal {G}[N])^{\mathrm {f}}$ and the quotient
$(\mathcal {G}[N])^\mu \subset (\mathcal {G}[N])^{\mathrm {f}}$ and the quotient ![]() ${(\mathcal {G}[N])^{\mathrm {ab}}} =(\mathcal {G}[N])^{\mathrm {f}}/(\mathcal {G}[N])^\mu $ is canonically isomorphic to
${(\mathcal {G}[N])^{\mathrm {ab}}} =(\mathcal {G}[N])^{\mathrm {f}}/(\mathcal {G}[N])^\mu $ is canonically isomorphic to ![]() $\mathcal {A}[N]$. (See also [Reference LanLan18, §3.4.2].)
$\mathcal {A}[N]$. (See also [Reference LanLan18, §3.4.2].)
Let ![]() ${\bar {\eta }}$ be a geometric point over
${\bar {\eta }}$ be a geometric point over ![]() $\eta $. The ordinary level structure
$\eta $. The ordinary level structure ![]() $\alpha _{p,\bar {\eta }}$ of
$\alpha _{p,\bar {\eta }}$ of ![]() $\mathcal {G}_{\bar {\eta }}$ gives rise to a filtration
$\mathcal {G}_{\bar {\eta }}$ gives rise to a filtration
(refer to text around equation (2.5.2)). We define a subset ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}\subset C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ in terms of the relative positions of
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}\subset C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ in terms of the relative positions of ![]() $\mathtt {F}^+_{2,\overline {\eta }}$ and
$\mathtt {F}^+_{2,\overline {\eta }}$ and ![]() $(\mathcal {G}_{\bar {\eta }}[p])^\mu $.
$(\mathcal {G}_{\bar {\eta }}[p])^\mu $.
Definition 4.3.1. Define ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ as the subset of
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ as the subset of ![]() $C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ consisting of g such that
$C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ consisting of g such that
for a geometric point ![]() $\bar {\eta }$ over a generic point
$\bar {\eta }$ over a generic point ![]() $\eta $ of
$\eta $ of ![]() $\mathfrak {X}_{g,n}$.
$\mathfrak {X}_{g,n}$.
One can check that the preceding definition does not depend on the choice of ![]() $\bar {\eta }$. Let
$\bar {\eta }$. Let
 $$ \begin{align*} {P^{\flat}_{\tt D}(\mathbb{Q}_p)} & =\left\{g\in P_{\mathtt{D}}(\mathbb{Q}_p)\,\middle|\, g^+=\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end{smallmatrix}\right) \text{ with }\left(\begin{smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{smallmatrix}\right) ^{-1}\left(\begin{smallmatrix}a_{23}\\ a_{33}\end{smallmatrix}\right) \in \mathbb{Z}^2_p \right\} \end{align*} $$
$$ \begin{align*} {P^{\flat}_{\tt D}(\mathbb{Q}_p)} & =\left\{g\in P_{\mathtt{D}}(\mathbb{Q}_p)\,\middle|\, g^+=\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end{smallmatrix}\right) \text{ with }\left(\begin{smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{smallmatrix}\right) ^{-1}\left(\begin{smallmatrix}a_{23}\\ a_{33}\end{smallmatrix}\right) \in \mathbb{Z}^2_p \right\} \end{align*} $$and
 $$ \begin{align*} P^{\flat}_{\mathtt{D}}(\mathbb{Z}_p)&=\left\{g_p\in P_{\mathtt{D}}(\mathbb{Z}_p)\,\middle|\, g^+_p=\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end{smallmatrix}\right) \text{ with }\left(\begin{smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{smallmatrix}\right) \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}_p) \right\}\\ &=P'(\mathbb{Z}_p) \left(\begin{smallmatrix}&&1\\1\\&1\\&&&1\end{smallmatrix}\right) \left(K^0_{p,n} \cap P_{\mathtt{D}}(\mathbb{Z}_p)\right). \end{align*} $$
$$ \begin{align*} P^{\flat}_{\mathtt{D}}(\mathbb{Z}_p)&=\left\{g_p\in P_{\mathtt{D}}(\mathbb{Z}_p)\,\middle|\, g^+_p=\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end{smallmatrix}\right) \text{ with }\left(\begin{smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{smallmatrix}\right) \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}_p) \right\}\\ &=P'(\mathbb{Z}_p) \left(\begin{smallmatrix}&&1\\1\\&1\\&&&1\end{smallmatrix}\right) \left(K^0_{p,n} \cap P_{\mathtt{D}}(\mathbb{Z}_p)\right). \end{align*} $$Proposition 4.3.2. We have
which is in a natural bijection with
Proof. Given ![]() $g_p\in P_{\mathtt {D}}(\mathbb {Z}_p)$ with
$g_p\in P_{\mathtt {D}}(\mathbb {Z}_p)$ with
 $$ \begin{align*} g_p^+&=\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&\ast\\a_{21}&a_{22}&a_{23}&\ast\\ a_{31}&a_{32}&a_{33}&\ast\\ &&&\ast\end{smallmatrix}\right) , &(g^{-1}_p)^+&=\left(\begin{smallmatrix}c_{11}&c_{12}&c_{13}&\ast\\c_{21}&c_{22}&c_{23}&\ast\\ c_{31}&c_{32}&c_{33}&\ast\\ &&&\ast\end{smallmatrix}\right) , &(g^{-1}_p)^-&=\left(\begin{smallmatrix}d_{11}&\ast & \ast & \ast\\ &\ast & \ast & \ast\\&\ast & \ast &\ast\\ &\ast & \ast & \ast\end{smallmatrix}\right) , \end{align*} $$
$$ \begin{align*} g_p^+&=\left(\begin{smallmatrix}a_{11}&a_{12}&a_{13}&\ast\\a_{21}&a_{22}&a_{23}&\ast\\ a_{31}&a_{32}&a_{33}&\ast\\ &&&\ast\end{smallmatrix}\right) , &(g^{-1}_p)^+&=\left(\begin{smallmatrix}c_{11}&c_{12}&c_{13}&\ast\\c_{21}&c_{22}&c_{23}&\ast\\ c_{31}&c_{32}&c_{33}&\ast\\ &&&\ast\end{smallmatrix}\right) , &(g^{-1}_p)^-&=\left(\begin{smallmatrix}d_{11}&\ast & \ast & \ast\\ &\ast & \ast & \ast\\&\ast & \ast &\ast\\ &\ast & \ast & \ast\end{smallmatrix}\right) , \end{align*} $$the corresponding ![]() $\mathtt {F}_{2,\bar {\eta }}$ is spanned by the image of
$\mathtt {F}_{2,\bar {\eta }}$ is spanned by the image of ![]() $x^+_1,w^+_1$ under
$x^+_1,w^+_1$ under ![]() $\alpha _{p,\bar {\eta }}$, and
$\alpha _{p,\bar {\eta }}$, and ![]() $\mathcal {T}_{\bar {\eta }}[p]$ is spanned by the image under
$\mathcal {T}_{\bar {\eta }}[p]$ is spanned by the image under ![]() $\alpha _{p,\bar {\eta }}$ of
$\alpha _{p,\bar {\eta }}$ of
 $$ \begin{align} (\mathtt{x}^+_1,\mathtt{w}^+_1,\mathtt{w}^+_2;\mathtt{x}^-_1)\begin{pmatrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\ c_{31}&c_{32}&c_{33}\\&&&d_{11}\end{pmatrix}\begin{pmatrix}1&0\\0&0\\0&0\\0&1\end{pmatrix}. \end{align} $$
$$ \begin{align} (\mathtt{x}^+_1,\mathtt{w}^+_1,\mathtt{w}^+_2;\mathtt{x}^-_1)\begin{pmatrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\ c_{31}&c_{32}&c_{33}\\&&&d_{11}\end{pmatrix}\begin{pmatrix}1&0\\0&0\\0&0\\0&1\end{pmatrix}. \end{align} $$Therefore, the condition ![]() $\mathtt {F}^+_{2,\overline {\eta }}\cap (\mathcal {G}_{\bar {\eta }}[p])^\mu =0$ is equivalent to the condition that
$\mathtt {F}^+_{2,\overline {\eta }}\cap (\mathcal {G}_{\bar {\eta }}[p])^\mu =0$ is equivalent to the condition that ![]() $c_{11}\mathtt {x}^+_1+c_{21}\mathtt {w}^+_1+c_{31}\mathtt {w}^+_2$ does not belong to
$c_{11}\mathtt {x}^+_1+c_{21}\mathtt {w}^+_1+c_{31}\mathtt {w}^+_2$ does not belong to ![]() $\mathrm {Span}_{\mathbb {F}_p}\{\mathtt {x}^+_1,\mathtt {w}^+_1\}$, which is equivalent to
$\mathrm {Span}_{\mathbb {F}_p}\{\mathtt {x}^+_1,\mathtt {w}^+_1\}$, which is equivalent to ![]() $c_{31}\in \mathbb {Z}^{\times }_p$. The condition
$c_{31}\in \mathbb {Z}^{\times }_p$. The condition ![]() $c_{31}\in \mathbb {Z}^{\times }_p$ for
$c_{31}\in \mathbb {Z}^{\times }_p$ for ![]() $(g^{-1}_p)^+$ is equivalent to the condition
$(g^{-1}_p)^+$ is equivalent to the condition ![]() $\left (\begin {smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}_p)$ for
$\left (\begin {smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end {smallmatrix}\right ) \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}_p)$ for ![]() $g^+_p$. This shows that
$g^+_p$. This shows that ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ equals equation (4.3.2). It is also easy to see that there is a natural bijection between equations (4.3.1) and (4.3.2).
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ equals equation (4.3.2). It is also easy to see that there is a natural bijection between equations (4.3.1) and (4.3.2).
Definition 4.3.3. Define
that is, the subspace of ![]() $V_{n,m}$ consisting of forms vanishing along all the boundary strata of
$V_{n,m}$ consisting of forms vanishing along all the boundary strata of ![]() $\mathscr {T}_n^{\mathrm {tor}}$ indexed by ordinary cusp labels outside
$\mathscr {T}_n^{\mathrm {tor}}$ indexed by ordinary cusp labels outside ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, and define
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, and define
4.4 The exact sequence for  $V^{\flat }_{n,m}$
$V^{\flat }_{n,m}$
When ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, the level
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, the level ![]() $K^{\prime }_{f,g,n}$ is independent of n, and we denote it by
$K^{\prime }_{f,g,n}$ is independent of n, and we denote it by ![]() $K^{\prime }_{f,g}$. We have
$K^{\prime }_{f,g}$. We have
 $$ \begin{align} \begin{aligned} K^{\prime p}_{f,g}&= \mathrm{Im} \left(P(\mathbb{A}^p_{\mathbb{Q},f})\cap g K^p_fg^{-1}\longrightarrow G'(\mathbb{A}^p_{\mathbb{Q},f})\right),\\ {K^{\prime}_{p,g}} &=\left\{h\in G'(\mathbb{Z}_p):h^+\equiv \begin{pmatrix}\ast &\ast\\ &\ast\end{pmatrix}\quad\mod p\right\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} K^{\prime p}_{f,g}&= \mathrm{Im} \left(P(\mathbb{A}^p_{\mathbb{Q},f})\cap g K^p_fg^{-1}\longrightarrow G'(\mathbb{A}^p_{\mathbb{Q},f})\right),\\ {K^{\prime}_{p,g}} &=\left\{h\in G'(\mathbb{Z}_p):h^+\equiv \begin{pmatrix}\ast &\ast\\ &\ast\end{pmatrix}\quad\mod p\right\}. \end{aligned} \end{align} $$Let ![]() ${M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})}$ be the space of classical automorphic forms on
${M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})}$ be the space of classical automorphic forms on ![]() $G'$ valued in
$G'$ valued in ![]() $\mathbb {Z}/p^m\mathbb {Z}$ of weight
$\mathbb {Z}/p^m\mathbb {Z}$ of weight ![]() $(0,0)$ and level
$(0,0)$ and level ![]() $K^{\prime }_{f,g}$ (which are functions valued in
$K^{\prime }_{f,g}$ (which are functions valued in ![]() $\mathbb {Z}/p^m\mathbb {Z}$ on the finite set
$\mathbb {Z}/p^m\mathbb {Z}$ on the finite set ![]() $G'(\mathbb {Q})\backslash G'(\mathbb {A}_{\mathbb {Q},f})/K^{\prime }_{f,g}$), and
$G'(\mathbb {Q})\backslash G'(\mathbb {A}_{\mathbb {Q},f})/K^{\prime }_{f,g}$), and ![]() $M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Q}_p/\mathbb {Z}_p)=\mathop {\varinjlim }\limits _mM_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$.
$M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Q}_p/\mathbb {Z}_p)=\mathop {\varinjlim }\limits _mM_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$.
Proposition 4.4.1. We have the exact sequences
 $$ \begin{align} 0\longrightarrow V^0_{n,m} \longrightarrow V^{\flat}_{n,m}\xrightarrow{\oplus\Phi_{g}} \bigoplus_{g\in C(K^p_f)} M_{(0,0)}(K^{\prime}_{f,g};\mathbb{Z}/p^m\mathbb{Z})\otimes\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)/U_{\mathcal{K},K^p_f}]\!] \longrightarrow 0 \end{align} $$
$$ \begin{align} 0\longrightarrow V^0_{n,m} \longrightarrow V^{\flat}_{n,m}\xrightarrow{\oplus\Phi_{g}} \bigoplus_{g\in C(K^p_f)} M_{(0,0)}(K^{\prime}_{f,g};\mathbb{Z}/p^m\mathbb{Z})\otimes\mathbb{Z}_p[\![ T_{\mathrm{so}}(\mathbb{Z}_p)/U_{\mathcal{K},K^p_f}]\!] \longrightarrow 0 \end{align} $$and

where the map ![]() ${\Phi _g}$ is obtained by restriction to the stratum
${\Phi _g}$ is obtained by restriction to the stratum ![]() $\mathscr {Z}_{g,n}$ (whose global sections are the same as the global sections of
$\mathscr {Z}_{g,n}$ (whose global sections are the same as the global sections of ![]() $\mathscr {Y}_{g,n}$, which can be identified with the
$\mathscr {Y}_{g,n}$, which can be identified with the ![]() $0$-dimensional Shimura variety
$0$-dimensional Shimura variety ![]() $\mathscr {S}_{G',K^{\prime }_{f,g}}$), and is sometimes called a Siegel operator.
$\mathscr {S}_{G',K^{\prime }_{f,g}}$), and is sometimes called a Siegel operator.
Proof. Let ![]() $\pi _n:\mathscr {T}^{\mathrm {tor}}_{n}\rightarrow \mathscr {T}^{\min }_{n}$ be the natural map. By [Reference LanLan18, Lem. 8.2.2.10], we have
$\pi _n:\mathscr {T}^{\mathrm {tor}}_{n}\rightarrow \mathscr {T}^{\min }_{n}$ be the natural map. By [Reference LanLan18, Lem. 8.2.2.10], we have
(Here, h is the map in the diagram (4.2.2).) Taking global sections over the affine scheme ![]() $\mathscr {T}^{\min }_{n,m}$, we get
$\mathscr {T}^{\min }_{n,m}$, we get
 $$ \begin{align} V_{n,m}/V^0_{n,m}=\bigoplus_{g\in C(K^p_fK^1_{p,n})_{\mathrm{ord}}} M_{(0,0)}(K^{\prime}_{f,g,n};\mathbb{Z}/p^m\mathbb{Z}). \end{align} $$
$$ \begin{align} V_{n,m}/V^0_{n,m}=\bigoplus_{g\in C(K^p_fK^1_{p,n})_{\mathrm{ord}}} M_{(0,0)}(K^{\prime}_{f,g,n};\mathbb{Z}/p^m\mathbb{Z}). \end{align} $$By definition, an element in ![]() $V_{n,m}$ belongs to
$V_{n,m}$ belongs to ![]() $V^{\flat }_{n,m}$ if and only if it vanishes along the strata associated to the cusp labels outside
$V^{\flat }_{n,m}$ if and only if it vanishes along the strata associated to the cusp labels outside ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, so
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, so
 $$ \begin{align} V^{\flat}_{n,m}/V^0_{n,m}=\bigoplus_{g\in C(K^p_fK^1_{p,n})^{\flat}_{\mathrm{ord}}} M_{(0,0)}(K^{\prime}_{f,g};\mathbb{Z}/p^m\mathbb{Z}). \end{align} $$
$$ \begin{align} V^{\flat}_{n,m}/V^0_{n,m}=\bigoplus_{g\in C(K^p_fK^1_{p,n})^{\flat}_{\mathrm{ord}}} M_{(0,0)}(K^{\prime}_{f,g};\mathbb{Z}/p^m\mathbb{Z}). \end{align} $$ The action of ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ on
$T_{\mathrm {so}}(\mathbb {Z}_p)$ on ![]() $V_{n,m}$ preserves
$V_{n,m}$ preserves ![]() $V^0_{n,m}$, so it descends to
$V^0_{n,m}$, so it descends to ![]() $V_{n,m}/V^0_{n,m}$. This action permutes the direct summands of the right-hand side of equation (4.4.4). More precisely, the corresponding action of
$V_{n,m}/V^0_{n,m}$. This action permutes the direct summands of the right-hand side of equation (4.4.4). More precisely, the corresponding action of ![]() $(a_1,a_2)\in T_{\mathrm {so}}(\mathbb {Z}_p)$ on the index set
$(a_1,a_2)\in T_{\mathrm {so}}(\mathbb {Z}_p)$ on the index set
sends ![]() $g=g^pg_p$ to
$g=g^pg_p$ to ![]() $g^pg_p t_{a_1,a_2}$, where
$g^pg_p t_{a_1,a_2}$, where ![]() $t_{a_1,a_2}\in G(\mathbb {Z}_p)$ with
$t_{a_1,a_2}\in G(\mathbb {Z}_p)$ with  $t^+_{a_1,a_2}=\left (\begin {smallmatrix}1\\&1\\&&a_1\\&&&a^{-1}_2\end {smallmatrix}\right ) $. It is easy to see that
$t^+_{a_1,a_2}=\left (\begin {smallmatrix}1\\&1\\&&a_1\\&&&a^{-1}_2\end {smallmatrix}\right ) $. It is easy to see that ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$-action on
$T_{\mathrm {so}}(\mathbb {Z}_p)$-action on ![]() $C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ preserves
$C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ preserves ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, so the
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, so the ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ on
$T_{\mathrm {so}}(\mathbb {Z}_p)$ on ![]() $V_{n,m}$ preserves
$V_{n,m}$ preserves ![]() $V^{\flat }_{n,m}$ and induces an action on
$V^{\flat }_{n,m}$ and induces an action on ![]() $V^{\flat }_{n,m}/V^0_{n,m}$.
$V^{\flat }_{n,m}/V^0_{n,m}$.
For given ![]() $g\in C(K^p_f)$, set
$g\in C(K^p_f)$, set
 $$ \begin{align} \begin{aligned} C(K^p_f K^1_{p,n})_{\mathrm{ord},g}&=\{\text{elements in } C(K^p_f K^1_{p,n})_{\mathrm{ord}} \text{ whose projection to } C(K^p_f) \text{ is } g\},\\ C(K^p_f K^1_{p,n})^{\flat}_{\mathrm{ord},g}&=\{\text{elements in } C(K^p_f K^1_{p,n})^{\flat}_{\mathrm{ord}} \text{ whose projection to } C(K^p_f) \text{ is } g\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} C(K^p_f K^1_{p,n})_{\mathrm{ord},g}&=\{\text{elements in } C(K^p_f K^1_{p,n})_{\mathrm{ord}} \text{ whose projection to } C(K^p_f) \text{ is } g\},\\ C(K^p_f K^1_{p,n})^{\flat}_{\mathrm{ord},g}&=\{\text{elements in } C(K^p_f K^1_{p,n})^{\flat}_{\mathrm{ord}} \text{ whose projection to } C(K^p_f) \text{ is } g\}. \end{aligned} \end{align} $$The ![]() $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module structures of
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module structures of ![]() $V_{n,m}/V^0_{n,m}$ (resp.
$V_{n,m}/V^0_{n,m}$ (resp. ![]() $V^{\flat }_{n,m}/V^0_{n,m}$) are determined by the
$V^{\flat }_{n,m}/V^0_{n,m}$) are determined by the ![]() $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-actions on
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-actions on ![]() $C(K^p_fK^1_{p,n})_{\mathrm {ord},g}$ (resp.
$C(K^p_fK^1_{p,n})_{\mathrm {ord},g}$ (resp. ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord},g}$). The
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord},g}$). The ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$-action on
$T_{\mathrm {so}}(\mathbb {Z}_p)$-action on ![]() $C(K^p_fK^1_{p,n})_{\mathrm {ord},g}$ has too many orbits, and the number of orbits grows with n, so
$C(K^p_fK^1_{p,n})_{\mathrm {ord},g}$ has too many orbits, and the number of orbits grows with n, so ![]() $V_{n,m}/V^0_{n,m}$ is not very nice as a
$V_{n,m}/V^0_{n,m}$ is not very nice as a ![]() $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module. In contrast, the
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module. In contrast, the ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$-action on
$T_{\mathrm {so}}(\mathbb {Z}_p)$-action on ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord},g}$ is transitive, factoring through
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord},g}$ is transitive, factoring through ![]() $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p/p^n\mathbb {Z})/U_{\mathcal {K},K^p_f}]\!]$, and the action of this quotient is free. Therefore, by fixing an element in
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p/p^n\mathbb {Z})/U_{\mathcal {K},K^p_f}]\!]$, and the action of this quotient is free. Therefore, by fixing an element in ![]() $P^{\flat }_{\mathtt {D}}(\mathbb {Z}_p)$, which we will always choose to be
$P^{\flat }_{\mathtt {D}}(\mathbb {Z}_p)$, which we will always choose to be  $\left (\begin {smallmatrix}&&1\\1\\&1\\&&&1\end {smallmatrix}\right ) $, we get the isomorphism
$\left (\begin {smallmatrix}&&1\\1\\&1\\&&&1\end {smallmatrix}\right ) $, we get the isomorphism
from which the exact sequence (4.4.2) follows. The exact sequence (4.4.3) follows from equation (4.4.2) by taking the direct limit.
4.5 Three propositions on the  $\mathbb {U}_p$-action on
$\mathbb {U}_p$-action on  and
and  .
.
We introduce some setting for the proof of the following propositions. Given ![]() $g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$, recall that
$g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$, recall that ![]() $\eta $ denotes a generic point of
$\eta $ denotes a generic point of ![]() $\mathfrak {X}_{g,n,m}$, and
$\mathfrak {X}_{g,n,m}$, and ![]() $\bar {\eta }$ denotes a geometric point over
$\bar {\eta }$ denotes a geometric point over ![]() $\eta $. Let
$\eta $. Let ![]() $(\mathcal {G}_{\bar {\eta }},i_{\bar {\eta }},\lambda _{\bar {\eta }},\alpha ^p_{\bar {\eta }},\alpha _{p,\bar {\eta }})$ be the pullback to
$(\mathcal {G}_{\bar {\eta }},i_{\bar {\eta }},\lambda _{\bar {\eta }},\alpha ^p_{\bar {\eta }},\alpha _{p,\bar {\eta }})$ be the pullback to ![]() $\bar {\eta }$ of the family of semiabelian schemes over
$\bar {\eta }$ of the family of semiabelian schemes over ![]() $\mathscr {T}^{\mathrm {tor}}_{n,m}$. Recall that certain Lagrangian subgroups
$\mathscr {T}^{\mathrm {tor}}_{n,m}$. Recall that certain Lagrangian subgroups ![]() $C\subset \mathcal {G}_{\bar {\eta }}[p^2]$ are used in the construction of
$C\subset \mathcal {G}_{\bar {\eta }}[p^2]$ are used in the construction of ![]() $\mathscr {C}^{\bullet }_{j,n,m}$ for defining
$\mathscr {C}^{\bullet }_{j,n,m}$ for defining ![]() $U^{\bullet }_{p,j}$ in §2.8. (Here,
$U^{\bullet }_{p,j}$ in §2.8. (Here, ![]() $(\bullet ,j)=(+,2),\,(+,3)$ or
$(\bullet ,j)=(+,2),\,(+,3)$ or ![]() $(-,1)$.) Let
$(-,1)$.) Let
be the tuple defined as in the construction of ![]() $\mathscr {C}^{\bullet }_{j,n,m}$. If
$\mathscr {C}^{\bullet }_{j,n,m}$. If ![]() $(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)$ is a basis of
$(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)$ is a basis of ![]() $\mathcal {G}_{\bar {\eta }}[p^n]$ compatible with
$\mathcal {G}_{\bar {\eta }}[p^n]$ compatible with ![]() $\alpha _{p,\bar {\eta }}$, then C is spanned by
$\alpha _{p,\bar {\eta }}$, then C is spanned by ![]() $(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n \gamma ^{\pm }_{C,p}$ with
$(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n \gamma ^{\pm }_{C,p}$ with ![]() $\gamma _{C,p}$ given as in equations (2.8.1), (2.8.2) and (2.8.3). From Mumford’s construction of the degenerating family over
$\gamma _{C,p}$ given as in equations (2.8.1), (2.8.2) and (2.8.3). From Mumford’s construction of the degenerating family over ![]() $\mathfrak {X}_{g,n,m}$, we see that the tuple (4.5.1), corresponds to a geometric point
$\mathfrak {X}_{g,n,m}$, we see that the tuple (4.5.1), corresponds to a geometric point ![]() $\bar {\eta }'$ over a generic point
$\bar {\eta }'$ over a generic point ![]() $\eta '$ of
$\eta '$ of ![]() $\mathfrak {X}_{g',n,m}$ with
$\mathfrak {X}_{g',n,m}$ with ![]() $g'=g\cdot \gamma _{C,p}$.
$g'=g\cdot \gamma _{C,p}$.
Proposition 4.5.1. The space ![]() is preserved by the
is preserved by the ![]() $\mathbb {U}_p$-operators.
$\mathbb {U}_p$-operators.
Proof. We shall show that ![]() $g'=g\cdot \gamma _{C,p}\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ only if
$g'=g\cdot \gamma _{C,p}\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ only if ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. By the definition of the
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. By the definition of the ![]() $\mathbb {U}_p$-operators, this will imply that if
$\mathbb {U}_p$-operators, this will imply that if ![]() vanishes along the strata outside
vanishes along the strata outside ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, then so does
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, then so does ![]() $U^{\bullet }_{p,j}(f)$. We use the description (4.3.1) for
$U^{\bullet }_{p,j}(f)$. We use the description (4.3.1) for ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. Consider the case
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. Consider the case ![]() $(\bullet ,j)=(+,2)$. Write
$(\bullet ,j)=(+,2)$. Write  $g^+_p=\left (\begin {smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end {smallmatrix}\right ) $ and
$g^+_p=\left (\begin {smallmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ &&&a_{44}\end {smallmatrix}\right ) $ and  $g^{\prime +}_p=g^+_p \cdot \gamma ^+_{C,p}= \left (\begin {smallmatrix}a^{\prime }_{11}&a^{\prime }_{12}&a^{\prime }_{13}&a^{\prime }_{14}\\ a^{\prime }_{21}&a^{\prime }_{22}&a^{\prime }_{23}&a^{\prime }_{24}\\ a^{\prime }_{31}&a^{\prime }_{32}&a^{\prime }_{33}&a^{\prime }_{34}\\ &&&a^{\prime }_{44}\end {smallmatrix}\right ) $ with
$g^{\prime +}_p=g^+_p \cdot \gamma ^+_{C,p}= \left (\begin {smallmatrix}a^{\prime }_{11}&a^{\prime }_{12}&a^{\prime }_{13}&a^{\prime }_{14}\\ a^{\prime }_{21}&a^{\prime }_{22}&a^{\prime }_{23}&a^{\prime }_{24}\\ a^{\prime }_{31}&a^{\prime }_{32}&a^{\prime }_{33}&a^{\prime }_{34}\\ &&&a^{\prime }_{44}\end {smallmatrix}\right ) $ with ![]() $\gamma ^+_{C,p}$ as in equation (2.8.1). We have
$\gamma ^+_{C,p}$ as in equation (2.8.1). We have
 $$ \begin{align} \begin{pmatrix}a^{\prime}_{11}&a^{\prime}_{12}&a^{\prime}_{13}&a^{\prime}_{14}\\ a^{\prime}_{21}&a^{\prime}_{22}&a^{\prime}_{23}&a^{\prime}_{24}\\ a^{\prime}_{31}&a^{\prime}_{32}&a^{\prime}_{33}&a^{\prime}_{34}\\ &&&a^{\prime}_{44}\end{pmatrix} = \begin{pmatrix}a_{11}&a_{12}&\frac{a_{13}+u_1a_{11}+u_2a_{12}}{p}&\ast\\ a_{21}&a_{22}&\frac{a_{23}+u_1a_{21}+u_2a_{22}}{p}&\ast\\ a_{31}&a_{32}&\frac{a_{33}+u_1a_{31}+u_2a_{32}}{p}&\ast\\ &&&\frac{a_{44}}{p}\end{pmatrix} \end{align} $$
$$ \begin{align} \begin{pmatrix}a^{\prime}_{11}&a^{\prime}_{12}&a^{\prime}_{13}&a^{\prime}_{14}\\ a^{\prime}_{21}&a^{\prime}_{22}&a^{\prime}_{23}&a^{\prime}_{24}\\ a^{\prime}_{31}&a^{\prime}_{32}&a^{\prime}_{33}&a^{\prime}_{34}\\ &&&a^{\prime}_{44}\end{pmatrix} = \begin{pmatrix}a_{11}&a_{12}&\frac{a_{13}+u_1a_{11}+u_2a_{12}}{p}&\ast\\ a_{21}&a_{22}&\frac{a_{23}+u_1a_{21}+u_2a_{22}}{p}&\ast\\ a_{31}&a_{32}&\frac{a_{33}+u_1a_{31}+u_2a_{32}}{p}&\ast\\ &&&\frac{a_{44}}{p}\end{pmatrix} \end{align} $$and
 $$ \begin{align} \begin{pmatrix}a^{\prime}_{21}&a^{\prime}_{22}\\a^{\prime}_{31}&a^{\prime}_{32}\end{pmatrix}^{-1}\begin{pmatrix}a^{\prime}_{23}\\a^{\prime}_{33}\end{pmatrix} =p^{-1}\left[\begin{pmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{pmatrix}^{-1}\begin{pmatrix}a_{23}\\a_{33}\end{pmatrix}+\begin{pmatrix}u_1\\u_2\end{pmatrix}\right]. \end{align} $$
$$ \begin{align} \begin{pmatrix}a^{\prime}_{21}&a^{\prime}_{22}\\a^{\prime}_{31}&a^{\prime}_{32}\end{pmatrix}^{-1}\begin{pmatrix}a^{\prime}_{23}\\a^{\prime}_{33}\end{pmatrix} =p^{-1}\left[\begin{pmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{pmatrix}^{-1}\begin{pmatrix}a_{23}\\a_{33}\end{pmatrix}+\begin{pmatrix}u_1\\u_2\end{pmatrix}\right]. \end{align} $$Since ![]() $u_1,u_2\in \mathbb {Z}_p$, the right-hand side can be integral only if
$u_1,u_2\in \mathbb {Z}_p$, the right-hand side can be integral only if ![]() $\left (\begin {smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end {smallmatrix}\right ) ^{-1}\left (\begin {smallmatrix}a_{23}\\a_{33}\end {smallmatrix}\right ) \in \mathbb {Z}^2_p$. Therefore,
$\left (\begin {smallmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end {smallmatrix}\right ) ^{-1}\left (\begin {smallmatrix}a_{23}\\a_{33}\end {smallmatrix}\right ) \in \mathbb {Z}^2_p$. Therefore, ![]() $g'=g\cdot \gamma _{C,p}\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ only if
$g'=g\cdot \gamma _{C,p}\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ only if ![]() $g \in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. The argument for the other two cases is similar.
$g \in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. The argument for the other two cases is similar.
Proposition 4.5.2. There exists a positive integer N such that the exact sequences in Proposition 4.4.1 are ![]() $(U^{\bullet }_{p,j})^N$-equivariant for
$(U^{\bullet }_{p,j})^N$-equivariant for ![]() $(\bullet ,j)=(+,2),(+,3),(-,1)$ in the sense that for all
$(\bullet ,j)=(+,2),(+,3),(-,1)$ in the sense that for all ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ and
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ and ![]() , we have
, we have
Proof. Take ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, and we use the setting described at the beginning of this subsection. In order to look at the image of
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, and we use the setting described at the beginning of this subsection. In order to look at the image of ![]() $U^{\bullet }_{p,j}f$ under the Siegel operator
$U^{\bullet }_{p,j}f$ under the Siegel operator ![]() $\Phi _g$, we consider the abelian quotients
$\Phi _g$, we consider the abelian quotients ![]() $\mathcal {A}_{\bar {\eta }}$ and
$\mathcal {A}_{\bar {\eta }}$ and ![]() $\mathcal {A}_{\bar {\eta }'}$ of the Raynaud extensions
$\mathcal {A}_{\bar {\eta }'}$ of the Raynaud extensions
Let
(See the beginning of §4.3 for the definition of ![]() $(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $ and
$(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $ and ![]() $(\mathcal {G}_{\bar {\eta }}[p^n])^{\mathrm {f}}$.) Then we have
$(\mathcal {G}_{\bar {\eta }}[p^n])^{\mathrm {f}}$.) Then we have
We use the description (4.1.3) and equation (4.3.2) for ![]() $C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ and
$C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ and ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. Write
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. Write ![]() $g=g^pg_p$ with
$g=g^pg_p$ with ![]() $g_p\in P_{\mathtt {D}}(\mathbb {Z}_p)$ and
$g_p\in P_{\mathtt {D}}(\mathbb {Z}_p)$ and
 $$ \begin{align} \begin{aligned} (g^{-1}_p)^+&=\left(\begin{smallmatrix}c_{11}&c_{12}&c_{13}&\ast\\c_{21}&c_{22}&c_{23}&\ast\\ c_{31}&c_{32}&c_{33}&\ast\\&&&\ast\end{smallmatrix}\right) , &(g^{-1}_p)^-&=\left(\begin{smallmatrix}d_{11}&\ast & \ast & \ast\\ &\ast & \ast & \ast\\&\ast & \ast & \ast\\&\ast & \ast & \ast\end{smallmatrix}\right). \end{aligned}\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} (g^{-1}_p)^+&=\left(\begin{smallmatrix}c_{11}&c_{12}&c_{13}&\ast\\c_{21}&c_{22}&c_{23}&\ast\\ c_{31}&c_{32}&c_{33}&\ast\\&&&\ast\end{smallmatrix}\right) , &(g^{-1}_p)^-&=\left(\begin{smallmatrix}d_{11}&\ast & \ast & \ast\\ &\ast & \ast & \ast\\&\ast & \ast & \ast\\&\ast & \ast & \ast\end{smallmatrix}\right). \end{aligned}\\[-15pt]\nonumber \end{align} $$The condition ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ implies that
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ implies that ![]() $c^{-1}_{31}c_{11},c^{-1}_{31}c_{21}\in \mathbb {Z}_p$. Thus, we see that
$c^{-1}_{31}c_{11},c^{-1}_{31}c_{21}\in \mathbb {Z}_p$. Thus, we see that ![]() $(\mathcal {G}_{\overline {\eta }}[p^n])^\mu $ is spanned by
$(\mathcal {G}_{\overline {\eta }}[p^n])^\mu $ is spanned by
(cf. equation (4.3.3)), and ![]() $(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$ is spanned by
$(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$ is spanned by
 $$ \begin{align} e^+_1,\quad e^+_2,\quad e^+_3,\quad e^-_1,\quad (e^-_2,e^-_3,e^-_4)\begin{pmatrix}-\iota_p(\bar{\zeta}_0)\\ &1\end{pmatrix}\begin{pmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end{pmatrix}.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} e^+_1,\quad e^+_2,\quad e^+_3,\quad e^-_1,\quad (e^-_2,e^-_3,e^-_4)\begin{pmatrix}-\iota_p(\bar{\zeta}_0)\\ &1\end{pmatrix}\begin{pmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end{pmatrix}.\\[-15pt]\nonumber \end{align} $$ We first consider the operator ![]() $U^+_{p,3}$. By a direct computation, we see that for
$U^+_{p,3}$. By a direct computation, we see that for ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, the p-part of
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, the p-part of ![]() $g'\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ is
$g'\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ is
 $$ \begin{align} g^{\prime+}_p=g^+_p\cdot\gamma^+_{C,p}=\left(\begin{smallmatrix}1&&&\ast\\ &1&&\ast\\ &&1&\ast\\&&&p^{-1} \end{smallmatrix}\right) g^+_p,\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} g^{\prime+}_p=g^+_p\cdot\gamma^+_{C,p}=\left(\begin{smallmatrix}1&&&\ast\\ &1&&\ast\\ &&1&\ast\\&&&p^{-1} \end{smallmatrix}\right) g^+_p,\\[-15pt]\nonumber \end{align} $$where ![]() $\ast \in \mathbb {Q}_p$. This shows that the cusp label
$\ast \in \mathbb {Q}_p$. This shows that the cusp label ![]() $g'$ is independent of C and belongs to
$g'$ is independent of C and belongs to ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. For given C spanned by
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. For given C spanned by ![]() $(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^{n-2}\gamma ^{\pm }_{C,p}$ with
$(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^{n-2}\gamma ^{\pm }_{C,p}$ with ![]() $\gamma _{C,p}^{\pm }$ as in (2.8.2), from the definition (4.5.4) and the basis (4.5.7) of
$\gamma _{C,p}^{\pm }$ as in (2.8.2), from the definition (4.5.4) and the basis (4.5.7) of ![]() $(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$, we see that
$(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$, we see that ![]() $C^{\mathrm {f}}$ is spanned by
$C^{\mathrm {f}}$ is spanned by
 $$\begin{align*}c^{-1}_{31}c_{11} e^+_1+c^{-1}_{31}c_{21}e^+_2+e^+_3,\quad e^-_1, \quad (e^-_2,e^-_3,e^-_4)\cdot p^{n-2}\begin{pmatrix}-\iota_p(\bar{\zeta}_0)\\ &1\end{pmatrix}\begin{pmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end{pmatrix}.\\[-15pt] \end{align*}$$
$$\begin{align*}c^{-1}_{31}c_{11} e^+_1+c^{-1}_{31}c_{21}e^+_2+e^+_3,\quad e^-_1, \quad (e^-_2,e^-_3,e^-_4)\cdot p^{n-2}\begin{pmatrix}-\iota_p(\bar{\zeta}_0)\\ &1\end{pmatrix}\begin{pmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end{pmatrix}.\\[-15pt] \end{align*}$$Its quotient ![]() $C^{\mathrm {ab}}$ is independent of the choice of C and is spanned by
$C^{\mathrm {ab}}$ is independent of the choice of C and is spanned by ![]() $(\epsilon ^-_1,\epsilon ^-_2)\cdot p^{n-2}$, with
$(\epsilon ^-_1,\epsilon ^-_2)\cdot p^{n-2}$, with ![]() $(\epsilon ^-_1,\epsilon ^-_2)$ the image of
$(\epsilon ^-_1,\epsilon ^-_2)$ the image of  $(e^-_2,e^-_3,e^-_4)\begin {pmatrix}-\iota _p(\bar {\zeta }_0)\\ &1\end {pmatrix}\left (\begin {smallmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end {smallmatrix}\right ) $under the quotient map
$(e^-_2,e^-_3,e^-_4)\begin {pmatrix}-\iota _p(\bar {\zeta }_0)\\ &1\end {pmatrix}\left (\begin {smallmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end {smallmatrix}\right ) $under the quotient map ![]() $\mathcal {G}^\natural _{\bar {\eta }}\rightarrow \mathcal {A}_{\bar {\eta }}$ which is a basis of
$\mathcal {G}^\natural _{\bar {\eta }}\rightarrow \mathcal {A}_{\bar {\eta }}$ which is a basis of ![]() $\mathcal {A}_{\bar {\eta }}[p^n]^-$. (Here, we identify
$\mathcal {A}_{\bar {\eta }}[p^n]^-$. (Here, we identify ![]() $(\mathcal {G}_{\bar {\eta }}[p^n])^{\mathrm {f}}$ with
$(\mathcal {G}_{\bar {\eta }}[p^n])^{\mathrm {f}}$ with ![]() $\mathcal {G}^\natural _{\bar {\eta }}[p^n]$ by the canonical isomorphism between them.) Thus, we get
$\mathcal {G}^\natural _{\bar {\eta }}[p^n]$ by the canonical isomorphism between them.) Thus, we get
Denote by ![]() $\left <p\right>^-$ the operator on
$\left <p\right>^-$ the operator on ![]() $M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$ induced by taking the quotient by
$M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$ induced by taking the quotient by ![]() $\mathcal {A}[p^2]^-$. Combining equations (4.5.8) and (4.5.9), we see that the trace cancels the normalizer in equation (2.8.5) due to the independence of the choice of C, and
$\mathcal {A}[p^2]^-$. Combining equations (4.5.8) and (4.5.9), we see that the trace cancels the normalizer in equation (2.8.5) due to the independence of the choice of C, and
With ![]() $K^p_f$ fixed, there exists
$K^p_f$ fixed, there exists ![]() $N_1\geq 1$, such that
$N_1\geq 1$, such that  $\left (\begin {smallmatrix} 1&&&\ast \\&1&&\ast \\&&1&\ast \\&&&p^{-N_1}\end {smallmatrix}\right ) _pg$ and g represent the same element in the double coset
$\left (\begin {smallmatrix} 1&&&\ast \\&1&&\ast \\&&1&\ast \\&&&p^{-N_1}\end {smallmatrix}\right ) _pg$ and g represent the same element in the double coset ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, and
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, and ![]() $(\left <p\right>^-)^{2N_1}=1$ on
$(\left <p\right>^-)^{2N_1}=1$ on ![]() $M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$. For such
$M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$. For such ![]() $N_1$, we deduce that
$N_1$, we deduce that
for all ![]() and
and ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. A similar calculation shows that that there exists
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. A similar calculation shows that that there exists ![]() $N_2\geq 1$ such that
$N_2\geq 1$ such that
for all ![]() and
and ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$.
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$.
It remains to consider ![]() $U^+_{p,2}$. Write
$U^+_{p,2}$. Write  $g^+_p=\left (\begin {smallmatrix}a_{11}&a_{12}&a_{13}&\ast \\a_{21}&a_{22}&a_{32}&\ast \\ a_{31}&a_{32}&a_{33}&\ast \\ &&&\ast \end {smallmatrix}\right ) $ and
$g^+_p=\left (\begin {smallmatrix}a_{11}&a_{12}&a_{13}&\ast \\a_{21}&a_{22}&a_{32}&\ast \\ a_{31}&a_{32}&a_{33}&\ast \\ &&&\ast \end {smallmatrix}\right ) $ and  $g^{\prime +}_p=g^+_p \cdot \gamma ^+_{C,p}= \left (\begin {smallmatrix}a^{\prime }_{11}&a^{\prime }_{12}&a^{\prime }_{13}&a^{\prime }_{14}\\ a^{\prime }_{21}&a^{\prime }_{22}&a^{\prime }_{23}&a^{\prime }_{24}\\ a^{\prime }_{31}&a^{\prime }_{32}&a^{\prime }_{33}&a^{\prime }_{34}\\ &&&a^{\prime }_{44}\end {smallmatrix}\right ) $ with
$g^{\prime +}_p=g^+_p \cdot \gamma ^+_{C,p}= \left (\begin {smallmatrix}a^{\prime }_{11}&a^{\prime }_{12}&a^{\prime }_{13}&a^{\prime }_{14}\\ a^{\prime }_{21}&a^{\prime }_{22}&a^{\prime }_{23}&a^{\prime }_{24}\\ a^{\prime }_{31}&a^{\prime }_{32}&a^{\prime }_{33}&a^{\prime }_{34}\\ &&&a^{\prime }_{44}\end {smallmatrix}\right ) $ with ![]() $\gamma _{C,p}^+$ as in (2.8.1). Then we have equations (4.5.2) and (4.5.3), and
$\gamma _{C,p}^+$ as in (2.8.1). Then we have equations (4.5.2) and (4.5.3), and ![]() $g'\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ if and only if
$g'\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ if and only if
 $$ \begin{align} \begin{pmatrix}u_1\\u_2\end{pmatrix}\equiv -\begin{pmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{pmatrix}^{-1}\begin{pmatrix}a_{23}\\a_{33}\end{pmatrix}\quad\mod p.\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} \begin{pmatrix}u_1\\u_2\end{pmatrix}\equiv -\begin{pmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{pmatrix}^{-1}\begin{pmatrix}a_{23}\\a_{33}\end{pmatrix}\quad\mod p.\\[-9pt]\nonumber \end{align} $$Now, suppose ![]() $g'\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, that is, the entries
$g'\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, that is, the entries ![]() $u_1,u_2$ in
$u_1,u_2$ in ![]() $\gamma ^{\pm }_{C,p}$ (see (2.8.1)) satisfy the congruence (4.5.10). Then we have
$\gamma ^{\pm }_{C,p}$ (see (2.8.1)) satisfy the congruence (4.5.10). Then we have  $ g^{\prime +}_p\in \left (\begin {smallmatrix}p^{-1}&\ast & \ast & \ast \\&1&&\ast \\&&1&\ast \\&&&p^{-1}\end {smallmatrix}\right ) g^+_p K^1_{p,n}, $and as an element in the double coset
$ g^{\prime +}_p\in \left (\begin {smallmatrix}p^{-1}&\ast & \ast & \ast \\&1&&\ast \\&&1&\ast \\&&&p^{-1}\end {smallmatrix}\right ) g^+_p K^1_{p,n}, $and as an element in the double coset ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$,
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, ![]() $g'$ represents the same element as
$g'$ represents the same element as  $\left (\begin {smallmatrix}p^{-1}&&&\\&1&&\\&&1&\\&&&p^{-1}\end {smallmatrix}\right ) g$ in
$\left (\begin {smallmatrix}p^{-1}&&&\\&1&&\\&&1&\\&&&p^{-1}\end {smallmatrix}\right ) g$ in ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. The congruence (4.5.10) implies that the
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. The congruence (4.5.10) implies that the ![]() $c_{ij}$’s in equation (4.5.5) satisfies
$c_{ij}$’s in equation (4.5.5) satisfies
From the definition (4.5.4) and the relation (4.5.11), by using the basis (4.5.7) of ![]() $(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$ and the basis of C in equation (2.8.1), we see that
$(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$ and the basis of C in equation (2.8.1), we see that ![]() $C^{\mathrm {f}}$ is spanned by
$C^{\mathrm {f}}$ is spanned by
 $$\begin{align*}c^{-1}_{31}c_{11} e^+_1+c^{-1}_{31}c_{21}e^+_2+e^+_3,\quad e^-_1, \quad (e^-_2,e^-_3,e^-_4)\cdot p^{n-2}\begin{pmatrix}-\iota_p(\bar{\zeta}_0)^{-1}\\ &1\end{pmatrix}\begin{pmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end{pmatrix}. \end{align*}$$
$$\begin{align*}c^{-1}_{31}c_{11} e^+_1+c^{-1}_{31}c_{21}e^+_2+e^+_3,\quad e^-_1, \quad (e^-_2,e^-_3,e^-_4)\cdot p^{n-2}\begin{pmatrix}-\iota_p(\bar{\zeta}_0)^{-1}\\ &1\end{pmatrix}\begin{pmatrix}0&1\\c^{-1}_{31}c_{11}&c^{-1}_{31}c_{21}\\1 &0\end{pmatrix}. \end{align*}$$Like in the case of ![]() $U^+_{p,3}$, we can deduce that
$U^+_{p,3}$, we can deduce that ![]() $C^{\mathrm {ab}}=\mathcal {A}_{\bar {\eta }}[p^n]^-$, and
$C^{\mathrm {ab}}=\mathcal {A}_{\bar {\eta }}[p^n]^-$, and
The independence of ![]() $C^{\mathrm {ab}}$ on the
$C^{\mathrm {ab}}$ on the ![]() $\ast $’s in
$\ast $’s in ![]() $\gamma ^+_{C,p}$ cancels the normalizer in equation (2.8.5), and we get
$\gamma ^+_{C,p}$ cancels the normalizer in equation (2.8.5), and we get
For fixed ![]() $K^p_f$, take
$K^p_f$, take ![]() $N_3$ such that
$N_3$ such that  $ \left (\begin {smallmatrix}p^{-1}&&&\\&1&&\\&&1&\\&&&p^{-1}\end {smallmatrix}\right ) ^{N_3}_pg $ and g represent the same element in the double coset
$ \left (\begin {smallmatrix}p^{-1}&&&\\&1&&\\&&1&\\&&&p^{-1}\end {smallmatrix}\right ) ^{N_3}_pg $ and g represent the same element in the double coset ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ and
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ and ![]() $(\left <p\right>^-)^{2N_3}=1$ on
$(\left <p\right>^-)^{2N_3}=1$ on ![]() $M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$. Then
$M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}/p^m\mathbb {Z})$. Then
for all ![]() and
and ![]() $g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. By taking
$g\in C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. By taking ![]() $N=N_1N_2N_3$, we conclude the proof.
$N=N_1N_2N_3$, we conclude the proof.
Proposition 4.5.3. ![]() $(U^+_{p,2})^mf\in V^{\flat }_{n,m}$ for all
$(U^+_{p,2})^mf\in V^{\flat }_{n,m}$ for all ![]() $f\in V_{n,m}$.
$f\in V_{n,m}$.
Proof. We shall show that for all ![]() $g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}- C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ and
$g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}- C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ and ![]() $f\in V_{n,m}$,
$f\in V_{n,m}$,
from which the proposition follows. For a given ![]() $g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}- C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, we use the setting described at the beginning of this subsection. As in the proof of Proposition 4.5.2, we consider
$g\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}- C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$, we use the setting described at the beginning of this subsection. As in the proof of Proposition 4.5.2, we consider ![]() $\mathcal {A}_{\bar {\eta }'}$, the abelian quotient of the Raynaud extension associated to
$\mathcal {A}_{\bar {\eta }'}$, the abelian quotient of the Raynaud extension associated to ![]() $\mathcal {G}_{\bar {\eta }'}=\mathcal {G}_{\bar {\eta }}/C$. We have
$\mathcal {G}_{\bar {\eta }'}=\mathcal {G}_{\bar {\eta }}/C$. We have
where ![]() $\mathcal {A}_{\bar {\eta }}$ is the abelian quotient of the Raynaud extension associated to
$\mathcal {A}_{\bar {\eta }}$ is the abelian quotient of the Raynaud extension associated to ![]() $\mathcal {G}_{\bar {\eta }}$, and
$\mathcal {G}_{\bar {\eta }}$, and ![]() $C^{\mathrm {ab}}$ is defined in equation (4.5.4). Since the
$C^{\mathrm {ab}}$ is defined in equation (4.5.4). Since the ![]() $\mathbb {U}_p$-operator considered here is
$\mathbb {U}_p$-operator considered here is ![]() $U^+_{p,2}$, the Lagrangian subgroup
$U^+_{p,2}$, the Lagrangian subgroup ![]() $C\subset \mathcal {G}_{\bar {\eta }}[p^2]$ is spanned by
$C\subset \mathcal {G}_{\bar {\eta }}[p^2]$ is spanned by ![]() $(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n \gamma ^{\pm }_{C,p}$ with
$(e^{\pm }_1,e^{\pm }_2,e^{\pm }_3,e^{\pm }_4)\cdot p^n \gamma ^{\pm }_{C,p}$ with ![]() $\gamma _{C,p}^{\pm }$ as in equation (2.8.1). We use the description (4.1.3) and equation (4.3.2) for
$\gamma _{C,p}^{\pm }$ as in equation (2.8.1). We use the description (4.1.3) and equation (4.3.2) for ![]() $C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ and
$C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ and ![]() $C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. Write
$C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$. Write  $(g^{-1}_p)^+=\left (\begin {smallmatrix}c_{11}&c_{12}&c_{13}&\ast \\c_{21}&c_{22}&c_{23}&\ast \\ c_{31}&c_{32}&c_{33}&\ast \\&&&\ast \end {smallmatrix}\right ) $,
$(g^{-1}_p)^+=\left (\begin {smallmatrix}c_{11}&c_{12}&c_{13}&\ast \\c_{21}&c_{22}&c_{23}&\ast \\ c_{31}&c_{32}&c_{33}&\ast \\&&&\ast \end {smallmatrix}\right ) $,  $(g^{-1}_p)^-=\left (\begin {smallmatrix}d_{11}&\ast & \ast & \ast \\ &\ast & \ast & \ast \\&\ast & \ast & \ast \\&\ast & \ast & \ast \end {smallmatrix}\right ) $(which are elements in
$(g^{-1}_p)^-=\left (\begin {smallmatrix}d_{11}&\ast & \ast & \ast \\ &\ast & \ast & \ast \\&\ast & \ast & \ast \\&\ast & \ast & \ast \end {smallmatrix}\right ) $(which are elements in ![]() $\operatorname {\mathrm {GL}}_4(\mathbb {Z}_p)$). The condition
$\operatorname {\mathrm {GL}}_4(\mathbb {Z}_p)$). The condition ![]() $g\notin C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ implies that
$g\notin C(K^p_fK^1_{p,n})^{\flat }_{\mathrm {ord}}$ implies that ![]() $c_{31}\in p\mathbb {Z}_p$ and
$c_{31}\in p\mathbb {Z}_p$ and ![]() $c_{11}$ or
$c_{11}$ or ![]() $c_{21}$ belongs to
$c_{21}$ belongs to ![]() $\mathbb {Z}^{\times }_p$.
$\mathbb {Z}^{\times }_p$.
Suppose ![]() $c_{11}\in \mathbb {Z}^{\times }_p$. The group
$c_{11}\in \mathbb {Z}^{\times }_p$. The group ![]() $(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $ is spanned by
$(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $ is spanned by
and ![]() $(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$ is spanned by
$(\mathcal {G}_{\overline {\eta }}[p^n])^{\mathrm {f}}$ is spanned by
 $$ \begin{align} e^+_1,\quad e^+_2,\quad e^+_3,\quad e^-_1,\quad (e^-_2,e^-_3,e^-_4)\begin{pmatrix}-\iota^c_p(\zeta_0)^{-1}\\ &1\end{pmatrix}\begin{pmatrix}c_{11}&0\\0&c_{11}\\-c_{21}&c_{31} \end{pmatrix}. \end{align} $$
$$ \begin{align} e^+_1,\quad e^+_2,\quad e^+_3,\quad e^-_1,\quad (e^-_2,e^-_3,e^-_4)\begin{pmatrix}-\iota^c_p(\zeta_0)^{-1}\\ &1\end{pmatrix}\begin{pmatrix}c_{11}&0\\0&c_{11}\\-c_{21}&c_{31} \end{pmatrix}. \end{align} $$By the definition of ![]() $C^{\mathrm {f}}$ in equation (4.5.4), a direct computation shows that
$C^{\mathrm {f}}$ in equation (4.5.4), a direct computation shows that ![]() $C^{\mathrm {f}}$ is spanned by
$C^{\mathrm {f}}$ is spanned by ![]() $(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $ plus
$(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $ plus
 $$ \begin{align} \left((c_{11}u_2-c_{21}u_1)e^+_2+c_{11} e^+_3\right)\cdot p^{n-1}, \quad (e^-_2,e^-_3,e^-_4)\begin{pmatrix}-\iota^c_p(\zeta_0)^{-1}\\ &1\end{pmatrix}\begin{pmatrix}c_{11}&0\\0&c_{11}\\-c_{21}&c_{31} \end{pmatrix} \begin{pmatrix}c_{11}&0\\c_{11}u_2-c_{21}u_1&p\end{pmatrix}. \end{align} $$
$$ \begin{align} \left((c_{11}u_2-c_{21}u_1)e^+_2+c_{11} e^+_3\right)\cdot p^{n-1}, \quad (e^-_2,e^-_3,e^-_4)\begin{pmatrix}-\iota^c_p(\zeta_0)^{-1}\\ &1\end{pmatrix}\begin{pmatrix}c_{11}&0\\0&c_{11}\\-c_{21}&c_{31} \end{pmatrix} \begin{pmatrix}c_{11}&0\\c_{11}u_2-c_{21}u_1&p\end{pmatrix}. \end{align} $$Hence, ![]() $C^{\mathrm {ab}}$ is spanned by the image of equation (4.5.15) modulo
$C^{\mathrm {ab}}$ is spanned by the image of equation (4.5.15) modulo ![]() $(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $. Let
$(\mathcal {G}_{\bar {\eta }}[p^n])^\mu $. Let ![]() $u^{\prime }_2=c_{11}u_2-c_{21}u_1$. The trace in equation (2.8.5) corresponds to a sum with
$u^{\prime }_2=c_{11}u_2-c_{21}u_1$. The trace in equation (2.8.5) corresponds to a sum with ![]() $u_1,u^{\prime }_2$ and the two
$u_1,u^{\prime }_2$ and the two ![]() $\ast $’s in
$\ast $’s in ![]() $\gamma _{C,p}$ varying in
$\gamma _{C,p}$ varying in ![]() $\mathbb {Z}/p\mathbb {Z}$. Since equation (4.5.15) depends only on
$\mathbb {Z}/p\mathbb {Z}$. Since equation (4.5.15) depends only on ![]() $u^{\prime }_2$, we see that
$u^{\prime }_2$, we see that ![]() $C^{\mathrm {ab}}$, and hence
$C^{\mathrm {ab}}$, and hence ![]() $\mathcal {A}_{\bar {\eta }'}$ depends only on
$\mathcal {A}_{\bar {\eta }'}$ depends only on ![]() $u^{\prime }_2$. Its independence of the two
$u^{\prime }_2$. Its independence of the two ![]() $\ast $’s implies that the sum over the two
$\ast $’s implies that the sum over the two ![]() $\ast $’s cancels the normalization factor in equation (2.8.5). Its independence of
$\ast $’s cancels the normalization factor in equation (2.8.5). Its independence of ![]() $u_1$ implies that the sum over
$u_1$ implies that the sum over ![]() $u_1$ contributes a factor p. Therefore, the evaluation of
$u_1$ contributes a factor p. Therefore, the evaluation of ![]() $\Phi _g\left (U^+_{p,2}f\right )$ at
$\Phi _g\left (U^+_{p,2}f\right )$ at ![]() $\bar {\eta }'$ is divisible by p. This shows the inclusion (4.5.12), hence the result in this case. The case
$\bar {\eta }'$ is divisible by p. This shows the inclusion (4.5.12), hence the result in this case. The case ![]() $c_{21}\in \mathbb {Z}^{\times }_p$ can be similarly treated.
$c_{21}\in \mathbb {Z}^{\times }_p$ can be similarly treated.
4.6 The ordinary projection on  and the fundamental exact sequence
and the fundamental exact sequence
In this section, we use the exact sequence in Proposition 4.4.1 and the three propositions proved in §4.5 to show that ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ converges for all
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ converges for all ![]() and that
and that ![]() is a free
is a free ![]() $\Lambda _{\mathrm {so}}$-module of finite rank and deduce the fundamental exact sequence in part (4) of Theorem 2.9.1.
$\Lambda _{\mathrm {so}}$-module of finite rank and deduce the fundamental exact sequence in part (4) of Theorem 2.9.1.
Theorem 4.6.1 (Vertical control theorem).
Let ![]() $U_p=U^+_{p,2}U^+_{p,3}U^-_{p,1}$. Then for each
$U_p=U^+_{p,2}U^+_{p,3}U^-_{p,1}$. Then for each ![]() ,
, ![]() $\lim \limits _{r\to \infty }(U_p)^{r!}f$ converges, and we can define the semiordinary projector as
$\lim \limits _{r\to \infty }(U_p)^{r!}f$ converges, and we can define the semiordinary projector as ![]() $e_{\mathrm {so}}=\lim \limits _{r\to \infty }(U_p)^{r!}$. The
$e_{\mathrm {so}}=\lim \limits _{r\to \infty }(U_p)^{r!}$. The ![]() $\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module
$\mathbb {Z}_p[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module ![]() is free of finite rank over
is free of finite rank over ![]() $\Lambda _{\mathrm {so}}$.
$\Lambda _{\mathrm {so}}$.
Proof. Given ![]() $f\in V_{n,m}$, we define the following finiteness property for f:
$f\in V_{n,m}$, we define the following finiteness property for f:
It is easy to see that the convergence of ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ follows from the property (F) for f. By Proposition 4.5.3, in order to show that all
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ follows from the property (F) for f. By Proposition 4.5.3, in order to show that all ![]() $f\in V_{n,m}$ satisfy (F), it suffices to show that all
$f\in V_{n,m}$ satisfy (F), it suffices to show that all ![]() $f\in V^{\flat }_{n,m}$ satisfy (F). Given
$f\in V^{\flat }_{n,m}$ satisfy (F). Given ![]() $f\in V^{\flat }_{n,m}$, it follows from Proposition 4.5.2 that
$f\in V^{\flat }_{n,m}$, it follows from Proposition 4.5.2 that ![]() $f'=U^N_pf-f$ belongs to
$f'=U^N_pf-f$ belongs to ![]() $V^0_{n,m}$. Proposition 3.0.2 implies that there exists
$V^0_{n,m}$. Proposition 3.0.2 implies that there exists ![]() $M\geq 0$ such that
$M\geq 0$ such that
Then
from which it follows that for all ![]() $r\geq 0$,
$r\geq 0$,
Hence, (F) holds for f. Therefore, we have proved that ![]() $\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ converges for all
$\lim \limits _{r\rightarrow \infty }(U_p)^{r!}f$ converges for all ![]() , and we can define the semiordinary projector
, and we can define the semiordinary projector ![]() $e_{\mathrm {so}}$ on
$e_{\mathrm {so}}$ on ![]() as
as
By Proposition 4.5.3, we have
Applying ![]() $e_{\mathrm {so}}$ to the Pontryagin dual of the exact sequence in Proposition 4.4.1 and using equation (4.6.2), we obtain the exact sequence
$e_{\mathrm {so}}$ to the Pontryagin dual of the exact sequence in Proposition 4.4.1 and using equation (4.6.2), we obtain the exact sequence
We know that ![]() $M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}_p)$ is a free
$M_{(0,0)}(K^{\prime }_{f,g};\mathbb {Z}_p)$ is a free ![]() $\mathbb {Z}_p$-module of finite rank, so the leftmost term in equation (4.6.3) is a free
$\mathbb {Z}_p$-module of finite rank, so the leftmost term in equation (4.6.3) is a free ![]() $\Lambda _{\mathrm {so}}$-module of finite rank. The rightmost term
$\Lambda _{\mathrm {so}}$-module of finite rank. The rightmost term ![]() is also a free
is also a free ![]() $\Lambda _{\mathrm {so}}$-module of finite rank by Theorem 3.0.7. Since
$\Lambda _{\mathrm {so}}$-module of finite rank by Theorem 3.0.7. Since ![]() $\mathrm {Ext}^1_{\Lambda _{\mathrm {so}}}(M,N)$ vanishes for free
$\mathrm {Ext}^1_{\Lambda _{\mathrm {so}}}(M,N)$ vanishes for free ![]() $\Lambda _{\mathrm {so}}$-modules M, we deduce that
$\Lambda _{\mathrm {so}}$-modules M, we deduce that ![]() , as a
, as a ![]() $\Lambda _{\mathrm {so}}$-module, is isomorphic to the direct sum of the terms on the two ends of equation (4.6.3) and therefore is a free
$\Lambda _{\mathrm {so}}$-module, is isomorphic to the direct sum of the terms on the two ends of equation (4.6.3) and therefore is a free ![]() $\Lambda _{\mathrm {so}}$-module of finite rank.
$\Lambda _{\mathrm {so}}$-module of finite rank.
Part (2) of Theorem 2.9.1 for noncuspidal semiordinary families can be proved in the same way as the cuspidal semiordinary families. The freeness of ![]() implies that applying
implies that applying ![]() $\operatorname {\mathrm {Hom}}_{\Lambda _{\mathrm {so}}}(\,\cdot \,,\Lambda _{\mathrm {so}})$ preserves the exactness of equation (4.6.3), and part (4) of Theorem 2.9.1 follows.
$\operatorname {\mathrm {Hom}}_{\Lambda _{\mathrm {so}}}(\,\cdot \,,\Lambda _{\mathrm {so}})$ preserves the exactness of equation (4.6.3), and part (4) of Theorem 2.9.1 follows.
4.7 The Fourier–Jacobi expansion
We introduce the Fourier–Jacobi expansions of p-adic forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$, which will be used in §7 for analyzing the Klingen Eisenstein family on
$\operatorname {\mathrm {GU}}(3,1)$, which will be used in §7 for analyzing the Klingen Eisenstein family on ![]() $\operatorname {\mathrm {GU}}(3,1)$ constructed in §5.
$\operatorname {\mathrm {GU}}(3,1)$ constructed in §5.
In §4.2, for an ordinary cusp label ![]() $g\in C(K^p_f K^1_{p,n})_{\mathrm {ord}}$, we described
$g\in C(K^p_f K^1_{p,n})_{\mathrm {ord}}$, we described ![]() $\mathfrak {X}_{g,n}$, the formal completion of
$\mathfrak {X}_{g,n}$, the formal completion of ![]() $\mathscr {T}^{\mathrm {tor}}_n$ along the boundary stratum
$\mathscr {T}^{\mathrm {tor}}_n$ along the boundary stratum ![]() $\mathscr {Z}_{g,n}$. From the description there, we see that
$\mathscr {Z}_{g,n}$. From the description there, we see that
 $$\begin{align*}H^0\left(\mathfrak{X}_{g,n},\mathcal{O}_{\mathfrak{X}_{g,n}}\right)=\left(\prod_{\beta} H^0\left(\mathscr{C}^{\mathrm{ord}}_{g,n},\mathcal{L}(\beta)\right)\right)^{\Gamma_g}, \end{align*}$$
$$\begin{align*}H^0\left(\mathfrak{X}_{g,n},\mathcal{O}_{\mathfrak{X}_{g,n}}\right)=\left(\prod_{\beta} H^0\left(\mathscr{C}^{\mathrm{ord}}_{g,n},\mathcal{L}(\beta)\right)\right)^{\Gamma_g}, \end{align*}$$where ![]() $\beta $ runs over
$\beta $ runs over ![]() $\mathbf {S}^{\vee }_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}\cap \mathbf {P}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}$, which can be identified with a subset of
$\mathbf {S}^{\vee }_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}\cap \mathbf {P}_{\Phi ^{(g)}_{K^p_fK^1_{p,n}}}$, which can be identified with a subset of ![]() $\operatorname {\mathrm {Her}}_1(\mathcal {K})_{\geq 0}$, and
$\operatorname {\mathrm {Her}}_1(\mathcal {K})_{\geq 0}$, and ![]() $\mathcal {L}(\beta )$ is the invertible sheaf over
$\mathcal {L}(\beta )$ is the invertible sheaf over ![]() $\mathscr {C}^{\mathrm {ord}}_{g,n}$ of
$\mathscr {C}^{\mathrm {ord}}_{g,n}$ of ![]() $\beta $-homogeneous functions on
$\beta $-homogeneous functions on ![]() $\Xi ^{\mathrm {ord}}_{g,n}$. Therefore, given
$\Xi ^{\mathrm {ord}}_{g,n}$. Therefore, given ![]() $g\in C(K^p_f K^1_{p,n})_{\mathrm {ord}}$ and
$g\in C(K^p_f K^1_{p,n})_{\mathrm {ord}}$ and ![]() $\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{\geq 0}$, the restriction to
$\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{\geq 0}$, the restriction to ![]() $\mathfrak {X}_{g,n}$ induces a map
$\mathfrak {X}_{g,n}$ induces a map
We consider ![]() $g=\mathbf {1}_4$ and
$g=\mathbf {1}_4$ and ![]() $\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{\geq 0}$. In this case, the p-component of level group for the Shimura variety
$\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{\geq 0}$. In this case, the p-component of level group for the Shimura variety ![]() $\mathscr {S}_{G',K^{\prime }_{f,\mathbf {1}_4,n}}$ in the diagram (4.2.2) is
$\mathscr {S}_{G',K^{\prime }_{f,\mathbf {1}_4,n}}$ in the diagram (4.2.2) is
 $$\begin{align*}K^{\prime}_{p,\mathbf{1}_4,n}=\left\{g\in \operatorname{\mathrm{GU}}(2)(\mathbb{Z}_p):g^+\equiv \begin{pmatrix}\ast & \ast\\0&1\end{pmatrix}\quad\mod p^n\right\}, \end{align*}$$
$$\begin{align*}K^{\prime}_{p,\mathbf{1}_4,n}=\left\{g\in \operatorname{\mathrm{GU}}(2)(\mathbb{Z}_p):g^+\equiv \begin{pmatrix}\ast & \ast\\0&1\end{pmatrix}\quad\mod p^n\right\}, \end{align*}$$(depending on n). Let
The map gives the map of taking the ![]() $\beta $-th Fourier–Jacobi coefficient of p-adic forms on
$\beta $-th Fourier–Jacobi coefficient of p-adic forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$ along the boundary stratum labeled by
$\operatorname {\mathrm {GU}}(3,1)$ along the boundary stratum labeled by ![]() $\mathbf {1}_4$:
$\mathbf {1}_4$:
5 The construction of the Klingen family
5.1 Some notation
Let ![]() ${\mathcal {K}_{\infty }}$ be the maximal abelian pro-p extension of
${\mathcal {K}_{\infty }}$ be the maximal abelian pro-p extension of ![]() $\mathcal {K}$ unramified outside p and
$\mathcal {K}$ unramified outside p and ![]() ${\Gamma _{\mathcal {K}}}=\operatorname {\mathrm {Gal}}(\mathcal {K}_{\infty }/\mathcal {K})$. Then
${\Gamma _{\mathcal {K}}}=\operatorname {\mathrm {Gal}}(\mathcal {K}_{\infty }/\mathcal {K})$. Then ![]() $\Gamma _{\mathcal {K}}\cong \mathbb {Z}^2_p$. Denote by
$\Gamma _{\mathcal {K}}\cong \mathbb {Z}^2_p$. Denote by ![]() ${\Omega _{\infty }}\in \mathbb {C}^{\times }$ (resp.
${\Omega _{\infty }}\in \mathbb {C}^{\times }$ (resp. ![]() ${\Omega _p}\in \hat {\mathbb {Z}}^{\mathrm {ur},\times }_p$) the complex complex multiplication (CM) period (p-adic CM period) with respect to the embeddings in equation (1.0.4) (cf. [Reference HsiehHsi14a, Section 2.8]). We also fix an isomorphism
${\Omega _p}\in \hat {\mathbb {Z}}^{\mathrm {ur},\times }_p$) the complex complex multiplication (CM) period (p-adic CM period) with respect to the embeddings in equation (1.0.4) (cf. [Reference HsiehHsi14a, Section 2.8]). We also fix an isomorphism ![]() $\overline {\mathbb {Q}}_p\cong \mathbb {C}$ compatible with the embeddings in equation (1.0.4). Let
$\overline {\mathbb {Q}}_p\cong \mathbb {C}$ compatible with the embeddings in equation (1.0.4). Let ![]() ${L}\subset \overline {\mathbb {Q}}_p$ be a sufficiently large finite extension of
${L}\subset \overline {\mathbb {Q}}_p$ be a sufficiently large finite extension of ![]() $\mathbb {Q}_p$, and denote by
$\mathbb {Q}_p$, and denote by ![]() ${\hat {\mathcal {O}}^{\mathrm {ur}}_L}$ the ring of integers of the completion of the maximal unramified extension of L.
${\hat {\mathcal {O}}^{\mathrm {ur}}_L}$ the ring of integers of the completion of the maximal unramified extension of L.
For our later use of theta correspondence for unitary groups, we also fix a Hecke character
such that
5.2 Our setup
Let ![]() ${\pi }$ be an irreducible cuspidal automorphic representation of
${\pi }$ be an irreducible cuspidal automorphic representation of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$ generated by a newform
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{\mathbb {Q}})$ generated by a newform ![]() ${f}$ of weight
${f}$ of weight ![]() $2$. Take a finite extension L of
$2$. Take a finite extension L of ![]() $\mathbb {Q}_p$ containing all the Hecke eigenvalues of f. We assume the following conditions on
$\mathbb {Q}_p$ containing all the Hecke eigenvalues of f. We assume the following conditions on ![]() $\pi $:
$\pi $:
• for all finite places v of
 $\mathbb {Q}$,
$\mathbb {Q}$,  $\pi _v$ is either unramified or Steinberg or Steinberg twisted by an unramified quadratic character of
$\pi _v$ is either unramified or Steinberg or Steinberg twisted by an unramified quadratic character of  $\mathbb {Q}^{\times }_v$,
$\mathbb {Q}^{\times }_v$,•
 $\pi _p$ is unramified,
$\pi _p$ is unramified,• there exists a prime q not split in
 $\mathcal {K}$ such that
$\mathcal {K}$ such that  $\pi $ is ramified at q, and if
$\pi $ is ramified at q, and if  $2$ does not split in
$2$ does not split in  $\mathcal {K}$, then
$\mathcal {K}$, then  $\pi $ is ramified at
$\pi $ is ramified at  $2$,
$2$,•
 $\bar {\rho }_{\pi }|_{\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})}$ is irreducible, (which is automatically true if
$\bar {\rho }_{\pi }|_{\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})}$ is irreducible, (which is automatically true if  $\pi $ is not ordinary at p because in this case
$\pi $ is not ordinary at p because in this case  $\bar {\rho }_{\pi }|_{G_{\mathcal {K}},\mathfrak {p}}\cong \bar {\rho }_{\pi }|_{G_{\mathbb {Q},p}}$ is irreducible by [Reference EdixhovenEdi92]), where
$\bar {\rho }_{\pi }|_{G_{\mathcal {K}},\mathfrak {p}}\cong \bar {\rho }_{\pi }|_{G_{\mathbb {Q},p}}$ is irreducible by [Reference EdixhovenEdi92]), where  $\bar {\rho }_{\pi }$ denotes the residual representation of the p-adic Galois representation
$\bar {\rho }_{\pi }$ denotes the residual representation of the p-adic Galois representation  $\rho _{\pi }:\operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q})\rightarrow \operatorname {\mathrm {GL}}_2(L)$.
$\rho _{\pi }:\operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q})\rightarrow \operatorname {\mathrm {GL}}_2(L)$.
We also fix
• an algebraic Hecke character
 ${\xi }:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of
${\xi }:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of  $\infty $-type
$\infty $-type  $\left (0,k_0\right )$ with
$\left (0,k_0\right )$ with  ${k_0}$ an even integer.
${k_0}$ an even integer.
5.3 The weight space
The weight space we will use for constructing the semiordinary Klingen Eisenstein family on ![]() $\operatorname {\mathrm {GU}}(3,1)$ is
$\operatorname {\mathrm {GU}}(3,1)$ is ![]() $\operatorname {\mathrm {Hom}}_{\mathrm {cont}}\big (\Gamma _{\mathcal {K}},\overline {\mathbb {Q}}^{\times }_p\big )$. By identifying
$\operatorname {\mathrm {Hom}}_{\mathrm {cont}}\big (\Gamma _{\mathcal {K}},\overline {\mathbb {Q}}^{\times }_p\big )$. By identifying ![]() $\Gamma _{\mathcal {K}}$ with a quotient of
$\Gamma _{\mathcal {K}}$ with a quotient of ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K},f}$, the arithmetic points in the weight space are p-adic avatars of the algebraic Hecke characters of
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K},f}$, the arithmetic points in the weight space are p-adic avatars of the algebraic Hecke characters of ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ whose p-adic avatars factor through
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ whose p-adic avatars factor through ![]() $\Gamma _{\mathcal {K}}$. (Given an algebraic Hecke character
$\Gamma _{\mathcal {K}}$. (Given an algebraic Hecke character ![]() $\chi :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of
$\chi :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of ![]() $\infty $-type
$\infty $-type ![]() $(k_1,k_2)$, its p-adic avatar is the continuous character
$(k_1,k_2)$, its p-adic avatar is the continuous character ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K},f}\longrightarrow \overline {\mathbb {Q}}^{\times }_p$ sending x to
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K},f}\longrightarrow \overline {\mathbb {Q}}^{\times }_p$ sending x to ![]() $\chi (x)x^{k_1}_{\mathfrak {p}} x^{k_2}_{\bar {\mathfrak {p}}}$.) We will use
$\chi (x)x^{k_1}_{\mathfrak {p}} x^{k_2}_{\bar {\mathfrak {p}}}$.) We will use ![]() ${\tau }$ to denote such Hecke characters.
${\tau }$ to denote such Hecke characters.
Given an algebraic Hecke character ![]() $\chi $, we denote by
$\chi $, we denote by ![]() $\chi _0$ its associated unitary Hecke character, that is,
$\chi _0$ its associated unitary Hecke character, that is,
and denote by ![]() $\chi _{p\text {-}\mathrm {adic}}$ its p-adic avatar. Applying this convention to
$\chi _{p\text {-}\mathrm {adic}}$ its p-adic avatar. Applying this convention to ![]() $\xi , \tau $, we get
$\xi , \tau $, we get ![]() ${\xi _0}$,
${\xi _0}$, ![]() ${\xi _{p\text {-}\mathrm {adic}}}$,
${\xi _{p\text {-}\mathrm {adic}}}$, ![]() ${\tau _0}$,
${\tau _0}$, ![]() ${\tau _{p\text {-}\mathrm {adic}}}$.
${\tau _{p\text {-}\mathrm {adic}}}$.
The interpolation points we will use are the ![]() $\tau $’s satisfying that
$\tau $’s satisfying that ![]() $\xi \tau $ has
$\xi \tau $ has ![]() $\infty $-type
$\infty $-type ![]() $(0,k)$ with k an even integer
$(0,k)$ with k an even integer ![]() $\geq 6$. (One can consider more general
$\geq 6$. (One can consider more general ![]() $\infty $-types by using Masss–Shimura differential operators. For our purpose here, only considering the case of
$\infty $-types by using Masss–Shimura differential operators. For our purpose here, only considering the case of ![]() $\infty $-type
$\infty $-type ![]() $(0,k)$ suffices.)
$(0,k)$ suffices.)
5.4 The groups
By the assumption on ![]() $\pi $ in §5.2, we can fix a prime
$\pi $ in §5.2, we can fix a prime ![]() ${q}$ such that
${q}$ such that
 $$\begin{align*}\left\{\begin{array}{ll} q \text{ does not split in } \mathcal{K} \text{ and } \pi_q \text{ is ramified}, &\text{if } 2 \text{ splits in } \mathcal{K},\\ q=2, &\text{if } 2 \text{ does not split in } \mathcal{K}. \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{\begin{array}{ll} q \text{ does not split in } \mathcal{K} \text{ and } \pi_q \text{ is ramified}, &\text{if } 2 \text{ splits in } \mathcal{K},\\ q=2, &\text{if } 2 \text{ does not split in } \mathcal{K}. \end{array} \right. \end{align*}$$Let ![]() ${D}$ be the quaternion algebra over
${D}$ be the quaternion algebra over ![]() $\mathbb {Q}$ ramified exactly at q and
$\mathbb {Q}$ ramified exactly at q and ![]() $\infty $, and let
$\infty $, and let ![]() $\pi ^D$ be the Jacquet–Langlands transfer of
$\pi ^D$ be the Jacquet–Langlands transfer of ![]() $\pi $ to
$\pi $ to ![]() $D^{\times }(\mathbb {A}_{\mathbb {Q}})$.
$D^{\times }(\mathbb {A}_{\mathbb {Q}})$.
We can take a square free positive integer ![]() ${\mathfrak {s}}$, coprime to
${\mathfrak {s}}$, coprime to ![]() $pD_{\mathcal {K}/\mathbb {Q}}$ and all the primes inert in
$pD_{\mathcal {K}/\mathbb {Q}}$ and all the primes inert in ![]() $\mathcal {K}$ where D splits such that
$\mathcal {K}$ where D splits such that ![]() $\mathrm {inv}_v(D)=(-\mathfrak {s},D_{\mathcal {K}/\mathbb {Q}})_v$, where
$\mathrm {inv}_v(D)=(-\mathfrak {s},D_{\mathcal {K}/\mathbb {Q}})_v$, where
is the Hilbert symbol. Define  ${\zeta _0}=\delta \begin {pmatrix}\mathfrak {s}\\&1\end {pmatrix}$ with
${\zeta _0}=\delta \begin {pmatrix}\mathfrak {s}\\&1\end {pmatrix}$ with ![]() $\delta $ the totally imaginary element in
$\delta $ the totally imaginary element in ![]() $\mathcal {K}$ with
$\mathcal {K}$ with ![]() $\delta ^2$ a p-adic unit as fixed in Notation. This
$\delta ^2$ a p-adic unit as fixed in Notation. This ![]() $\zeta _0$ is a skew-Hermitian matrix. Define the unitary group
$\zeta _0$ is a skew-Hermitian matrix. Define the unitary group ![]() $\operatorname {\mathrm {U}}(2)$ (resp. similitude unitary group
$\operatorname {\mathrm {U}}(2)$ (resp. similitude unitary group ![]() $\operatorname {\mathrm {GU}}(2)$) over
$\operatorname {\mathrm {GU}}(2)$) over ![]() $\mathbb {Z}$ as: for all
$\mathbb {Z}$ as: for all ![]() $\mathbb {Z}$-algebra R,
$\mathbb {Z}$-algebra R,
We have

and we view both ![]() $D^{\times }$ and
$D^{\times }$ and ![]() $\operatorname {\mathrm {GU}}(2)$ as subgroups of
$\operatorname {\mathrm {GU}}(2)$ as subgroups of ![]() $\mathrm {Res}_{\mathcal {K}/\mathbb {Q}}\operatorname {\mathrm {GL}}_2(\mathcal {K})$. Then the homomorphism
$\mathrm {Res}_{\mathcal {K}/\mathbb {Q}}\operatorname {\mathrm {GL}}_2(\mathcal {K})$. Then the homomorphism
induces an isomorphism
Given an automorphic form on ![]() $\phi $ on
$\phi $ on ![]() $D^{\times }$ with central character
$D^{\times }$ with central character ![]() $\chi _1$, by picking an extension
$\chi _1$, by picking an extension ![]() $\chi $ of
$\chi $ of ![]() $\chi _1$ to
$\chi _1$ to ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$, one obtains an automorphic form
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$, one obtains an automorphic form ![]() $\phi ^{\operatorname {\mathrm {GU}}(2)}$ on
$\phi ^{\operatorname {\mathrm {GU}}(2)}$ on ![]() $\operatorname {\mathrm {GU}}(2)$ by equation (5.4.3).
$\operatorname {\mathrm {GU}}(2)$ by equation (5.4.3).
We denote by ![]() ${\pi ^{D}}$ the Jacquet–Langlands transfer of
${\pi ^{D}}$ the Jacquet–Langlands transfer of ![]() $\pi $ to
$\pi $ to ![]() $D^{\times }$, and by
$D^{\times }$, and by ![]() ${f^D}$ the unique automorphic form on
${f^D}$ the unique automorphic form on ![]() $D^{\times }$ which is a newform for the action of
$D^{\times }$ which is a newform for the action of ![]() $D^{\times }(\mathbb {Q}_v)\simeq \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ for all
$D^{\times }(\mathbb {Q}_v)\simeq \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ for all ![]() $v\neq q,\infty $ and takes value
$v\neq q,\infty $ and takes value ![]() $1$ at
$1$ at ![]() $\mathbf {1}_2$. By our assumption,
$\mathbf {1}_2$. By our assumption, ![]() $\pi ^D$ has trivial central character. We can extend
$\pi ^D$ has trivial central character. We can extend ![]() $f^D$ to a form
$f^D$ to a form ![]() ${f^{\operatorname {\mathrm {GU}}(2)}}$ via equation (5.4.3) and the trivial character and denote by
${f^{\operatorname {\mathrm {GU}}(2)}}$ via equation (5.4.3) and the trivial character and denote by ![]() ${\pi ^{\operatorname {\mathrm {GU}}(2)}}$ the automorphic representation of
${\pi ^{\operatorname {\mathrm {GU}}(2)}}$ the automorphic representation of ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ generated by
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ generated by ![]() $f^{\operatorname {\mathrm {GU}}(2)}$.
$f^{\operatorname {\mathrm {GU}}(2)}$.
Define the unitary group ![]() $\operatorname {\mathrm {U}}(3,1)$ (resp. similitude unitary group
$\operatorname {\mathrm {U}}(3,1)$ (resp. similitude unitary group ![]() $\operatorname {\mathrm {GU}}(3,1)$) over
$\operatorname {\mathrm {GU}}(3,1)$) over ![]() $\mathbb {Z}$ as
$\mathbb {Z}$ as

Let
 $$ \begin{align} {P_{\operatorname{\mathrm{GU}}(3,1)}} =\left\{\begin{pmatrix}x&\ast & \ast\\ &g&\ast\\&&\nu(g)\bar{x}^{-1}\end{pmatrix}\in\operatorname{\mathrm{GU}}(3,1): g\in \operatorname{\mathrm{GU}}(2),\,\,x\in \mathrm{Res}_{\mathcal{K}/\mathbb{Q}}\mathbb{G}_m\right\}, \end{align} $$
$$ \begin{align} {P_{\operatorname{\mathrm{GU}}(3,1)}} =\left\{\begin{pmatrix}x&\ast & \ast\\ &g&\ast\\&&\nu(g)\bar{x}^{-1}\end{pmatrix}\in\operatorname{\mathrm{GU}}(3,1): g\in \operatorname{\mathrm{GU}}(2),\,\,x\in \mathrm{Res}_{\mathcal{K}/\mathbb{Q}}\mathbb{G}_m\right\}, \end{align} $$the (standard) Klingen parabolic subgroup of ![]() $\operatorname {\mathrm {GU}}(3,1)$. Its Levi subgroup is
$\operatorname {\mathrm {GU}}(3,1)$. Its Levi subgroup is
(Over ![]() $\mathbb {Q}$, the groups
$\mathbb {Q}$, the groups ![]() $\operatorname {\mathrm {GU}}(2)$ and
$\operatorname {\mathrm {GU}}(2)$ and ![]() $\operatorname {\mathrm {GU}}(3,1)$ are the same as the groups defined in equation (2.1.1) written with respect to the basis
$\operatorname {\mathrm {GU}}(3,1)$ are the same as the groups defined in equation (2.1.1) written with respect to the basis ![]() $\mathtt {w_1,w_2}$ and
$\mathtt {w_1,w_2}$ and ![]() $\mathtt {x_1,w_1,w_2,y_1}$.)
$\mathtt {x_1,w_1,w_2,y_1}$.)
Define the unitary group ![]() $\operatorname {\mathrm {U}}(1)$ over
$\operatorname {\mathrm {U}}(1)$ over ![]() $\mathbb {Z}$ by
$\mathbb {Z}$ by
The projection ![]() $\varrho _{\mathfrak {p}}:\mathcal {K}_p=\mathcal {K}\otimes \mathbb {Q}_p\rightarrow \mathbb {Q}_p$ induces maps
$\varrho _{\mathfrak {p}}:\mathcal {K}_p=\mathcal {K}\otimes \mathbb {Q}_p\rightarrow \mathbb {Q}_p$ induces maps
and they are all isomorphisms. We denote the inverse maps by ![]() ${\varrho ^{-1}_{\mathfrak {p}}}$:
${\varrho ^{-1}_{\mathfrak {p}}}$:
5.5 The Klingen Eisenstein series and the doubling method
We briefly recall the definition of Klingen Eisenstein series and Garrett’s (generalized) doubling method formula which expresses a Klingen Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,1)$ as an integral involving a Siegel Eisenstein series on
$\operatorname {\mathrm {GU}}(3,1)$ as an integral involving a Siegel Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,3)$.
$\operatorname {\mathrm {GU}}(3,3)$.
5.5.1 The Klingen Eisenstein series on  $\operatorname {\mathrm {GU}}(3,1)$
$\operatorname {\mathrm {GU}}(3,1)$
Let ![]() $U_{P_{\operatorname {\mathrm {GU}}(3,1)}}$ be the unipotent subgroup of the Klingen parabolic subgroup
$U_{P_{\operatorname {\mathrm {GU}}(3,1)}}$ be the unipotent subgroup of the Klingen parabolic subgroup ![]() $P_{\operatorname {\mathrm {GU}}(3,1)}$ in equation (5.4.4). For a unitary character
$P_{\operatorname {\mathrm {GU}}(3,1)}$ in equation (5.4.4). For a unitary character ![]() $\xi _0\tau _0:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ and a complex number s, define
$\xi _0\tau _0:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ and a complex number s, define ![]() $I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ as the space of smooth K-finite functions (where K is a maximal compact subgroup of
$I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ as the space of smooth K-finite functions (where K is a maximal compact subgroup of ![]() $\operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$)
$\operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$)
satisfying
(i)
 $F(s,\xi _0\tau _0)\left (\begin {pmatrix}x\\&\mathbf {1}_2\\&&\overline {x}^{-1}\end {pmatrix}g\right )=\xi _0\tau _0(x)|x\bar {x}|^{s+\frac {3}{2}}_{\mathbb {A}_{\mathbb {Q}}}$ for all
$F(s,\xi _0\tau _0)\left (\begin {pmatrix}x\\&\mathbf {1}_2\\&&\overline {x}^{-1}\end {pmatrix}g\right )=\xi _0\tau _0(x)|x\bar {x}|^{s+\frac {3}{2}}_{\mathbb {A}_{\mathbb {Q}}}$ for all  $x\in \mathbb {A}^{\times }_{\mathcal {K}}$,
$x\in \mathbb {A}^{\times }_{\mathcal {K}}$,  $g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$,
$g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$,(ii) for all
 $g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$, the function
$g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$, the function  $g_1\mapsto F(s,\xi _0\tau _0)\left (\begin {pmatrix}1\\&g_1\\&&\nu (g_1)\end {pmatrix}g\right )$ is an automorphic form on
$g_1\mapsto F(s,\xi _0\tau _0)\left (\begin {pmatrix}1\\&g_1\\&&\nu (g_1)\end {pmatrix}g\right )$ is an automorphic form on  $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$.
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$.
The Klingen Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,1)$ attached to
$\operatorname {\mathrm {GU}}(3,1)$ attached to ![]() $F(s,\xi _0\tau _0)\in I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ is defined as
$F(s,\xi _0\tau _0)\in I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ is defined as
 $$ \begin{align*} {E^{\mathrm{Kling}}(g;F(s,\xi_0\tau_0))} = \sum_{\gamma\in P_{\operatorname{\mathrm{GU}}(3,1)}(\mathbb{Q})\backslash \operatorname{\mathrm{GU}}(3,1)(\mathbb{Q})} F(s,\xi_0\tau_0)(\gamma g). \end{align*} $$
$$ \begin{align*} {E^{\mathrm{Kling}}(g;F(s,\xi_0\tau_0))} = \sum_{\gamma\in P_{\operatorname{\mathrm{GU}}(3,1)}(\mathbb{Q})\backslash \operatorname{\mathrm{GU}}(3,1)(\mathbb{Q})} F(s,\xi_0\tau_0)(\gamma g). \end{align*} $$ If the cuspidal automorphic form in (ii) belongs to ![]() $\pi ^{\operatorname {\mathrm {GU}}(2)}$, the Galois representation attached to
$\pi ^{\operatorname {\mathrm {GU}}(2)}$, the Galois representation attached to ![]() (where we assume that
(where we assume that ![]() $\xi \tau $ has
$\xi \tau $ has ![]() $\infty $-type
$\infty $-type ![]() $(0,k)$) is
$(0,k)$) is
where the Hecke characters of ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ are viewed as characters of
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ are viewed as characters of ![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})$. The congruences between this Klingen Eisenstein series and cuspidal forms on
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})$. The congruences between this Klingen Eisenstein series and cuspidal forms on ![]() $\operatorname {\mathrm {GU}}(3,1)$ can be used to construct elements in the Selmer group for
$\operatorname {\mathrm {GU}}(3,1)$ can be used to construct elements in the Selmer group for ![]() $\rho _{\pi }(\epsilon ^2_{\mathrm {cyc}})|_{\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})}\otimes \xi ^{-1}\tau ^{-1}$.
$\rho _{\pi }(\epsilon ^2_{\mathrm {cyc}})|_{\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})}\otimes \xi ^{-1}\tau ^{-1}$.
5.5.2 The Siegel Eisenstein series on  $\operatorname {\mathrm {GU}}(3,3)$
$\operatorname {\mathrm {GU}}(3,3)$
Let ![]() $\operatorname {\mathrm {GU}}(3,3)$ be the similitude unitary group over
$\operatorname {\mathrm {GU}}(3,3)$ be the similitude unitary group over ![]() $\mathbb {Z}$ defined by
$\mathbb {Z}$ defined by

The group ![]() $\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m} \operatorname {\mathrm {GU}}(2)=\{(g_1,g_2)\in \operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2):\nu (g_1)=\nu (g_2)\}$ embeds into H by
$\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m} \operatorname {\mathrm {GU}}(2)=\{(g_1,g_2)\in \operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2):\nu (g_1)=\nu (g_2)\}$ embeds into H by
 $$ \begin{align} \begin{aligned} {\imath} : \operatorname{\mathrm{GU}}(3,1)\times_{\mathbb{G}_m} \operatorname{\mathrm{GU}}(2)&\longrightarrow \operatorname{\mathrm{GU}}(3,3)\\ (g_1,g_2)&\longrightarrow \mathcal{S}^{-1}\begin{pmatrix}g_1\\ &g_2\end{pmatrix}\mathcal{S}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\imath} : \operatorname{\mathrm{GU}}(3,1)\times_{\mathbb{G}_m} \operatorname{\mathrm{GU}}(2)&\longrightarrow \operatorname{\mathrm{GU}}(3,3)\\ (g_1,g_2)&\longrightarrow \mathcal{S}^{-1}\begin{pmatrix}g_1\\ &g_2\end{pmatrix}\mathcal{S}, \end{aligned} \end{align} $$where  ${\mathcal {S}}=\begin {pmatrix}1&\\ &\mathbf {1}_2&&-\frac {\zeta _0}{2}\\&&1\\ &-\mathbf {1}_2&&-\frac {\zeta _0}{2}\end {pmatrix}$.
${\mathcal {S}}=\begin {pmatrix}1&\\ &\mathbf {1}_2&&-\frac {\zeta _0}{2}\\&&1\\ &-\mathbf {1}_2&&-\frac {\zeta _0}{2}\end {pmatrix}$.
Let ![]() ${Q_{\operatorname {\mathrm {GU}}(3,3)}}$ be the (standard) Siegel parabolic subgroup of
${Q_{\operatorname {\mathrm {GU}}(3,3)}}$ be the (standard) Siegel parabolic subgroup of ![]() $\operatorname {\mathrm {GU}}(3,3)$. For a
$\operatorname {\mathrm {GU}}(3,3)$. For a ![]() $\mathbb {Z}$-algebra R,
$\mathbb {Z}$-algebra R,

For a place v of ![]() $\mathbb {Q}$, a unitary character
$\mathbb {Q}$, a unitary character ![]() $\xi _{0,v}\tau _{0,v}$ of
$\xi _{0,v}\tau _{0,v}$ of ![]() $\mathcal {K}^{\times }_v$ and a complex number s, the degenerate principal series
$\mathcal {K}^{\times }_v$ and a complex number s, the degenerate principal series ![]() $I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _{0,v}\tau _{0,v})$ is defined as the space consisting of smooth
$I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _{0,v}\tau _{0,v})$ is defined as the space consisting of smooth ![]() $\operatorname {\mathrm {GU}}(3,3)(\mathbb {Z}_v)$-finite functions
$\operatorname {\mathrm {GU}}(3,3)(\mathbb {Z}_v)$-finite functions ![]() $ f_v(s,\xi _{0,v}\tau _{0,v}):\operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v)\longrightarrow \mathbb {C}$ satisfying
$ f_v(s,\xi _{0,v}\tau _{0,v}):\operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v)\longrightarrow \mathbb {C}$ satisfying
 $$ \begin{align*} f_v(s,\xi_{0,v}\tau_{0,v})\left(\begin{pmatrix}A&B\\ 0&D\end{pmatrix}g\right)=\xi_{0,v} \tau_{0,v}(\det A)|\det A D^{-1}|^{s+\frac{3}{2}}_vf(g) \end{align*} $$
$$ \begin{align*} f_v(s,\xi_{0,v}\tau_{0,v})\left(\begin{pmatrix}A&B\\ 0&D\end{pmatrix}g\right)=\xi_{0,v} \tau_{0,v}(\det A)|\det A D^{-1}|^{s+\frac{3}{2}}_vf(g) \end{align*} $$for all  $g\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v),\,\begin {pmatrix}A&B\\ 0&D\end {pmatrix}\in Q_{\operatorname {\mathrm {GU}}(3,3)}(\mathbb {Q}_v)$.
$g\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v),\,\begin {pmatrix}A&B\\ 0&D\end {pmatrix}\in Q_{\operatorname {\mathrm {GU}}(3,3)}(\mathbb {Q}_v)$.
Given a unitary character ![]() $\xi _0\tau _0:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ and a section
$\xi _0\tau _0:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ and a section ![]() $f(s,\xi _0\tau _{0})=\bigotimes ^{\prime }_v f_v(s,\xi _{0,v}\tau _{0,v})$ inside
$f(s,\xi _0\tau _{0})=\bigotimes ^{\prime }_v f_v(s,\xi _{0,v}\tau _{0,v})$ inside ![]() $\bigotimes ^{\prime }_v I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _{0,v}\tau _{0,v})$, the Siegel Eisenstein series on
$\bigotimes ^{\prime }_v I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _{0,v}\tau _{0,v})$, the Siegel Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,3)$ attached to
$\operatorname {\mathrm {GU}}(3,3)$ attached to ![]() $f(s,\xi _{0}\tau _0)$ is defined as
$f(s,\xi _{0}\tau _0)$ is defined as
 $$ \begin{align*} {E^{\mathrm{Sieg}}(g;f(s,\xi_0\tau_0))}&=\sum_{\gamma\in Q_{\operatorname{\mathrm{GU}}(3,3)}(\mathbb{Q})\backslash \operatorname{\mathrm{GU}}(3,3)(\mathbb{Q})} f(s,\xi_0\tau_0)(\gamma g). \end{align*} $$
$$ \begin{align*} {E^{\mathrm{Sieg}}(g;f(s,\xi_0\tau_0))}&=\sum_{\gamma\in Q_{\operatorname{\mathrm{GU}}(3,3)}(\mathbb{Q})\backslash \operatorname{\mathrm{GU}}(3,3)(\mathbb{Q})} f(s,\xi_0\tau_0)(\gamma g). \end{align*} $$5.5.3 The (generalized) doubling method formula
Theorem 5.5.1 [Reference Gan and IchinoGar89].
Let ![]() $\xi _0\tau _0:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ be a unitary character. For a section
$\xi _0\tau _0:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ be a unitary character. For a section ![]() $f(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)}}(s,\xi _0\tau _0)$ and a cuspidal automorphic form
$f(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)}}(s,\xi _0\tau _0)$ and a cuspidal automorphic form ![]() $\varphi $ on
$\varphi $ on ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$,
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$,
 $$\begin{align*}\begin{aligned} \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}E^{\mathrm{Sieg}}\big(\imath\left(g,g_1t\right);f(s,\xi_0\tau_0)\big)\varphi\left(g_1t\right)(\xi_0\tau_0)^{-1}(\det g_1t)\,dg_1 {\,=\,}E^{\mathrm{Kling}}\big(g;F(f(s,\xi_0\tau_0),\varphi)\big), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}E^{\mathrm{Sieg}}\big(\imath\left(g,g_1t\right);f(s,\xi_0\tau_0)\big)\varphi\left(g_1t\right)(\xi_0\tau_0)^{-1}(\det g_1t)\,dg_1 {\,=\,}E^{\mathrm{Kling}}\big(g;F(f(s,\xi_0\tau_0),\varphi)\big), \end{aligned} \end{align*}$$where t is an element of ![]() $\operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ with
$\operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ with ![]() $\nu (t)=\nu (g)$ (and it is easy to see that the left-hand side does not depend on the choice of t), and
$\nu (t)=\nu (g)$ (and it is easy to see that the left-hand side does not depend on the choice of t), and ![]() $F(f(s,\xi _0\tau _0),\varphi )$ is the section in
$F(f(s,\xi _0\tau _0),\varphi )$ is the section in ![]() $I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ defined by
$I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ defined by
 $$ \begin{align*} {F(f(s,\xi_0\tau_0),\varphi)}(g)&=\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f(s,\tau_0)(\imath(g,g_1t))\,\varphi(g_1t)(\xi_0\tau_0)^{-1}(\det g_1t)\,dg_1. \end{align*} $$
$$ \begin{align*} {F(f(s,\xi_0\tau_0),\varphi)}(g)&=\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f(s,\tau_0)(\imath(g,g_1t))\,\varphi(g_1t)(\xi_0\tau_0)^{-1}(\det g_1t)\,dg_1. \end{align*} $$5.6 The auxiliary data for the Klingen family
Let ![]() ${\Sigma }$ be the set of finite places of
${\Sigma }$ be the set of finite places of ![]() $\mathbb {Q}$ containing the prime
$\mathbb {Q}$ containing the prime ![]() $2$, the prime q, the finite places
$2$, the prime q, the finite places ![]() $v\neq p$ where
$v\neq p$ where ![]() $\pi $ or
$\pi $ or ![]() $\xi $ or
$\xi $ or ![]() $\mathcal {K}/\mathbb {Q}$ is ramified and the primes dividing
$\mathcal {K}/\mathbb {Q}$ is ramified and the primes dividing ![]() $\mathfrak {s}$. We denote by
$\mathfrak {s}$. We denote by ![]() ${\Sigma _{\mathrm {s}}}$ the set of primes in
${\Sigma _{\mathrm {s}}}$ the set of primes in ![]() $\Sigma $ split in
$\Sigma $ split in ![]() $\mathcal {K}$ and
$\mathcal {K}$ and ![]() ${\Sigma _{\mathrm {ns}}}$ the set of primes in
${\Sigma _{\mathrm {ns}}}$ the set of primes in ![]() $\Sigma $ nonsplit in
$\Sigma $ nonsplit in ![]() $\mathcal {K}$.
$\mathcal {K}$.
The Klingen Eisenstein family we will construct is not of the optimal level. It depends on some auxiliary data which are chosen such that we can prove the desired properties of its nondegenerate Fourier–Jacobi coefficients. In this subsection, we fix these auxiliary data.
The Siegel Eisenstein family on ![]() $\operatorname {\mathrm {GU}}(3,3)$ we will use for constructing the Klingen Eisenstein family depends on the choice of
$\operatorname {\mathrm {GU}}(3,3)$ we will use for constructing the Klingen Eisenstein family depends on the choice of ![]() $\ell ,\ell ',c_v$,
$\ell ,\ell ',c_v$, ![]() $v\in \Sigma \cup \{\ell ,\ell '\}$. We will define a space (5.6.11) depending on
$v\in \Sigma \cup \{\ell ,\ell '\}$. We will define a space (5.6.11) depending on ![]() $\chi _{h,v}$,
$\chi _{h,v}$, ![]() $v\in \Sigma _{\mathrm {s}}\cup \{\ell \}$, from which we will choose an automorphic form on
$v\in \Sigma _{\mathrm {s}}\cup \{\ell \}$, from which we will choose an automorphic form on ![]() $\operatorname {\mathrm {GU}}(2)$ to pair with the restriction of the Siegel Eisenstein family to
$\operatorname {\mathrm {GU}}(2)$ to pair with the restriction of the Siegel Eisenstein family to ![]() $\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m}\operatorname {\mathrm {GU}}(2)$. The characters
$\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m}\operatorname {\mathrm {GU}}(2)$. The characters ![]() $\chi _{\theta },\chi _h$ will show up in our analysis of nondegenerate Fourier coefficients.
$\chi _{\theta },\chi _h$ will show up in our analysis of nondegenerate Fourier coefficients.
Before choosing the auxiliary data, we first introduce a proposition on certain Schwartz functions in the Schrödinger model of Weil representations of ![]() $\operatorname {\mathrm {U}}(2,1)$. Let
$\operatorname {\mathrm {U}}(2,1)$. Let ![]() $V,V^-$ (resp.
$V,V^-$ (resp. ![]() $W_{\beta }$) be the two-dimensional skew-Hermitian spaces (resp. one-dimensional Hermitian space) over
$W_{\beta }$) be the two-dimensional skew-Hermitian spaces (resp. one-dimensional Hermitian space) over ![]() $\mathcal {K}$, and
$\mathcal {K}$, and ![]() $e_1,e_2\in V\otimes W_{\beta }$,
$e_1,e_2\in V\otimes W_{\beta }$, ![]() $e^-_1,e^-_2\in V^-\otimes W_{\beta }$ as in §7.1. We have
$e^-_1,e^-_2\in V^-\otimes W_{\beta }$ as in §7.1. We have ![]() $\operatorname {\mathrm {U}}(V\oplus V^-)\cong \operatorname {\mathrm {U}}(2,2)$ and
$\operatorname {\mathrm {U}}(V\oplus V^-)\cong \operatorname {\mathrm {U}}(2,2)$ and ![]() $\operatorname {\mathrm {U}}(W_{\beta })\cong \operatorname {\mathrm {U}}(1)$.
$\operatorname {\mathrm {U}}(W_{\beta })\cong \operatorname {\mathrm {U}}(1)$.
Proposition 5.6.1. Let v be a finite place of ![]() $\mathbb {Q}$ nonsplit in
$\mathbb {Q}$ nonsplit in ![]() $\mathcal {K}/\mathbb {Q}$. Denote by
$\mathcal {K}/\mathbb {Q}$. Denote by
the Weil representation of ![]() $\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_v)\times \operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$ on the Schrödinger model
$\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_v)\times \operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$ on the Schrödinger model
(with respect to ![]() $\lambda _{W_{\beta }}=\lambda $). Let
$\lambda _{W_{\beta }}=\lambda $). Let
be the intertwining map between Schrödinger models.
For ![]() $\beta =1$ and
$\beta =1$ and ![]() $m>\max \{\mathrm {ord}_v(\mathrm {cond}(\lambda _v)),3\}$, there exists a character
$m>\max \{\mathrm {ord}_v(\mathrm {cond}(\lambda _v)),3\}$, there exists a character ![]() $\chi _v:\operatorname {\mathrm {U}}(1)(\mathbb {Q}^{\times }_v)\rightarrow \mathbb {C}^{\times }$ of conductor at least
$\chi _v:\operatorname {\mathrm {U}}(1)(\mathbb {Q}^{\times }_v)\rightarrow \mathbb {C}^{\times }$ of conductor at least ![]() $\varpi _v^{\max \{\mathrm {ord}_v(\mathrm {cond}(\lambda _v)),3\}+1}$, a Schwartz function
$\varpi _v^{\max \{\mathrm {ord}_v(\mathrm {cond}(\lambda _v)),3\}+1}$, a Schwartz function ![]() $\phi _{1,v}$ on
$\phi _{1,v}$ on ![]() $\mathbb {Q}_v e_1\oplus \mathbb {Q}_v e_2$, and
$\mathbb {Q}_v e_1\oplus \mathbb {Q}_v e_2$, and ![]() $u_1,\dots ,u_t\in \operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$,
$u_1,\dots ,u_t\in \operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$, ![]() $b_1,\dots ,b_t\in \mathbb {C}$ such that the function
$b_1,\dots ,b_t\in \mathbb {C}$ such that the function
 $$\begin{align*}y\longmapsto \sum_{j=1}^t b_j\int_{\mathbb{Q}_v e_1\oplus\mathbb{Q}_v e_2} \mathscr{T}^{-1}\left(\omega_{\beta,v}\left(\begin{pmatrix}\mathbf{1}_2&q^{-m}\cdot\mathbf{1}_2\\0&\mathbf{1}_2\end{pmatrix} ,u_j\right) \Phi_{0,v}\right)(x,y)\cdot \phi_{1,v}(x)\,dx \end{align*}$$
$$\begin{align*}y\longmapsto \sum_{j=1}^t b_j\int_{\mathbb{Q}_v e_1\oplus\mathbb{Q}_v e_2} \mathscr{T}^{-1}\left(\omega_{\beta,v}\left(\begin{pmatrix}\mathbf{1}_2&q^{-m}\cdot\mathbf{1}_2\\0&\mathbf{1}_2\end{pmatrix} ,u_j\right) \Phi_{0,v}\right)(x,y)\cdot \phi_{1,v}(x)\,dx \end{align*}$$is nonzero and belongs to the ![]() $\chi _v\lambda ^2_v|_{\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)}$-eigenspace for the action of
$\chi _v\lambda ^2_v|_{\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)}$-eigenspace for the action of ![]() $\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$, where
$\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$, where ![]() $\Phi _{0,v}$ is the characteristic function of
$\Phi _{0,v}$ is the characteristic function of ![]() $\mathcal {O}_{K,v}\frac {e_1+e^-_1}{2}\oplus \mathcal {O}_{\mathcal {K},v}\frac {e_2+e^-_2}{2}$.
$\mathcal {O}_{K,v}\frac {e_1+e^-_1}{2}\oplus \mathcal {O}_{\mathcal {K},v}\frac {e_2+e^-_2}{2}$.
Proof. [Reference WanWan20, Lemma 6.26].
We fix:
– primes
 $\ell ,\ell '\neq 2,p$ such that
$\ell ,\ell '\neq 2,p$ such that  $\ell $ splits in
$\ell $ splits in  $\mathcal {K}/\mathbb {Q}$,
$\mathcal {K}/\mathbb {Q}$,  $\ell '$ is inert in
$\ell '$ is inert in  $\mathcal {K}/\mathbb {Q}$, and
$\mathcal {K}/\mathbb {Q}$, and  $\pi _{\ell },\pi _{\ell '}$ are unramified,
$\pi _{\ell },\pi _{\ell '}$ are unramified,– a positive integer
 ${c_v}$ for each place
${c_v}$ for each place  $v\in \Sigma \cup \{\ell ,\ell '\}$,
$v\in \Sigma \cup \{\ell ,\ell '\}$,– auxiliary Hecke characters
 ${\chi _{\theta },\chi _h}:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of
${\chi _{\theta },\chi _h}:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of  $\infty $-type
$\infty $-type  $(0,0)$ with
$(0,0)$ with  $\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$
$\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$
satisfying the following properties:
(1)
 $\chi _{\theta },\chi _h$ are unramified away from
$\chi _{\theta },\chi _h$ are unramified away from  $\Sigma \cup \{p,\ell ,\ell '\}$ and
$\Sigma \cup \{p,\ell ,\ell '\}$ and  $\chi _h\chi ^c_{\theta }$ is unramified at q;
$\chi _h\chi ^c_{\theta }$ is unramified at q;(2)
 $\chi _{\theta ,\mathfrak {p}},\chi _{h,\bar {\mathfrak {p}}}$ are unramified, and
$\chi _{\theta ,\mathfrak {p}},\chi _{h,\bar {\mathfrak {p}}}$ are unramified, and  $\chi _{h,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p}=\chi ^{-1}_{\theta ,\bar {\mathfrak {p}}}|_{\mathbb {Z}^{\times }_p}=\xi _{0,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p}$;
$\chi _{h,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p}=\chi ^{-1}_{\theta ,\bar {\mathfrak {p}}}|_{\mathbb {Z}^{\times }_p}=\xi _{0,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p}$;(3) For
 $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$,
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$,  $$ \begin{align*} &c_v>\max\{\mathrm{ord}_v(\mathrm{cond}(\pi_v)),\mathrm{ord}_v(\mathrm{cond}(\lambda_v)),3\}\\ &\chi_{\theta,v}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}=\text{a } \chi_v \text{ as in Proposition}\ 5.6.1\ \text{with } m=c_v, \\ &\mathrm{ord}_v\left(\mathrm{cond}(\chi_{h,v}\chi^c_{\theta,v})\right),\,\mathrm{ord}_v\left(\mathrm{cond}((\lambda^2_v\chi_{h,v}\chi_{\theta,v})\right)> \mathrm{ord}_v(\mathrm{cond}(\pi_v)),\text{ if } v\neq q,\\ &\mathrm{ord}_v\left(\mathrm{cond}(\chi_{\theta,v})|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\right)\geq \max\{\mathrm{ord}_v\left(\mathrm{cond}(\chi_{h,v})|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\right), \mathrm{ord}_v(\mathrm{cond}(\lambda_v)+1\}; \end{align*} $$
$$ \begin{align*} &c_v>\max\{\mathrm{ord}_v(\mathrm{cond}(\pi_v)),\mathrm{ord}_v(\mathrm{cond}(\lambda_v)),3\}\\ &\chi_{\theta,v}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}=\text{a } \chi_v \text{ as in Proposition}\ 5.6.1\ \text{with } m=c_v, \\ &\mathrm{ord}_v\left(\mathrm{cond}(\chi_{h,v}\chi^c_{\theta,v})\right),\,\mathrm{ord}_v\left(\mathrm{cond}((\lambda^2_v\chi_{h,v}\chi_{\theta,v})\right)> \mathrm{ord}_v(\mathrm{cond}(\pi_v)),\text{ if } v\neq q,\\ &\mathrm{ord}_v\left(\mathrm{cond}(\chi_{\theta,v})|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\right)\geq \max\{\mathrm{ord}_v\left(\mathrm{cond}(\chi_{h,v})|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\right), \mathrm{ord}_v(\mathrm{cond}(\lambda_v)+1\}; \end{align*} $$(4) For
 $v=\mathfrak {v}\overline {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\cup \{\ell \}$,
$v=\mathfrak {v}\overline {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\cup \{\ell \}$,  $\chi _{\theta ,\mathfrak {v}}$ is unramified, and
$\chi _{\theta ,\mathfrak {v}}$ is unramified, and  $$ \begin{align*} &\mathrm{ord}_{\bar{\mathfrak{v}}}(\mathrm{cond} (\chi_{\theta,\bar{\mathfrak{v}}}))\geq 2\mathrm{ord}_v(\mathrm{cond}( \pi_v))+2, \\ &\mathrm{ord}_{\mathfrak{v}}\left(\mathrm{cond}((\chi_{h}\chi^c_{\theta})_{\mathfrak{v}}\right) =\left\{\begin{array}{ll}\mathrm{ord}_{\mathfrak{v}}\left(\mathrm{cond}(\chi_{\theta,{\bar{\mathfrak{v}}} })\right)-\mathrm{ord}_v(\mathrm{cond}(\pi_v)), &\pi_v\text{ ramified,}\\ \mathrm{ord}_{\mathfrak{v}}\left(\mathrm{cond}(\chi_{\theta,{\bar{\mathfrak{v}}} })\right)-1, &\pi_v\text{ unramified};\end{array} \right.\\ &c_v>\max\Big\{\mathrm{ord}_{\bar{\mathfrak{v}}}(\mathrm{cond}(\chi_{\theta,\bar{\mathfrak{v}}})), \mathrm{ord}_{\mathfrak{v}}(\mathrm{cond}(\xi_{0,\mathfrak{v}})),\mathrm{ord}_{\bar{\mathfrak{v}}} (\mathrm{cond}(\xi_{0,\bar{\mathfrak{v}}})), \mathrm{ord}_{\bar{\mathfrak{v}}}(\mathrm{cond}(\lambda_{\bar{\mathfrak{v}}}))\Big\} \end{align*} $$
$$ \begin{align*} &\mathrm{ord}_{\bar{\mathfrak{v}}}(\mathrm{cond} (\chi_{\theta,\bar{\mathfrak{v}}}))\geq 2\mathrm{ord}_v(\mathrm{cond}( \pi_v))+2, \\ &\mathrm{ord}_{\mathfrak{v}}\left(\mathrm{cond}((\chi_{h}\chi^c_{\theta})_{\mathfrak{v}}\right) =\left\{\begin{array}{ll}\mathrm{ord}_{\mathfrak{v}}\left(\mathrm{cond}(\chi_{\theta,{\bar{\mathfrak{v}}} })\right)-\mathrm{ord}_v(\mathrm{cond}(\pi_v)), &\pi_v\text{ ramified,}\\ \mathrm{ord}_{\mathfrak{v}}\left(\mathrm{cond}(\chi_{\theta,{\bar{\mathfrak{v}}} })\right)-1, &\pi_v\text{ unramified};\end{array} \right.\\ &c_v>\max\Big\{\mathrm{ord}_{\bar{\mathfrak{v}}}(\mathrm{cond}(\chi_{\theta,\bar{\mathfrak{v}}})), \mathrm{ord}_{\mathfrak{v}}(\mathrm{cond}(\xi_{0,\mathfrak{v}})),\mathrm{ord}_{\bar{\mathfrak{v}}} (\mathrm{cond}(\xi_{0,\bar{\mathfrak{v}}})), \mathrm{ord}_{\bar{\mathfrak{v}}}(\mathrm{cond}(\lambda_{\bar{\mathfrak{v}}}))\Big\} \end{align*} $$(5) If
 $q=\mathfrak {q}^2$ is ramified in
$q=\mathfrak {q}^2$ is ramified in  $\mathcal {K}/\mathbb {Q}$,
$\mathcal {K}/\mathbb {Q}$,  $$\begin{align*}(\chi_{h}\chi^c_{\theta})_q(\varpi_{\mathfrak{q}})=\chi_q(q), \end{align*}$$
$$\begin{align*}(\chi_{h}\chi^c_{\theta})_q(\varpi_{\mathfrak{q}})=\chi_q(q), \end{align*}$$where
 $\varpi _{\mathfrak {q}}$ is a uniformizer of
$\varpi _{\mathfrak {q}}$ is a uniformizer of  $\mathcal {K}_{\mathfrak {q}}$ and
$\mathcal {K}_{\mathfrak {q}}$ and  $\chi _q$ is the unramified quadratic character of
$\chi _q$ is the unramified quadratic character of  $\mathcal {K}^{\times }_q$ such that
$\mathcal {K}^{\times }_q$ such that  $\pi _q\cong \text {Steinberg}\otimes \chi _q$;
$\pi _q\cong \text {Steinberg}\otimes \chi _q$;(6) Furthermore, the value
(5.6.1) $$ \begin{align} \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^4\pi^{-3}\cdot \gamma_p\left(\frac{1}{2},\pi_{p}\times \left(\lambda^2\chi_h\chi_{\theta}\right)_{\bar{\mathfrak{p}}}\right)^{-1} L\left(\frac{1}{2},\mathrm{BC}(\pi)\times\lambda^2\chi_h\chi_{\theta}\right) \end{align} $$
$$ \begin{align} \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^4\pi^{-3}\cdot \gamma_p\left(\frac{1}{2},\pi_{p}\times \left(\lambda^2\chi_h\chi_{\theta}\right)_{\bar{\mathfrak{p}}}\right)^{-1} L\left(\frac{1}{2},\mathrm{BC}(\pi)\times\lambda^2\chi_h\chi_{\theta}\right) \end{align} $$is a p-adic unit, and
(5.6.2) $$ \begin{align} L^q\left(\frac{1}{2},\mathrm{BC}(\pi)\times\chi_h\chi^c_{\theta}\right)\neq 0. \end{align} $$
$$ \begin{align} L^q\left(\frac{1}{2},\mathrm{BC}(\pi)\times\chi_h\chi^c_{\theta}\right)\neq 0. \end{align} $$For some algebraic Hecke character
 $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that  $\tau _{p\text {-}\mathrm {adic}}$ factors through
$\tau _{p\text {-}\mathrm {adic}}$ factors through  $\Gamma _{\mathcal {K}}$ and
$\Gamma _{\mathcal {K}}$ and  $\xi \tau $ has
$\xi \tau $ has  $\infty $-type
$\infty $-type  $(0,k)$,
$(0,k)$,  $k\geq 2$, the values (5.6.3)
$k\geq 2$, the values (5.6.3) $$ \begin{align} \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^k(2\pi i)^{1-k}\Gamma(k-1)\cdot\gamma_{\bar{\mathfrak{p}}}\left(\frac{k-2}{2},\chi_h\chi_{\theta}^c\xi_0\tau_0\right)^{-1} L^{p\infty} \left(\frac{k-2}{2},\chi_h\chi_{\theta}^c\xi_0\tau_0\right), \end{align} $$(5.6.4)
$$ \begin{align} \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^k(2\pi i)^{1-k}\Gamma(k-1)\cdot\gamma_{\bar{\mathfrak{p}}}\left(\frac{k-2}{2},\chi_h\chi_{\theta}^c\xi_0\tau_0\right)^{-1} L^{p\infty} \left(\frac{k-2}{2},\chi_h\chi_{\theta}^c\xi_0\tau_0\right), \end{align} $$(5.6.4) $$ \begin{align} \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{k-2}(2\pi i)^{2-k}\Gamma(k-2) \cdot L_{\mathfrak{p}}\left(\frac{k-2}{2},\lambda^2\chi_h\chi_{\theta}\xi^c_0\tau^c_0\right) L^{p\infty} \left(\frac{k-2}{2},\lambda^2\chi_h\chi_{\theta}\xi^c_0\tau^c_0\right), \end{align} $$(5.6.5)
$$ \begin{align} \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{k-2}(2\pi i)^{2-k}\Gamma(k-2) \cdot L_{\mathfrak{p}}\left(\frac{k-2}{2},\lambda^2\chi_h\chi_{\theta}\xi^c_0\tau^c_0\right) L^{p\infty} \left(\frac{k-2}{2},\lambda^2\chi_h\chi_{\theta}\xi^c_0\tau^c_0\right), \end{align} $$(5.6.5) $$ \begin{align} 1-(\chi_h\chi_{\theta}^c\xi_0\tau_0)_q(q)q^{-\frac{k-2}{2}}, \end{align} $$
$$ \begin{align} 1-(\chi_h\chi_{\theta}^c\xi_0\tau_0)_q(q)q^{-\frac{k-2}{2}}, \end{align} $$are all p-adic units.
We can first fix places ![]() $\ell ,\ell '$ and positive integers
$\ell ,\ell '$ and positive integers ![]() $c_v$ for
$c_v$ for ![]() $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$. Next, we can choose
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$. Next, we can choose ![]() $\chi _{\theta ,1},\chi _{h,1}$ satisfying the conditions (1)–(5) except the last one in (4). (The inert prime
$\chi _{\theta ,1},\chi _{h,1}$ satisfying the conditions (1)–(5) except the last one in (4). (The inert prime ![]() $\ell '$ is introduced to ensure the existence.) Then we apply the mod p nonvanishing results—[Reference HsiehHsi14b] for the L-values in equation (5.6.1), [Reference Hida and TilouineHsi12] for the L-values in equations (5.6.3)(5.6.4) and in [Reference HungHun17] for the L-value in equation (5.6.2)—to choose a character
$\ell '$ is introduced to ensure the existence.) Then we apply the mod p nonvanishing results—[Reference HsiehHsi14b] for the L-values in equation (5.6.1), [Reference Hida and TilouineHsi12] for the L-values in equations (5.6.3)(5.6.4) and in [Reference HungHun17] for the L-value in equation (5.6.2)—to choose a character ![]() $\nu $ of
$\nu $ of ![]() $\ell $-power conductor such that
$\ell $-power conductor such that ![]() $\chi _{\theta }=\chi _{\theta ,1}\nu $,
$\chi _{\theta }=\chi _{\theta ,1}\nu $, ![]() $\chi _h=\chi _{h,1}\nu $ satisfy (1)–(6) except the last one in (4). (The conditions in (3) on the conductors at nonsplit primes and the condition (5) implies that the local root numbers are
$\chi _h=\chi _{h,1}\nu $ satisfy (1)–(6) except the last one in (4). (The conditions in (3) on the conductors at nonsplit primes and the condition (5) implies that the local root numbers are ![]() $+1$ as required for applying [Reference HsiehHsi14b, Reference HungHun17]. Our assumption that
$+1$ as required for applying [Reference HsiehHsi14b, Reference HungHun17]. Our assumption that ![]() $\xi $ has
$\xi $ has ![]() $\infty $-type
$\infty $-type ![]() $(0,k_0)$ with
$(0,k_0)$ with ![]() $k_0$ even implies that the L-values in equations (5.6.3)(5.6.4) fall into the nonresidually self-dual case for which [Reference Hida and TilouineHsi12, Theorem B] can be applied. Since we only need the L-value in equation (5.6.2) to be nonvanishing rather than mod p nonvanishing, we can choose a prime
$k_0$ even implies that the L-values in equations (5.6.3)(5.6.4) fall into the nonresidually self-dual case for which [Reference Hida and TilouineHsi12, Theorem B] can be applied. Since we only need the L-value in equation (5.6.2) to be nonvanishing rather than mod p nonvanishing, we can choose a prime ![]() $p'\neq \ell $, different from p, such that the results in [Reference HungHun17] apply.) Then we fix positive integers
$p'\neq \ell $, different from p, such that the results in [Reference HungHun17] apply.) Then we fix positive integers ![]() $c_v$ for
$c_v$ for ![]() $v\in \Sigma _{\mathrm {s}}\cup \{\ell \}$. (The strategy outlined in §7.5 explains why we need to make such a choice of the auxiliary
$v\in \Sigma _{\mathrm {s}}\cup \{\ell \}$. (The strategy outlined in §7.5 explains why we need to make such a choice of the auxiliary ![]() $\chi _{\theta },\chi _h$.)
$\chi _{\theta },\chi _h$.)
With our fixed ![]() $c_v$’s for all
$c_v$’s for all ![]() $v\in \Sigma \cup \{\ell ,\ell '\}$, define
$v\in \Sigma \cup \{\ell ,\ell '\}$, define
and the tame level group ![]() $K^{\prime p}_f\subset \operatorname {\mathrm {GU}}(2)(\widehat {\mathbb {Z}}^{(p)})$ as
$K^{\prime p}_f\subset \operatorname {\mathrm {GU}}(2)(\widehat {\mathbb {Z}}^{(p)})$ as
Given an open subgroup ![]() $K^{\prime }_p\subset \operatorname {\mathrm {GU}}(2)(\mathbb {Z}_p)$ and a ring R, let
$K^{\prime }_p\subset \operatorname {\mathrm {GU}}(2)(\mathbb {Z}_p)$ and a ring R, let
the space of R-valued automorphic forms on ![]() $\operatorname {\mathrm {GU}}(2)$ of weight
$\operatorname {\mathrm {GU}}(2)$ of weight ![]() $(0,0)$ and level
$(0,0)$ and level ![]() $K^{\prime p}_fK^{\prime }_p$.
$K^{\prime p}_fK^{\prime }_p$.
We also define the following twist of the form ![]() $f^{\operatorname {\mathrm {GU}}(2)}$:
$f^{\operatorname {\mathrm {GU}}(2)}$:
 $$ \begin{align} {f^{\operatorname{\mathrm{GU}}(2)}_{\chi_h}} = \prod_{\substack{v=\mathfrak{v}\bar{\mathfrak{v}}\in\Sigma_{\mathrm{s}}\cup\{\ell\}}} \sum_{n\in(\mathbb{Z}_v/q^{t_v}_v\mathbb{Z}_v)^{\times}}\chi_{h,\bar{\mathfrak{v}}}(-n)\,R\left(\begin{pmatrix}1\\n&1\end{pmatrix}_{\mathfrak{v}}\begin{pmatrix}q^{-t_v}_v\\&1\end{pmatrix}_{\mathfrak{v}}\right)f^{\operatorname{\mathrm{GU}}(2)}, \end{align} $$
$$ \begin{align} {f^{\operatorname{\mathrm{GU}}(2)}_{\chi_h}} = \prod_{\substack{v=\mathfrak{v}\bar{\mathfrak{v}}\in\Sigma_{\mathrm{s}}\cup\{\ell\}}} \sum_{n\in(\mathbb{Z}_v/q^{t_v}_v\mathbb{Z}_v)^{\times}}\chi_{h,\bar{\mathfrak{v}}}(-n)\,R\left(\begin{pmatrix}1\\n&1\end{pmatrix}_{\mathfrak{v}}\begin{pmatrix}q^{-t_v}_v\\&1\end{pmatrix}_{\mathfrak{v}}\right)f^{\operatorname{\mathrm{GU}}(2)}, \end{align} $$where ![]() $t_v=\mathrm {ord}_{\bar {\mathfrak {v}}}(\mathrm {cond}(\chi _{h,\bar {\mathfrak {v}}}))$. We have
$t_v=\mathrm {ord}_{\bar {\mathfrak {v}}}(\mathrm {cond}(\chi _{h,\bar {\mathfrak {v}}}))$. We have ![]() $f^{\operatorname {\mathrm {GU}}(2)}_{\chi _h}\in M_{\operatorname {\mathrm {GU}}(2)}\left (K^{\prime p}_f\operatorname {\mathrm {GU}}(2)(\mathbb {Z}_p);\mathcal {O}_L\right )$. Let
$f^{\operatorname {\mathrm {GU}}(2)}_{\chi _h}\in M_{\operatorname {\mathrm {GU}}(2)}\left (K^{\prime p}_f\operatorname {\mathrm {GU}}(2)(\mathbb {Z}_p);\mathcal {O}_L\right )$. Let
denote the space generated by ![]() $f^{\operatorname {\mathrm {GU}}(2)}_{\chi _h}$ and the action of
$f^{\operatorname {\mathrm {GU}}(2)}_{\chi _h}$ and the action of ![]() $\operatorname {\mathrm {GU}}(\mathbb {Q}_v)$,
$\operatorname {\mathrm {GU}}(\mathbb {Q}_v)$, ![]() $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$.
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$.
Remark 5.6.2. In the sentence beginning ‘the twist at the split’, please define CM. We will choose a ![]() $\varphi $ inside the space
$\varphi $ inside the space
to pair with the Siegel Eisenstein family on ![]() $\operatorname {\mathrm {GU}}(3,3)$ to get the Klingen Eisenstein family on
$\operatorname {\mathrm {GU}}(3,3)$ to get the Klingen Eisenstein family on ![]() $\operatorname {\mathrm {GU}}(3,1)$. The twist at the split primes is to make the nebentypus match those of the auxiliary CM families
$\operatorname {\mathrm {GU}}(3,1)$. The twist at the split primes is to make the nebentypus match those of the auxiliary CM families ![]() $ \boldsymbol {\theta }$ and
$ \boldsymbol {\theta }$ and ![]() $\boldsymbol {h}$ constructed from our chosen auxiliary characters
$\boldsymbol {h}$ constructed from our chosen auxiliary characters ![]() $\chi _{\theta }$ and
$\chi _{\theta }$ and ![]() $\chi _h$. The flexibility at the nonsplit primes is to ensure the nonvanishing of the local triple product integrals at the nonsplit primes.
$\chi _h$. The flexibility at the nonsplit primes is to ensure the nonvanishing of the local triple product integrals at the nonsplit primes.
5.7 The choice of the local sections for the Siegel Eisenstein series on  $\operatorname {\mathrm {GU}}(3,3)$
$\operatorname {\mathrm {GU}}(3,3)$
With ![]() $c_v$’s chosen in §5.6, given an algebraic Hecke character
$c_v$’s chosen in §5.6, given an algebraic Hecke character ![]() $\tau $ such that
$\tau $ such that ![]() $\xi \tau $ has
$\xi \tau $ has ![]() $\infty $-type
$\infty $-type ![]() $(0,k)$ with k an even integer
$(0,k)$ with k an even integer ![]() $\geq 6$, we make the following choices of
$\geq 6$, we make the following choices of ![]() $f(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)}}(s,\xi _0\tau _0)$ so that after a suitable normalization,
$f(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)}}(s,\xi _0\tau _0)$ so that after a suitable normalization, ![]() can be interpolated by a two-variable p-adic family when
can be interpolated by a two-variable p-adic family when ![]() $\tau $ varies.
$\tau $ varies.
5.7.1 The Archimedean place
We choose ![]() $f_{\infty }(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},\infty }(s,\tau _0)$ as
$f_{\infty }(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},\infty }(s,\tau _0)$ as
 $$ \begin{align*} f_{\infty}(s,\xi_0\tau_0)\left(g=\begin{pmatrix}A&B\\ C&D\end{pmatrix}\right)=&\,(\det g)^k|\det(g)|_{\mathbb{C}}^{\frac{s}{2}+\frac{3}{4}-\frac{k}{4}}\\ &\times\det\left(C\left(\begin{smallmatrix}i\\&\frac{\zeta_0}{2}\end{smallmatrix}\right) +D\right)^{-k}\left\|\det\left(C \left(\begin{smallmatrix}i\\ &\frac{\zeta_0}{2}\end{smallmatrix}\right) +D\right)\right| {}_{\mathbb{C}}^{-s-\frac{3}{2}+\frac{k}{2}}. \end{align*} $$
$$ \begin{align*} f_{\infty}(s,\xi_0\tau_0)\left(g=\begin{pmatrix}A&B\\ C&D\end{pmatrix}\right)=&\,(\det g)^k|\det(g)|_{\mathbb{C}}^{\frac{s}{2}+\frac{3}{4}-\frac{k}{4}}\\ &\times\det\left(C\left(\begin{smallmatrix}i\\&\frac{\zeta_0}{2}\end{smallmatrix}\right) +D\right)^{-k}\left\|\det\left(C \left(\begin{smallmatrix}i\\ &\frac{\zeta_0}{2}\end{smallmatrix}\right) +D\right)\right| {}_{\mathbb{C}}^{-s-\frac{3}{2}+\frac{k}{2}}. \end{align*} $$5.7.2 Unramified places
For ![]() $v\notin \Sigma \cup \{p,\ell ,\ell '\}$, we choose
$v\notin \Sigma \cup \{p,\ell ,\ell '\}$, we choose ![]() $f_v(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\tau _0)$ to be the standard spherical section, that is, the section that is invariant under the right translation of
$f_v(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\tau _0)$ to be the standard spherical section, that is, the section that is invariant under the right translation of ![]() $\operatorname {\mathrm {GU}}(3,3)(\mathbb {Z}_v)$ and takes value
$\operatorname {\mathrm {GU}}(3,3)(\mathbb {Z}_v)$ and takes value ![]() $1$ at
$1$ at ![]() $\mathbf {1}_6$.
$\mathbf {1}_6$.
5.7.3 Places  $v\in \Sigma \cup \{\ell ,\ell '\}$
$v\in \Sigma \cup \{\ell ,\ell '\}$
We choose ![]() $f_v(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\tau _0)$ as
$f_v(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\tau _0)$ as

where ![]() $c_v$ is the fixed positive integer in §5.6.
$c_v$ is the fixed positive integer in §5.6.
5.7.4 The place p
We have the isomorphisms
 $$ \begin{align*} \operatorname{\mathrm{U}}(3,3)(\mathbb{Q}_p)&\longrightarrow \operatorname{\mathrm{GL}}_6(\mathbb{Q}_p), & g=\big(a_{ij}\big)&\longmapsto \big(\varrho_{\mathfrak{p}}(a_{ij})\big),\\ \operatorname{\mathrm{Her}}_3(\mathcal{K}_p)&\longrightarrow M_{3,3}(\mathbb{Q}_p), &x=\big(x_{ij}\big)&\longmapsto \varrho_{\mathfrak{p}}(x)=\big(\varrho_{\mathfrak{p}}(x_{ij})\big), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{U}}(3,3)(\mathbb{Q}_p)&\longrightarrow \operatorname{\mathrm{GL}}_6(\mathbb{Q}_p), & g=\big(a_{ij}\big)&\longmapsto \big(\varrho_{\mathfrak{p}}(a_{ij})\big),\\ \operatorname{\mathrm{Her}}_3(\mathcal{K}_p)&\longrightarrow M_{3,3}(\mathbb{Q}_p), &x=\big(x_{ij}\big)&\longmapsto \varrho_{\mathfrak{p}}(x)=\big(\varrho_{\mathfrak{p}}(x_{ij})\big), \end{align*} $$and we will often use them to identify ![]() $\operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_p)$ with
$\operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_p)$ with ![]() $\operatorname {\mathrm {GL}}_6(\mathbb {Q}_p)$ and
$\operatorname {\mathrm {GL}}_6(\mathbb {Q}_p)$ and ![]() $\operatorname {\mathrm {Her}}_3(\mathcal {K}_p)$ with
$\operatorname {\mathrm {Her}}_3(\mathcal {K}_p)$ with ![]() $M_{3,3}(\mathbb {Q}_p)$.
$M_{3,3}(\mathbb {Q}_p)$.
For ![]() $x\in \operatorname {\mathrm {Her}}_3(\mathcal {K}_p)$, we write
$x\in \operatorname {\mathrm {Her}}_3(\mathcal {K}_p)$, we write ![]() $\varrho _{\mathfrak {p}}(x)$ as
$\varrho _{\mathfrak {p}}(x)$ as  $\begin {pmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\end {pmatrix}$. Define the Schwartz function
$\begin {pmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\end {pmatrix}$. Define the Schwartz function ![]() $\alpha _{\xi \tau ,p}$ on
$\alpha _{\xi \tau ,p}$ on ![]() $\operatorname {\mathrm {Her}}_3(\mathcal {K}_p)$ as
$\operatorname {\mathrm {Her}}_3(\mathcal {K}_p)$ as

and let ![]() $\mathcal {F}^{-1}\alpha _{\xi \tau ,p}$ be the inverse Fourier transform of
$\mathcal {F}^{-1}\alpha _{\xi \tau ,p}$ be the inverse Fourier transform of ![]() $\alpha _{\xi \tau ,p}$, that is,
$\alpha _{\xi \tau ,p}$, that is,
 $$\begin{align*}\mathcal{F}^{-1}\alpha_{\xi\tau,p}(x)=\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}_p)} \alpha_{\xi\tau,p}(y)\,\mathbf{e}_p(\mathrm{Tr}\, xy)\,dy, \end{align*}$$
$$\begin{align*}\mathcal{F}^{-1}\alpha_{\xi\tau,p}(x)=\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}_p)} \alpha_{\xi\tau,p}(y)\,\mathbf{e}_p(\mathrm{Tr}\, xy)\,dy, \end{align*}$$where ![]() $\mathbf {e}_p$ is the additive character in equation (1.0.5). (A simple computation shows that
$\mathbf {e}_p$ is the additive character in equation (1.0.5). (A simple computation shows that

if ![]() $(\xi _0\tau _0)_{\mathfrak {p}}$ has conductor
$(\xi _0\tau _0)_{\mathfrak {p}}$ has conductor ![]() $p^t$,
$p^t$, ![]() $t\geq 1$.) In order to define the
$t\geq 1$.) In order to define the ![]() $f_p(s,\xi _0\tau _0)$ for our purpose, we first define the section
$f_p(s,\xi _0\tau _0)$ for our purpose, we first define the section

which belongs to ![]() $I_{Q_{\operatorname {\mathrm {GU}}(3,3)},p}(-s,(\xi _0\tau _0)^{-c})$ and is supported on the big cell
$I_{Q_{\operatorname {\mathrm {GU}}(3,3)},p}(-s,(\xi _0\tau _0)^{-c})$ and is supported on the big cell
 $$\begin{align*}Q_{\operatorname{\mathrm{GU}}(3,3)(\mathbb{Q}_p)}\begin{pmatrix}0&-\mathbf{1}_3\\\mathbf{1}_3&0\end{pmatrix}Q_{\operatorname{\mathrm{GU}}(3,3)(\mathbb{Q}_p)}. \end{align*}$$
$$\begin{align*}Q_{\operatorname{\mathrm{GU}}(3,3)(\mathbb{Q}_p)}\begin{pmatrix}0&-\mathbf{1}_3\\\mathbf{1}_3&0\end{pmatrix}Q_{\operatorname{\mathrm{GU}}(3,3)(\mathbb{Q}_p)}. \end{align*}$$We choose ![]() $f_p(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},p}(s,\xi _0\tau _0)$ as
$f_p(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},p}(s,\xi _0\tau _0)$ as
 $$ \begin{align} \begin{aligned} f_p(s,\xi_0\tau_0)(g)=&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\\ &\times M_p\left(-s,(\xi_0\tau_0)^{-c}\right)f^{\text{big-cell}}_p\left(-s,(\xi_0\tau_0)^{-c}\right)(g\Upsilon_p), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} f_p(s,\xi_0\tau_0)(g)=&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\\ &\times M_p\left(-s,(\xi_0\tau_0)^{-c}\right)f^{\text{big-cell}}_p\left(-s,(\xi_0\tau_0)^{-c}\right)(g\Upsilon_p), \end{aligned} \end{align} $$where ![]() ${\xi ^{\mathbb {Q}}_0}$ (resp.
${\xi ^{\mathbb {Q}}_0}$ (resp. ![]() ${\tau ^{\mathbb {Q}}_0}$) denotes the restriction of
${\tau ^{\mathbb {Q}}_0}$) denotes the restriction of ![]() $\xi _0$ (resp.
$\xi _0$ (resp. ![]() $\tau _0$) to
$\tau _0$) to ![]() $\mathbb {Q}^{\times }\backslash \mathbb {A}^{\times }_{\mathbb {Q}}$, and
$\mathbb {Q}^{\times }\backslash \mathbb {A}^{\times }_{\mathbb {Q}}$, and ![]() $M_p\left (-s,(\xi _0\tau _0)^{-c}\right )$ is the intertwining operator, that is,
$M_p\left (-s,(\xi _0\tau _0)^{-c}\right )$ is the intertwining operator, that is,
 $$ \begin{align} \begin{aligned} &M_p\left(-s,(\xi_0\tau_0)^{-c}\right)f^{\text{big-cell}}_p(-s,(\xi_0\tau_0)^{-c})(g\Upsilon_p)\\ =&\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}_p)} f^{\text{big-cell}}_p(-s,(\xi\tau_0)^{-c})\left(\begin{pmatrix}&-\mathbf{1}_3\\\mathbf{1}_3\end{pmatrix}\begin{pmatrix}\mathbf{1}_3&y\\&\mathbf{1}_3\end{pmatrix}g\Upsilon_p\right)\,dy, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &M_p\left(-s,(\xi_0\tau_0)^{-c}\right)f^{\text{big-cell}}_p(-s,(\xi_0\tau_0)^{-c})(g\Upsilon_p)\\ =&\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}_p)} f^{\text{big-cell}}_p(-s,(\xi\tau_0)^{-c})\left(\begin{pmatrix}&-\mathbf{1}_3\\\mathbf{1}_3\end{pmatrix}\begin{pmatrix}\mathbf{1}_3&y\\&\mathbf{1}_3\end{pmatrix}g\Upsilon_p\right)\,dy, \end{aligned} \end{align} $$and ![]() ${\Upsilon _p}$ is the element in
${\Upsilon _p}$ is the element in ![]() $\operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_p)$ such that
$\operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_p)$ such that
 $$\begin{align*}\varrho_{\mathfrak{p}}(\Upsilon_p)= \begin{pmatrix} 1&\\&\mathbf{1}_2&&-\frac{\zeta_0}{2}\\&&1\\&-\mathbf{1}_2&&-\frac{\zeta_0}{2} \end{pmatrix}^{-1}. \end{align*}$$
$$\begin{align*}\varrho_{\mathfrak{p}}(\Upsilon_p)= \begin{pmatrix} 1&\\&\mathbf{1}_2&&-\frac{\zeta_0}{2}\\&&1\\&-\mathbf{1}_2&&-\frac{\zeta_0}{2} \end{pmatrix}^{-1}. \end{align*}$$Remark 5.7.1. When ![]() $(\xi ^{\mathbb {Q}}_0\tau ^{\mathbb {Q}}_0)_p$ is ramified with conductor
$(\xi ^{\mathbb {Q}}_0\tau ^{\mathbb {Q}}_0)_p$ is ramified with conductor ![]() $p^t$,
$p^t$,
 $$ \begin{align*} &\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\\ =&\,\mathfrak{g}\left((\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_p^{-1}\right)^{-3}(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_p(p)^{-3t}p^{(6s+6)t}. \end{align*} $$
$$ \begin{align*} &\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\\ =&\,\mathfrak{g}\left((\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_p^{-1}\right)^{-3}(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_p(p)^{-3t}p^{(6s+6)t}. \end{align*} $$Combining this with equation (5.7.2), one can see that the formula for the section ![]() $f_p(s,\xi _0\tau _0)$ in equation (5.7.3) agrees with the formula in [Reference WanWan20, (6-5)].)
$f_p(s,\xi _0\tau _0)$ in equation (5.7.3) agrees with the formula in [Reference WanWan20, (6-5)].)
Remark 5.7.2. For the unitary group attached to  $\begin {pmatrix}&\mathbf {1}_n\\-\mathbf {1}_n\end {pmatrix}$ and
$\begin {pmatrix}&\mathbf {1}_n\\-\mathbf {1}_n\end {pmatrix}$ and ![]() $\beta \in \operatorname {\mathrm {Her}}_n(\mathcal {K})$, the factor for the functional equation of the
$\beta \in \operatorname {\mathrm {Her}}_n(\mathcal {K})$, the factor for the functional equation of the ![]() $\beta $-th local Fourier coefficients of the degenerate principal series inducing
$\beta $-th local Fourier coefficients of the degenerate principal series inducing ![]() $(\xi _0\tau _{0})^{-c}_p|\cdot |_{\mathcal {K}_p}^{-s}$ is
$(\xi _0\tau _{0})^{-c}_p|\cdot |_{\mathcal {K}_p}^{-s}$ is
 $$ \begin{align} \begin{aligned} &c_{n,p}(-s,(\xi_0\tau_0)^{-c},\beta)\\ =&\,c_{\beta,p}\cdot (\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_{p}(\det\beta)|\det\beta|^{2s}_{\mathbb{Q}_p}\cdot\prod_{j=1}^n\gamma_p\left(-2s+1-j,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}^{n+j}\right)^{-1}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &c_{n,p}(-s,(\xi_0\tau_0)^{-c},\beta)\\ =&\,c_{\beta,p}\cdot (\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_{p}(\det\beta)|\det\beta|^{2s}_{\mathbb{Q}_p}\cdot\prod_{j=1}^n\gamma_p\left(-2s+1-j,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}^{n+j}\right)^{-1}, \end{aligned} \end{align} $$where ![]() $c_{\beta ,p}$ is a constant independent of s and
$c_{\beta ,p}$ is a constant independent of s and ![]() $\xi _0\tau _0$. This factor also shows up in the functional equation of the doubling zeta integrals. Note that in our choice of
$\xi _0\tau _0$. This factor also shows up in the functional equation of the doubling zeta integrals. Note that in our choice of ![]() $f_p(s,\xi _0\tau _0)$ in equation (5.7.3), the product of gamma factors is exactly the product of gamma factors in
$f_p(s,\xi _0\tau _0)$ in equation (5.7.3), the product of gamma factors is exactly the product of gamma factors in ![]() $c_{3,p}(-s,(\xi _0\tau _0)^{-c},\beta )$.
$c_{3,p}(-s,(\xi _0\tau _0)^{-c},\beta )$.
Next, we construct a p-adic family interpolating these ![]() $E^{\mathrm {Sieg}}(-;f(s,\xi _0\tau _0))\big |_{s=\frac {k-3}{2}}$ with
$E^{\mathrm {Sieg}}(-;f(s,\xi _0\tau _0))\big |_{s=\frac {k-3}{2}}$ with ![]() $f(s,\xi _0\tau _0)$ chosen as above. We will construct p-adic families of automorphic forms as measures on
$f(s,\xi _0\tau _0)$ chosen as above. We will construct p-adic families of automorphic forms as measures on ![]() $\Gamma _{\mathcal {K}}$ valued in the space of p-adic forms. The next subsection introduces some notions about p-adic measures.
$\Gamma _{\mathcal {K}}$ valued in the space of p-adic forms. The next subsection introduces some notions about p-adic measures.
5.8 p-adic measures and p-adic families of automorphic forms
For a p-adically complete ![]() $\mathcal {O}_L$-module M and a compact abelian group Y with totally disconnected topology, denote by
$\mathcal {O}_L$-module M and a compact abelian group Y with totally disconnected topology, denote by ![]() $\mathcal {M} eas(Y,M)$ the space of M-valued p-adic measures on Y. Given
$\mathcal {M} eas(Y,M)$ the space of M-valued p-adic measures on Y. Given ![]() $\mu \in \mathcal {M} eas(Y,M)$ and a continuous function
$\mu \in \mathcal {M} eas(Y,M)$ and a continuous function ![]() $\eta :Y\rightarrow R$ with R a p-adically complete
$\eta :Y\rightarrow R$ with R a p-adically complete ![]() $\mathcal {O}_L$-algebra, we write
$\mathcal {O}_L$-algebra, we write
to denote the value of ![]() $\mu $ at
$\mu $ at ![]() $\eta $, which is an element in
$\eta $, which is an element in ![]() $R\widehat {\otimes }_{\mathcal {O}_L}M$.
$R\widehat {\otimes }_{\mathcal {O}_L}M$.
For each ![]() $y\in Y$, we have the delta measure
$y\in Y$, we have the delta measure ![]() $\delta _y\in \mathcal {M} eas(Y,M)$ defined by
$\delta _y\in \mathcal {M} eas(Y,M)$ defined by
Given ![]() $M_1,M_2$ and
$M_1,M_2$ and ![]() $\mu _i\in \mathcal {M} eas(Y,M_i)$,
$\mu _i\in \mathcal {M} eas(Y,M_i)$, ![]() $i=1,2$, the convolution
$i=1,2$, the convolution ![]() $\mu _1\ast \mu _2\in \mathcal {M} eas(Y,M_1\widehat {\otimes }M_2)$ is defined by
$\mu _1\ast \mu _2\in \mathcal {M} eas(Y,M_1\widehat {\otimes }M_2)$ is defined by
If ![]() $\chi $ is a continuous character of Y valued in
$\chi $ is a continuous character of Y valued in ![]() $\mathcal {O}^{\times }_{\bar {L}}$, then
$\mathcal {O}^{\times }_{\bar {L}}$, then
Let A be a group with a homomorphism ![]() $A\rightarrow Y$ and an action on M. Then the group A acts on
$A\rightarrow Y$ and an action on M. Then the group A acts on ![]() $\mathcal {M} eas(Y,M)$ in two ways:
$\mathcal {M} eas(Y,M)$ in two ways:
– A acts on
 $\mathcal {M} eas(Y,M)$ via its action on M,
$\mathcal {M} eas(Y,M)$ via its action on M,– A acts on
 $\mathcal {M} eas(Y,M)$ via the homomorphism
$\mathcal {M} eas(Y,M)$ via the homomorphism  $A\rightarrow Y$ and the translation of Y on itself.
$A\rightarrow Y$ and the translation of Y on itself.
Define
 $$ \begin{align} {\mathcal{M} eas(Y,M)^\natural}=\left\{\begin{array}{ll}p\text{-adic measures in } \mathcal{M} eas(Y,M) \text{ on which}\\ \text{the two actions of } A \text{ are compatible}\end{array}\right\}. \end{align} $$
$$ \begin{align} {\mathcal{M} eas(Y,M)^\natural}=\left\{\begin{array}{ll}p\text{-adic measures in } \mathcal{M} eas(Y,M) \text{ on which}\\ \text{the two actions of } A \text{ are compatible}\end{array}\right\}. \end{align} $$ In our applications, Y will be taken to be ![]() $\Gamma _{\mathcal {K}}$ or
$\Gamma _{\mathcal {K}}$ or ![]() $U_{\mathcal {K},p}=1+p\mathcal {O}_{\mathcal {K},p}$, A will be taken to be
$U_{\mathcal {K},p}=1+p\mathcal {O}_{\mathcal {K},p}$, A will be taken to be ![]() $\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$, which we identify with
$\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$, which we identify with ![]() $\mathcal {O}^{\times }_{\mathcal {K},p}$ via
$\mathcal {O}^{\times }_{\mathcal {K},p}$ via ![]() $(\varrho _{\mathfrak {p}},\varrho _{\bar {\mathfrak {p}}})$, and M will be taken to be either
$(\varrho _{\mathfrak {p}},\varrho _{\bar {\mathfrak {p}}})$, and M will be taken to be either ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L$ or spaces of p-adic forms on unitary groups. Next, we introduce the spaces of p-adic families of automorphic forms we will use.
$\hat {\mathcal {O}}^{\mathrm {ur}}_L$ or spaces of p-adic forms on unitary groups. Next, we introduce the spaces of p-adic families of automorphic forms we will use.
5.8.1 p-adic families on  $\operatorname {\mathrm {GU}}(3,1)$
$\operatorname {\mathrm {GU}}(3,1)$
Define the tame level group
 $$ \begin{align*} K_v&=\Big\{g\in\operatorname{\mathrm{GU}}(3,1)(\mathbb{Z}_v):g\equiv\mathbf{1}_4\quad\mod q^{2c_v+\mathrm{ord}_v(\mathfrak{s}\delta)}_v \Big\},\\ K^p_f&=\bigotimes_{v\notin\Sigma\cup\{\infty,\ell,\ell',p\}}\operatorname{\mathrm{GU}}(3,1)(\mathbb{Z}_v)\bigotimes_{v\in\Sigma\cup\{\ell,\ell'\}}K_v. \end{align*} $$
$$ \begin{align*} K_v&=\Big\{g\in\operatorname{\mathrm{GU}}(3,1)(\mathbb{Z}_v):g\equiv\mathbf{1}_4\quad\mod q^{2c_v+\mathrm{ord}_v(\mathfrak{s}\delta)}_v \Big\},\\ K^p_f&=\bigotimes_{v\notin\Sigma\cup\{\infty,\ell,\ell',p\}}\operatorname{\mathrm{GU}}(3,1)(\mathbb{Z}_v)\bigotimes_{v\in\Sigma\cup\{\ell,\ell'\}}K_v. \end{align*} $$Let ![]() ${V_{\operatorname {\mathrm {GU}}(3,1)}}=\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n V_{n,m}$ (with
${V_{\operatorname {\mathrm {GU}}(3,1)}}=\mathop {\varprojlim }\limits _m\mathop {\varinjlim }\limits _n V_{n,m}$ (with ![]() $V_{n,m}$ defined in §2.6) of tame level
$V_{n,m}$ defined in §2.6) of tame level ![]() $K^p_f$. In equation (5.8.4), put
$K^p_f$. In equation (5.8.4), put ![]() $Y=\Gamma _{\mathcal {K}}$,
$Y=\Gamma _{\mathcal {K}}$, ![]() $A=\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ with the homomorphism
$A=\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ with the homomorphism
and ![]() $M=V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }$, the component of
$M=V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }$, the component of ![]() $V_{\operatorname {\mathrm {GU}}(3,1)}$ on which the kernel of equation (5.8.5) acts through the character
$V_{\operatorname {\mathrm {GU}}(3,1)}$ on which the kernel of equation (5.8.5) acts through the character ![]() $\xi _{p\text {-}\mathrm {adic}}$. We make
$\xi _{p\text {-}\mathrm {adic}}$. We make ![]() $(a_1,a_2)\in \mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ act on
$(a_1,a_2)\in \mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ act on ![]() $V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }$ by the usual action of
$V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }$ by the usual action of  $ \varrho ^{-1}_{\mathfrak {p}}\left (\begin {smallmatrix}1\\&1\\&&a_1\\&&&a_2\end {smallmatrix}\right ) \in T_{\mathrm {so}}(\mathbb {Z}_p)\subset \operatorname {\mathrm {U}}(3,1)(\mathbb {Z}_p) $ on
$ \varrho ^{-1}_{\mathfrak {p}}\left (\begin {smallmatrix}1\\&1\\&&a_1\\&&&a_2\end {smallmatrix}\right ) \in T_{\mathrm {so}}(\mathbb {Z}_p)\subset \operatorname {\mathrm {U}}(3,1)(\mathbb {Z}_p) $ on ![]() $V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }$ multiplied by the scalar
$V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }$ multiplied by the scalar ![]() $\xi ^{-1}_{p\text {-}\mathrm {adic},p}(a_1,a_2)$. (Here,
$\xi ^{-1}_{p\text {-}\mathrm {adic},p}(a_1,a_2)$. (Here, ![]() $\varrho ^{-1}_{\mathfrak {p}}$ is the isomorphism in equation (5.4.5), and this action factors through the quotient of
$\varrho ^{-1}_{\mathfrak {p}}$ is the isomorphism in equation (5.4.5), and this action factors through the quotient of ![]() $\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ by the kernel of equation (5.8.5).) Then we get
$\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ by the kernel of equation (5.8.5).) Then we get
the ![]() $\xi _{p\text {-}\mathrm {adic}}$-component of the space of p-adic families on
$\xi _{p\text {-}\mathrm {adic}}$-component of the space of p-adic families on ![]() $\operatorname {\mathrm {GU}}(3,1)$. The compatibility of the two actions of
$\operatorname {\mathrm {GU}}(3,1)$. The compatibility of the two actions of ![]() $\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ implies that the value at
$\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ implies that the value at ![]() $\tau _{p\text {-}\mathrm {adic}}$ of an element in equation (5.8.6) is a p-adic form with p-adic nebentypus
$\tau _{p\text {-}\mathrm {adic}}$ of an element in equation (5.8.6) is a p-adic form with p-adic nebentypus
(By saying p-adic nebentypus, we refer to the usual action of  $\varrho ^{-1}_{\mathfrak {p}}\left (\begin {smallmatrix}a_1&\ast & \ast & \ast \\&a_2&\ast & \ast \\&&a_3&\ast \\&&&a_4\end {smallmatrix}\right ) \in \operatorname {\mathrm {U}}(3,1)(\mathbb {Z}_p)$ on
$\varrho ^{-1}_{\mathfrak {p}}\left (\begin {smallmatrix}a_1&\ast & \ast & \ast \\&a_2&\ast & \ast \\&&a_3&\ast \\&&&a_4\end {smallmatrix}\right ) \in \operatorname {\mathrm {U}}(3,1)(\mathbb {Z}_p)$ on ![]() $V_{\operatorname {\mathrm {GU}}(3,1)}$.)
$V_{\operatorname {\mathrm {GU}}(3,1)}$.)
The base change to ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L$ of the space (5.8.6) contains the subspace of semiordinary families:
$\hat {\mathcal {O}}^{\mathrm {ur}}_L$ of the space (5.8.6) contains the subspace of semiordinary families:
which is naturally equipped with an ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$-module structure. The Klingen Eisenstein family we will construct belongs to this space. (It is tautological that an element in equation (5.8.7) gives rise to an element in
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$-module structure. The Klingen Eisenstein family we will construct belongs to this space. (It is tautological that an element in equation (5.8.7) gives rise to an element in ![]() $\xi _{p\text {-}\mathrm {adic}}$-component of
$\xi _{p\text {-}\mathrm {adic}}$-component of ![]() ; see §8.1.)
; see §8.1.)
5.8.2 p-adic families on  $\operatorname {\mathrm {GU}}(3,3)$
$\operatorname {\mathrm {GU}}(3,3)$
Let ![]() ${V_{\operatorname {\mathrm {GU}}(3,3)}}$ be the space of p-adic forms on
${V_{\operatorname {\mathrm {GU}}(3,3)}}$ be the space of p-adic forms on ![]() $\operatorname {\mathrm {GU}}(3,3)$ defined by considering global sections of the structure sheaf on the Igusa towers for the Shimura variety of
$\operatorname {\mathrm {GU}}(3,3)$ defined by considering global sections of the structure sheaf on the Igusa towers for the Shimura variety of ![]() $\operatorname {\mathrm {GU}}(3,3)$. We will construct a Siegel Eisenstein family in
$\operatorname {\mathrm {GU}}(3,3)$. We will construct a Siegel Eisenstein family in
5.8.3 p-adic families on  $\operatorname {\mathrm {U}}(2)$
$\operatorname {\mathrm {U}}(2)$
For constructing the Klingen Eisenstein family, we use an automorphic form ![]() $\varphi $ in the space (5.6.11), which is spherical at p and does not vary over the weight space. It is when analyzing the nondegenerate Fourier–Jacobi coefficients of our Klingen Eisenstein family that we need auxiliary p-adic families on
$\varphi $ in the space (5.6.11), which is spherical at p and does not vary over the weight space. It is when analyzing the nondegenerate Fourier–Jacobi coefficients of our Klingen Eisenstein family that we need auxiliary p-adic families on ![]() $\operatorname {\mathrm {U}}(2)$.
$\operatorname {\mathrm {U}}(2)$.
Let
 $$ \begin{align*} N_p(\mathbb{Z}_p)&=\left\{g\in \operatorname{\mathrm{U}}(2)(\mathbb{Z}_p):\varrho_{\mathfrak{p}}(g)=\begin{pmatrix}\ast & \ast\\0&1\end{pmatrix}\right\},\\ N^{\prime}_p(\mathbb{Z}_p)&=\left\{g\in \operatorname{\mathrm{U}}(2)(\mathbb{Z}_p):\varrho_{\mathfrak{p}}(g)=\begin{pmatrix}1&\ast\\0&\ast\end{pmatrix}\right\}.\\[-16pt] \end{align*} $$
$$ \begin{align*} N_p(\mathbb{Z}_p)&=\left\{g\in \operatorname{\mathrm{U}}(2)(\mathbb{Z}_p):\varrho_{\mathfrak{p}}(g)=\begin{pmatrix}\ast & \ast\\0&1\end{pmatrix}\right\},\\ N^{\prime}_p(\mathbb{Z}_p)&=\left\{g\in \operatorname{\mathrm{U}}(2)(\mathbb{Z}_p):\varrho_{\mathfrak{p}}(g)=\begin{pmatrix}1&\ast\\0&\ast\end{pmatrix}\right\}.\\[-16pt] \end{align*} $$We define the following two spaces of p-adic forms on ![]() $\operatorname {\mathrm {U}}(2)$ of tame level
$\operatorname {\mathrm {U}}(2)$ of tame level ![]() $K^{\prime p}_f\cap \operatorname {\mathrm {U}}(2)(\widehat {\mathbb {Z}}^{(p)})$:
$K^{\prime p}_f\cap \operatorname {\mathrm {U}}(2)(\widehat {\mathbb {Z}}^{(p)})$:
 $$ \begin{align*} {V_{\operatorname{\mathrm{U}}(2)}}&=\left\{\text{continuous functions }\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q},f})/\big(K^{\prime p}_f\cap\operatorname{\mathrm{U}}(2)(\widehat{\mathbb{Z}}^{(p)})\big) N_p(\mathbb{Z}_p)\rightarrow \mathcal{O}_L \right\},\\ {V^{\prime}_{\operatorname{\mathrm{U}}(2)}}&=\left\{\text{continuous functions }\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q},f})/\big(K^{\prime p}_f\cap\operatorname{\mathrm{U}}(2)(\widehat{\mathbb{Z}}^{(p)})\big) N^{\prime}_p(\mathbb{Z}_p)\rightarrow \mathcal{O}_L \right\}, \end{align*} $$
$$ \begin{align*} {V_{\operatorname{\mathrm{U}}(2)}}&=\left\{\text{continuous functions }\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q},f})/\big(K^{\prime p}_f\cap\operatorname{\mathrm{U}}(2)(\widehat{\mathbb{Z}}^{(p)})\big) N_p(\mathbb{Z}_p)\rightarrow \mathcal{O}_L \right\},\\ {V^{\prime}_{\operatorname{\mathrm{U}}(2)}}&=\left\{\text{continuous functions }\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q},f})/\big(K^{\prime p}_f\cap\operatorname{\mathrm{U}}(2)(\widehat{\mathbb{Z}}^{(p)})\big) N^{\prime}_p(\mathbb{Z}_p)\rightarrow \mathcal{O}_L \right\}, \end{align*} $$and let ![]() ${V_{\operatorname {\mathrm {U}}(2),\,\xi }}$ (resp.
${V_{\operatorname {\mathrm {U}}(2),\,\xi }}$ (resp. ![]() ${V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}}$) denote the subspace of
${V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}}$) denote the subspace of ![]() $V_{\operatorname {\mathrm {U}}(2)}$ (resp.
$V_{\operatorname {\mathrm {U}}(2)}$ (resp. ![]() $V^{\prime }_{\operatorname {\mathrm {U}}(2)}$) on which the kernel of equation (5.8.5) acts through the character
$V^{\prime }_{\operatorname {\mathrm {U}}(2)}$) on which the kernel of equation (5.8.5) acts through the character ![]() $(\mathrm {triv},\xi _{p\text {-}\mathrm {adic},\mathfrak {p}})$ (resp.
$(\mathrm {triv},\xi _{p\text {-}\mathrm {adic},\mathfrak {p}})$ (resp. ![]() $(\xi ^{-1}_{p\text {-}\mathrm {adic},\mathfrak {p}},\mathrm {triv})$). We have the operator
$(\xi ^{-1}_{p\text {-}\mathrm {adic},\mathfrak {p}},\mathrm {triv})$). We have the operator ![]() $U_p$ acting on
$U_p$ acting on ![]() $\mathtt {F}\in V_{\operatorname {\mathrm {U}}(2),\,\xi }$ (resp.
$\mathtt {F}\in V_{\operatorname {\mathrm {U}}(2),\,\xi }$ (resp. ![]() $\mathtt {F}\in V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}$) as
$\mathtt {F}\in V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}$) as
 $$\begin{align*}(U_p\mathtt{F})(g)=\sum_{x\in\mathbb{Z}/p\mathbb{Z}}\mathtt{F}\left(g\varrho^{-1}_{\mathfrak{p}}\begin{pmatrix}p&x\\&1\end{pmatrix}\right) \end{align*}$$
$$\begin{align*}(U_p\mathtt{F})(g)=\sum_{x\in\mathbb{Z}/p\mathbb{Z}}\mathtt{F}\left(g\varrho^{-1}_{\mathfrak{p}}\begin{pmatrix}p&x\\&1\end{pmatrix}\right) \end{align*}$$with ![]() $\varrho ^{-1}_{\mathfrak {p}}$ the isomorphism in equation (5.4.5). The ordinary projection is defined as
$\varrho ^{-1}_{\mathfrak {p}}$ the isomorphism in equation (5.4.5). The ordinary projection is defined as ![]() ${e_{\mathrm {ord}}} = \lim \limits _{n\rightarrow \infty }U^{n!}_p$.
${e_{\mathrm {ord}}} = \lim \limits _{n\rightarrow \infty }U^{n!}_p$.
In equation (5.8.4), put ![]() $Y=\Gamma _{\mathcal {K}}$,
$Y=\Gamma _{\mathcal {K}}$, ![]() $A=\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ with the homomorphism
$A=\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ with the homomorphism ![]() $A\rightarrow Y$ as in equation (5.8.5), and
$A\rightarrow Y$ as in equation (5.8.5), and ![]() $M=V_{\operatorname {\mathrm {U}}(2),\,\xi }$ on which we make
$M=V_{\operatorname {\mathrm {U}}(2),\,\xi }$ on which we make ![]() $(a_1,a_2)\in \mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ act by the right translation of
$(a_1,a_2)\in \mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ act by the right translation of  $\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}1\\&a_1\end {pmatrix}$ multiplied by the scalar
$\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}1\\&a_1\end {pmatrix}$ multiplied by the scalar ![]() $\xi ^{-1}_{p\text {-}\mathrm {adic},\mathfrak {p}}(a_1)$. (This action factors through the quotient of
$\xi ^{-1}_{p\text {-}\mathrm {adic},\mathfrak {p}}(a_1)$. (This action factors through the quotient of ![]() $\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ by the kernel of equation (5.8.5).) Then we get
$\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ by the kernel of equation (5.8.5).) Then we get
The evaluation at ![]() $\tau _{p\text {-}\mathrm {adic}}$ of an element in equation (5.8.8) is a p-adic form on
$\tau _{p\text {-}\mathrm {adic}}$ of an element in equation (5.8.8) is a p-adic form on ![]() $\operatorname {\mathrm {U}}(2)$ with p-adic nebentypus
$\operatorname {\mathrm {U}}(2)$ with p-adic nebentypus
The nondegenerate Fourier–Jacobi coefficients of our Klingen Eisenstein family are p-adic measures on ![]() $\Gamma _{\mathcal {K}}$ valued in p-adic Jacobi forms on
$\Gamma _{\mathcal {K}}$ valued in p-adic Jacobi forms on ![]() $\operatorname {\mathrm {U}}(2)$. Pairing them with a fixed Jacobi form on
$\operatorname {\mathrm {U}}(2)$. Pairing them with a fixed Jacobi form on ![]() $\operatorname {\mathrm {U}}(2)$ gives an element in equation (5.8.8). (See §7.6.)
$\operatorname {\mathrm {U}}(2)$ gives an element in equation (5.8.8). (See §7.6.)
We will also need to consider some auxiliary p-adic families which are p-adic measures on ![]() $U_{\mathcal {K},p}=1+p\mathcal {O}_{\mathcal {K},p}$ valued in
$U_{\mathcal {K},p}=1+p\mathcal {O}_{\mathcal {K},p}$ valued in ![]() $V_{\operatorname {\mathrm {U}}(2),\,\xi }$ and
$V_{\operatorname {\mathrm {U}}(2),\,\xi }$ and ![]() $V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}$. We will fix
$V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}$. We will fix ![]() $\mathtt {N}$, a power of p, such that raising to the
$\mathtt {N}$, a power of p, such that raising to the ![]() $\mathtt {N}$-th power maps
$\mathtt {N}$-th power maps ![]() $\Gamma _{\mathcal {K}}$ into
$\Gamma _{\mathcal {K}}$ into ![]() $U_{\mathcal {K},p}$. (See §7.7.1 for an explanation why we need to consider
$U_{\mathcal {K},p}$. (See §7.7.1 for an explanation why we need to consider ![]() $U_{\mathcal {K},p}$ and fix such an
$U_{\mathcal {K},p}$ and fix such an ![]() $\mathtt {N}$.)
$\mathtt {N}$.)
Put ![]() $Y=U_{\mathcal {K},p}=1+p\mathcal {O}_{\mathcal {K},p}$,
$Y=U_{\mathcal {K},p}=1+p\mathcal {O}_{\mathcal {K},p}$, ![]() $A=\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ with the homomorphism
$A=\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p$ with the homomorphism
and ![]() $M=e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }$ (resp.
$M=e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }$ (resp. ![]() $e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}$) in equation (5.8.4), on which we make
$e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}$) in equation (5.8.4), on which we make ![]() $(a_1,a_2)\in A$ act through the right translation by
$(a_1,a_2)\in A$ act through the right translation by  $\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}1\\&a_1\end {pmatrix}$ (resp.
$\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}1\\&a_1\end {pmatrix}$ (resp.  $\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}a^{-1}_1\\&1\end {pmatrix}$) multiplied by the scalar
$\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}a^{-1}_1\\&1\end {pmatrix}$) multiplied by the scalar ![]() $\xi ^{-1}_{p\text {-}\mathrm {adic},\mathfrak {p}}(a_1)$ (resp.
$\xi ^{-1}_{p\text {-}\mathrm {adic},\mathfrak {p}}(a_1)$ (resp. ![]() $\xi _{p\text {-}\mathrm {adic},\mathfrak {p}}(a_1)$). Then we get
$\xi _{p\text {-}\mathrm {adic},\mathfrak {p}}(a_1)$). Then we get
 $$ \begin{align} \mathcal{M} eas\left(U_{\mathcal{K},p},e_{\mathrm{ord}} V_{\operatorname{\mathrm{U}}(2),\,\xi}\right)^\natural \quad \left(\text{resp. } \mathcal{M} eas\left(U_{\mathcal{K},p},e_{\mathrm{ord}} V^{\prime}_{\operatorname{\mathrm{U}}(2),\,\xi^{-1}}\right)^\natural\right). \end{align} $$
$$ \begin{align} \mathcal{M} eas\left(U_{\mathcal{K},p},e_{\mathrm{ord}} V_{\operatorname{\mathrm{U}}(2),\,\xi}\right)^\natural \quad \left(\text{resp. } \mathcal{M} eas\left(U_{\mathcal{K},p},e_{\mathrm{ord}} V^{\prime}_{\operatorname{\mathrm{U}}(2),\,\xi^{-1}}\right)^\natural\right). \end{align} $$For ![]() $\tau _{p\text {-}\mathrm {adic}}\in \operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (\Gamma _{\mathcal {K}},\overline {\mathbb {Q}}^{\times }_p\right )$, the evaluation at
$\tau _{p\text {-}\mathrm {adic}}\in \operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (\Gamma _{\mathcal {K}},\overline {\mathbb {Q}}^{\times }_p\right )$, the evaluation at ![]() $\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}}$ of an element in equation (5.8.8) is a p-adic form on
$\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}}$ of an element in equation (5.8.8) is a p-adic form on ![]() $\operatorname {\mathrm {U}}(2)$ with nebentypus
$\operatorname {\mathrm {U}}(2)$ with nebentypus
We will construct auxiliary CM families
in §7.7 and use them to study the nondegenerate Fourier–Jacobi coefficients of the Klingen Eisenstein family (which are elements in equation (5.8.8) and gives rise to measures on ![]() $U_{\mathcal {K},p}$ by the map (7.7.1).)
$U_{\mathcal {K},p}$ by the map (7.7.1).)
5.9 The p-adic family of Siegel Eisenstein series on  $\operatorname {\mathrm {GU}}(3,3)$
$\operatorname {\mathrm {GU}}(3,3)$
We normalize the Siegel Eisenstein series ![]() (with
(with ![]() $f(s,\xi _0\tau _0)$ chosen as in §5.7) as
$f(s,\xi _0\tau _0)$ chosen as in §5.7) as

where
 $$ \begin{align} \begin{aligned} d^{\,\Sigma\cup\{\infty,p,\ell,\ell'\}}_3(s,\xi_0\tau_0)&=\prod_{v\notin \Sigma \cup\{p,\ell,\ell'\}} d_{3,v}(s,\xi_0\tau_0), \\ {d_{3,v}(s,\xi_0\tau_0)} &=\prod_{j=1}^3 L_v\left(2s+j,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0}\eta^{3-j}_{\mathcal{K}/\mathbb{Q}}\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} d^{\,\Sigma\cup\{\infty,p,\ell,\ell'\}}_3(s,\xi_0\tau_0)&=\prod_{v\notin \Sigma \cup\{p,\ell,\ell'\}} d_{3,v}(s,\xi_0\tau_0), \\ {d_{3,v}(s,\xi_0\tau_0)} &=\prod_{j=1}^3 L_v\left(2s+j,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0}\eta^{3-j}_{\mathcal{K}/\mathbb{Q}}\right). \end{aligned} \end{align} $$Theorem 5.9.1. There exists a p-adic measure ![]() ${\boldsymbol {E}^{\mathrm {Sieg}}}\in \mathcal {M} eas\left (\Gamma _{\mathcal {K}},V_{\operatorname {\mathrm {GU}}(3,3)}\right )$ such that
${\boldsymbol {E}^{\mathrm {Sieg}}}\in \mathcal {M} eas\left (\Gamma _{\mathcal {K}},V_{\operatorname {\mathrm {GU}}(3,3)}\right )$ such that
for all algebraic Hecke character ![]() $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that its p-adic avatar
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that its p-adic avatar ![]() $\tau _{p\text {-}\mathrm {adic}}$ factors through
$\tau _{p\text {-}\mathrm {adic}}$ factors through ![]() $\Gamma _{\mathcal {K}}$ and
$\Gamma _{\mathcal {K}}$ and ![]() $\xi \tau $ has
$\xi \tau $ has ![]() $\infty $-type
$\infty $-type ![]() $\left (0,k\right )$ with
$\left (0,k\right )$ with ![]() $k\geq 6$ even.
$k\geq 6$ even.
Proof. The measure is constructed by interpolating the q-expansions of the ![]() $E^{\mathrm {Sieg}}_{\xi \tau }$’s. First, we record the formulas for the Fourier coefficients in [Reference WanWan20, §§6E-6H]. Given
$E^{\mathrm {Sieg}}_{\xi \tau }$’s. First, we record the formulas for the Fourier coefficients in [Reference WanWan20, §§6E-6H]. Given ![]() $\beta \in \operatorname {\mathrm {Her}}_3(\mathcal {K})$ and
$\beta \in \operatorname {\mathrm {Her}}_3(\mathcal {K})$ and ![]() $g\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {A}_{\mathbb {Q}})$, let
$g\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {A}_{\mathbb {Q}})$, let
 $$\begin{align*}W_{\beta,v}\big(g_v,f_v(s,\xi_0\tau_0)\big)=\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}_v)}f_v(s,\xi_0\tau_0)\left(\begin{pmatrix}&-\mathbf{1}_3\\\mathbf{1}_3\end{pmatrix}\begin{pmatrix}\mathbf{1}_3&\varsigma\\0&\mathbf{1}_3\end{pmatrix}g_v\right)\mathbf{e}_v(-\mathrm{Tr}\,\beta\varsigma)\,d\varsigma \end{align*}$$
$$\begin{align*}W_{\beta,v}\big(g_v,f_v(s,\xi_0\tau_0)\big)=\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}_v)}f_v(s,\xi_0\tau_0)\left(\begin{pmatrix}&-\mathbf{1}_3\\\mathbf{1}_3\end{pmatrix}\begin{pmatrix}\mathbf{1}_3&\varsigma\\0&\mathbf{1}_3\end{pmatrix}g_v\right)\mathbf{e}_v(-\mathrm{Tr}\,\beta\varsigma)\,d\varsigma \end{align*}$$(where ![]() $\mathbf {e}_v$ is the additive character in equation (1.0.5)), and
$\mathbf {e}_v$ is the additive character in equation (1.0.5)), and
 $$\begin{align*}E^{\mathrm{Sieg}}_{\beta}\big(g;f(s,\xi_0\tau_0)\big) =\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}\backslash\mathbb{A}_{\mathcal{K}})}E^{\mathrm{Sieg}}\left(\begin{pmatrix}\mathbf{1}_3&\varsigma\\0&\mathbf{1}_3\end{pmatrix}g;f(s,\xi_0\tau_0)\right)\mathbf{e}_{\mathbb{A}_{\mathbb{Q}}}(-\mathrm{Tr}\,\beta\varsigma)\,d\varsigma. \end{align*}$$
$$\begin{align*}E^{\mathrm{Sieg}}_{\beta}\big(g;f(s,\xi_0\tau_0)\big) =\int_{\operatorname{\mathrm{Her}}_3(\mathcal{K}\backslash\mathbb{A}_{\mathcal{K}})}E^{\mathrm{Sieg}}\left(\begin{pmatrix}\mathbf{1}_3&\varsigma\\0&\mathbf{1}_3\end{pmatrix}g;f(s,\xi_0\tau_0)\right)\mathbf{e}_{\mathbb{A}_{\mathbb{Q}}}(-\mathrm{Tr}\,\beta\varsigma)\,d\varsigma. \end{align*}$$Because the sections at ![]() $v\in \Sigma \cup \{\ell ,\ell '\}$ are chosen to be supported on the big cell, for
$v\in \Sigma \cup \{\ell ,\ell '\}$ are chosen to be supported on the big cell, for ![]() $g\in Q_{\operatorname {\mathrm {GU}}(3,3)}(\mathbb {A}_{\mathbb {Q}})$, we have
$g\in Q_{\operatorname {\mathrm {GU}}(3,3)}(\mathbb {A}_{\mathbb {Q}})$, we have
For our choice of ![]() $f_v(s,\xi _0\tau _0)$ in §5.7, the formulas for
$f_v(s,\xi _0\tau _0)$ in §5.7, the formulas for ![]() $W_{\beta ,v}\big (g_v,f_v(s,\xi _0\tau _0)\big )$ are as follows.
$W_{\beta ,v}\big (g_v,f_v(s,\xi _0\tau _0)\big )$ are as follows.
– The Archimedean place.

– ![]() $v\notin \Sigma \cup \{p,\ell ,\ell '\}$. For
$v\notin \Sigma \cup \{p,\ell ,\ell '\}$. For ![]() $\det \beta \neq 0$,
$\det \beta \neq 0$,

where ![]() $h_{v,D^{-1}\beta A}\in \mathbb {Z}[X]$ is a monic polynomial depending only on v and
$h_{v,D^{-1}\beta A}\in \mathbb {Z}[X]$ is a monic polynomial depending only on v and ![]() $D^{-1}\beta A$, and is the constant polynomial when when
$D^{-1}\beta A$, and is the constant polynomial when when ![]() $D^{-1}\beta A$ belongs to
$D^{-1}\beta A$ belongs to ![]() $\operatorname {\mathrm {GL}}_3(\mathcal {O}_{\mathcal {K},v})$.
$\operatorname {\mathrm {GL}}_3(\mathcal {O}_{\mathcal {K},v})$.
– ![]() $v\in \Sigma \cup \{\ell ,\ell '\}$.
$v\in \Sigma \cup \{\ell ,\ell '\}$.

– The place p. An easy computation shows that
The functional equation for ![]() $W_{\beta ,p}$ in [Reference Lapid and RallisLR05, (14)] implies that
$W_{\beta ,p}$ in [Reference Lapid and RallisLR05, (14)] implies that
 $$ \begin{align*} &W_{\beta,p}\left(g;M_p\left(-s,\xi^{-c}_0\tau^{-c}_{0}\right)f^{\text{big-cell}}_p(-s,\xi^{-1}_0\tau^{-1}_0)\right)\\ =&\,c_{3,p}(-s,\xi^{-c}_0\tau^{-c}_{0},\beta)\cdot W_{\beta,p}\left(g;f^{\text{big-cell}}_p(-s,\xi^{-c}_0\tau^{-c}_0)\right) \end{align*} $$
$$ \begin{align*} &W_{\beta,p}\left(g;M_p\left(-s,\xi^{-c}_0\tau^{-c}_{0}\right)f^{\text{big-cell}}_p(-s,\xi^{-1}_0\tau^{-1}_0)\right)\\ =&\,c_{3,p}(-s,\xi^{-c}_0\tau^{-c}_{0},\beta)\cdot W_{\beta,p}\left(g;f^{\text{big-cell}}_p(-s,\xi^{-c}_0\tau^{-c}_0)\right) \end{align*} $$with ![]() $c_{3,p}(-s,\xi ^{-c}_0\tau ^{-c}_{0},\beta )$ defined as in equation (5.7.5). It follows that
$c_{3,p}(-s,\xi ^{-c}_0\tau ^{-c}_{0},\beta )$ defined as in equation (5.7.5). It follows that
Denote by ![]() $E^{\mathrm {Sieg}}_{\xi \tau ,\beta }\big (\mathrm {diag}(A,D)\big )$ the
$E^{\mathrm {Sieg}}_{\xi \tau ,\beta }\big (\mathrm {diag}(A,D)\big )$ the ![]() $\beta $-th coefficient in the (p-adic) q-expansion of
$\beta $-th coefficient in the (p-adic) q-expansion of ![]() $E^{\mathrm {Sieg}}_{\xi \tau }$ at the (
$E^{\mathrm {Sieg}}_{\xi \tau }$ at the (![]() $0$-dimensional) cusp indexed by
$0$-dimensional) cusp indexed by ![]() $\mathrm {diag}(A,D)\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {A}^p_{\mathcal {K},f})$. From the above formulas for the local Fourier coefficients at the p and
$\mathrm {diag}(A,D)\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {A}^p_{\mathcal {K},f})$. From the above formulas for the local Fourier coefficients at the p and ![]() $\infty $, we see that
$\infty $, we see that ![]() $E^{\mathrm {Sieg}}_{\xi \tau ,\beta }\big (\mathrm {diag}(A,D)\big )$ is nonzero only for
$E^{\mathrm {Sieg}}_{\xi \tau ,\beta }\big (\mathrm {diag}(A,D)\big )$ is nonzero only for ![]() $\beta $ inside
$\beta $ inside
 $$\begin{align*}\mathfrak{S}_3=\left\{\beta\in\operatorname{\mathrm{Her}}_3(\mathcal{O}_{\mathcal{K}})_{>0}:\varrho_{\mathfrak{p}}(\beta_{21})\in\mathbb{Z}^{\times}_p,\,\begin{pmatrix}\varrho_{\mathfrak{p}}(\beta_{21})&\varrho_{\mathfrak{p}}(\beta_{22})\\\varrho_{\mathfrak{p}}(\beta_{31})&\varrho_{\mathfrak{p}}(\beta_{32})\end{pmatrix}\in\operatorname{\mathrm{GL}}_2(\mathbb{Z}_p)\right\}, \end{align*}$$
$$\begin{align*}\mathfrak{S}_3=\left\{\beta\in\operatorname{\mathrm{Her}}_3(\mathcal{O}_{\mathcal{K}})_{>0}:\varrho_{\mathfrak{p}}(\beta_{21})\in\mathbb{Z}^{\times}_p,\,\begin{pmatrix}\varrho_{\mathfrak{p}}(\beta_{21})&\varrho_{\mathfrak{p}}(\beta_{22})\\\varrho_{\mathfrak{p}}(\beta_{31})&\varrho_{\mathfrak{p}}(\beta_{32})\end{pmatrix}\in\operatorname{\mathrm{GL}}_2(\mathbb{Z}_p)\right\}, \end{align*}$$and for ![]() $\beta \in \mathfrak {S}_3$, combining the above formulas gives
$\beta \in \mathfrak {S}_3$, combining the above formulas gives

(Note that thanks to the condition that ![]() $\xi \tau $ has
$\xi \tau $ has ![]() $\infty $-type
$\infty $-type ![]() $(0,k)$, we have
$(0,k)$, we have ![]() $(\xi \tau )_{p\text {-}\mathrm {adic},\mathfrak {p}}=(\xi \tau )_{\mathfrak {p}}$ and
$(\xi \tau )_{p\text {-}\mathrm {adic},\mathfrak {p}}=(\xi \tau )_{\mathfrak {p}}$ and ![]() $(\xi \tau )_{p\text {-}\mathrm {adic}}|_{\mathcal {O}^{\times }_{\mathcal {K},\mathfrak {p}}}=\xi _0\tau _0|_{\mathcal {O}^{\times }_{\mathcal {K},\mathfrak {p}}}$.)
$(\xi \tau )_{p\text {-}\mathrm {adic}}|_{\mathcal {O}^{\times }_{\mathcal {K},\mathfrak {p}}}=\xi _0\tau _0|_{\mathcal {O}^{\times }_{\mathcal {K},\mathfrak {p}}}$.)
The factors on the right-hand side of equation (5.9.3) are interpolated by ![]() $\delta $-measures in
$\delta $-measures in ![]() $\mathcal {M} eas\left (\Gamma _{\mathcal {K}},\mathcal {O}_L\right )$. The convolution of those
$\mathcal {M} eas\left (\Gamma _{\mathcal {K}},\mathcal {O}_L\right )$. The convolution of those ![]() $\delta $-measures gives an element in
$\delta $-measures gives an element in ![]() $\mathcal {M} eas\left (\Gamma _{\mathcal {K}},\mathcal {O}_L\right )$ which interpolates the Fourier coefficient
$\mathcal {M} eas\left (\Gamma _{\mathcal {K}},\mathcal {O}_L\right )$ which interpolates the Fourier coefficient ![]() $E^{\mathrm {Sieg}}_{\xi \tau ,\beta }\big (\mathrm {diag}(A,D)\big )$. (See equations (5.8.1)(5.8.2)(5.8.3) for the definitions of
$E^{\mathrm {Sieg}}_{\xi \tau ,\beta }\big (\mathrm {diag}(A,D)\big )$. (See equations (5.8.1)(5.8.2)(5.8.3) for the definitions of ![]() $\delta $-measures and the convolution of p-adic measures.) We see that there exists a p-adic measure
$\delta $-measures and the convolution of p-adic measures.) We see that there exists a p-adic measure
 $$\begin{align*}\boldsymbol{E}^{\mathrm{Sieg}}\in \mathcal{M} eas\Big(\Gamma_{\mathcal{K}},\bigoplus\limits_{p\text{-adic cusps}}\mathcal{O}_L[\![\mathfrak{S}_3]\!] \Big)\\[-9pt] \end{align*}$$
$$\begin{align*}\boldsymbol{E}^{\mathrm{Sieg}}\in \mathcal{M} eas\Big(\Gamma_{\mathcal{K}},\bigoplus\limits_{p\text{-adic cusps}}\mathcal{O}_L[\![\mathfrak{S}_3]\!] \Big)\\[-9pt] \end{align*}$$that interpolates the p-adic q-expansions of ![]() $E^{\mathrm {Sieg}}_{\xi \tau }$. By the q-expansion principle and the fact that the
$E^{\mathrm {Sieg}}_{\xi \tau }$. By the q-expansion principle and the fact that the ![]() $E^{\mathrm {Sieg}}_{\xi \tau }$’s are automorphic forms on
$E^{\mathrm {Sieg}}_{\xi \tau }$’s are automorphic forms on ![]() $\operatorname {\mathrm {GU}}(3,3)$, we deduce that
$\operatorname {\mathrm {GU}}(3,3)$, we deduce that ![]() $\boldsymbol {E}^{\mathrm {Sieg}}$ belongs to
$\boldsymbol {E}^{\mathrm {Sieg}}$ belongs to ![]() $\mathcal {M} eas\left (\Gamma _{\mathcal {K}},V_{\operatorname {\mathrm {GU}}(3,3)}\right )$. (Here, we view the space of p-adic measures valued in
$\mathcal {M} eas\left (\Gamma _{\mathcal {K}},V_{\operatorname {\mathrm {GU}}(3,3)}\right )$. (Here, we view the space of p-adic measures valued in ![]() $V_{\operatorname {\mathrm {GU}}(3,3)}$ as a subspace of the space of p-adic measures valued in copies of
$V_{\operatorname {\mathrm {GU}}(3,3)}$ as a subspace of the space of p-adic measures valued in copies of ![]() $\mathcal {O}_L[\![\mathfrak {S}]\!]$ via the embedding of
$\mathcal {O}_L[\![\mathfrak {S}]\!]$ via the embedding of ![]() $V_{\operatorname {\mathrm {GU}}(3,3)}$ into the
$V_{\operatorname {\mathrm {GU}}(3,3)}$ into the ![]() $\mathcal {O}_L$-module of q-expansions.)
$\mathcal {O}_L$-module of q-expansions.)
5.10 The semiordinary family of Klingen Eisenstein series
Let ![]() $E^{\mathrm {Sieg}}_{\xi \tau }\big |_{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ be the automorphic form obtained by the composition of the restriction from
$E^{\mathrm {Sieg}}_{\xi \tau }\big |_{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ be the automorphic form obtained by the composition of the restriction from ![]() $\operatorname {\mathrm {GU}}(3,3)$ to
$\operatorname {\mathrm {GU}}(3,3)$ to ![]() $\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m}\operatorname {\mathrm {GU}}(2)$ via the embedding (5.5.1) and the extension by zero from
$\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m}\operatorname {\mathrm {GU}}(2)$ via the embedding (5.5.1) and the extension by zero from ![]() $\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m}\operatorname {\mathrm {GU}}(2)$ to
$\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m}\operatorname {\mathrm {GU}}(2)$ to ![]() $\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)$. Define the twist
$\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)$. Define the twist ![]() $E^{\mathrm {Sieg}}_{\xi \tau }\big |^\star _{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ as
$E^{\mathrm {Sieg}}_{\xi \tau }\big |^\star _{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ as
Then by our choice of the section ![]() $f_p(s,\xi _0\tau _0)$, we see that
$f_p(s,\xi _0\tau _0)$, we see that
with  ${K^{\prime }_{p,0}}=\left \{g\in \operatorname {\mathrm {GU}}(2)(\mathbb {Z}_p):\varrho _{\mathfrak {p}}(g)=\begin {pmatrix}\ast & \ast \\ p\ast & \ast \end {pmatrix}\right \}$. (Note that
${K^{\prime }_{p,0}}=\left \{g\in \operatorname {\mathrm {GU}}(2)(\mathbb {Z}_p):\varrho _{\mathfrak {p}}(g)=\begin {pmatrix}\ast & \ast \\ p\ast & \ast \end {pmatrix}\right \}$. (Note that ![]() $K^{\prime }_{p,0}$ equals the
$K^{\prime }_{p,0}$ equals the ![]() $K^{\prime }_{p,g}$ in equation (4.4.1). See equation (5.6.8) for the definition of
$K^{\prime }_{p,g}$ in equation (4.4.1). See equation (5.6.8) for the definition of ![]() $M_{\operatorname {\mathrm {GU}}(2)}\left (K^{\prime p}_fK^{\prime }_{p,0};\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )$.)
$M_{\operatorname {\mathrm {GU}}(2)}\left (K^{\prime p}_fK^{\prime }_{p,0};\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )$.)
Therefore, by applying a twist of ![]() $(\xi \tau )^{-1}_{p\text {-}\mathrm {adic}}\circ \,\det $ to the family
$(\xi \tau )^{-1}_{p\text {-}\mathrm {adic}}\circ \,\det $ to the family ![]() $\boldsymbol {E}^{\mathrm {Sieg}}\big |_{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ on the second factor, we obtain the p-adic family
$\boldsymbol {E}^{\mathrm {Sieg}}\big |_{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ on the second factor, we obtain the p-adic family
interpolating ![]() $E^{\mathrm {Sieg}}_{\xi \tau }\big |^\star _{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ when
$E^{\mathrm {Sieg}}_{\xi \tau }\big |^\star _{\operatorname {\mathrm {GU}}(3,1)\times \operatorname {\mathrm {GU}}(2)}$ when ![]() $\tau $ varies. (To see that it belongs to the
$\tau $ varies. (To see that it belongs to the ![]() $^\natural $-subspace, one just needs to check the nebentypus.)
$^\natural $-subspace, one just needs to check the nebentypus.)
Attached to a ![]() $\varphi $ in the space (5.6.11) is a linear functional
$\varphi $ in the space (5.6.11) is a linear functional

where the integral is understood as a sum over the finite set ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {Q})\backslash \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q},f})/K^{\prime p}_fK^{\prime }_{p,0}$. Applying the linear functional
$\operatorname {\mathrm {GU}}(2)(\mathbb {Q})\backslash \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q},f})/K^{\prime p}_fK^{\prime }_{p,0}$. Applying the linear functional
to equation (5.10.1) gives a family
Proposition 5.10.1. For ![]() $\tau _{p\text {-}\mathrm {adic}}$ satisfying the conditions in Theorem 5.9.1, the evaluation of the family
$\tau _{p\text {-}\mathrm {adic}}$ satisfying the conditions in Theorem 5.9.1, the evaluation of the family ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ at
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ at ![]() $\tau _{p\text {-}\mathrm {adic}}$ is a Klingen Eisenstein series on
$\tau _{p\text {-}\mathrm {adic}}$ is a Klingen Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,1)$ inducing
$\operatorname {\mathrm {GU}}(3,1)$ inducing ![]() $\xi _0\tau _0|\cdot |^{\frac {k-3}{2}}\boxtimes \pi ^{\operatorname {\mathrm {GU}}(2)}$, more precisely, the automorphic form
$\xi _0\tau _0|\cdot |^{\frac {k-3}{2}}\boxtimes \pi ^{\operatorname {\mathrm {GU}}(2)}$, more precisely, the automorphic form
 $$ \begin{align} g\longmapsto \left.\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})/\operatorname{\mathrm{U}}(2)(\mathbb{R})} E^{\mathrm{Sieg}}\big(\imath(g,g_2);f(s,\xi_0\tau_0)\big)\varphi(g_2)(\xi_0\tau_0)^{-1}(\det g_2)\,dg_2\,\right| {}_{s=\frac{k-3}{2}} \end{align} $$
$$ \begin{align} g\longmapsto \left.\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})/\operatorname{\mathrm{U}}(2)(\mathbb{R})} E^{\mathrm{Sieg}}\big(\imath(g,g_2);f(s,\xi_0\tau_0)\big)\varphi(g_2)(\xi_0\tau_0)^{-1}(\det g_2)\,dg_2\,\right| {}_{s=\frac{k-3}{2}} \end{align} $$normalized by the factor in equation (5.9.1).
Moreover, ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\in \mathcal {M} eas\left (\Gamma _{\mathcal {K}},e_{\mathrm {so}} V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }\widehat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^\natural \otimes _{\mathbb {Z}}\mathbb {Q}$, that is, is a semiordinary family.
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\in \mathcal {M} eas\left (\Gamma _{\mathcal {K}},e_{\mathrm {so}} V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }\widehat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^\natural \otimes _{\mathbb {Z}}\mathbb {Q}$, that is, is a semiordinary family.
Proof. From the construction of the family ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$, it is easy to see that its evaluation
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$, it is easy to see that its evaluation ![]() $\tau _{p\text {-}\mathrm {adic}}$ satisfying the conditions in Theorem 5.9.1 equals the form given in equation (5.10.3) normalized by the factor in equation (5.9.1). By the doubling method formula (Theorem 5.5.1), we know that equation (5.10.3) is a Klingen Eisenstein series inducing
$\tau _{p\text {-}\mathrm {adic}}$ satisfying the conditions in Theorem 5.9.1 equals the form given in equation (5.10.3) normalized by the factor in equation (5.9.1). By the doubling method formula (Theorem 5.5.1), we know that equation (5.10.3) is a Klingen Eisenstein series inducing ![]() $\xi _0\tau _0|\cdot |^{\frac {k-3}{2}}\boxtimes \pi ^{\operatorname {\mathrm {GU}}(2)}$.
$\xi _0\tau _0|\cdot |^{\frac {k-3}{2}}\boxtimes \pi ^{\operatorname {\mathrm {GU}}(2)}$.
In order to show that ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ is a semiordinary family, for all
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ is a semiordinary family, for all ![]() $\tau $ satisfying the conditions in Theorem 5.9.1 and
$\tau $ satisfying the conditions in Theorem 5.9.1 and ![]() $(\xi \tau )_{\mathfrak {p}}$ ramified, we look at the action of
$(\xi \tau )_{\mathfrak {p}}$ ramified, we look at the action of ![]() $\mathbb {U}_p$-operators on the form (5.10.3), which has weight
$\mathbb {U}_p$-operators on the form (5.10.3), which has weight ![]() $(0,0,0;k)$. Given integers
$(0,0,0;k)$. Given integers ![]() $m,m',m"\geq 0$, by the formula for adelic
$m,m',m"\geq 0$, by the formula for adelic ![]() $\mathbb {U}_p$-operators in equation (2.8.8) and our choice of the local section at p in §5.7, the action of
$\mathbb {U}_p$-operators in equation (2.8.8) and our choice of the local section at p in §5.7, the action of ![]() $(U^+_{p,2})^{m}(U^+_{p,3})^{m'}(U^-_{p,1})^{m"}$ on the form (5.10.3) can be computed by considering
$(U^+_{p,2})^{m}(U^+_{p,3})^{m'}(U^-_{p,1})^{m"}$ on the form (5.10.3) can be computed by considering
 $$ \begin{align} p^{2m+km"}\int_{N(\mathbb{Z}_p)} f^{\text{big-cell}}_p\left(\frac{3-k}{2},(\xi_0\tau_0)^{-c}\right)\left(gu\left(\begin{smallmatrix}p^{m+m'}\\&p^{m+m'}\\&&p^{m'}\\&&&p^{-m"}\\&&&&1\\&&&&&1\end{smallmatrix}\right) \right)\,du, \end{align} $$
$$ \begin{align} p^{2m+km"}\int_{N(\mathbb{Z}_p)} f^{\text{big-cell}}_p\left(\frac{3-k}{2},(\xi_0\tau_0)^{-c}\right)\left(gu\left(\begin{smallmatrix}p^{m+m'}\\&p^{m+m'}\\&&p^{m'}\\&&&p^{-m"}\\&&&&1\\&&&&&1\end{smallmatrix}\right) \right)\,du, \end{align} $$where we identify ![]() $\operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_p)$ with
$\operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_p)$ with ![]() $\operatorname {\mathrm {GL}}_6(\mathbb {Q}_p)$ via
$\operatorname {\mathrm {GL}}_6(\mathbb {Q}_p)$ via ![]() $\varrho _{\mathfrak {p}}:\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p$. Writing
$\varrho _{\mathfrak {p}}:\mathcal {K}\otimes _{\mathbb {Q}}\mathbb {Q}_p\rightarrow \mathbb {Q}_p$. Writing  $g=\begin {pmatrix}A&B\\C&D\end {pmatrix}$ in
$g=\begin {pmatrix}A&B\\C&D\end {pmatrix}$ in ![]() $3\times 3$ blocks, we have
$3\times 3$ blocks, we have
 $$ \begin{align} \begin{aligned} (5.10.4) =&\,p^{2m+km"}\cdot \left((\xi\tau)_{\mathfrak{p}}(p)p^{3}\right)^{2m+3m'} \left((\xi\tau)_{\bar{\mathfrak{p}}}(p)p^{3}\right)^{m"}\\ &\times p^{-4m-3m'-3m"}\sum_{u_1,u_2\in \mathbb{Z}/p^m\mathbb{Z}}\sum_{\substack{{v_1,v_2\in\mathbb{Z}/p^{m+m'+m"}}\\ v_3\in\mathbb{Z}/p^{m'+m"}\mathbb{Z}}}\\ &\quad(\mathcal{F}^{-1}\alpha_{\xi\tau,p}) \left(\left(\begin{smallmatrix}p^{-m-m'}\\&p^{-m-m'}\\&&p^{-m'}\end{smallmatrix}\right) \left(\begin{smallmatrix}1&&-u_1\\&1&-u_2\\&&1\end{smallmatrix}\right) \left(C^{-1}D+\left(\begin{smallmatrix}v_1&0&0\\v_2&0&0\\v_3&0&0\end{smallmatrix}\right) \right)\left(\begin{smallmatrix}p^{-m"}\\&1\\&&1\end{smallmatrix}\right) \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (5.10.4) =&\,p^{2m+km"}\cdot \left((\xi\tau)_{\mathfrak{p}}(p)p^{3}\right)^{2m+3m'} \left((\xi\tau)_{\bar{\mathfrak{p}}}(p)p^{3}\right)^{m"}\\ &\times p^{-4m-3m'-3m"}\sum_{u_1,u_2\in \mathbb{Z}/p^m\mathbb{Z}}\sum_{\substack{{v_1,v_2\in\mathbb{Z}/p^{m+m'+m"}}\\ v_3\in\mathbb{Z}/p^{m'+m"}\mathbb{Z}}}\\ &\quad(\mathcal{F}^{-1}\alpha_{\xi\tau,p}) \left(\left(\begin{smallmatrix}p^{-m-m'}\\&p^{-m-m'}\\&&p^{-m'}\end{smallmatrix}\right) \left(\begin{smallmatrix}1&&-u_1\\&1&-u_2\\&&1\end{smallmatrix}\right) \left(C^{-1}D+\left(\begin{smallmatrix}v_1&0&0\\v_2&0&0\\v_3&0&0\end{smallmatrix}\right) \right)\left(\begin{smallmatrix}p^{-m"}\\&1\\&&1\end{smallmatrix}\right) \right). \end{aligned} \end{align} $$A direct computation by using the formula (5.7.2) shows that when ![]() $(\xi \tau )_{\mathfrak {p}}$ is ramified
$(\xi \tau )_{\mathfrak {p}}$ is ramified
 $$ \begin{align} \begin{aligned} &\sum_{u_1,u_2}\sum_{v_1,v_2,v_3}(\mathcal{F}^{-1}\alpha_{\xi\tau,p})\left(\left(\begin{smallmatrix}p^{-m-m'}\\&p^{-m-m'}\\&&p^{-m'}\end{smallmatrix}\right) \left(\begin{smallmatrix}1&&-u_1\\&1&-u_2\\&&1\end{smallmatrix}\right) \left(C^{-1}D+\left(\begin{smallmatrix}v_1&0&0\\v_2&0&0\\v_3&0&0\end{smallmatrix}\right) \right)\left(\begin{smallmatrix}p^{-m"}\\&1\\&&1\end{smallmatrix}\right) \right)\\ =&\,p^{2m}(\mathcal{F}^{-1}\alpha_{\xi\tau,p})\left(C^{-1}D\left(\begin{smallmatrix}1\\&p^{-m-m'}\\&&p^{-m-m'}\end{smallmatrix}\right) \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\sum_{u_1,u_2}\sum_{v_1,v_2,v_3}(\mathcal{F}^{-1}\alpha_{\xi\tau,p})\left(\left(\begin{smallmatrix}p^{-m-m'}\\&p^{-m-m'}\\&&p^{-m'}\end{smallmatrix}\right) \left(\begin{smallmatrix}1&&-u_1\\&1&-u_2\\&&1\end{smallmatrix}\right) \left(C^{-1}D+\left(\begin{smallmatrix}v_1&0&0\\v_2&0&0\\v_3&0&0\end{smallmatrix}\right) \right)\left(\begin{smallmatrix}p^{-m"}\\&1\\&&1\end{smallmatrix}\right) \right)\\ =&\,p^{2m}(\mathcal{F}^{-1}\alpha_{\xi\tau,p})\left(C^{-1}D\left(\begin{smallmatrix}1\\&p^{-m-m'}\\&&p^{-m-m'}\end{smallmatrix}\right) \right). \end{aligned} \end{align} $$Combining equations (5.10.5) and (5.10.6), we obtain
 $$ \begin{align*} (5.10.4) = &\,p^{6m+6m'}(\xi\tau)_{\mathfrak{p}}(p)^{2m+3m'}\left((\xi\tau)_{\bar{\mathfrak{p}}}(p)p^k\right)^{m"}\cdot \left(\xi\tau)_{\bar{\mathfrak{p}}}(p)p^3\right)^{-2m-2m'}\\ &\times f^{\text{big-cell}}_p\left(\frac{3-k}{2},(\xi_0\tau_0)^{-c}\right)\left(g\left(\begin{smallmatrix}\mathbf{1}_4\\&p^{-m-m'}\cdot\mathbf{1}_2\end{smallmatrix}\right) \right),\\ =&\,(\xi\tau)_{\mathfrak{p}}(p)^{m'}\left((\xi\tau)_{\bar{\mathfrak{p}}}(p)p^k\right)^{m"}\cdot (\xi\tau)_{\bar{\mathfrak{p}}}(\xi\tau)^{-1}_{{\mathfrak{p}}}(p)^{-2m-2m'}\\ &\times f^{\text{big-cell}}_p\left(\frac{3-k}{2},(\xi_0\tau_0)^{-c}\right)\left(g\left(\begin{smallmatrix}\mathbf{1}_4\\&p^{-m-m'}\cdot\mathbf{1}_2\end{smallmatrix}\right) \right), \end{align*} $$
$$ \begin{align*} (5.10.4) = &\,p^{6m+6m'}(\xi\tau)_{\mathfrak{p}}(p)^{2m+3m'}\left((\xi\tau)_{\bar{\mathfrak{p}}}(p)p^k\right)^{m"}\cdot \left(\xi\tau)_{\bar{\mathfrak{p}}}(p)p^3\right)^{-2m-2m'}\\ &\times f^{\text{big-cell}}_p\left(\frac{3-k}{2},(\xi_0\tau_0)^{-c}\right)\left(g\left(\begin{smallmatrix}\mathbf{1}_4\\&p^{-m-m'}\cdot\mathbf{1}_2\end{smallmatrix}\right) \right),\\ =&\,(\xi\tau)_{\mathfrak{p}}(p)^{m'}\left((\xi\tau)_{\bar{\mathfrak{p}}}(p)p^k\right)^{m"}\cdot (\xi\tau)_{\bar{\mathfrak{p}}}(\xi\tau)^{-1}_{{\mathfrak{p}}}(p)^{-2m-2m'}\\ &\times f^{\text{big-cell}}_p\left(\frac{3-k}{2},(\xi_0\tau_0)^{-c}\right)\left(g\left(\begin{smallmatrix}\mathbf{1}_4\\&p^{-m-m'}\cdot\mathbf{1}_2\end{smallmatrix}\right) \right), \end{align*} $$and the corresponding Siegel Eisenstein series paired with ![]() $\varphi \cdot (\xi _0\tau _0)^{-1}\circ \det $ over
$\varphi \cdot (\xi _0\tau _0)^{-1}\circ \det $ over ![]() $\operatorname {\mathrm {U}}(2)$ gives
$\operatorname {\mathrm {U}}(2)$ gives
Here, we use the condition that ![]() $\varphi $ has trivial central character. Both
$\varphi $ has trivial central character. Both ![]() $(\xi \tau )_{\mathfrak {p}}(p)$ and
$(\xi \tau )_{\mathfrak {p}}(p)$ and ![]() $(\xi \tau )_{\bar {\mathfrak {p}}}(p)p^k$ are p-adic units, so the form (5.10.3) is an eigenvector for the action of
$(\xi \tau )_{\bar {\mathfrak {p}}}(p)p^k$ are p-adic units, so the form (5.10.3) is an eigenvector for the action of ![]() $(U^+_{p,2})^{m}(U^+_{p,3})^{m'}(U^-_{p,1})^{m"}$ with eigenvalue a p-adic unit. This shows that the evaluations of the Klingen Eisenstein family
$(U^+_{p,2})^{m}(U^+_{p,3})^{m'}(U^-_{p,1})^{m"}$ with eigenvalue a p-adic unit. This shows that the evaluations of the Klingen Eisenstein family ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ at all
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ at all ![]() $\tau $ satisfying the conditions in Theorem 5.9.1 with
$\tau $ satisfying the conditions in Theorem 5.9.1 with ![]() $(\xi \tau )_{\mathfrak {p}}$ ramified are semiordinary. Hence,
$(\xi \tau )_{\mathfrak {p}}$ ramified are semiordinary. Hence, ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ is semiordinary.
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ is semiordinary.
6 The degenerate Fourier–Jacobi coefficients of the Klingen family
This section is devoted to proving Theorem 6.1.1, which states that the degenerate Fourier–Jacobi coefficients of ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ are divisible by the p-adic L-function attached to
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ are divisible by the p-adic L-function attached to ![]() $\mathrm {BC}(\pi )$.
$\mathrm {BC}(\pi )$.
6.1 The divisibility of the degenerate Fourier–Jacobi coefficients by p-adic L-functions
Given a cusp label ![]() $g\in C(K^p_f)$, we have the map
$g\in C(K^p_f)$, we have the map
(which corresponds to the map ![]() $\Phi _g$ in the fundamental exact sequence in part (4) of Theorem 2.9.1). Here,
$\Phi _g$ in the fundamental exact sequence in part (4) of Theorem 2.9.1). Here, ![]() $K^{\prime p}_{f,g}$ is an open subgroup of
$K^{\prime p}_{f,g}$ is an open subgroup of ![]() $\operatorname {\mathrm {GU}}(2)(\widehat {\mathbb {Z}}^{(p)})$ depending on the cusp label
$\operatorname {\mathrm {GU}}(2)(\widehat {\mathbb {Z}}^{(p)})$ depending on the cusp label ![]() $g\in C(K^p_f)$. Applying it to our Klingen Eisenstein family
$g\in C(K^p_f)$. Applying it to our Klingen Eisenstein family ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$, we get
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$, we get
Evaluating it at ![]() $g'\in \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q},f})$ gives
$g'\in \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q},f})$ gives
By the work of Kubota–Leopoldt on p-adic L-functions for Dirichlet characters, there exists a (unique) p-adic L-function ![]() ${\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}}\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]$ satisfying the interpolation property:
${\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}}\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]$ satisfying the interpolation property:
for all algebraic Hecke character ![]() $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that ![]() $\tau _{p\text {-}\mathrm {adic}}$ factors through
$\tau _{p\text {-}\mathrm {adic}}$ factors through ![]() $\Gamma _{\mathcal {K}}$ and
$\Gamma _{\mathcal {K}}$ and ![]() $\tau ^{\mathbb {Q}}_{\infty }=\mathrm {sgn}^k|\cdot |^k_{\mathbb {R}}$.
$\tau ^{\mathbb {Q}}_{\infty }=\mathrm {sgn}^k|\cdot |^k_{\mathbb {R}}$.
By [Reference Eischen and LiuEW16] (and the Archimedean computation in [Reference Eischen and WanEL]), there exists a (unique) p-adic L-function ![]() ${\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }}\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ satisfying the interpolation property: for all algebraic Hecke character
${\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }}\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ satisfying the interpolation property: for all algebraic Hecke character ![]() $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that ![]() $\tau _{p\text {-}\mathrm {adic}}$ factors through
$\tau _{p\text {-}\mathrm {adic}}$ factors through ![]() $\Gamma _{\mathcal {K}}$ and
$\Gamma _{\mathcal {K}}$ and ![]() $\xi \tau $ has
$\xi \tau $ has ![]() $\infty $-type
$\infty $-type ![]() $\left (k_1,k_2\right )$ with
$\left (k_1,k_2\right )$ with ![]() $k_1,k_2\in \mathbb {Z}$,
$k_1,k_2\in \mathbb {Z}$, ![]() $k_1\leq 0$,
$k_1\leq 0$, ![]() $k_2\geq 2-k_1$,
$k_2\geq 2-k_1$,
 $$ \begin{align} \begin{aligned} &\mathcal{L}^{\Sigma\,\cup\{\ell,\ell'\}}_{\pi,\mathcal{K},\xi}(\tau_{p\text{-}\mathrm{adic}})\\ =&\, \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{2(k_2-k_1)}\frac{\Gamma(k_2)\Gamma(k_2-1)}{(2\pi i)^{2k_2-1}} \cdot \gamma_p\left(\frac{3-(k_1+k_2)}{2},\pi^{\vee}_{p}\times (\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\\ &\times L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(\frac{k_1+k_2-1}{2},\mathrm{BC}(\pi)\times\xi_0\tau_0\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\mathcal{L}^{\Sigma\,\cup\{\ell,\ell'\}}_{\pi,\mathcal{K},\xi}(\tau_{p\text{-}\mathrm{adic}})\\ =&\, \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{2(k_2-k_1)}\frac{\Gamma(k_2)\Gamma(k_2-1)}{(2\pi i)^{2k_2-1}} \cdot \gamma_p\left(\frac{3-(k_1+k_2)}{2},\pi^{\vee}_{p}\times (\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\\ &\times L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(\frac{k_1+k_2-1}{2},\mathrm{BC}(\pi)\times\xi_0\tau_0\right). \end{aligned} \end{align} $$Theorem 6.1.1. Suppose that ![]() $\varphi $ belongs to the space (5.6.11). Then for all cusp labels
$\varphi $ belongs to the space (5.6.11). Then for all cusp labels ![]() $g\in C(K^p_f)$ and
$g\in C(K^p_f)$ and ![]() $g'\in \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q},f})$, we have
$g'\in \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q},f})$, we have
in ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
Proof. For ![]() $\tau $ as in Theorem 5.9.1, that is,
$\tau $ as in Theorem 5.9.1, that is, ![]() $\tau _{p\text {-}\mathrm {adic}}$ factoring through
$\tau _{p\text {-}\mathrm {adic}}$ factoring through ![]() $\Gamma _{\mathcal {K}}$ and
$\Gamma _{\mathcal {K}}$ and ![]() $\xi \tau $ has
$\xi \tau $ has ![]() $\infty $-type
$\infty $-type ![]() $\left (0,k\right )$ with
$\left (0,k\right )$ with ![]() $k\geq 6$ even), let
$k\geq 6$ even), let ![]() $E^{\mathrm {Kling}}_{\varphi ,\xi \tau }$ be the classical Klingen Eisenstein series whose corresponding p-adic form is
$E^{\mathrm {Kling}}_{\varphi ,\xi \tau }$ be the classical Klingen Eisenstein series whose corresponding p-adic form is ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }(\tau _{p\text {-}\mathrm {adic}})$. The theorem is proved by computing
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }(\tau _{p\text {-}\mathrm {adic}})$. The theorem is proved by computing ![]() $\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(\tau _{p\text {-}\mathrm {adic}})$ with
$\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(\tau _{p\text {-}\mathrm {adic}})$ with
The value of ![]() $\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(\tau _{p\text {-}\mathrm {adic}})$ at
$\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(\tau _{p\text {-}\mathrm {adic}})$ at ![]() $g'\in \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ is the
$g'\in \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ is the ![]() $0$-th Fourier–Jacobi coefficient of the
$0$-th Fourier–Jacobi coefficient of the ![]() $E^{\mathrm {Kling}}_{\varphi ,\xi \tau }$ at
$E^{\mathrm {Kling}}_{\varphi ,\xi \tau }$ at
 $$\begin{align*}x=\left(\begin{smallmatrix}1\\&g'\\&&\nu(g')\end{smallmatrix}\right) k_{\Sigma_f,\ell,\ell'}\,w_{3,p} \end{align*}$$
$$\begin{align*}x=\left(\begin{smallmatrix}1\\&g'\\&&\nu(g')\end{smallmatrix}\right) k_{\Sigma_f,\ell,\ell'}\,w_{3,p} \end{align*}$$multiplied by ![]() $\left (\frac {\Omega _p}{\Omega _{\infty }}\right )^{2k}$, where
$\left (\frac {\Omega _p}{\Omega _{\infty }}\right )^{2k}$, where ![]() $w_{3,p}\in \operatorname {\mathrm {U}}(3,1)(\mathbb {Q}_p)$ is defined by
$w_{3,p}\in \operatorname {\mathrm {U}}(3,1)(\mathbb {Q}_p)$ is defined by
 $$\begin{align*}\varrho_{\mathfrak{p}}(w_{3,p})=\begin{pmatrix}&&1\\1\\&1\\&&&1\end{pmatrix}. \end{align*}$$
$$\begin{align*}\varrho_{\mathfrak{p}}(w_{3,p})=\begin{pmatrix}&&1\\1\\&1\\&&&1\end{pmatrix}. \end{align*}$$Note that ![]() $w_{3,p}\in \operatorname {\mathrm {U}}(3,1)(\mathbb {Q}_p)$ is also our fixed element in
$w_{3,p}\in \operatorname {\mathrm {U}}(3,1)(\mathbb {Q}_p)$ is also our fixed element in ![]() $P^{\flat }_{\mathtt {D}}(\mathbb {Z}_p)$ for obtaining the isomorphism (4.4.7)).
$P^{\flat }_{\mathtt {D}}(\mathbb {Z}_p)$ for obtaining the isomorphism (4.4.7)).
By the description of ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }(\tau _{p\text {-}\mathrm {adic}})$ in equation (5.10.3) and the doubling method formula (Theorem 5.5.1), we have
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }(\tau _{p\text {-}\mathrm {adic}})$ in equation (5.10.3) and the doubling method formula (Theorem 5.5.1), we have
with ![]() $F(f(s,\xi _0\tau _0),\varphi )$ the section in
$F(f(s,\xi _0\tau _0),\varphi )$ the section in ![]() $I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ given by
$I_{P_{\operatorname {\mathrm {GU}}(3,1)}}(s,\xi _0\tau _0)$ given by
 $$ \begin{align*} F(f(s,\tau_0),\varphi)(x)&=\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f(s,\xi_0\tau_0)(\imath(x,g_1t))\varphi(g_1t)(\xi_0\tau_0)^{-1}(\det g_1t)\,dg_1\\ &=\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f(s,\xi_0\tau_0)\left(\imath\left(k_{\Sigma_f,\ell,\ell'}\,w_{3,p},g_1\right)\right)\varphi(g'g_1)(\xi_0\tau_0)^{-1}(\det g_1)\,dg_1, \end{align*} $$
$$ \begin{align*} F(f(s,\tau_0),\varphi)(x)&=\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f(s,\xi_0\tau_0)(\imath(x,g_1t))\varphi(g_1t)(\xi_0\tau_0)^{-1}(\det g_1t)\,dg_1\\ &=\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f(s,\xi_0\tau_0)\left(\imath\left(k_{\Sigma_f,\ell,\ell'}\,w_{3,p},g_1\right)\right)\varphi(g'g_1)(\xi_0\tau_0)^{-1}(\det g_1)\,dg_1, \end{align*} $$where t is an element in ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ with
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ with ![]() $\nu (t)=\nu (x)$. What we need to compute is
$\nu (t)=\nu (x)$. What we need to compute is
 $$ \begin{align} \int_{U_{P_{\operatorname{\mathrm{GU}}(3,1)}}(\mathbb{Q})\big\backslash U_{P_{\operatorname{\mathrm{GU}}(3,1)}}(\mathbb{A}_{\mathbb{Q}})} E^{\mathrm{Kling}}\big(ux;F(f(s,\xi_0\tau_0),\varphi)\big)\,du. \end{align} $$
$$ \begin{align} \int_{U_{P_{\operatorname{\mathrm{GU}}(3,1)}}(\mathbb{Q})\big\backslash U_{P_{\operatorname{\mathrm{GU}}(3,1)}}(\mathbb{A}_{\mathbb{Q}})} E^{\mathrm{Kling}}\big(ux;F(f(s,\xi_0\tau_0),\varphi)\big)\,du. \end{align} $$It follows from [Reference Mœglin and WaldspurgerMW94, II.1.7] that
The Archimedean computation in [Reference WanWan15, Corollary 5.11] shows that for our choice of ![]() $f_{\infty }(s,\xi _0\tau _0)$ in §5.7 and
$f_{\infty }(s,\xi _0\tau _0)$ in §5.7 and ![]() $k\geq 6$,
$k\geq 6$,
We reduce to compute ![]() $F(f(s,\xi _0\tau _0),\varphi )(x)$. Take arbitrary
$F(f(s,\xi _0\tau _0),\varphi )(x)$. Take arbitrary ![]() $\varphi '\in \bar {\pi }^{\operatorname {\mathrm {GU}}(2)}$ spherical away from
$\varphi '\in \bar {\pi }^{\operatorname {\mathrm {GU}}(2)}$ spherical away from ![]() $\Sigma \,\cup \{\ell ,\ell '\}$ and factorizable with respect to an isomorphism
$\Sigma \,\cup \{\ell ,\ell '\}$ and factorizable with respect to an isomorphism ![]() $\bar {\pi }^{\operatorname {\mathrm {GU}}(2)}\simeq \bigotimes _v \bar {\pi }^{\operatorname {\mathrm {GU}}(2)}_{v}$. Put
$\bar {\pi }^{\operatorname {\mathrm {GU}}(2)}\simeq \bigotimes _v \bar {\pi }^{\operatorname {\mathrm {GU}}(2)}_{v}$. Put

Then we have

where for ![]() $g_v\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Q}_v)$,
$g_v\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Q}_v)$,
 $$ \begin{align} \begin{aligned} &Z_v\left(f_v(s,\xi_0\tau_0),g_v,\varphi_{v},\varphi^{\prime}_v\right)\\ =&\,\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_v)}f_v(s,\xi_0\tau_0)(\imath(g_v,g_1))(\xi_0\tau_0)^{-1}_{v}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_v(g_1)\varphi_{v},\varphi^{\prime}_v\right>\,dg_1. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &Z_v\left(f_v(s,\xi_0\tau_0),g_v,\varphi_{v},\varphi^{\prime}_v\right)\\ =&\,\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_v)}f_v(s,\xi_0\tau_0)(\imath(g_v,g_1))(\xi_0\tau_0)^{-1}_{v}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_v(g_1)\varphi_{v},\varphi^{\prime}_v\right>\,dg_1. \end{aligned} \end{align} $$ The restriction of ![]() to
to ![]() $\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_v)$ is a section in the degenerate principal series of
$\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_v)$ is a section in the degenerate principal series of ![]() $\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_v)$ inducing
$\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_v)$ inducing ![]() $\xi _0\tau _0|\cdot |^{s+\frac {1}{2}}_{\mathbb {A}_{\mathcal {K}}}$. Hence, the integral (6.1.5) is essentially a doubling zeta integral. We have the following formulas.
$\xi _0\tau _0|\cdot |^{s+\frac {1}{2}}_{\mathbb {A}_{\mathcal {K}}}$. Hence, the integral (6.1.5) is essentially a doubling zeta integral. We have the following formulas.
– The Archimedean place.
 $$ \begin{align*} Z_{\infty}\left(f_{\infty}(s,\xi_0\tau_0),\mathbf{1}_4,\varphi_{\infty},\varphi^{\prime}_{\infty}\right) =\left<\varphi_{\infty},\varphi^{\prime}_{\infty}\right> \end{align*} $$
$$ \begin{align*} Z_{\infty}\left(f_{\infty}(s,\xi_0\tau_0),\mathbf{1}_4,\varphi_{\infty},\varphi^{\prime}_{\infty}\right) =\left<\varphi_{\infty},\varphi^{\prime}_{\infty}\right> \end{align*} $$because
 ,
,  $\varphi _{\infty }$,
$\varphi _{\infty }$,  $\varphi ^{\prime }_{\infty }$ are all invariant under
$\varphi ^{\prime }_{\infty }$ are all invariant under  $\operatorname {\mathrm {U}}(2)(\mathbb {R})$.
$\operatorname {\mathrm {U}}(2)(\mathbb {R})$.–
 $v\notin \Sigma \,\cup \{\ell ,\ell ',p\}$.
$v\notin \Sigma \,\cup \{\ell ,\ell ',p\}$.  $$ \begin{align*} Z_v\left(f_v(s,\xi_0\tau_0),\mathbf{1}_4,\varphi_{v},\varphi^{\prime}_v\right) =d_{2,v}\left(s+\frac{1}{2},\xi_0\tau_0\right)^{-1}\cdot L_v\left(s+1,\mathrm{BC}(\pi)\times\xi_0\tau_{0}\right) \end{align*} $$
$$ \begin{align*} Z_v\left(f_v(s,\xi_0\tau_0),\mathbf{1}_4,\varphi_{v},\varphi^{\prime}_v\right) =d_{2,v}\left(s+\frac{1}{2},\xi_0\tau_0\right)^{-1}\cdot L_v\left(s+1,\mathrm{BC}(\pi)\times\xi_0\tau_{0}\right) \end{align*} $$with
 $$\begin{align*}{d_{2,v}\left(s,\xi_0\tau_0\right)} = \prod_{j=1}^2 L_v(2s+1+j,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0}\eta^{2-j}_{\mathcal{K}/\mathbb{Q}}). \end{align*}$$
$$\begin{align*}{d_{2,v}\left(s,\xi_0\tau_0\right)} = \prod_{j=1}^2 L_v(2s+1+j,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0}\eta^{2-j}_{\mathcal{K}/\mathbb{Q}}). \end{align*}$$This follows from the standard formula for unramified local doubling zeta integrals [Reference Lapid and RallisLR05, Proposition 3, Remark 3].
–
 $v\in \Sigma \,\cup \{\ell ,\ell '\}$. By [Reference WanWan20, Lemma 6.20] or an easy direct computation, one can see that for
$v\in \Sigma \,\cup \{\ell ,\ell '\}$. By [Reference WanWan20, Lemma 6.20] or an easy direct computation, one can see that for  $\varphi $ in the space (5.6.11),
$\varphi $ in the space (5.6.11),  $$\begin{align*}Z_v\left(f_v(s,\xi_0\tau_0),k_v,\varphi_v,\varphi^{\prime}_v\right)=0, \quad\text{if }k_v\notin P_{\operatorname{\mathrm{U}}(3,1)}(\mathbb{Z}_v)\begin{pmatrix}&&1\\&\mathbf{1}_2\\-1\end{pmatrix} P_{\operatorname{\mathrm{U}}(3,1)}(\mathbb{Z}_v), \end{align*}$$
$$\begin{align*}Z_v\left(f_v(s,\xi_0\tau_0),k_v,\varphi_v,\varphi^{\prime}_v\right)=0, \quad\text{if }k_v\notin P_{\operatorname{\mathrm{U}}(3,1)}(\mathbb{Z}_v)\begin{pmatrix}&&1\\&\mathbf{1}_2\\-1\end{pmatrix} P_{\operatorname{\mathrm{U}}(3,1)}(\mathbb{Z}_v), \end{align*}$$and for
 $k_v$ such that
$k_v$ such that  $Z_v\left (f_v(s,\xi _0\tau _0),k_v,\varphi _v,\varphi ^{\prime }_v\right )\neq 0$,
$Z_v\left (f_v(s,\xi _0\tau _0),k_v,\varphi _v,\varphi ^{\prime }_v\right )\neq 0$,  $$ \begin{align*} Z_v\left(f_v(s,\xi_0\tau_0),k_v,\varphi_{v},\varphi^{\prime}_v\right) =\mathrm{vol}(\mathfrak{Y}_{c_v})\cdot\left((\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_v(q_v)|q_v|^{s+\frac{3}{2}}_v\right)^{-c_v}\left<\varphi_{v},\varphi^{\prime}_v\right>, \end{align*} $$
$$ \begin{align*} Z_v\left(f_v(s,\xi_0\tau_0),k_v,\varphi_{v},\varphi^{\prime}_v\right) =\mathrm{vol}(\mathfrak{Y}_{c_v})\cdot\left((\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)_v(q_v)|q_v|^{s+\frac{3}{2}}_v\right)^{-c_v}\left<\varphi_{v},\varphi^{\prime}_v\right>, \end{align*} $$where
 $\mathfrak {Y}_{c_v}$ is an open subgroup of
$\mathfrak {Y}_{c_v}$ is an open subgroup of  $\{k^{\prime }_v\in \operatorname {\mathrm {U}}(2)(\mathbb {Z}_v):k^{\prime }_v\equiv \mathbf {1}_2\ \ \mod q^{c_v}_v\}$, and
$\{k^{\prime }_v\in \operatorname {\mathrm {U}}(2)(\mathbb {Z}_v):k^{\prime }_v\equiv \mathbf {1}_2\ \ \mod q^{c_v}_v\}$, and  $c_v$ is the positive integer in the definition of
$c_v$ is the positive integer in the definition of  $f_v(s,\xi _0\tau _0)$ in equation (5.7.1).
$f_v(s,\xi _0\tau _0)$ in equation (5.7.1).– The place p.
(6.1.6) $$ \begin{align} Z_p\left(f_p(s,\xi_0\tau_0),w_{3,p},\varphi_p,\varphi^{\prime}_p\right) =\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right) \gamma_p\left(-s,\pi_p\times(\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\left<\varphi_{p},\varphi^{\prime}_p\right>. \end{align} $$
$$ \begin{align} Z_p\left(f_p(s,\xi_0\tau_0),w_{3,p},\varphi_p,\varphi^{\prime}_p\right) =\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right) \gamma_p\left(-s,\pi_p\times(\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\left<\varphi_{p},\varphi^{\prime}_p\right>. \end{align} $$See §6.2 for the computation. Note that we only need the value at
 $w_{3,p}\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Q}_p)$ rather than a general
$w_{3,p}\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Q}_p)$ rather than a general  $k_p\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Z}_p)$. This significantly simplifies the computation. The value at a general
$k_p\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Z}_p)$. This significantly simplifies the computation. The value at a general  $k_p\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Z}_p)$ can be difficult to compute since intertwining operators are not easy to compute completely.
$k_p\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {Z}_p)$ can be difficult to compute since intertwining operators are not easy to compute completely.
Combining the local formulas, since ![]() $\varphi '$ is arbitrary, we see that for
$\varphi '$ is arbitrary, we see that for ![]() $\tau $ as in Theorem 5.9.1,
$\tau $ as in Theorem 5.9.1, ![]() $F(f(s,\xi _0\tau _0),\varphi )(x)\big |_{s=\frac {k-3}{2}}$ is either
$F(f(s,\xi _0\tau _0),\varphi )(x)\big |_{s=\frac {k-3}{2}}$ is either ![]() $0$ or equals
$0$ or equals
 $$ \begin{align*} &d^{\,\Sigma\,\cup\{\infty,p,\ell,\ell'\}}_3(s,\xi_0\tau_0)^{-1} \cdot C_{\Sigma\cup\{\ell,\ell'\}}\cdot \gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right) L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(2s+1,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0\right)\\ &\times \gamma_p\left(-s,\pi_p\times(\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right) L^{\Sigma\,\cup\{\infty,\ell,\ell',p\}}\left(s+1,\mathrm{BC}(\pi)\times\xi_0\tau_0\right)\Big|_{s=\frac{k-3}{2}}\cdot \varphi(g') \end{align*} $$
$$ \begin{align*} &d^{\,\Sigma\,\cup\{\infty,p,\ell,\ell'\}}_3(s,\xi_0\tau_0)^{-1} \cdot C_{\Sigma\cup\{\ell,\ell'\}}\cdot \gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right) L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(2s+1,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0\right)\\ &\times \gamma_p\left(-s,\pi_p\times(\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right) L^{\Sigma\,\cup\{\infty,\ell,\ell',p\}}\left(s+1,\mathrm{BC}(\pi)\times\xi_0\tau_0\right)\Big|_{s=\frac{k-3}{2}}\cdot \varphi(g') \end{align*} $$for some ![]() $C_{\Sigma \cup \{\ell ,\ell '\}}\in L$ independent of
$C_{\Sigma \cup \{\ell ,\ell '\}}\in L$ independent of ![]() $\tau $. Combining this formula with the normalization (5.9.1), we see that at all
$\tau $. Combining this formula with the normalization (5.9.1), we see that at all ![]() $\tau _{a\text {-}\mathrm {adic}}$ as in Theorem 5.9.1, if
$\tau _{a\text {-}\mathrm {adic}}$ as in Theorem 5.9.1, if ![]() $\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(g')$ is nonzero, then its value agree with the value of
$\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(g')$ is nonzero, then its value agree with the value of ![]() $C_{\Sigma \cup \{\ell ,\ell '\}}\cdot \mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$. Evaluations at these
$C_{\Sigma \cup \{\ell ,\ell '\}}\cdot \mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$. Evaluations at these ![]() $\tau _{p\text {-}\mathrm {adic}}$’s uniquely determine elements in
$\tau _{p\text {-}\mathrm {adic}}$’s uniquely determine elements in ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$. Therefore,
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$. Therefore, ![]() $\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(g')$ is either
$\Phi _{g}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }\right )(g')$ is either ![]() $0$ or equals
$0$ or equals ![]() $C_{\Sigma \cup \{\ell ,\ell '\}}\cdot \mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$, and in particular the desired divisibility holds in
$C_{\Sigma \cup \{\ell ,\ell '\}}\cdot \mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$, and in particular the desired divisibility holds in ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
6.2 The computation of local zeta integrals at p
The ramification conditions in [Reference WanWan20, Definition 6.30] on ![]() $\xi _{0,p}\tau _{0,p}$ and the characters from which
$\xi _{0,p}\tau _{0,p}$ and the characters from which ![]() $\pi _p$ is induced are not satisfied in our case here because our
$\pi _p$ is induced are not satisfied in our case here because our ![]() $\pi _p$ is unramified. Those conditions are used in loc.cit to simplify the computation involving the intertwining operators. Here, we use the functional equation for doubling zeta integrals to handle the intertwining operator and compute
$\pi _p$ is unramified. Those conditions are used in loc.cit to simplify the computation involving the intertwining operators. Here, we use the functional equation for doubling zeta integrals to handle the intertwining operator and compute ![]() $Z_p\left (f_p(s,\xi _0\tau _0),w_{3,p},\varphi _p,\varphi ^{\prime }_p\right )$.
$Z_p\left (f_p(s,\xi _0\tau _0),w_{3,p},\varphi _p,\varphi ^{\prime }_p\right )$.
Proof of equation (6.1.6).
Inside the degenerate principal series on ![]() $\operatorname {\mathrm {GU}}(2,2)(\mathbb {Q}_p)$ inducing the character
$\operatorname {\mathrm {GU}}(2,2)(\mathbb {Q}_p)$ inducing the character ![]() $(\xi _0\tau _0)^{-c}_{p}|\cdot |^{-s}$, we define the section
$(\xi _0\tau _0)^{-c}_{p}|\cdot |^{-s}$, we define the section ![]() $f_p^{\operatorname {\mathrm {U}}(2,2)}(-s,(\xi _0\tau _0)^{-c})$ as
$f_p^{\operatorname {\mathrm {U}}(2,2)}(-s,(\xi _0\tau _0)^{-c})$ as

where the Schwartz function ![]() $\alpha _{\xi \tau ,p}$ is defined in equation (5.7.2). Then we have
$\alpha _{\xi \tau ,p}$ is defined in equation (5.7.2). Then we have

where ![]() $\jmath :\operatorname {\mathrm {U}}(2,2)\rightarrow \operatorname {\mathrm {U}}(3,3)$ is defined as
$\jmath :\operatorname {\mathrm {U}}(2,2)\rightarrow \operatorname {\mathrm {U}}(3,3)$ is defined as
 $$\begin{align*}\jmath\begin{pmatrix}A&B\\C&D\end{pmatrix}=\begin{pmatrix}1\\&A&&B\\&&1\\&C&&D\end{pmatrix}. \end{align*}$$
$$\begin{align*}\jmath\begin{pmatrix}A&B\\C&D\end{pmatrix}=\begin{pmatrix}1\\&A&&B\\&&1\\&C&&D\end{pmatrix}. \end{align*}$$To see equation (6.2.1), writing  $g_2=\begin {pmatrix}A&B\\C&D\end {pmatrix}$, we have
$g_2=\begin {pmatrix}A&B\\C&D\end {pmatrix}$, we have

and

It follows that the integrand of the left-hand side of equation (6.2.1) equals

so

Put  $\mathcal {S}_0=\begin {pmatrix}1&-\frac {\zeta _0}{2}\\-1 &-\frac {\zeta _0}{2}\end {pmatrix}$ and
$\mathcal {S}_0=\begin {pmatrix}1&-\frac {\zeta _0}{2}\\-1 &-\frac {\zeta _0}{2}\end {pmatrix}$ and ![]() $\Upsilon _{0,p}$ to be the element in
$\Upsilon _{0,p}$ to be the element in ![]() $\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_p)$ such that
$\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_p)$ such that ![]() $\varrho _{\mathfrak {p}}(\Upsilon _{0,p})=\mathcal {S}^{-1}_0$. Set
$\varrho _{\mathfrak {p}}(\Upsilon _{0,p})=\mathcal {S}^{-1}_0$. Set
 $$ \begin{align} \imath_0:\operatorname{\mathrm{U}}(2)\times\operatorname{\mathrm{U}}(2)&\longrightarrow \operatorname{\mathrm{U}}(2,2), &\imath_0(g_1,g^{\prime}_1)=\mathcal{S}^{-1}_0\begin{pmatrix}g_1\\&g^{\prime}_1\end{pmatrix}. \end{align} $$
$$ \begin{align} \imath_0:\operatorname{\mathrm{U}}(2)\times\operatorname{\mathrm{U}}(2)&\longrightarrow \operatorname{\mathrm{U}}(2,2), &\imath_0(g_1,g^{\prime}_1)=\mathcal{S}^{-1}_0\begin{pmatrix}g_1\\&g^{\prime}_1\end{pmatrix}. \end{align} $$By the definition of the intertwining operator ![]() $M_p(-s,\xi \tau ^{-1}_0(\xi _0\tau _0)^{-c})$ (in equations (5.7.4)) and (6.2.1),
$M_p(-s,\xi \tau ^{-1}_0(\xi _0\tau _0)^{-c})$ (in equations (5.7.4)) and (6.2.1),

and
 $$ \begin{align*} &f_p(s,\xi_0\tau_0)\left(\imath(w_{3,p},g_1)\right)\\ =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\\ &\times M^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right) f^{\operatorname{\mathrm{U}}(2,2)}_p(\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right). \end{align*} $$
$$ \begin{align*} &f_p(s,\xi_0\tau_0)\left(\imath(w_{3,p},g_1)\right)\\ =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\\ &\times M^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right) f^{\operatorname{\mathrm{U}}(2,2)}_p(\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right). \end{align*} $$By the functional equation of the local doubling zeta integral [Reference Lapid and RallisLR05, (19)(25)],
 $$ \begin{align*} &\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)}M^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right) f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)\\ &\hspace{15em}\times(\xi_0\tau_0)^c_{p}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_p(g_1)\varphi_{p},\varphi^{\prime}_p\right>\,dg_1\\ =&\,c_{2,p}\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c},\left(\begin{smallmatrix}&\mathbf{1}_2\\\mathbf{1}_2\end{smallmatrix}\right) \right)\gamma_p\left(-s,\mathrm{BC}(\pi)\times (\xi_0\tau_0)^{-c}\right)\\ &\times\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)} f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)(\xi_0\tau_0)^{c}_{p}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_p(g_1)\varphi_{p},\varphi^{\prime}_p\right>\,dg_1, \end{align*} $$
$$ \begin{align*} &\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)}M^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right) f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)\\ &\hspace{15em}\times(\xi_0\tau_0)^c_{p}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_p(g_1)\varphi_{p},\varphi^{\prime}_p\right>\,dg_1\\ =&\,c_{2,p}\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c},\left(\begin{smallmatrix}&\mathbf{1}_2\\\mathbf{1}_2\end{smallmatrix}\right) \right)\gamma_p\left(-s,\mathrm{BC}(\pi)\times (\xi_0\tau_0)^{-c}\right)\\ &\times\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)} f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)(\xi_0\tau_0)^{c}_{p}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_p(g_1)\varphi_{p},\varphi^{\prime}_p\right>\,dg_1, \end{align*} $$with the factor
 $$\begin{align*}c_{2,p}\left(-s-\frac{-1}{2},(\xi_0\tau_0)^{-c},\left(\begin{smallmatrix}&\mathbf{1}_2\\\mathbf{1}_2\end{smallmatrix}\right) \right)=\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)^{-1}\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)^{-1}\right)^{-1} \end{align*}$$
$$\begin{align*}c_{2,p}\left(-s-\frac{-1}{2},(\xi_0\tau_0)^{-c},\left(\begin{smallmatrix}&\mathbf{1}_2\\\mathbf{1}_2\end{smallmatrix}\right) \right)=\gamma_p\left(-2s-1,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)^{-1}\eta_{\mathcal{K}/\mathbb{Q}}\right)^{-1}\gamma_p\left(-2s-2,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0)^{-1}\right)^{-1} \end{align*}$$as defined in equation (5.7.5). Therefore,
 $$ \begin{align} \begin{aligned} &Z_p\left(f_p(s,\xi_0\tau_0),w_{3,p},\varphi_p,\varphi^{\prime}_p\right)\\ =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-s,\mathrm{BC}(\pi)\times (\xi_0\tau_0)^{-c}\right)\\ &\times\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)} f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)(\xi_0\tau_0)^{c}_{p}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_p(g_1)\varphi_{p},\varphi^{\prime}_p\right>\,dg_1. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &Z_p\left(f_p(s,\xi_0\tau_0),w_{3,p},\varphi_p,\varphi^{\prime}_p\right)\\ =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-s,\mathrm{BC}(\pi)\times (\xi_0\tau_0)^{-c}\right)\\ &\times\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)} f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)(\xi_0\tau_0)^{c}_{p}(\det g_1)\left<\pi^{\operatorname{\mathrm{GU}}(2)}_p(g_1)\varphi_{p},\varphi^{\prime}_p\right>\,dg_1. \end{aligned} \end{align} $$By noting that
 $$\begin{align*}f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)=\mathcal{F}^{-1}\alpha_{\xi\tau,p}\begin{pmatrix}0&g_1\\0&0\end{pmatrix} \end{align*}$$
$$\begin{align*}f^{\operatorname{\mathrm{U}}(2,2)}_p\left(-s-\frac{1}{2},(\xi_0\tau_0)^{-c}\right)\left(\imath_0(1,g_1)\Upsilon_{0,p}\right)=\mathcal{F}^{-1}\alpha_{\xi\tau,p}\begin{pmatrix}0&g_1\\0&0\end{pmatrix} \end{align*}$$and using the formula (5.7.2) for ![]() $\mathcal {F}^{-1}\alpha _{\xi \tau ,p}$ and that
$\mathcal {F}^{-1}\alpha _{\xi \tau ,p}$ and that ![]() $\varphi _p$ is spherical, an easy computation shows that
$\varphi _p$ is spherical, an easy computation shows that
where ![]() $p^t$,
$p^t$, ![]() $t\geq 1$, is the conductor of
$t\geq 1$, is the conductor of ![]() $(\xi _0\tau _0)_{\mathfrak {p}}$. Since
$(\xi _0\tau _0)_{\mathfrak {p}}$. Since ![]() $\pi _p$ is unramified with trivial central character, we have
$\pi _p$ is unramified with trivial central character, we have
Combining equations (6.2.3), (6.2.4) and (6.2.5), we get
 $$ \begin{align*} (6.2.3) =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-s,\mathrm{BC}(\pi)\times (\xi_0\tau_0)^{-c}\right) \gamma_p\left(s+1,\pi_p\times(\xi_0\tau_0)_{\mathfrak{p}}\right)\cdot \left<\varphi_{p},\varphi^{\prime}_p\right>\\ =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right) \gamma_p\left(-s,\pi_p\times(\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\cdot \left<\varphi_{p},\varphi^{\prime}_p\right>.\\[-36pt] \end{align*} $$
$$ \begin{align*} (6.2.3) =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right)\gamma_p\left(-s,\mathrm{BC}(\pi)\times (\xi_0\tau_0)^{-c}\right) \gamma_p\left(s+1,\pi_p\times(\xi_0\tau_0)_{\mathfrak{p}}\right)\cdot \left<\varphi_{p},\varphi^{\prime}_p\right>\\ =&\,\gamma_p\left(-2s,(\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_{0})^{-1}\right) \gamma_p\left(-s,\pi_p\times(\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\cdot \left<\varphi_{p},\varphi^{\prime}_p\right>.\\[-36pt] \end{align*} $$7 The nondegenerate Fourier–Jacobi coefficients of the Klingen family
The map (4.7.3) of taking the ![]() $\beta $-th Fourier–Jacobi coefficient along the boundary stratum indexed by the cusp label
$\beta $-th Fourier–Jacobi coefficient along the boundary stratum indexed by the cusp label ![]() $\mathbf {1}_4\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ induces
$\mathbf {1}_4\in C(K^p_fK^1_{p,n})_{\mathrm {ord}}$ induces
For ![]() $u\in \bigotimes _{v\in \Sigma _{\mathrm {ns}}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$, let
$u\in \bigotimes _{v\in \Sigma _{\mathrm {ns}}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$, let
(The group ![]() $\operatorname {\mathrm {GU}}(3,1)(\mathbb {A}^p_f)$ acts on the Igusa tower and acts on
$\operatorname {\mathrm {GU}}(3,1)(\mathbb {A}^p_f)$ acts on the Igusa tower and acts on ![]() $V_{\operatorname {\mathrm {GU}}(3,1)}$, and
$V_{\operatorname {\mathrm {GU}}(3,1)}$, and ![]() $\left (\begin {smallmatrix}u\\&\mathbf {1}_2\\&&u\end {smallmatrix}\right ) \boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ denotes the action of
$\left (\begin {smallmatrix}u\\&\mathbf {1}_2\\&&u\end {smallmatrix}\right ) \boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ denotes the action of ![]() $\left (\begin {smallmatrix}u\\&\mathbf {1}_2\\&&u\end {smallmatrix}\right ) $ on
$\left (\begin {smallmatrix}u\\&\mathbf {1}_2\\&&u\end {smallmatrix}\right ) $ on ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$.) The goal of this section is to prove Proposition 7.11.3 on the nonvanishing properties of the
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$.) The goal of this section is to prove Proposition 7.11.3 on the nonvanishing properties of the ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$’s.
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$’s.
In §7.1-§7.2, we briefly recall some basics we will use about Weil representations, theta series, Jacobi forms and p-adic Petersson inner products. In §7.4 and §7.5, we unfold the Siegel Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,3)$ to compute the nondegenerate Fourier–Jacobi coefficients of the Klingen Eisenstein series on
$\operatorname {\mathrm {GU}}(3,3)$ to compute the nondegenerate Fourier–Jacobi coefficients of the Klingen Eisenstein series on ![]() $\operatorname {\mathrm {GU}}(3,1)$, and sketch our strategy for relating them to certain L-values, for which we can apply mod p nonvanishing results. Following that strategy, we need to choose an auxiliary Jacobi form on
$\operatorname {\mathrm {GU}}(3,1)$, and sketch our strategy for relating them to certain L-values, for which we can apply mod p nonvanishing results. Following that strategy, we need to choose an auxiliary Jacobi form on ![]() $\operatorname {\mathrm {U}}(2)$ and two CM families on
$\operatorname {\mathrm {U}}(2)$ and two CM families on ![]() $\operatorname {\mathrm {U}}(2)$. §7.6-§7.10 are about constructing the auxiliary Jacobi form and CM families and some other technical preparations. The desired nonvanishing property is proved in §7.11.
$\operatorname {\mathrm {U}}(2)$. §7.6-§7.10 are about constructing the auxiliary Jacobi form and CM families and some other technical preparations. The desired nonvanishing property is proved in §7.11.
7.1 The Schrödinger model of Weil representation and the intertwining maps for different polarizations
The nondegenerate terms in the Fourier–Jacobi expansion of an automorphic form on ![]() $\operatorname {\mathrm {GU}}(3,1)(\mathbb {A})$ are Jacobi forms on the Jacobi group associated
$\operatorname {\mathrm {GU}}(3,1)(\mathbb {A})$ are Jacobi forms on the Jacobi group associated ![]() $\operatorname {\mathrm {GU}}(2)$.
$\operatorname {\mathrm {GU}}(2)$.
Let V (resp. ![]() $V^-$) be the two-dimensional skew-Hermitian space
$V^-$) be the two-dimensional skew-Hermitian space ![]() $(\mathcal {K}^2,\zeta _0)$ (resp.
$(\mathcal {K}^2,\zeta _0)$ (resp. ![]() $(\mathcal {K}^2,-\zeta _0)$). We write elements in
$(\mathcal {K}^2,-\zeta _0)$). We write elements in ![]() $V,V^-$ as row vectors and fix the basis
$V,V^-$ as row vectors and fix the basis ![]() $v_1=(1,0),v_2=(0,1)$ for V (resp.
$v_1=(1,0),v_2=(0,1)$ for V (resp. ![]() $v^-_1=(1,0),v^-_2=(0,1)$ for
$v^-_1=(1,0),v^-_2=(0,1)$ for ![]() $V^-$). With respect to the fixed basis, the unitary groups
$V^-$). With respect to the fixed basis, the unitary groups ![]() $\operatorname {\mathrm {U}}(V)$ and
$\operatorname {\mathrm {U}}(V)$ and ![]() $\operatorname {\mathrm {U}}(V^-)$ are naturally identified with our
$\operatorname {\mathrm {U}}(V^-)$ are naturally identified with our ![]() $\operatorname {\mathrm {U}}(2)$ (defined in equation (5.4.1)).
$\operatorname {\mathrm {U}}(2)$ (defined in equation (5.4.1)).
We fix the basis ![]() $v_1,v_2,v^-_1,v^-_2$ for
$v_1,v_2,v^-_1,v^-_2$ for ![]() $V\oplus V^-$ and identify
$V\oplus V^-$ and identify ![]() $\operatorname {\mathrm {U}}(V\oplus V^-)$ with the unitary group whose R-points are
$\operatorname {\mathrm {U}}(V\oplus V^-)$ with the unitary group whose R-points are

Define the unitary group ![]() $\operatorname {\mathrm {U}}(2,2)$ as
$\operatorname {\mathrm {U}}(2,2)$ as

We fix the isomorphism
 $$ \begin{align*} \operatorname{\mathrm{U}}(V\oplus V^-)&\longrightarrow \operatorname{\mathrm{U}}(2,2), &g&\longmapsto \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}g \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{U}}(V\oplus V^-)&\longrightarrow \operatorname{\mathrm{U}}(2,2), &g&\longmapsto \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}g \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}, \end{align*} $$which induces the embedding
 $$ \begin{align*} \operatorname{\mathrm{U}}(2)\times\operatorname{\mathrm{U}}(2)&\longrightarrow\operatorname{\mathrm{U}}(2,2), &(g_1,g_2)&\longmapsto \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&g_2\end{pmatrix} \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{U}}(2)\times\operatorname{\mathrm{U}}(2)&\longrightarrow\operatorname{\mathrm{U}}(2,2), &(g_1,g_2)&\longmapsto \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&g_2\end{pmatrix} \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}. \end{align*} $$For a nonzero ![]() $\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})$, denote by
$\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})$, denote by ![]() $W_{\beta }$ the one-dimensional Hermitian space
$W_{\beta }$ the one-dimensional Hermitian space ![]() $(\mathcal {K},\beta )$. Fix a basis
$(\mathcal {K},\beta )$. Fix a basis ![]() $w_{\beta }=1$ for
$w_{\beta }=1$ for ![]() $W_{\beta }$, and we can identify
$W_{\beta }$, and we can identify ![]() $\operatorname {\mathrm {U}}(W_{\beta })$ with the group
$\operatorname {\mathrm {U}}(W_{\beta })$ with the group ![]() $\operatorname {\mathrm {U}}(1)$ defined by
$\operatorname {\mathrm {U}}(1)$ defined by
We consider the Weil representations for the dual pairs ![]() $\operatorname {\mathrm {U}}(2)\times \operatorname {\mathrm {U}}(1)$ and
$\operatorname {\mathrm {U}}(2)\times \operatorname {\mathrm {U}}(1)$ and ![]() $\operatorname {\mathrm {U}}(2,2)\times \operatorname {\mathrm {U}}(1)$. The space
$\operatorname {\mathrm {U}}(2,2)\times \operatorname {\mathrm {U}}(1)$. The space ![]() $V\otimes _{\mathcal {K}} W_{\beta }$ is a four-dimensional
$V\otimes _{\mathcal {K}} W_{\beta }$ is a four-dimensional ![]() $\mathbb {Q}$-vector space equipped with a nondegenerate symplectic pairing induced from the skew-Hermitian form on V and the Hermitian form on
$\mathbb {Q}$-vector space equipped with a nondegenerate symplectic pairing induced from the skew-Hermitian form on V and the Hermitian form on ![]() $W_{\beta }$. The group
$W_{\beta }$. The group ![]() $\operatorname {\mathrm {U}}(V)\times \operatorname {\mathrm {U}}(W_{\beta })$ embeds into
$\operatorname {\mathrm {U}}(V)\times \operatorname {\mathrm {U}}(W_{\beta })$ embeds into ![]() $\operatorname {\mathrm {Sp}}(V\otimes _{\mathcal {K}} W_{\beta })$ and forms a reductive dual pair. Let
$\operatorname {\mathrm {Sp}}(V\otimes _{\mathcal {K}} W_{\beta })$ and forms a reductive dual pair. Let ![]() $\widetilde {\operatorname {\mathrm {Sp}}}(V\otimes _{\mathcal {K}} W_{\beta })$ denote the metaplectic group. Given a pair of Hecke characters
$\widetilde {\operatorname {\mathrm {Sp}}}(V\otimes _{\mathcal {K}} W_{\beta })$ denote the metaplectic group. Given a pair of Hecke characters ![]() $\lambda _V,\lambda _{W_{\beta }}:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that
$\lambda _V,\lambda _{W_{\beta }}:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ such that ![]() $\lambda _V|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta _{\mathcal {K}/\mathbb {Q}}^{\dim _{\mathcal {K}} V}$ and
$\lambda _V|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta _{\mathcal {K}/\mathbb {Q}}^{\dim _{\mathcal {K}} V}$ and ![]() $\lambda _{W_{\beta }}|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta ^{\dim _{\mathcal {K}} W_{\beta }}_{\mathcal {K}/\mathbb {Q}}$, there is a splitting
$\lambda _{W_{\beta }}|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta ^{\dim _{\mathcal {K}} W_{\beta }}_{\mathcal {K}/\mathbb {Q}}$, there is a splitting
for all places v of ![]() $\mathbb {Q}$. The Weil representation of
$\mathbb {Q}$. The Weil representation of ![]() $\widetilde {\operatorname {\mathrm {Sp}}}(V_v\otimes _{\mathcal {K}} W_{\beta ,v})$ (with respect to our fixed additive character
$\widetilde {\operatorname {\mathrm {Sp}}}(V_v\otimes _{\mathcal {K}} W_{\beta ,v})$ (with respect to our fixed additive character ![]() $\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}:\mathbb {Q}\backslash \mathbb {A}_{\mathbb {Q}}\rightarrow \mathbb {C}^{\times }$ in equation (1.0.5)) induces the Weil representation of
$\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}:\mathbb {Q}\backslash \mathbb {A}_{\mathbb {Q}}\rightarrow \mathbb {C}^{\times }$ in equation (1.0.5)) induces the Weil representation of ![]() $\operatorname {\mathrm {U}}(V_v)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$. Similarly, with respect to
$\operatorname {\mathrm {U}}(V_v)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$. Similarly, with respect to ![]() $\lambda _{V^-},\lambda _{V\oplus V^-}:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ satisfying
$\lambda _{V^-},\lambda _{V\oplus V^-}:\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ satisfying ![]() $\lambda _{V^-}|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta _{\mathcal {K}/\mathbb {Q}}^{\dim _{\mathcal {K}} V^-}$,
$\lambda _{V^-}|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta _{\mathcal {K}/\mathbb {Q}}^{\dim _{\mathcal {K}} V^-}$, ![]() $\lambda _{V\oplus V^-} |_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta _{\mathcal {K}/\mathbb {Q}}^{\dim _{\mathcal {K}} V+\dim _{\mathcal {K}} V^-}$, we have the Weil representations of
$\lambda _{V\oplus V^-} |_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\eta _{\mathcal {K}/\mathbb {Q}}^{\dim _{\mathcal {K}} V+\dim _{\mathcal {K}} V^-}$, we have the Weil representations of ![]() $\operatorname {\mathrm {U}}(V^-_v)\times U(W_{\beta ,v})$ and
$\operatorname {\mathrm {U}}(V^-_v)\times U(W_{\beta ,v})$ and ![]() $\operatorname {\mathrm {U}}(V\oplus V^-_v)\times U(W_{\beta ,v})$.
$\operatorname {\mathrm {U}}(V\oplus V^-_v)\times U(W_{\beta ,v})$.
We choose our ![]() $\lambda _V,\lambda _{V^-},\lambda _{W_{\beta }}$ as
$\lambda _V,\lambda _{V^-},\lambda _{W_{\beta }}$ as
where ![]() $\lambda $ is the Hecke character fixed in §5.1.
$\lambda $ is the Hecke character fixed in §5.1.
Remark 7.1.1. In some literature, instead of ![]() $\lambda _V=\lambda _{V^-}=\lambda ^2$,
$\lambda _V=\lambda _{V^-}=\lambda ^2$, ![]() $\lambda _V=\lambda _{V^-}=\mathrm {triv}$ is used.
$\lambda _V=\lambda _{V^-}=\mathrm {triv}$ is used.
Put
Then ![]() $\mathbb {Q} e_1\oplus \mathbb {Q} e_2$ is a maximal isotropic subspace of the symplectic space
$\mathbb {Q} e_1\oplus \mathbb {Q} e_2$ is a maximal isotropic subspace of the symplectic space ![]() $V\otimes _{\mathcal {K}} W_{\beta }$. We have the polarizations
$V\otimes _{\mathcal {K}} W_{\beta }$. We have the polarizations
(where ![]() $\delta $ is our fixed totally imaginary element in
$\delta $ is our fixed totally imaginary element in ![]() $\mathcal {K}$.) The Schrödinger model of the Weil representation of
$\mathcal {K}$.) The Schrödinger model of the Weil representation of ![]() $\operatorname {\mathrm {U}}(V_v)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$ is an action of
$\operatorname {\mathrm {U}}(V_v)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$ is an action of ![]() $\operatorname {\mathrm {U}}(V_v)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$ on
$\operatorname {\mathrm {U}}(V_v)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$ on
, the space of Schwartz functions on ![]() $\mathbb {Q}_v e_1\oplus \mathbb {Q}_v e_2$. We write this action as
$\mathbb {Q}_v e_1\oplus \mathbb {Q}_v e_2$. We write this action as
Similarly, we have the polarization
and the Schrödinger model
For a place ![]() $v=\mathfrak {v}\bar {\mathfrak {v}}$ split in
$v=\mathfrak {v}\bar {\mathfrak {v}}$ split in ![]() $\mathcal {K}$, we have
$\mathcal {K}$, we have ![]() $\mathcal {K}_v\simeq \mathcal {K}_{\mathfrak {v}}\times \mathcal {K}_{\bar {\mathfrak {v}}}$ with
$\mathcal {K}_v\simeq \mathcal {K}_{\mathfrak {v}}\times \mathcal {K}_{\bar {\mathfrak {v}}}$ with ![]() $\mathcal {K}_{\mathfrak {v}}\simeq \mathcal {K}_{\bar {\mathfrak {v}}}\simeq \mathbb {Q}_v$. In addition to the above polarizations, we also consider the polarizations
$\mathcal {K}_{\mathfrak {v}}\simeq \mathcal {K}_{\bar {\mathfrak {v}}}\simeq \mathbb {Q}_v$. In addition to the above polarizations, we also consider the polarizations
 $$ \begin{align*} V_v\otimes W_{\beta,v}&=\big(\mathcal{K}_{\mathfrak{v}} e_1\oplus\mathcal{K}_{\mathfrak{v}} e_2\big)\oplus \big(\mathcal{K}_{\bar{\mathfrak{v}}} e_1\oplus\mathcal{K}_{\bar{\mathfrak{v}}} e_2\big),\\ V^-_v\otimes W_{\beta,v}&=\big(\mathcal{K}_{\mathfrak{v}} e^-_1\oplus\mathcal{K}_{\mathfrak{v}} e^-_2\big)\oplus \big(\mathcal{K}_{\bar{\mathfrak{v}}} e^-_1\oplus\mathcal{K}_{\bar{\mathfrak{v}}} e^-_2\big), \end{align*} $$
$$ \begin{align*} V_v\otimes W_{\beta,v}&=\big(\mathcal{K}_{\mathfrak{v}} e_1\oplus\mathcal{K}_{\mathfrak{v}} e_2\big)\oplus \big(\mathcal{K}_{\bar{\mathfrak{v}}} e_1\oplus\mathcal{K}_{\bar{\mathfrak{v}}} e_2\big),\\ V^-_v\otimes W_{\beta,v}&=\big(\mathcal{K}_{\mathfrak{v}} e^-_1\oplus\mathcal{K}_{\mathfrak{v}} e^-_2\big)\oplus \big(\mathcal{K}_{\bar{\mathfrak{v}}} e^-_1\oplus\mathcal{K}_{\bar{\mathfrak{v}}} e^-_2\big), \end{align*} $$and the intertwining maps
For ![]() $V\oplus V^-$, we have the polarization:
$V\oplus V^-$, we have the polarization:
Writing an element in ![]() $\mathcal {K}_v(e_1+e^-_1)\oplus \mathcal {K}_v(e_2+e^-_2)$ as
$\mathcal {K}_v(e_1+e^-_1)\oplus \mathcal {K}_v(e_2+e^-_2)$ as ![]() $X\in M_{1,2}(\mathcal {K}_v)$, for the Schrödinger model,
$X\in M_{1,2}(\mathcal {K}_v)$, for the Schrödinger model, ![]() $(g,u)\in \operatorname {\mathrm {U}}(2,2)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$,
$(g,u)\in \operatorname {\mathrm {U}}(2,2)\times \operatorname {\mathrm {U}}(W_{\beta ,v})$,
we have the following formulas:

7.2 The Heisenberg group and Jacobi forms
Jacobi forms on ![]() $\operatorname {\mathrm {U}}(2)$ and
$\operatorname {\mathrm {U}}(2)$ and ![]() $\operatorname {\mathrm {U}}(2,2)$ show up in our computation of the nondegenerate Fourier–Jacobi coefficients of the evaluations at classical points of the Klingen family
$\operatorname {\mathrm {U}}(2,2)$ show up in our computation of the nondegenerate Fourier–Jacobi coefficients of the evaluations at classical points of the Klingen family ![]() $\boldsymbol {E}^{\mathrm {Kling}}$.
$\boldsymbol {E}^{\mathrm {Kling}}$.
First, we introduce Jacobi forms on ![]() $\operatorname {\mathrm {U}}(2)$. Recall that V is the skew-Hermitian space
$\operatorname {\mathrm {U}}(2)$. Recall that V is the skew-Hermitian space ![]() $(\mathcal {K}^2,\zeta _0)$. Denote by
$(\mathcal {K}^2,\zeta _0)$. Denote by ![]() ${H(V)}$ the Heisenberg group associated to V. For a
${H(V)}$ the Heisenberg group associated to V. For a ![]() $\mathbb {Q}$-algebra R
$\mathbb {Q}$-algebra R
and the multiplication is

It is easy to see that ![]() $H(V)$ is isomorphic to
$H(V)$ is isomorphic to ![]() $U_{P_{\operatorname {\mathrm {GU}}(3,1)}}$ via
$U_{P_{\operatorname {\mathrm {GU}}(3,1)}}$ via

The Jacobi group associated to V is the semidirect product ![]() $H(V)\rtimes \operatorname {\mathrm {U}}(V)$, which we identify with a subgroup of
$H(V)\rtimes \operatorname {\mathrm {U}}(V)$, which we identify with a subgroup of ![]() $P_{\operatorname {\mathrm {GU}}(3,1)}$ by
$P_{\operatorname {\mathrm {GU}}(3,1)}$ by
where for ![]() $g_1\in \operatorname {\mathrm {U}}(V)$,
$g_1\in \operatorname {\mathrm {U}}(V)$,
 $$\begin{align*}m(g_1)=\begin{pmatrix}1\\&g_1\\&&1\end{pmatrix}. \end{align*}$$
$$\begin{align*}m(g_1)=\begin{pmatrix}1\\&g_1\\&&1\end{pmatrix}. \end{align*}$$ A Jacobi form on ![]() $H(V)\rtimes \operatorname {\mathrm {U}}(V)$ or a Jacobi form on
$H(V)\rtimes \operatorname {\mathrm {U}}(V)$ or a Jacobi form on ![]() $\operatorname {\mathrm {U}}(V)$ of index
$\operatorname {\mathrm {U}}(V)$ of index ![]() $\beta $ is a smooth function on
$\beta $ is a smooth function on ![]() $H(V)(\mathbb {Q})\rtimes \operatorname {\mathrm {U}}(V)(\mathbb {Q})\backslash H(V)(\mathbb {A}_{\mathbb {Q}})\rtimes \operatorname {\mathrm {U}}(V)(\mathbb {A}_{\mathbb {Q}})$ such that
$H(V)(\mathbb {Q})\rtimes \operatorname {\mathrm {U}}(V)(\mathbb {Q})\backslash H(V)(\mathbb {A}_{\mathbb {Q}})\rtimes \operatorname {\mathrm {U}}(V)(\mathbb {A}_{\mathbb {Q}})$ such that
– for all
 $\sigma \in \mathbb {A}_{\mathbb {Q}}$, the left translation by
$\sigma \in \mathbb {A}_{\mathbb {Q}}$, the left translation by  $\big ((0,\sigma ),\mathbf {1}_2\big )$ equals the multiplication by
$\big ((0,\sigma ),\mathbf {1}_2\big )$ equals the multiplication by  $\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}(\beta \sigma )$,
$\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}(\beta \sigma )$,– the right translation of a maximal compact subgroup and the action of the center of the universal enveloping Lie algebra at
 $\infty $ satisfy finiteness conditions.
$\infty $ satisfy finiteness conditions.
It is easy to see that a Jacobi form of index ![]() $\beta $ holomorphic at
$\beta $ holomorphic at ![]() $\infty $ of weight
$\infty $ of weight ![]() $(0,0)$ corresponds a section in
$(0,0)$ corresponds a section in ![]() $H^0\left (\mathscr {C},\mathcal {L}(\beta )\right )$ with
$H^0\left (\mathscr {C},\mathcal {L}(\beta )\right )$ with ![]() $\mathscr {C}$ a torsor over the Shimura variety of
$\mathscr {C}$ a torsor over the Shimura variety of ![]() $\operatorname {\mathrm {GU}}(2)$ of an abelian scheme isogeneous to the universal abelian scheme, and
$\operatorname {\mathrm {GU}}(2)$ of an abelian scheme isogeneous to the universal abelian scheme, and ![]() $\mathcal {L}(\beta )$ the invertible sheaf over
$\mathcal {L}(\beta )$ the invertible sheaf over ![]() $\mathscr {C}$ of
$\mathscr {C}$ of ![]() $\beta $-homogeneous functions.
$\beta $-homogeneous functions.
We will also need Jacobi forms on ![]() $\operatorname {\mathrm {U}}(2,2)$. Denote by
$\operatorname {\mathrm {U}}(2,2)$. Denote by ![]() $\mathbb {V}$ the skew-Hermitian space
$\mathbb {V}$ the skew-Hermitian space ![]() $\mathcal {K}^4$ equipped with the skew-Hermitian form
$\mathcal {K}^4$ equipped with the skew-Hermitian form  $\begin {pmatrix}&\mathbf {1}_2\\-\mathbf {1}_2\end {pmatrix}$, and by
$\begin {pmatrix}&\mathbf {1}_2\\-\mathbf {1}_2\end {pmatrix}$, and by ![]() ${H(\mathbb {V})}$ its associated Heisenberg group whose R-points for a
${H(\mathbb {V})}$ its associated Heisenberg group whose R-points for a ![]() $\mathbb {Q}$-algebra R are
$\mathbb {Q}$-algebra R are
We write an element in ![]() $H(\mathbb {V})(R)$ as
$H(\mathbb {V})(R)$ as ![]() $(x,y,\sigma )$,
$(x,y,\sigma )$, ![]() $x,y\in R\otimes _{\mathbb {Q}}\mathcal {K}^2$,
$x,y\in R\otimes _{\mathbb {Q}}\mathcal {K}^2$, ![]() $\sigma \in R$. The multiplication is given by
$\sigma \in R$. The multiplication is given by

The Jacobi group associated to ![]() $\mathbb {V}$ is the semidirect product
$\mathbb {V}$ is the semidirect product ![]() $H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(\mathbb {V})$.
$H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(\mathbb {V})$.
Denote by ![]() $P_{\operatorname {\mathrm {GU}}(3,3)}$ the parabolic subgroup of
$P_{\operatorname {\mathrm {GU}}(3,3)}$ the parabolic subgroup of ![]() $\operatorname {\mathrm {GU}}(3,3)$ consisting of elements whose entries in the first column are all
$\operatorname {\mathrm {GU}}(3,3)$ consisting of elements whose entries in the first column are all ![]() $0$ except the
$0$ except the ![]() $(1,1)$ entry, and denote by
$(1,1)$ entry, and denote by ![]() $U_{P_{\operatorname {\mathrm {GU}}(3,3)}}$ its unipotent subgroup. We identify
$U_{P_{\operatorname {\mathrm {GU}}(3,3)}}$ its unipotent subgroup. We identify ![]() $H(\mathbb {V})$ with
$H(\mathbb {V})$ with ![]() $U_{P_{\operatorname {\mathrm {GU}}(3,3)}}$ by
$U_{P_{\operatorname {\mathrm {GU}}(3,3)}}$ by

and identify ![]() $H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$ with a subgroup of
$H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$ with a subgroup of ![]() $P_{\operatorname {\mathrm {GU}}(3,3)}$ by
$P_{\operatorname {\mathrm {GU}}(3,3)}$ by
where for  $g=\begin {pmatrix}A&B\\C&D\end {pmatrix}\in \operatorname {\mathrm {U}}(2,2)$,
$g=\begin {pmatrix}A&B\\C&D\end {pmatrix}\in \operatorname {\mathrm {U}}(2,2)$,
 $$ \begin{align} m(g)=\begin{pmatrix} 1\\&A&&B\\&&1\\&C&&D\end{pmatrix}.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} m(g)=\begin{pmatrix} 1\\&A&&B\\&&1\\&C&&D\end{pmatrix}.\\[-15pt]\nonumber \end{align} $$Similarly as above, we define Jacobi forms on ![]() $\operatorname {\mathrm {U}}(\mathbb {V})$ of index
$\operatorname {\mathrm {U}}(\mathbb {V})$ of index ![]() $\beta $ to be smooth functions on
$\beta $ to be smooth functions on ![]() $H(\mathbb {V})(\mathbb {Q})\rtimes \operatorname {\mathrm {U}}(\mathbb {V})(\mathbb {Q})\backslash H(\mathbb {V})(\mathbb {A}_{\mathbb {Q}})\rtimes \operatorname {\mathrm {U}}(\mathbb {V})(\mathbb {A}_{\mathbb {Q}})$ on which the left translation of
$H(\mathbb {V})(\mathbb {Q})\rtimes \operatorname {\mathrm {U}}(\mathbb {V})(\mathbb {Q})\backslash H(\mathbb {V})(\mathbb {A}_{\mathbb {Q}})\rtimes \operatorname {\mathrm {U}}(\mathbb {V})(\mathbb {A}_{\mathbb {Q}})$ on which the left translation of ![]() $\big ((0,0,\sigma ),\mathbf {1}_4\big )$ equal the multiplication of
$\big ((0,0,\sigma ),\mathbf {1}_4\big )$ equal the multiplication of ![]() $\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}(\beta \sigma )$ plus finiteness conditions for the right translation of a maximal compact subgroup and the center of the universal enveloping Lie algebra at
$\mathbf {e}_{\mathbb {A}_{\mathbb {Q}}}(\beta \sigma )$ plus finiteness conditions for the right translation of a maximal compact subgroup and the center of the universal enveloping Lie algebra at ![]() $\infty $.
$\infty $.
We have the following embedding of skew-Hermitian spaces
 $$ \begin{align*} V&\longrightarrow \mathbb{V}, &x&\longmapsto \left(x,-\frac{x\zeta_0}{2}\right).\\[-15pt] \end{align*} $$
$$ \begin{align*} V&\longrightarrow \mathbb{V}, &x&\longmapsto \left(x,-\frac{x\zeta_0}{2}\right).\\[-15pt] \end{align*} $$It induces the embedding of unitary groups
 $$ \begin{align*} \operatorname{\mathrm{U}}(V)&\longrightarrow\operatorname{\mathrm{U}}(\mathbb{V})=\operatorname{\mathrm{U}}(2,2), &g_1&\longrightarrow \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\ -\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&\mathbf{1}_2\end{pmatrix}\begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}\\[-15pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{U}}(V)&\longrightarrow\operatorname{\mathrm{U}}(\mathbb{V})=\operatorname{\mathrm{U}}(2,2), &g_1&\longrightarrow \begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\ -\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&\mathbf{1}_2\end{pmatrix}\begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}\\[-15pt] \end{align*} $$and induces an embedding of the Jacobi groups
 $$ \begin{align} \begin{aligned} H(V)\rtimes \operatorname{\mathrm{U}}(V)&\longrightarrow H(\mathbb{V})\rtimes \operatorname{\mathrm{U}}(\mathbb{V}), \\ \left((x,\sigma),\begin{pmatrix}a&b\\c&d\end{pmatrix}\right)&\longmapsto \left(\left(x,-\frac{x\zeta_0}{2},\sigma\right),\begin{pmatrix} \mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&\mathbf{1}_2\end{pmatrix}\begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} H(V)\rtimes \operatorname{\mathrm{U}}(V)&\longrightarrow H(\mathbb{V})\rtimes \operatorname{\mathrm{U}}(\mathbb{V}), \\ \left((x,\sigma),\begin{pmatrix}a&b\\c&d\end{pmatrix}\right)&\longmapsto \left(\left(x,-\frac{x\zeta_0}{2},\sigma\right),\begin{pmatrix} \mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&\mathbf{1}_2\end{pmatrix}\begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}\right). \end{aligned} \end{align} $$From this embedding, we also get the embedding
 $$ \begin{align} \begin{aligned} \big(H(V)\rtimes \operatorname{\mathrm{U}}(V)\big)\times\operatorname{\mathrm{U}}(V^-)&\longrightarrow H(\mathbb{V})\rtimes \operatorname{\mathrm{U}}(\mathbb{V}), \\ \big(((x,\sigma),g_1),g_2\big)&\longmapsto \left(\left(x,-\frac{x\zeta_0}{2},\sigma\right),\begin{pmatrix} \mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&g_2\end{pmatrix}\begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big(H(V)\rtimes \operatorname{\mathrm{U}}(V)\big)\times\operatorname{\mathrm{U}}(V^-)&\longrightarrow H(\mathbb{V})\rtimes \operatorname{\mathrm{U}}(\mathbb{V}), \\ \big(((x,\sigma),g_1),g_2\big)&\longmapsto \left(\left(x,-\frac{x\zeta_0}{2},\sigma\right),\begin{pmatrix} \mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}^{-1}\begin{pmatrix}g_1\\&g_2\end{pmatrix}\begin{pmatrix}\mathbf{1}_2&-\frac{\zeta_0}{2}\\-\mathbf{1}_2&-\frac{\zeta_0}{2}\end{pmatrix}\right). \end{aligned} \end{align} $$ The embeddings (7.2.2)(7.2.3)(7.2.6) are compatible with the embedding ![]() $\imath $ in equation (5.5.1) in the sense that the following diagram commutes:
$\imath $ in equation (5.5.1) in the sense that the following diagram commutes:

7.3 Theta series
Given a Schwartz function ![]() (with
(with ![]() for all most all finite places v), we define the theta series
for all most all finite places v), we define the theta series ![]() , which is an automorphic form on
, which is an automorphic form on ![]() $\operatorname {\mathrm {U}}(V)(\mathbb {A}_{\mathbb {Q}})$, as
$\operatorname {\mathrm {U}}(V)(\mathbb {A}_{\mathbb {Q}})$, as
We can also define the Jacobi theta series ![]() , which is a Jacobi form on
, which is a Jacobi form on ![]() $H(V)\rtimes \operatorname {\mathrm {U}}(2)$, as
$H(V)\rtimes \operatorname {\mathrm {U}}(2)$, as

Similarly, given ![]() , we can define the theta series
, we can define the theta series ![]() on
on ![]() $\operatorname {\mathrm {U}}(V^-)(\mathbb {A}_{\mathbb {Q}})$.
$\operatorname {\mathrm {U}}(V^-)(\mathbb {A}_{\mathbb {Q}})$.
7.4 The unfolding
Given a holomorphic automorphic form ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $\operatorname {\mathrm {GU}}(3,1)(\mathbb {A})$ and
$\operatorname {\mathrm {GU}}(3,1)(\mathbb {A})$ and ![]() $g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ and
$g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ and ![]() $\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{>0}=\mathbb {Q}_{>0}$, the
$\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{>0}=\mathbb {Q}_{>0}$, the ![]() $\beta $-th Fourier–Jacobi coefficient of
$\beta $-th Fourier–Jacobi coefficient of ![]() $\mathcal {F}$ at g is defined as
$\mathcal {F}$ at g is defined as
 $$ \begin{align*} a_{\beta}(g;\mathcal{F})=\int_{\sigma\in\operatorname{\mathrm{Her}}_1(\mathcal{K})\backslash\operatorname{\mathrm{Her}}_1(\mathbb{A}_{\mathcal{K}})} \mathcal{F}\left(\begin{pmatrix}1&&\sigma\\&\mathbf{1}_2\\ &&1\end{pmatrix} g\right)\mathbf{e}_{\mathbb{A}}(-\beta\sigma)\,d\sigma. \end{align*} $$
$$ \begin{align*} a_{\beta}(g;\mathcal{F})=\int_{\sigma\in\operatorname{\mathrm{Her}}_1(\mathcal{K})\backslash\operatorname{\mathrm{Her}}_1(\mathbb{A}_{\mathcal{K}})} \mathcal{F}\left(\begin{pmatrix}1&&\sigma\\&\mathbf{1}_2\\ &&1\end{pmatrix} g\right)\mathbf{e}_{\mathbb{A}}(-\beta\sigma)\,d\sigma. \end{align*} $$With ![]() $g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ fixed, the function
$g\in \operatorname {\mathrm {GU}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ fixed, the function
 $$ \begin{align*} H(V)(\mathbb{A}_{\mathbb{Q}})\rtimes \operatorname{\mathrm{U}}(V)(\mathbb{A}_{\mathbb{Q}})&\longrightarrow \mathbb{C}\\ \big((x,\sigma),g_1\big)&\longmapsto a_{\beta}\big(u(x,\sigma)m(g_1);\mathcal{F}\big) \end{align*} $$
$$ \begin{align*} H(V)(\mathbb{A}_{\mathbb{Q}})\rtimes \operatorname{\mathrm{U}}(V)(\mathbb{A}_{\mathbb{Q}})&\longrightarrow \mathbb{C}\\ \big((x,\sigma),g_1\big)&\longmapsto a_{\beta}\big(u(x,\sigma)m(g_1);\mathcal{F}\big) \end{align*} $$is a Jacobi form on ![]() $H(V)\ltimes \operatorname {\mathrm {U}}(V)$ of index
$H(V)\ltimes \operatorname {\mathrm {U}}(V)$ of index ![]() $\beta $.
$\beta $.
The Klingen Eisenstein family ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ interpolates a normalization of the Klingen Eisenstein series
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ interpolates a normalization of the Klingen Eisenstein series ![]() , which can be expressed as the integral in equation (5.10.3). We can compute its
, which can be expressed as the integral in equation (5.10.3). We can compute its ![]() $\beta $-th Fourier–Jacobi coefficients by first computing
$\beta $-th Fourier–Jacobi coefficients by first computing
 $$ \begin{align} \begin{aligned} &E^{\mathrm{Sieg}}_{\beta}(g;f(s,\xi_0\tau_0))\\ =&\,\int_{\operatorname{\mathrm{Her}}_1(\mathcal{K})\backslash\operatorname{\mathrm{Her}}_1(\mathbb{A}_{\mathcal{K}})}E^{\mathrm{Sieg}} \left(\begin{pmatrix}1&&\sigma\\&\mathbf{1}_2\\ &&1\\ &&&\mathbf{1}_2\end{pmatrix}g;f(s,\xi_0\tau_0)\right)\mathbf{e}_{\mathbb{A}_{\mathbb{Q}}}(-\beta\sigma)\,d\sigma, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &E^{\mathrm{Sieg}}_{\beta}(g;f(s,\xi_0\tau_0))\\ =&\,\int_{\operatorname{\mathrm{Her}}_1(\mathcal{K})\backslash\operatorname{\mathrm{Her}}_1(\mathbb{A}_{\mathcal{K}})}E^{\mathrm{Sieg}} \left(\begin{pmatrix}1&&\sigma\\&\mathbf{1}_2\\ &&1\\ &&&\mathbf{1}_2\end{pmatrix}g;f(s,\xi_0\tau_0)\right)\mathbf{e}_{\mathbb{A}_{\mathbb{Q}}}(-\beta\sigma)\,d\sigma, \end{aligned} \end{align} $$and then pairing its restriction to ![]() $\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m} \operatorname {\mathrm {GU}}(2)$ with
$\operatorname {\mathrm {GU}}(3,1)\times _{\mathbb {G}_m} \operatorname {\mathrm {GU}}(2)$ with ![]() $\varphi $ on
$\varphi $ on ![]() $\operatorname {\mathrm {GU}}(2)$. By unfolding the Siegel Eisenstein series in the integrand on the right-hand side of equation (7.4.1), it’s not difficult to show that
$\operatorname {\mathrm {GU}}(2)$. By unfolding the Siegel Eisenstein series in the integrand on the right-hand side of equation (7.4.1), it’s not difficult to show that

where ![]() is the embedding of
is the embedding of ![]() $\operatorname {\mathrm {U}}(2,2)$ into
$\operatorname {\mathrm {U}}(2,2)$ into ![]() $\operatorname {\mathrm {U}}(3,3)$ as defined in equation (7.2.4). (cf [Reference WanWan15, Section 3C1])
$\operatorname {\mathrm {U}}(3,3)$ as defined in equation (7.2.4). (cf [Reference WanWan15, Section 3C1])
Definition 7.4.1. For ![]() $g_v\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v)$,
$g_v\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v)$, ![]() $x_v\in \mathcal {K}^2_v$ and
$x_v\in \mathcal {K}^2_v$ and ![]() $f_v(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _0\tau _0)$, define
$f_v(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _0\tau _0)$, define

For ![]() $g\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {A}_{\mathbb {Q}})$,
$g\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {A}_{\mathbb {Q}})$, ![]() $x\in \mathbb {A}^2_{\mathcal {K}}$ and
$x\in \mathbb {A}^2_{\mathcal {K}}$ and ![]() $f(s,\xi _0\tau _0) =\otimes _v f_v(s,\xi _0\tau _{0})$, let
$f(s,\xi _0\tau _0) =\otimes _v f_v(s,\xi _0\tau _{0})$, let
The unfolding result (7.4.2) gives the following proposition.
Proposition 7.4.2. Let ![]() $\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{>0}$ and
$\beta \in \operatorname {\mathrm {Her}}_1(\mathcal {K})_{>0}$ and ![]() $f(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)}}(s,\xi _0\tau _0)$. The
$f(s,\xi _0\tau _0)\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)}}(s,\xi _0\tau _0)$. The ![]() $\beta $-th Fourier–Jacobi coefficient of the Siegel Eisenstein series
$\beta $-th Fourier–Jacobi coefficient of the Siegel Eisenstein series ![]() at
at ![]() $g\in \operatorname {\mathrm {U}}(3,3)(\mathbb {A}_{\mathbb {Q}})$ equals
$g\in \operatorname {\mathrm {U}}(3,3)(\mathbb {A}_{\mathbb {Q}})$ equals
 $$\begin{align*}E^{\mathrm{Sieg}}_{\beta}(g;f(s,\xi_0\tau_0))=\sum_{\gamma\in Q_{\operatorname{\mathrm{U}}(2,2)}(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2,2)(\mathbb{Q})}\sum_{x\in\mathcal{K}^2} \mathrm{FJ}_{\beta}\big(m(\gamma)g,x;f(s,\xi_0\tau_0)\big), \end{align*}$$
$$\begin{align*}E^{\mathrm{Sieg}}_{\beta}(g;f(s,\xi_0\tau_0))=\sum_{\gamma\in Q_{\operatorname{\mathrm{U}}(2,2)}(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2,2)(\mathbb{Q})}\sum_{x\in\mathcal{K}^2} \mathrm{FJ}_{\beta}\big(m(\gamma)g,x;f(s,\xi_0\tau_0)\big), \end{align*}$$with ![]() $\mathrm {FJ}_{\beta }$ defined as in Definition 7.4.1 and
$\mathrm {FJ}_{\beta }$ defined as in Definition 7.4.1 and ![]() the embedding (7.2.4).
the embedding (7.2.4).
One can easily check that ![]() $\mathrm {FJ}_{\beta ,v}$ satisfies
$\mathrm {FJ}_{\beta ,v}$ satisfies

Comparing them with the formulas in equation (7.1.7) for the Schrödinger model of Weil representations, we see that for a fixed ![]() $g_v\in \operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_v)$,
$g_v\in \operatorname {\mathrm {U}}(3,3)(\mathbb {Q}_v)$, ![]() $\mathrm {FJ}_{\beta ,v}\big (u(x_v,y_v,\sigma _v)\,m(g_{1,v})g_v,x_0;f_v(s,\xi _0\tau _{0})\big )$ is essentially (a finite sum of) the product
$\mathrm {FJ}_{\beta ,v}\big (u(x_v,y_v,\sigma _v)\,m(g_{1,v})g_v,x_0;f_v(s,\xi _0\tau _{0})\big )$ is essentially (a finite sum of) the product
with ![]() $f_{2,v}\left (s,\xi _0\tau _{0}\lambda ^{-1}\right )$ a section in the degenerate principal series
$f_{2,v}\left (s,\xi _0\tau _{0}\lambda ^{-1}\right )$ a section in the degenerate principal series ![]() $I_{Q_{\operatorname {\mathrm {U}}(2,2),v}}\left (s,\xi _0\tau _{0}\lambda ^{-1}\right )$,
$I_{Q_{\operatorname {\mathrm {U}}(2,2),v}}\left (s,\xi _0\tau _{0}\lambda ^{-1}\right )$, ![]() $\Phi _v$ a Schwartz function on
$\Phi _v$ a Schwartz function on ![]() $\mathcal {K}^2_v$ and
$\mathcal {K}^2_v$ and ![]() $\omega _{\beta ,v}$ the Weil representation of
$\omega _{\beta ,v}$ the Weil representation of ![]() $\operatorname {\mathrm {U}}(2,2)$ briefly recalled in §7.1. Both
$\operatorname {\mathrm {U}}(2,2)$ briefly recalled in §7.1. Both ![]() $f_{2,v}\left (s,\xi _0\tau _0\lambda ^{-1}\right )$ and
$f_{2,v}\left (s,\xi _0\tau _0\lambda ^{-1}\right )$ and ![]() $\Phi _v$ are determined by
$\Phi _v$ are determined by ![]() $f_v(s,\xi _0\tau _{0})\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _0\tau _0)$ and
$f_v(s,\xi _0\tau _{0})\in I_{Q_{\operatorname {\mathrm {GU}}(3,3)},v}(s,\xi _0\tau _0)$ and ![]() $g_v\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v)$. The computation at an unramified place v gives
$g_v\in \operatorname {\mathrm {GU}}(3,3)(\mathbb {Q}_v)$. The computation at an unramified place v gives

Therefore, the Jacobi form on ![]() $H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$ given by
$H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$ given by
is essentially (a finite sum of) the product
with ![]() $E^{\mathrm {Sieg}}_2\left (s,\xi _0\tau _{0}\lambda ^{-1}\right )$ a Siegel Eisenstein series on
$E^{\mathrm {Sieg}}_2\left (s,\xi _0\tau _{0}\lambda ^{-1}\right )$ a Siegel Eisenstein series on ![]() $\operatorname {\mathrm {U}}(2,2)$ and
$\operatorname {\mathrm {U}}(2,2)$ and ![]() $\Theta ^J$ a Jacobi theta function on the
$\Theta ^J$ a Jacobi theta function on the ![]() $H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$. The restriction of
$H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$. The restriction of ![]() $\Theta ^J$ from
$\Theta ^J$ from ![]() $H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$ to
$H(\mathbb {V})\rtimes \operatorname {\mathrm {U}}(2,2)$ to ![]() $\big (H(V)\rtimes \operatorname {\mathrm {U}}(2)\big )\times \operatorname {\mathrm {U}}(2)$ via equation (7.2.3) is essentially (a finite sum of)
$\big (H(V)\rtimes \operatorname {\mathrm {U}}(2)\big )\times \operatorname {\mathrm {U}}(2)$ via equation (7.2.3) is essentially (a finite sum of) ![]() $\theta ^J_3\boxtimes \theta _2$, with
$\theta ^J_3\boxtimes \theta _2$, with ![]() $\theta ^J_3$ (resp.
$\theta ^J_3$ (resp. ![]() $\theta _2$) a Jacobi theta function (resp. theta function) on
$\theta _2$) a Jacobi theta function (resp. theta function) on ![]() $H(V)\rtimes \operatorname {\mathrm {U}}(2)$ (resp.
$H(V)\rtimes \operatorname {\mathrm {U}}(2)$ (resp. ![]() $\operatorname {\mathrm {U}}(2)$) attached to a Schwartz function
$\operatorname {\mathrm {U}}(2)$) attached to a Schwartz function ![]() $\phi _3$ (resp.
$\phi _3$ (resp. ![]() $\phi _2$) on
$\phi _2$) on ![]() $\mathbb {A}_{\mathcal {K}}$. Therefore,
$\mathbb {A}_{\mathcal {K}}$. Therefore,

Here, ![]() $\approx $ means equal up to normalizations and more precise formulas for local sections are needed to be an actual identity. We will also use the notation
$\approx $ means equal up to normalizations and more precise formulas for local sections are needed to be an actual identity. We will also use the notation ![]() $\approx $ several times in the next section. All the identities with
$\approx $ several times in the next section. All the identities with ![]() $\approx $ are only for the purpose of illustrating the ideas of relating the nondegenerate Fourier–Jacobi coefficients with L-values and will not be used for our rigorous analysis of
$\approx $ are only for the purpose of illustrating the ideas of relating the nondegenerate Fourier–Jacobi coefficients with L-values and will not be used for our rigorous analysis of ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$ starting from §7.6.
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$ starting from §7.6.
7.5 Our strategy of analyzing the nondegenerate Fourier–Jacobi coefficients of the Klingen Eisenstein family
Before we move on to the involved computations, we give a brief explanation of how we choose the auxiliary data to study the pairing of equation (7.4.3) with ![]() $\varphi $. The discussion in this section should also explain why the choices of the auxiliary data in §5.6 are made for constructing
$\varphi $. The discussion in this section should also explain why the choices of the auxiliary data in §5.6 are made for constructing ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ and guaranteeing that its nondegenerate Fourier–Jacobi coefficients satisfy the nonvanishing properties needed for applications.
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ and guaranteeing that its nondegenerate Fourier–Jacobi coefficients satisfy the nonvanishing properties needed for applications.
7.5.1 Choosing the auxiliary  $\theta ^J_1$
$\theta ^J_1$
The first step to analyze equation (7.4.3) is to pick a suitable Schwartz function ![]() $\phi _1$ on
$\phi _1$ on ![]() $\mathbb {A}_{\mathcal {K}}$, to which we can associate a Jacobi theta function
$\mathbb {A}_{\mathcal {K}}$, to which we can associate a Jacobi theta function ![]() ${\theta ^J_1}$ on
${\theta ^J_1}$ on ![]() $H(V)\rtimes \operatorname {\mathrm {U}}(2)$ (defined as in equation (7.3.1)), and define the linear functional
$H(V)\rtimes \operatorname {\mathrm {U}}(2)$ (defined as in equation (7.3.1)), and define the linear functional
by
Applying ![]() $l_{\theta ^J_1}$ to equation (7.4.3), we obtain an automorphic form on
$l_{\theta ^J_1}$ to equation (7.4.3), we obtain an automorphic form on ![]() $\operatorname {\mathrm {U}}(2)\times \operatorname {\mathrm {U}}(2)$ whose value at
$\operatorname {\mathrm {U}}(2)\times \operatorname {\mathrm {U}}(2)$ whose value at ![]() $(g_1,g_2)$ equals
$(g_1,g_2)$ equals
It is a standard fact that for two Schwartz functions ![]() $\phi ,\phi '$ on
$\phi ,\phi '$ on ![]() $\mathbb {A}_{\mathcal {K}}$,
$\mathbb {A}_{\mathcal {K}}$,
 $$\begin{align*}\int_{H(V)(\mathbb{Q})\backslash H(V)(\mathbb{A})} \theta^J_{\phi}\big((x,\sigma),g_1\big)\overline{\theta^J_{\phi'}\big((x,\sigma),g_1\big)}\,dxd\sigma=\left<\phi,\overline{\phi'}\right>=\int_{\mathcal{K}\backslash\mathbb{A}_{\mathcal{K}}} \phi(x)\overline{\phi'(x)}\,dx,\\[-9pt] \end{align*}$$
$$\begin{align*}\int_{H(V)(\mathbb{Q})\backslash H(V)(\mathbb{A})} \theta^J_{\phi}\big((x,\sigma),g_1\big)\overline{\theta^J_{\phi'}\big((x,\sigma),g_1\big)}\,dxd\sigma=\left<\phi,\overline{\phi'}\right>=\int_{\mathcal{K}\backslash\mathbb{A}_{\mathcal{K}}} \phi(x)\overline{\phi'(x)}\,dx,\\[-9pt] \end{align*}$$independent of ![]() $g_1\in \operatorname {\mathrm {U}}(2)$. Thanks to this fact, from equations (7.4.3) and (7.5.2) we obtain
$g_1\in \operatorname {\mathrm {U}}(2)$. Thanks to this fact, from equations (7.4.3) and (7.5.2) we obtain

Here, ![]() $1\boxtimes \theta _2$ denotes the automorphic form on
$1\boxtimes \theta _2$ denotes the automorphic form on ![]() $\operatorname {\mathrm {U}}(2)\times \operatorname {\mathrm {U}}(2)$ which is the constant function
$\operatorname {\mathrm {U}}(2)\times \operatorname {\mathrm {U}}(2)$ which is the constant function ![]() $1$ on the first factor and
$1$ on the first factor and ![]() $\theta _2$ on the second factor.
$\theta _2$ on the second factor.
For an automorphic form on ![]() $\mathtt {F}$ on
$\mathtt {F}$ on ![]() $\operatorname {\mathrm {U}}(2)$ and a Hecke character
$\operatorname {\mathrm {U}}(2)$ and a Hecke character ![]() $\chi :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$, we use the notation
$\chi :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$, we use the notation ![]() $\mathtt {F}^\chi $ to denote the form
$\mathtt {F}^\chi $ to denote the form
Our Klingen Eisenstein series ![]() is obtained by pairing the restriction of the Siegel Eisenstein series with
is obtained by pairing the restriction of the Siegel Eisenstein series with ![]() $\varphi ^{\overline {\xi _0\tau }_0}$, so we have
$\varphi ^{\overline {\xi _0\tau }_0}$, so we have

where ![]() $\left <\cdot ,\cdot \right>_{1\times \operatorname {\mathrm {U}}(2)}$ means integration over the second copy of
$\left <\cdot ,\cdot \right>_{1\times \operatorname {\mathrm {U}}(2)}$ means integration over the second copy of ![]() $\operatorname {\mathrm {U}}(2)$.
$\operatorname {\mathrm {U}}(2)$.
The standard doubling method formula [Reference Lapid and RallisLR05] implies
 $$\begin{align*}\left.E^{\mathrm{Sieg}}_2\left(s,\xi_0\tau_{0}\lambda^{-1}\right)\right| {}_{\operatorname{\mathrm{U}}(2)\times\operatorname{\mathrm{U}}(2)}\approx \sum_h \frac{L\left(s+\frac{1}{2},\mathrm{BC}(\pi_{h})\times\xi_0\tau_0\lambda^{-1}\right)}{L\left(2s+1,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0\right)\,L\left(2s+2,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0\eta_{\mathcal{K}/\mathbb{Q}}\right)}\frac{\overline{h} \boxtimes h^{\xi_0\tau_0\overline{\lambda}}}{\left<\overline{h},h\right>}, \end{align*}$$
$$\begin{align*}\left.E^{\mathrm{Sieg}}_2\left(s,\xi_0\tau_{0}\lambda^{-1}\right)\right| {}_{\operatorname{\mathrm{U}}(2)\times\operatorname{\mathrm{U}}(2)}\approx \sum_h \frac{L\left(s+\frac{1}{2},\mathrm{BC}(\pi_{h})\times\xi_0\tau_0\lambda^{-1}\right)}{L\left(2s+1,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0\right)\,L\left(2s+2,\xi^{\mathbb{Q}}_0\tau^{\mathbb{Q}}_0\eta_{\mathcal{K}/\mathbb{Q}}\right)}\frac{\overline{h} \boxtimes h^{\xi_0\tau_0\overline{\lambda}}}{\left<\overline{h},h\right>}, \end{align*}$$where h runs over a certain orthonormal basis of automorphic forms on ![]() $\operatorname {\mathrm {U}}(2)$ of certain level. By picking an h, we have
$\operatorname {\mathrm {U}}(2)$ of certain level. By picking an h, we have
 $$ \begin{align} \begin{aligned} &\left<l_{\theta^J_1}\left(E^{\mathrm{Kling}}_{\beta}\big(-;F(f(s,\xi_0\tau_0),\varphi)\big)\right),h\right>\\ \approx &\,\left<\phi_1,\phi_3\right>\frac{L\left(s+\frac{1}{2},\mathrm{BC}(\pi_h)\times\xi_0\tau_0\lambda^{-1}\right)}{d_3(s,\xi_0\tau_0)}\left<\theta_2\varphi^{\overline{\xi_0\tau_0}},h^{\xi_0\tau_0\overline{\lambda}}\right>\\ =&\,\left<\phi_1,\phi_3\right>\frac{L\left(s+\frac{1}{2},\mathrm{BC}(\pi_h)\times\xi_0\tau_0\lambda^{-1}\right)}{d_3(s,\xi_0\tau_0)}\left<\theta_2^{\overline{\lambda}}\varphi,h\right>, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left<l_{\theta^J_1}\left(E^{\mathrm{Kling}}_{\beta}\big(-;F(f(s,\xi_0\tau_0),\varphi)\big)\right),h\right>\\ \approx &\,\left<\phi_1,\phi_3\right>\frac{L\left(s+\frac{1}{2},\mathrm{BC}(\pi_h)\times\xi_0\tau_0\lambda^{-1}\right)}{d_3(s,\xi_0\tau_0)}\left<\theta_2\varphi^{\overline{\xi_0\tau_0}},h^{\xi_0\tau_0\overline{\lambda}}\right>\\ =&\,\left<\phi_1,\phi_3\right>\frac{L\left(s+\frac{1}{2},\mathrm{BC}(\pi_h)\times\xi_0\tau_0\lambda^{-1}\right)}{d_3(s,\xi_0\tau_0)}\left<\theta_2^{\overline{\lambda}}\varphi,h\right>, \end{aligned} \end{align} $$where ![]() $d_3(s,\xi _0\tau _0)$ is as in equation (5.9.2). The Petersson inner product
$d_3(s,\xi _0\tau _0)$ is as in equation (5.9.2). The Petersson inner product ![]() $\left <\theta _2^{\overline {\lambda }}\varphi ,h\right>$ is related to the central value of a triple product L-function by Ichino’s formula.
$\left <\theta _2^{\overline {\lambda }}\varphi ,h\right>$ is related to the central value of a triple product L-function by Ichino’s formula.
7.5.2 Choosing auxiliary h and  $\theta $ and relating to L-values
$\theta $ and relating to L-values
We will choose suitable CM forms h and ![]() $\theta $ on
$\theta $ on ![]() $\operatorname {\mathrm {U}}(2)$ such that we can apply the available mod p nonvanishing results to study
$\operatorname {\mathrm {U}}(2)$ such that we can apply the available mod p nonvanishing results to study ![]() $L\left (s+\frac {1}{2},\mathrm {BC}(\pi _h)\times \xi _0\tau _0\lambda ^{-1}\right )$ and
$L\left (s+\frac {1}{2},\mathrm {BC}(\pi _h)\times \xi _0\tau _0\lambda ^{-1}\right )$ and ![]() $\left <\theta _2^{\overline {\lambda }}\varphi ,h\right>$ in equation (7.5.6).
$\left <\theta _2^{\overline {\lambda }}\varphi ,h\right>$ in equation (7.5.6).
Let ![]() $\chi _h$ and
$\chi _h$ and ![]() $\chi _{\theta }$ be two unitary Hecke characters of
$\chi _{\theta }$ be two unitary Hecke characters of ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ such that
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ such that ![]() $\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$ (as chosen in §5.6). Let
$\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$ (as chosen in §5.6). Let ![]() $h_0$ be the theta lift of
$h_0$ be the theta lift of ![]() $\chi ^{-1}_h|_{\operatorname {\mathrm {U}}(1)}$ to
$\chi ^{-1}_h|_{\operatorname {\mathrm {U}}(1)}$ to ![]() $\operatorname {\mathrm {U}}(2)$, and h be the automorphic form on
$\operatorname {\mathrm {U}}(2)$, and h be the automorphic form on ![]() $\operatorname {\mathrm {U}}(2)$ obtained from
$\operatorname {\mathrm {U}}(2)$ obtained from ![]() $h_0$ by
$h_0$ by
Thanks to the condition ![]() $\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$, the definition of
$\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$, the definition of ![]() $h(g)$ does not depend on the choice of
$h(g)$ does not depend on the choice of ![]() $a\in \mathbb {A}^{\times }_{\mathcal {K}}$.
$a\in \mathbb {A}^{\times }_{\mathcal {K}}$.
The form ![]() $\theta _2$ does not generate an irreducible representation of
$\theta _2$ does not generate an irreducible representation of ![]() $\operatorname {\mathrm {U}}(2)$. Let
$\operatorname {\mathrm {U}}(2)$. Let ![]() $\theta $ be the projection of
$\theta $ be the projection of ![]() $\theta _2$ to its
$\theta _2$ to its ![]() $\chi _{\theta }\lambda ^2|_{\operatorname {\mathrm {U}}(1)}$-eigenspace for the action of the center of
$\chi _{\theta }\lambda ^2|_{\operatorname {\mathrm {U}}(1)}$-eigenspace for the action of the center of ![]() $\operatorname {\mathrm {U}}(2)$. Then
$\operatorname {\mathrm {U}}(2)$. Then ![]() $\theta $ is a theta lift of
$\theta $ is a theta lift of ![]() $\chi _{\theta }\lambda ^2|_{\operatorname {\mathrm {U}}(1)}$. Since our
$\chi _{\theta }\lambda ^2|_{\operatorname {\mathrm {U}}(1)}$. Since our ![]() $\varphi $ is assumed to have the trivial central character and h has the central character
$\varphi $ is assumed to have the trivial central character and h has the central character ![]() $\chi ^{-1}_{\theta }|_{\operatorname {\mathrm {U}}(1)}$, we have
$\chi ^{-1}_{\theta }|_{\operatorname {\mathrm {U}}(1)}$, we have
By [Reference GarrettGI14, Theorem C.5], with the choice of the splitting characters for the theta correspondence between ![]() $\operatorname {\mathrm {U}}(2)$ and
$\operatorname {\mathrm {U}}(2)$ and ![]() $\operatorname {\mathrm {U}}(1)$ as in equation (7.1.2), we have
$\operatorname {\mathrm {U}}(1)$ as in equation (7.1.2), we have
 $$ \begin{align} \begin{aligned} \mathrm{BC}\left(\pi_{h}\right)&=\mathrm{BC}\left(\pi_{h_0}\right)\otimes\chi_h\chi^c_{\theta}=\left(\mathrm{BC}\left(\chi^{-1}_h|_{\operatorname{\mathrm{U}}(1)}\right)\lambda^{-1}\oplus \lambda\right)\otimes\chi_h\chi^c_{\theta}\\ &=\left(\chi^{-1}_h\chi^c_h\lambda^{-1}\oplus\lambda\right)\otimes\chi_h\chi^c_{\theta}=\chi^c_h\chi^c_{\theta}\lambda^{-1}\oplus \chi_h\chi^c_{\theta}\lambda, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathrm{BC}\left(\pi_{h}\right)&=\mathrm{BC}\left(\pi_{h_0}\right)\otimes\chi_h\chi^c_{\theta}=\left(\mathrm{BC}\left(\chi^{-1}_h|_{\operatorname{\mathrm{U}}(1)}\right)\lambda^{-1}\oplus \lambda\right)\otimes\chi_h\chi^c_{\theta}\\ &=\left(\chi^{-1}_h\chi^c_h\lambda^{-1}\oplus\lambda\right)\otimes\chi_h\chi^c_{\theta}=\chi^c_h\chi^c_{\theta}\lambda^{-1}\oplus \chi_h\chi^c_{\theta}\lambda, \end{aligned} \end{align} $$and
Thus, we have
 $$ \begin{align} \begin{aligned} &L\left(s+\frac{1}{2},\mathrm{BC}(\pi_h)\times\lambda^{-1}\xi_0\tau_0\right)\\ =&\,L\left(s+\frac{1}{2},\lambda^{-2}\chi^c_h\chi^c_{\theta}\xi_0\tau_0\right)\,L\left(s+\frac{1}{2},\chi_h\chi^c_{\theta}\xi_0\tau_0\right)\\ =&\,L\left(s+\frac{1}{2},\lambda^2\chi_h\chi_{\theta}\xi^c_0\tau^c_0\right)\,L\left(s+\frac{1}{2},\chi_h\chi^c_{\theta}\xi_0\tau_0\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &L\left(s+\frac{1}{2},\mathrm{BC}(\pi_h)\times\lambda^{-1}\xi_0\tau_0\right)\\ =&\,L\left(s+\frac{1}{2},\lambda^{-2}\chi^c_h\chi^c_{\theta}\xi_0\tau_0\right)\,L\left(s+\frac{1}{2},\chi_h\chi^c_{\theta}\xi_0\tau_0\right)\\ =&\,L\left(s+\frac{1}{2},\lambda^2\chi_h\chi_{\theta}\xi^c_0\tau^c_0\right)\,L\left(s+\frac{1}{2},\chi_h\chi^c_{\theta}\xi_0\tau_0\right). \end{aligned} \end{align} $$By the triple product formula,
 $$ \begin{align} \begin{aligned} \left<\theta^{\bar{\lambda}}\varphi,h\right>\left<\tilde{\theta}^\lambda_3\tilde{\varphi},\tilde{h}_3\right> &\approx \frac{\big<\varphi,\tilde{\varphi}\big>}{L(1,\pi,\mathrm{Ad})}\, \frac{\big<h,\tilde{h}_3\big>}{\zeta_{\mathcal{K}}(1)\,L(1,\chi_h\chi^{-1}_h\lambda^2)}\, \frac{\big<\theta,\tilde{\theta}_3\big>}{\zeta_{\mathcal{K}}(1)\, L(1,\chi_{\theta}\chi^{-c}_{\theta}\lambda^2)}\\ &\quad\times L\left(\frac{1}{2},\mathrm{BC}(\pi)\times\chi_h\chi_{\theta}\lambda^2\right)L\left(\frac{1}{2},\mathrm{BC}(\pi)\times \chi_h\chi^c_{\theta}\right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left<\theta^{\bar{\lambda}}\varphi,h\right>\left<\tilde{\theta}^\lambda_3\tilde{\varphi},\tilde{h}_3\right> &\approx \frac{\big<\varphi,\tilde{\varphi}\big>}{L(1,\pi,\mathrm{Ad})}\, \frac{\big<h,\tilde{h}_3\big>}{\zeta_{\mathcal{K}}(1)\,L(1,\chi_h\chi^{-1}_h\lambda^2)}\, \frac{\big<\theta,\tilde{\theta}_3\big>}{\zeta_{\mathcal{K}}(1)\, L(1,\chi_{\theta}\chi^{-c}_{\theta}\lambda^2)}\\ &\quad\times L\left(\frac{1}{2},\mathrm{BC}(\pi)\times\chi_h\chi_{\theta}\lambda^2\right)L\left(\frac{1}{2},\mathrm{BC}(\pi)\times \chi_h\chi^c_{\theta}\right), \end{aligned} \end{align} $$where ![]() $\tilde {\varphi }$ (resp.
$\tilde {\varphi }$ (resp. ![]() $\tilde {h}_3$,
$\tilde {h}_3$, ![]() $\tilde {\theta }_3$) are suitable forms taken from the dual representation of
$\tilde {\theta }_3$) are suitable forms taken from the dual representation of ![]() $\pi ^{\operatorname {\mathrm {U}}(2)}=\pi _{\varphi }$ (resp.
$\pi ^{\operatorname {\mathrm {U}}(2)}=\pi _{\varphi }$ (resp. ![]() $\pi _{h}$,
$\pi _{h}$, ![]() $\pi _{\theta }$). (In our case here, the triple product L-function for
$\pi _{\theta }$). (In our case here, the triple product L-function for ![]() $\pi ^D\times \pi ^D_{\theta }\times \pi ^D_h$ factorizes as the product of the two L-functions in equation (7.5.12). Also, note that Ichino’s triple product formula is for automorphic forms on
$\pi ^D\times \pi ^D_{\theta }\times \pi ^D_h$ factorizes as the product of the two L-functions in equation (7.5.12). Also, note that Ichino’s triple product formula is for automorphic forms on ![]() $D^{\times }$, we actually need to relate the integral on
$D^{\times }$, we actually need to relate the integral on ![]() $\operatorname {\mathrm {U}}(2)$ for
$\operatorname {\mathrm {U}}(2)$ for ![]() $\left <\theta ^{\bar {\lambda }}\varphi ,h\right>\left <\tilde {\theta }^\lambda _3\tilde {\varphi },\tilde {h}_3\right>$ to an integral on
$\left <\theta ^{\bar {\lambda }}\varphi ,h\right>\left <\tilde {\theta }^\lambda _3\tilde {\varphi },\tilde {h}_3\right>$ to an integral on ![]() $D^{\times }$. In §7.10, we discuss extending automorphic forms on
$D^{\times }$. In §7.10, we discuss extending automorphic forms on ![]() $\operatorname {\mathrm {U}}(2)$ to
$\operatorname {\mathrm {U}}(2)$ to ![]() $\operatorname {\mathrm {GU}}(2)$. Thanks to equation (5.4.3), the integral over
$\operatorname {\mathrm {GU}}(2)$. Thanks to equation (5.4.3), the integral over ![]() $\operatorname {\mathrm {GU}}(2)$ is the same as the integral over
$\operatorname {\mathrm {GU}}(2)$ is the same as the integral over ![]() $D^{\times }$.)
$D^{\times }$.)
Combining equations (7.5.6)(7.5.8)(7.5.11)(7.5.12), we get

The relation between ![]() $E^{\mathrm {Kling}}_{\beta }\big (-;F(f(s,\xi _0\tau _0),\varphi )\big )$ and L-values illustrated in equation (7.5.13) explains the nonvanishing conditions on the L-values in equations (5.6.1)(5.6.2)(5.6.3)(5.6.4) in our choice of the auxiliary Hecke characters
$E^{\mathrm {Kling}}_{\beta }\big (-;F(f(s,\xi _0\tau _0),\varphi )\big )$ and L-values illustrated in equation (7.5.13) explains the nonvanishing conditions on the L-values in equations (5.6.1)(5.6.2)(5.6.3)(5.6.4) in our choice of the auxiliary Hecke characters ![]() $\chi _{\theta }$ and
$\chi _{\theta }$ and ![]() $\chi _h$ in §5.6.
$\chi _h$ in §5.6.
In the following, guided by the strategy described in this section, we carry out the necessary local computations and the construction of the auxiliary objects to prove the desired property of ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$ with
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$ with ![]() $\beta =1$. The computation is place by place, and we have the following cases:
$\beta =1$. The computation is place by place, and we have the following cases:
– For the Archimedean place, we only need to consider the cases for which there are standard choices of local sections and computations are easy.
– For unramified places, we have the standard formulas for spherical sections.
– For the place p and the places in
 $\Sigma _{\mathrm {s}}\cup \{\ell \}$, we compute precise formulas.
$\Sigma _{\mathrm {s}}\cup \{\ell \}$, we compute precise formulas.– For the places in
 $\Sigma _{\mathrm {ns}}\cup \{\ell '\}$, we do not attempt to compute precise formulas. At these places, the local data actually do not change when
$\Sigma _{\mathrm {ns}}\cup \{\ell '\}$, we do not attempt to compute precise formulas. At these places, the local data actually do not change when  $\tau $ varies in a p-adic family, and we only make sure that local integrals contribute a nonzero scalar.
$\tau $ varies in a p-adic family, and we only make sure that local integrals contribute a nonzero scalar.
7.6 The auxiliary Jacobi form  $\theta ^J_1$
$\theta ^J_1$
Given a Schwartz function ![]() $\phi $ on
$\phi $ on ![]() $\mathbb {A}^2_{\mathbb {Q}}$ such that
$\mathbb {A}^2_{\mathbb {Q}}$ such that ![]() $\phi _{\infty }$ is the standard Gaussian function, let
$\phi _{\infty }$ is the standard Gaussian function, let ![]() $\theta ^J$ be its associated Jacobi form on
$\theta ^J$ be its associated Jacobi form on ![]() $\operatorname {\mathrm {U}}(2)$ (as defined in equation (7.3.1)). The map attached to this
$\operatorname {\mathrm {U}}(2)$ (as defined in equation (7.3.1)). The map attached to this ![]() $\theta ^J$ defined in equation (7.5.1) extends to
$\theta ^J$ defined in equation (7.5.1) extends to ![]() $V^{J,\beta }_{\operatorname {\mathrm {GU}}(2)}$ and induces
$V^{J,\beta }_{\operatorname {\mathrm {GU}}(2)}$ and induces
Apply it to ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$ (defined in equation (7.0.1)), we get
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}$ (defined in equation (7.0.1)), we get
Proposition 7.6.1. Let ![]() $\beta =1\in \operatorname {\mathrm {Her}}_1(\mathcal {K})$. There exists a Schwartz function
$\beta =1\in \operatorname {\mathrm {Her}}_1(\mathcal {K})$. There exists a Schwartz function ![]() $\phi _1$ on
$\phi _1$ on ![]() $\mathbb {A}^2_{\mathbb {Q}}$ with
$\mathbb {A}^2_{\mathbb {Q}}$ with ![]() $\phi _{1,\infty }$ the standard Gaussian function, elements
$\phi _{1,\infty }$ the standard Gaussian function, elements ![]() $u_1,\dots ,u_r\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)\left (\mathbb {Q}_v\right )$, and constants
$u_1,\dots ,u_r\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)\left (\mathbb {Q}_v\right )$, and constants ![]() $b_1,\dots ,b_r\in \mathcal {O}_L$, (all independent of
$b_1,\dots ,b_r\in \mathcal {O}_L$, (all independent of ![]() $\tau $), such that, denoting
$\tau $), such that, denoting ![]() $l_{\theta ^J_1}$ the map (7.6.1) attached to the Jacobi form
$l_{\theta ^J_1}$ the map (7.6.1) attached to the Jacobi form ![]() ${\theta ^J_1}$ corresponding to
${\theta ^J_1}$ corresponding to ![]() $\phi _1$,
$\phi _1$,
 $$\begin{align*}l_{\theta^J_1}\left(\sum_i b_i\boldsymbol{E}^{\mathrm{Kling}}_{\varphi,\beta,u_i}\right)\in \mathcal{M} eas\left(\Gamma_{\mathcal{K}},V_{\operatorname{\mathrm{U}}(2),\,\xi}\right)^\natural\\[-15pt] \end{align*}$$
$$\begin{align*}l_{\theta^J_1}\left(\sum_i b_i\boldsymbol{E}^{\mathrm{Kling}}_{\varphi,\beta,u_i}\right)\in \mathcal{M} eas\left(\Gamma_{\mathcal{K}},V_{\operatorname{\mathrm{U}}(2),\,\xi}\right)^\natural\\[-15pt] \end{align*}$$satisfies the following interpolation properties: For all ![]() $\tau $ such that
$\tau $ such that ![]() $\xi \tau $ is ramified at
$\xi \tau $ is ramified at ![]() $\mathfrak {p}$ and satisfies the conditions in Theorem 5.9.1,
$\mathfrak {p}$ and satisfies the conditions in Theorem 5.9.1,

with ![]() (independent of
(independent of ![]() $\tau $ except
$\tau $ except ![]() $v=p$) and
$v=p$) and ![]() $f_2(s,\xi _0\tau _0\lambda ^{-1})\in \bigotimes _vI_{Q_{\operatorname {\mathrm {U}}(2,2)},v}(s,\xi _0\tau _0\lambda ^{-1})$ described as follows:
$f_2(s,\xi _0\tau _0\lambda ^{-1})\in \bigotimes _vI_{Q_{\operatorname {\mathrm {U}}(2,2)},v}(s,\xi _0\tau _0\lambda ^{-1})$ described as follows:
–
 $v=\infty $.
$v=\infty $.  $$ \begin{align*} \phi_{2,\xi\tau,\infty}(y_1,y_2)&=\frac{\mathfrak{s}^{1/4}\mathrm{Nm}(\delta)^{1/4}}{2} e^{-2\pi\sqrt{\mathrm{Nm}(\delta)}\,\left(\begin{smallmatrix}y_1&y_2\end{smallmatrix}\right) \zeta_0\left(\begin{smallmatrix}y_1\\y_2\end{smallmatrix}\right) },\\ f_{2,\infty}(s,\xi_0\tau_0\lambda^{-1})\left(g'=\begin{pmatrix}A&B\\C&D\end{pmatrix}\right)&= \frac{(-2\pi i)^k}{\Gamma(k)}\cdot \det\left(C\frac{\zeta_0}{2}+D\right)^{-k}\left|C\frac{\zeta_0}{2}+D\right| {}^{-s+1+\frac{k}{2}}_{\mathbb{C}}\\[-15pt] \end{align*} $$
$$ \begin{align*} \phi_{2,\xi\tau,\infty}(y_1,y_2)&=\frac{\mathfrak{s}^{1/4}\mathrm{Nm}(\delta)^{1/4}}{2} e^{-2\pi\sqrt{\mathrm{Nm}(\delta)}\,\left(\begin{smallmatrix}y_1&y_2\end{smallmatrix}\right) \zeta_0\left(\begin{smallmatrix}y_1\\y_2\end{smallmatrix}\right) },\\ f_{2,\infty}(s,\xi_0\tau_0\lambda^{-1})\left(g'=\begin{pmatrix}A&B\\C&D\end{pmatrix}\right)&= \frac{(-2\pi i)^k}{\Gamma(k)}\cdot \det\left(C\frac{\zeta_0}{2}+D\right)^{-k}\left|C\frac{\zeta_0}{2}+D\right| {}^{-s+1+\frac{k}{2}}_{\mathbb{C}}\\[-15pt] \end{align*} $$–
 $v\notin \Sigma \cup \{\ell ,\ell ',p\}$.
$v\notin \Sigma \cup \{\ell ,\ell ',p\}$. 
–
 $v=\mathfrak {v}\overline {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\cup \{\ell \}$.
$v=\mathfrak {v}\overline {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\cup \{\ell \}$.  (7.6.3)
(7.6.3)
–
 $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$.
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$.  $$ \begin{align*} \phi_{2,\xi\tau,v}=&\,\text{a nonzero Schwartz function on } \mathbb{Q}^2_v \text{ inside the } \chi_{\theta}\lambda^2|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace}\\ &\,\text{for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v), \text{ invariant under } K_v, \text{ independent of } \tau,\\ f_{2,v}(s,\xi_0\tau_0\lambda^{-1})=&\,\text{same as equation}\ \textit{(}7.6.3\textit{)}. \end{align*} $$
$$ \begin{align*} \phi_{2,\xi\tau,v}=&\,\text{a nonzero Schwartz function on } \mathbb{Q}^2_v \text{ inside the } \chi_{\theta}\lambda^2|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace}\\ &\,\text{for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v), \text{ invariant under } K_v, \text{ independent of } \tau,\\ f_{2,v}(s,\xi_0\tau_0\lambda^{-1})=&\,\text{same as equation}\ \textit{(}7.6.3\textit{)}. \end{align*} $$– The place p.
(7.6.4)

where
•
 $M^{\prime }_p\left (-s,(\xi _0\tau _0\lambda )^{-c}\right ):I_{Q_{\operatorname {\mathrm {U}}(2,2)},p}\left (-s,(\xi _0\tau _0\lambda )^{-c}\right )\rightarrow I_{Q_{\operatorname {\mathrm {U}}(2,2)},p}(s,\xi _0\tau _0\lambda ^{-1})$ is the intertwining operator,
$M^{\prime }_p\left (-s,(\xi _0\tau _0\lambda )^{-c}\right ):I_{Q_{\operatorname {\mathrm {U}}(2,2)},p}\left (-s,(\xi _0\tau _0\lambda )^{-c}\right )\rightarrow I_{Q_{\operatorname {\mathrm {U}}(2,2)},p}(s,\xi _0\tau _0\lambda ^{-1})$ is the intertwining operator,•
 $\Upsilon ^{\prime }_p$ is the element in
$\Upsilon ^{\prime }_p$ is the element in  $\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_p)$ with
$\operatorname {\mathrm {U}}(2,2)(\mathbb {Q}_p)$ with  $\varrho _{\mathfrak {p}}(\Upsilon ^{\prime }_p)=\begin {pmatrix}\mathbf {1}_1&-\frac {\zeta _0}{2}\\-\mathbf {1}_2&-\frac {\zeta _0}{2}\end {pmatrix}^{-1}$,
$\varrho _{\mathfrak {p}}(\Upsilon ^{\prime }_p)=\begin {pmatrix}\mathbf {1}_1&-\frac {\zeta _0}{2}\\-\mathbf {1}_2&-\frac {\zeta _0}{2}\end {pmatrix}^{-1}$,• writing
 $t=\mathrm {ord}_p(\mathrm {cond}(\xi _{\mathfrak {p}}\tau _{\mathfrak {p}}))$,
$t=\mathrm {ord}_p(\mathrm {cond}(\xi _{\mathfrak {p}}\tau _{\mathfrak {p}}))$,  $\varrho _{\mathfrak {p}}(x)=\begin {pmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end {pmatrix}$, with
$\varrho _{\mathfrak {p}}(x)=\begin {pmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end {pmatrix}$, with
 $\alpha ^{\prime }_{\xi \tau ,p}$ the Schwartz function on
$\alpha ^{\prime }_{\xi \tau ,p}$ the Schwartz function on  $\operatorname {\mathrm {Her}}_2(\mathcal {K}_p)$ defined as
$\operatorname {\mathrm {Her}}_2(\mathcal {K}_p)$ defined as 
Proof. This proposition is proved in [Reference WanWan20, sections 6.E-6.H] by computing ![]() $\mathrm {FJ}_{\beta ,v}\big (g,x;f_v(s,\xi _0\tau _0)\big )$ place by place. The place
$\mathrm {FJ}_{\beta ,v}\big (g,x;f_v(s,\xi _0\tau _0)\big )$ place by place. The place ![]() $\infty $ is done in Lemmas 6.9 and 6.11 and the unramified places are done in Lemma 6.18. (Note that, at the unramified places, we have
$\infty $ is done in Lemmas 6.9 and 6.11 and the unramified places are done in Lemma 6.18. (Note that, at the unramified places, we have ![]() $d_{2,v}(s,\xi _0\tau _0\lambda ^{-1})=\frac {d_{3,v}(s,\xi _0\tau _0)}{L_v(2s+3,\xi ^{\mathbb {Q}}_0\tau ^{\mathbb {Q}}_0)}$.) The places in
$d_{2,v}(s,\xi _0\tau _0\lambda ^{-1})=\frac {d_{3,v}(s,\xi _0\tau _0)}{L_v(2s+3,\xi ^{\mathbb {Q}}_0\tau ^{\mathbb {Q}}_0)}$.) The places in ![]() $\Sigma _{\mathrm {s}}\cup \{\ell \}$ are done in Lemmas 6.22 and 6.24, and the places in
$\Sigma _{\mathrm {s}}\cup \{\ell \}$ are done in Lemmas 6.22 and 6.24, and the places in ![]() $\Sigma _{\mathrm {ns}}\cup \{\ell '\}$ are done in Lemmas 6.22 and 6.26. Note that Lemma 6.26 loc.cit is already recalled in Proposition 5.6.1 and in §5.6 we choose
$\Sigma _{\mathrm {ns}}\cup \{\ell '\}$ are done in Lemmas 6.22 and 6.26. Note that Lemma 6.26 loc.cit is already recalled in Proposition 5.6.1 and in §5.6 we choose ![]() $\chi _{\theta }$ such that at
$\chi _{\theta }$ such that at ![]() $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$ we have nonzero
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$ we have nonzero ![]() $\phi _{2,\xi \tau ,v}$ described in this proposition. The place p is done from Lemma 6.35 to the end of the Section 6.H. The Schwartz function
$\phi _{2,\xi \tau ,v}$ described in this proposition. The place p is done from Lemma 6.35 to the end of the Section 6.H. The Schwartz function ![]() $\phi _{2,\tau _0,p}$ is the
$\phi _{2,\tau _0,p}$ is the ![]() $\phi ^{\prime }_{2,p}$ given below Definition 6.38. Note that our
$\phi ^{\prime }_{2,p}$ given below Definition 6.38. Note that our ![]() $\mathrm {FJ}_{\beta ,v}\big (g,x;f_v(s,\xi _0\tau _0)\big )$ defined in Definition 7.4.1 equals
$\mathrm {FJ}_{\beta ,v}\big (g,x;f_v(s,\xi _0\tau _0)\big )$ defined in Definition 7.4.1 equals ![]() $\mathrm {FJ}_{\beta }(f_{sieg,v};z,x,g\eta ^{-1},1)$ in [Reference WanWan20] with
$\mathrm {FJ}_{\beta }(f_{sieg,v};z,x,g\eta ^{-1},1)$ in [Reference WanWan20] with ![]() $z=s$ and
$z=s$ and  $\eta =\begin {pmatrix}&\mathbf {1}_2\\-\mathbf {1}_2\end {pmatrix}$, so the results in loc.cit all contain the extra
$\eta =\begin {pmatrix}&\mathbf {1}_2\\-\mathbf {1}_2\end {pmatrix}$, so the results in loc.cit all contain the extra ![]() $\eta $ but the formulas in this proposition do not.
$\eta $ but the formulas in this proposition do not.
At the place p, in fact the pairing of ![]() $\phi _{1,p}(x)$ and
$\phi _{1,p}(x)$ and ![]() $\mathrm {FJ}_{\beta ,p}\big (g,(x,y)_p;f_p(s,\xi _0\tau _0\big )$ along x does not directly equal
$\mathrm {FJ}_{\beta ,p}\big (g,(x,y)_p;f_p(s,\xi _0\tau _0\big )$ along x does not directly equal ![]() $\phi _{2,\tau ,p}(y)\cdot f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})(g)$ but equals the average
$\phi _{2,\tau ,p}(y)\cdot f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})(g)$ but equals the average
 $$ \begin{align} \int_{\mathbb{Z}_p}\omega_{\beta,p}\left(\varrho_{\mathfrak{p}}^{-1}\begin{pmatrix}1&0\\n&1\end{pmatrix},1\right)\phi_{2,\tau,p}(y)\cdot f_{2,p}(s,\tau_0\lambda^{-1})\left(g\Upsilon^{\prime}_p\begin{pmatrix}1&\\&1\\&&1&\\&&n&1\end{pmatrix}\right)\,dn. \end{align} $$
$$ \begin{align} \int_{\mathbb{Z}_p}\omega_{\beta,p}\left(\varrho_{\mathfrak{p}}^{-1}\begin{pmatrix}1&0\\n&1\end{pmatrix},1\right)\phi_{2,\tau,p}(y)\cdot f_{2,p}(s,\tau_0\lambda^{-1})\left(g\Upsilon^{\prime}_p\begin{pmatrix}1&\\&1\\&&1&\\&&n&1\end{pmatrix}\right)\,dn. \end{align} $$Meanwhile, ![]() $\varphi $ is spherical at p, in particular invariant under the right translation by
$\varphi $ is spherical at p, in particular invariant under the right translation by  $\begin {pmatrix}1&\\\mathbb {Z}_p&1\end {pmatrix}$, so replacing equation (7.6.5) by
$\begin {pmatrix}1&\\\mathbb {Z}_p&1\end {pmatrix}$, so replacing equation (7.6.5) by ![]() $\phi _{2,\tau ,p}(y)\cdot f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})(g)$ does not change the resulting Petersson inner product with
$\phi _{2,\tau ,p}(y)\cdot f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})(g)$ does not change the resulting Petersson inner product with ![]() $\varphi $ over
$\varphi $ over ![]() $\operatorname {\mathrm {U}}(V^-)=\operatorname {\mathrm {U}}(2)$.
$\operatorname {\mathrm {U}}(V^-)=\operatorname {\mathrm {U}}(2)$.
The Schwartz function (7.6.4) is the ![]() $(v_3,v_4)$-part of
$(v_3,v_4)$-part of ![]() $\Phi _{\mathcal {D},p}$, the Schwartz function on
$\Phi _{\mathcal {D},p}$, the Schwartz function on ![]() $\mathbb {Q}^4_p$ defined and appearing in [Reference WanWan20, Lemma 6.37, Definition 6.36]. As mentioned above, our formula in the proposition corresponds to replacing g by
$\mathbb {Q}^4_p$ defined and appearing in [Reference WanWan20, Lemma 6.37, Definition 6.36]. As mentioned above, our formula in the proposition corresponds to replacing g by ![]() $g\eta ^{-1}$ in the formula in loc.cit, so there is a translation by
$g\eta ^{-1}$ in the formula in loc.cit, so there is a translation by  $\begin {pmatrix}&-1\\ 1 \end {pmatrix}$in the theta series in equation (7.6.2).
$\begin {pmatrix}&-1\\ 1 \end {pmatrix}$in the theta series in equation (7.6.2).
7.7 The construction of the auxiliary CM families  $ h,\tilde {h}_3,\theta ,\tilde {\theta }_3$
$ h,\tilde {h}_3,\theta ,\tilde {\theta }_3$
Besides ![]() $\theta ^J_1$, our strategy described in §7.5 also includes auxiliary CM forms. We want to construct a CM family
$\theta ^J_1$, our strategy described in §7.5 also includes auxiliary CM forms. We want to construct a CM family ![]() $\boldsymbol {h}$ on
$\boldsymbol {h}$ on ![]() $\operatorname {\mathrm {U}}(V)=\operatorname {\mathrm {U}}(2)$ and pair it with
$\operatorname {\mathrm {U}}(V)=\operatorname {\mathrm {U}}(2)$ and pair it with ![]() $l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$. The splitting characters for the theta correspondence between
$l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$. The splitting characters for the theta correspondence between ![]() $\operatorname {\mathrm {U}}(2)$ and
$\operatorname {\mathrm {U}}(2)$ and ![]() $\operatorname {\mathrm {U}}(1)$ are chosen as in equation (7.1.2).
$\operatorname {\mathrm {U}}(1)$ are chosen as in equation (7.1.2).
7.7.1 The auxiliary group  $U_{\mathcal {K},p}$
$U_{\mathcal {K},p}$
First, we note that for ![]() $\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1, the nebentypus of
$\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1, the nebentypus of ![]() $l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$ at p is
$l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$ at p is ![]() $\left (\mathrm {triv},(\xi _0\tau _0)_{\mathfrak {p}}|_{\mathbb {Z}^{\times }_p}\right )$, that is,
$\left (\mathrm {triv},(\xi _0\tau _0)_{\mathfrak {p}}|_{\mathbb {Z}^{\times }_p}\right )$, that is,  $\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}\ast & \ast \\0&a_2\end {pmatrix}\in \operatorname {\mathrm {U}}(2)(\mathbb {Z}_p)$acts by
$\varrho ^{-1}_{\mathfrak {p}}\begin {pmatrix}\ast & \ast \\0&a_2\end {pmatrix}\in \operatorname {\mathrm {U}}(2)(\mathbb {Z}_p)$acts by ![]() $(\xi _0\tau _0)_{\mathfrak {p}}(a_2)$). In order to get a CM family
$(\xi _0\tau _0)_{\mathfrak {p}}(a_2)$). In order to get a CM family ![]() $\boldsymbol {h}$ with the correct nebentypus to pair with
$\boldsymbol {h}$ with the correct nebentypus to pair with ![]() $l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$, we want Hecke characters of
$l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$, we want Hecke characters of ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ unramified away from
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ unramified away from ![]() $p\infty $ with restriction
$p\infty $ with restriction ![]() $\left (\tau _{0,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p},\mathrm {triv}\right )$ on
$\left (\tau _{0,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p},\mathrm {triv}\right )$ on ![]() $\mathcal {O}^{\times }_{\mathcal {K},p}$. However, in general there is no canonical way to extend local characters
$\mathcal {O}^{\times }_{\mathcal {K},p}$. However, in general there is no canonical way to extend local characters ![]() $\left (\tau _{0,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p},\mathrm {triv}\right )$ of
$\left (\tau _{0,\mathfrak {p}}|_{\mathbb {Z}^{\times }_p},\mathrm {triv}\right )$ of ![]() $\mathcal {O}^{\times }_{\mathcal {K},p}$ to global Hecke characters. Hence, we need to consider an auxiliary group
$\mathcal {O}^{\times }_{\mathcal {K},p}$ to global Hecke characters. Hence, we need to consider an auxiliary group ![]() $U_{\mathcal {K},p}$ and the nonstandard type of p-adic measures defined in equation (5.8.9).
$U_{\mathcal {K},p}$ and the nonstandard type of p-adic measures defined in equation (5.8.9).
Let ![]() ${U_{\mathcal {K},p}} = 1+p\mathcal {O}_{\mathcal {K},p}$ and
${U_{\mathcal {K},p}} = 1+p\mathcal {O}_{\mathcal {K},p}$ and ![]() ${U_{\mathcal {K},\mathfrak {p}}} = 1+p\mathcal {O}_{\mathcal {K},\mathfrak {p}}$,
${U_{\mathcal {K},\mathfrak {p}}} = 1+p\mathcal {O}_{\mathcal {K},\mathfrak {p}}$, ![]() ${U_{\mathcal {K},\bar {\mathfrak {p}}}} = 1 + p\mathcal {O}_{\mathcal {K},\bar {\mathfrak {p}}}$. Then the natural map
${U_{\mathcal {K},\bar {\mathfrak {p}}}} = 1 + p\mathcal {O}_{\mathcal {K},\bar {\mathfrak {p}}}$. Then the natural map
is an injection. We can pick ![]() ${\tt N}$, a nonnegative power of p, such that raising to the
${\tt N}$, a nonnegative power of p, such that raising to the ![]() $\mathtt {N}$-th power maps
$\mathtt {N}$-th power maps ![]() $\Gamma _{\mathcal {K}}$ into
$\Gamma _{\mathcal {K}}$ into ![]() $U_{\mathcal {K},p}$. Define
$U_{\mathcal {K},p}$. Define
Then given a (local) p-adic character ![]() $\epsilon :U_{\mathcal {K},\mathfrak {p}}\rightarrow \overline {\mathbb {Q}}_p^{\times }$, the composition
$\epsilon :U_{\mathcal {K},\mathfrak {p}}\rightarrow \overline {\mathbb {Q}}_p^{\times }$, the composition
is a (global) p-adic character of ![]() $\Gamma _{\mathcal {K}}$ whose restriction back to
$\Gamma _{\mathcal {K}}$ whose restriction back to ![]() $U_{\mathcal {K},p}=U_{\mathcal {K},\mathfrak {p}}\times U_{\mathcal {K},\bar {\mathfrak {p}}}$ is
$U_{\mathcal {K},p}=U_{\mathcal {K},\mathfrak {p}}\times U_{\mathcal {K},\bar {\mathfrak {p}}}$ is ![]() $\left (\epsilon ^{\mathtt {N}},\mathrm {triv}\right )$.
$\left (\epsilon ^{\mathtt {N}},\mathrm {triv}\right )$.
In particular, for an algebraic Hecke character ![]() $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ of ![]() $\infty $-type
$\infty $-type ![]() $\left (0,k\right )$ whose p-adic avatar
$\left (0,k\right )$ whose p-adic avatar ![]() $\tau _{p\text {-}\mathrm {adic}}$ factors through
$\tau _{p\text {-}\mathrm {adic}}$ factors through ![]() $\Gamma _{\mathcal {K}}$, we can define
$\Gamma _{\mathcal {K}}$, we can define
Then
is a p-adic Hecke character of ![]() $\Gamma _{\mathcal {K}}$ with
$\Gamma _{\mathcal {K}}$ with
Because ![]() $\tau $ has
$\tau $ has ![]() $\infty $-type
$\infty $-type ![]() $(0,k)$, the local character
$(0,k)$, the local character ![]() $\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},\mathfrak {p}}}$ is of finite order, and it follows that the (global) character
$\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},\mathfrak {p}}}$ is of finite order, and it follows that the (global) character
is also of finite order. Hence, it takes values in ![]() $\overline {\mathbb {Q}}^{\times }$ and is also an algebraic Hecke character of
$\overline {\mathbb {Q}}^{\times }$ and is also an algebraic Hecke character of ![]() $\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ of
$\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}$ of ![]() $\infty $-type
$\infty $-type ![]() $\left (0,0\right )$. (From the definition of p-adic avatars recalled in §5.3, we can see that the p-adic avatar of a Hecke character of
$\left (0,0\right )$. (From the definition of p-adic avatars recalled in §5.3, we can see that the p-adic avatar of a Hecke character of ![]() $\infty $-type
$\infty $-type ![]() $(0,0)$ is itself.)
$(0,0)$ is itself.)
The map
induces a map
(See §5.8.3 for the definition of these spaces of p-adic measures.) We have
for every ![]() $\tau _{p\text {-}\mathrm {adic}}\in \operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (\Gamma _{\mathcal {K}},\overline {\mathbb {Q}}^{\times }_p\right )$. In order to show the nonvanishing property of
$\tau _{p\text {-}\mathrm {adic}}\in \operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (\Gamma _{\mathcal {K}},\overline {\mathbb {Q}}^{\times }_p\right )$. In order to show the nonvanishing property of ![]() $l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$ in Proposition 7.11.3, it suffices to show the nonvanishing property for
$l_{\theta ^J_{1}}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$ in Proposition 7.11.3, it suffices to show the nonvanishing property for
.
Next, we construct auxiliary CM families ![]() $\boldsymbol {h}$,
$\boldsymbol {h}$, ![]() $\tilde {\boldsymbol {h}}_3$,
$\tilde {\boldsymbol {h}}_3$, ![]() $ \boldsymbol {\theta }$,
$ \boldsymbol {\theta }$, ![]() $\tilde { \boldsymbol {\theta }}_3$ on
$\tilde { \boldsymbol {\theta }}_3$ on ![]() $\operatorname {\mathrm {U}}(2)$ as p-adic measures on
$\operatorname {\mathrm {U}}(2)$ as p-adic measures on ![]() $U_{\mathcal {K},p}$.
$U_{\mathcal {K},p}$.
7.7.2 The auxiliary CM families h and  $\tilde {h}_3$
$\tilde {h}_3$
Proposition 7.7.1. There exist a CM family ![]() ${\boldsymbol {h}_0}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$ and a CM family
${\boldsymbol {h}_0}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$ and a CM family ![]() ${\boldsymbol {h}^{\prime }_0}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$ such that for every
${\boldsymbol {h}^{\prime }_0}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$ such that for every ![]() $\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1 sufficiently ramified at p,
$\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1 sufficiently ramified at p,

the theta lift of
(resp.
) to ![]() $\operatorname {\mathrm {U}}(2)$) with respect to the Schwartz function
$\operatorname {\mathrm {U}}(2)$) with respect to the Schwartz function ![]() $\phi _{h,\tau }$ (resp.
$\phi _{h,\tau }$ (resp. ![]() $\phi ^{\prime }_{h,\tau }$) on
$\phi ^{\prime }_{h,\tau }$) on ![]() $\mathbb {A}^2_{\mathbb {Q}}$ described as follows:
$\mathbb {A}^2_{\mathbb {Q}}$ described as follows:
–
 $v\notin \Sigma \cup \{\ell ,\ell ',p\}$.
$v\notin \Sigma \cup \{\ell ,\ell ',p\}$.  $$\begin{align*}\phi_{h,\tau,v}=\phi^{\prime}_{h,\tau,v}=\phi_{2,\xi\tau^{\mathtt{N}},v} \text{ in Proposition}\ 7.6.1. \end{align*}$$
$$\begin{align*}\phi_{h,\tau,v}=\phi^{\prime}_{h,\tau,v}=\phi_{2,\xi\tau^{\mathtt{N}},v} \text{ in Proposition}\ 7.6.1. \end{align*}$$–
 $v=\mathfrak {v}\bar {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\cup \{\ell \}$. We have
$v=\mathfrak {v}\bar {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\cup \{\ell \}$. We have  .
. 
–
 $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$. We have
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$. We have  .
.  $$ \begin{align*} \phi_{h,\tau,v}=&\,\text{a Schwartz function on } \mathbb{Q}^2_v \text{ invariant under } K_v, \text{ independent of } \tau,\\ &\,\text{belonging to the } \chi^{-1}_{h,v}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v),\\ \phi^{\prime}_{h,\tau,v}=&\,\text{a Schwartz function on } \mathbb{Q}^2_v \text{ invariant under } K_v,, \text{independent of } \tau, \\ &\,\text{belonging to the } \chi_{h,v}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v),\\ &\,\text{and }\int_{\mathbb{Q}^2_v}\phi_{h,\tau,v}(y)\phi^{\prime}_{h,\tau,v}(y)\,dy\neq 0. \end{align*} $$
$$ \begin{align*} \phi_{h,\tau,v}=&\,\text{a Schwartz function on } \mathbb{Q}^2_v \text{ invariant under } K_v, \text{ independent of } \tau,\\ &\,\text{belonging to the } \chi^{-1}_{h,v}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v),\\ \phi^{\prime}_{h,\tau,v}=&\,\text{a Schwartz function on } \mathbb{Q}^2_v \text{ invariant under } K_v,, \text{independent of } \tau, \\ &\,\text{belonging to the } \chi_{h,v}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v),\\ &\,\text{and }\int_{\mathbb{Q}^2_v}\phi_{h,\tau,v}(y)\phi^{\prime}_{h,\tau,v}(y)\,dy\neq 0. \end{align*} $$–
 $v=p$. We have
$v=p$. We have  . Let
. Let  $t=\mathrm {ord}_p\left (\mathrm {cond}\left ((\xi _0\tau ^{\mathtt {N}}_0)_{\mathfrak {p}}\right )\right )$.
$t=\mathrm {ord}_p\left (\mathrm {cond}\left ((\xi _0\tau ^{\mathtt {N}}_0)_{\mathfrak {p}}\right )\right )$. 
Proof. See [Reference WanWan20, §8B]. The idea of constructing ![]() $\boldsymbol {h}_0$ (resp.
$\boldsymbol {h}_0$ (resp. ![]() $\boldsymbol {h}^{\prime }_0$) is to first use suitably chosen Schwartz functions to construct a family of theta series on
$\boldsymbol {h}^{\prime }_0$) is to first use suitably chosen Schwartz functions to construct a family of theta series on ![]() $\operatorname {\mathrm {U}}(2,2)$ by interpolating the q-expansions and then restrict the family to
$\operatorname {\mathrm {U}}(2,2)$ by interpolating the q-expansions and then restrict the family to ![]() $\operatorname {\mathrm {U}}(V)\times \operatorname {\mathrm {U}}(V^-)$ and evaluate at a suitable point
$\operatorname {\mathrm {U}}(V)\times \operatorname {\mathrm {U}}(V^-)$ and evaluate at a suitable point ![]() $u_{aux}\in \operatorname {\mathrm {U}}(V)(\mathbb {A}_{\mathbb {Q}})$ (resp.
$u_{aux}\in \operatorname {\mathrm {U}}(V)(\mathbb {A}_{\mathbb {Q}})$ (resp. ![]() $u^{\prime }_{aux}\in \operatorname {\mathrm {U}}(V^-)(\mathbb {A}_{\mathbb {Q}})$) to get the desired family on
$u^{\prime }_{aux}\in \operatorname {\mathrm {U}}(V^-)(\mathbb {A}_{\mathbb {Q}})$) to get the desired family on ![]() $\operatorname {\mathrm {U}}(V^-)$ (resp.
$\operatorname {\mathrm {U}}(V^-)$ (resp. ![]() $\operatorname {\mathrm {U}}(V)$).
$\operatorname {\mathrm {U}}(V)$).
Definition 7.7.2. The map (7.5.7) between automorphic forms on ![]() $\operatorname {\mathrm {U}}(2)$ defined in terms of the tame character
$\operatorname {\mathrm {U}}(2)$ defined in terms of the tame character ![]() $\chi _h\chi ^c_{\theta }$ extends to a map from
$\chi _h\chi ^c_{\theta }$ extends to a map from ![]() $V_{\operatorname {\mathrm {U}}(2)}$ to
$V_{\operatorname {\mathrm {U}}(2)}$ to ![]() $V_{\operatorname {\mathrm {U}}(2)}$. Applying this twisting map to
$V_{\operatorname {\mathrm {U}}(2)}$. Applying this twisting map to ![]() $\boldsymbol {h}_0$ in Proposition 7.7.1 defines the CM family
$\boldsymbol {h}_0$ in Proposition 7.7.1 defines the CM family ![]() ${\boldsymbol {h}}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$.
${\boldsymbol {h}}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$.
Replacing ![]() $\chi _h\chi ^c_{\theta }$ by
$\chi _h\chi ^c_{\theta }$ by ![]() $\chi ^{-1}_h\chi ^{-c}_{\theta }$ and applying the corresponding twisting map to
$\chi ^{-1}_h\chi ^{-c}_{\theta }$ and applying the corresponding twisting map to ![]() $\boldsymbol {h}^{\prime }_0$ in Proposition 7.7.1 defines the CM family
$\boldsymbol {h}^{\prime }_0$ in Proposition 7.7.1 defines the CM family ![]() ${\tilde {\boldsymbol {h}}_3}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$.
${\tilde {\boldsymbol {h}}_3}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$.
7.7.3 The auxiliary CM families  $\theta $ and
$\theta $ and  $\tilde {\theta }_3$
$\tilde {\theta }_3$
We construct a CM family ![]() $ \boldsymbol {\theta }$ whose specializations are closely related to the theta series
$ \boldsymbol {\theta }$ whose specializations are closely related to the theta series ![]() $\theta (\phi _{2,\tau })$ in Proposition 7.6.1. (The theta series
$\theta (\phi _{2,\tau })$ in Proposition 7.6.1. (The theta series ![]() $\theta (\phi _{2,\tau })$ is not an eigenform and does not belong to the theta lift of one character of
$\theta (\phi _{2,\tau })$ is not an eigenform and does not belong to the theta lift of one character of ![]() $\operatorname {\mathrm {U}}(1)$. The specialization of
$\operatorname {\mathrm {U}}(1)$. The specialization of ![]() $ \boldsymbol {\theta }$ at
$ \boldsymbol {\theta }$ at ![]() $\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}}$ is essentially the projection of
$\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}}$ is essentially the projection of ![]() $\theta (\phi _{2,\tau ^{\mathtt {N}}})$ to the theta lift of
$\theta (\phi _{2,\tau ^{\mathtt {N}}})$ to the theta lift of ![]() .) We also construct a CM family
.) We also construct a CM family ![]() $\tilde { \boldsymbol {\theta }}_3$ dual to
$\tilde { \boldsymbol {\theta }}_3$ dual to ![]() $ \boldsymbol {\theta }$.
$ \boldsymbol {\theta }$.
Proposition 7.7.3. (1) There exists a CM family ![]() ${ \boldsymbol {\theta }}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^\natural \otimes _{\mathbb {Z}}\mathbb {Q}$ and also a CM family
${ \boldsymbol {\theta }}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V_{\operatorname {\mathrm {U}}(2),\,\xi }\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^\natural \otimes _{\mathbb {Z}}\mathbb {Q}$ and also a CM family ![]() ${\tilde { \boldsymbol {\theta }}_3}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$ such that for every
${\tilde { \boldsymbol {\theta }}_3}\in \mathcal {M} eas\left (U_{\mathcal {K},p},e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2),\,\xi ^{-1}}\,\hat {\otimes }\,\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )^{\natural }\otimes _{\mathbb {Z}}\mathbb {Q}$ such that for every ![]() $\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1 ramified at p,
$\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1 ramified at p,

the theta lift of ![]() (resp.
(resp. ![]() ) to
) to ![]() $\operatorname {\mathrm {U}}(2)$ with respect to the Schwartz function
$\operatorname {\mathrm {U}}(2)$ with respect to the Schwartz function ![]() $\phi _{\theta ,\tau }$ (resp.
$\phi _{\theta ,\tau }$ (resp. ![]() $\phi ^{\prime }_{\theta ,\tau }$) on
$\phi ^{\prime }_{\theta ,\tau }$) on ![]() $\mathbb {A}^2_{\mathbb {Q}}$ described as follows:
$\mathbb {A}^2_{\mathbb {Q}}$ described as follows:
–
 $v\notin \Sigma \,\cup \,\{\ell ,\ell ',p\}$.
$v\notin \Sigma \,\cup \,\{\ell ,\ell ',p\}$.  $$ \begin{align*} \phi_{\theta,\tau,v}=\phi^{\prime}_{\theta,\tau,v}=\phi_{2,\xi\tau^{\mathtt{N}},v} \text{in Proposition 7.6.1}. \end{align*} $$
$$ \begin{align*} \phi_{\theta,\tau,v}=\phi^{\prime}_{\theta,\tau,v}=\phi_{2,\xi\tau^{\mathtt{N}},v} \text{in Proposition 7.6.1}. \end{align*} $$–
 $v=\mathfrak {v}\bar {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\,\cup \,\{\ell '\}$. We have
$v=\mathfrak {v}\bar {\mathfrak {v}}\in \Sigma _{\mathrm {s}}\,\cup \,\{\ell '\}$. We have  and
and  $\chi _{\theta ,\mathfrak {v}}$ unramified.
$\chi _{\theta ,\mathfrak {v}}$ unramified. 
–
 $v\in \Sigma _{\mathrm {ns}}\,\cup \,\{\ell '\}$. We have
$v\in \Sigma _{\mathrm {ns}}\,\cup \,\{\ell '\}$. We have  .
.  $$ \begin{align*} \phi_{\theta,\tau,v}&=\phi_{2,\xi\tau^{\mathtt{N}},v} \text{in Proposition 7.6.1},\\ \phi^{\prime}_{\theta,\tau,v}&=\text{a Schwartz function on } \mathbb{Q}^2_v \text{ invariant under } K_v, \text{independent of } \tau,\\ &\quad\text{belonging to the } \chi^{-1}_{\theta}\lambda^{-2}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v), \\ &\quad\text{and }\int_{\mathbb{Q}^2_v}\phi_{\theta,\tau,v}(y) \phi^{\prime}_{\theta,\tau,v}(y)\,dy\neq 0.\\[-15pt] \end{align*} $$
$$ \begin{align*} \phi_{\theta,\tau,v}&=\phi_{2,\xi\tau^{\mathtt{N}},v} \text{in Proposition 7.6.1},\\ \phi^{\prime}_{\theta,\tau,v}&=\text{a Schwartz function on } \mathbb{Q}^2_v \text{ invariant under } K_v, \text{independent of } \tau,\\ &\quad\text{belonging to the } \chi^{-1}_{\theta}\lambda^{-2}|_{\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v)}\text{-eigenspace for the action of } \operatorname{\mathrm{U}}(1)(\mathbb{Q}_v), \\ &\quad\text{and }\int_{\mathbb{Q}^2_v}\phi_{\theta,\tau,v}(y) \phi^{\prime}_{\theta,\tau,v}(y)\,dy\neq 0.\\[-15pt] \end{align*} $$–
 $v=p$. We have
$v=p$. We have  . Let
. Let  $t=\mathrm {ord}_p\left (\mathrm {cond}\left ((\xi _0\tau ^{\mathtt { N}}_0)_{\mathfrak {p}}\right )\right )$.
$t=\mathrm {ord}_p\left (\mathrm {cond}\left ((\xi _0\tau ^{\mathtt { N}}_0)_{\mathfrak {p}}\right )\right )$. 
where
 $\phi _{2,\tau ^{\mathtt {N}},p}$ is as in Proposition 7.6.1.
$\phi _{2,\tau ^{\mathtt {N}},p}$ is as in Proposition 7.6.1.
(2) The specialization ![]() $ \boldsymbol {\theta }\left (\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}}\right )$ equals the projection of
$ \boldsymbol {\theta }\left (\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}}\right )$ equals the projection of  $\sum \limits _{n\in \mathbb {Z}/p^t\mathbb {Z}}\theta (\phi _{2,\tau ^{\mathtt {N}}})\left (g\begin {pmatrix}1&0\\n&1\end {pmatrix}\right )$ to the
$\sum \limits _{n\in \mathbb {Z}/p^t\mathbb {Z}}\theta (\phi _{2,\tau ^{\mathtt {N}}})\left (g\begin {pmatrix}1&0\\n&1\end {pmatrix}\right )$ to the ![]() -eigenspace for the action of the center of
-eigenspace for the action of the center of ![]() $\operatorname {\mathrm {U}}(2)$. (Note that the projection of a theta series to the
$\operatorname {\mathrm {U}}(2)$. (Note that the projection of a theta series to the ![]() -eigenspace for the action of the center is a theta lift of
-eigenspace for the action of the center is a theta lift of ![]() .)
.)
Proof. See [Reference WanWan20, §8B]. The idea is the same as the construction of ![]() $\boldsymbol {h}_0$ and
$\boldsymbol {h}_0$ and ![]() $\boldsymbol {h}^{\prime }_0$, and (2) follows immediately from (1).
$\boldsymbol {h}^{\prime }_0$, and (2) follows immediately from (1).
7.8 p-adic Petersson inner product on  $\operatorname {\mathrm {U}}(2)$
$\operatorname {\mathrm {U}}(2)$
We need p-adic Petersson inner product for families on ![]() $\operatorname {\mathrm {U}}(2)$. Let
$\operatorname {\mathrm {U}}(2)$. Let ![]() $V_{\operatorname {\mathrm {U}}(2)}$,
$V_{\operatorname {\mathrm {U}}(2)}$, ![]() $e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2)}$ be as defined in §5.8.3, an
$e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2)}$ be as defined in §5.8.3, an ![]() $K^{\prime }_{p,0}(p^n)\subset \operatorname {\mathrm {U}}(2)(\mathbb {Z}_p)$ be the subgroup consisting of g with
$K^{\prime }_{p,0}(p^n)\subset \operatorname {\mathrm {U}}(2)(\mathbb {Z}_p)$ be the subgroup consisting of g with  $\mathfrak {p}(g)\equiv \begin {pmatrix}\ast & \ast \\0&\ast \end {pmatrix}$ mod
$\mathfrak {p}(g)\equiv \begin {pmatrix}\ast & \ast \\0&\ast \end {pmatrix}$ mod ![]() $p^n$. Following [Reference HsiehHsi21, p.33], we can define a p-adic Petersson inner product
$p^n$. Following [Reference HsiehHsi21, p.33], we can define a p-adic Petersson inner product
such that for all ![]() $\phi \in V_{\operatorname {\mathrm {U}}(2)}$ with
$\phi \in V_{\operatorname {\mathrm {U}}(2)}$ with ![]() $K^{\prime }_{p,0}(p^n)$-nebentypus
$K^{\prime }_{p,0}(p^n)$-nebentypus ![]() $(\mathrm {triv},\chi )$ and
$(\mathrm {triv},\chi )$ and ![]() $\phi '\in e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2)}$ with
$\phi '\in e_{\mathrm {ord}} V^{\prime }_{\operatorname {\mathrm {U}}(2)}$ with ![]() $K^{\prime }_{p,0}(p^n)$-nebentypus
$K^{\prime }_{p,0}(p^n)$-nebentypus ![]() $(\chi ',\mathrm {triv})$,
$(\chi ',\mathrm {triv})$,
 $$\begin{align*}{\left<\phi',\phi\right>_{p\text{-}\mathrm{adic}}} =\left\{\begin{array}{ll} \sum\limits_{g}\, (U^{-n}_p\phi')\left(g\varrho^{-1}_{\mathfrak{p}}\begin{pmatrix}&1\\-p^n\end{pmatrix}\right)\phi\left(g\right), &\chi\chi'=\mathrm{triv},\\[1.5em] 0, &\chi\chi'\neq\mathrm{triv}, \end{array} \right.\\[-15pt] \end{align*}$$
$$\begin{align*}{\left<\phi',\phi\right>_{p\text{-}\mathrm{adic}}} =\left\{\begin{array}{ll} \sum\limits_{g}\, (U^{-n}_p\phi')\left(g\varrho^{-1}_{\mathfrak{p}}\begin{pmatrix}&1\\-p^n\end{pmatrix}\right)\phi\left(g\right), &\chi\chi'=\mathrm{triv},\\[1.5em] 0, &\chi\chi'\neq\mathrm{triv}, \end{array} \right.\\[-15pt] \end{align*}$$where in the summation, g runs over the finite set ![]() $\operatorname {\mathrm {U}}(2)(\mathbb {Q})\backslash \operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q},f})/K^{\prime p}_f K^{\prime }_{p,0}(p^n)$. A useful property of this p-adic Petersson inner product is that
$\operatorname {\mathrm {U}}(2)(\mathbb {Q})\backslash \operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q},f})/K^{\prime p}_f K^{\prime }_{p,0}(p^n)$. A useful property of this p-adic Petersson inner product is that
if ![]() $\phi '$ has central character
$\phi '$ has central character ![]() $\omega _{\phi '}$. Here,
$\omega _{\phi '}$. Here, ![]() $\varrho ^{-1}_{\mathfrak {p}}$ is the isomorphism from
$\varrho ^{-1}_{\mathfrak {p}}$ is the isomorphism from ![]() $\mathbb {Q}^{\times }_p$ to
$\mathbb {Q}^{\times }_p$ to ![]() $\operatorname {\mathrm {U}}(1)(\mathbb {Q}_p)$.
$\operatorname {\mathrm {U}}(1)(\mathbb {Q}_p)$.
The p-adic Petersson inner product in equation (7.8.1) induces the p-adic Petersson inner product for p-adic families on ![]() $\operatorname {\mathrm {U}}(2)$:
$\operatorname {\mathrm {U}}(2)$:

7.9 The Rallis inner product formulas for  $\big <\boldsymbol \theta ,\tilde {\theta }_3\big>_{p\text {-}\mathrm {adic}}$ and
$\big <\boldsymbol \theta ,\tilde {\theta }_3\big>_{p\text {-}\mathrm {adic}}$ and  $\big <\boldsymbol h,\tilde {h}_3\big>_{p\text {-}\mathrm {adic}}$.
$\big <\boldsymbol h,\tilde {h}_3\big>_{p\text {-}\mathrm {adic}}$.
From the description of our strategy in §7.5, in particular equation (7.5.13), we see that we need a formula relating ![]() $\big < \boldsymbol {\theta },\tilde { \boldsymbol {\theta }}_2\big>_{p\text {-}\mathrm {adic}}$ and
$\big < \boldsymbol {\theta },\tilde { \boldsymbol {\theta }}_2\big>_{p\text {-}\mathrm {adic}}$ and ![]() $\big <\boldsymbol {h},\tilde {\boldsymbol {h}}_3\big>_{p\text {-}\mathrm {adic}}$ to certain p-adic L-functions.
$\big <\boldsymbol {h},\tilde {\boldsymbol {h}}_3\big>_{p\text {-}\mathrm {adic}}$ to certain p-adic L-functions.
Let ![]() ${\mathcal {L}_3,\mathcal {L}_4}\in \mathcal {M} eas\left (U_{\mathcal {K},p},\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}\simeq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the L-function interpolating the special value at
${\mathcal {L}_3,\mathcal {L}_4}\in \mathcal {M} eas\left (U_{\mathcal {K},p},\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}\simeq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the L-function interpolating the special value at ![]() $s=1$ of
$s=1$ of ![]() $L\left (s,\pi ^{\operatorname {\mathrm {GL}}_2}_{\theta },\mathrm {Ad}\right )$,
$L\left (s,\pi ^{\operatorname {\mathrm {GL}}_2}_{\theta },\mathrm {Ad}\right )$, ![]() $L\left (s,\pi ^{\operatorname {\mathrm {GL}}_2}_h,\mathrm {Ad}\right )$, which factorize as
$L\left (s,\pi ^{\operatorname {\mathrm {GL}}_2}_h,\mathrm {Ad}\right )$, which factorize as

More precisely, for ![]() $\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1,
$\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1,

The existence of ![]() $\mathcal {L}_3,\mathcal {L}_4$ follows from Katz p-adic L-functions [Reference KatzKat78, Reference HsiehHT93].
$\mathcal {L}_3,\mathcal {L}_4$ follows from Katz p-adic L-functions [Reference KatzKat78, Reference HsiehHT93].
Proposition 7.9.1. There exists ![]() $C_{\theta },C_h\in L^{\times }$ such that
$C_{\theta },C_h\in L^{\times }$ such that
(See equation (7.8.2) for the definition of the p-adic Petersson inner product for families.)
Proof. The proof is the same as [Reference WanWan20, Proposition 8.9], which computes the specializations of the left-hand side by using the Rallis inner product formula.
7.10 Extending CM forms on  $\operatorname {\mathrm {U}}(2)$ to
$\operatorname {\mathrm {U}}(2)$ to  $\operatorname {\mathrm {GU}}(2)$
$\operatorname {\mathrm {GU}}(2)$
Let ![]() $H=\operatorname {\mathrm {GU}}(2)(\mathbb {Q})Z_{\operatorname {\mathrm {GU}}(2)}(\mathbb {A}_{\mathbb {Q}})\operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q}})$. Then H is a subgroup of
$H=\operatorname {\mathrm {GU}}(2)(\mathbb {Q})Z_{\operatorname {\mathrm {GU}}(2)}(\mathbb {A}_{\mathbb {Q}})\operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q}})$. Then H is a subgroup of ![]() $\operatorname {\mathrm {GU}}(\mathbb {A}_{\mathbb {Q}})$ of index
$\operatorname {\mathrm {GU}}(\mathbb {A}_{\mathbb {Q}})$ of index ![]() $2$ consisting of
$2$ consisting of ![]() $g\in \operatorname {\mathrm {GU}}(2)(\mathbb {A})$ with
$g\in \operatorname {\mathrm {GU}}(2)(\mathbb {A})$ with ![]() $\nu (g)\in \mathbb {Q}^{\times }\mathrm {Nm}(\mathbb {A}^{\times }_{\mathcal {K}})$. Suppose that
$\nu (g)\in \mathbb {Q}^{\times }\mathrm {Nm}(\mathbb {A}^{\times }_{\mathcal {K}})$. Suppose that ![]() $\phi $ is an automorphic form on
$\phi $ is an automorphic form on ![]() $\operatorname {\mathrm {U}}(2)$ and generates an irreducible automorphic representation
$\operatorname {\mathrm {U}}(2)$ and generates an irreducible automorphic representation ![]() $\pi _{\phi }$ of
$\pi _{\phi }$ of ![]() $\operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q}})$. Let
$\operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q}})$. Let ![]() $\omega :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ be a Hecke character extending the central character of
$\omega :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ be a Hecke character extending the central character of ![]() $\pi _{\phi }$. We can first extend
$\pi _{\phi }$. We can first extend ![]() $\phi $ to a function on H by
$\phi $ to a function on H by
and then extend this function by zero from H to ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$. We denote this extension of
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$. We denote this extension of ![]() $\phi $ to
$\phi $ to ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ by
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ by ![]() $\breve {\phi }$. This
$\breve {\phi }$. This ![]() $\breve {\phi }$ is an automorphic form on
$\breve {\phi }$ is an automorphic form on ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$.
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$.
Proposition 7.10.1. Suppose that ![]() $\pi _{\phi }$ is a theta lift from
$\pi _{\phi }$ is a theta lift from ![]() $\operatorname {\mathrm {U}}(1)$. Then
$\operatorname {\mathrm {U}}(1)$. Then ![]() $\breve {\phi }$ generates an irreducible automorphic representation
$\breve {\phi }$ generates an irreducible automorphic representation ![]() $\pi _{\breve {\phi }}$ of
$\pi _{\breve {\phi }}$ of ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A})$. Moreover, if
$\operatorname {\mathrm {GU}}(2)(\mathbb {A})$. Moreover, if ![]() $\phi \in \pi _{\phi }$ is a pure tensor in
$\phi \in \pi _{\phi }$ is a pure tensor in ![]() $\pi _{\phi }\simeq \bigotimes _v\pi _{\phi ,v}$, then
$\pi _{\phi }\simeq \bigotimes _v\pi _{\phi ,v}$, then ![]() $\breve {\phi }$ is also a pure tensor in
$\breve {\phi }$ is also a pure tensor in ![]() $\pi _{\breve {\phi }}\simeq \bigotimes _v\pi _{\breve {\phi },v}$.
$\pi _{\breve {\phi }}\simeq \bigotimes _v\pi _{\breve {\phi },v}$.
Proof. Let ![]() $\pi _{\breve {\phi }}$ be the automorphic representation of
$\pi _{\breve {\phi }}$ be the automorphic representation of ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ generated by
$\operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ generated by ![]() $\breve {\phi }$, and
$\breve {\phi }$, and ![]() $\pi ^D_{\breve {\phi }}$ be the corresponding automorphic representation of
$\pi ^D_{\breve {\phi }}$ be the corresponding automorphic representation of ![]() $D^{\times }(\mathbb {A}_{\mathbb {Q}})$ (via equation (5.4.3)). Let
$D^{\times }(\mathbb {A}_{\mathbb {Q}})$ (via equation (5.4.3)). Let ![]() $\sigma $ be an irreducible direct summand of
$\sigma $ be an irreducible direct summand of ![]() $\pi ^D_{\breve {\phi }}$ and
$\pi ^D_{\breve {\phi }}$ and ![]() $\mathrm {BC}(\sigma )$ be the base change to
$\mathrm {BC}(\sigma )$ be the base change to ![]() $\operatorname {\mathrm {GL}}(2)_{/\mathcal {K}}$. Then for each prime
$\operatorname {\mathrm {GL}}(2)_{/\mathcal {K}}$. Then for each prime ![]() $\mathfrak {v}$ of
$\mathfrak {v}$ of ![]() $\mathcal {K}$ over a split prime v in
$\mathcal {K}$ over a split prime v in ![]() $\mathbb {Q}$, we have
$\mathbb {Q}$, we have ![]() $\mathrm {BC}(\sigma )_{\mathfrak {v}}\cong \omega _{\mathfrak {v}}\lambda ^{-1}_{\mathfrak {v}}\oplus \omega ^c_{\mathfrak {v}}\lambda ^{-c}_{\mathfrak {v}}$. Therefore,
$\mathrm {BC}(\sigma )_{\mathfrak {v}}\cong \omega _{\mathfrak {v}}\lambda ^{-1}_{\mathfrak {v}}\oplus \omega ^c_{\mathfrak {v}}\lambda ^{-c}_{\mathfrak {v}}$. Therefore, ![]() $\mathrm {BC}(\sigma )\cong \mathrm {BC}(\pi ^D_{\omega })$ with
$\mathrm {BC}(\sigma )\cong \mathrm {BC}(\pi ^D_{\omega })$ with ![]() $\pi ^D_{\omega }$ the automorphic representation of
$\pi ^D_{\omega }$ the automorphic representation of ![]() $D^{\times }(\mathbb {A}_{\mathbb {Q}})$ corresponding to the theta lift of
$D^{\times }(\mathbb {A}_{\mathbb {Q}})$ corresponding to the theta lift of ![]() $\omega $ from
$\omega $ from ![]() $\operatorname {\mathrm {GU}}(1)$ to
$\operatorname {\mathrm {GU}}(1)$ to ![]() $\operatorname {\mathrm {GU}}(2)$ ([Reference RamakrishnanRam15, Corollary B]). It follows that
$\operatorname {\mathrm {GU}}(2)$ ([Reference RamakrishnanRam15, Corollary B]). It follows that ![]() $\sigma = \pi ^D_{\omega }$, and we see that all the irreducible direct summands of
$\sigma = \pi ^D_{\omega }$, and we see that all the irreducible direct summands of ![]() $\pi ^D_{\breve {\phi }}$ are isomorphic. Hence,
$\pi ^D_{\breve {\phi }}$ are isomorphic. Hence, ![]() $\pi ^D_{\breve {\phi }}$ is irreducible and so is
$\pi ^D_{\breve {\phi }}$ is irreducible and so is ![]() $\pi _{\breve {\phi }}$. (See also [Reference WanWan20, Lemma 8.1].)
$\pi _{\breve {\phi }}$. (See also [Reference WanWan20, Lemma 8.1].)
Since ![]() $\breve {\phi }$ is obtained by extension by zero, it belongs to the direct summand
$\breve {\phi }$ is obtained by extension by zero, it belongs to the direct summand ![]() $\pi _{\phi }$ in
$\pi _{\phi }$ in ![]() $\pi _{\breve {\phi }}|_{\operatorname {\mathrm {U}}(2)}$. Hence,
$\pi _{\breve {\phi }}|_{\operatorname {\mathrm {U}}(2)}$. Hence, ![]() $\phi $ being a pure tensor in
$\phi $ being a pure tensor in ![]() $\pi _{\phi }$ implies that
$\pi _{\phi }$ implies that ![]() $\breve {\phi }$ is a pure tensor in
$\breve {\phi }$ is a pure tensor in ![]() $\pi _{\breve {\phi }}$.
$\pi _{\breve {\phi }}$.
The above extension from ![]() $\operatorname {\mathrm {U}}(2)$ to
$\operatorname {\mathrm {U}}(2)$ to ![]() $\operatorname {\mathrm {GU}}(2)$ also works for p-adic automorphic forms. We denote by
$\operatorname {\mathrm {GU}}(2)$ also works for p-adic automorphic forms. We denote by ![]() ${\breve {\boldsymbol {h}}}$ the extension of
${\breve {\boldsymbol {h}}}$ the extension of ![]() $\boldsymbol {h}$ whose specialization at
$\boldsymbol {h}$ whose specialization at ![]() $\tau _{p\text {-}\mathrm {adic}}$ is the extension by zero of
$\tau _{p\text {-}\mathrm {adic}}$ is the extension by zero of ![]() $\boldsymbol {h}(\tau _{p\text {-}\mathrm {adic}})$ to
$\boldsymbol {h}(\tau _{p\text {-}\mathrm {adic}})$ to ![]() $\operatorname {\mathrm {GU}}(2)$ with respect to the character
$\operatorname {\mathrm {GU}}(2)$ with respect to the character ![]() . Similarly, we denote by
. Similarly, we denote by ![]() ${\breve {\tilde {\boldsymbol {h}}}_3}$ (resp.
${\breve {\tilde {\boldsymbol {h}}}_3}$ (resp. ![]() ${\breve { \boldsymbol {\theta }}},{\breve {\tilde { \boldsymbol {\theta }}}_3}$) the extension of
${\breve { \boldsymbol {\theta }}},{\breve {\tilde { \boldsymbol {\theta }}}_3}$) the extension of ![]() $\tilde {\boldsymbol {h}}_3$ whose specialization at
$\tilde {\boldsymbol {h}}_3$ whose specialization at ![]() $\tau _{p\text {-}\mathrm {adic}}$ is the extension by zero of
$\tau _{p\text {-}\mathrm {adic}}$ is the extension by zero of ![]() $\tilde {\boldsymbol {h}}_3(\tau _{p\text {-}\mathrm {adic}})$ to
$\tilde {\boldsymbol {h}}_3(\tau _{p\text {-}\mathrm {adic}})$ to ![]() $\operatorname {\mathrm {GU}}(2)$ with respect to the character
$\operatorname {\mathrm {GU}}(2)$ with respect to the character ![]() (resp.
(resp. ![]() ).
).
7.11 The nonvanishing property of the degenerate Fourier–Jacobi coefficients of the Klingen Eisenstein family
Let ![]() ${\mathcal {L}_5,\mathcal {L}_6}\in \mathcal {M} eas\left (U_{\mathcal {K},p},\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}\simeq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the Katz p-adic L-functions interpolating special values of
${\mathcal {L}_5,\mathcal {L}_6}\in \mathcal {M} eas\left (U_{\mathcal {K},p},\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}\simeq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the Katz p-adic L-functions interpolating special values of ![]() $L\left (s,\chi _h\chi ^c_{\theta }\xi _0\tau ^{\mathtt {N}}_0\right )$,
$L\left (s,\chi _h\chi ^c_{\theta }\xi _0\tau ^{\mathtt {N}}_0\right )$,
. In particular, for a Hecke character ![]() $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ as in Theorem 5.9.1,
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ as in Theorem 5.9.1,

The product of ![]() $\mathcal {L}_5\mathcal {L}_6$ interpolates the special values of
$\mathcal {L}_5\mathcal {L}_6$ interpolates the special values of ![]() $L(s,\mathrm {BC}(\pi _h)\times \xi _0\tau _0\lambda ^{-1})$, where
$L(s,\mathrm {BC}(\pi _h)\times \xi _0\tau _0\lambda ^{-1})$, where ![]() $\pi _h$ is the automorphic representation associated to specializations of the CM family
$\pi _h$ is the automorphic representation associated to specializations of the CM family ![]() $\boldsymbol {h}$. Note that the restriction of
$\boldsymbol {h}$. Note that the restriction of
to ![]() $\mathcal {O}^{\times }_{\mathcal {K},p}$ is
$\mathcal {O}^{\times }_{\mathcal {K},p}$ is ![]() $\left (\xi _{0,\mathfrak {p}}\xi _{0,\bar {\mathfrak {p}}}\tau ^{\mathtt {N}}_{0,\mathfrak {p}}\tau ^{\mathtt {N}}_{0,\bar {\mathfrak {p}}},\mathrm {triv}\right )$, so
$\left (\xi _{0,\mathfrak {p}}\xi _{0,\bar {\mathfrak {p}}}\tau ^{\mathtt {N}}_{0,\mathfrak {p}}\tau ^{\mathtt {N}}_{0,\bar {\mathfrak {p}}},\mathrm {triv}\right )$, so ![]() $\mathcal {L}_6$ is essentially of one variable. In fact,
$\mathcal {L}_6$ is essentially of one variable. In fact, ![]() $\mathcal {L}_6$ is the so-called ‘improved’ p-adic L-function, for which the local factor at p in the interpolation formula is a partial local L-factor instead of a partial local
$\mathcal {L}_6$ is the so-called ‘improved’ p-adic L-function, for which the local factor at p in the interpolation formula is a partial local L-factor instead of a partial local ![]() $\gamma $-factor.
$\gamma $-factor.
Proposition 7.11.1. For ![]() $\varphi $ inside the space (5.6.11), an operator
$\varphi $ inside the space (5.6.11), an operator ![]() $\mathscr {T}_{\mathrm {ns}}\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)\big (\mathbb {Q}_v\big )\right ]$ such that
$\mathscr {T}_{\mathrm {ns}}\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)\big (\mathbb {Q}_v\big )\right ]$ such that ![]() $\mathscr {T}_{\mathrm {ns}}\boldsymbol {h}$ is still invariant under the tame level group
$\mathscr {T}_{\mathrm {ns}}\boldsymbol {h}$ is still invariant under the tame level group ![]() $K^{\prime p}_f$ (defined equation (5.6.7)), and
$K^{\prime p}_f$ (defined equation (5.6.7)), and ![]() $u_1,\dots ,u_r\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$,
$u_1,\dots ,u_r\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$, ![]() $b_1,\dots ,b_r\in \mathcal {O}_L$ as in Proposition 7.6.1,
$b_1,\dots ,b_r\in \mathcal {O}_L$ as in Proposition 7.6.1,

where ![]() $ \boldsymbol {\theta }^{\bar {\lambda }}= \boldsymbol {\theta }\cdot (\bar {\lambda }\circ \det )$ and
$ \boldsymbol {\theta }^{\bar {\lambda }}= \boldsymbol {\theta }\cdot (\bar {\lambda }\circ \det )$ and ![]() $\mathcal {C}_1\in \left (\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}\right )^{\times }$.
$\mathcal {C}_1\in \left (\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}\right )^{\times }$.
Proof. The identity is proved by comparing the evaluations of both sides at ![]() $\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1. For such a
$\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1. For such a ![]() $\tau _{p\text {-}\mathrm {adic}}$, put
$\tau _{p\text {-}\mathrm {adic}}$, put ![]() $\theta _{\tau }= \boldsymbol {\theta }(\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}})$ and
$\theta _{\tau }= \boldsymbol {\theta }(\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}})$ and ![]() $h_{\tau }=\boldsymbol {h}(\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}})$, which are classical ordinary CM forms. The description of
$h_{\tau }=\boldsymbol {h}(\tau _{p\text {-}\mathrm {adic}}|_{U_{\mathcal {K},p}})$, which are classical ordinary CM forms. The description of ![]() $l_{\theta ^J_1}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$ in Proposition 7.6.1 and the definition of the p-adic Petersson inner product in §7.8 imply that
$l_{\theta ^J_1}\left (\sum _i b_i\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u_i}\right )$ in Proposition 7.6.1 and the definition of the p-adic Petersson inner product in §7.8 imply that
 $$ \begin{align} \begin{aligned} &\left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{-2\mathtt{N} k+2}\cdot\text{LHS of equation}\ (7.11.1)\ \text{evaluated at } \tau_{p\text{-}\mathrm{adic}}\\ =&\,d^{\Sigma\,\cup\{p,\ell,\ell'\}}_2\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right) \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}\theta_{\tau}\left(g_2\varrho^{-1}_{\mathfrak{p}} \begin{pmatrix} &1 \\ -1 \end{pmatrix} \right)\varphi^{\bar{\xi}_0\bar{\tau}^{\mathtt{N}}_0}(g_2) \\ &\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})} E^{\mathrm{Sieg}}_2\left(\imath_0(g_1,g_2);f_2(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\xi^{-1}_0\tau^{-\mathtt{N}}_0\lambda(\det g_1)\\ &\hspace{8em}\times \left.(U^{-m}_p \mathscr{T}_{\mathrm{ns}} \breve{h}_{\tau})\left( g_1\begin{pmatrix}&1 &\\ -p^m\end{pmatrix}_p \right)\,dg_1dg_2\,\right| {}_{s=\frac{\mathtt{N} k-3}{2}}\\ =&\,\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}) \backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}\theta^{\bar{\lambda}}_{\tau}\left(g_2\right)\varphi(g_2)\, h^{\prime}_{\tau}(g_2)\,dg_2 \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{-2\mathtt{N} k+2}\cdot\text{LHS of equation}\ (7.11.1)\ \text{evaluated at } \tau_{p\text{-}\mathrm{adic}}\\ =&\,d^{\Sigma\,\cup\{p,\ell,\ell'\}}_2\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right) \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}\theta_{\tau}\left(g_2\varrho^{-1}_{\mathfrak{p}} \begin{pmatrix} &1 \\ -1 \end{pmatrix} \right)\varphi^{\bar{\xi}_0\bar{\tau}^{\mathtt{N}}_0}(g_2) \\ &\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})} E^{\mathrm{Sieg}}_2\left(\imath_0(g_1,g_2);f_2(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\xi^{-1}_0\tau^{-\mathtt{N}}_0\lambda(\det g_1)\\ &\hspace{8em}\times \left.(U^{-m}_p \mathscr{T}_{\mathrm{ns}} \breve{h}_{\tau})\left( g_1\begin{pmatrix}&1 &\\ -p^m\end{pmatrix}_p \right)\,dg_1dg_2\,\right| {}_{s=\frac{\mathtt{N} k-3}{2}}\\ =&\,\int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}) \backslash \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}\theta^{\bar{\lambda}}_{\tau}\left(g_2\right)\varphi(g_2)\, h^{\prime}_{\tau}(g_2)\,dg_2 \end{aligned} \end{align} $$with ![]() $\imath _0$ defined in equation (6.2.2) and
$\imath _0$ defined in equation (6.2.2) and
 $$ \begin{align*} \begin{aligned} h^{\prime}_{\tau}(g_2)= d^{\Sigma\,\cup\{p,\ell,\ell'\}}_2\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)^{-1} &\cdot\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f_{2,v}\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\left(\imath_0\left(\begin{pmatrix}&1\\-1\end{pmatrix}_pg,1\right)\right)\\ &\hspace{6em}\times\left.(U^{-m}_p \mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau})\left(g_2g\begin{pmatrix}&1&\\-p^m\end{pmatrix}_p\right)\,dg\,\right| {}_{s=\frac{\mathtt{N} k-3}{2}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} h^{\prime}_{\tau}(g_2)= d^{\Sigma\,\cup\{p,\ell,\ell'\}}_2\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)^{-1} &\cdot\int_{\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})}f_{2,v}\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\left(\imath_0\left(\begin{pmatrix}&1\\-1\end{pmatrix}_pg,1\right)\right)\\ &\hspace{6em}\times\left.(U^{-m}_p \mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau})\left(g_2g\begin{pmatrix}&1&\\-p^m\end{pmatrix}_p\right)\,dg\,\right| {}_{s=\frac{\mathtt{N} k-3}{2}}, \end{aligned} \end{align*} $$where m is any sufficiently large integer. The integral over g is essentially doubling local zeta integral.
By using the same computation results in the proof of Theorem 6.1.1 for all ![]() $v\neq p$, we obtain
$v\neq p$, we obtain
 $$ \begin{align} \begin{aligned} h^{\prime}_{\tau}(g_2)=&\,\mathcal{C}_1(\tau_{p\text{-}\mathrm{adic}})\cdot \frac{\Gamma(\mathtt{N} k-1)\Gamma(\mathtt{N} k-2)}{(2\pi i)^{2\mathtt{N} k-3}}\cdot L^{p\infty}\left(\frac{\mathtt{N} k-2}{2},\mathrm{BC}(\pi_{h_{\tau}})\times \xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\\ &\times \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)}f_{2,p}\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\left(\imath_0\left(\begin{pmatrix}&1\\-1\end{pmatrix}_p g,1\right)\right)\\ &\hspace{6em}\times\left.(U^{-m}_p \mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau})\left(g_2g\begin{pmatrix}&1&\\-p^m\end{pmatrix}_p\right)\,dg\,\right| {}_{s=\frac{\mathtt{N} k-3}{2}}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} h^{\prime}_{\tau}(g_2)=&\,\mathcal{C}_1(\tau_{p\text{-}\mathrm{adic}})\cdot \frac{\Gamma(\mathtt{N} k-1)\Gamma(\mathtt{N} k-2)}{(2\pi i)^{2\mathtt{N} k-3}}\cdot L^{p\infty}\left(\frac{\mathtt{N} k-2}{2},\mathrm{BC}(\pi_{h_{\tau}})\times \xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\\ &\times \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q}_p)}f_{2,p}\left(s,\xi_0\tau^{\mathtt{N}}_0\lambda^{-1}\right)\left(\imath_0\left(\begin{pmatrix}&1\\-1\end{pmatrix}_p g,1\right)\right)\\ &\hspace{6em}\times\left.(U^{-m}_p \mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau})\left(g_2g\begin{pmatrix}&1&\\-p^m\end{pmatrix}_p\right)\,dg\,\right| {}_{s=\frac{\mathtt{N} k-3}{2}}, \end{aligned} \end{align} $$where ![]() $\mathcal {C}_1$ is the product of
$\mathcal {C}_1$ is the product of
• the local doubling zeta integrals at
 $v\in \Sigma \,\cup \{\ell ,\ell '\}$, which is a nonzero constant in L by our choice, and
$v\in \Sigma \,\cup \{\ell ,\ell '\}$, which is a nonzero constant in L by our choice, and• the element in
 $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]$ interpolating
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]$ interpolating  $L_q\left (\frac {\mathtt {N} k-2}{2},\chi _h\chi ^c_{\theta }\xi _0\tau ^{\mathtt {N}}_0\right )^{-1}$, which is a unit by our assumption on equation (5.6.5).
$L_q\left (\frac {\mathtt {N} k-2}{2},\chi _h\chi ^c_{\theta }\xi _0\tau ^{\mathtt {N}}_0\right )^{-1}$, which is a unit by our assumption on equation (5.6.5).
Our choice of ![]() $\chi _h$,
$\chi _h$, ![]() $\chi _{\theta }$ implies that
$\chi _{\theta }$ implies that ![]() $L_v\left (s,\mathrm {BC}(\pi _{h_{\tau }})\times \xi _0\tau _0\lambda ^{-1}\right )=1$ for
$L_v\left (s,\mathrm {BC}(\pi _{h_{\tau }})\times \xi _0\tau _0\lambda ^{-1}\right )=1$ for ![]() $v\in \Sigma \,\cup \{\ell ,\ell '\}$. The computation at p is slightly different from that in the construction of p-adic L-functions because the section
$v\in \Sigma \,\cup \{\ell ,\ell '\}$. The computation at p is slightly different from that in the construction of p-adic L-functions because the section ![]() $f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})$ is slightly different from the one for p-adic L-functions. The Schwartz function
$f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})$ is slightly different from the one for p-adic L-functions. The Schwartz function ![]() $\alpha ^{\prime }_{\xi \tau ,p}$ in the description of
$\alpha ^{\prime }_{\xi \tau ,p}$ in the description of ![]() $f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})$ in Proposition 7.6.1 only requires
$f_{2,p}(s,\xi _0\tau _0\lambda ^{-1})$ in Proposition 7.6.1 only requires ![]() $x_{12}$ to be supported on
$x_{12}$ to be supported on ![]() $p^{-t}\mathbb {Z}^{\times }_p$. Unlike the section for constructing p-adic L-functions,
$p^{-t}\mathbb {Z}^{\times }_p$. Unlike the section for constructing p-adic L-functions, ![]() $\alpha ^{\prime }_{\xi \tau ,p}$ does not require the whole
$\alpha ^{\prime }_{\xi \tau ,p}$ does not require the whole  $\begin {pmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end {pmatrix}$ to be supported on
$\begin {pmatrix}x_{11}&x_{12}\\x_{21}&x_{22}\end {pmatrix}$ to be supported on ![]() $p^{-t}\operatorname {\mathrm {GL}}_2(\mathbb {Z}_p)$. (In fact,
$p^{-t}\operatorname {\mathrm {GL}}_2(\mathbb {Z}_p)$. (In fact, ![]() $f_{2,p}(s,\tau _0\lambda ^{-1})$ is essentially of the same type as the section in [Reference Liu and RossoLR20, Table 2 on p.210] for constructing the ‘improved’ p-adic L-function.) The computation at p is done in [Reference WanWan20, 6I], and plugging it into equation (7.11.3), we get
$f_{2,p}(s,\tau _0\lambda ^{-1})$ is essentially of the same type as the section in [Reference Liu and RossoLR20, Table 2 on p.210] for constructing the ‘improved’ p-adic L-function.) The computation at p is done in [Reference WanWan20, 6I], and plugging it into equation (7.11.3), we get

Plugging this into equation (7.11.2), we see that the evaluations at ![]() $\tau _{p\text {-}\mathrm {adic}}$ of the two sides of equation (7.11.1) are equal.
$\tau _{p\text {-}\mathrm {adic}}$ of the two sides of equation (7.11.1) are equal.
We introduce some more p-adic L-functions. Let ![]() ${\mathcal {L}_1}\in \mathcal {M} eas\left (U_{\mathcal {K},p},\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}\simeq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the p-adic L-function interpolating the central values of
${\mathcal {L}_1}\in \mathcal {M} eas\left (U_{\mathcal {K},p},\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}\simeq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ U_{\mathcal {K},p}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the p-adic L-function interpolating the central values of
, that is, for ![]() $\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1,
$\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1,

The existence of such a p-adic L-function follows from [Reference HsiehHsi14b]. Let
 $$\begin{align*}{\mathcal{L}_2}=\pi^{-2}\left<f,\bar{f}\right>^{-1}\cdot L^\infty\left(\frac{1}{2},\mathrm{BC}(\pi)\times \chi_h\chi^c_{\theta}\right)\in L^{\mathrm{ur}}. \end{align*}$$
$$\begin{align*}{\mathcal{L}_2}=\pi^{-2}\left<f,\bar{f}\right>^{-1}\cdot L^\infty\left(\frac{1}{2},\mathrm{BC}(\pi)\times \chi_h\chi^c_{\theta}\right)\in L^{\mathrm{ur}}. \end{align*}$$The product of ![]() $\mathcal {L}_1\mathcal {L}_2$ interpolates the central values of
$\mathcal {L}_1\mathcal {L}_2$ interpolates the central values of ![]() $L\left (s,\pi \times \pi ^{\operatorname {\mathrm {GL}}_2}_h\times \pi ^{\operatorname {\mathrm {GL}}_2}_{\theta ^{\bar {\lambda }}}\right )$ with h,
$L\left (s,\pi \times \pi ^{\operatorname {\mathrm {GL}}_2}_h\times \pi ^{\operatorname {\mathrm {GL}}_2}_{\theta ^{\bar {\lambda }}}\right )$ with h, ![]() $\theta $ specializations of the CM families
$\theta $ specializations of the CM families ![]() $\boldsymbol {h}$,
$\boldsymbol {h}$, ![]() $ \boldsymbol {\theta }$.
$ \boldsymbol {\theta }$.
Note that because ![]() $\pi $ has trivial central character and
$\pi $ has trivial central character and ![]() $\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$, when
$\chi _h\chi ^c_{\theta }|_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\mathrm {triv}$, when ![]() $\mathrm {cond}\left (\xi _{0,p}\tau ^{\mathtt {N}}_{0,\mathfrak {p}}\right )=p^t$,
$\mathrm {cond}\left (\xi _{0,p}\tau ^{\mathtt {N}}_{0,\mathfrak {p}}\right )=p^t$,

Combining equation(7.11.4), the above interpolation formulas for ![]() $\mathcal {L}_1,\mathcal {L}_2$, and the interpolation formulas for
$\mathcal {L}_1,\mathcal {L}_2$, and the interpolation formulas for ![]() $\mathcal {L}_3,\mathcal {L}_4$ in §7.9, we see that when
$\mathcal {L}_3,\mathcal {L}_4$ in §7.9, we see that when ![]() $\mathrm {cond}\left (\xi _{0,p}\tau ^{\mathtt {N}}_{0,\mathfrak {p}}\right )=p^t$,
$\mathrm {cond}\left (\xi _{0,p}\tau ^{\mathtt {N}}_{0,\mathfrak {p}}\right )=p^t$,

Proposition 7.11.2. There exist operators ![]() $\mathscr {T}_{\mathrm {ns}},\mathscr {T}^{\prime }_{\mathrm {ns}} \in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)\big (\mathbb {Q}_v\big )\right ]$, and
$\mathscr {T}_{\mathrm {ns}},\mathscr {T}^{\prime }_{\mathrm {ns}} \in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)\big (\mathbb {Q}_v\big )\right ]$, and ![]() $\varphi $ inside the space (5.6.11),
$\varphi $ inside the space (5.6.11), ![]() $\varphi '$ inside the space (5.6.10) such that
$\varphi '$ inside the space (5.6.10) such that ![]() $\mathscr {T}_{\mathrm {ns}}\boldsymbol {h}$ is invariant under the tame level group
$\mathscr {T}_{\mathrm {ns}}\boldsymbol {h}$ is invariant under the tame level group ![]() $K^{\prime p}_f$ (defined in equation (5.6.7)) and
$K^{\prime p}_f$ (defined in equation (5.6.7)) and
 $$ \begin{align} \begin{aligned} &\left<\left(\mathscr{T}_{\mathrm{ns}}\breve{\boldsymbol{h}}\right)|_{\operatorname{\mathrm{U}}(2)},\boldsymbol{\theta}^{\bar{\lambda}} \varphi\right>_{p\text{-}\mathrm{adic}} \left<\Big(\mathscr{T}^{\prime}_{\mathrm{ns}}\breve{\tilde{\boldsymbol{h}}}_3\Big)|_{\operatorname{\mathrm{U}}(2)},\tilde{\boldsymbol{\theta}}^{\lambda}_3 \varphi'\right>_{p\text{-}\mathrm{adic}}\\ =&\,C_2\cdot \big<\boldsymbol{\theta},\tilde{\boldsymbol{\theta}}_3\big>_{p\text{-}\mathrm{adic}}\big<\boldsymbol{h},\tilde{\boldsymbol{h}}_3\big>_{p\text{-}\mathrm{adic}} \cdot \frac{\mathcal{L}_1\mathcal{L}_2}{\mathcal{L}_3\mathcal{L}_4} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left<\left(\mathscr{T}_{\mathrm{ns}}\breve{\boldsymbol{h}}\right)|_{\operatorname{\mathrm{U}}(2)},\boldsymbol{\theta}^{\bar{\lambda}} \varphi\right>_{p\text{-}\mathrm{adic}} \left<\Big(\mathscr{T}^{\prime}_{\mathrm{ns}}\breve{\tilde{\boldsymbol{h}}}_3\Big)|_{\operatorname{\mathrm{U}}(2)},\tilde{\boldsymbol{\theta}}^{\lambda}_3 \varphi'\right>_{p\text{-}\mathrm{adic}}\\ =&\,C_2\cdot \big<\boldsymbol{\theta},\tilde{\boldsymbol{\theta}}_3\big>_{p\text{-}\mathrm{adic}}\big<\boldsymbol{h},\tilde{\boldsymbol{h}}_3\big>_{p\text{-}\mathrm{adic}} \cdot \frac{\mathcal{L}_1\mathcal{L}_2}{\mathcal{L}_3\mathcal{L}_4} \end{aligned} \end{align} $$with ![]() $C_2\in L^{\times }$.
$C_2\in L^{\times }$.
Proof. For ![]() $\mathscr {T}_{\mathrm {ns}},\mathscr {T}^{\prime }_{\mathrm {ns}} \in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)\big (\mathbb {Q}_v\big )\right ]$ and
$\mathscr {T}_{\mathrm {ns}},\mathscr {T}^{\prime }_{\mathrm {ns}} \in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)\big (\mathbb {Q}_v\big )\right ]$ and ![]() $\varphi ,\varphi '$ in equation (5.6.11) corresponding to pure tensors in
$\varphi ,\varphi '$ in equation (5.6.11) corresponding to pure tensors in ![]() $\bigotimes _v\pi ^{\operatorname {\mathrm {GU}}(2)}_v$, we consider evaluations at
$\bigotimes _v\pi ^{\operatorname {\mathrm {GU}}(2)}_v$, we consider evaluations at ![]() $\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1 with
$\tau _{p\text {-}\mathrm {adic}}$ as in Theorem 5.9.1 with ![]() $\mathrm {cond}(\tau _{\mathfrak {p}})=p^t$. Put
$\mathrm {cond}(\tau _{\mathfrak {p}})=p^t$. Put ![]() $\theta _{\tau }= \boldsymbol {\theta }(\tau _{p\text {-}\mathrm {adic}})$ and
$\theta _{\tau }= \boldsymbol {\theta }(\tau _{p\text {-}\mathrm {adic}})$ and ![]() $h_{\tau }=\boldsymbol {h}(\tau _{p\text {-}\mathrm {adic}})$.
$h_{\tau }=\boldsymbol {h}(\tau _{p\text {-}\mathrm {adic}})$.
 $$ \begin{align} \begin{aligned} \begin{array}{ll}\text{LHS of equation}\ (7.11.6)\\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\end{array} =& \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})} \theta^{\bar{\lambda}}_{\tau}(g) \,\varphi(g) \,\left(\mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau}\right)\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg\\ &\times \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})} \tilde{\theta}^{\lambda}_{\tau}(g) \, \varphi'(g) \,\left(\mathscr{T}^{\prime}_{\mathrm{ns}}\breve{\tilde{h}}_{\tau}\right)\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{array}{ll}\text{LHS of equation}\ (7.11.6)\\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\end{array} =& \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})} \theta^{\bar{\lambda}}_{\tau}(g) \,\varphi(g) \,\left(\mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau}\right)\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg\\ &\times \int_{\operatorname{\mathrm{U}}(2)(\mathbb{Q})\backslash\operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q}})} \tilde{\theta}^{\lambda}_{\tau}(g) \, \varphi'(g) \,\left(\mathscr{T}^{\prime}_{\mathrm{ns}}\breve{\tilde{h}}_{\tau}\right)\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg. \end{aligned} \end{align} $$We can replace ![]() $\theta ^{\bar {\lambda }}_{\tau }$ (resp.
$\theta ^{\bar {\lambda }}_{\tau }$ (resp. ![]() $\tilde {\theta }^\lambda _{\tau }$) in the integrand by
$\tilde {\theta }^\lambda _{\tau }$) in the integrand by ![]() $\breve {\theta }^{\bar {\lambda }}_{\tau }$ (resp.
$\breve {\theta }^{\bar {\lambda }}_{\tau }$ (resp. ![]() $\breve {\tilde {\theta }}^\lambda _{\tau }$), its extension by zero to
$\breve {\tilde {\theta }}^\lambda _{\tau }$), its extension by zero to ![]() $\operatorname {\mathrm {GU}}(2)$ with respect the character
$\operatorname {\mathrm {GU}}(2)$ with respect the character ![]() $\chi _{\theta }\tau _{\mathfrak {p},\tau _{\mathtt {N}}}$ (resp.
$\chi _{\theta }\tau _{\mathfrak {p},\tau _{\mathtt {N}}}$ (resp. ![]() $\chi ^{-1}_{\theta }\tau ^{-1}_{\mathfrak {p},\tau _{\mathtt {N}}}$) (as described at the beginning of §7.10) and replace the domain of integration by
$\chi ^{-1}_{\theta }\tau ^{-1}_{\mathfrak {p},\tau _{\mathtt {N}}}$) (as described at the beginning of §7.10) and replace the domain of integration by ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {Q})Z_{\operatorname {\mathrm {GU}}(2)}(\mathbb {A}_{\mathbb {Q}})\backslash \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$. Thanks to equation (5.4.3), we can further replace
$\operatorname {\mathrm {GU}}(2)(\mathbb {Q})Z_{\operatorname {\mathrm {GU}}(2)}(\mathbb {A}_{\mathbb {Q}})\backslash \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$. Thanks to equation (5.4.3), we can further replace ![]() $\operatorname {\mathrm {GU}}(2)(\mathbb {Q})Z_{\operatorname {\mathrm {GU}}(2)}(\mathbb {A}_{\mathbb {Q}})\backslash \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ by
$\operatorname {\mathrm {GU}}(2)(\mathbb {Q})Z_{\operatorname {\mathrm {GU}}(2)}(\mathbb {A}_{\mathbb {Q}})\backslash \operatorname {\mathrm {GU}}(2)(\mathbb {A}_{\mathbb {Q}})$ by ![]() $D^{\times }(\mathbb {Q})Z_D(\mathbb {A}_{\mathbb {Q}})\backslash D^{\times }(\mathbb {A}_{\mathbb {Q}})$. Then for
$D^{\times }(\mathbb {Q})Z_D(\mathbb {A}_{\mathbb {Q}})\backslash D^{\times }(\mathbb {A}_{\mathbb {Q}})$. Then for ![]() $\mathscr {T}_{\mathrm {ns}},\mathscr {T}^{\prime }_{\mathrm {ns}}\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]\subset \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)(\mathbb {Q}_v)\right ]$, we can rewrite equation (7.11.7) as
$\mathscr {T}_{\mathrm {ns}},\mathscr {T}^{\prime }_{\mathrm {ns}}\in \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]\subset \bigotimes \limits _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\mathcal {O}_L\left [\operatorname {\mathrm {GU}}(2)(\mathbb {Q}_v)\right ]$, we can rewrite equation (7.11.7) as
 $$ \begin{align} \begin{aligned} \begin{array}{ll}\text{LHS of equation}\ (7.11.6)\\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\end{array} =&\int_{\mathbb{A}^{\times}_{\mathbb{Q}}\backslash D^{\times}(\mathbb{A}_{\mathbb{Q}})} \breve{\theta}^{\bar{\lambda}}_{\tau}(g) \,\varphi(g) \,(\mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau})\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg\\ &\times\int_{\mathbb{A}^{\times}_{\mathbb{Q}}\backslash D^{\times}(\mathbb{A}_{\mathbb{Q}})} \breve{\tilde{\theta}}^{\lambda}_{\tau}(g) \,\varphi'(g) \,(\mathscr{T}^{\prime}_{\mathrm{ns}}\breve{\tilde{h}}_{\tau})\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \begin{array}{ll}\text{LHS of equation}\ (7.11.6)\\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\end{array} =&\int_{\mathbb{A}^{\times}_{\mathbb{Q}}\backslash D^{\times}(\mathbb{A}_{\mathbb{Q}})} \breve{\theta}^{\bar{\lambda}}_{\tau}(g) \,\varphi(g) \,(\mathscr{T}_{\mathrm{ns}}\breve{h}_{\tau})\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg\\ &\times\int_{\mathbb{A}^{\times}_{\mathbb{Q}}\backslash D^{\times}(\mathbb{A}_{\mathbb{Q}})} \breve{\tilde{\theta}}^{\lambda}_{\tau}(g) \,\varphi'(g) \,(\mathscr{T}^{\prime}_{\mathrm{ns}}\breve{\tilde{h}}_{\tau})\left(g\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) _{\scriptscriptstyle p}\right)\,dg. \end{aligned} \end{align} $$This is the triple product integral.
Let
Then ![]() $F_{\tau }$ generates
$F_{\tau }$ generates ![]() $\Pi _{\tau }=\pi ^D_{\theta ^{\bar {\lambda }}_{\tau }}\otimes \pi ^D_{h_{\tau }}\otimes \pi ^D$, where
$\Pi _{\tau }=\pi ^D_{\theta ^{\bar {\lambda }}_{\tau }}\otimes \pi ^D_{h_{\tau }}\otimes \pi ^D$, where ![]() $\pi ^D_{\theta ^{\bar {\lambda }}_{\tau }}$ (resp.
$\pi ^D_{\theta ^{\bar {\lambda }}_{\tau }}$ (resp. ![]() $\pi ^D_{h_{\tau }}$,
$\pi ^D_{h_{\tau }}$, ![]() $\pi ^D$) is the automorphic representation of
$\pi ^D$) is the automorphic representation of ![]() $D^{\times }(\mathbb {A}_{\mathbb {Q}})$ generated by the restriction of
$D^{\times }(\mathbb {A}_{\mathbb {Q}})$ generated by the restriction of ![]() $\breve {\theta }^{\bar {\lambda }}_{\tau }$ (resp.
$\breve {\theta }^{\bar {\lambda }}_{\tau }$ (resp. ![]() $\breve {h}_{\tau }$,
$\breve {h}_{\tau }$, ![]() $\varphi $) to
$\varphi $) to ![]() $D^{\times }$, and
$D^{\times }$, and ![]() $F^{\prime }_{\tau }$ generates
$F^{\prime }_{\tau }$ generates ![]() $\tilde {\Pi }_{\tau }$, the contragredient representation of
$\tilde {\Pi }_{\tau }$, the contragredient representation of ![]() $\Pi _{\tau }$. By the isomorphism (5.4.3) and Proposition 7.10.1, we know that
$\Pi _{\tau }$. By the isomorphism (5.4.3) and Proposition 7.10.1, we know that ![]() $\pi ^D_{\theta ^{\bar {\lambda }}_{\tau }}$,
$\pi ^D_{\theta ^{\bar {\lambda }}_{\tau }}$, ![]() $\pi ^D_{h_{\tau }}$ are irreducible and
$\pi ^D_{h_{\tau }}$ are irreducible and ![]() $\breve {\theta }^{\bar {\lambda }}_{\tau }$,
$\breve {\theta }^{\bar {\lambda }}_{\tau }$, ![]() $\breve {h}_{\tau }$ are pure tensors. By the definition of
$\breve {h}_{\tau }$ are pure tensors. By the definition of ![]() $\varphi $, we know that
$\varphi $, we know that ![]() $\pi ^D_{\varphi }=\pi ^D$. Hence,
$\pi ^D_{\varphi }=\pi ^D$. Hence, ![]() $\Pi _{\tau }$ (resp.
$\Pi _{\tau }$ (resp. ![]() $\tilde {\Pi }_{\tau }$) is irreducible, and the image of
$\tilde {\Pi }_{\tau }$) is irreducible, and the image of ![]() $F_{\tau }$ (resp.
$F_{\tau }$ (resp. ![]() $F^{\prime }_{\tau }$) under
$F^{\prime }_{\tau }$) under ![]() $\Pi _{\tau }\simeq \bigotimes _v \Pi _{\tau ,v}$ (
$\Pi _{\tau }\simeq \bigotimes _v \Pi _{\tau ,v}$ (![]() $\tilde {\Pi }_{\tau }\simeq \bigotimes _v\tilde {\Pi }_{\tau ,v}$) is a pure tensor
$\tilde {\Pi }_{\tau }\simeq \bigotimes _v\tilde {\Pi }_{\tau ,v}$) is a pure tensor ![]() $\bigotimes _v F_{\tau ,v}$ (resp.
$\bigotimes _v F_{\tau ,v}$ (resp. ![]() $\bigotimes _v F^{\prime }_{\tau ,v}$). By Ichino’s triple product formula [Reference IchinoIch08], equation (7.11.8) becomes
$\bigotimes _v F^{\prime }_{\tau ,v}$). By Ichino’s triple product formula [Reference IchinoIch08], equation (7.11.8) becomes
 $$ \begin{align} \begin{aligned} &\text{LHS of equation}\ (7.11.6)\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\\ =&\,\prod_v \int_{\mathbb{A}^{\times}_{\mathbb{Q}}\backslash D^{\times}(\mathbb{A}_{\mathbb{Q}})} \big<\Pi_v(g_v)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg_v\\ =&\,\big<f^D,\bar{f}^D\big>\big<\theta_{\tau},\tilde{\theta}_{3,\tau}\big>_{p\text{-}\mathrm{adic}}\big<h_{\tau},\tilde{h}_{3,\tau}\big>_{p\text{-}\mathrm{adic}} \cdot \frac{\zeta^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}(2)^2\cdot L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(\frac{1}{2},\Pi\right)}{L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(1,\Pi,\mathrm{Ad}\right)}\\ &\times \prod_{v\in \Sigma\,\cup\{\infty,\ell,\ell'\}} \frac{\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)}\big<\Pi_v(g)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg}{\big<f^D_v,\bar{f}^D_v\big>_v\big<\theta_{\tau,v},\tilde{\theta}_{3,\tau,v}\big>_v\big<h_{\tau,v},\tilde{h}_{3,\tau,v}\big>_v}\\ &\times \frac{\int_{\mathbb{Q}^{\times}_p\backslash D^{\times}(\mathbb{Q}_p)}\big<\Pi_p(g)F_{\tau,p},F^{\prime}_{\tau,p}\big>_p\,dg}{\big<f^D_p,\bar{f}^D_p\big>_p\big<\theta_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{\theta}_{3,\tau,v}\big>_p\big<h_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{h}_{3,\tau,p}\big>_p}. \end{aligned}\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} &\text{LHS of equation}\ (7.11.6)\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\\ =&\,\prod_v \int_{\mathbb{A}^{\times}_{\mathbb{Q}}\backslash D^{\times}(\mathbb{A}_{\mathbb{Q}})} \big<\Pi_v(g_v)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg_v\\ =&\,\big<f^D,\bar{f}^D\big>\big<\theta_{\tau},\tilde{\theta}_{3,\tau}\big>_{p\text{-}\mathrm{adic}}\big<h_{\tau},\tilde{h}_{3,\tau}\big>_{p\text{-}\mathrm{adic}} \cdot \frac{\zeta^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}(2)^2\cdot L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(\frac{1}{2},\Pi\right)}{L^{\Sigma\,\cup\{\infty,p,\ell,\ell'\}}\left(1,\Pi,\mathrm{Ad}\right)}\\ &\times \prod_{v\in \Sigma\,\cup\{\infty,\ell,\ell'\}} \frac{\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)}\big<\Pi_v(g)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg}{\big<f^D_v,\bar{f}^D_v\big>_v\big<\theta_{\tau,v},\tilde{\theta}_{3,\tau,v}\big>_v\big<h_{\tau,v},\tilde{h}_{3,\tau,v}\big>_v}\\ &\times \frac{\int_{\mathbb{Q}^{\times}_p\backslash D^{\times}(\mathbb{Q}_p)}\big<\Pi_p(g)F_{\tau,p},F^{\prime}_{\tau,p}\big>_p\,dg}{\big<f^D_p,\bar{f}^D_p\big>_p\big<\theta_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{\theta}_{3,\tau,v}\big>_p\big<h_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{h}_{3,\tau,p}\big>_p}. \end{aligned}\\[-16pt]\nonumber \end{align} $$We have the following results for the local integrals at ![]() $v\in \Sigma \,\cup \{\infty ,p,\ell ,\ell '\}$:
$v\in \Sigma \,\cup \{\infty ,p,\ell ,\ell '\}$:
–
 $v\in \Sigma _{\mathrm {s}}\cup \{\infty ,\ell \}$.
$v\in \Sigma _{\mathrm {s}}\cup \{\infty ,\ell \}$.  $$\begin{align*}\frac{\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)\phi_v,\phi^{\prime}_v\big>_v\,dg}{\big<f^D_v,\bar{f}^D_v\big>_v\big<\theta_{\tau,v},\tilde{\theta}_{3,\tau,v}\big>_v\big<h_{\tau,v},\tilde{h}_{3,\tau,v}\big>_v}=\text{a nonzero constant independent of } \tau.\\[-16pt] \end{align*}$$
$$\begin{align*}\frac{\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)\phi_v,\phi^{\prime}_v\big>_v\,dg}{\big<f^D_v,\bar{f}^D_v\big>_v\big<\theta_{\tau,v},\tilde{\theta}_{3,\tau,v}\big>_v\big<h_{\tau,v},\tilde{h}_{3,\tau,v}\big>_v}=\text{a nonzero constant independent of } \tau.\\[-16pt] \end{align*}$$For
 $v=\infty $, the integral is
$v=\infty $, the integral is  $1$ because
$1$ because  $\Pi _{\infty }$ is the trivial representation. For
$\Pi _{\infty }$ is the trivial representation. For  $v=\Sigma _{\mathrm {s}}\cup \{\ell \}$, this is [Reference WanWan20, Lemmas 8.13-8.17]. Note that the twist at
$v=\Sigma _{\mathrm {s}}\cup \{\ell \}$, this is [Reference WanWan20, Lemmas 8.13-8.17]. Note that the twist at  $v\in \Sigma _{\mathrm {s}}\cup \{\ell \}$ in equation (5.6.9) guarantees that the local integrals are nonzero constants.
$v\in \Sigma _{\mathrm {s}}\cup \{\ell \}$ in equation (5.6.9) guarantees that the local integrals are nonzero constants.–
 $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$. There exist
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$. There exist  $\mathscr {T}_v,\mathscr {T}^{\prime }_v\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]\subset \mathcal {O}_L \left [\operatorname {\mathrm {GU}}(2)(\mathbb {Q}_v)\right ]$ and
$\mathscr {T}_v,\mathscr {T}^{\prime }_v\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]\subset \mathcal {O}_L \left [\operatorname {\mathrm {GU}}(2)(\mathbb {Q}_v)\right ]$ and  $\varphi _v,\varphi ^{\prime }_v\in \pi ^{\operatorname {\mathrm {GU}}(2)}_v$ such that
$\varphi _v,\varphi ^{\prime }_v\in \pi ^{\operatorname {\mathrm {GU}}(2)}_v$ such that  $\varphi _v$ and
$\varphi _v$ and  $\mathscr {T}_v\boldsymbol {h}$ are invariant under the level group
$\mathscr {T}_v\boldsymbol {h}$ are invariant under the level group  $K_v$ (defined in equation (5.6.6)) and
$K_v$ (defined in equation (5.6.6)) and  $$\begin{align*}\frac{\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg}{\big<f^D_v,\bar{f}^D_v\big>_v\big<\theta_{\tau,v},\tilde{\theta}_{3,\tau,v}\big>_v\big<h_{\tau,v},\tilde{h}_{3,\tau,v}\big>_v}=\text{a nonzero constant independent of } \tau\\[-16pt] \end{align*}$$
$$\begin{align*}\frac{\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg}{\big<f^D_v,\bar{f}^D_v\big>_v\big<\theta_{\tau,v},\tilde{\theta}_{3,\tau,v}\big>_v\big<h_{\tau,v},\tilde{h}_{3,\tau,v}\big>_v}=\text{a nonzero constant independent of } \tau\\[-16pt] \end{align*}$$This is proved in the following §7.12.
–
 $v=p$.
$v=p$.  $$ \begin{align*} &\frac{\int_{\mathbb{Q}^{\times}_p\backslash D^{\times}(\mathbb{Q}_p)}\big<\Pi_p(g)F_{\tau,p},F^{\prime}_{\tau,p}\big>_p\,dg}{\big<f^D_p,\bar{f}^D_p\big>_p\big<\theta_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{\theta}_{3,\tau,v}\big>_p\big<h_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{h}_{3,\tau,p}\big>_p}\\ =&\, p^{-t}\,\frac{\zeta_p(2)^2\cdot L_p\left(\frac{1}{2},\mathrm{BC}(\pi)\times\chi_h\chi^c_{\theta}\right)}{L_p\left(1,\eta_{\mathcal{K}/\mathbb{Q}}\right)^2\cdot L_p\left(1,\pi,\mathrm{Ad}\right)}. \end{align*} $$
$$ \begin{align*} &\frac{\int_{\mathbb{Q}^{\times}_p\backslash D^{\times}(\mathbb{Q}_p)}\big<\Pi_p(g)F_{\tau,p},F^{\prime}_{\tau,p}\big>_p\,dg}{\big<f^D_p,\bar{f}^D_p\big>_p\big<\theta_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{\theta}_{3,\tau,v}\big>_p\big<h_{\tau,p},\left(\begin{smallmatrix}&1\\-p^t\end{smallmatrix}\right) \tilde{h}_{3,\tau,p}\big>_p}\\ =&\, p^{-t}\,\frac{\zeta_p(2)^2\cdot L_p\left(\frac{1}{2},\mathrm{BC}(\pi)\times\chi_h\chi^c_{\theta}\right)}{L_p\left(1,\eta_{\mathcal{K}/\mathbb{Q}}\right)^2\cdot L_p\left(1,\pi,\mathrm{Ad}\right)}. \end{align*} $$This is a direct consequence of [Reference HsiehHsi21, Proposition 6.3]. We also use the formulas for local norms of the chosen vectors in the proof of Lemma 6.4 of loc.cit..
Plug these results on local integrals into equation (7.11.9) and compare with equation (7.11.5), we see that
 $$ \begin{align*} &\begin{array}{ll}\text{LHS of equation}\ (7.11.6)\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\end{array}\\ =&\,C_2\cdot \big<\theta_{\tau},\tilde{\theta}_{3,\tau}\big>_{p\text{-}\mathrm{adic}}\big<h_{\tau},\tilde{h}_{3,\tau}\big>_{p\text{-}\mathrm{adic}}\cdot \left(\frac{\mathcal{L}_1\mathcal{L}_2}{\mathcal{L}_3\mathcal{L}_4}\right)\left(\tau_{p\text{-}\mathrm{adic}}|_{U_{\mathcal{K},p}}\right) \end{align*} $$
$$ \begin{align*} &\begin{array}{ll}\text{LHS of equation}\ (7.11.6)\ \text{valued at } \tau_{p\text{-}\mathrm{adic}}\end{array}\\ =&\,C_2\cdot \big<\theta_{\tau},\tilde{\theta}_{3,\tau}\big>_{p\text{-}\mathrm{adic}}\big<h_{\tau},\tilde{h}_{3,\tau}\big>_{p\text{-}\mathrm{adic}}\cdot \left(\frac{\mathcal{L}_1\mathcal{L}_2}{\mathcal{L}_3\mathcal{L}_4}\right)\left(\tau_{p\text{-}\mathrm{adic}}|_{U_{\mathcal{K},p}}\right) \end{align*} $$with ![]() $C_2\in L^{\times }$ the product of
$C_2\in L^{\times }$ the product of
• the local triple product integrals divided by the norms at
 $v\in \Sigma \cup \{\ell ,\ell '\}$, which are nonzero constants,
$v\in \Sigma \cup \{\ell ,\ell '\}$, which are nonzero constants,•
 $\prod \limits _{v\in \Sigma \,\cup \{\ell ,\ell '\}} \Big (\frac {\zeta _v(2)^2 L_v\left (\frac {1}{2},\Pi \right )}{L_v\left (1,\Pi ,\mathrm {Ad}\right )}\Big )^{-1}$, which, by our choice of the Hecke characters
$\prod \limits _{v\in \Sigma \,\cup \{\ell ,\ell '\}} \Big (\frac {\zeta _v(2)^2 L_v\left (\frac {1}{2},\Pi \right )}{L_v\left (1,\Pi ,\mathrm {Ad}\right )}\Big )^{-1}$, which, by our choice of the Hecke characters  $\chi _{\theta },\chi _h$, equals
$\chi _{\theta },\chi _h$, equals  $L_q\left (\frac {1}{2},\mathrm {BC}(\pi )\times \chi _h\chi ^c_{\theta }\right )^{-1} \prod \limits _{v\in \Sigma \,\cup \{\ell ,\ell '\}} \zeta _v(2)^{-2}L_v\left (1,\eta _{\mathcal {K}/\mathbb {Q}}\right )^2 L_v\left (1,\pi ,\mathrm {Ad}\right )$, a nonzero constant,
$L_q\left (\frac {1}{2},\mathrm {BC}(\pi )\times \chi _h\chi ^c_{\theta }\right )^{-1} \prod \limits _{v\in \Sigma \,\cup \{\ell ,\ell '\}} \zeta _v(2)^{-2}L_v\left (1,\eta _{\mathcal {K}/\mathbb {Q}}\right )^2 L_v\left (1,\pi ,\mathrm {Ad}\right )$, a nonzero constant,•
 $\left (\pi \frac {L^\infty \left (1,\pi ,\mathrm {Ad}\right )}{\left <f,\bar {f}\right>}\cdot \big <f^D,\bar {f}^D\big>\right )^{-1}\in \mathbb {Q}^{\times }$.
$\left (\pi \frac {L^\infty \left (1,\pi ,\mathrm {Ad}\right )}{\left <f,\bar {f}\right>}\cdot \big <f^D,\bar {f}^D\big>\right )^{-1}\in \mathbb {Q}^{\times }$.
Given ![]() $g\in \operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q},f})$, evaluating a p-adic form at g induces a map
$g\in \operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q},f})$, evaluating a p-adic form at g induces a map
Denote by ![]() $l_{\theta ^J_1}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}\right )(g)\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ the image of
$l_{\theta ^J_1}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}\right )(g)\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ the image of ![]() $l_{\theta ^J_1}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}\right )$ under this map.
$l_{\theta ^J_1}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}\right )$ under this map.
Proposition 7.11.3. Let ![]() $\beta =1\in \operatorname {\mathrm {Her}}_1(\mathcal {K})$,
$\beta =1\in \operatorname {\mathrm {Her}}_1(\mathcal {K})$, ![]() $\theta ^J_1$ be the Fourier–Jacobi form on
$\theta ^J_1$ be the Fourier–Jacobi form on ![]() $\operatorname {\mathrm {U}}(2)$ as in Proposition 7.6.1 and
$\operatorname {\mathrm {U}}(2)$ as in Proposition 7.6.1 and ![]() $\varphi $ be an automorphic form on
$\varphi $ be an automorphic form on ![]() $\operatorname {\mathrm {U}}(2)$ as in Proposition 7.11.2. Let
$\operatorname {\mathrm {U}}(2)$ as in Proposition 7.11.2. Let ![]() $J\subseteq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the ideal generated by
$J\subseteq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ be the ideal generated by
 $$ \begin{align*} &l_{\theta^J_1}\left(\boldsymbol{E}^{\mathrm{Kling}}_{\varphi,\beta,u}\right)(g), &g\in \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q},f}),\quad u\in\hspace{-.5em}\bigotimes_{v\in\Sigma_{\mathrm{ns}}\cup\{\ell'\}}\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v). \end{align*} $$
$$ \begin{align*} &l_{\theta^J_1}\left(\boldsymbol{E}^{\mathrm{Kling}}_{\varphi,\beta,u}\right)(g), &g\in \operatorname{\mathrm{U}}(2)(\mathbb{A}_{\mathbb{Q},f}),\quad u\in\hspace{-.5em}\bigotimes_{v\in\Sigma_{\mathrm{ns}}\cup\{\ell'\}}\operatorname{\mathrm{U}}(1)(\mathbb{Q}_v). \end{align*} $$Then ![]() $J=\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
$J=\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
Proof. Suppose that ![]() $J\neq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$. Then J is contained in a maximal ideal of
$J\neq \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$. Then J is contained in a maximal ideal of ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ so is contained in the maximal ideal associated to a p-adic character
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ so is contained in the maximal ideal associated to a p-adic character ![]() $\kappa :\Gamma _{\mathcal {K}}\rightarrow \overline {\mathbb {Q}}^{\times }_p$. Let
$\kappa :\Gamma _{\mathcal {K}}\rightarrow \overline {\mathbb {Q}}^{\times }_p$. Let ![]() $\kappa ':\Gamma _{\mathcal {K}}\rightarrow \overline {\mathbb {Q}}^{\times }_p$ be a p-adic character whose
$\kappa ':\Gamma _{\mathcal {K}}\rightarrow \overline {\mathbb {Q}}^{\times }_p$ be a p-adic character whose ![]() $\mathtt {N}$-th power is
$\mathtt {N}$-th power is ![]() $\kappa $. Then
$\kappa $. Then
for all ![]() $u\in \bigotimes _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$. Then it follows from Propositions 7.11.1 and 7.11.2 that
$u\in \bigotimes _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$. Then it follows from Propositions 7.11.1 and 7.11.2 that
 $$\begin{align*}\left( \big<\boldsymbol{\theta},\tilde{\boldsymbol{\theta}}_3\big>_{p\text{-}\mathrm{adic}}\big<\boldsymbol{h},\tilde{\boldsymbol{h}}_3\big>_{p\text{-}\mathrm{adic}} \cdot \frac{\mathcal{L}_1\mathcal{L}_2\mathcal{L}_5\mathcal{L}_6}{\mathcal{L}_3\mathcal{L}_4}\right)(\kappa'|_{U_{\mathcal{K},p}})=0, \end{align*}$$
$$\begin{align*}\left( \big<\boldsymbol{\theta},\tilde{\boldsymbol{\theta}}_3\big>_{p\text{-}\mathrm{adic}}\big<\boldsymbol{h},\tilde{\boldsymbol{h}}_3\big>_{p\text{-}\mathrm{adic}} \cdot \frac{\mathcal{L}_1\mathcal{L}_2\mathcal{L}_5\mathcal{L}_6}{\mathcal{L}_3\mathcal{L}_4}\right)(\kappa'|_{U_{\mathcal{K},p}})=0, \end{align*}$$which, combining with Proposition 7.9.1, implies that
However, the condition (3) in our choice of ![]() $\chi _h,\chi _{\theta }$ in §5.6 implies that
$\chi _h,\chi _{\theta }$ in §5.6 implies that ![]() $\mathcal {L}_1\mathcal {L}_2\mathcal {L}_5\mathcal {L}_6$ is a unit in
$\mathcal {L}_1\mathcal {L}_2\mathcal {L}_5\mathcal {L}_6$ is a unit in ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ so is nonzero at all characters in
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ so is nonzero at all characters in ![]() $\operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (U_{\mathcal {K},p},\overline {\mathbb {Q}}^{\times }_p\right )$. We get a contradiction. Therefore,
$\operatorname {\mathrm {Hom}}_{\mathrm {cont}}\left (U_{\mathcal {K},p},\overline {\mathbb {Q}}^{\times }_p\right )$. We get a contradiction. Therefore, ![]() $J=\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
$J=\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$.
7.12 The local triple product integrals at nonsplit places
Lemma 7.12.1. Let v be a place of ![]() $\mathbb {Q}$ nonsplit in
$\mathbb {Q}$ nonsplit in ![]() $\mathcal {K}$ and
$\mathcal {K}$ and ![]() $\sigma :\mathcal {K}^{\times }_v\rightarrow \mathbb {C}^{\times }$ be a character nontrivial on the kernel of
$\sigma :\mathcal {K}^{\times }_v\rightarrow \mathbb {C}^{\times }$ be a character nontrivial on the kernel of ![]() $\mathrm {Nm}_{\mathcal {K}_v/\mathbb {Q}_v}$. Let
$\mathrm {Nm}_{\mathcal {K}_v/\mathbb {Q}_v}$. Let ![]() $\pi _{\sigma }$ be the dihedral supercuspidal representation of
$\pi _{\sigma }$ be the dihedral supercuspidal representation of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ obtained by the theta lift of
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ obtained by the theta lift of ![]() $\sigma $. (See [Reference SchmidtSch02, §1.2] for the precise definition.) Then by [Reference SchmidtSch02, Theorem in §2.3.2], we have the formula for the conductor of
$\sigma $. (See [Reference SchmidtSch02, §1.2] for the precise definition.) Then by [Reference SchmidtSch02, Theorem in §2.3.2], we have the formula for the conductor of ![]() $\pi _{\sigma }$:
$\pi _{\sigma }$:
 $$ \begin{align} c(\pi_{\sigma})=\left\{\begin{array}{ll} 2\mathrm{cond}(\sigma), &v\text{ inert,}\\ \mathrm{cond}(\sigma)+1, &v\text{ ramified}. \end{array} \right. \end{align} $$
$$ \begin{align} c(\pi_{\sigma})=\left\{\begin{array}{ll} 2\mathrm{cond}(\sigma), &v\text{ inert,}\\ \mathrm{cond}(\sigma)+1, &v\text{ ramified}. \end{array} \right. \end{align} $$Let W be the Kirillov model of ![]() $\pi _{\sigma }$ with respect to the additive character
$\pi _{\sigma }$ with respect to the additive character ![]() $\mathbf {e}_v^{\pm 1}$ of
$\mathbf {e}_v^{\pm 1}$ of ![]() $\mathbb {Q}_v$. (W consists of Schwartz functions on
$\mathbb {Q}_v$. (W consists of Schwartz functions on ![]() $\mathbb {Q}^{\times }_v$ since
$\mathbb {Q}^{\times }_v$ since ![]() $\pi _{\sigma }$ is supercuspidal.) For
$\pi _{\sigma }$ is supercuspidal.) For ![]() $w\in W$, define
$w\in W$, define
 $$ \begin{align} n(w)=\min\left\{n\in\mathbb{Z}: w \text{ is fixed by } \begin{pmatrix}1&0\\ \varpi^{n}_v\mathbb{Z}_v&1\end{pmatrix}\right\}. \end{align} $$
$$ \begin{align} n(w)=\min\left\{n\in\mathbb{Z}: w \text{ is fixed by } \begin{pmatrix}1&0\\ \varpi^{n}_v\mathbb{Z}_v&1\end{pmatrix}\right\}. \end{align} $$Let ![]() $\vartheta $ be a character of
$\vartheta $ be a character of ![]() $\mathbb {Z}^{\times }_v$ and
$\mathbb {Z}^{\times }_v$ and ![]() $\vartheta ^*$ be its extension to
$\vartheta ^*$ be its extension to ![]() $\mathbb {Q}^{\times }_v$ taking value
$\mathbb {Q}^{\times }_v$ taking value ![]() $1$ at
$1$ at ![]() $\varpi _v$. For each integer m, define
$\varpi _v$. For each integer m, define ![]() $w^m_{\vartheta }\in W$ as
$w^m_{\vartheta }\in W$ as
Then the following hold:
(1) Let
 $w=\sum \limits _{m=l_1}^{l_2} c_m w^m_{\vartheta }$ with
$w=\sum \limits _{m=l_1}^{l_2} c_m w^m_{\vartheta }$ with  $c_{l_2}\neq 0$. Then
$c_{l_2}\neq 0$. Then  $n(w)=n(w^{l_2}_{\vartheta })=n(w^0_{\vartheta })+l_2$.
$n(w)=n(w^{l_2}_{\vartheta })=n(w^0_{\vartheta })+l_2$.(2) We have
 $$ \begin{align*} n(w^m_{\vartheta})&=m+c(\pi_{\sigma}\otimes\vartheta^{*-1}) =\left\{\begin{array}{ll} m+2\mathrm{cond}(\sigma\cdot\vartheta^{*-1}\circ \mathrm{Nm}_{\mathcal{K}_v/\mathbb{Q}_v}), &v \text{ inert},\\ m+\mathrm{cond}(\sigma\cdot\vartheta^{*-1}\circ\mathrm{Nm}_{\mathcal{K}_v/\mathbb{Q}_v})+1, &v \text{ ramified}. \end{array} \right. \end{align*} $$
$$ \begin{align*} n(w^m_{\vartheta})&=m+c(\pi_{\sigma}\otimes\vartheta^{*-1}) =\left\{\begin{array}{ll} m+2\mathrm{cond}(\sigma\cdot\vartheta^{*-1}\circ \mathrm{Nm}_{\mathcal{K}_v/\mathbb{Q}_v}), &v \text{ inert},\\ m+\mathrm{cond}(\sigma\cdot\vartheta^{*-1}\circ\mathrm{Nm}_{\mathcal{K}_v/\mathbb{Q}_v})+1, &v \text{ ramified}. \end{array} \right. \end{align*} $$
Proof. The action ![]() $B(\mathbb {Q}_v)\subset \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ on W has the formula:
$B(\mathbb {Q}_v)\subset \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ on W has the formula:
 $$ \begin{align} \begin{pmatrix}a&b\\ 0 &d\end{pmatrix}\cdot w(x)&=\omega_{\sigma}(d)\,\mathbf{e}_v^{\pm 1}(bd^{-1}x)\,w(ad^{-1}x), &w\in W, \end{align} $$
$$ \begin{align} \begin{pmatrix}a&b\\ 0 &d\end{pmatrix}\cdot w(x)&=\omega_{\sigma}(d)\,\mathbf{e}_v^{\pm 1}(bd^{-1}x)\,w(ad^{-1}x), &w\in W, \end{align} $$where ![]() $\omega _{\sigma }$ is the central character of
$\omega _{\sigma }$ is the central character of ![]() $\sigma $ .
$\sigma $ .
(1) It is easy to see that  $\begin {pmatrix}\varpi ^l_v\\&1\end {pmatrix}\cdot w^m_{\vartheta } =w^{m-l}_{\vartheta }$. Thus,
$\begin {pmatrix}\varpi ^l_v\\&1\end {pmatrix}\cdot w^m_{\vartheta } =w^{m-l}_{\vartheta }$. Thus, ![]() $n(w^m_{\vartheta })=n(w^0_{\vartheta })+m$. It follows that
$n(w^m_{\vartheta })=n(w^0_{\vartheta })+m$. It follows that ![]() $n(w^m_{\vartheta })\leq n(w^{l_2}_{\vartheta })$ for all
$n(w^m_{\vartheta })\leq n(w^{l_2}_{\vartheta })$ for all ![]() $m\leq l_2$, so
$m\leq l_2$, so ![]() $n(w)\leq n(w^{l_2}_{\vartheta })$. On the other hand, if
$n(w)\leq n(w^{l_2}_{\vartheta })$. On the other hand, if ![]() $n(w)\leq n(w^{l_2}_{\vartheta })-1$, then
$n(w)\leq n(w^{l_2}_{\vartheta })-1$, then  $n(w^{l_2}_{\vartheta })=n\Big (c^{-1}_{l_2}(w-\sum \limits _{l_1}^{l_2-1}c_m w^m_{\vartheta })\Big )\leq n(w^{l_2}_{\vartheta })-1$. This is a contradiction. Hence,
$n(w^{l_2}_{\vartheta })=n\Big (c^{-1}_{l_2}(w-\sum \limits _{l_1}^{l_2-1}c_m w^m_{\vartheta })\Big )\leq n(w^{l_2}_{\vartheta })-1$. This is a contradiction. Hence, ![]() $n(w)= n(w^{l_2}_{\vartheta })$.
$n(w)= n(w^{l_2}_{\vartheta })$.
(2) Let ![]() $W'$ the representation of
$W'$ the representation of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ whose underlying
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ whose underlying ![]() $\mathbb {C}$-vector space equals that of W with the action of
$\mathbb {C}$-vector space equals that of W with the action of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ defined as the action of
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ defined as the action of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ on W twisted by
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ on W twisted by ![]() $\vartheta ^{*-1}\circ \det $, that is, for
$\vartheta ^{*-1}\circ \det $, that is, for ![]() $g\in \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ and
$g\in \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$ and ![]() $w\in W'$, the action of g on w gives
$w\in W'$, the action of g on w gives ![]() $\vartheta ^{*-1}(\det g)(g\cdot w)$, where
$\vartheta ^{*-1}(\det g)(g\cdot w)$, where ![]() $g\cdot w$ denotes the action of g on w viewed as an element in W. Then
$g\cdot w$ denotes the action of g on w viewed as an element in W. Then ![]() $W'\cong \pi _{\sigma }\otimes \vartheta ^{*-1}$. Suppose that
$W'\cong \pi _{\sigma }\otimes \vartheta ^{*-1}$. Suppose that ![]() $w'\in W'$ is the new vector, then
$w'\in W'$ is the new vector, then  $\begin {pmatrix}\mathbb {Z}^{\times }_v&\mathbb {Z}_v\\0&d\end {pmatrix}$,
$\begin {pmatrix}\mathbb {Z}^{\times }_v&\mathbb {Z}_v\\0&d\end {pmatrix}$, ![]() $d\in \mathbb {Z}^{\times }_v$, acts on it by the scalar
$d\in \mathbb {Z}^{\times }_v$, acts on it by the scalar ![]() $\sigma \vartheta ^{-2}(d)$, and we have
$\sigma \vartheta ^{-2}(d)$, and we have  $w'=\sum \limits _{m=l_1}^{l_2}c_m w^m_{\vartheta }$ with
$w'=\sum \limits _{m=l_1}^{l_2}c_m w^m_{\vartheta }$ with ![]() $c_{l_1}\neq 0$ for some
$c_{l_1}\neq 0$ for some ![]() $l_1\geq 0$. (In this equality, we view
$l_1\geq 0$. (In this equality, we view ![]() $w^m_{\vartheta }$ as a vector in
$w^m_{\vartheta }$ as a vector in ![]() $W'$. From the formula (7.12.3) and the definition of
$W'$. From the formula (7.12.3) and the definition of ![]() $w^m_{\vartheta }$, we know that the invariance of
$w^m_{\vartheta }$, we know that the invariance of ![]() $w'$ under the action of
$w'$ under the action of  $\begin {pmatrix}1&\mathbb {Z}_v\\0&1\end {pmatrix}$ implies that
$\begin {pmatrix}1&\mathbb {Z}_v\\0&1\end {pmatrix}$ implies that ![]() $l_1\geq 0$.) Then
$l_1\geq 0$.) Then
where the first inequality follows from the definition of new vectors with ![]() $w^0_{\vartheta }$ viewed as a vector in
$w^0_{\vartheta }$ viewed as a vector in ![]() $W'$, the middle equality is because
$W'$, the middle equality is because ![]() $w'$ is the new vector, and the right equality follows from (1). Equation (7.12.4) implies that
$w'$ is the new vector, and the right equality follows from (1). Equation (7.12.4) implies that ![]() $l_1=l_2=0$,
$l_1=l_2=0$, ![]() $w^0_{\vartheta }$ is the new vector in
$w^0_{\vartheta }$ is the new vector in ![]() $W'$, and
$W'$, and ![]() $ n(w^0_{\vartheta })=c(\pi _{\sigma }\otimes \vartheta ^{*-1})$. Since
$ n(w^0_{\vartheta })=c(\pi _{\sigma }\otimes \vartheta ^{*-1})$. Since ![]() $n(w^m_{\vartheta })=n(w^0_{\vartheta })+m$, we see that
$n(w^m_{\vartheta })=n(w^0_{\vartheta })+m$, we see that ![]() $n(w^m_{\vartheta })=m+c(\pi _{\sigma }\otimes \vartheta ^{*-1})$.
$n(w^m_{\vartheta })=m+c(\pi _{\sigma }\otimes \vartheta ^{*-1})$.
Proposition 7.12.2. For ![]() $v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$, there exist
$v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}$, there exist ![]() $\mathscr {T}_v,\mathscr {T}^{\prime }_v\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]\subset \mathcal {O}_L \left [\operatorname {\mathrm {GU}}(2)(\mathbb {Q}_v)\right ]$ and
$\mathscr {T}_v,\mathscr {T}^{\prime }_v\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]\subset \mathcal {O}_L \left [\operatorname {\mathrm {GU}}(2)(\mathbb {Q}_v)\right ]$ and ![]() $\varphi _v,\varphi ^{\prime }_v\in \pi ^D_v$ such that
$\varphi _v,\varphi ^{\prime }_v\in \pi ^D_v$ such that ![]() $\varphi _v$ and
$\varphi _v$ and ![]() $\mathscr {T}_v\boldsymbol {h}$ are invariant under the level group
$\mathscr {T}_v\boldsymbol {h}$ are invariant under the level group ![]() $K_v$ (defined in equation (5.6.6)), and
$K_v$ (defined in equation (5.6.6)), and
 $$ \begin{align} \int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg=\text{a nonzero constant independent of } \tau,\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} \int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)F_{\tau,v},F^{\prime}_{\tau,v}\big>_v\,dg=\text{a nonzero constant independent of } \tau,\\[-9pt]\nonumber \end{align} $$where
Proof. Let v be a place in ![]() $\Sigma _{\mathrm {ns}}\cup \{\ell '\}$. Then
$\Sigma _{\mathrm {ns}}\cup \{\ell '\}$. Then ![]() $\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)\subset \mathcal {O}^{\times }_{\mathcal {K},v}$ and
$\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)\subset \mathcal {O}^{\times }_{\mathcal {K},v}$ and ![]() is trivial. From the construction of
is trivial. From the construction of ![]() $\boldsymbol {h},\tilde {\boldsymbol {h}}_3$ in §7.7.2 and
$\boldsymbol {h},\tilde {\boldsymbol {h}}_3$ in §7.7.2 and ![]() $ \boldsymbol {\theta },\tilde { \boldsymbol {\theta }}_3$ in §7.7.3, we see that
$ \boldsymbol {\theta },\tilde { \boldsymbol {\theta }}_3$ in §7.7.3, we see that ![]() $\pi _{h_{\tau },v}$,
$\pi _{h_{\tau },v}$, ![]() $\pi _{\theta _{\tau },v}$ and
$\pi _{\theta _{\tau },v}$ and ![]() $h_{\tau ,v},\tilde {h}_{3,\tau ,v},\theta _{\tau ,v},\tilde {\theta }_{3,\tau ,v}$ do not change when
$h_{\tau ,v},\tilde {h}_{3,\tau ,v},\theta _{\tau ,v},\tilde {\theta }_{3,\tau ,v}$ do not change when ![]() $\tau $ varies. It follows that the left-hand side of equation (7.12.5) is independent of
$\tau $ varies. It follows that the left-hand side of equation (7.12.5) is independent of ![]() $\tau $.
$\tau $.
Next, we show the nonvanishing. By our choice of ![]() $\chi _h,\chi _{\theta }$, we have
$\chi _h,\chi _{\theta }$, we have ![]() $\operatorname {\mathrm {Hom}}_{D^{\times }(\mathbb {Q}_v)}\left (\Pi _v,\mathbb {C}\right )\neq 0$. By [Reference PrasadPra90, Theorem 1.4], we can pick
$\operatorname {\mathrm {Hom}}_{D^{\times }(\mathbb {Q}_v)}\left (\Pi _v,\mathbb {C}\right )\neq 0$. By [Reference PrasadPra90, Theorem 1.4], we can pick ![]() $\mathscr {T}^{\prime }_v\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]$ and
$\mathscr {T}^{\prime }_v\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]$ and ![]() $\varphi ^{\prime }_v\in \pi ^D_v$ such that the linear functional
$\varphi ^{\prime }_v\in \pi ^D_v$ such that the linear functional
 $$ \begin{align} \mathscr{L}_{F^{\prime}_{\tau,v}}:\Pi_v\longrightarrow \mathbb{C}, \quad\quad \mathscr{L}_{F^{\prime}_{\tau,v}}(F_v)=\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)F_v,F^{\prime}_{\tau,v}\big>_v\,dg\\[-9pt]\nonumber \end{align} $$
$$ \begin{align} \mathscr{L}_{F^{\prime}_{\tau,v}}:\Pi_v\longrightarrow \mathbb{C}, \quad\quad \mathscr{L}_{F^{\prime}_{\tau,v}}(F_v)=\int_{\mathbb{Q}^{\times}_v\backslash D^{\times}(\mathbb{Q}_v)} \big<\Pi_v(g)F_v,F^{\prime}_{\tau,v}\big>_v\,dg\\[-9pt]\nonumber \end{align} $$is nonzero and spans the one-dimensional space ![]() $\operatorname {\mathrm {Hom}}_{D^{\times }(\mathbb {Q}_v)}\left (\Pi _v,\mathbb {C}\right )$. What we need to show is that there exists
$\operatorname {\mathrm {Hom}}_{D^{\times }(\mathbb {Q}_v)}\left (\Pi _v,\mathbb {C}\right )$. What we need to show is that there exists ![]() $\mathscr {T}_v\breve {h}_{\tau ,v}\in \pi ^D_{h_{\tau },v}$ and
$\mathscr {T}_v\breve {h}_{\tau ,v}\in \pi ^D_{h_{\tau },v}$ and ![]() $\varphi _v\in \pi ^D_v$ invariant under the level group
$\varphi _v\in \pi ^D_v$ invariant under the level group ![]() $K_v$ defined in equation (5.6.6) such that
$K_v$ defined in equation (5.6.6) such that ![]() $\mathscr {L}_{F^{\prime }_{\tau ,v}}\left (\breve {\theta }^{\bar {\lambda }}_{\tau ,v}\otimes \varphi _v\otimes \mathscr {T}_v\breve {h}_{\tau ,v}\right )\neq 0$. Since
$\mathscr {L}_{F^{\prime }_{\tau ,v}}\left (\breve {\theta }^{\bar {\lambda }}_{\tau ,v}\otimes \varphi _v\otimes \mathscr {T}_v\breve {h}_{\tau ,v}\right )\neq 0$. Since ![]() $\breve {\theta }^{\bar {\lambda }}_{\tau ,v}$ is invariant under
$\breve {\theta }^{\bar {\lambda }}_{\tau ,v}$ is invariant under ![]() $K_v$, it suffices to show that there exists
$K_v$, it suffices to show that there exists ![]() $\mathscr {T}_v\breve {h}_{\tau ,v}\in \pi ^D_{h_{\tau },v}$ invariant under
$\mathscr {T}_v\breve {h}_{\tau ,v}\in \pi ^D_{h_{\tau },v}$ invariant under ![]() $K_v$ such that the linear functional
$K_v$ such that the linear functional
is nonzero. There are two cases.
Case 1: ![]() $v\neq q$,
$v\neq q$, ![]() $D^{\times }(\mathbb {Q}_v)\cong \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$. Recall that at the beginning of §5.4, we have fixed the positive integer
$D^{\times }(\mathbb {Q}_v)\cong \operatorname {\mathrm {GL}}_2(\mathbb {Q}_v)$. Recall that at the beginning of §5.4, we have fixed the positive integer ![]() $\mathfrak {s}$ and the totally imaginary element
$\mathfrak {s}$ and the totally imaginary element ![]() $\delta $ in
$\delta $ in ![]() $\mathcal {K}$, and
$\mathcal {K}$, and ![]() $\operatorname {\mathrm {U}}(2)$ is the unitary group for the skew-Hermitian form
$\operatorname {\mathrm {U}}(2)$ is the unitary group for the skew-Hermitian form  $\zeta _0=\delta \begin {pmatrix}\mathfrak {s}\\&1\end {pmatrix}$. By our assumption on
$\zeta _0=\delta \begin {pmatrix}\mathfrak {s}\\&1\end {pmatrix}$. By our assumption on ![]() $\mathfrak {s}$, there exists
$\mathfrak {s}$, there exists ![]() $\mathfrak {r}\in \mathcal {O}^{\times }_{\mathcal {K},v}$ such that
$\mathfrak {r}\in \mathcal {O}^{\times }_{\mathcal {K},v}$ such that ![]() $\mathrm {Nm}_{\mathcal {K}_v/\mathbb {Q}_v}(\mathfrak {r})=-\mathfrak {s}$. We fix the following isomorphism
$\mathrm {Nm}_{\mathcal {K}_v/\mathbb {Q}_v}(\mathfrak {r})=-\mathfrak {s}$. We fix the following isomorphism
 $$ \begin{align*} \mathfrak{i}:\operatorname{\mathrm{GU}}(2)(\mathbb{Q}_v)&\stackrel{\cong}{\longrightarrow}\operatorname{\mathrm{GU}}(1,1)(\mathbb{Q}_v), &g&\longmapsto \begin{pmatrix}\frac{\delta}{2}&\frac{\delta\mathfrak{r}}{2}\\1&-\mathfrak{r}\end{pmatrix}g\begin{pmatrix}\frac{\delta}{2}&\frac{\delta\mathfrak{r}}{2}\\1&-\mathfrak{r}\end{pmatrix}^{-1}, \end{align*} $$
$$ \begin{align*} \mathfrak{i}:\operatorname{\mathrm{GU}}(2)(\mathbb{Q}_v)&\stackrel{\cong}{\longrightarrow}\operatorname{\mathrm{GU}}(1,1)(\mathbb{Q}_v), &g&\longmapsto \begin{pmatrix}\frac{\delta}{2}&\frac{\delta\mathfrak{r}}{2}\\1&-\mathfrak{r}\end{pmatrix}g\begin{pmatrix}\frac{\delta}{2}&\frac{\delta\mathfrak{r}}{2}\\1&-\mathfrak{r}\end{pmatrix}^{-1}, \end{align*} $$where ![]() $\operatorname {\mathrm {GU}}(1,1)$ denotes the unitary group attached to the skew-Hermitian form
$\operatorname {\mathrm {GU}}(1,1)$ denotes the unitary group attached to the skew-Hermitian form  $\begin {pmatrix}&1\\-1\end {pmatrix}.$Let
$\begin {pmatrix}&1\\-1\end {pmatrix}.$Let ![]() $K^{\operatorname {\mathrm {GL}}_2}_v=\mathfrak {i}(K_v)\cap \operatorname {\mathrm {GL}}_2(\mathbb {Z}_v)$. By our assumptions in §5.2,
$K^{\operatorname {\mathrm {GL}}_2}_v=\mathfrak {i}(K_v)\cap \operatorname {\mathrm {GL}}_2(\mathbb {Z}_v)$. By our assumptions in §5.2, ![]() $v\neq 2$. One can check that
$v\neq 2$. One can check that
 $$ \begin{align*} K^{\operatorname{\mathrm{GL}}_2}_v=\begin{pmatrix}1+\varpi^{c_v}_v\mathbb{Z}_v&\varpi^{c_v+\epsilon_v}_v\mathbb{Z}_v\\\varpi^{c_v}_v\mathbb{Z}_v&1+\varpi^{c_v}_v\mathbb{Z}_v\end{pmatrix}\subset\operatorname{\mathrm{GL}}_2(\mathbb{Z}_v),\\[-16pt] \end{align*} $$
$$ \begin{align*} K^{\operatorname{\mathrm{GL}}_2}_v=\begin{pmatrix}1+\varpi^{c_v}_v\mathbb{Z}_v&\varpi^{c_v+\epsilon_v}_v\mathbb{Z}_v\\\varpi^{c_v}_v\mathbb{Z}_v&1+\varpi^{c_v}_v\mathbb{Z}_v\end{pmatrix}\subset\operatorname{\mathrm{GL}}_2(\mathbb{Z}_v),\\[-16pt] \end{align*} $$where  $\epsilon _v=\begin {cases}0,&v\text { inert}\\ 1,&v\text { ramified}\end {cases}$.
$\epsilon _v=\begin {cases}0,&v\text { inert}\\ 1,&v\text { ramified}\end {cases}$.
Given a character ![]() $\chi _v:\mathbb {Q}^{\times }_v\rightarrow \mathbb {C}^{\times }$, we denote also by
$\chi _v:\mathbb {Q}^{\times }_v\rightarrow \mathbb {C}^{\times }$, we denote also by ![]() $\chi _v$ the character
$\chi _v$ the character ![]() $B(\mathbb {Q}_v)\rightarrow \mathbb {C}^{\times }$,
$B(\mathbb {Q}_v)\rightarrow \mathbb {C}^{\times }$,  $\begin {pmatrix}a&b\\0&d\end {pmatrix}\mapsto \chi _v(ad^{-1})$, and
$\begin {pmatrix}a&b\\0&d\end {pmatrix}\mapsto \chi _v(ad^{-1})$, and ![]() $\operatorname {\mathrm {Ind}}_{B}^{\operatorname {\mathrm {GL}}_2}(\chi _v)$ the (normalized) induction of
$\operatorname {\mathrm {Ind}}_{B}^{\operatorname {\mathrm {GL}}_2}(\chi _v)$ the (normalized) induction of ![]() $\chi _v$. By our assumption on
$\chi _v$. By our assumption on ![]() $\pi $,
$\pi $, ![]() $\pi _v$ is either isomorphic to
$\pi _v$ is either isomorphic to ![]() $\operatorname {\mathrm {Ind}}_{B}^{\operatorname {\mathrm {GL}}(2)}(\chi _v)$ for an unramified character
$\operatorname {\mathrm {Ind}}_{B}^{\operatorname {\mathrm {GL}}(2)}(\chi _v)$ for an unramified character ![]() $\chi _v\neq |\cdot |^{\pm 1/2}_{\mathbb {Q}_v}$ or is isomorphic to the irreducible quotient of
$\chi _v\neq |\cdot |^{\pm 1/2}_{\mathbb {Q}_v}$ or is isomorphic to the irreducible quotient of ![]() $\operatorname {\mathrm {Ind}}_{B}^{\operatorname {\mathrm {GL}}(2)}(\chi _v)$ with
$\operatorname {\mathrm {Ind}}_{B}^{\operatorname {\mathrm {GL}}(2)}(\chi _v)$ with ![]() $\chi _v=|\cdot |^{-1/2}_{\mathbb {Q}_v}$. Let
$\chi _v=|\cdot |^{-1/2}_{\mathbb {Q}_v}$. Let ![]() $\psi _1=\mathbf {e}_v$, the additive character of
$\psi _1=\mathbf {e}_v$, the additive character of ![]() $\mathbb {Q}_v$ defined in equation (1.0.5),
$\mathbb {Q}_v$ defined in equation (1.0.5), ![]() $\psi _2=\bar {\mathbf {e}}_v$, and
$\psi _2=\bar {\mathbf {e}}_v$, and ![]() $W_{1}$ (resp.
$W_{1}$ (resp. ![]() $W_{2}$) be the Kirillov model of
$W_{2}$) be the Kirillov model of ![]() $\pi _1=\pi ^D_{\theta ^{\bar {\lambda }}_{\tau },v}$ (resp.
$\pi _1=\pi ^D_{\theta ^{\bar {\lambda }}_{\tau },v}$ (resp. ![]() $\pi _2=\pi ^D_{h_{\tau },v}$) with respect to
$\pi _2=\pi ^D_{h_{\tau },v}$) with respect to ![]() $\psi _1$ (resp.
$\psi _1$ (resp. ![]() $\psi _2$). We have
$\psi _2$). We have
 $$ \begin{align} \begin{aligned} \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{GL}}_2(\mathbb{Q}_v)}\left(W_1\otimes W_2,\tilde{\pi}\right)&\cong \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{GL}}_2(\mathbb{Q}_v)}\left(W_1\otimes W_2,\operatorname{\mathrm{Ind}}^{\operatorname{\mathrm{GL}}_2}_B (\chi^{-1}_v)\right)\\ &\cong \operatorname{\mathrm{Hom}}_{B(\mathbb{Q}_v)}\left(W_1\otimes W_2,\chi^{-1}_v|\cdot|^{1/2}_{\mathbb{Q}_v}\right), \end{aligned}\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{GL}}_2(\mathbb{Q}_v)}\left(W_1\otimes W_2,\tilde{\pi}\right)&\cong \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{GL}}_2(\mathbb{Q}_v)}\left(W_1\otimes W_2,\operatorname{\mathrm{Ind}}^{\operatorname{\mathrm{GL}}_2}_B (\chi^{-1}_v)\right)\\ &\cong \operatorname{\mathrm{Hom}}_{B(\mathbb{Q}_v)}\left(W_1\otimes W_2,\chi^{-1}_v|\cdot|^{1/2}_{\mathbb{Q}_v}\right), \end{aligned}\\[-16pt]\nonumber \end{align} $$where the second isomorphism is deduced from the Frobenius reciprocity, and when ![]() $\chi _v=|\cdot |^{-1/2}_{\mathbb {Q}_v}$, the first isomorphism is because by our choice of
$\chi _v=|\cdot |^{-1/2}_{\mathbb {Q}_v}$, the first isomorphism is because by our choice of ![]() $\chi _{\theta },\chi _h$,
$\chi _{\theta },\chi _h$, ![]() $W_1\not \cong \tilde {W}_2$. It is easy to see that the map
$W_1\not \cong \tilde {W}_2$. It is easy to see that the map
 $$ \begin{align} \mathscr{L}(w_1,w_2)= \int_{\mathbb{Q}^{\times}_v} w_1(x)w_2(x)\cdot\chi_v(x)|x|^{-1/2}_{\mathbb{Q}_v}\,d^{\times} x, \quad\quad w_1\in W_1,\,w_2\in W_2\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} \mathscr{L}(w_1,w_2)= \int_{\mathbb{Q}^{\times}_v} w_1(x)w_2(x)\cdot\chi_v(x)|x|^{-1/2}_{\mathbb{Q}_v}\,d^{\times} x, \quad\quad w_1\in W_1,\,w_2\in W_2\\[-16pt]\nonumber \end{align} $$is a nonzero element in the second line of equation (7.12.8), which is one dimensional, so it equals the image of ![]() in the second line of equation (7.12.8) up to a nonzero scalar. Hence, showing the existence of
in the second line of equation (7.12.8) up to a nonzero scalar. Hence, showing the existence of ![]() $\mathscr {T}_v\breve {h}_{\tau ,v}\in \pi ^D_{h_{\tau },v}$ invariant under
$\mathscr {T}_v\breve {h}_{\tau ,v}\in \pi ^D_{h_{\tau },v}$ invariant under ![]() $K_v$ such that equation (7.12.7) is nonzero reduces to showing the existence of
$K_v$ such that equation (7.12.7) is nonzero reduces to showing the existence of ![]() invariant under
invariant under ![]() $K^{\operatorname {\mathrm {GL}}_2}_v$ such that
$K^{\operatorname {\mathrm {GL}}_2}_v$ such that ![]() , where
, where ![]() is the vector invariant under
is the vector invariant under ![]() $K^{\operatorname {\mathrm {GL}}_2}_v$ corresponding to
$K^{\operatorname {\mathrm {GL}}_2}_v$ corresponding to ![]() $\breve {\theta }^{\bar {\lambda }}_{\tau ,v}\in \pi ^D_{\theta ^{\bar {\lambda }}_{\tau },v}$.
$\breve {\theta }^{\bar {\lambda }}_{\tau ,v}\in \pi ^D_{\theta ^{\bar {\lambda }}_{\tau },v}$.
For a character ![]() $\vartheta :\mathbb {Z}^{\times }_v\rightarrow \mathbb {C}^{\times }$, put
$\vartheta :\mathbb {Z}^{\times }_v\rightarrow \mathbb {C}^{\times }$, put

the projection of
to the ![]() $\vartheta $-eigenspace for the action of
$\vartheta $-eigenspace for the action of ![]() $\mathrm {diag}(\mathbb {Z}^{\times }_v,1)$. Let
$\mathrm {diag}(\mathbb {Z}^{\times }_v,1)$. Let ![]() $\vartheta ^*$ be the extension of
$\vartheta ^*$ be the extension of ![]() $\vartheta $ to
$\vartheta $ to ![]() $\mathbb {Q}^{\times }_v$ taking value
$\mathbb {Q}^{\times }_v$ taking value ![]() $1$ at
$1$ at ![]() $\varpi _v$. For each integer m, put define
$\varpi _v$. For each integer m, put define ![]() $w^m_{j,\vartheta }\in W_j$,
$w^m_{j,\vartheta }\in W_j$, ![]() $j=1,2$, as
$j=1,2$, as
Then we have
with ![]() $c_m\in \mathbb {C}$ finitely many nonzero m, and
$c_m\in \mathbb {C}$ finitely many nonzero m, and
. We can take a ![]() $\vartheta $ of conductor
$\vartheta $ of conductor ![]() $\leq \varpi ^{c_v}_v$ such that
$\leq \varpi ^{c_v}_v$ such that
. This
is still invariant under ![]() $K^{\operatorname {\mathrm {GL}}_2}_v$. By the formula (7.12.3) and (1) of Lemma 7.12.1, we deduce that
$K^{\operatorname {\mathrm {GL}}_2}_v$. By the formula (7.12.3) and (1) of Lemma 7.12.1, we deduce that

with ![]() $n(w^0_{1,\vartheta })$ defined as in equation (7.12.2). Take
$n(w^0_{1,\vartheta })$ defined as in equation (7.12.2). Take ![]() $-(c_v+\epsilon _v)\leq m_0\leq c_v-n(w^0_{1,\vartheta })$ such that
$-(c_v+\epsilon _v)\leq m_0\leq c_v-n(w^0_{1,\vartheta })$ such that ![]() $c_{m_0}\neq 0$. Then
$c_{m_0}\neq 0$. Then
and by the formula (7.12.3), we know that ![]() $w^{m_0}_{2,\vartheta ^{-1}}$ is invariant under
$w^{m_0}_{2,\vartheta ^{-1}}$ is invariant under  $\begin {pmatrix}1+\varpi ^{c_v}_v\mathbb {Z}_v&\varpi ^{c_v+\epsilon _v}_v\mathbb {Z}_v\\0&1+\varpi ^{c_v}_v\end {pmatrix}$, and by (2) of Lemma 7.12.1, we know that
$\begin {pmatrix}1+\varpi ^{c_v}_v\mathbb {Z}_v&\varpi ^{c_v+\epsilon _v}_v\mathbb {Z}_v\\0&1+\varpi ^{c_v}_v\end {pmatrix}$, and by (2) of Lemma 7.12.1, we know that
By our choice of ![]() $\chi _{\theta },\chi _h$ and the formula (7.12.1), we have
$\chi _{\theta },\chi _h$ and the formula (7.12.1), we have ![]() $c(\pi _1\otimes \vartheta ^{*-1})\geq c(\pi _2\otimes \vartheta ^{*})$. Hence,
$c(\pi _1\otimes \vartheta ^{*-1})\geq c(\pi _2\otimes \vartheta ^{*})$. Hence, ![]() $ n(w^{m_0}_{2,\vartheta ^{-1}})\geq c_v$, and
$ n(w^{m_0}_{2,\vartheta ^{-1}})\geq c_v$, and ![]() $w^{m_0}_{2,\vartheta ^{-1}}$ is invariant under
$w^{m_0}_{2,\vartheta ^{-1}}$ is invariant under  $\begin {pmatrix}1&0\\ \varpi ^{c_v}_v\mathbb {Z}_v&1\end {pmatrix}$. Therefore,
$\begin {pmatrix}1&0\\ \varpi ^{c_v}_v\mathbb {Z}_v&1\end {pmatrix}$. Therefore,
is the desired vector in ![]() $W_2$ invariant under
$W_2$ invariant under ![]() $K^{\operatorname {\mathrm {GL}}_2}_v$ such that
$K^{\operatorname {\mathrm {GL}}_2}_v$ such that
.
Case 2: ![]() $v=q$,
$v=q$, ![]() $D^{\times }(\mathbb {Q}_q)$ modulo its center is compact and
$D^{\times }(\mathbb {Q}_q)$ modulo its center is compact and ![]() $\pi ^D_v$ is one-dimensional isomorphic to
$\pi ^D_v$ is one-dimensional isomorphic to ![]() $\chi _q\circ \mathrm {Nm}_D$, where
$\chi _q\circ \mathrm {Nm}_D$, where ![]() $\chi _q$ is the unramified quadratic character in condition (5) in the choice of
$\chi _q$ is the unramified quadratic character in condition (5) in the choice of ![]() $\chi _{\theta },\chi _h$ at the beginning of §5.6, and
$\chi _{\theta },\chi _h$ at the beginning of §5.6, and ![]() $\mathrm {Nm}_D$ denotes the norm of D. By our choice of
$\mathrm {Nm}_D$ denotes the norm of D. By our choice of ![]() $\chi _{\theta },\chi _h$, we have
$\chi _{\theta },\chi _h$, we have
It follows that there exists ![]() $\mathscr {T}_q\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]$ such that equation (7.12.7) is nonzero. Since
$\mathscr {T}_q\in \mathcal {O}_L\left [D^{\times }(\mathbb {Q}_v)\right ]$ such that equation (7.12.7) is nonzero. Since ![]() $K_v$ is a normal subgroup of
$K_v$ is a normal subgroup of ![]() $D^{\times }(\mathbb {Q}_q)$,
$D^{\times }(\mathbb {Q}_q)$, ![]() $\mathscr {T}_q\breve {h}_{\tau ,q}$ is still invariant under
$\mathscr {T}_q\breve {h}_{\tau ,q}$ is still invariant under ![]() $K_v$.
$K_v$.
8 Proof of Greenberg–Iwasawa main conjecture
8.1 The Klingen Eisenstein ideal
Let ![]() be the
be the ![]() $\mathcal {O}_L[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module of semiordinary families on
$\mathcal {O}_L[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module of semiordinary families on ![]() $\operatorname {\mathrm {GU}}(3,1)$ of tame level
$\operatorname {\mathrm {GU}}(3,1)$ of tame level ![]() $K^p_f$ as in Theorem 2.9.1. Identifying
$K^p_f$ as in Theorem 2.9.1. Identifying ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ with
$T_{\mathrm {so}}(\mathbb {Z}_p)$ with ![]() $\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p\simeq \mathcal {O}^{\times }_{\mathcal {K},p}$, we have the map
$\mathbb {Z}^{\times }_p\times \mathbb {Z}^{\times }_p\simeq \mathcal {O}^{\times }_{\mathcal {K},p}$, we have the map
with kernel ![]() $\mu _p\times \mu _p$. Denote by
$\mu _p\times \mu _p$. Denote by ![]() (resp.
(resp. ![]() ${\mathcal {M}_{\mathrm {so},\,\xi }}$) the sub-
${\mathcal {M}_{\mathrm {so},\,\xi }}$) the sub-![]() $\mathcal {O}_L[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module of
$\mathcal {O}_L[\![ T_{\mathrm {so}}(\mathbb {Z}_p)]\!]$-module of ![]() (resp.
(resp. ![]() $\mathcal {M}_{\mathrm {so}}$) on which
$\mathcal {M}_{\mathrm {so}}$) on which ![]() $\mu _p\times \mu _p$ acts through
$\mu _p\times \mu _p$ acts through ![]() $\xi _{p\text {-}\mathrm {adic}}$. We make
$\xi _{p\text {-}\mathrm {adic}}$. We make ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ act on
$T_{\mathrm {so}}(\mathbb {Z}_p)$ act on ![]() and
and ![]() $\mathcal {M}_{\mathrm {so},\,\xi }$ through its usual action multiplied by the character
$\mathcal {M}_{\mathrm {so},\,\xi }$ through its usual action multiplied by the character ![]() $\xi ^{-1}_{p\text {-}\mathrm {adic}}$. Then this action factors through the image of
$\xi ^{-1}_{p\text {-}\mathrm {adic}}$. Then this action factors through the image of ![]() $T_{\mathrm {so}}(\mathbb {Z}_p)$ in
$T_{\mathrm {so}}(\mathbb {Z}_p)$ in ![]() $\Gamma _{\mathcal {K}}$ under the map (8.1.1). Let
$\Gamma _{\mathcal {K}}$ under the map (8.1.1). Let ![]() ,
, ![]() ${\mathcal {M}^0_{\mathrm {so},\,\xi }}\subset \mathcal {M}_{\mathrm {so},\,\xi }$ be the cuspidal part. We consider the
${\mathcal {M}^0_{\mathrm {so},\,\xi }}\subset \mathcal {M}_{\mathrm {so},\,\xi }$ be the cuspidal part. We consider the ![]() $\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$-modules
$\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$-modules
 $$ \begin{align*} {\mathcal{M}_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}} &= \mathcal{M}_{\mathrm{so},\,\xi}\otimes_{\mathcal{O}_L[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]} \hat{\mathcal{O}}^{\mathrm{ur}}_L[\![\Gamma_{\mathcal{K}}]\!],\\ {\mathcal{M}^0_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}} &= \mathcal{M}^0_{\mathrm{so},\,\xi}\otimes_{\mathcal{O}_L[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]} \hat{\mathcal{O}}^{\mathrm{ur}}_L[\![\Gamma_{\mathcal{K}}]\!].\\[-15pt] \end{align*} $$
$$ \begin{align*} {\mathcal{M}_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}} &= \mathcal{M}_{\mathrm{so},\,\xi}\otimes_{\mathcal{O}_L[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]} \hat{\mathcal{O}}^{\mathrm{ur}}_L[\![\Gamma_{\mathcal{K}}]\!],\\ {\mathcal{M}^0_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}} &= \mathcal{M}^0_{\mathrm{so},\,\xi}\otimes_{\mathcal{O}_L[\![ T_{\mathrm{so}}(\mathbb{Z}_p)]\!]} \hat{\mathcal{O}}^{\mathrm{ur}}_L[\![\Gamma_{\mathcal{K}}]\!].\\[-15pt] \end{align*} $$ The semiordinary Klingen Eisenstein family ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ constructed in §5.10 belongs to the space
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ constructed in §5.10 belongs to the space ![]() $\mathcal {M} eas\left (\Gamma _{\mathcal {K}},e_{\mathrm {so}} V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }\widehat {\otimes }\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}$. By the natural pairing between
$\mathcal {M} eas\left (\Gamma _{\mathcal {K}},e_{\mathrm {so}} V_{\operatorname {\mathrm {GU}}(3,1),\,\xi }\widehat {\otimes }\hat {\mathcal {O}}^{\mathrm {ur}}_L\right )\otimes _{\mathbb {Z}}\mathbb {Q}$. By the natural pairing between ![]() $V_{\operatorname {\mathrm {GU}}(3,1),\mathrm {so}}$ and the space
$V_{\operatorname {\mathrm {GU}}(3,1),\mathrm {so}}$ and the space
in Theorem 2.9.1, we see that there is a natural map
and it induces a ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$-linear Hecke-equivariant map
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$-linear Hecke-equivariant map
Therefore, we can view ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ as an element in
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ as an element in ![]() $\mathcal {M}_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\otimes _{\mathbb {Z}}\mathbb {Q}$. Let
$\mathcal {M}_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\otimes _{\mathbb {Z}}\mathbb {Q}$. Let ![]() $\mathbb {T}$ be the abstract algebra generated by the unramified Hecke algebras away from
$\mathbb {T}$ be the abstract algebra generated by the unramified Hecke algebras away from ![]() $\Sigma \cup \{p,\ell ,\ell '\}$ and
$\Sigma \cup \{p,\ell ,\ell '\}$ and ![]() $\mathbb {U}_p$-operators at p. Then
$\mathbb {U}_p$-operators at p. Then ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ is an eigen-family for the action of
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$ is an eigen-family for the action of ![]() $\mathbb {T}$, and we denote by
$\mathbb {T}$, and we denote by ![]() $\lambda _{\mathrm {Eis},\pi ,\xi }:\mathbb {T}\rightarrow \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ the corresponding eigen-system.
$\lambda _{\mathrm {Eis},\pi ,\xi }:\mathbb {T}\rightarrow \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ the corresponding eigen-system.
Let ![]() ${\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}}$ be the reduced Hecke algebra generated by
${\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}}$ be the reduced Hecke algebra generated by ![]() $\mathbb {T}$ acting on
$\mathbb {T}$ acting on ![]() $\mathcal {M}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$. Let
$\mathcal {M}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$. Let ![]() ${\mathcal {I}_{\mathrm {Eis},\pi ,\xi }}\subset \mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$ be the ideal generated by the images of
${\mathcal {I}_{\mathrm {Eis},\pi ,\xi }}\subset \mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$ be the ideal generated by the images of ![]() $T-\lambda _{\mathrm {Eis},\pi ,\xi }(T)$ in
$T-\lambda _{\mathrm {Eis},\pi ,\xi }(T)$ in ![]() $\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$,
$\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$, ![]() $T\in \mathbb {T}$. We define the Klingen Eisenstein ideal as
$T\in \mathbb {T}$. We define the Klingen Eisenstein ideal as
It measures the congruences between the Hecke eigen-systems in ![]() $\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$ and the Hecke eigen-system
$\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$ and the Hecke eigen-system ![]() $\lambda _{\mathrm {Eis},\pi ,\xi }$ attached to
$\lambda _{\mathrm {Eis},\pi ,\xi }$ attached to ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$.
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$.
Theorem 8.1.1. Let ![]() $\varphi $ be as in Proposition 7.11.2. Let P be a height one prime ideal of
$\varphi $ be as in Proposition 7.11.2. Let P be a height one prime ideal of ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ such that
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ such that ![]() $P\cap \hat {\mathcal {O}}^{\mathrm {ur}}_L=(0)$. Then
$P\cap \hat {\mathcal {O}}^{\mathrm {ur}}_L=(0)$. Then
(where ![]() $\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}},\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ are the p-adic L-function satisfying the interpolation property in equation (6.1.1)(6.1.2)).
$\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}},\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ are the p-adic L-function satisfying the interpolation property in equation (6.1.1)(6.1.2)).
Proof. By Theorem 2.9.1, we have the fundamental exact sequence
 $$\begin{align*}0\rightarrow\mathcal{M}^0_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}\rightarrow \mathcal{M}_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}\rightarrow \bigoplus\limits_{g\in C(K^p_f)} M_{\operatorname{\mathrm{GU}}(2)}\left(K^{\prime p}_{f,g}K^{\prime}_{p,0},\hat{\mathcal{O}}^{\mathrm{ur}}_L\right)\otimes_{\mathbb{Z}_p}\mathbb{Z}_p[\![ \Gamma_{\mathcal{K}}]\!] \rightarrow 0. \end{align*}$$
$$\begin{align*}0\rightarrow\mathcal{M}^0_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}\rightarrow \mathcal{M}_{\mathrm{so},\,\xi,\Gamma_{\mathcal{K}}}\rightarrow \bigoplus\limits_{g\in C(K^p_f)} M_{\operatorname{\mathrm{GU}}(2)}\left(K^{\prime p}_{f,g}K^{\prime}_{p,0},\hat{\mathcal{O}}^{\mathrm{ur}}_L\right)\otimes_{\mathbb{Z}_p}\mathbb{Z}_p[\![ \Gamma_{\mathcal{K}}]\!] \rightarrow 0. \end{align*}$$Combining it with Theorem 6.1.1 on the degenerate Fourier–Jacobi coefficients of ![]() $\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$, we deduce that there exists
$\boldsymbol {E}^{\mathrm {Kling}}_{\varphi }$, we deduce that there exists ![]() $\boldsymbol {E}'\in \mathcal {M}_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$ such that
$\boldsymbol {E}'\in \mathcal {M}_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}$ such that
Let P be a height one prime ideal of ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ such that
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ such that
By Proposition 7.11.3, for ![]() $\beta =1$, there exists
$\beta =1$, there exists ![]() $g\in \operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q}})$ and
$g\in \operatorname {\mathrm {U}}(2)(\mathbb {A}_{\mathbb {Q}})$ and ![]() $u\in \bigotimes _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$ such that
$u\in \bigotimes _{v\in \Sigma _{\mathrm {ns}}\cup \{\ell '\}}\operatorname {\mathrm {U}}(1)(\mathbb {Q}_v)$ such that ![]() $l_{\theta ^J_1}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}\right )(g)\notin P$. Then
$l_{\theta ^J_1}\left (\boldsymbol {E}^{\mathrm {Kling}}_{\varphi ,\beta ,u}\right )(g)\notin P$. Then ![]() $l_{\theta ^J_1}\left (\boldsymbol {F}_{\beta ,u}\right )(g)\notin P$, and we have the
$l_{\theta ^J_1}\left (\boldsymbol {F}_{\beta ,u}\right )(g)\notin P$, and we have the ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]_P$-linear map
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]_P$-linear map
which sends the image of ![]() $T\in \mathbb {T}$ in
$T\in \mathbb {T}$ in ![]() $\left (\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\right )_P$ to
$\left (\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\right )_P$ to
 $$ \begin{align*} \frac{l_{\theta^J_1}\left((T\cdot \boldsymbol{F})_{\beta,u}\right)(g)}{l_{\theta^J_1}\left(\boldsymbol{F}_{\beta,u}\right)(g)}\equiv \frac{l_{\theta^J_1}\left((T\cdot \boldsymbol{E}^{\mathrm{Kling}}_{\varphi})_{\beta,u}\right)(g)}{l_{\theta^J_1}\left(\boldsymbol{E}^{\mathrm{Kling}}_{\varphi,\beta,u}\right)(g)}\equiv \lambda_{\mathrm{Eis},\pi,\xi}(T) \quad\mod P^m. \end{align*} $$
$$ \begin{align*} \frac{l_{\theta^J_1}\left((T\cdot \boldsymbol{F})_{\beta,u}\right)(g)}{l_{\theta^J_1}\left(\boldsymbol{F}_{\beta,u}\right)(g)}\equiv \frac{l_{\theta^J_1}\left((T\cdot \boldsymbol{E}^{\mathrm{Kling}}_{\varphi})_{\beta,u}\right)(g)}{l_{\theta^J_1}\left(\boldsymbol{E}^{\mathrm{Kling}}_{\varphi,\beta,u}\right)(g)}\equiv \lambda_{\mathrm{Eis},\pi,\xi}(T) \quad\mod P^m. \end{align*} $$We see that equation (8.1.2) factors through ![]() $\left (\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\right )_P\Big /\mathcal {I}_{\mathrm {Eis},\pi ,\xi } \left (\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\right )_P$. It follows that the composition
$\left (\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\right )_P\Big /\mathcal {I}_{\mathrm {Eis},\pi ,\xi } \left (\mathbb {T}^0_{\mathrm {so},\,\xi ,\Gamma _{\mathcal {K}}}\right )_P$. It follows that the composition
factors through ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P/\mathcal {E}_{\pi ,\xi }\hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P$. By the definition of equation (8.1.2), we also know that the composition (8.1.3) is the natural projection. Hence, we deduce that
$\hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P/\mathcal {E}_{\pi ,\xi }\hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P$. By the definition of equation (8.1.2), we also know that the composition (8.1.3) is the natural projection. Hence, we deduce that ![]() $\mathcal {E}_{\pi ,\xi } \hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P\subset P^m \hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P$, and
$\mathcal {E}_{\pi ,\xi } \hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P\subset P^m \hat {\mathcal {O}}^{\mathrm {ur}}_{\mathcal {K}}[\![\Gamma _{\mathcal {K}}]\!]_P$, and
8.2 The main theorem
By relaxing the conditions at ![]() $v\in \Sigma \cup \{\ell ,\ell '\}$ in the definition of
$v\in \Sigma \cup \{\ell ,\ell '\}$ in the definition of ![]() $\mathrm {Sel}_{\pi ,\mathcal {K},\xi }$ in equation (1.0.1) and
$\mathrm {Sel}_{\pi ,\mathcal {K},\xi }$ in equation (1.0.1) and ![]() $X_{\pi ,\mathcal {K},\xi }$ in equation (1.0.2), we define the
$X_{\pi ,\mathcal {K},\xi }$ in equation (1.0.2), we define the ![]() $\Sigma \cup \{\ell ,\ell '\}$-primitive Selmer group:
$\Sigma \cup \{\ell ,\ell '\}$-primitive Selmer group:
 $$ \begin{align*} {\mathrm{Sel}^{\Sigma\,\cup\{\ell,\ell'\}}_{\pi,\mathcal{K},\xi}}=\ker\left\{ \begin{aligned} &H^1\big(\mathcal{K},T_{\pi,\mathcal{K},\xi}\otimes_{\mathcal{O}_L}\mathcal{O}_L[\![\Gamma_{\mathcal{K}}]\!]^*\big)\\ &\quad\longrightarrow \hspace{-2em}\prod_{\substack{\mathfrak{v} \neq\mathfrak{p}\\ \mathfrak{v}\,\nmid \text{ places in } \Sigma\cup\{\ell,\ell'\}}}\hspace{-1em}H^1 \big(I_{\mathfrak{v}}, T_{\pi,\mathcal{K},\xi}\otimes_{\mathcal{O}_L}\mathcal{O}_L [\![\Gamma_{\mathcal{K}}]\!]^*\big)\end{aligned}\right\}.\\[-15pt] \end{align*} $$
$$ \begin{align*} {\mathrm{Sel}^{\Sigma\,\cup\{\ell,\ell'\}}_{\pi,\mathcal{K},\xi}}=\ker\left\{ \begin{aligned} &H^1\big(\mathcal{K},T_{\pi,\mathcal{K},\xi}\otimes_{\mathcal{O}_L}\mathcal{O}_L[\![\Gamma_{\mathcal{K}}]\!]^*\big)\\ &\quad\longrightarrow \hspace{-2em}\prod_{\substack{\mathfrak{v} \neq\mathfrak{p}\\ \mathfrak{v}\,\nmid \text{ places in } \Sigma\cup\{\ell,\ell'\}}}\hspace{-1em}H^1 \big(I_{\mathfrak{v}}, T_{\pi,\mathcal{K},\xi}\otimes_{\mathcal{O}_L}\mathcal{O}_L [\![\Gamma_{\mathcal{K}}]\!]^*\big)\end{aligned}\right\}.\\[-15pt] \end{align*} $$and
Denote by ![]() $\Gamma ^+_{\mathcal {K}}$ the rank one
$\Gamma ^+_{\mathcal {K}}$ the rank one ![]() $\mathbb {Z}_p$-module of
$\mathbb {Z}_p$-module of ![]() $\Gamma _{\mathcal {K}}$ on which the complex conjugation acts by
$\Gamma _{\mathcal {K}}$ on which the complex conjugation acts by ![]() $+1$, and put
$+1$, and put
Theorem 8.2.1. For an imaginary quadratic field ![]() $\mathcal {K}$, a prime
$\mathcal {K}$, a prime ![]() $p\geq 3$ split in
$p\geq 3$ split in ![]() $\mathcal {K}$ and
$\mathcal {K}$ and ![]() $\pi $,
$\pi $, ![]() $\xi $ as in §5.2,
$\xi $ as in §5.2,
as ideals of ![]() . (Here
. (Here ![]() $\mathcal {L}^{\Sigma \cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ is the p-adic L-function constructed in [Reference Eischen and LiuEW16] with the interpolation properties described in equation (6.1.2).)
$\mathcal {L}^{\Sigma \cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ is the p-adic L-function constructed in [Reference Eischen and LiuEW16] with the interpolation properties described in equation (6.1.2).)
Proof. We can assume that the module ![]() $X^{\Sigma \cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$ is
$X^{\Sigma \cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$ is ![]() -torsion (since otherwise its characteristic ideal is defined to be
-torsion (since otherwise its characteristic ideal is defined to be ![]() $(0)$ and the inclusion (8.2.2) automatically holds). We need to show that given a height one prime ideal
$(0)$ and the inclusion (8.2.2) automatically holds). We need to show that given a height one prime ideal ![]() $P\subset \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]$ such that
$P\subset \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![ \Gamma _{\mathcal {K}}]\!]$ such that ![]() $P\cap \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]=(0)$, we have the inequality
$P\cap \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]=(0)$, we have the inequality
By Theorem 8.1.1, we reduce to showing that
We have the following setup.
•
 $A_0=\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ and
$A_0=\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ and  $A=\hat {A}_{0,P}$.
$A=\hat {A}_{0,P}$.•
 $R_0=\mathbb {T}^0_{\mathrm {so},\xi ,\Gamma _{\mathcal {K}}}$, a prime ideal
$R_0=\mathbb {T}^0_{\mathrm {so},\xi ,\Gamma _{\mathcal {K}}}$, a prime ideal  $Q\subset R$ such that
$Q\subset R$ such that  $Q\cap A_0=P$, and
$Q\cap A_0=P$, and  $R=\hat {R}_{0,Q}$.
$R=\hat {R}_{0,Q}$.•
 $H=G_{\mathbb {Q}}=\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$ and
$H=G_{\mathbb {Q}}=\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$ and  $G=G_{\mathcal {K}}=\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})$.
$G=G_{\mathcal {K}}=\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathcal {K})$.
The following data give us the setup (1)–(5) on [Reference WanWan20, page 478].
(1) Let
 $\nu :H\rightarrow A^{\times }_0$ be the trivial character.
$\nu :H\rightarrow A^{\times }_0$ be the trivial character.(2)
 $\chi =\xi \Psi _{\mathcal {K}}:G\rightarrow A^{\times }_0$, with
$\chi =\xi \Psi _{\mathcal {K}}:G\rightarrow A^{\times }_0$, with  $\chi \not \equiv \chi ^{-c}$ modulo the maximal ideal of
$\chi \not \equiv \chi ^{-c}$ modulo the maximal ideal of  $A_0$ by the choice of
$A_0$ by the choice of  $\xi $.
$\xi $.(3)
 $\rho :G\rightarrow \mathrm {Aut}_A(V)$, a Galois representation obtained from the two-dimensional Galois representation
$\rho :G\rightarrow \mathrm {Aut}_A(V)$, a Galois representation obtained from the two-dimensional Galois representation  $\rho _{\pi }:H\rightarrow \operatorname {\mathrm {GL}}(V_{\pi })$ with
$\rho _{\pi }:H\rightarrow \operatorname {\mathrm {GL}}(V_{\pi })$ with  $V=T_{\pi }\otimes _{\mathcal {O}_L} A$ and
$V=T_{\pi }\otimes _{\mathcal {O}_L} A$ and  $T_{\pi }\subset V_{\pi }$ a G-stable lattice.
$T_{\pi }\subset V_{\pi }$ a G-stable lattice.(4)
 $\sigma :G\rightarrow \mathrm {Aut}_{R\otimes _A F}(M)$, a Galois representation on
$\sigma :G\rightarrow \mathrm {Aut}_{R\otimes _A F}(M)$, a Galois representation on  $M=(R\otimes _A \mathrm {Frac}(A))^4$ obtained as the pseudo-representation associated to
$M=(R\otimes _A \mathrm {Frac}(A))^4$ obtained as the pseudo-representation associated to  $R_0$ as in [Reference SprungSU14, Proposition 7.2.1]
$R_0$ as in [Reference SprungSU14, Proposition 7.2.1](5)
 $I=\mathcal {E}_{\pi ,\xi }A_P$ and
$I=\mathcal {E}_{\pi ,\xi }A_P$ and  $J=\ker (R\rightarrow A/I)$, where the map
$J=\ker (R\rightarrow A/I)$, where the map  $R\rightarrow A$ is defined as the map (8.1.2) and is surjective, and
$R\rightarrow A$ is defined as the map (8.1.2) and is surjective, and  $A/I=R/J$.
$A/I=R/J$.
Moreover, the data satisfy the properties (6)–(9) on [Reference WanWan20, page 478]. Properties (6)–(8) are checked in the same way as loc.cit.
Property (9) is about the irreducibility of ![]() $\sigma $. It requires that, for each
$\sigma $. It requires that, for each ![]() $\mathrm {Frac}(A)$-algebra homomorphism
$\mathrm {Frac}(A)$-algebra homomorphism ![]() $\lambda :R\otimes _A\mathrm {Frac(A)}\rightarrow K$, K a finite extension of
$\lambda :R\otimes _A\mathrm {Frac(A)}\rightarrow K$, K a finite extension of ![]() $\mathrm {Frac}(A)$, the representation
$\mathrm {Frac}(A)$, the representation ![]() $\sigma _{\lambda }:G\rightarrow \operatorname {\mathrm {GL}}_4(K)$ obtained from
$\sigma _{\lambda }:G\rightarrow \operatorname {\mathrm {GL}}_4(K)$ obtained from ![]() $\sigma $ via
$\sigma $ via ![]() $\lambda $ is either absolutely irreducible or contains an absolutely irreducible two-dimensional subrepresentation whose trace is congruent to
$\lambda $ is either absolutely irreducible or contains an absolutely irreducible two-dimensional subrepresentation whose trace is congruent to ![]() $\chi +\chi ^{-c}$ mod I. It can be checked as follows. Let
$\chi +\chi ^{-c}$ mod I. It can be checked as follows. Let ![]() be the pseudo representation giving rise to
be the pseudo representation giving rise to ![]() $\sigma $. Suppose that
$\sigma $. Suppose that ![]() $\sigma $ does not satisfy (9). Then
$\sigma $ does not satisfy (9). Then ![]() with
with ![]() $\delta _1,\delta _2$ characters and
$\delta _1,\delta _2$ characters and ![]() $\delta _3$ a two-dimensional pseudo-representation with irreducible residual representation is
$\delta _3$ a two-dimensional pseudo-representation with irreducible residual representation is ![]() $\mathrm {Tr} \bar {\rho }_{\pi }$. Take an arithmetic point
$\mathrm {Tr} \bar {\rho }_{\pi }$. Take an arithmetic point ![]() $x:\mathbb {T}^0_{\mathrm {so},\xi ,\Gamma _{\mathcal {K}}}\rightarrow \overline {\mathbb {Q}}_p$ corresponding to an automorphic representation
$x:\mathbb {T}^0_{\mathrm {so},\xi ,\Gamma _{\mathcal {K}}}\rightarrow \overline {\mathbb {Q}}_p$ corresponding to an automorphic representation ![]() $\Pi $ of
$\Pi $ of ![]() $\operatorname {\mathrm {U}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ generated by a classical semiordinary cuspidal automorphic form fixed by
$\operatorname {\mathrm {U}}(3,1)(\mathbb {A}_{\mathbb {Q}})$ generated by a classical semiordinary cuspidal automorphic form fixed by ![]() $K^0_{p,1}$ of weight
$K^0_{p,1}$ of weight ![]() $(0,0,t^+;t^-)$,
$(0,0,t^+;t^-)$, ![]() $0\gg t^+\gg -t^-$. We can associate a two-dimensional (irreducible) Galois representation
$0\gg t^+\gg -t^-$. We can associate a two-dimensional (irreducible) Galois representation ![]() $\rho _{3,x}: G {\rightarrow } {\operatorname {\mathrm {GL}}}_2(\overline {\mathbb {Q}}_p)$ to the specialization of
$\rho _{3,x}: G {\rightarrow } {\operatorname {\mathrm {GL}}}_2(\overline {\mathbb {Q}}_p)$ to the specialization of ![]() $\delta _3$ at x. As in [Reference SprungSU14, Theorem 7.5], a twist of
$\delta _3$ at x. As in [Reference SprungSU14, Theorem 7.5], a twist of ![]() $\rho _{3,x}$ descends to
$\rho _{3,x}$ descends to ![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$, which we denote by
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$, which we denote by ![]() $\rho ^{\prime }_{3,x}:\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q}){\rightarrow } {\operatorname {\mathrm {GL}}}_2(\overline {\mathbb {Q}}_p)$.
$\rho ^{\prime }_{3,x}:\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q}){\rightarrow } {\operatorname {\mathrm {GL}}}_2(\overline {\mathbb {Q}}_p)$.
If ![]() $\pi $ is ordinary at p, then
$\pi $ is ordinary at p, then ![]() $\Pi $ is ordinary at p. By the argument in [Reference SprungSU14, Theorem 7.5], we know that
$\Pi $ is ordinary at p. By the argument in [Reference SprungSU14, Theorem 7.5], we know that ![]() $\rho ^{\prime }_{3,x}$ is modular and
$\rho ^{\prime }_{3,x}$ is modular and ![]() $\Pi $ is cuspidal associated to parabolic subgroup (CAP), but the condition on the weights
$\Pi $ is cuspidal associated to parabolic subgroup (CAP), but the condition on the weights ![]() $(0,0,t^+;t^-)$ excludes this possibility ([Reference HarrisHar84, Theorem 2.5.6]).
$(0,0,t^+;t^-)$ excludes this possibility ([Reference HarrisHar84, Theorem 2.5.6]).
If ![]() $\pi $ is not ordinary at p, then
$\pi $ is not ordinary at p, then ![]() $\bar {\rho }_{\pi }|_{G_{\mathcal {K},\mathfrak {p}}}\cong \bar {\rho }_{\pi }|_{G_{\mathbb {Q},p}}$ is irreducible by [Reference EdixhovenEdi92]. Since
$\bar {\rho }_{\pi }|_{G_{\mathcal {K},\mathfrak {p}}}\cong \bar {\rho }_{\pi }|_{G_{\mathbb {Q},p}}$ is irreducible by [Reference EdixhovenEdi92]. Since ![]() $\bar {\rho }_{\Pi }\cong \bar {\rho }_{\pi }|_G\oplus \text {two characters}$, we deduce that the semisimplification of
$\bar {\rho }_{\Pi }\cong \bar {\rho }_{\pi }|_G\oplus \text {two characters}$, we deduce that the semisimplification of ![]() $\rho _{\Pi }|_{G_{\mathcal {K},\mathfrak {p}}}$ is not a direct sum of four characters. Identify
$\rho _{\Pi }|_{G_{\mathcal {K},\mathfrak {p}}}$ is not a direct sum of four characters. Identify ![]() $\operatorname {\mathrm {U}}(3,1)(\mathbb {Q}_p)$ with
$\operatorname {\mathrm {U}}(3,1)(\mathbb {Q}_p)$ with ![]() $\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$, and let
$\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)$, and let ![]() $Q\subset \operatorname {\mathrm {GL}}_4$ be a parabolic subgroup with its Levi subgroup isomorphic to
$Q\subset \operatorname {\mathrm {GL}}_4$ be a parabolic subgroup with its Levi subgroup isomorphic to ![]() $\operatorname {\mathrm {GL}}_2\times \operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_1$. As in the proof of Proposition 3.0.5, it follows from the theory of Jacquet modules that
$\operatorname {\mathrm {GL}}_2\times \operatorname {\mathrm {GL}}_1\times \operatorname {\mathrm {GL}}_1$. As in the proof of Proposition 3.0.5, it follows from the theory of Jacquet modules that ![]() $\Pi _p$ is isomorphic to a subquotient of
$\Pi _p$ is isomorphic to a subquotient of ![]() $\operatorname {\mathrm {Ind}}^{\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)}_{Q(\mathbb {Q}_p)}\sigma \boxtimes \chi \boxtimes \chi '$ with
$\operatorname {\mathrm {Ind}}^{\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)}_{Q(\mathbb {Q}_p)}\sigma \boxtimes \chi \boxtimes \chi '$ with ![]() $\chi ,\chi '$ characters of
$\chi ,\chi '$ characters of ![]() $\mathbb {Q}^{\times }_p$ and
$\mathbb {Q}^{\times }_p$ and ![]() $\sigma $ an irreducible admissible representation of
$\sigma $ an irreducible admissible representation of ![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$ containing a nonzero vector fixed by the Iwahori subgroup. Since the semisimplification of
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$ containing a nonzero vector fixed by the Iwahori subgroup. Since the semisimplification of ![]() $\rho _{\Pi }|_{G_{\mathcal {K},p}}$ is not a direct sum of four characters,
$\rho _{\Pi }|_{G_{\mathcal {K},p}}$ is not a direct sum of four characters, ![]() $\sigma $ is not Steinberg or a twist of Steinberg, and must be unramified. Hence,
$\sigma $ is not Steinberg or a twist of Steinberg, and must be unramified. Hence, ![]() $\Pi _p$ is isomorphic to a subquotient of
$\Pi _p$ is isomorphic to a subquotient of ![]() $\operatorname {\mathrm {Ind}}^{\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)}_{B(\mathbb {Q}_p)}\chi _1\boxtimes \chi _2\boxtimes \chi _3\boxtimes \chi _4$ with
$\operatorname {\mathrm {Ind}}^{\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)}_{B(\mathbb {Q}_p)}\chi _1\boxtimes \chi _2\boxtimes \chi _3\boxtimes \chi _4$ with ![]() $\chi _1,\chi _2,\chi _3,\chi _4$ unramified characters of
$\chi _1,\chi _2,\chi _3,\chi _4$ unramified characters of ![]() $\mathbb {Q}^{\times }_p$. Let
$\mathbb {Q}^{\times }_p$. Let ![]() $\alpha _j=\chi _j(p)$,
$\alpha _j=\chi _j(p)$, ![]() $1\leq j\leq 4$. We can assume that
$1\leq j\leq 4$. We can assume that ![]() $\mathrm {val}_p(\alpha _1)\leq \mathrm {val}_p(\alpha _2)\leq \mathrm {val}_p(\alpha _3)\leq \mathrm {val}_p(\alpha _4)$. The semiordinarity of
$\mathrm {val}_p(\alpha _1)\leq \mathrm {val}_p(\alpha _2)\leq \mathrm {val}_p(\alpha _3)\leq \mathrm {val}_p(\alpha _4)$. The semiordinarity of ![]() $\Pi $ at p implies that
$\Pi $ at p implies that
and the integrality of the operator ![]() $U^+_{p,1}$ (defined in equation (3.0.7)) implies that
$U^+_{p,1}$ (defined in equation (3.0.7)) implies that
Thanks to the condition ![]() $0\gg t^+\gg -t^-$, equations (8.2.5) and (8.2.6) imply that
$0\gg t^+\gg -t^-$, equations (8.2.5) and (8.2.6) imply that ![]() $\alpha _i\alpha ^{-1}_j\neq p^{\pm 1}$ unless
$\alpha _i\alpha ^{-1}_j\neq p^{\pm 1}$ unless ![]() $\{i,j\}=\{1,2\}$ and
$\{i,j\}=\{1,2\}$ and ![]() $\mathrm {val}_p(\alpha _1)=-\frac {1}{2}$,
$\mathrm {val}_p(\alpha _1)=-\frac {1}{2}$, ![]() $\mathrm {val}_p(\alpha _2)=\frac {1}{2}$. However,
$\mathrm {val}_p(\alpha _2)=\frac {1}{2}$. However, ![]() $\mathrm {val}_p(\alpha _1)=-\frac {1}{2}$,
$\mathrm {val}_p(\alpha _1)=-\frac {1}{2}$, ![]() $\mathrm {val}_p(\alpha _2)=\frac {1}{2}$ imply that
$\mathrm {val}_p(\alpha _2)=\frac {1}{2}$ imply that ![]() $\Pi $ is ordinary at p and this contradicts that
$\Pi $ is ordinary at p and this contradicts that ![]() $\rho _{\Pi }|_{G_{\mathcal {K},\mathfrak {p}}}$ is not a direct sum of four characters. Therefore, we have
$\rho _{\Pi }|_{G_{\mathcal {K},\mathfrak {p}}}$ is not a direct sum of four characters. Therefore, we have ![]() $\alpha _i\alpha ^{-1}_j\neq p^{\pm 1}$ for all
$\alpha _i\alpha ^{-1}_j\neq p^{\pm 1}$ for all ![]() $i,j$, so
$i,j$, so ![]() $\operatorname {\mathrm {Ind}}^{\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)}_{Q(\mathbb {Q}_p)}\sigma \boxtimes \chi \boxtimes \chi '$ is irreducible and
$\operatorname {\mathrm {Ind}}^{\operatorname {\mathrm {GL}}_4(\mathbb {Q}_p)}_{Q(\mathbb {Q}_p)}\sigma \boxtimes \chi \boxtimes \chi '$ is irreducible and ![]() $\Pi _p$ is unramified. It follows that
$\Pi _p$ is unramified. It follows that ![]() $\rho _{\Pi }|_{G_{\mathcal {K},\mathfrak {p}}}$ is crystalline, so
$\rho _{\Pi }|_{G_{\mathcal {K},\mathfrak {p}}}$ is crystalline, so ![]() $\rho ^{\prime }_{3,x}|_{G_{\mathbb {Q},p}}$ is crystalline. Also,
$\rho ^{\prime }_{3,x}|_{G_{\mathbb {Q},p}}$ is crystalline. Also, ![]() $\bar {\rho }^{\prime }_{3,x}\equiv \bar {\rho }_{\pi }$ is not induced from a Galois character for
$\bar {\rho }^{\prime }_{3,x}\equiv \bar {\rho }_{\pi }$ is not induced from a Galois character for ![]() $\mathbb {Q}\left (\sqrt {(-1)^{(p-1)/2}p}\right )$, because its restriction to
$\mathbb {Q}\left (\sqrt {(-1)^{(p-1)/2}p}\right )$, because its restriction to ![]() $I_p$ has semisimplification
$I_p$ has semisimplification ![]() $\omega ^i_2\oplus \omega ^{pi}_2$ with
$\omega ^i_2\oplus \omega ^{pi}_2$ with ![]() $\omega _2$ the fundamental character of level
$\omega _2$ the fundamental character of level ![]() $2$ and
$2$ and ![]() $i\equiv 1\mod (p-1)$ (since
$i\equiv 1\mod (p-1)$ (since ![]() $\rho _{\pi }|_{G_{\mathbb {Q},p}}$ is crystalline of weight
$\rho _{\pi }|_{G_{\mathbb {Q},p}}$ is crystalline of weight ![]() $(0,1)$), and if
$(0,1)$), and if ![]() $\bar {\pi }$ was induced from a Galois character for
$\bar {\pi }$ was induced from a Galois character for ![]() $\mathbb {Q}\left (\sqrt {(-1)^{(p-1)/2}p}\right )$, i must be a multiple of
$\mathbb {Q}\left (\sqrt {(-1)^{(p-1)/2}p}\right )$, i must be a multiple of ![]() $\frac {p+1}{2}$, which is impossible when p is odd. Thus, we can apply [Reference KisinKis09], we deduce that
$\frac {p+1}{2}$, which is impossible when p is odd. Thus, we can apply [Reference KisinKis09], we deduce that ![]() $\rho ^{\prime }_{3,x}$ is modular. Then
$\rho ^{\prime }_{3,x}$ is modular. Then ![]() $\Pi $ is CAP, that is, it has the same system of Hecke eigenvalues as a Klingen-type Eisenstein series. This is impossible thanks to the condition on the weights
$\Pi $ is CAP, that is, it has the same system of Hecke eigenvalues as a Klingen-type Eisenstein series. This is impossible thanks to the condition on the weights ![]() $(0,0,t^+;t^-)$ by [Reference HarrisHar84, Theorem 2.5.6]. Property (9) is verified.
$(0,0,t^+;t^-)$ by [Reference HarrisHar84, Theorem 2.5.6]. Property (9) is verified.
Let
 $$ \begin{align*} X^{\Sigma\,\cup\{\ell,\ell'\}}_{\xi\circ\mathrm{Nm}}=\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left( \ker\bigg\{H^1\bigg(\mathbb{Q},\xi\Psi_{\mathcal{K}}\circ \mathrm{Nm}\right)\rightarrow \hspace{-1em}\prod_{v\notin\Sigma\cup\{\ell,\ell'\}}\hspace{-1em} H^1\bigg(I_v,\xi\Psi_{\mathcal{K}}\circ \mathrm{Nm}\bigg)\bigg\},\,\mathbb{Q}_p/\mathbb{Z}_p\bigg), \end{align*} $$
$$ \begin{align*} X^{\Sigma\,\cup\{\ell,\ell'\}}_{\xi\circ\mathrm{Nm}}=\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}\left( \ker\bigg\{H^1\bigg(\mathbb{Q},\xi\Psi_{\mathcal{K}}\circ \mathrm{Nm}\right)\rightarrow \hspace{-1em}\prod_{v\notin\Sigma\cup\{\ell,\ell'\}}\hspace{-1em} H^1\bigg(I_v,\xi\Psi_{\mathcal{K}}\circ \mathrm{Nm}\bigg)\bigg\},\,\mathbb{Q}_p/\mathbb{Z}_p\bigg), \end{align*} $$where ![]() $\xi \Psi _{\mathcal {K}}\circ \mathrm {Nm}$ is understood as a character of
$\xi \Psi _{\mathcal {K}}\circ \mathrm {Nm}$ is understood as a character of ![]() $\operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q})$ valued in
$\operatorname {\mathrm {Gal}}(\bar {\mathbb {Q}}/\mathbb {Q})$ valued in ![]() $\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]*$. With the input (1)–(5) satisfying the properties (6)–(9), applying the lattice construction [Reference WanWan20, Proposition 9.2], one proves that if
$\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]*$. With the input (1)–(5) satisfying the properties (6)–(9), applying the lattice construction [Reference WanWan20, Proposition 9.2], one proves that if ![]() $P\subset \mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ is a height one prime such that
$P\subset \mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ is a height one prime such that ![]() $\mathrm {ord}_P\left (\mathcal {E}_{\pi ,\xi }\right )>0$ and
$\mathrm {ord}_P\left (\mathcal {E}_{\pi ,\xi }\right )>0$ and ![]() $\left (X_{\xi \circ \mathrm {Nm}}\otimes _{\mathbb {Z}}\mathbb {Q})\right )_P=0$, then the inequality (8.2.4) holds. It follows that for all height one prime ideals
$\left (X_{\xi \circ \mathrm {Nm}}\otimes _{\mathbb {Z}}\mathbb {Q})\right )_P=0$, then the inequality (8.2.4) holds. It follows that for all height one prime ideals ![]() $P\subset \mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ with
$P\subset \mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ with ![]() $P\cap \mathcal {O}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]=(0)$, the desired inequality (8.2.3) holds.
$P\cap \mathcal {O}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]=(0)$, the desired inequality (8.2.3) holds.
(The congruence ideal ![]() $\mathcal {E}_{\pi ,\xi }$ is bounded by the product
$\mathcal {E}_{\pi ,\xi }$ is bounded by the product ![]() $\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$ and is expected to give a bound for the product of the characteristic ideals of
$\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$ and is expected to give a bound for the product of the characteristic ideals of ![]() $X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi \circ \mathrm {Nm}}$ and
$X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi \circ \mathrm {Nm}}$ and ![]() $X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$. Although, the characteristic ideals of
$X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }$. Although, the characteristic ideals of ![]() $X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi \circ \mathrm {Nm}}$ is known to be generated by
$X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi \circ \mathrm {Nm}}$ is known to be generated by ![]() $\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}$ by the Iwasawa main conjecture proved in [Reference Mazur and WilesMW84], the lattice construction argument in [Reference SprungSU14, Reference WanWan20] only proves the desired bound for
$\mathcal {L}^{\Sigma \,\cup \{\ell ,\ell '\}}_{\xi ,\mathbb {Q}}$ by the Iwasawa main conjecture proved in [Reference Mazur and WilesMW84], the lattice construction argument in [Reference SprungSU14, Reference WanWan20] only proves the desired bound for ![]() $\mathrm {ord}_P\left (\mathrm {char}_{\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]}\left (X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }\right )\right )$ when
$\mathrm {ord}_P\left (\mathrm {char}_{\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]}\left (X^{\Sigma \,\cup \{\ell ,\ell '\}}_{\pi ,\mathcal {K},\xi }\right )\right )$ when ![]() $\left (X_{\xi \circ \mathrm {Nm}}\otimes _{\mathbb {Z}}\mathbb {Q})\right )_P=0$. In [Reference WanWan20], height one primes in
$\left (X_{\xi \circ \mathrm {Nm}}\otimes _{\mathbb {Z}}\mathbb {Q})\right )_P=0$. In [Reference WanWan20], height one primes in ![]() $\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ do not need to be excluded thanks to Lemma 9.3 in loc.cit and the fact that
$\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]\otimes _{\mathbb {Z}}\mathbb {Q}$ do not need to be excluded thanks to Lemma 9.3 in loc.cit and the fact that ![]() $\mathcal {L}_{\pi ,\mathcal {K},\xi }$ is not contained in any height one prime ideal in
$\mathcal {L}_{\pi ,\mathcal {K},\xi }$ is not contained in any height one prime ideal in ![]() $\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ by [Reference HsiehHsi14b]. However, in our case with
$\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ by [Reference HsiehHsi14b]. However, in our case with ![]() $\pi $ fixed instead of moving in a family, we cannot prove an analogue of Lemma 9.3 in [Reference WanWan20].)
$\pi $ fixed instead of moving in a family, we cannot prove an analogue of Lemma 9.3 in [Reference WanWan20].)
Next, we deduce partial results towards Conjecture 1.0.2 from Theorem 8.2.1. We first introduce the following integral primitive p-adic L-function.
Proposition 8.2.2. Suppose that ![]() $\xi $ (fixed in §5.2) further satisfies the following conditions:
$\xi $ (fixed in §5.2) further satisfies the following conditions:
–
 $ \xi _{\mathfrak {p}}\not \equiv \xi _{\bar {\mathfrak {p}}}$ modulo the maximal ideal of
$ \xi _{\mathfrak {p}}\not \equiv \xi _{\bar {\mathfrak {p}}}$ modulo the maximal ideal of  $\mathcal {O}_L$ (so that
$\mathcal {O}_L$ (so that  $\mathrm {Ind}^{\mathbb {Q}}_{\mathcal {K}} \rho _{\xi }$, the p-adic Galois representation corresponding to a CM eigenform associated to
$\mathrm {Ind}^{\mathbb {Q}}_{\mathcal {K}} \rho _{\xi }$, the p-adic Galois representation corresponding to a CM eigenform associated to  $\xi $, is residually absolutely irreducible and the two characters of
$\xi $, is residually absolutely irreducible and the two characters of  $\left (\mathrm {Ind}^{\mathbb {Q}}_{\mathcal {K}} \xi \right )|_{G_{\mathbb {Q},p}}$ on the diagonal are distinct),
$\left (\mathrm {Ind}^{\mathbb {Q}}_{\mathcal {K}} \xi \right )|_{G_{\mathbb {Q},p}}$ on the diagonal are distinct),– the conductor of
 $\xi $ is only divisible by primes split in
$\xi $ is only divisible by primes split in  $\mathcal {K}/\mathbb {Q}$.
$\mathcal {K}/\mathbb {Q}$.
Then there exists a p-adic L-function ![]() $\mathcal {L}_{\pi ,\mathcal {K},\xi }\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ such that for all algebraic Hecke characters
$\mathcal {L}_{\pi ,\mathcal {K},\xi }\in \hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]$ such that for all algebraic Hecke characters ![]() $\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ with
$\tau :\mathcal {K}^{\times }\backslash \mathbb {A}^{\times }_{\mathcal {K}}\rightarrow \mathbb {C}^{\times }$ with ![]() $\tau _{p\text {-}\mathrm {adic}}$ factoring through
$\tau _{p\text {-}\mathrm {adic}}$ factoring through ![]() $\Gamma _{\mathcal {K}}$ and
$\Gamma _{\mathcal {K}}$ and ![]() $\xi \tau $ of
$\xi \tau $ of ![]() $\infty $-type
$\infty $-type ![]() $\left (k_1,k_2\right )$ with
$\left (k_1,k_2\right )$ with ![]() $k_1,k_2\in \mathbb {Z}$,
$k_1,k_2\in \mathbb {Z}$, ![]() $k_1\leq 0$,
$k_1\leq 0$, ![]() $k_2\geq 2-k_1$,
$k_2\geq 2-k_1$,
 $$ \begin{align*} \mathcal{L}_{\pi,\mathcal{K},\xi}(\tau_{p\text{-}\mathrm{adic}}) =&\, \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{2(k_2-k_1)}\frac{\Gamma(k_2)\Gamma(k_2-1)}{(2\pi i)^{2k_2-1}} \cdot \gamma_p\left(\frac{3-(k_1+k_2)}{2},\pi^{\vee}_{p}\times (\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\\ &\times L^{\{\infty,p\}}\left(\frac{k_1+k_2-1}{2},\mathrm{BC}(\pi)\times\xi_0\tau_0\right). \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\pi,\mathcal{K},\xi}(\tau_{p\text{-}\mathrm{adic}}) =&\, \left(\frac{\Omega_p}{\Omega_{\infty}}\right)^{2(k_2-k_1)}\frac{\Gamma(k_2)\Gamma(k_2-1)}{(2\pi i)^{2k_2-1}} \cdot \gamma_p\left(\frac{3-(k_1+k_2)}{2},\pi^{\vee}_{p}\times (\xi_0\tau_0)^{-1}_{\bar{\mathfrak{p}}}\right)\\ &\times L^{\{\infty,p\}}\left(\frac{k_1+k_2-1}{2},\mathrm{BC}(\pi)\times\xi_0\tau_0\right). \end{align*} $$Proof. When both modular forms are ordinary and move in Hida families, the three-variable (nonintegral) p-adic Rankin–Selberg p-adic L-function is constructed in [Reference Harris, Lan, Taylor and ThorneHid91], and the integral p-adic L-function obtained by multiplying a generator of a congruence ideal is constructed in [Reference WanWan20, Definition 7.8] when the dominant-weight family is CM, and in [Reference Castella and WanCH20] for the general case under the assumption that the Galois representation associated to the weight-dominant form is residually absolutely irreducible and residually p-distinguished, which guarantees that its associated congruence ideals is principal. In fact, when the form of nondominant weight, that is, our f here) is fixed, the ordinarity assumption on it is not necessary for constructing the two-variable p-adic Rankin–Selberg p-adic L-function.
Like in [Reference WanWan20, Definition 7.8], we let ![]() $\xi '=\xi \cdot (\chi ^{\mathrm {tw}}_{g_{\xi }}\circ \mathrm {Nm}_{\mathcal {K}/\mathbb {Q}})$ with
$\xi '=\xi \cdot (\chi ^{\mathrm {tw}}_{g_{\xi }}\circ \mathrm {Nm}_{\mathcal {K}/\mathbb {Q}})$ with ![]() $\chi ^{\mathrm {tw}}_{g_{\xi }}$ a finite-order Dirichlet character unramified outside
$\chi ^{\mathrm {tw}}_{g_{\xi }}$ a finite-order Dirichlet character unramified outside ![]() $\Sigma \cup \{p\}$ such that the automorphic representation of
$\Sigma \cup \{p\}$ such that the automorphic representation of ![]() $\operatorname {\mathrm {GL}}(2,\mathbb {A}_{\mathbb {Q}})$ corresponding to
$\operatorname {\mathrm {GL}}(2,\mathbb {A}_{\mathbb {Q}})$ corresponding to ![]() $\xi '$ is minimal in the sense of [Reference HsiehHT93, Section 7] at all finite places. Denote by
$\xi '$ is minimal in the sense of [Reference HsiehHT93, Section 7] at all finite places. Denote by ![]() $\mathbf {g}_{\xi '}$ the ordinary CM family associated to
$\mathbf {g}_{\xi '}$ the ordinary CM family associated to ![]() $\xi '\Psi _{\mathcal {K}}$.
$\xi '\Psi _{\mathcal {K}}$.
In [Reference Harris, Lan, Taylor and ThorneHid91], a three-variable Eisenstein measure valued in p-adic modular forms is constructed. Denote by ![]() $\boldsymbol {E}$ the restriction of the three-variable Eisenstein measure to the two-variable weight space corresponding to f being fixed. Let
$\boldsymbol {E}$ the restriction of the three-variable Eisenstein measure to the two-variable weight space corresponding to f being fixed. Let ![]() $f'$ be the twist of f by
$f'$ be the twist of f by ![]() $\chi ^{\mathrm {tw},-1}_{g_{\xi }}$. Then the product
$\chi ^{\mathrm {tw},-1}_{g_{\xi }}$. Then the product ![]() $f'\boldsymbol {E}$ gives a two-variable p-adic measure valued in p-adic modular forms. We can apply to it the ordinary projector and get an ordinary family
$f'\boldsymbol {E}$ gives a two-variable p-adic measure valued in p-adic modular forms. We can apply to it the ordinary projector and get an ordinary family ![]() $e_{\mathrm {ord}}(f\boldsymbol {E})$. Applying the Hecke projector
$e_{\mathrm {ord}}(f\boldsymbol {E})$. Applying the Hecke projector ![]() to
to ![]() $e_{\mathrm {ord}}(f\boldsymbol {E})$ and taking the first Fourier coefficient gives an element in
$e_{\mathrm {ord}}(f\boldsymbol {E})$ and taking the first Fourier coefficient gives an element in ![]() $\mathcal {L}^{\mathrm {frac}}_{\pi ,\mathcal {K},\xi }\in \mathrm {Frac}\left (\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\right )$. Under the assumptions on
$\mathcal {L}^{\mathrm {frac}}_{\pi ,\mathcal {K},\xi }\in \mathrm {Frac}\left (\hat {\mathcal {O}}^{\mathrm {ur}}_L[\![\Gamma _{\mathcal {K}}]\!]\right )$. Under the assumptions on ![]() $\xi $, the same argument in [Reference WanWan20, Definition 7.8] shows that the desired p-adic L-function (up to a p-adic unit) can be obtained by multiplying
$\xi $, the same argument in [Reference WanWan20, Definition 7.8] shows that the desired p-adic L-function (up to a p-adic unit) can be obtained by multiplying ![]() $\mathrm {Cl}_{\mathcal {K}}\cdot \mathcal {L}^{\mathrm {Katz}}_{\mathcal {K},\xi }$ to
$\mathrm {Cl}_{\mathcal {K}}\cdot \mathcal {L}^{\mathrm {Katz}}_{\mathcal {K},\xi }$ to ![]() $\mathcal {L}^{\mathrm {frac}}_{\pi ,\mathcal {K},\xi }$.
$\mathcal {L}^{\mathrm {frac}}_{\pi ,\mathcal {K},\xi }$.
Theorem 8.2.3. Let ![]() $\mathcal {K}$ be an imaginary quadratic field,
$\mathcal {K}$ be an imaginary quadratic field, ![]() $p\geq 3$ be a prime split in
$p\geq 3$ be a prime split in ![]() $\mathcal {K}$, and
$\mathcal {K}$, and ![]() $\pi $,
$\pi $, ![]() $\xi $ as in §5.2 with
$\xi $ as in §5.2 with ![]() $\xi $ also satisfying the conditions in Proposition 8.2.2.
$\xi $ also satisfying the conditions in Proposition 8.2.2.
(1) As ideals of
 ,
, 
(where the ring
 is defined in equation (8.2.1), the
is defined in equation (8.2.1), the  $\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$-module
$\mathcal {O}_L[\![\Gamma _{\mathcal {K}}]\!]$-module  $X_{\pi ,\mathcal {K},\xi }$ and its characteristic ideal are defined in §1, and the p-adic L-function
$X_{\pi ,\mathcal {K},\xi }$ and its characteristic ideal are defined in §1, and the p-adic L-function  $\mathcal {L}_{\pi ,\mathcal {K},\xi }$ is given in Proposition 8.2.2).
$\mathcal {L}_{\pi ,\mathcal {K},\xi }$ is given in Proposition 8.2.2).(2) If
 $\xi $ further satisfies:
$\xi $ further satisfies:–
 $\xi |_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\omega ^2$ with
$\xi |_{\mathbb {A}^{\times }_{\mathbb {Q}}}=\omega ^2$ with  $\omega :\mathbb {Q}^{\times }\backslash \mathbb {A}^{\times }_{\mathbb {Q}}\rightarrow \mathbb {C}^{\times }$ the Teichmüller character, and
$\omega :\mathbb {Q}^{\times }\backslash \mathbb {A}^{\times }_{\mathbb {Q}}\rightarrow \mathbb {C}^{\times }$ the Teichmüller character, and  $k_0\equiv 0 \mod 2(p-1)$,
$k_0\equiv 0 \mod 2(p-1)$,– for every finite place of
 $\mathbb {Q}$ nonsplit in
$\mathbb {Q}$ nonsplit in  $\mathcal {K}$,
$\mathcal {K}$,  $\epsilon _v\left (\frac {1}{2},\mathrm {BC}(\pi )\times \xi _0\right )=1$,
$\epsilon _v\left (\frac {1}{2},\mathrm {BC}(\pi )\times \xi _0\right )=1$,
then
 $$\begin{align*}\big(\mathcal{L}_{\pi,\mathcal{K},\xi}\big)\supset \mathrm{char}_{\mathcal{O}^{\mathrm{ur}}_L[\![\Gamma_{\mathcal{K}}]\!] }\big(X_{\pi,\mathcal{K},\xi}\big). \end{align*}$$
$$\begin{align*}\big(\mathcal{L}_{\pi,\mathcal{K},\xi}\big)\supset \mathrm{char}_{\mathcal{O}^{\mathrm{ur}}_L[\![\Gamma_{\mathcal{K}}]\!] }\big(X_{\pi,\mathcal{K},\xi}\big). \end{align*}$$
(1) By the same argument as in the proof of [Reference Jetchev, Skinner and WanJSW17, Theorem 6.1.6], which uses the fact that the sizes of the unramified cohomology groups at primes outside p are controlled by the local Euler factors of the p-adic L-functions, the inclusion in (1) follows from Theorem 8.2.1.
(2) With those further conditions on
 $\xi $, one can use the vanishing of the anticyclotomic
$\xi $, one can use the vanishing of the anticyclotomic  $\mu $-invariant proved in [Reference HsiehHsi14b] to deduce that the
$\mu $-invariant proved in [Reference HsiehHsi14b] to deduce that the  $\mathcal {L}_{\pi ,\mathcal {K},\xi }$ is not divisible by any height one prime ideal in
$\mathcal {L}_{\pi ,\mathcal {K},\xi }$ is not divisible by any height one prime ideal in  $\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]$. Thus, the inclusion in (1) implies the inclusion in (2).
$\mathcal {O}^{\mathrm {ur}}_L[\![\Gamma ^+_{\mathcal {K}}]\!]$. Thus, the inclusion in (1) implies the inclusion in (2).
Acknowledgments
We would like to thank Eric Urban for pointing out to us the possibility of developing the semiordinary Hida theory needed in this paper. We also thank Ming-Lun Hsieh, Kai-Wen Lan and Christopher Skinner for useful communications. We also thank the referees for their careful reading of the paper and many useful suggestions.
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
F. C. was partially supported by the NSF grant DMS-1946136 and DMS-2101458. Z. L. was partially supported by the NSF grant DMS-2001527. X. W. was partially supported by National key R&D Program of China 2020YFA0712600, CAS Project for Young Scientists in Basic Research, Grant No. YSBR-033, and NSFC grants 11688101, 11621061.