Symposium - International Astronomical Union, Rotation of the Earth
- This volume was published under a former title. See this journal's title history.
Other
Preface
-
- Published online by Cambridge University Press:
- 27 June 2016, p. v
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Introduction
Introduction: Past and Future of Research Methods in Problems of the Earth's Rotation (Presidential Address)
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. xi-xxii
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
Creep in the Earth and Planets (Invited Lecture)
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 1-9
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Revised Values (1941–1961) of the Coordinates of the Pole Referred to the CIO
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 10-11
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
New Determination of the Polar Motion from 1890 to 1969
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 12-13
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
General Considerations about the Revision of All the Calculations of the International Latitude Service
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 14-18
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Analysis of Pole Position from 1846 to 1970∗
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 19-32
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Spectral Analyses of the Chandler Wobble
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 33-38
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The Variation of Latitude
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 39-42
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Analysis of the Chandler Period of Polar Coordinates Calculated by the Orlov Method
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 43-45
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Other
Comments on the Changes in Amplitude of the Chandlerian Wobble
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 46-48
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Research Article
An Interpretation of the Ambiguity between Annual Terms Obtained by Time and Latitude Observations
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 49-55
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Comparisons between Results of Polar Coordinates Derived from Time Data and Those from Latitude Ones
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 56-57
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
On the Short Period Terms in the UT1 and Those in the Polar Motion
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 58-60
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
On the Regularity of Fluctuations in Annual and Secular Polar Motions
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 61-67
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Separating the Secular Motion of the Pole from Continental Drift Where and What to Observe?
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 68-77
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Non-Periodic Latitude Variations and the Secular Motion of the Earth's Pole
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 78-85
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Secular and Nonpolar Variation of Washington Latitude
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 86-96
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Secular and Long-Term Variations of the Polar Motion
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 97-100
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Accuracy of Doppler Determinations of Station Positions
-
- Published online by Cambridge University Press:
- 27 June 2016, pp. 101-103
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

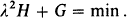
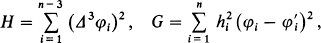
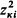 for this series. The polar coordinates obtained in the second approximation are denoted by
for this series. The polar coordinates obtained in the second approximation are denoted by