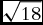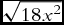Premodern algebra, in Greek, Arabic, Latin, and Italian, was a numerical problem-solving technique. To work out a problem by algebra, an unknown number was named in terms of the given names of the powers, the conditions of the problem were applied to set up an equation, and this was then simplified and solved. While this broad approach is comparable to modern algebra, premodern algebraists – and for the time being I mean those who practiced algebra before the sixteenth century – did not solve their problems the same way we do today. Some of the steps they took differ from ours, their phrasing of certain operations makes little sense when interpreted through our symbolic solutions, and even their notations exhibit differences that cannot be attributed to local variation.
One example of a difference in practice is that premodern algebraists consistently worked out their operations before setting up equations, where we do not hesitate to include operations in equations (see Oaks Reference Oaks2009; Oaks Reference Oaks2010; Christianidis and Oaks Reference Christianidis and Oaks2013). And to simplify an equation like 10 − x = 4x Arabic algebraists would “restore” the 10, and then add the x to the 4x. We have no reason to restore quantities (whatever that would mean) that have something subtracted from them.Footnote 1 And in notation a “1” is always given for the coefficient of a term when there is one of them: where we write just x, Italian abbacists wrote “1ρ”.Footnote 2
Taken together, these and other differences in procedure, wording, and notation point to a different understanding of monomials, polynomials, and equations. Premodern polynomials, for example, were treated as collections or aggregations of the names of the powers of the unknown, and not as the linear combinations of the powers that we work with today. Particularly relevant for the present study is that the interpretation of notation was determined by the rhetorical version it represented. This meant that the signs for the powers of the unknown functioned differently than ours do today. The abbacist “ρ”, for example, does not stand for the value of the unknown the way our x does, but indicates a kind of number.
In this article I focus on one particular difference in practice: that premodern algebraists in Arabic, Latin, and Italian did not allow the “number” (coefficient) of a term to be irrational. They restricted their coefficients to (positive) rational numbers, even if irrational numbers were commonplace and unquestioned in medieval logistic. As an example, we multiply
![]() $\sqrt {18} $
by x to get
$\sqrt {18} $
by x to get
![]() $\sqrt {18} x$
, but Maestro Biaggio, a fifteenth century abbacist, writes instead the rhetorical equivalent of
$\sqrt {18} x$
, but Maestro Biaggio, a fifteenth century abbacist, writes instead the rhetorical equivalent of
![]() $\sqrt {18{x^2}} $
.Footnote
3
Here the “number” of x
2’s is rational, while the square root of the term is perfectly valid as an irrational number (the value of x is found in this problem to be
$\sqrt {18{x^2}} $
.Footnote
3
Here the “number” of x
2’s is rational, while the square root of the term is perfectly valid as an irrational number (the value of x is found in this problem to be
![]() $\sqrt {200} - 10$
).
$\sqrt {200} - 10$
).
This conceptual framework of premodern algebra was inherited by European algebraists in the sixteenth century. The symptomatic differences in practice, wording, and notation that distinguish it from modern algebra remained in force, too, but with one exception: some algebraists now allowed their coefficients to be irrational. This first occurs in a limited way in Christoff Rudolff (1525), then more abundantly in Girolamo Cardano (Reference Cardano1539), and later in Johann Scheubel (Reference Scheubel1550), Pedro Nuñez (Reference Nuñez1567), Rafael Bombelli (1572), and Simon Stevin (Reference Stevin1585). But most algebraists, including Michael Stifel, Jacques Peletier, and Niccolò Tartaglia, continued with the old way by putting the whole term under the root.
This development was not a step toward the modern algebra of Viète, Fermat, and Descartes. The appearance of irrational coefficients and the controversies that it sparked took place entirely within the conceptual context of premodern algebra, where polynomials remained aggregations and “coefficients” were at least nominally regarded as numbers that count the term. It is only in this context that the issue makes sense, so this is the conceptual setting in which the various texts must be assessed. When Viète later devised an algebra founded in geometry he created a radically new notation to go with it, and it is out of this that Descartes's notation and its subsequent incarnations emerged.
I begin by reviewing the ways medieval algebraists expressed monomials affected by irrational numbers. The medieval practice is presented in the context of the aggregations interpretation with particular attention to notation, and this is put into broader perspective by a comparison with how fractions and multitudes of roots were expressed in arithmetic. Then I examine sixteenth century books to show how the restriction on “coefficients” was relaxed in some algebraists. Contemporary attitudes are then brought to light by examining a debate over this issue in mid-seventeenth-century Italy in which the participants cite the earlier algebraists. I conclude by addressing two related questions: What change had occurred in algebra that allowed some sixteenth-century algebraists to work with irrational coefficients? And what effect did this change have on the medieval concepts?
Some Preliminary Remarks
Premodern algebra is almost always presented in the manuscripts in rhetorical form. Natural language by its nature admits ambiguities in meaning, but when expressing algebra this meaning is controlled in important ways by the mathematics. For example, we know that Abū Kāmil's “a root of five hundred māls” corresponds to our
![]() $\sqrt {500{x^2}} $
and not
$\sqrt {500{x^2}} $
and not
![]() $\sqrt {500} {x^2}$
because interpreting it as the latter is mathematically wrong in the context of the problem being solved. The examples I have chosen to quote in this article are mathematically unambiguous. Abū Kāmil's phrase, for instance, is the result of multiplying “ten things” by “a root of five,” which corresponds to our 10x by
$\sqrt {500} {x^2}$
because interpreting it as the latter is mathematically wrong in the context of the problem being solved. The examples I have chosen to quote in this article are mathematically unambiguous. Abū Kāmil's phrase, for instance, is the result of multiplying “ten things” by “a root of five,” which corresponds to our 10x by
![]() $\sqrt 5 $
. Even taking into consideration the conceptual differences between the Arabic words and our modern notation, the underlying computations still have to make sense.
$\sqrt 5 $
. Even taking into consideration the conceptual differences between the Arabic words and our modern notation, the underlying computations still have to make sense.
The sources for this study consist of every medieval Arabic, Latin, Italian, and early modern European book treating algebra down to 1630 that I could locate, plus a few from later in the seventeenth century. I consulted 33 books in medieval Arabic, seven in medieval Latin (not including translations of al-Khwārizmī and Abū Kāmil), 27 in Italian (fourteenth and fifteenth centuries), and more than fifty written in Latin and European vernacular languages between 1500 and 1630. The reference list shows only works from which I cite passages or give references.
A word on the word “coefficient”: Algebraists before Viète called the coefficient the “number” or “quantity” of a term. For example, Ibn al-Hāʾim (1387) begins his rule for finding x
2 in the equation x
2 = 4x + 5 with: “The square of the number (ʿidda) of roots is sixteen” (Ibn al-Hāʾim 2003, 95:2). Maestro Dardi (1344), after arriving at the equation
![]() $\sqrt {8{x^2}} = \frac{2}{3}{x^3}$
, writes “Multiply the quantity (quantità) of cubes by itself, which is 2/3.”Footnote
4
Most often, though, algebraists would simply write “the roots” or “the cubes” to mean the number of roots or cubes.
$\sqrt {8{x^2}} = \frac{2}{3}{x^3}$
, writes “Multiply the quantity (quantità) of cubes by itself, which is 2/3.”Footnote
4
Most often, though, algebraists would simply write “the roots” or “the cubes” to mean the number of roots or cubes.
It is important to keep in mind that what is at stake in this article is not the concept of an irrational number, but rather the concept of an algebraic monomial. To use modern terminology, I investigate how algebraists understood the relationship between the power of the unknown and the coefficient. Irrationals come into play because it is with them that we see a difference in practice. The concepts of irrational numbers presented in some sixteenth-century books like those of Regiomontanus (1533), Stifel (Reference Stifel1544), and Stevin (Reference Stevin1585)Footnote 5 appear to have no connection with the introduction of irrational coefficients that we find in Rudolff 1525, Cardano Reference Cardano1539, Stevin Reference Stevin1585, etc. This is not surprising. The rules for operating with irrational roots were already well-established in the ninth century, and irrationals had remained a staple of calculation in practical arithmetic and algebra ever since. Whatever musings on the nature of irrationals we find in sixteenth-century authors would have had no effect on actual calculations, and it is with calculations that I am concerned.
Last, modern notation can still be useful to clarify the medieval operations as long as one keeps the medieval concepts in mind. Thus I use it throughout this article.
Monomials in Medieval Algebra and the Aggregations Interpretation
To show the ways that Arabic algebraists constructed and worked with monomials I need to first outline the main features of medieval algebraic problem solving, including the way they conceived of the polynomials that make up the two sides of an equation. The name given to the first-degree unknown in Arabic algebra is shayʾ (“thing”), though it is sometimes called jidhr (“root”). This corresponds to our “x.” Its square, our x 2, is called a māl, literally “sum of money,” “treasure,” “property,” “wealth.”Footnote 6 The cube of a “thing” is called a kaʿb (“cube”), and higher powers are written as some combination of māl and kaʿb, like māl kaʿb for x 5 and māl māl māl māl for x 8. Units are often counted in dirhams, a silver coin, but also with words meaning “units” or “in number,” and often the term is dropped altogether. So “ten dirhams,” “ten units,” “ten in number,” and simply “ten” all mean the number 10.
In books that describe algebra in detail the explanation of the various rules is followed by a collection of solved problems. There are some notable differences between how medieval algebraists solved problems and how we solve them today. One difference is that although these algebraists worked freely with irrational roots, they would not allow them to serve as the “number” of a term. As an example of how medieval algebraists worked with monomials involving roots I present the enunciation and the first solution to problem (41) from Abū Kāmil's late ninth century Book of Algebra.Footnote 7 The enunciation reads:
Ten: you divided it into two parts. You divided each one of the parts by the other, and you added them, so it yielded a root of five dirhams.
To reformulate this in modern algebraic notation we can name the parts a and b, so a + b = 10 and the condition states that
![]() $\frac{a}{b} + \frac{b}{a} = \sqrt 5 $
. In the solution Abū Kāmil names one of the parts “a thing,” and then he manipulates the operations in terms of the names of the powers to form an equation:
$\frac{a}{b} + \frac{b}{a} = \sqrt 5 $
. In the solution Abū Kāmil names one of the parts “a thing,” and then he manipulates the operations in terms of the names of the powers to form an equation:
Its rule is that you make one of the parts a thing [x], and the other ten less a thing [10 − x]. So multiply each one of them by itself and add them, so it yields a hundred dirhams and two māls less twenty things [100 + 2x
2 − 20x]. Keep this in mind. Then multiply one of the parts by the other, which is a thing by ten less a thing, so it yields ten things less a māl [10x − x
2]. Multiply this by a root of five, so it yields: a root of five hundred māls less a root of five māls māl equal a hundred dirhams and two māls less twenty roots [
![]() $\sqrt {500{x^2}} - \sqrt {5{x^4}} = 100 + 2{x^2} - 20x$
].
$\sqrt {500{x^2}} - \sqrt {5{x^4}} = 100 + 2{x^2} - 20x$
].
The equation is then simplified and solved:
So restore a root of five hundred māls by a root of five māls māl and add it to a hundred dirhams and two māls less twenty things. And restore the hundred dirhams and two māls less twenty things by the twenty things and add it to a root of five hundred māls.Footnote
8
It yields: twenty things and a root of five hundred māls equal a hundred dirhams and two māls and a root of five māls māl [
![]() $20x + \sqrt {500{x^2}} = 100 + 2{x^2} + \sqrt {5{x^4}} $
].
$20x + \sqrt {500{x^2}} = 100 + 2{x^2} + \sqrt {5{x^4}} $
].
Return everything you have to one māl, which is that you multiply the two māls and a root of five māls māl by a root of five dirhams less two dirhams [
![]() $\sqrt 5 - 2$
]. You multiply it by a root of five dirhams less two dirhams because if you divided a dirham by two and a root of five, it resulted in one root of five less two dirhams, as is clear to you.Footnote
9
So you multiply everything you have by a root of five less two dirhams to get: a māl and a root of fifty thousand dirhams less two hundred dirhams equal ten things [
$\sqrt 5 - 2$
]. You multiply it by a root of five dirhams less two dirhams because if you divided a dirham by two and a root of five, it resulted in one root of five less two dirhams, as is clear to you.Footnote
9
So you multiply everything you have by a root of five less two dirhams to get: a māl and a root of fifty thousand dirhams less two hundred dirhams equal ten things [
![]() ${x^2} + \sqrt {50000} - 200 = 10x$
].
${x^2} + \sqrt {50000} - 200 = 10x$
].
Then halve the things,Footnote
10
so it yields five. Multiply it by itself, so it yields twenty-five dirhams. Subtract from it a root of fiftyFootnote
11
thousand dirhams less two hundred dirhams. This leaves two hundred twenty-five dirhams less a root of fifty thousand. A root of that subtracted from fiveFootnote
12
is one of the two parts, and added to five is the other part [
![]() $5 - \sqrt {225 - \sqrt {50000} } $
and
$5 - \sqrt {225 - \sqrt {50000} } $
and
![]() $5 + \sqrt {225 - \sqrt {50000} } $
].
$5 + \sqrt {225 - \sqrt {50000} } $
].
In the first part of the solution Abū Kāmil multiplies the
![]() $\sqrt 5 $
by “ten things less a māl” (10x − x
2) to get “a root of five hundred māls less a root of five māls māl” (
$\sqrt 5 $
by “ten things less a māl” (10x − x
2) to get “a root of five hundred māls less a root of five māls māl” (
![]() $\sqrt {500{x^2}} - \sqrt {5{x^4}} $
). We would put the powers outside the square roots like this:
$\sqrt {500{x^2}} - \sqrt {5{x^4}} $
). We would put the powers outside the square roots like this:
![]() $\sqrt {500} x - \sqrt 5 {x^2}$
. Abū Kāmil, instead, insists on taking the square roots of the whole terms.Footnote
13
Once the operations have been performed he sets up and simplifies his equation, which in modern notation is
$\sqrt {500} x - \sqrt 5 {x^2}$
. Abū Kāmil, instead, insists on taking the square roots of the whole terms.Footnote
13
Once the operations have been performed he sets up and simplifies his equation, which in modern notation is
![]() $20x + \sqrt {500{x^2}} = 100 + 2{x^2} + \sqrt {5{x^4}} $
. Instead, we would write it as (
$20x + \sqrt {500{x^2}} = 100 + 2{x^2} + \sqrt {5{x^4}} $
. Instead, we would write it as (
![]() $20 + \sqrt {500} )x = 100 + (2 + \sqrt 5 ){x^2}$
. In our version it is much easier to identify the linear and quadratic terms. Even with his formulation Abū Kāmil understands that to set the “number” of māls to 1 he must multiply everything by the reciprocal of
$20 + \sqrt {500} )x = 100 + (2 + \sqrt 5 ){x^2}$
. In our version it is much easier to identify the linear and quadratic terms. Even with his formulation Abū Kāmil understands that to set the “number” of māls to 1 he must multiply everything by the reciprocal of
![]() $2 + \sqrt 5 $
.
$2 + \sqrt 5 $
.
Abū Kāmil does not work with fractions in this problem, but many problems in Arabic algebra are solved with fractions. One example is this equation from al-Khwārizmī’s problem (25): “twenty-five parts of a hundred forty-four parts of a māl and sixteen dirhams less three roots and a third of a root equal. . .a thing” (
![]() $\frac{{25}}{{144}}{x^2} + 16 - 3\frac{1}{3}x = x$
) (al-Khwārizmī Reference Rashed2009, 187.6-8; my translation).Footnote
14
$\frac{{25}}{{144}}{x^2} + 16 - 3\frac{1}{3}x = x$
) (al-Khwārizmī Reference Rashed2009, 187.6-8; my translation).Footnote
14
Clearly the Arabic “number” of a term does not possess the same meaning as our modern coefficient. I explain this in some detail in my “Polynomials and Equations in Arabic Algebra” (Oaks Reference Oaks2009, §5), and more succinctly in “Medieval Arabic Algebra as an Artificial Language.” There I explain medieval polynomials by decoding al-Karajī’s equation “. . .ten things less a māl, and that equals four things and five dirhams” (Saidan Reference Saidan1986, 202.8) (10x − x 2 = 4x + 5):
Medieval algebraists conceived of polynomials differently than we do today. For us, a polynomial is constructed from the powers of x with the operations of scalar multiplication and addition/subtraction. In other words, it is a linear combination of the powers. By contrast, Arabic polynomials contain no operations at all. In the expression “four things,” the “four” is not multiplied by “things.” Instead, it merely indicates how many things are present. Think of “four things” like “four bottles.”
Further, the phrase “four things and five dirhams” entails no addition, but is a collection of nine items of two different kinds. Think of it like “four bottles and five cans.” The wa (“and”) connecting the things and the dirhams is the common conjunction. It does not take the meaning of the modern word “plus.”
The “ten things less a māl” on the other side of the equation describes an amount which is a māl short of “ten things.” Think of it as a collection of ten items which have been diminished by a māl. Similarly, if I take a bite out of an apple, I can describe the result as “an apple less a bite.” “Ten things less a māl,” like the bitten apple, is a static object: it is only our description of it which seems to imply a subtraction. Illā (“less”) is the negative counterpart to “and.” It does not mean “minus.” (Oaks Reference Oaks2007, 548)Footnote 15
Even grammatically the number of a term is “how many” there are. Premodern algebraists, in Arabic, Latin, and Italian, speak of “a thing,” making the noun singular when there is one, and “two things,” “three things,” etc., making “thing” plural when there is more than one. It would make no sense to multiply “a root of five” by “a thing” and get “a root of five things” (
![]() $\sqrt 5 x$
). One can talk about the aggregation “five māls,” though, and because this represents a number, its root can be taken. So the result of the multiplication is “a root of five māls” (
$\sqrt 5 x$
). One can talk about the aggregation “five māls,” though, and because this represents a number, its root can be taken. So the result of the multiplication is “a root of five māls” (
![]() $\sqrt {5{x^2}} $
). To borrow a phrase from Jacob Klein, the number of a term is “a determinate number of determinate things” (Klein 1968, 131), where these “things” are the species, or powers of the unknown: dirhams, things, māls, cubes, etc.
$\sqrt {5{x^2}} $
). To borrow a phrase from Jacob Klein, the number of a term is “a determinate number of determinate things” (Klein 1968, 131), where these “things” are the species, or powers of the unknown: dirhams, things, māls, cubes, etc.
Abū Kāmil may present the solution to his problem rhetorically, but he would have worked out the calculations in some kind of notation on a dust-board or another erasable surface. Books were regarded as transcriptions of lectures, and since notation serves no purpose when reading aloud, it is not written in the manuscripts. We know of the Arabic algebraic notation that developed in the western part of the Islamic world around the twelfth century only because some textbook authors show it to instruct students in its use. Even there the problems and solutions are still written out in words. In Italian algebra notation starts to creep into the rhetorical presentations, but the declinations of the signs and the words that appear within it suggest that it was intended to be pronounced. Only in the sixteenth century do we begin to see notation shed its dependence on the rhetorical parts of the text (Oaks Reference Oaks2010; Oaks Reference Oaks2012).
Premodern concepts are naturally reflected in the algebraic notations found in Greek and medieval manuscripts, and they remained in force in books treating algebra in sixteenth-century Europe.Footnote
16
What is important for this study is the relationship between the coefficient and the power. As an example, consider the equation “1
![]() + 8
+ 8
![]() – 24 æquatur 72” from Michael Stifel's 1544 Arithmetica Integra (Stifel Reference Stifel1544, fol. 241b). The first-degree unknown is shown by the cossic symbol “
– 24 æquatur 72” from Michael Stifel's 1544 Arithmetica Integra (Stifel Reference Stifel1544, fol. 241b). The first-degree unknown is shown by the cossic symbol “
![]() ”, and the second-degree unknown with the symbol “
”, and the second-degree unknown with the symbol “
![]() ”. Translated into modern notation the equation is x
2 + 8x − 24 = 72. Stifel's version may look tantalizingly modern, but the “8
”. Translated into modern notation the equation is x
2 + 8x − 24 = 72. Stifel's version may look tantalizingly modern, but the “8
![]() ”, for instance, was not read like our “8x.” There the “8” and the “
”, for instance, was not read like our “8x.” There the “8” and the “
![]() ” play different roles than their modern counterparts. Where our x represents the value of the first-degree unknown, Stifel's
” play different roles than their modern counterparts. Where our x represents the value of the first-degree unknown, Stifel's
![]() denotes a kind or denomination (denominatio) of number (Stifel Reference Stifel1544, fol. 228ff; see also fol. 7b). In fact, as Stifel himself notes, the cossic signs are much like denominations of coins (Stifel Reference Stifel1544, fol. 79bff; fol. 231a).Footnote
17
Writing “1
denotes a kind or denomination (denominatio) of number (Stifel Reference Stifel1544, fol. 228ff; see also fol. 7b). In fact, as Stifel himself notes, the cossic signs are much like denominations of coins (Stifel Reference Stifel1544, fol. 79bff; fol. 231a).Footnote
17
Writing “1
![]() + 8
+ 8
![]() ” is like writing “1 euro and 8 dollars,” a particular amount of money. We do not include a coefficient of “1” for the x
2 in our x
2 + 8x because x
2 denotes the value of a particular unknown number. But Stifel could not write “
” is like writing “1 euro and 8 dollars,” a particular amount of money. We do not include a coefficient of “1” for the x
2 in our x
2 + 8x because x
2 denotes the value of a particular unknown number. But Stifel could not write “
![]() + 8
+ 8
![]() ” because it would be like saying “euros and 8 dollars.” This leaves unanswered the question of how many euros there are. Premodern polynomials are inventories in which each denomination or kind requires a number (coefficient) to go with it. By itself
” because it would be like saying “euros and 8 dollars.” This leaves unanswered the question of how many euros there are. Premodern polynomials are inventories in which each denomination or kind requires a number (coefficient) to go with it. By itself
![]() is a kind of number, and only with a coefficient, like “1
is a kind of number, and only with a coefficient, like “1
![]() ” or “8
” or “8
![]() ”, does it stand for a value. This is why Stifel and others consistently place a “1” before a sign when there is only one of them. An important consequence of this is that the cossic signs
”, does it stand for a value. This is why Stifel and others consistently place a “1” before a sign when there is only one of them. An important consequence of this is that the cossic signs
![]() and
and
![]() are not subject to operations the way our x and x
2 are. Only with a coefficient can they be multiplied, added, etc. to form algebraic expressions. For this reason in particular the concatenation of the number with the sign cannot mean multiplication. Simple numbers like the 24 and 72 in Stifel's equation require no particular sign. The entire polynomial “1
are not subject to operations the way our x and x
2 are. Only with a coefficient can they be multiplied, added, etc. to form algebraic expressions. For this reason in particular the concatenation of the number with the sign cannot mean multiplication. Simple numbers like the 24 and 72 in Stifel's equation require no particular sign. The entire polynomial “1
![]() + 8
+ 8
![]() – 24” is a collection of nine objects of two different kinds, diminished by 24 objects of a third kind.
– 24” is a collection of nine objects of two different kinds, diminished by 24 objects of a third kind.
From Arabic to Latin and Italian
The practice of applying roots to entire terms in algebra was consistently applied throughout the medieval period. ʿAlī al-Sulamī (ca. 10th century), for example, multiplies “a thing” by “a root of twenty” to get “a root of twenty māls” (ʿAlī al-Sulamī, ff. 61b-62a; see also fol. 97a). At one point al-Karajī (early 11th century) multiplies “a root of ten by ten less two things” to get “a root of a thousand dirhams less a root of forty māls” (Problem (II.49) (Saidan Reference Saidan1986, 204.2). In the western part of the Islamic world Ibn al-Bannāʾ (d. 1321) multiplies
![]() $\sqrt 3 $
by 5x to get
$\sqrt 3 $
by 5x to get
![]() $\sqrt {75{x^2}} $
(Saidan Reference Saidan1986, 537.10). Similar examples can also be found in the works of al-Māhānī (mid 9th century), al-Samawʾal (12th century), and Ibn al-Hāʿim (1387).Footnote
18
Other algebraists do not show the right kinds of computations to illustrate this, including among others al-Khwārizmī, Ibn Turk, al-Khayyām, Sharaf al-Dīn al-Ṭūsī, Ibn Badr, and al-ʿĀmilī.
$\sqrt {75{x^2}} $
(Saidan Reference Saidan1986, 537.10). Similar examples can also be found in the works of al-Māhānī (mid 9th century), al-Samawʾal (12th century), and Ibn al-Hāʿim (1387).Footnote
18
Other algebraists do not show the right kinds of computations to illustrate this, including among others al-Khwārizmī, Ibn Turk, al-Khayyām, Sharaf al-Dīn al-Ṭūsī, Ibn Badr, and al-ʿĀmilī.
Most medieval Latin texts are translations or adaptations from Arabic, so it should be no surprise that the “number” of a term is always rational there, too. In problem <113> of the Liber Mensurationum, a twelfth-century translation from Arabic, the side of an equilateral triangle is named a rem (“thing”), making the altitude “radix trium quartarum census” (
![]() $\sqrt {\frac{3}{4}{x^2}} $
) (Busard Reference Busard1968, 111). In his Liber Abaci (1228) Fibonacci took over many problems involving roots from Abū Kāmil, but he also included some that are not currently known from any Arabic source. In one of these, problem (66), he multiplies “res, et denari 10; que multiplicata in radicem de 5, faciunt radicem 5 censuum, et radicem 500 denariorum”
$\sqrt {\frac{3}{4}{x^2}} $
) (Busard Reference Busard1968, 111). In his Liber Abaci (1228) Fibonacci took over many problems involving roots from Abū Kāmil, but he also included some that are not currently known from any Arabic source. In one of these, problem (66), he multiplies “res, et denari 10; que multiplicata in radicem de 5, faciunt radicem 5 censuum, et radicem 500 denariorum”
![]() $( {x + 10} ) \cdot \sqrt 5 \to \sqrt {5{x^2}} + \sqrt {500} $
) (Fibonacci Reference Boncompagni1857, 430.27; Fibonacci Reference Sigler2002, 582.33). Jean de Murs's 1343 Liber Quadripartitum also reproduces many problems that ultimately come from Abū Kāmil, and he shows the same treatment of roots (Jean de Murs Reference l'Huillier1990, 408, 414, 442, 450, 452). Other Latin books, like the Liber Augmenti et Diminutionis and the Liber Mahameleth, show no examples of an irrational root multiplied by an algebraic term.
$( {x + 10} ) \cdot \sqrt 5 \to \sqrt {5{x^2}} + \sqrt {500} $
) (Fibonacci Reference Boncompagni1857, 430.27; Fibonacci Reference Sigler2002, 582.33). Jean de Murs's 1343 Liber Quadripartitum also reproduces many problems that ultimately come from Abū Kāmil, and he shows the same treatment of roots (Jean de Murs Reference l'Huillier1990, 408, 414, 442, 450, 452). Other Latin books, like the Liber Augmenti et Diminutionis and the Liber Mahameleth, show no examples of an irrational root multiplied by an algebraic term.
When multiplying a monomial by a root, Italian abbacists work the product as it was done in Arabic. Maestro Benedetto of Florence (1463) gives a full explanation of the product of
![]() $\sqrt {12} $
by 8x (Note: censo is the Italian translation of the Arabic māl.):
$\sqrt {12} $
by 8x (Note: censo is the Italian translation of the Arabic māl.):
Multiply the root of 12 by 8 things. First you render the root of 12 rational, whereby you multiply the root of 12 by itself, making 12. And similarly you multiply 8 things by itself, making 64 censi. And you multiply 12 by 64 censi to make 768 censi, and you say that this multiplication is the root of 768 censi, and the same goes for each of the other names.Footnote 19
The same treatment is found in every abbacus book I have seen that deals with such computations, down through Luca Pacioli's 1494 Summa de Arithmetica. Among many examples, Pacioli posits the side of a square as “una cosa” (i.e. “a thing,” or x), and he calculates its diagonal as “radice di 2 censi” (“root of two censi,” or
![]() $\sqrt {2{x^2}} $
). In this problem he sets up the equation “the censo is equal to 4 things and root of 8 censi” (
$\sqrt {2{x^2}} $
). In this problem he sets up the equation “the censo is equal to 4 things and root of 8 censi” (
![]() ${x^2} = 4x + \sqrt {8{x^2}} $
), where the right side of the equation is obtained from doubling
${x^2} = 4x + \sqrt {8{x^2}} $
), where the right side of the equation is obtained from doubling
![]() $2x + \sqrt {2{x^2}} $
.Footnote
20
$2x + \sqrt {2{x^2}} $
.Footnote
20
An interesting slip-up occurs in an anonymous fourteenth-century Trattato di Geometria Pratica. At one point in the solution to problem [246] the author wants to calculate
![]() $( {45 + {x^2}} ) - {( {\sqrt {27} - x} )^2}$
, after which the result is to be divided by 12. In the excerpt translated below, the
$( {45 + {x^2}} ) - {( {\sqrt {27} - x} )^2}$
, after which the result is to be divided by 12. In the excerpt translated below, the
![]() $\sqrt {27} - x$
is squared, resulting in
$\sqrt {27} - x$
is squared, resulting in
![]() $27 - \sqrt {108} x + {x^2}$
. Note the irrational number of cose! Then the remainder after subtracting is found to be
$27 - \sqrt {108} x + {x^2}$
. Note the irrational number of cose! Then the remainder after subtracting is found to be
![]() $18 + \sqrt {108} x$
, which is then divided by 12. As the author is about to divide the
$18 + \sqrt {108} x$
, which is then divided by 12. As the author is about to divide the
![]() $\sqrt {108} x$
he notices that the term is not proper, so he converts it to
$\sqrt {108} x$
he notices that the term is not proper, so he converts it to
![]() $\sqrt {108{x^2}} $
and then proceeds with the division, getting
$\sqrt {108{x^2}} $
and then proceeds with the division, getting
![]() $\sqrt {\frac{3}{4}{x^2}} $
(in this book “1/c” means “1 cosa”, and “1/z” means “1 zenso,” a variation on censo):
$\sqrt {\frac{3}{4}{x^2}} $
(in this book “1/c” means “1 cosa”, and “1/z” means “1 zenso,” a variation on censo):
multiplying the root of 27 less 1/c by itself makes 27 less the root of 108 co[se] and plusFootnote 21 1/z. Subtracting it from 45 [and] 1/z leaves 18 plus the root of 108/c. You must divide by double the base, which is Ab, which is by 2 by 6, making 12. Divide 18 by 12 to get 1 1/2; divide the root of 108/c, which is to say 108/z and not co[se]. Divide [the root of] 108/z by 12: render 12 a root, which is 144, to get 3/4, and the root of 3/4 of z comes out.Footnote 22
In all other instances in this book, including the calculations later in the same problem on the next two pages, the whole term is put under the root.Footnote 23
Recall that to multiply a root by a quantity, Maestro Benedetto first made the quantity a root by squaring it. In the medieval Italian books this was done even when the quantity had more than one term. In problem (27) of an anonymous Trattato d'Algibra from the 1390’s the author needs to multiply 25 − x
2 by
![]() $\sqrt {14} $
. Rather than multiply the
$\sqrt {14} $
. Rather than multiply the
![]() $\sqrt {14} $
by each term as Abū Kāmil would have done, this algebraist first converts 25 − x
2 into
$\sqrt {14} $
by each term as Abū Kāmil would have done, this algebraist first converts 25 − x
2 into
![]() $\sqrt {625 - 50{x^2} + {x^4}} $
, and then multiplies it by
$\sqrt {625 - 50{x^2} + {x^4}} $
, and then multiplies it by
![]() $\sqrt {14} $
to get
$\sqrt {14} $
to get
![]() $\sqrt {8750 - 700{x^2} + 14{x^4}} $
:
$\sqrt {8750 - 700{x^2} + 14{x^4}} $
:
for such a multiplication it is necessary to render the 25 less a censo into a root, which will be the root of 625 less 50 censi plus a censo di censo, and this quantity multiplied against the root of 14 makes the root of 8750 less 700 censi plus 14 censi di censi.Footnote 24
I have found only two other examples of an Italian abbacist multiplying an irrational root by a polynomial, and in both cases the operation is performed the same way. Piero della Francesca, in his Trattato d'Abaco (ca. 1470–80), multiplies
![]() $\sqrt {18} $
by 10 − 2x to get
$\sqrt {18} $
by 10 − 2x to get
![]() $\sqrt {1800 - 720x + 72{x^2}} $
, and Raffaello Canacci, in his Ragionamenti d'Algebra i problemi (ca. 1495), multiplies 15 − x by
$\sqrt {1800 - 720x + 72{x^2}} $
, and Raffaello Canacci, in his Ragionamenti d'Algebra i problemi (ca. 1495), multiplies 15 − x by
![]() $\sqrt {18} $
to get
$\sqrt {18} $
to get
![]() $\sqrt {18{x^2} - 540x + 4050} $
(Piero della Francesca Reference Arrrighi1970, 164; Canacci Reference Canacci and Procissi1983, 25.31).
$\sqrt {18{x^2} - 540x + 4050} $
(Piero della Francesca Reference Arrrighi1970, 164; Canacci Reference Canacci and Procissi1983, 25.31).
Nicholas Chuquet, too, follows the traditional way in his Triparty en la Science des Nombres, composed in French in 1484. For example, at one point he writes “Ores multiplie .1.1 par R.2 72.
![]() ${\rm{\tilde{m}}}$
. 1. si auras R.2 72.2
${\rm{\tilde{m}}}$
. 1. si auras R.2 72.2
![]() ${\rm{\tilde{m}}}$
. 1.1”. In modern notation this is
${\rm{\tilde{m}}}$
. 1.1”. In modern notation this is
![]() $x \cdot ( {\sqrt {72} - 1} ) \to \sqrt {72{x^2}} - x$
(Marre Reference Marre1880, 813.15).
$x \cdot ( {\sqrt {72} - 1} ) \to \sqrt {72{x^2}} - x$
(Marre Reference Marre1880, 813.15).
The problems in Abū Kāmil's Book of Algebra continued to be translated and copied in medieval Europe. His problem (41), translated in the previous section, reappears several times. It is of course in the Latin translation preserved in a fourteenth-century manuscript and in the fifteenth-century Hebrew translation of his book, and it is also found in Fibonacci's Liber Abaci, Jean de Murs's Liber Quadripartitum, and in a fifteenth-century medieval Italian translation of Fibonacci's chapter on algebra (Sesiano Reference Sesiano, Folkerts and Hogendijk1993, l. 2426; Levey Reference Levey1966, 150; Fibonacci Reference Boncompagni1857, 434.26; Fibonacci Reference Sigler2002, 587.4; Jean de Murs Reference l'Huillier1990, 441; Salomone Reference Salomone1984, 58, 63).Footnote 25 The same treatment of roots is found in all these incarnations.
So far I am aware of no counterexamples to my claim that medieval algebraists forbid the number of a term to be irrational. The anonymous Italian abbacist nearly provided one, but he caught and corrected his error. Because someone else may have made the same kind of error, there may be a counterexample or two lurking in some book I have not consulted. Such counterexamples, if they are found, would not alter the fact that algebraists in Arabic, Latin, and Italian deliberately and routinely insisted on rational coefficients. That practice, which might seem odd to us, is a natural outcome of their concept of a monomial.
Multitudes of Roots and Fractions in Arithmetic
This idea of “a number of” a particular object was not restricted to algebra. It also applies to the ways medieval mathematicians expressed roots and fractions. It will be worthwhile to take a digression into arithmetic now to explain this, not just for the broader arithmetical context it provides, but also because it will give us the background to understand a transition in the way roots of numbers were expressed by some European mathematicians beginning with Descartes.
Let us back up and look at Abū Kāmil's answer to problem (41):
![]() $5 - \sqrt {225 - \sqrt {50000} } $
and
$5 - \sqrt {225 - \sqrt {50000} } $
and
![]() $5 + \sqrt {225 - \sqrt {50000} } $
. His “root of fifty thousand” is the result of multiplying 100 by
$5 + \sqrt {225 - \sqrt {50000} } $
. His “root of fifty thousand” is the result of multiplying 100 by
![]() $\sqrt 5 $
. He says “a root of fifty thousand” (
$\sqrt 5 $
. He says “a root of fifty thousand” (
![]() $\sqrt {50000} $
) and not “a hundred roots of five” (
$\sqrt {50000} $
) and not “a hundred roots of five” (
![]() $100\sqrt 5 $
), which we would prefer, because “a hundred roots of five” is a hundred numbers. To express it as a single number he squares the 100 and multiplies it by the five to get “a root of fifty thousand.” While
$100\sqrt 5 $
), which we would prefer, because “a hundred roots of five” is a hundred numbers. To express it as a single number he squares the 100 and multiplies it by the five to get “a root of fifty thousand.” While
![]() $100\sqrt 5 $
is a perfectly acceptable number to us, medieval algebraists preferred one root to a multitude of roots.
$100\sqrt 5 $
is a perfectly acceptable number to us, medieval algebraists preferred one root to a multitude of roots.
Multitudes of roots crop up sometimes in the course of solving problems, and they are always converted to a single root in the end. ʿAlī al-Sulamī, for example, poses the problem of adding
![]() $\sqrt {10} $
,
$\sqrt {10} $
,
![]() $\sqrt {40} $
,
$\sqrt {40} $
,
![]() $\sqrt {90} $
and
$\sqrt {90} $
and
![]() $\sqrt {250} $
. He converts the second, third, and fourth numbers to “two roots of ten,” “three roots of ten,” and “five roots of ten” respectively, and then he adds them all to get “eleven roots of ten.” He then gives the instruction to “make this the root of one number,” and his answer is
$\sqrt {250} $
. He converts the second, third, and fourth numbers to “two roots of ten,” “three roots of ten,” and “five roots of ten” respectively, and then he adds them all to get “eleven roots of ten.” He then gives the instruction to “make this the root of one number,” and his answer is
![]() $\sqrt {1210} $
(ʿAlī al-Sulamī, fol. 29b.8).
$\sqrt {1210} $
(ʿAlī al-Sulamī, fol. 29b.8).
Al-Hawārī expresses the idea of multitudes in his commentary on Ibn al-Bannāʾ’s Talkhīṣ (1305): “Add half the root of twenty to two roots of five. Half the root of twenty is less than one root, so we convert it to one root, as seen in the chapter on division. After working the multiplication it becomes a root of five. And two roots of five are more than one root, so we convert it to one root, to get a root of twenty” ([al-Hawārī Reference Abdeljaouad and Oaks2013, 179.20).Footnote 26
Al-Khwārizmī explains how to convert a multitude of roots and fractions of a root into a single root in his algebra book. To double the root of a quantity “you multiply two by two, then by the quantity. The root of the result becomes twice the root of that quantity” (al-Khwārizmī Reference Rashed2009, 131; my translation). He gives similar instructions for triple the root, half of the root, etc. Later, in the chapter on mensuration, he multiplies 5 by
![]() $\sqrt {75} $
by squaring the five, and then multiplying the 25 by 75 to get
$\sqrt {75} $
by squaring the five, and then multiplying the 25 by 75 to get
![]() $\sqrt {1875} $
(al-Khwārizmī Reference Rashed2009, 219). Here is one more example, from al-Karajī (1011/12 CE): “Two roots of ten is a root of what quantity? Multiply two by two to get four. Multiply it by ten to get forty. So a root of forty is two roots of ten” (Saidan Reference Saidan1986, 121.19). Think of “two roots of ten” as the pair (
$\sqrt {1875} $
(al-Khwārizmī Reference Rashed2009, 219). Here is one more example, from al-Karajī (1011/12 CE): “Two roots of ten is a root of what quantity? Multiply two by two to get four. Multiply it by ten to get forty. So a root of forty is two roots of ten” (Saidan Reference Saidan1986, 121.19). Think of “two roots of ten” as the pair (
![]() $\sqrt {10} $
$\sqrt {10} $
![]() $\sqrt {10} $
), and not as the single number
$\sqrt {10} $
), and not as the single number
![]() $2\sqrt {10} $
.
$2\sqrt {10} $
.
This rule is likewise applied in all medieval Latin and Italian books I have seen. This next problem comes from an anonymous fourteenth-century Trattato dell'Alcibra Amuchabile:
I want to multiply 3 by the root of 34. Do it like this: you must render the 3, which is the number, to a root, and say 3 by 3 makes nine. Then you must multiply the root of nine by the root of 34. Nine by 34 makes 306, and you say that multiplying 3 by the root of 34 makes the root of 306, and it is done.Footnote 27
Mathematicians continued to write single roots throughout the sixteenth century. Cardano multiplies “R cu 5” by 10 to get “R cu 5000”
![]() $(\sqrt[3]{5} \cdot 10 \to \sqrt[3]{{5000}})$
(Cardano Reference Cardano1539, 188); Bombelli writes “2 via R.q. 5 fa R.q. 20” (
$(\sqrt[3]{5} \cdot 10 \to \sqrt[3]{{5000}})$
(Cardano Reference Cardano1539, 188); Bombelli writes “2 via R.q. 5 fa R.q. 20” (
![]() $2 \cdot \sqrt 5 \to \sqrt {20} $
) (Bombelli Reference Bombelli1966, 159); and Stevin doubles
$2 \cdot \sqrt 5 \to \sqrt {20} $
) (Bombelli Reference Bombelli1966, 159); and Stevin doubles
![]() $\sqrt {735} $
to get
$\sqrt {735} $
to get
![]() $\sqrt {2940} $
(Stevin Reference Stevin1585, 207). Two examples of many in Viète show that he prefers
$\sqrt {2940} $
(Stevin Reference Stevin1585, 207). Two examples of many in Viète show that he prefers
![]() $\sqrt {59319} $
to our
$\sqrt {59319} $
to our
![]() $39\sqrt {39} $
and
$39\sqrt {39} $
and
![]() $\sqrt {32} $
to
$\sqrt {32} $
to
![]() $4\sqrt 2 $
(Viète Reference Viète1615, 7, 118; Viète 1646, 87, 153). Mathematicians in the early seventeenth century continued this practice, including Christoph Clavius (Reference Clavius1608), Albert Girard (Reference Girard1629), Marino Ghetaldi (Reference Ghetaldi1630), and Thomas Harriot (Reference Harriot1631). Harriot, for instance, writes
$4\sqrt 2 $
(Viète Reference Viète1615, 7, 118; Viète 1646, 87, 153). Mathematicians in the early seventeenth century continued this practice, including Christoph Clavius (Reference Clavius1608), Albert Girard (Reference Girard1629), Marino Ghetaldi (Reference Ghetaldi1630), and Thomas Harriot (Reference Harriot1631). Harriot, for instance, writes
![]() $\sqrt {18252} $
instead of
$\sqrt {18252} $
instead of
![]() $78\sqrt 3 $
(Harriot Reference Harriot1631, 101; Girard Reference Girard1629, 23; Ghetaldi Reference Ghetaldi1630, 221, 224). The earliest modern treatment of roots I have found is in René Descartes's La Geometrie (French, 1637). On page 379 he writes the equation “
$78\sqrt 3 $
(Harriot Reference Harriot1631, 101; Girard Reference Girard1629, 23; Ghetaldi Reference Ghetaldi1630, 221, 224). The earliest modern treatment of roots I have found is in René Descartes's La Geometrie (French, 1637). On page 379 he writes the equation “
![]() ${x^3}\ - \ \sqrt 3 xx + \frac{{26}}{{27}}x\ - \ \frac{8}{{27\sqrt 3 }}$
${x^3}\ - \ \sqrt 3 xx + \frac{{26}}{{27}}x\ - \ \frac{8}{{27\sqrt 3 }}$
![]() 0”; and on page 380 he writes the numbers “
0”; and on page 380 he writes the numbers “
![]() $\frac{2}{9}\sqrt 3 $
”, “
$\frac{2}{9}\sqrt 3 $
”, “
![]() $\frac{1}{3}\sqrt 3 $
”, and “
$\frac{1}{3}\sqrt 3 $
”, and “
![]() $\frac{4}{9}\sqrt 3 $
”. I will come back to this development below.
$\frac{4}{9}\sqrt 3 $
”. I will come back to this development below.
Multitudes of numbers extend even to fractions. In Arabic there are two basic ways of expressing fractions. If the denominator is ten or less, they say it just as we do, as “seven tenths” or “three fourths.” In this latter fraction the “three” indicates how many “fourths” there are. Even our own words “numerator” and “denominator” reflect this conception. The “denominator” is the name or kind of object, and the “numerator” is their number. In Arabic, when the denominator is larger than ten and the fraction cannot be reduced to some combination of smaller fractions, the language of “parts” is used. For
![]() $\frac{4}{{13}}$
one says “four parts of thirteen parts of a dirham.” Here it is the “parts” that are counted. A “dirham” (i.e. the unit) is partitioned into 13 equal parts, and the fraction is four of those parts. In medieval Italian the texts generally show fractions the way we do, using Arabic numerals and the division bar.
$\frac{4}{{13}}$
one says “four parts of thirteen parts of a dirham.” Here it is the “parts” that are counted. A “dirham” (i.e. the unit) is partitioned into 13 equal parts, and the fraction is four of those parts. In medieval Italian the texts generally show fractions the way we do, using Arabic numerals and the division bar.
So in medieval arithmetic and algebra, numbers can be counted just like bricks, chickens, and shoes. “Five chickens,” “five sevenths,” “five roots of three,” and “five things” (5x) are all collections of five objects. Only in the case of roots is it possible to turn the multitude into a single number. It is clear, then, why medieval algebraists never allowed the “number” of a term to be irrational even if it complicates the expressions. It simply makes no sense to speak of a first degree term as “a root of three things.” Our
![]() $\sqrt 3 x$
is perfectly fine because the
$\sqrt 3 x$
is perfectly fine because the
![]() $\sqrt 3 $
is regarded as a number multiplied by the x, or as a quantity that scales the x. It is not how many x’s there are.
$\sqrt 3 $
is regarded as a number multiplied by the x, or as a quantity that scales the x. It is not how many x’s there are.
Irrational Coefficients in Sixteenth-Century European Algebra
Just as the case in Arabic, Italian algebra was largely the domain of practitioners. It was not taught in the early universities, and only in the sixteenth century did it draw the serious attention of more theoretically minded mathematicians. Many significant advances were made then, most notably the solutions to general cubic and quartic equations, which are linked to the introduction of negative and complex numbers. One development that has gone unnoticed is that some sixteenth-century algebraists began to allow the “number” of a term to be irrational.
The earliest text I know to deviate from the medieval rule is Christoff Rudolff's 1525 Coss.Footnote
28
Rudolff makes the adjustment in four instances in 240 problems. In each case the “number” of the term is a binomial. In one problem he multiplies “1
![]() + 2 + √ 2
+ 2 + √ 2
![]() ” by “1
” by “1
![]() ” to get “1
” to get “1
![]() + 2 + √ 2
+ 2 + √ 2
![]() ”, or in modern notation,
”, or in modern notation,
![]() $( {x + 2 + \sqrt 2 } ) \cdot x \to {x^2} + ( {2 + \sqrt 2 } )x$
. He adds this comment in parentheses immediately after: “Note that the binomial would be taken as a quantity, or would be spoken as 2 + √2,
$( {x + 2 + \sqrt 2 } ) \cdot x \to {x^2} + ( {2 + \sqrt 2 } )x$
. He adds this comment in parentheses immediately after: “Note that the binomial would be taken as a quantity, or would be spoken as 2 + √2,
![]() ” (Kaunzner & Röttel Reference Kaunzner and Röttel2006, 113, 243a).Footnote
29
Rudolff is aware that it is not customary for the “quantity” of a term to be “deaf” (i.e. irrational), so he has taken the step of treating it as if it were “spoken.” Had he followed the old way he would have expressed the product as “1
” (Kaunzner & Röttel Reference Kaunzner and Röttel2006, 113, 243a).Footnote
29
Rudolff is aware that it is not customary for the “quantity” of a term to be “deaf” (i.e. irrational), so he has taken the step of treating it as if it were “spoken.” Had he followed the old way he would have expressed the product as “1
![]() + 2
+ 2
![]() + √ 2
+ √ 2
![]() ”, where the last term corresponds to our
”, where the last term corresponds to our
![]() $\sqrt {2{x^2}} $
, like we saw in Abū Kāmil.
$\sqrt {2{x^2}} $
, like we saw in Abū Kāmil.
In the other instances Rudolff multiplies the binomials
![]() $8 + \sqrt {20} $
,
$8 + \sqrt {20} $
,
![]() $18 + \sqrt {648} $
, and
$18 + \sqrt {648} $
, and
![]() $10 + \sqrt {18} $
by “1
$10 + \sqrt {18} $
by “1
![]() ” to get “8 + √ 20
” to get “8 + √ 20
![]() ”, “18 + √ 648
”, “18 + √ 648
![]() ”, and “10 + √ 18
”, and “10 + √ 18
![]() ” respectively (Kaunzner & Röttel Reference Kaunzner and Röttel2006, 62, 63, 118, 196d, 197c, 249b). Rudolff's notation is not ambiguous because he uses the symbol “
” respectively (Kaunzner & Röttel Reference Kaunzner and Röttel2006, 62, 63, 118, 196d, 197c, 249b). Rudolff's notation is not ambiguous because he uses the symbol “
![]() ” for units. Thus “1
” for units. Thus “1
![]() + 2 + √ 2
+ 2 + √ 2
![]() ” means
” means
![]() ${x^2} + ( {2 + \sqrt 2 } )x$
, while “1
${x^2} + ( {2 + \sqrt 2 } )x$
, while “1
![]() + 2
+ 2
![]() + √ 2
+ √ 2
![]() ” would be
” would be
![]() ${x^2} + 2 + \sqrt {2x} $
. In all other cases Rudolff follows tradition by putting everything under the root. In one problem, for example, he takes the square root of “
${x^2} + 2 + \sqrt {2x} $
. In all other cases Rudolff follows tradition by putting everything under the root. In one problem, for example, he takes the square root of “
![]() $\frac{3}{2}$
$\frac{3}{2}$
![]() ” (
” (
![]() $\frac{3}{2}{x^2}$
) to get “
$\frac{3}{2}{x^2}$
) to get “
![]() $\surd \frac{3}{2}$
$\surd \frac{3}{2}$
![]() ” (Kaunzner & Röttel Reference Kaunzner and Röttel2006, 107, 235d).
” (Kaunzner & Röttel Reference Kaunzner and Röttel2006, 107, 235d).
Marco Aurel translates many of Rudolff's problems in his Libro Primero de Arithmetica Algebratica (Spanish, 1552), including his first, third, and fourth problems with irrational binomials (Aurel Reference Aurel1552, ff. 106b, 122a, 133a). He translates Rudolff's explanation as “nota el binomio 2 + √2, se toma por sola 1 quantidad, y al presente por
![]() ” (Aurel Reference Aurel1552, fol. 122a). Also, one of Rudolff's examples is found among the many problems translated by George Henischus in his Arithmetica Perfecta et Demonstrata (Latin, 1609) (Henischus Reference Henischus1609, 374).Footnote
30
Like Rudolff, both Aurel and Henischus put the whole term under the root in other problems. Both authors appear to have merely copied Rudolff, and may have had no opinion about his binomial coefficients. (I discuss Stifel's edition of Rudolff's book below.)
” (Aurel Reference Aurel1552, fol. 122a). Also, one of Rudolff's examples is found among the many problems translated by George Henischus in his Arithmetica Perfecta et Demonstrata (Latin, 1609) (Henischus Reference Henischus1609, 374).Footnote
30
Like Rudolff, both Aurel and Henischus put the whole term under the root in other problems. Both authors appear to have merely copied Rudolff, and may have had no opinion about his binomial coefficients. (I discuss Stifel's edition of Rudolff's book below.)
Girolamo Cardano is the next algebraist after Rudolff to admit irrational numbers of terms. In his Practica Arithmetice, & Mensurandi Singularis (Latin, 1539), Cardano makes allowance not just for binomials, but for any irrational number. He explains that when taking the root of “ce” (the abbreviation for censo, the second degree) or “ce ce” (the abbreviation for the fourth degree), one puts the root after the “co” (the abbreviation for the first degree cosa) or the “ce” (“R” is an abbreviation for Radix, “Root”):
R of a number is a number, such as R 10 is R 10. R censuum is co, such as R 7 ce is co R 7. R ce ce is ce, as R 10 ce ce is ce R 10.Footnote 31 (Cardano Reference Cardano1539, ff. 90b last line, 91a.14, 98a.28)
This way he can write the old “R 7 ce” (
![]() $\sqrt {7{x^2}} $
) as “co R 7” (
$\sqrt {7{x^2}} $
) as “co R 7” (
![]() $\sqrt 7 x$
). He puts the irrational number after the power in some of his subsequent problems, though he retains the old way in others. Three examples are “10 m R 24 æquantur R 6 ce” (
$\sqrt 7 x$
). He puts the irrational number after the power in some of his subsequent problems, though he retains the old way in others. Three examples are “10 m R 24 æquantur R 6 ce” (
![]() $10 - \sqrt {24} = \sqrt {6{x^2}} $
), “co R cu 8” (
$10 - \sqrt {24} = \sqrt {6{x^2}} $
), “co R cu 8” (
![]() $\sqrt[3]{8}x$
), and “R 4 ce que sit co R 4” (
$\sqrt[3]{8}x$
), and “R 4 ce que sit co R 4” (
![]() $\sqrt {4{x^2}} $
, which is
$\sqrt {4{x^2}} $
, which is
![]() $\sqrt 4 x$
). He applied the same scheme in his Ars Magna of 1545. There, for example, we find “rebus R 12” for
$\sqrt 4 x$
). He applied the same scheme in his Ars Magna of 1545. There, for example, we find “rebus R 12” for
![]() $\sqrt {12} x$
(Cardano Reference Cardano1545, fol. 11a.11). And one later example from his 1570 De Regula Aliza is the equation “cubus æquatur rebus, R cu.100 p.: 10” (
$\sqrt {12} x$
(Cardano Reference Cardano1545, fol. 11a.11). And one later example from his 1570 De Regula Aliza is the equation “cubus æquatur rebus, R cu.100 p.: 10” (
![]() ${x^3} = \sqrt[3]{{100}}x + 10$
) (Cardano Reference Cardano1570, 19.10).
${x^3} = \sqrt[3]{{100}}x + 10$
) (Cardano Reference Cardano1570, 19.10).
Pedro Nuñez follows Cardano by putting the root after the name of the term in his Libro de Algebra en Arithmetica y Geometria (Spanish, 1567). He explains:
Since things are the roots of censos, as was shown, to say R 5 ce [
![]() $\sqrt {5{x^2}} $
] is like co R 5 [
$\sqrt {5{x^2}} $
] is like co R 5 [
![]() $\sqrt 5 x$
]. The proof is very clear, because certainly multiplying co R 5 by itself gives us 5 ce [
$\sqrt 5 x$
]. The proof is very clear, because certainly multiplying co R 5 by itself gives us 5 ce [
![]() ${( {\sqrt 5 x} )^2} \to 5{x^2}$
] and we get the same by multiplying R 5 ce [
${( {\sqrt 5 x} )^2} \to 5{x^2}$
] and we get the same by multiplying R 5 ce [
![]() $\sqrt {5{x^2}} $
] by itself. And for the same reason R 7 ce ce will be ce R 7 [
$\sqrt {5{x^2}} $
] by itself. And for the same reason R 7 ce ce will be ce R 7 [
![]() $\sqrt {7{x^4}} = \sqrt 7 {x^2}$
] (Nuñez Reference Nuñez1567, fol. 141a.9).Footnote
32
$\sqrt {7{x^4}} = \sqrt 7 {x^2}$
] (Nuñez Reference Nuñez1567, fol. 141a.9).Footnote
32
Like Cardano, Nuñez writes roots both ways. Later on the page he has “1 ce es ygual a 2
![]() ${\rm{\tilde{p}}}$
R 8 ce. . . Porque tanto vale como dezir, que 1 ce es ygual a 2
${\rm{\tilde{p}}}$
R 8 ce. . . Porque tanto vale como dezir, que 1 ce es ygual a 2
![]() ${\rm{\tilde{p}}}$
co R 8. . .” (
${\rm{\tilde{p}}}$
co R 8. . .” (
![]() ${x^2} = 2 + \sqrt {8{x^2}} $
. . .This is the same as saying that
${x^2} = 2 + \sqrt {8{x^2}} $
. . .This is the same as saying that
![]() ${x^2} = 2 + \sqrt 8 x$
).Footnote
33
${x^2} = 2 + \sqrt 8 x$
).Footnote
33
Johann Scheubel uses irrational coefficients in his Brevis Regularum Algebrae Descriptio (Latin, 1550).Footnote
34
Because he never puts an entire term under a root, he can keep the number on the left. He uses the abbreviation “ra.” for radix, the name of the first-degree unknown, and “pri.” for prima, the name of the second-degree unknown. In one problem he multiplies “√448 N – 1 ra.” by “1 radix” to get “√448 radicum – 1 pri” (
![]() $( {\sqrt {448} - x} ) \cdot x \to \sqrt {448} x - {x^2}$
) (Scheubel Reference Scheubel1550, 66). Like Rudolff, his symbol for units (N) prevents ambiguity. His “32 – √512 ra” (Scheubel Reference Scheubel1550, 56) corresponds to our
$( {\sqrt {448} - x} ) \cdot x \to \sqrt {448} x - {x^2}$
) (Scheubel Reference Scheubel1550, 66). Like Rudolff, his symbol for units (N) prevents ambiguity. His “32 – √512 ra” (Scheubel Reference Scheubel1550, 56) corresponds to our
![]() $( {32 - \sqrt {512} } )x$
, while “√448 N – 1 radice” is
$( {32 - \sqrt {512} } )x$
, while “√448 N – 1 radice” is
![]() $\sqrt {448} - x$
(ibid., 66).
$\sqrt {448} - x$
(ibid., 66).
Rafael Bombelli consistently puts the root on the left in his L'Algebra (Italian, 1572). He explains how to multiply an irrational root (“R.q.”) by a monomial (a dignità, or “rank”) in terms of the example
![]() $\sqrt 5 \cdot 2x \to \sqrt {20} x$
, which he prefaces with a warning against those who also square the rank:
$\sqrt 5 \cdot 2x \to \sqrt {20} x$
, which he prefaces with a warning against those who also square the rank:
Sometimes it happens that a R.q. is multiplied by a rank, and it is the position of some authors that one must square them both, which even if they manage to do many times, nevertheless it carries the ranks so far that there is no type [Capitolo] that matches it.Footnote
35
So in order not to encounter this setback, keep the following in mind. Multiply R.q. 5 by 2
![]() [
[
![]() $\sqrt 5 $
by 2x]. This proposal is like multiplying tanti [i.e. a first degree term] by number, since these R.q. are themselves number (though they can only be named in power, for they do not have a side), so that multiplying 2 by R.q. 5 makes R.q. 20 [
$\sqrt 5 $
by 2x]. This proposal is like multiplying tanti [i.e. a first degree term] by number, since these R.q. are themselves number (though they can only be named in power, for they do not have a side), so that multiplying 2 by R.q. 5 makes R.q. 20 [
![]() $\sqrt {20} $
], whose sign you put next to
$\sqrt {20} $
], whose sign you put next to
![]() , and will make R.q. 20
, and will make R.q. 20
![]() [
[
![]() $\sqrt {20} x$
]. (Bombelli Reference Bombelli1966, 158–159; Bombelli Reference Bombelli1579, 206)Footnote
36
$\sqrt {20} x$
]. (Bombelli Reference Bombelli1966, 158–159; Bombelli Reference Bombelli1579, 206)Footnote
36
Here is how he takes the square root of an even-power term:
and if you have to take the side [i.e. square root] of 20
![]() [20x
2], take half of the
[20x
2], take half of the
![]() which is 1 and put it in the semicircle to get
which is 1 and put it in the semicircle to get
![]() . Then you take the side of 20, which will be R.q. 20, and this you put next to
. Then you take the side of 20, which will be R.q. 20, and this you put next to
![]() , making R.q. 20
, making R.q. 20
![]() [
[
![]() $\sqrt {20} x$
]. (Bombelli Reference Bombelli1966, 159.24; Bombelli Reference Bombelli1579, 207)Footnote
37
$\sqrt {20} x$
]. (Bombelli Reference Bombelli1966, 159.24; Bombelli Reference Bombelli1579, 207)Footnote
37
He then adds that when the power is odd, one uses his version of parentheses. These consist of an “L” for “(”, and an “
![]() ” for “)”. So the square root of “6
” for “)”. So the square root of “6
![]() ” (6x
3) is “R.q. L 6
” (6x
3) is “R.q. L 6
![]()
![]() ” (Bombelli Reference Bombelli1966, 159 last line).
” (Bombelli Reference Bombelli1966, 159 last line).
Simon Stevin, on the other hand, employs the symbol “
![]() ” to separate an irrational root from the symbol of the power in his L'Arithmetique (French, 1585). His √9
” to separate an irrational root from the symbol of the power in his L'Arithmetique (French, 1585). His √9
![]() ② corresponds to our
② corresponds to our
![]() $\sqrt 9 {x^2}$
, while √9② is
$\sqrt 9 {x^2}$
, while √9② is
![]() $\sqrt {9{x^2}} $
.
$\sqrt {9{x^2}} $
.
For √9
![]() ②, which is to say root of 9 seconds, the √ refers only to 9, & points to ②, where the dividing mark is denoted by
②, which is to say root of 9 seconds, the √ refers only to 9, & points to ②, where the dividing mark is denoted by
![]() : thus √9
: thus √9
![]() ② is valued as much (seeing that √9 makes 3) as 3 ②. But when the radical number is an incommensurable arithmetical number, like √5
② is valued as much (seeing that √9 makes 3) as 3 ②. But when the radical number is an incommensurable arithmetical number, like √5
![]() ②, it must remain as it is. But without this dividing mark
②, it must remain as it is. But without this dividing mark
![]() , like √9②, it will be like saying root of nine seconds. Considering (because there is no division mark) that the √ refers to 9, and to ②, √9② is valued as 3 ①. For example, √③8③ [
, like √9②, it will be like saying root of nine seconds. Considering (because there is no division mark) that the √ refers to 9, and to ②, √9② is valued as 3 ①. For example, √③8③ [
![]() $\sqrt[3]{{8{x^3}}}$
] is valued as 2 ①. (Stevin Reference Stevin1585, 40)Footnote
38
$\sqrt[3]{{8{x^3}}}$
] is valued as 2 ①. (Stevin Reference Stevin1585, 40)Footnote
38
I checked all printed books dealing with algebra I could locate down to 1630, which is about the time Viète's algebra nova became widely known. In the four and a half decades after Stevin's L'Arithmetique I found only two other books admitting irrational numbers of terms, both from 1620. Clément Cyriaque de Mangin appended algebraic treatments to practical geometry problems in his edition of Jean Errard's La Geometrie et Pratique Generale d'Icelle. In one problem, for example, he squares “√21 + 1R – 2” (
![]() $\sqrt {21} + x - 2$
) to get “1q + √84R + 25 – 4R – √336” (
$\sqrt {21} + x - 2$
) to get “1q + √84R + 25 – 4R – √336” (
![]() ${x^2} + \sqrt {84} x + 25 - 4x - \sqrt {336} $
). Pietro Antonio Cataldi's Elementi delle Quantità Algebratiche shows the new way in many examples. In one of these he squares “5 cose piu rad 7” (
${x^2} + \sqrt {84} x + 25 - 4x - \sqrt {336} $
). Pietro Antonio Cataldi's Elementi delle Quantità Algebratiche shows the new way in many examples. In one of these he squares “5 cose piu rad 7” (
![]() $5x + \sqrt 7 $
) to get “25 censi piu rad 700 cose piu 7” (
$5x + \sqrt 7 $
) to get “25 censi piu rad 700 cose piu 7” (
![]() $25{x^2} + \sqrt {700} x + 7$
). (Cyriaque de Mangin Reference Cyriaque de Mangin1620, 52; Cataldi Reference Cataldi1620, 15). Cataldi's use of the letter “L” for parentheses shows that he was influenced by Bombelli.
$25{x^2} + \sqrt {700} x + 7$
). (Cyriaque de Mangin Reference Cyriaque de Mangin1620, 52; Cataldi Reference Cataldi1620, 15). Cataldi's use of the letter “L” for parentheses shows that he was influenced by Bombelli.
Algebraists Who Continued to Follow the Traditional Way
Many prominent sixteenth-century algebraists continued with the old way. Michael Stifel works only with roots of entire terms in his Arithmetica Integra (Latin, 1544). For example, in one problem he multiplies “1
![]() ” by “√
” by “√
![]() 12500” to get “√
12500” to get “√
![]() 12500
12500
![]() ” (
” (
![]() $x \cdot \sqrt {12500} \to \sqrt {12500{x^2}} $
. Note that “√
$x \cdot \sqrt {12500} \to \sqrt {12500{x^2}} $
. Note that “√
![]() ” is the sign for square root) (Stifel Reference Stifel1544, fol. 287a).Footnote
39
In this book he criticizes Rudolff's notational innovation:
” is the sign for square root) (Stifel Reference Stifel1544, fol. 287a).Footnote
39
In this book he criticizes Rudolff's notational innovation:
Note here that in the clause √
![]() 648
648
![]() , the sign
, the sign
![]() that you see placed on the right side is considered to be a sign for
that you see placed on the right side is considered to be a sign for
![]() because of the sign √
because of the sign √
![]() which is on the left side. If, for example, 6 is multiplied by 1
which is on the left side. If, for example, 6 is multiplied by 1
![]() , the result is 6
, the result is 6
![]() . But if √
. But if √
![]() 6 is multiplied by 1
6 is multiplied by 1
![]() , the result is √
, the result is √
![]() 6
6
![]() and not √
and not √
![]() 6
6
![]() , as Christoph wanted. When √
, as Christoph wanted. When √
![]() 6 is multiplied by 1
6 is multiplied by 1
![]() then √
then √
![]() 1
1
![]() takes the place of 1
takes the place of 1
![]() . I give this warning because of the numbers my reader might see in the way Christoph works out his problem 46, so that we may know that my numbers are correct as placed. So √
. I give this warning because of the numbers my reader might see in the way Christoph works out his problem 46, so that we may know that my numbers are correct as placed. So √
![]() 648
648
![]() + 18
+ 18
![]() should be taken as a number of roots not because of the addition sign, as Christoph seems to have thought, but because each part refers to a number of roots. (Stifel Reference Stifel1544, ff. 283a-b) Footnote
40
should be taken as a number of roots not because of the addition sign, as Christoph seems to have thought, but because each part refers to a number of roots. (Stifel Reference Stifel1544, ff. 283a-b) Footnote
40
Later, in his 1553 edition of Rudolff's Coss, Stifel converted the four binomials to the old way. For example, he writes “8
![]() + √ 20
+ √ 20
![]() ” in place of Rudolff's “8 + √ 20
” in place of Rudolff's “8 + √ 20
![]() ” (Rudolff Reference Rudolff and Stifel1553, ff. 201a, 206a, 386b, 409a).
” (Rudolff Reference Rudolff and Stifel1553, ff. 201a, 206a, 386b, 409a).
Niccolò Tartaglia explains that one must take the roots of entire terms his La Sesta Parte del General Trattato di Numeri, et Misure (Italian, 1560):
For example, the R of 3 ce cannot be taken, but is represented in this way: R 3 ce, and similarly the R of 5 ce is R 5 ce, and so forth for the other non-square numbers. (Tartaglia Reference Tartaglia1560, fol. 3b) Footnote 41
Here “R 3 ce” corresponds to our
![]() $\sqrt {3{x^2}} $
. He puts this into practice in his problems. For example, at one point he multiplies “R
$\sqrt {3{x^2}} $
. He puts this into practice in his problems. For example, at one point he multiplies “R
![]() $\frac{3}{4}$
cen.” (
$\frac{3}{4}$
cen.” (
![]() $\sqrt {\frac{3}{4}{x^2}} $
) by “
$\sqrt {\frac{3}{4}{x^2}} $
) by “
![]() $\frac{1}{2}$
co” (
$\frac{1}{2}$
co” (
![]() $\frac{1}{2}x$
) to get “R
$\frac{1}{2}x$
) to get “R
![]() $\frac{3}{{16}}$
ce ce” (
$\frac{3}{{16}}$
ce ce” (
![]() $\sqrt {\frac{3}{{16}}{x^4}} $
) (Tartaglia Reference Tartaglia1560, fol. 32b).Footnote
42
$\sqrt {\frac{3}{{16}}{x^4}} $
) (Tartaglia Reference Tartaglia1560, fol. 32b).Footnote
42
Christoph Clavius, too, consistently works with the old way in his Algebra (Latin, 1608). In one problem he multiplies
![]() $150 - \sqrt {4500} $
by x to get
$150 - \sqrt {4500} $
by x to get
![]() $150x - \sqrt {4500{x^2}} $
(Clavius Reference Clavius1608, 367–8).
$150x - \sqrt {4500{x^2}} $
(Clavius Reference Clavius1608, 367–8).
François Viète works with two different kinds of algebra. One of them, his logistice numerosa, corresponds to traditional numerical algebra, and the other, logistice speciosa, is his new algebra founded in geometry. Viète has only one opportunity to express an irrational number of a term among the samples of logistice numerosa in his works, but he neither follows the new way, nor does he put the whole term under the root. In chapter 5 of De Emendatione Æquationum (Latin, 1615) he writes the equation “1C. – lc. 18. in 1N. æquatur 6” (Viète Reference Viète1615, 91; Viète 1646, 140),Footnote
43
or in our notation,
![]() $1{x^3} - \sqrt[3]{{18}} \cdot 1x = 6$
. Viète writes the preposition in (“by”) to indicate that the
$1{x^3} - \sqrt[3]{{18}} \cdot 1x = 6$
. Viète writes the preposition in (“by”) to indicate that the
![]() $\sqrt[3]{{18}}$
is multiplied by the “1N”. This
$\sqrt[3]{{18}}$
is multiplied by the “1N”. This
![]() $\sqrt[3]{{18}}$
is not the “number” of the term, since Viète still retains the “1” before the “N.” This “1C. – lc. 18. in 1N” is Viète's numerical version of “A cubus – Lc. B solido-solidi in A” (
$\sqrt[3]{{18}}$
is not the “number” of the term, since Viète still retains the “1” before the “N.” This “1C. – lc. 18. in 1N” is Viète's numerical version of “A cubus – Lc. B solido-solidi in A” (
![]() ${A^3} - \sqrt[3]{{{B^{SS}}}} \cdot A$
),Footnote
44
so he has simply transferred the operation from logistice speciosa to the version in logistice numerosa.
${A^3} - \sqrt[3]{{{B^{SS}}}} \cdot A$
),Footnote
44
so he has simply transferred the operation from logistice speciosa to the version in logistice numerosa.
Other books exhibiting the traditional way include: Étienne de la Roche's L'Arismethique Nouellement Composee (French, 1520), Francesco Ghaligai's Summa de Arithmetica (Italian, 1548), Jacques Peletier's L'Algebre (French, 1554) and De Occulta Parte Numerorum Libri Duo (Latin, 1560), M. Valentin Mennher de Kempten's Practique pour Brievement Apprendre à Ciffrer, & Tenir Livre de Comptes, avec la Regle de Coss, & Geometrie (French, 1556), Juan Pérez De Moya's Tratado Mathematicasen que Secontienen Cosas de Arithmetica, Geometria, Cosmographia, etc. (Spanish, 1573), Anton Schultze's Arithmetica oder Rechenbuch (German, 1600), Nicolaus Petri's Practique om te Leeren Rekenen (Dutch, 1605), Christophorus Dibuadius's In Arithmeticam Irrationalium (Latin, 1605), Anthoni Smyters's Arithmetica (German, 1612), Ludolf van Ceulen's Fundamenta Arithmetica et Geometrica (Latin, 1615), Joannes Lantz's Institutionum Arithmeticarum (Latin, 1619), Claude Gaspar Bachet's Diophanti Alexandrini Arithmeticorum Libri sex et De Numeris Multangulis Liber Unus (Latin, 1621), Hermann Follinus's Algebra sive Liber de Rebus Occultis (Latin, 1622), and D. Henrion's Sommaire de l'Algebre (French, 1623).Footnote 45 In his Coss (German, 1525 MS) Adam Ries puts the whole terms under roots, but he does not operate with radicals enough to know if he might have admitted irrational numbers of terms (Ries Reference Ries, Kaunzner and Wußing1992, 417–420).
The 1984 edition of Dionigi Gori's 1544 Libro e Trattato della Praticha d'Alcibra appears to show the new way, but the two instances are due to transcription errors and problems with the manuscript (Gori Reference Gori and Rigatelli1984, 23, 25).Footnote 46 Likewise the Arithmetica by Gielis Van den Hoecke (Dutch, 1545, originally published 1537) appears to apply the new way on fol. 91a, but a comparison with fol. 85b shows that it is a misprint. Cajori also notes misprints in the one passage he translates from this book (Cajori 1928–29 vol. 1, 138; Hoecke Reference Hoecke1545).
Some books do not show the right kinds of calculations to know whether their authors subscribed to the new way or not. These include Heinrich Schreiber's Ayn new kunstlich Buech (German, 1521) and Ein new künstlichbehend und gewiss Rechenbüchlin (German, 1544), Francesco Feliciano's Libro Arithmetica & Geometria (Italian, 1545), Bento Fernandes's Tratado da Arte de Arismetica (Spanish, 1555), Casparo Peucer's Logistice Astronomica (Latin, 1556), Robert Recorde's The Whetstone of Witte (English, 1557), Jean Borrel's Logistica (Latin, 1559), Petrus Ramus's Algebra (Latin, 1560) and Arithmetices Libri Duo, et Algebræ Totidem (Latin, 1592), Wilhelm Klebiz's Insulæ Melitensis (Latin, 1565), Henricus Brucaeus's Mathematicarum Exercitationum Libri Duo (Latin, 1575), Guillaume Gosselin's De Arte Magna (Latin, 1577),Footnote 47 Bernard Salignac's Degalensis Arithmeticæ (Latin, 1580), Zacharias Lochner's Tractätlein (German, 1583), Ioseppo Unicorno's De l'Arithmetica Universale (Italian, 1598), Nicolaus Raimarus Ursus's Arithmetica Analytica (German, 1601), Heinrich Roselen's Wolgegrünt Kunst und artig Rechenbuch von allerhand Regulen des Kauffmanschafft (German, 1629), and Albert Girard's Invention Nouvelle en l'Algebre (French, 1629).
Coefficients in Viète's algebra nova and Its Successors
Our word “coefficient” originated with François Viète's 1591 Isagoge in Artem Analyticem. In his logistice speciosa the word coëfficiens refers to a known yet undetermined magnitude multiplied by a power of an unknown magnitude. One purpose of coefficients is to make the terms in an equation homogeneous. Take for example the equation “A cubus plus B plano ter in A, æquetur D solido” (A 3 + 3BP · A = DS ) (Viète Reference Viète1615, 10). The “A cubus” is a third-degree term, so to make the second term homogeneous with it the first degree unknown A is multiplied by (3 copies of) the two-dimensional coefficient “B plano.” The “ter” (“thrice”) is not a coefficient, but functions like the medieval “number” of the term to say how many B plano's are multiplied by the A. Note that the “A cubus” is not preceded by a “1”. This is because it represents a value, and not a kind or denomination. Also, the coefficients are explicitly multiplied by the terms, as indicated by the preposition “in.” Viète's notation is modern in these fundamental respects.
Viète's logistice speciosa is an algebra founded in magnitudes (magnitudines). In order to show an equation numerically he switches to logistice numerosa. Here the coefficients are given specific numerical values and the equations are expressed with the premodern notation Viète borrowed from Xylander's translation of Diophantus (1575). The equation above is rewritten as “1C + 6N æquatur 7” (x 3 + 6x = 7). The “1” placed before the “C” is one indication that the “C” and “N” represent kinds, while the numbers 1 and 6 tell how many of each of them is present. In Viète's works the coefficients in logistice speciosa are always letters, while those in logistice numerosa are always numbers.
Starting with Descartes some algebraists assumed a unit line, which allowed numbers to serve as coefficients in their versions of logistice speciosa. Like in Viète, their symbols for the unknowns or variables no longer stand for kinds, but for the numerical values themselves. We have already seen above Descartes's equation “
![]() ${x^3} - \sqrt 3 xx + \frac{{26}}{{27}}x - \frac{8}{{27\sqrt 3 }}$
${x^3} - \sqrt 3 xx + \frac{{26}}{{27}}x - \frac{8}{{27\sqrt 3 }}$
![]() 0”, where the x
3 requires no “1” before it, and the
0”, where the x
3 requires no “1” before it, and the
![]() $\sqrt 3 $
is a coefficient multiplied by the xx. Two other examples are Abraham de Graaf's equation xx
$\sqrt 3 $
is a coefficient multiplied by the xx. Two other examples are Abraham de Graaf's equation xx
![]()
![]() $\frac{1}{2}y + y\surd 1\frac{1}{4}$
from his De Beginselen van de Algebra of Stelkonst (Dutch, 1672) and John Wallis's equation 78√3 = 3ddd√3 + 3dee√3 from A Treatise of Algebra both Historical and Practical (Reference Wallis1685) (de Graaf Reference de Graaf1672, 160; Wallis Reference Wallis1685, 178). In Wallis's “3dee√3” the 3, the d, the two e’s and the √3 all signify the values of numbers that are understood to be multiplied by one another by virtue of concatenation. The roots appear on the right in these two equations only to prevent the topless √ from being applied to the whole term.
$\frac{1}{2}y + y\surd 1\frac{1}{4}$
from his De Beginselen van de Algebra of Stelkonst (Dutch, 1672) and John Wallis's equation 78√3 = 3ddd√3 + 3dee√3 from A Treatise of Algebra both Historical and Practical (Reference Wallis1685) (de Graaf Reference de Graaf1672, 160; Wallis Reference Wallis1685, 178). In Wallis's “3dee√3” the 3, the d, the two e’s and the √3 all signify the values of numbers that are understood to be multiplied by one another by virtue of concatenation. The roots appear on the right in these two equations only to prevent the topless √ from being applied to the whole term.
In any numerical algebra that ultimately derives from Viète's logistice speciosa there is no difficulty with irrational coefficients because all elements in a term are understood to be multiplied together. Irrational numbers of terms only pose a problem in cossic, or pre-Viètan algebra, where the coefficient is understood to count the term.
With the adaptation of logistice speciosa to numbers the notion of a single root vs. a multitude of roots vanishes. Descartes writes
![]() $\frac{8}{{27\sqrt 3 }}$
instead of
$\frac{8}{{27\sqrt 3 }}$
instead of
![]() $\frac{{64}}{{243}}$
, de Graaf shows 2√17 rather than √68, and Wallis has 14√2 instead of √392 (de Graaf Reference de Graaf1672, 163; Wallis Reference Wallis1685, 177). For these mathematicians “2√17” is a number composed through multiplication of 2 by √17. It is not two roots of 17. Those algebraists who restricted their logistice speciosa to magnitudes continued writing single roots. Viète wrote
$\frac{{64}}{{243}}$
, de Graaf shows 2√17 rather than √68, and Wallis has 14√2 instead of √392 (de Graaf Reference de Graaf1672, 163; Wallis Reference Wallis1685, 177). For these mathematicians “2√17” is a number composed through multiplication of 2 by √17. It is not two roots of 17. Those algebraists who restricted their logistice speciosa to magnitudes continued writing single roots. Viète wrote
![]() $\sqrt {59319} $
and Harriot
$\sqrt {59319} $
and Harriot
![]() $\sqrt {18252} $
because for them the old logistice numerosa, founded on a concept of polynomials as aggregations, still reigned over numbers. And of course practitioners of cossic algebra in the seventeenth century likewise also continued to work with single roots.
$\sqrt {18252} $
because for them the old logistice numerosa, founded on a concept of polynomials as aggregations, still reigned over numbers. And of course practitioners of cossic algebra in the seventeenth century likewise also continued to work with single roots.
Cossic Algebra post-Viète: Benedetto Maghetti's quesiti
The old and new algebras coexisted for many decades after Viète's ideas began to take hold around 1630. To name just four examples, Carlo Renaldini's Opus Mathematicum (Latin, 1655), J. R. Brasser's Regula Cos, of Algebra (Dutch, 1663), Andrés Puig's Arithmetica Especulativa, y Practica, y Arte de Algebra (Spanish, 1672), and Giuseppe Maria Figatelli's Trattato Aritmetico (Italian, 1678) all teach algebra the traditional way. In these authors we find the same mix of the old and new ways of representing irrational roots of terms. Renaldini follows the new way, Brasser and Figatelli follow the old way, and Puig does not perform the right operations for us to know (Renaldini Reference Renaldini1655, 109; Brasser Reference Brasser1663, 35; Figatelli Reference Figatelli1678, 218).
The same mathematician could even be found working with both cossic algebra and Viète's logistice speciosa, as Giovanni Camillo Gloriosi did in his Exercitationum Mathematicarum Decas Tertia, henceforth terza Deca, as it was called in Italian (Latin, 1639). In the first exercitatio, Gloriosi cites Viète and Ghetaldi by name, and he presents theorems using Viète's notation. In the third exercitatio, on the other hand, all work is done with pre-Viètan concepts and notation.
I will not give lists of every post-1630 book with cossic algebra to show who followed the old way and who followed the new way. Rather, I will give an account of a controversy over this issue that erupted in Italy toward the middle of the century that gives us an idea of how contemporary mathematicians understood the issue. In 1638 Benedetto Maghetti, a physician in Ancona, published a collection of nine questions (quesiti) in a single folio titled “To all those who practice mathematics.”Footnote 48 The quesiti were posted all over Italy and in a couple of neighboring countries. The first eight quesiti ask for the square, cube, fourth, or fifth root of a given polynomial in order to solve an equation, and the ninth asks for a number satisfying a certain condition. The purpose of these questions, stated on the same sheet, was “to teach the way to extract roots of such composite numbers, both with and without algebraic ranks,” in other words, to find the roots of polynomials.Footnote 49
The second and seventh quesiti show that Maghetti followed the new way of writing terms. Here is the second quesito:
Question II. The square root of 9cc – 24qc + 46qq – 40c – rq180c + 25q + rq320q – rq500N + 5 = 94368 – rq5. One wants the square root without parentheses, as is always intended, and the value of 1N.Footnote 50
Maghetti is asking for the square root of the polynomial on the left side of the equation, which in modern notation is
![]() $9{x^6} - 24{x^5} + 46{x^4} - 40{x^3} - \sqrt {180} {x^3} + 25{x^2} + \sqrt {320} {x^2} - \sqrt {500} x + 5$
. This root is then equated to the number
$9{x^6} - 24{x^5} + 46{x^4} - 40{x^3} - \sqrt {180} {x^3} + 25{x^2} + \sqrt {320} {x^2} - \sqrt {500} x + 5$
. This root is then equated to the number
![]() $94368 - \sqrt 5 $
and the equation is then solved.
$94368 - \sqrt 5 $
and the equation is then solved.
Maghetti published his solutions and explained his techniques the following year in his 184-page book Analisi o Risolutione de Quesiti. He finds the square root of the polynomial in the second quesito to be “3c – 4q + 5N – rq5” (
![]() $3{x^3} - 4{x^2} + 5x - \sqrt 5 $
) (Maghetti Reference Maghetti1639, 123). Maghetti was aware that writing terms with roots as he does might cause some controversy, so he defends his position early in the book:
$3{x^3} - 4{x^2} + 5x - \sqrt 5 $
) (Maghetti Reference Maghetti1639, 123). Maghetti was aware that writing terms with roots as he does might cause some controversy, so he defends his position early in the book:
Multiplying rq3 by 2N makes rq12N [
![]() $\sqrt 3 \cdot 2x \to \sqrt {12} x$
], which gives rise to a doubt: whether having to square the 2, the number of N, means that one must also square the rank [i.e. the power], and say rq4q [
$\sqrt 3 \cdot 2x \to \sqrt {12} x$
], which gives rise to a doubt: whether having to square the 2, the number of N, means that one must also square the rank [i.e. the power], and say rq4q [
![]() $\sqrt {4{x^2}} $
].
$\sqrt {4{x^2}} $
].
If I must say what I feel, I believe that one can do either one, because either way one can take the square root, or cube root, etc.Footnote 51
Maghetti then mentions that Bombelli allows for irrational numbers of terms while Clavius performs the operation in the traditional way. He concludes “I am persuaded to follow Bombelli, and others can follow who they want.”Footnote 52
One of those who answered Maghetti's quesiti was Gloriosi, whose solutions occupy the fifth exercitatio in the terza Deca. Gloriosi was committed to the old way of expressing terms with irrational roots, so he asserts that the polynomial in the second quesito should have been written “9CC – 24QC + 46QQ – 40C – Rq.180CC + 25Q + Rq.320QQ – Rq.500Q + 5” (Gloriosi Reference Gloriosi1639, 111–2). To account for Maghetti's “error,” Gloriosi suggested “Perhaps it was from neglect (per incuriam) that our author thought that 3C – 4Q + 5N, multiplied by Rq.5, makes Rq.45C – Rq.80Q + Rq.125N, which is not true. It is in fact Rq.45CC – Rq.80QQ + Rq.125Q.”Footnote 53 Gloriosi justified his correction by citing the abbacus rule that if two terms to be multiplied are of “different natures” (diversæ naturæ), they must be reduced to one nature before multiplying. In this case a term expressed with a root is of a different nature than one without a root. As Maestro Benedetto explained above, both terms should be squared, and then one takes the root of their product. But of course the issue at hand is not about the process of multiplication, but about how to express the result.
The terza Deca was published just a short time before Maghetti's Analisi, so Maghetti had not yet seen it when he wrote his book (Maghetti Reference Maghetti1639, 180–1; Gloriosi Reference Gloriosi1641, 47, 56).Footnote 54 When Maghetti finally did read Gloriosi's remarks he responded with his Apologia, a short treatise of 39 pages published in 1640. Now, instead of writing that people can choose whatever notation they want, he maintains that his is the correct way. He explains his position already on the title page: “Where it is proven with very sure demonstrations that one must not square the rank while multiplying a number with rank by a square root, nor cube with a cube root, nor square the square with a fourth root, etc.”Footnote 55 Maghetti writes that he “must respond to that fraternal warning made by Giovanni Camillo Gloriosi at the end of the fifth exercitatione of his terza Deca.”Footnote 56 He felt particularly insulted by Gloriosi's accusation that it was from neglect that he wrote his polynomials the way he did. In the first 17 pages of the book, where he sets out his defense, Maghetti cites the offending phrase five times.
Maghetti was undoubtedly pleased to find that Gloriosi himself had followed the new way in the sixth exercitatione of the terza Deca (Maghetti Reference Maghetti1640, 6). There, on page 127, Gloriosi gives instructions that are remarkably close to Bombelli's: “When the number does not have a root, and the power has an even index, then the sign of the root is prefixed to the number, and the index is halved, and this gives rise to the sought-after root.”Footnote 57 Gloriosi then gives the example that the square root of “28Q” is to be written as “R28N.” Maghetti does not cite it, but Gloriosi writes after this that if the index of the power is odd, one uses parentheses. The examples are “33C” and “25C,” whose roots are written as “R(33C)” and “R(25C)” respectively. In other places Gloriosi follows the old way. Just before this, on page 125, he multiplies “R24” by “1Q” to get “R24QQ.” After explaining his reasoning again, Maghetti concludes “From this one sees that that which I have written and thought & is true, is not otherwise from neglect.”Footnote 58 In his subsequent arguments Maghetti simply presumes that his reading of the notation is correct.
The debate did not stop there. Gloriosi responded to Maghetti's Apologia with another treatise, his 56-page Responsio Ioannis Camilli Gloriosi ad Apologiam Benedicti Maghetti, published in 1641. Gloriosi was in a bind for having applied the new way in his terza Deca. So he reformulated his argument by appealing to the need to avoid ambiguity, first criticizing those authorities who follow the new way. Gloriosi calls Bombelli's notation uncertain and ambiguous (“incerti & ambigui”), and the operations of Nuñes and Stevin are said to be illegitimate and to breed confusion (“operatio illegitima est, & confusionem parit”) (Gloriosi Reference Gloriosi1641, 10). Of course the notations of these mathematicians were not ambiguous at all, but this claim allowed Gloriosi to address his own ambiguity in the terza Deca. He writes that “uncertainty and ambiguity are introduced to algebraic operations if the sign of the radical does not refer to the whole term,”Footnote 59 and this leads him to propose a convention: that the “radical sign refer to the whole term, to the number as well as the rank.”Footnote 60
Like Maghetti, in all his subsequent arguments Gloriosi simply presumes that his reading of the notation is correct to show that his opponent is wrong. This way he is able to accuse Maghetti of “mixing the cards” and to make remarks like “I say that my procedure is good and his is false.”Footnote 61
Salvator Grisio, working in Rome, was another person who attacked Maghetti's way of writing terms with irrational roots. Grisio's 1641 book Antanalisi a Quesiti Stampati nell'Analisi di Benedetto Maghetti devotes 144 pages to the issue. Grisio takes Maghetti's claim that “rq3 by 2N makes rq12N” as implying that 2N multiplied by 2N gives 4N (Grisio Reference Grisio1641, 5). This is because he assumes that Maghetti follows the abbacus rule that one squares the 2N before multiplying by the rq3, when in fact he only squares the 2. Throughout the book Grisio presumes that the R must apply to the whole term. He does not seem to understand that it can be a matter of convention.
Grisio appeals to many authorities to support his view. He admits that Bombelli explains the multiplications in a way that conforms with Maghetti, but he asserts that Bombelli does not follow this rule in practice. The example he quotes is Bombelli's multiplication of “RQ(4N.–6.)” by “3N” (
![]() $\sqrt {4x - 6} $
by 3x), resulting in “RQ.(36C–54Q.)” (
$\sqrt {4x - 6} $
by 3x), resulting in “RQ.(36C–54Q.)” (
![]() $\sqrt {36{x^3} - 54{x^2}} $
).Footnote
62
But this is an example with parentheses, which Bombelli explains along with his other notations. Bombelli does in fact apply his rule for monomials in his worked-out problems, but mainly near the end.Footnote
63
Grisio later comments on Cardano's way of putting the irrational root after the name, he mentions that Stifel condemns Rudolff's binomial coefficients, and he writes that Stevins's separation mark “
$\sqrt {36{x^3} - 54{x^2}} $
).Footnote
62
But this is an example with parentheses, which Bombelli explains along with his other notations. Bombelli does in fact apply his rule for monomials in his worked-out problems, but mainly near the end.Footnote
63
Grisio later comments on Cardano's way of putting the irrational root after the name, he mentions that Stifel condemns Rudolff's binomial coefficients, and he writes that Stevins's separation mark “
![]() ” “is not a necessary thing, and serves nothing.”Footnote
64
Despite Grisio's familiarity with the algebraic literature from Pacioli down to his own time, he misses the point entirely.
” “is not a necessary thing, and serves nothing.”Footnote
64
Despite Grisio's familiarity with the algebraic literature from Pacioli down to his own time, he misses the point entirely.
Even farther from any understanding of the issue is the Sicilian priest Pietro Emmanuele, who published the short book Risposta alli Quesiti di Benedetto Maghetti in Palermo, also in 1641. I have not located any copy of this book, but many quotations from it are preserved in Daniele Spinola's La Bietolata (Italian, 1647), a dialogue ridiculing Emmanuele's work.Footnote 65
Emmanuele does not address the issue of irrational numbers of terms. Rather, he sets his sights on solving Maghetti's questions philosophically (filosoficamente), that is, through alchemy. It is true that Emmanuele does not touch on the main topic of this paper, but I describe his project anyway in order to complete what we know about the influence of Maghetti's quesiti.
Emmanuele laments “that algebra, abounding in mathematical precepts, has no place in philosophy,” so he wants to show “that the way to solve those quesiti is veiled (like Arcanum) in the enigma of Apollo when he taught the art of foretelling to Cassandra.”Footnote 66 The allegory is spelled out a few pages later. Apollo (the incarnation of Philosophy, i.e. alchemy), being in love with Cassandra (Arithmetic), teaches her the art of foretelling (solving equations). But once she has learned the art she refuses Apollo's love (Arithmetic shuns Philosophy). Thus Emmanuele sets out to restore Philosophy to Arithmetic.
Spinola gives many quotations of Emmanuele's analysis of the first quesito, which is the last one Emmanuele solves. In this quesito Maghetti asks for the square root of “4qcc + 12qqc + 25cc + 44qc + 46qq + 40c + 25q” and for the value of 1N when its root is equal to 969514 (Gloriosi Reference Gloriosi1639, 107).Footnote 67 Emmanuele has no intention of solving the problem mathematically. Instead, he interprets the finding of the “root” (radice) as being the search for the “principle & origin of the thing.”Footnote 68 He writes that
the art of making the philosopher's stone is hidden in the figurate numbers according to their mystical signification. . .
The first name of the said septinomial is 4QCC, of which the 4 is the number of Mercury, and the figure QCC (according to Diophantus) has exponent eight, the appropriate number of the element of fire.Footnote 69
The analysis continues in this way for each term of the polynomial, and its root is found to be “the production of Mercury.”Footnote 70
Not only does Emmanuele extract the “root” of the polynomial “philosophically,” but he also proposes to find the value of 1N by “leaving Diophantus and following Pythagoras.”Footnote 71 So he treats the number 969514 similarly. He notes that the sum of its digits is 34, which leads him to a four by four magic square and to the “temperament of the philosophical Mercury.” He concludes that the value of 1N “will be the priceless stone.”Footnote 72 Spinola writes “Whoever believes this is crazy”.Footnote 73
Synthesis
At this point it is natural to ask one of those inherently deep and complex questions about scientific development: What caused some sixteenth-century algebraists to allow for irrational numbers of terms? It is not simply that these mathematicians decided to introduce a new convention in notation. The very way algebraists conceived of monomials forbids coefficients from being irrational. So while Rudolff's notational innovation may have simplified the solutions of some problems, it was a violation of how monomials had been understood for centuries.
I suspect that in part the development was made possible by the fact that in the early sixteenth century algebraic notation was in the process of becoming autonomous from speech, allowing syntax to take precedence over semantics. With notation replacing verbal expositions for calculations some algebraists could view their notation more formally and take algebra in directions that would have been absurd if expressed rhetorically. This formal treatment of algebraic notation is an example of what Frits Staal has called the “generosity” of an artificial language.Footnote 74 It was in a similar vein that some of the same mathematicians began working with complex and negative numbers around the same time.
If the introduction of irrational coefficients were accompanied by a corresponding shift in algebraic concepts, in other words, if it were something more than just a formal extension of the notational syntax, then the foundation of the medieval aggregations interpretation of polynomials would have been compromised. But I do not see any evidence that this happened. In terms like Cardano's “co R 8,” the irrational number (here “R 8”, or
![]() $\sqrt 8 $
) was still treated as if it were the number that counts the term. Two features of sixteenth-century algebra suggest this. First, the medieval relationship between the number and the sign for the power was retained (see Oaks Reference Oaks2010, 47; Oaks Reference Oaks2012). A “
$\sqrt 8 $
) was still treated as if it were the number that counts the term. Two features of sixteenth-century algebra suggest this. First, the medieval relationship between the number and the sign for the power was retained (see Oaks Reference Oaks2010, 47; Oaks Reference Oaks2012). A “
![]() ”, “co,” “ra,.” “
”, “co,” “ra,.” “
![]() ,” or “①” does not stand alone if there is only one of them, but the “1” is always written: “1
,” or “①” does not stand alone if there is only one of them, but the “1” is always written: “1
![]() ”, “1 co,” “1 ra.,” “1
”, “1 co,” “1 ra.,” “1
![]() ,” and “1 ①.”Footnote
75
If, by contrast, irrational coefficients were thought of as scalars, or as numbers multiplied by the power, then the signs would have ceased to be kinds of number and would have become values, allowing for them to operate alone like Viète's A or Descartes's x. In fact, the only two algebraists who offer brief explanations of their irrational coefficients still situate them in premodern terms. Rudolff urges his readers to regard irrational coefficients as if they were “spoken,” and Bombelli asserts that irrational roots, “though they can only be named in power,” are still numbers, so they too can serve as coefficients.
,” and “1 ①.”Footnote
75
If, by contrast, irrational coefficients were thought of as scalars, or as numbers multiplied by the power, then the signs would have ceased to be kinds of number and would have become values, allowing for them to operate alone like Viète's A or Descartes's x. In fact, the only two algebraists who offer brief explanations of their irrational coefficients still situate them in premodern terms. Rudolff urges his readers to regard irrational coefficients as if they were “spoken,” and Bombelli asserts that irrational roots, “though they can only be named in power,” are still numbers, so they too can serve as coefficients.
Second, algebraists continued to solve problems by working the operations before setting up equations.Footnote 76 Irrational numbers of terms did not open the door for operations in equations, which is further evidence that a term like “co R 8” does not denote the multiplication of “co” by “R 8.” Although these irrational numbers look and behave more like modern coefficients than their medieval counterparts, the conceptual shift that that we might associate with them appears not to have occurred. That would come only with the new algebra of Viète, Descartes, and Fermat, in which operations are an integral part of equations.
The debate between Maghetti, Gloriosi, and Grisio over irrational numbers of terms took place after the publication of Descartes's La Geometrie in 1637. In hindsight it was a debate framed in terms of an algebra that was already out of date. Yet Gloriosi for one was not a mathematician who lingered behind the times. He was not only aware of recent developments in algebra, but he took an active part in them. What made the debate relevant was that traditional algebra was still widely practiced in the middle years of the seventeenth century, and at that time no one could have foreseen its demise in the coming decades. With its demise the debate over irrational numbers of terms passed away unresolved.