Research Article
The rank of syzygies under the action by a finite group
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-12
-
- Article
-
- You have access
- Export citation
Remarks to the uniqueness problem of meromorphic maps into PN(C), I
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-24
-
- Article
-
- You have access
- Export citation
Remarks to the uniqueness problem of meromorphic maps into PN(C), II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 25-41
-
- Article
-
- You have access
- Export citation
p-Adic properties of Siegel modular forms of degree 2
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 43-60
-
- Article
-
- You have access
- Export citation
On the central class field mod
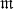 of Galois extensions of an algebraic number field
of Galois extensions of an algebraic number field
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 61-85
-
- Article
-
- You have access
- Export citation
A remark concerning the 2-adic number field
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 87-90
-
- Article
-
- You have access
- Export citation
Remarks on the curvature of hypersurfaces in Cn
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 91-95
-
- Article
-
- You have access
- Export citation
Some examples of stochastically stable homeomorphisms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 97-105
-
- Article
-
- You have access
- Export citation
Local energy decays for wave equations with time-dependent coefficients
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 107-123
-
- Article
-
- You have access
- Export citation
On the decay of the local energy for wave equations with a moving obstacle
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 125-147
-
- Article
-
- You have access
- Export citation
On the Doi-Naganuma lifting associated with imaginary quadratic fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 149-167
-
- Article
-
- You have access
- Export citation
A remark on the Grothendieck-Lefschetz theorem about the Picard group
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 169-179
-
- Article
-
- You have access
- Export citation
Construction of a solution of a certain evolution equation II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 181-198
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 71 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 71 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

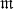 of Galois extensions of an algebraic number field
of Galois extensions of an algebraic number field
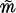 whose degree is some power of a prime
whose degree is some power of a prime 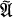 be the module of
be the module of 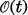 has been studied by Cooper [1] and Cooper and Strauss [2] etc. In their works it has been assumed that the obstacle
has been studied by Cooper [1] and Cooper and Strauss [2] etc. In their works it has been assumed that the obstacle