Research Article
The Fourth-Order Q-Curvature Flow on Closed 3-Manifolds
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation
The Carathéodory–Cartan–Kaup–Wu Theorem on an Infinite-Dimensional Hilbert Space
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 17-30
-
- Article
-
- You have access
- Export citation
Positive Toeplitz Operators of Schatten–Herz Type
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 31-62
-
- Article
-
- You have access
- Export citation
Truncated Microsupport and Hyperbolic Inequalities
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 63-91
-
- Article
-
- You have access
- Export citation
On the K-Theory of the Coordinate Axes in the Plane
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 93-109
-
- Article
-
- You have access
- Export citation
Finiteness of Entire Functions Sharing a Finite Set
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 111-122
-
- Article
-
- You have access
- Export citation
Hilbert-Kunz Multiplicity and Reduction Mod p
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 123-141
-
- Article
-
- You have access
- Export citation
Some estimates for the Bergman Kernel and Metric in Terms of Logarithmic Capacity
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 143-150
-
- Article
-
- You have access
- Export citation
Unboundedness of the Ball Bilinear Multiplier Operator
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 151-159
-
- Article
-
- You have access
- Export citation
On the Complement of Levi-Flats in Kähler Manifolds of Dimension ≥ 3
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 161-169
-
- Article
-
- You have access
- Export citation
Toeplitz Algebras on Strongly Pseudoconvex Domains
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 171-186
-
- Article
-
- You have access
- Export citation

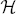 with a fixed point
with a fixed point 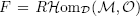 , where
, where 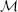 is a coherent
is a coherent 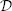 -module, we obtain new estimates for the truncated microsupport of real analytic and hyperfunction solutions. When
-module, we obtain new estimates for the truncated microsupport of real analytic and hyperfunction solutions. When 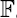
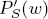 has distinct
has distinct 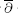 -equation, it is shown that compact Kähler manifolds of dimension ≥ 3 admit no Levi flat real analytic hypersurfaces whose complements are Stein.
-equation, it is shown that compact Kähler manifolds of dimension ≥ 3 admit no Levi flat real analytic hypersurfaces whose complements are Stein.