Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kechris, Alexander S.
1973.
Measure and category in effective descriptive set theory.
Annals of Mathematical Logic,
Vol. 5,
Issue. 4,
p.
337.
Yasuda, Yutaka
1986.
Structure Theory for Projective Sets in the Plane With Countable Sections.
Mathematical Logic Quarterly,
Vol. 32,
Issue. 31-34,
p.
481.
Iljazović, Zvonko
and
Validžić, Lucija
2017.
Computable neighbourhoods of points in semicomputable manifolds.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 4,
p.
840.
Iljazović, Zvonko
and
Pažek, Bojan
2018.
Warsaw discs and semicomputability.
Topology and its Applications,
Vol. 239,
Issue. ,
p.
308.
Iljazović, Zvonko
and
Sušić, Igor
2018.
Semicomputable manifolds in computable topological spaces.
Journal of Complexity,
Vol. 45,
Issue. ,
p.
83.
Čičković, Eugen
Iljazović, Zvonko
and
Validžić, Lucija
2019.
Chainable and circularly chainable semicomputable sets in computable topological spaces.
Archive for Mathematical Logic,
Vol. 58,
Issue. 7-8,
p.
885.
Horvat, Marko
Iljazović, Zvonko
and
Pažek, Bojan
2020.
Computability of pseudo-cubes.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 8,
p.
102823.
Iljazović, Zvonko
2020.
Computability of graphs.
Mathematical Logic Quarterly,
Vol. 66,
Issue. 1,
p.
51.
Čelar, Matea
and
Iljazović, Zvonko
2021.
Computability of Products of Chainable Continua.
Theory of Computing Systems,
Vol. 65,
Issue. 2,
p.
410.
Čačić, Vedran
Horvat, Marko
and
Iljazović, Zvonko
2021.
Computable subcontinua of semicomputable chainable Hausdorff continua.
Theoretical Computer Science,
Vol. 892,
Issue. ,
p.
155.
Čelar, Matea
and
IljazoviĆ, Zvonko
2022.
Computability of glued manifolds.
Journal of Logic and Computation,
Vol. 32,
Issue. 1,
p.
65.
Iljazović, Zvonko
and
Jelić, Matea
2024.
Computable approximations of a chainable continuum with a computable endpoint.
Archive for Mathematical Logic,
Vol. 63,
Issue. 1-2,
p.
181.
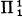 sets which have positive measure (or which are not meager, i.e., of the second Baire category) have been obtained by several authors. For example, every non-meager
sets which have positive measure (or which are not meager, i.e., of the second Baire category) have been obtained by several authors. For example, every non-meager 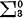 set must have a recursive element (Shoenfield-Hinman, Hinman [2]) but there exists a non-meager
set must have a recursive element (Shoenfield-Hinman, Hinman [2]) but there exists a non-meager 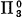 set (as well as of measure 1) that contains no recursive element (Shoenfield [7]), and every
set (as well as of measure 1) that contains no recursive element (Shoenfield [7]), and every 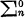 set (i.e., arithmetic set) of positive measure contains an arithmetic element (Sacks [5], and Tanaka [12]).
set (i.e., arithmetic set) of positive measure contains an arithmetic element (Sacks [5], and Tanaka [12]).

